Интервалы задаются через точку с запятой (; ). При задании интервалов и шага можно использовать математические выражения (прим. -4pi; (5/6)pi) или слово «авто» или оставить поля пустыми (эквивалентно «авто»)
Округление:
Таблица точек функции f(x) = 2/x
Показать/скрыть таблицу точек
| -10 | -0.2 |
| -9.5 | -0.21 |
| -9 | -0.22 |
| -8.5 | -0.24 |
| -8 | -0.25 |
| -7.5 | -0.27 |
| -7 | -0.29 |
| -6.5 | -0.31 |
| -6 | -0.33 |
| -5.5 | -0.36 |
| -5 | -0.4 |
| -4.5 | -0.44 |
| -4 | -0.5 |
| -3.5 | -0.57 |
| -3 | -0.67 |
| -2.5 | -0.8 |
| -2 | -1 |
| -1.5 | -1.33 |
| -1 | -2 |
| -0.5 | -4 |
| 0 | отсутствует: деление на 0 |
| 0 | -4 |
| 0.5 | 4 |
| 1 | 2 |
| 1.5 | 1.33 |
| 2 | 1 |
| 2.5 | 0.8 |
| 3 | 0.67 |
| 3.5 | 0.57 |
| 4 | 0.5 |
| 4.5 | 0.44 |
| 5 | 0.4 |
| 5.5 | 0.36 |
| 6 | 0.33 |
| 6.5 | 0.31 |
| 7 | 0.29 |
| 7.5 | 0.27 |
| 8 | 0.25 |
| 8.5 | 0.24 |
| 9 | 0.22 |
| 9.5 | 0.21 |
| 10 | 0.2 |
График построен по уравнению, но можно воспользоваться таблицой точек, чтобы построить такой же график по точкам.
Как читать график? Фон. Зона интереса.
Источник: kalku.ru
Калькулятор графиков. График функции онлайн
Используя этот онлайн калькулятор для рисования графиков функции, вы сможете очень просто и быстро нарисовать график функции.
Воспользовавшись онлайн калькулятором для рисования графиков, вы получите удобное решение вашей задачи, которое позволит понять алгоритм решения задач на графики и закрепить пройденный материал.
Начертить график функции
| y = | frac+cos (x) |
Параметрический y ( t ), x ( t )
В полярной системе координат r ( θ )
Для рисования графиков выполните следующие действия:
- введите значения функции y ( x ), используя стандартные математические операции и математические функции.
- Если необходимо начертить более одного графика, добавьте еще функции и введите их значения
- ВВедите интервал значений для переменной x .
- Нажмите кнопку «Нарисовать график».
- Через несколько секунд вы увидите график функции.
Таблица стандартных функций для калькулятора графиков
Оператор
Компьютерная графика простыми словами
Описание
Простейшие математические операции
- 0.5 — правильная запись;
- 0,5 — неправильная запись .
Элементарные функции
Тригонометрические функции
Некоторые константы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Источник: ru.onlinemschool.com
Построение графиков функций онлайн Справка
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн.
Источник: yotx.ru
Как построить график функции
с помощью геометрических преобразований графиков?
Долгое время мне не хватало решимости подойти к детальной разработке раздела о полном исследовании функции, поскольку тема весьма обширна и предполагает построение большого количества графиков. Но после аналитической геометрии не страшны уже и чертежи ядерной электростанции, поэтому без колебаний возьмём в свои руки острозаточенные карандаши и длинные линейки. Не беспокойтесь по поводу значительного размера веб страницы – здесь очень много чертежей и важнейшей прикладной информации, которая потребуется в будущем.
Чайникам и вновь прибывшим посетителям рекомендую, прежде всего, ознакомительную статью Графики и свойства элементарных функций, где мы рассмотрели основные методы и правила построения графиков. И следующая ступень посвящения – геометрические преобразования графиков функций.
Что это такое? Рассмотрим какую-нибудь элементарную функцию, например, . Подавляющему большинству читателей не составит труда построить кубическую параболу, но что делать, если требуется начертить график функции или ? Интуиция подсказывает, что совершенно не нужно тратить уйму времени и проводить полное исследование функции, достаточно выполнить некоторые геометрические преобразования кубической параболы . График функции можно сжимать/растягивать, сдвигать вдоль осей, симметрично отображать. То есть, несколько волшебных пассов, и кривые готовы!
Зачем это нужно? Вы скажете, что можно применить метод поточечного построения, о котором я так много говорил в методичке о графиках функций. Вот взять ту же функцию и построить её по точкам! Да, способ рабочий.
Однако знания геометрических преобразований позволят вам быстро понять, как расположен график, а в несложных случаях вроде практически мгновенно его нарисовать! Навыки грамотно разбираться с чертежами потребуются в различных задачах высшей математики, например, при исследовании функции на непрерывность, нахождении площади фигуры, объема тела вращения, в ходе вычисления двойных интегралов и т.д.
Кроме того, поточечное построение бывает не всегда удобным, так, значения периодической функции можно находить до нервного смеха. Конечно, существуют специальные программы для построения графиков, онлайн сервисы, но они далеко не всегда бывают под рукой.
Иногда на практике задание встречается отдельно, примерная формулировка такова: «построить график функции, используя преобразования графиков элементарных функций». Дана, скажем, функция . Задача состоит в том, чтобы с помощью геометрических преобразований ветки логарифма получить график функции .
Среди прочего материала мы рассмотрим функции с модулем, незаслуженно обойдённые вниманием на первом уроке. По существу, модуль тоже влечёт вполне определённое преобразование графика функции.
Перед тем как перейти непосредственно к примерам напомню некоторые теоретические моменты. В начале статьи о дифференцировании неявной функции я сформулировал определение функции одной переменной . Актуализирую два особо нужных сейчас термина: «икс» – независимая переменная или АРГУМЕНТ, «игрек» – зависимая переменная или ФУНКЦИЯ. При этом функцию можно обозначать как через «игрек», так равноценно и через «эф от икс», например:
Данный технический момент уже упоминался на уроке Типовые задачи с производной. Разницы особой нет, но есть традиции, и в теме «Функции и графики» значительно чаще используется обозначение .
Арсенал преобразований графиков разнообразен как набор пыток святой инквизиции, и опытные читатели могут сразу выбрать свою участь:)
ну а начинающим лучше изучить всё по порядку:
Сжатие (растяжение) графика к (от) оси ординат.
Симметричное отображение графика относительно оси
Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов:
Сжатие графика функции к оси ординат
Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.
Правило: чтобы построить график функции , где , нужно график функции сжать к оси в раз.
И первой на эшафот взойдёт функция, которой я недавно грозился:
Построить график функции .
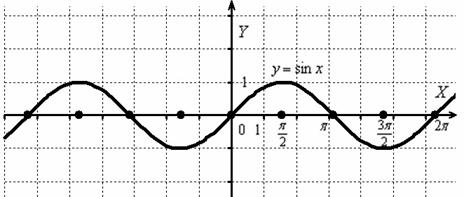
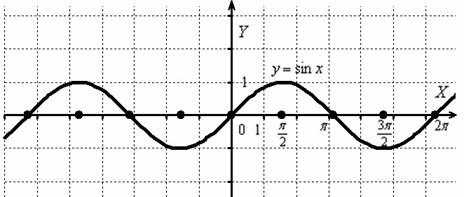
Сначала изобразим график синуса, его период равен :
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
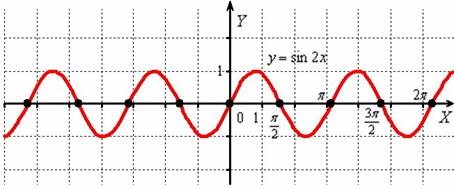
Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси в 2 раза:
То есть, график функции получается путём сжатия графика к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
Смотрим на чертёж, и видим, что это действительно так.
Аналогичную блиц-проверку полезно осуществлять в любом другом примере! Более того, она лучше поможет усвоить суть того или иного преобразования.
Построить график функции
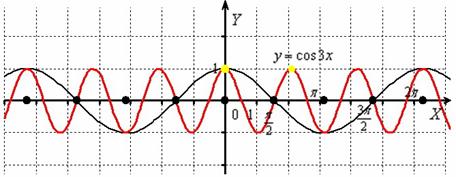
«Чёрная гармошка» сжимается к оси в 3 раза:
Итоговый график проведён красным цветом.
Исходный период косинуса закономерно уменьшается в три раза: (отграничен жёлтыми точками).
Растяжение графика функции от оси ординат
Это противоположное действие, теперь баян не сжимается, а растягивается.
Случай имеет место, когда АРГУМЕНТ функции умножается на число .
Правило: чтобы построить график функции , где , нужно график функции растянуть от оси в раз.
Продолжим мучить синус:
Построить график функции
Берём в руки нашу «бесконечную гармошку»:
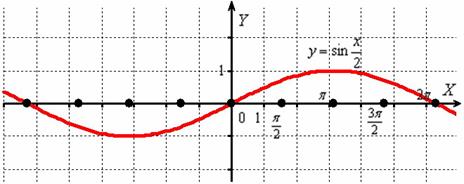
И растягиваем её от оси в 2 раза:
То есть, график функции получается путём растяжения графика от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: , он толком даже не вместился на данный чертёж.
Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций:
Построить графики функций
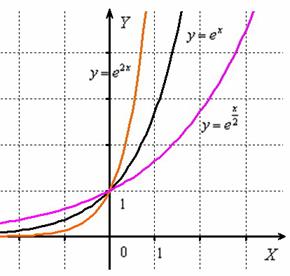
График функции получается путём сжатия графика экспоненты к оси в два раза. А график – путём растяжения графика экспоненты от оси в два раза:
В качестве ассоциации можете опять поиграть на «баяне» .
Продолжаем систематизировать умножение аргумента функции на число:
Мы рассмотрели два случая – сжатие () и растяжение ().
Очевидно, что нет практического смысла рассматривать значения . Есть более интересный вопрос: что происходит, когда аргумент умножается на отрицательное число? Ответ будет получен чуть позже, а пока рассмотрим распространённый частный случай, когда :
Симметричное отображение графика функции относительно оси ординат
АРГУМЕНТ функции меняет знак.
Правило: чтобы построить график функции , нужно график отобразить симметрично относительно оси .
Наглядный пример уже встречался на уроке Графики и свойства элементарных функций (вспоминаем ). Распечатаем ещё один комплект:
Построить график функции
График функции получается путём симметричного отображения графика относительно оси ординат:
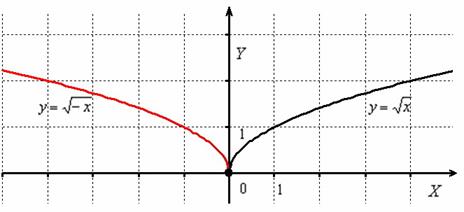
Как видите, всё просто.
Если при умножении аргумента на число значение параметра отрицательно и не равно минус единице, то построение выполняется в два шага. Например: . На первом шаге выполняем сжатие графика к оси ординат в 2 раза: . На втором шаге график отображаем симметрично относительно оси ординат: . Конкретный пример обязательно рассмотрим ниже.
А следующий параграф посвящается одному интересному человеку из дворовой компании моего далёкого детства. Он вытягивал руки в стороны, открывал рот и прыгал влево/вправо по проезжей части. Водители крутили виском у пальца, сигналили, но догнать его так никто и не смог.
Сдвиг графика влево/вправо вдоль оси абсцисс
Если к АРГУМЕНТУ функции добавляется константа, то происходит сдвиг (параллельный перенос) графика вдоль оси . Рассмотрим функцию и положительное число :
Правила:
1) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц влево;
2) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц вправо.
Построить график функции
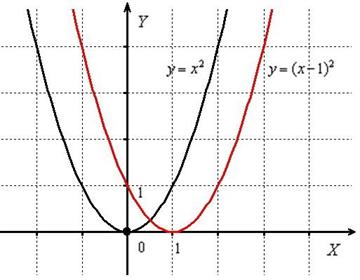
Берём параболу и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
«Опознавательным маячком» служит значение , именно здесь находится вершина параболы .
Теперь, думаю, ни у кого не возникнет трудностей с построением графика (демонстрационный пример начала урока) – кубическую параболу нужно сдвинуть на 2 единицы влево.
Вот ещё один характерный случай:
Построить график функции
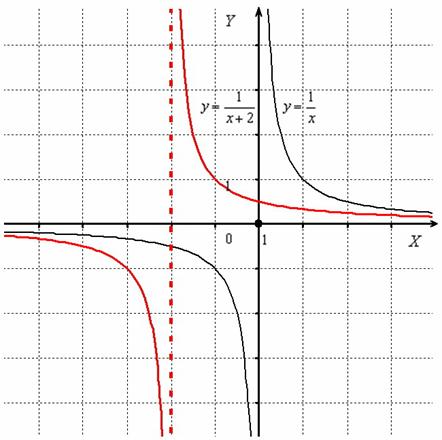
Гиперболу (чёрный цвет) сдвинем вдоль оси на 2 единицы влево:
Перемещение гиперболы «выдаёт» значение, которое не входит в область определения функции. В данном примере , и уравнение прямой задаёт вертикальную асимптоту (красный пунктир) графика функции (красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
Вернёмся к тригонометрическим функциям:
Построить график функции
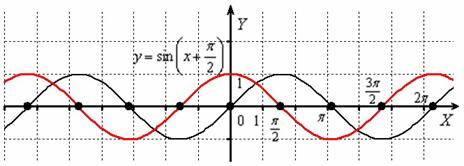
График синуса (чёрный цвет) сдвинем вдоль оси на влево:
Внимательно присмотримся к полученному красному графику …. Это в точности график косинуса ! По сути, мы получили геометрическую иллюстрацию формулы приведения , и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции получается путём сдвига синусоиды вдоль оси на единиц влево (о чём уже говорилось на уроке Графики и свойства элементарных функций). Аналогично можно убедиться в справедливости любой другой формулы приведения.
Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: , при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения , а потом сдвигаем на единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
Аргумент функции необходимо представить в виде и последовательно выполнить следующие преобразования:
1) График функции сжимаем (или растягиваем) к оси (от оси) ординат: (если , то график дополнительно следует отобразить симметрично относительно оси ).
2) График полученной функции сдвигаем влево (или вправо) вдоль оси абсцисс на (. ) единиц, в результате чего будет построен искомый график .
Построить график функции
Представим функцию в виде и выполним следующие преобразования: синусоиду (чёрный цвет):
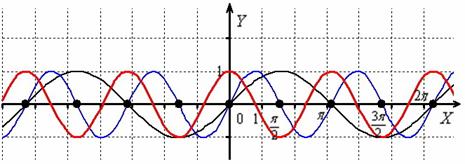
1) сожмём к оси в два раза: (синий цвет);
2) сдвинем вдоль оси на (. ) влево: (красный цвет):
Пример вроде бы несложный, а пролететь с параллельным переносом легче лёгкого. График сдвигается на , а вовсе не на .
Продолжаем расправляться с функциями начала урока:
Построить график функции
Представим функцию в виде . В данном случае: Построение проведём в три шага. График натурального логарифма :
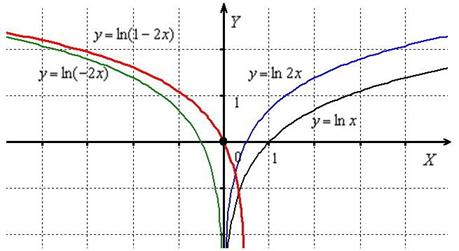
1) сожмём к оси в 2 раза: ;
2) отобразим симметрично относительно оси : ;
3) сдвинем вдоль оси на (. ) вправо: :
Для самоконтроля в итоговую функцию можно подставить пару значений «икс», например, и свериться с полученным графиком.
В рассмотренных параграфах события происходили «горизонтально» – гармонь играет, ноги пляшут влево/вправо. Но похожие преобразования происходят и в «вертикальном» направлении – вдоль оси . Принципиальное отличие состоит в том, что связаны они не с АРГУМЕНТОМ, а с САМОЙ ФУНКЦИЕЙ.
Растяжение (сжатие) графика ВДОЛЬ оси ординат.
Симметричное отображение графика относительно оси абсцисс
Структура второй части статьи будет очень похожа.
1) Если ФУНКЦИЯ умножается на число , то происходит растяжение её графика вдоль оси ординат.
Правило: чтобы построить график функции , где , нужно график функции растянуть вдоль оси в раз.
2) Если ФУНКЦИЯ умножается на число , то происходит сжатие её графика вдоль оси ординат.
Правило: чтобы построить график функции , где , нужно график функции сжать вдоль оси в раз.
Догадайтесь, какую функцию я буду снова пытать =)
Построить графики функций .
Берём синусоиду за макушку/пятки:
И вытягиваем её вдоль оси в 2 раза:
Период функции не изменился и составляет , а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: .
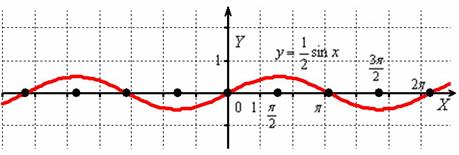
Теперь сожмём синусоиду вдоль оси в 2 раза:
Аналогично, период не изменился, но область значений функции «сплющилась» в два раза: .
Нет, у меня нет какого-то пристрастного отношения к синусоиде, просто я хотел продемонстрировать, чем отличаются графики функций (Примеры № 1, 3) от только что построенных собратьев . Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
И, конечно же, классический пример растяжения/сжатия параболы:
Построить графики функций .
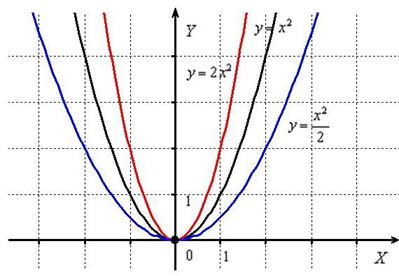
Возьмём рога молодого оленя и вытянем их вверх вдоль оси в два раза: . Затем сожмём вдоль оси ординат в 2 раза:
И снова заметьте, что значения функции увеличиваются в 2 раза, а значения уменьшаются во столько же раз (исключение составляет точка ).
Отпустим в тундру удивлённое животное и продолжим изучать умножение функции на число: . Случаи не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай :
Если ФУНКЦИЯ меняет знак на противоположный, то её график отображается симметрично относительно оси абсцисс.
Правило: чтобы построить график функции , нужно график отобразить симметрично относительно оси .
Построить график функции
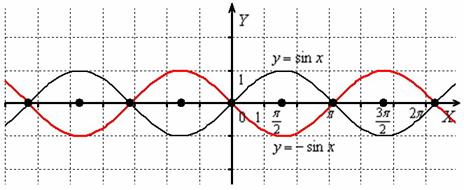
Отобразим синусоиду симметрично относительно оси :
Ещё более наглядно симметрия просматривается у следующей типовой функции:
Построить график функции
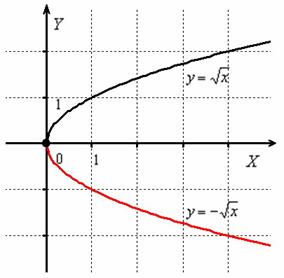
График функции получается путём симметричного отображения графика относительно оси абсцисс:
Функции задают две ветви параболы, которая «лежит на боку». Обратная функция задаёт параболу целиком. С подобными графиками часто приходится иметь дело при нахождении площадей фигур, построении областей интегрирования двойных интегралов и в некоторых других задачах.
При умножении функции на отрицательное число , , построение графика следует выполнить в два этапа: сжатие (или растяжение) вдоль оси ординат, а потом – симметричное отображение относительно оси абсцисс. Конкретные примеры увидим в следующем топике.
Сдвиг графика вверх/вниз вдоль оси ординат
Настала пора дать передышку ногам и сесть в лифт.
Если к ФУНКЦИИ добавляется константа, то происходит сдвиг (параллельный перенос) её графика вдоль оси . Рассмотрим функцию и положительное число :
Правила:
1) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц вверх;
2) чтобы построить график функции , нужно график сдвинуть ВДОЛЬ оси на единиц вниз.
Построить графики функций .
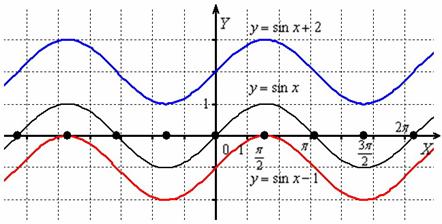
В комментариях, думаю, нет особой необходимости:
Комбинационное построение графика в общем случае осуществляется очевидным образом:
1) График функции растягиваем (сжимаем) вдоль оси . Если множитель отрицателен, дополнительно осуществляем симметричное отображение относительно оси .
2) Полученный на первом шаге график сдвигаем вверх или вниз в соответствии со значением константы .
Построить график функции
График косинуса (чёрный цвет):
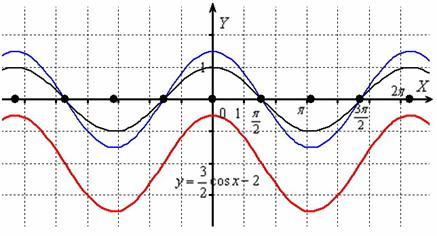
1) Растягиваем вдоль оси в 1,5 раза: (синий цвет);
2) Сдвигаем вдоль оси на 2 единицы вниз: :
Простой, но весьма распространённый кадр:
Построить график функции
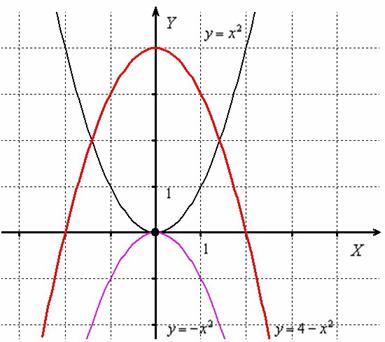
1) отобразим симметрично относительно оси абсцисс: ;
2) сдвинем вдоль оси на 4 единицы вверх: :
Да, конечно, данную кривую легко построить и поточечно, но такие параболы очень часто встречаются в практических заданиях, поэтому весьма полезно сразу представлять, как они расположены.
Аналогичный трехходовой пример с растяжением и симметричным отображением графика относительно оси :
Построить график функции
График экспоненциальной функции :
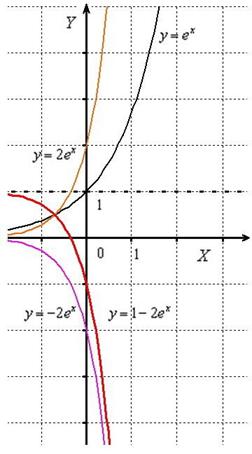
1) растянем вдоль оси в 2 раза: ;
2) отобразим симметрично относительно оси абсцисс: ;
3) сдвинем вдоль оси на 1 единицу вверх: :
Заметьте, что в результате последнего преобразования горизонтальная асимптота графика тоже «уехала» вверх на 1 единицу. Аналогичный факт мы уже наблюдали при сдвиге гиперболы (см. Пример № 7).
Систематизируем всю информацию:
Общая схема построения графика функции
с помощью геометрических преобразований
Рассмотрим функцию , которая «базируется» на некоторой функции . Для многих читателей алгоритм построения графика уже понятен:
– на первом шаге выполняем преобразования, связанные с АРГУМЕНТОМ функции (см. первые два параграфа), в результате чего получаем график функции ;
– на втором шаге выполняем только что рассмотренные преобразования, связанные с самой ФУНКЦИЕЙ, и получаем график .
Завершим самое длинное построение данного урока:
Пример 19 (концовка Примера 10)
Построить график функции
В примере № 10 мы выполнили построение графика , то есть полностью разобрались с аргументом функции. И сейчас осталось выполнить завершающие шаги.
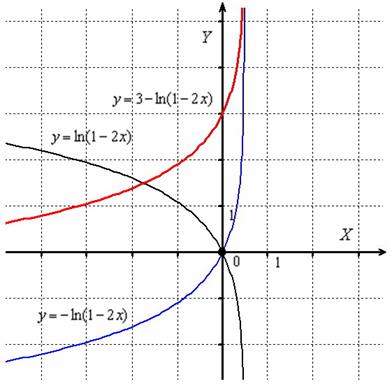
4) отобразим симметрично относительно оси : ;
5) сдвинем вдоль оси на 3 единицы вверх: :
На практике, к счастью, построения почти всегда более коротки, например:
– кубическую параболу сдвигаем вдоль оси на 5 единиц вправо и сжимаем вдоль оси в 3 раза.
– график экспоненты отображаем симметрично относительно оси ординат, затем – симметрично относительно оси абсцисс.
– график функции смещаем влево на 5 единиц, затем – вверх на 1 единицу.
И т.д. Некоторые геометрические преобразования можно поменять местами, но это возможно далеко не всегда! Поэтому «чайникам» лучше придерживаться алгоритма, изложенного в начале параграфа.
Весь материал статьи, который носит в бОльшей степени всё-таки справочный характер, потребуется для выполнения чертежей в других задачах, но время от времени на практике рассматриваемое задание встречается отдельно, причём, бывает, в «сыром» виде:
Построить график функции с помощью преобразований графиков элементарных функций
Методику быстрого построения параболы я разобрал на первом уроке о графиках функций, однако здесь по условию необходимо применить вполне определённый способ.
На первом шаге представим функцию в виде . Для этого используем так называемый метод выделения полного квадрата. Советую не пренебрегать задачей, поскольку типовой приём потребуется и в будущем, например, при нахождении интегралов от некоторых дробей.
Идея состоит в том, чтобы искусственно преобразовать функцию ТАК, чтобы воспользоваться одной из формул сокращенного умножения либо .
Начнём преобразования. Коэффициент при выносим за скобку:
Очевидно, что выражение сведётся к формуле . В скобках конструируем :
Таким образом, . Теперь организуем , для этого в скобках прибавим и вычтем :
Последнее слагаемое выносим из скобок:
Используем формулу и суммируем два последних слагаемых:
В целях проверки целесообразно раскрыть скобки и убедиться, что получится исходная функция:
Построим график . Параболу :
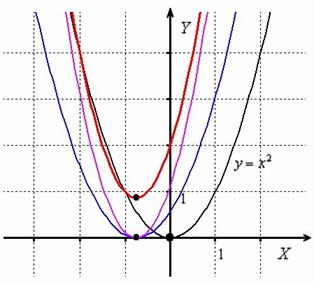
1) Сдвинем вдоль оси на влево: (синий цвет);
2) Вытянем вдоль оси в 2 раза: (малиновый цвет);
3) Сдвинем вдоль оси на вверх: (красный цвет):
Рассмотрим ещё один типовой трюк:
Построить график функции с помощью преобразований графиков элементарных функций.
Сначала сведём функцию к виду . Все действия я закомментирую:
(1) В знаменателе выносим –1 за скобки. Это необходимо, чтобы аргумент функции представить «в привычном» порядке .
(2) Минус знаменателя поставим перед дробью. В числителе проведём искусственное преобразование – прибавим и вычтем единицу. Это необходимо для почленного деления на следующем шаге.
(3) Почленно делим числитель на знаменатель. Возьмите на заметку рассмотренный приём, он используется при интегрировании дробей.
(4) Раскрываем скобки.
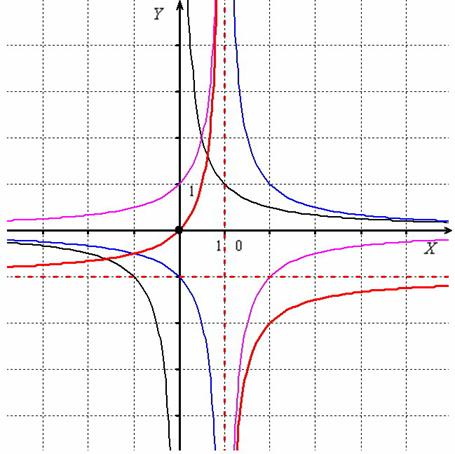
Проведём построение. График гиперболы (чёрный цвет):
1) Сдвинем вправо на 1 единицу: (синий цвет);
2) Отобразим симметрично относительно оси абсцисс: (малиновый цвет);
3) Сдвинем вдоль оси на единицу вниз: (красный цвет):
Перейдём к заключительной части урока, в которой речь пойдёт о модуле. Хотел её сделать отдельной небольшой страничкой или pdf-кой, да потом передумал, чего уж тут мелочиться. Хотя эта статья далеко не рекордная по количеству букв, солидную часть объема занимают чертежи.
Графики функций с модулем
Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.
Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.
Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.
Правило: график функции получается из графика функции следующим образом: при график функции сохраняется, а при «сохранённая часть» отображается симметрично относительно оси .
Построить график функции
И снова вечная картина:
Согласно правилу, при график сохраняется:
И сохранившаяся часть отображается симметрично относительно оси в левую полуплоскость:
Действительно, функция – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.
Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:
То есть, правая волна графика задаётся функцией , а левая волна – функцией (см. Пример 13).
Построить график функции
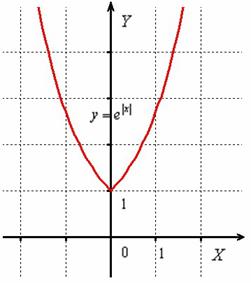
Аналогично, ветвь «обычной» экспоненты правой полуплоскости отображаем симметрично относительно оси в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .
Модуль не имеет смысл «навешивать» на аргумент чётной функции: и т.п. (проанализируйте, почему).
И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.
Правило: график функции получается из графика функции следующим образом: часть графика , лежащая НАД осью сохраняется, а часть графика , лежащая ПОД осью отображается симметрично относительно данной оси.
Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)
Построить график функции
Сначала начертим прямую, известную широкому кругу лиц:
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси – отображается симметрично в верхнюю полуплоскость:
Модуль функции также раскрывается аналитически в кусочном виде:
Внимание! Формула отличается от формулы предыдущего пункта!
В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .
Кстати, – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и к самой функции: . Изучим более «жизненную» ситуацию:
Построить график функции
Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси в верхнюю полуплоскость:
Согласно формуле , распишем функцию аналитически в кусочном виде: .
Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.
На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .
Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:
Построить график функции .
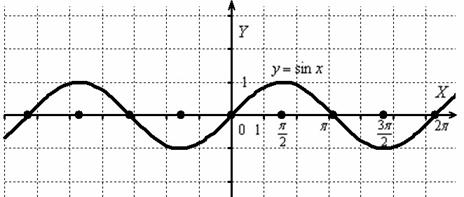
Изобразим сами знаете что =)
И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :
Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.
Распишем функцию в кусочном виде:
Решив два простейших школьных неравенства , получаем:
, где – любое целое число.
Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)
(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Zaochnik.com – профессиональная помощь студентам,
cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Источник: www.mathprofi.ru