Для решения физических и инженерных задач при проектировании несущих конструкций многоэтажных сооружений в строительной отрасли принято использовать численные методы. Одним из самых распространенных и эффективных из них как в России, так и во всем мире является метод конечных элементов (МКЭ). Ведущее положение этого метода объясняется широкой областью и относительной простотой его применения: независимостью расчета от типа конструкции и физических свойств применяемых материалов, упрощенной системой учета взаимодействия расчетных конструкций с окружающей их средой, возможностью автоматизации расчета на любом его этапе.
История появления метода конечных элементов
Метод конечных элементов в строительстве впервые на практике был использован в начале 50-х годов двадцатого века. Изначально его развитие происходило в двух независимых друг от друга направлениях: инженерном и математическом. На раннем этапе становления формулировки метода отталкивались только от принципов строительной механики, и это существенно ограничивало область его применения. И лишь после формулировки основ МКЭ с возможностью небольших отклонений, стало возможным его использование и в решении других задач. Активному развитию метода конечных элементов способствовал и прогресс в области компьютерной техники, а также появляющаяся возможность его использования в большинстве областей науки и практики.
Жить такой жизнью очень просто

Этапы развития метода:
1. В развитии метода конечных элементов свои роли сыграли как вариационные основы механики, так и математические методы, которые были основаны на вариационных принципах. Разбитие задачи с помощью вариационного метода Ритца было впервые применено Рихардом Курантом в 1943 году, и только в 50-е годы двадцатого века увидели свет такие же работы других ученых (Поли, Герша и других).
2. Весомый вклад в развитие метода был сделан Джоном (Иоаннисом) Аргирисом. Именно он к расчету стержневых систем применил матричную формулировку на базе основных энергетических принципов, определил матрицу податливости и обратную ей матрицу жесткости. Научные труды Аргириса и его коллег, которые были опубликованы с 1954 по 1960 годы, стали отправной точкой для матричного отображения известных в то время численных методов и позволили применять их с помощью электронно-вычислительных машин для расчетов конструкций.
3. Современная концепция метода была изложена группой американских ученых (Тэрнером, Клаффом, Мартином и Топпом) в 1956 году. Они, решая задачу теории упругости на плоскости, применили новый элемент треугольной формы и сформировали для него не только матрицу жесткости, но и вектор узловых сил.
Название же метода конечных элементов, под которым его знают и по сей день, ввел в действие ученый Клафф в 1960 году. В следующее пятилетие после этого было опубликовано множество работ по нахождению конечных элементов для двумерных и трехмерных конструкций, среди авторов следует отметить таких ученых, как Р. Мак-Лей, Р. Мелош, Дж. Бесселин, Ф. де Веубеке, М. Джонс, Т. Пиан. В 1967 году увидела свет и первая монография, посвященная методу конечных элементов, под авторством И. Чанга и О. Зенкевича.
Вебинар по BIM: «Информационное моделирование в строительстве. Первое знакомство»
4. Математическая теория метода появилась лишь в 70-х годах, ее зарождение прослеживается в трудах таких ученых, как И. Бабушки, Р. Галлагер, Ж. Дек-лу, Дж. Оден, Г. Стренг, Дж. Фикс. Весомый вклад был внесен и российскими учеными. Так, например, В.Г.Корнеев сопоставил математические сущности метода конечных элементов и вариационно-разностного метода и указал на их совпадение.
Над той же темой трудился Л.А.Розин. А А.С.Сахаровым была разработана моментная схема КЭ.
5. Последнее время, особенно последние десятилетия, характеризуются активным развитием и применением метода конечных элементов для расчета динамики конструкций, оптимизации проектирования и учета нелинейного поведения.
Суть метода конечных элементов
Перед началом выполнения расчета конструкции следует представить ее в виде, понятном электронному мозгу, то есть компьютеру. И так как компьютер может оперировать только с цифрами, то и конструкция должна быть представлена именно в цифровом варианте. Таким образом, нужно создать математическую модель, которая будет не только полностью соответствовать рассчитываемой конструкции, но и состоять только из цифр. Целью работы будет решение этой математической модели и определение неизвестных.
Суть метода конечных элементов заключается в разбиении всей области, занимаемой конструкцией, на некоторое количество малых подобластей с конечным размером. Эти подобласти носят название конечных элементов, а само разбиение называется дискретизацией.
Форма конечных элементов будет зависеть от типа самой конструкции и характера деформации. Например, конечными элементами в расчете стержневых конструкций (ферм, балок или рам) будут участки стержней, при расчетах двумерных континуальных систем (пластин, плит или оболочек) — прямоугольные или треугольные подобласти, а при расчете трехмерных конструкций (массивов или толстых плит) — подобласти в виде тетраэдров или параллелепипедов. Но в отличие от настоящей конструкции в такой дискретной модели связывание конечных элементов происходит только в отдельных узлах (точках) некоторым известным количеством узловых параметров.
Функционалом энергии всей конструкции при дискретизации будет алгебраическая сумма отдельных функционалов конечных элементов, и для каждой подобласти должен быть задан независимый от других закон распределения требуемых для решения функций. С помощью этих законов возможно выражение перемещений (искомых непрерывных величин) в пределах заданного конечного элемента через значения величин в конечных точках.
Число узлов и число их возможных перемещений (степень свободы) для конечного элемента могут варьироваться, но меньше минимального количества, необходимого для рассмотрения состояний конечных элементов под действием напряжения или деформации в данной принятой модели, их быть не должно. Степени свободы конечных элементов определяются числом независимых перемещений во всех их узлах. Степень свободы всей рассчитываемой конструкции и, как следствие, алгебраический порядок уравнений системы будет определяться суммированием числа перемещений всех известных ее узлов. Исходя из того, что основные неизвестные в расчете методом перемещений — искомые узловые перемещения, то понятия степени свободы конечных элементов и конструкции целиком становятся особо важными в методе конечных элементов.
Способ дискретизации рассматриваемой области, количество конечных элементов, число их степеней свободы, а также форма используемых приближенных функций оказывают непосредственное влияние на точность расчета всей конструкции. Таким образом, метод конечных элементов, как наиболее алгебраический, помогает не только при расчете отдельных строительных конструкций, но и в целом при решении строительных задач.

Пример расчета континуальных двумерных конструкций
Рассмотрим пример расчета континуальных двумерных конструкций (пластин или плит) методом конечных элементов, которое заключается в выполнении следующих этапов:
Источник: www.it-nv.ru
Понятие о методе конечных элементов
Метод конечных элементов – это метод расчета сооружений, основанный на рассмотрении сооружения как совокупности типовых элементов, называемых конечными элементами (КЭ).
В дискретном методе мы рассмотрели три типовых стержневых элементов, которые используются и в МКЭ как конечные элементы. Например, элемент 3-его типа в МКЭ называется ферменным (рис. 14.1 а), а 1-го типа – плоским стержневым конечным элементом (рис. 14.1 б). При расчете пространственных рам используется КЭ бруса (рис. 14.1 в).
В расчетах плоских тел (плит или пластин) используются треугольный (рис. 14.1 г) или четырехугольный (рис. 14.1 д) конечные элементы. При расчете пространственных сооружений могут использоваться призменный КЭ (рис. 14.1 е) или тетраэдальный КЭ (рис. 14.1 ж) и др.
Для расчета различных сооружений разработано множество других КЭ.

МКЭ – дискретный метод. В этом методе сооружение делится на определенное число КЭ, соединенных между собой в узлах конечно-элементной модели. А нагрузка, действующая на сооружение, переносится в узлы. Это позволяет определять НДС сооружения через узловые усилия и перемещения конечно-элементной модели.
Как мы знаем, можно выбирать разные расчетные схемы сооружения. Но и в пределах одной расчетной схемы можно выбирать разные расчетные модели по МКЭ, потому что сооружение можно разбить не только на разное количество однотипных КЭ, но и представить его как комбинацию различных типов КЭ. С другой стороны, при расчете сооружения могут быть реализованы различные варианты МКЭ в формах метода сил, метода перемещений и смешанного метода. В настоящее время широкое распространение получил МКЭ в форме метода перемещений.
Вариационные основы МКЭ
При решении многих задач статики, динамики и устойчивости сооружений определяется их полная потенциальная энергия U:
Здесь W – работа внешних сил, V – работа внутренних сил. Обычно все они представляются в виде функций, зависящих от перемещений, деформаций, напряжений элементов расчетной модели сооружения.
Исследование этого выражения позволяет выявить важные законы механики, называемые принципами. Например, в теоретической механике известен принцип Лагранжа-Дирихле: для того чтобы механическая система находилась в равновесии, ее полная потенциальная энергия должна быть постоянной. Из этого принципа следует, что приращение полной потенциальной энергии системы, находящейся в равновесии, должно равняться нулю:
Вычисление приращения функции обычно заменяется вычислением его приближенного значения − дифференциала. В этом случае получается вариационное уравнение Лагранжа
где символ означает вариацию, вычисление которого схоже с вычислением дифференциала функции. Это уравнение позволяет свести задачу определения НДС сооружения к отысканию экстремума полной потенциальной энергии.
С учетом (1) вариационное уравнение Лагранжа принимает вид
Оно формулируется как принцип Лагранжа: вариация работы внутренних сил равна вариации работы внешних сил.
Принцип Лагранжа используется для сведения континуальной задачи расчета сооружений к дискретной задаче путем аппроксимации (приближенного определения) непрерывных полей перемещений, деформаций, напряжений внутри конечного элемента по его узловым перемещениям.
В строительной механике используются и другие вариационные принципы, аналогичные принципу Лагранжа, такие как принципы Кастильяно, Рейсснера, Ху-Вашицу и др. Однако мы воспользуемся только вариационным принципом Лагранжа как основой варианта МКЭ в форме метода перемещений.
Аппроксимация КЭ
Имея КЭ разного типа, при выборе конечно-элементной модели сооружения можно вводить узлы с разным числом степеней свободы. Например, в плоской системе могут рассматриваться узлы как с тремя степенями свободы (рис. 14.2 а), так и с двумя (рис. 14.2 б) или даже с одной степенью свободы.
В первом случае учитываются два линейных (поступательных) и одно угловое перемещение узла, во втором – два линейных перемещения, а в третьем − лишь одно поступательное перемещение. В пространственной системе узлы могут иметь шесть (рис. 14.2 в) или три степени свободы (рис. 14.2 г).
Для упорядочения степеней свободы и соответствующих перемещений узлов КЭ все они нумеруются в определенном порядке и собираются в общий вектор перемещений u.
Чтобы воспользоваться принципом Лагранжа, вводятся так называемые координатные функции, аппроксимирующие непрерывное поле перемещений внутри КЭ через перемещения ее узлов:
Здесь – вектор перемещений внутренних точек КЭ,C– матрица координатных функций, – вектор коэффициентов. Элементы матрицы C выбираются в виде полиномов, непрерывных внутри КЭ. Если в полиноме учитывается минимальное число членов, то такой КЭ называется симплекс-элементом. При учете большего числа членов полинома КЭ называется комплекс-элементом.
В качестве простейшего примера рассмотрим ферменный КЭ с узлами i и j (рис. 14.3 а) в местной системе координат . Его узлы имеют по одной поступательной степени свободы по оси и соответствующие им узловые перемещения и . Допустим, что в узлах КЭ приложены силы и (рис. 14.3 б).
Перемещения внутренних точек элемента будем аппроксимировать полиномом первой степени
Запишем его в матричной форме:
где называется матрицей координатных функций, а является вектором неизвестных коэффициентов.
Подставив и в наш полином, получим два равенства:
С другой стороны, и (рис. 14.3 б). Учитывая их, предыдущие равенства перепишем так:
Тогда их можно записать в матричной форме
и представить как матричное уравнение
связывающее вектор узловых перемещений и вектор координат через представленную выше матрицу .
Входящая сюда матрица H называется матрицей форм. Она позволяет аппроксимировать поле перемещений внутренних точек КЭ через перемещения узлов.
По аналогии с перемещениями поле внутренних усилий в КЭ можно аппроксимировать через вектор узловых сил по формуле
Например, для рассмотренного КЭ имеем
Матрица жесткости КЭ
Известные в механике геометрические и физические соотношения для континуальных систем можно записать в виде, аналогичном рассмотренным ранее уравнениям дискретного подхода. Например,
для дискретной системы: для континуальной системы: , , , .
Здесь и – вектора деформаций и напряжений, а и – матрицы равновесия и податливости континуальной системы. В отличие от дискретного подхода, уравнения континуального подхода удовлетворяются во всех точках системы.
При рассмотрении конечного элемента как континуальной системы принцип Лагранжа можно записать в виде
где левая и правая части представляют возможные работы внутренних и внешних сил, а интегрирование ведется по объему КЭ V.
После этого осуществляется переход к дискретной модели КЭ с использованием матрицы форм H. Тогда после ряда преобразований получается матричное уравнение, связывающее вектор узловых перемещений u с вектором узловых усилий P КЭ:
в которой симметричная квадратная матрица
называется матрицей жесткости конечного элемента. Физический смысл элемента kij этой матрицы – это реакция (реактивная сила), возникающая в i-ом направлении отзаданного единичного перемещения в j-ом направлении.
К примеру, для рассмотренного ферменного КЭ, находящегося в одноосном напряженном состоянии, геометрическое уравнение будет . Сравнив его с матричным уравнением , видим, что матрица равновесия является дифференциальным оператором с одним членом, т.е. . Из уравнения связи между деформацией и напряжением видно, что матрица податливости будет .
Для определения матрицы жесткости КЭ вычислим:
Интегрирование по объему V сводится к интегрированию по длине l КЭ, т.к. (F − площадь сечения КЭ). Тогда
При рассмотрении прямоугольного КЭ толщиной t и размерами 2a и 2b с четырьмя узлами i, j, k, m и восемью узловыми перемещениями (рис. 14.4), матрица жесткости будет иметь размеры 8´8.
Для краткости записи матрицу жесткости этого КЭ можно представить в блочной форме с 16 блоками одинаковой размерности 2´2:
Здесь μ – коэффициент Пуассона. Элементы каждого блока матрицы K определяются по разным формулам. Например,
В о п р о с ы
1. Какой из подходов механики реализуется в МКЭ?
2. Какие основные типы КЭ используются в МКЭ?
3. Как формулируется принцип Лагранжа?
4. Для чего нужны координатные функции и матрицы форм?
5. Что такое функция формы?
6. Как определяется матрица жесткости КЭ?
7. Какой физический смысл имеют элементы матрицы жесткости?
Л е к ц и я 15
Перечень документов по охране труда. Сроки хранения: Итак, перечень документов по охране труда выглядит следующим образом.
Методы исследования в анатомии и физиологии: Гиппократ около 460- около 370гг. до н.э. ученый изучал.
Источник: poisk-ru.ru
Способы применения плитных КЭ при проектировании строительных конструкций
В библиотеке КЭ ЛИРА САПР есть несколько видов КЭ пластинчатых элементов, которые условно можно разделить на три группы:
- Плиты (КЭ 11…15, 19);
- Балки-стенки (КЭ 21…24,27,30);
- Оболочки (КЭ 41,42,44);
Выбор каждого из типов КЭ зависит от следующих параметров:
- Признак схемы решаемой задачи;
- Конструктивная схема здания или сооружения и её влияние на пространственную работу;
В рамках данной статьи рассмотрим несколько случаев расчёта строительных конструкций и применение соответствующих типов КЭ.
Различия в работе КЭ плит, балок-стенок и оболочек
Ключевое отличие КЭ плит, балок-стенок и оболочек друг от друга заключается в наличии или отсутствии определённых степеней свободы в узлах элемента. Различия в работе данных типов КЭ показаны в видео https://youtu.be/mSOl2SKs-Qw
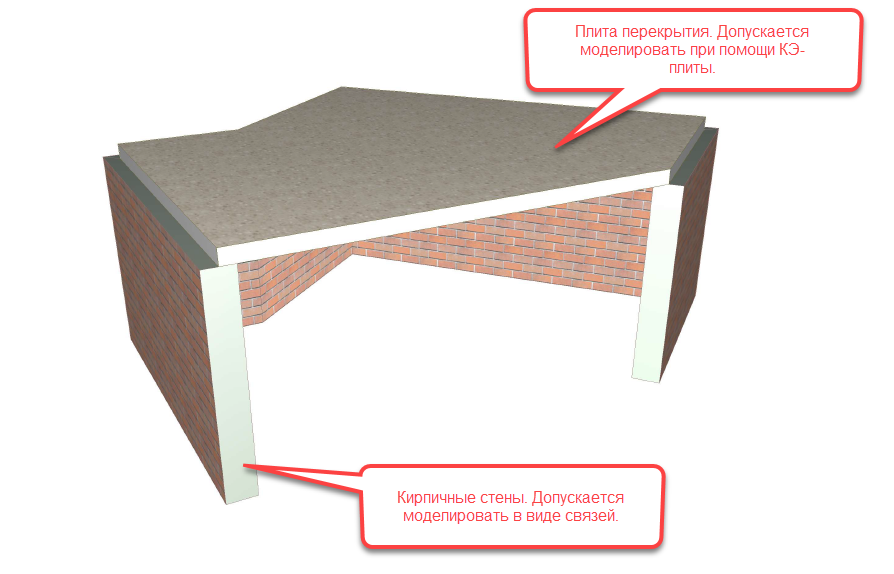
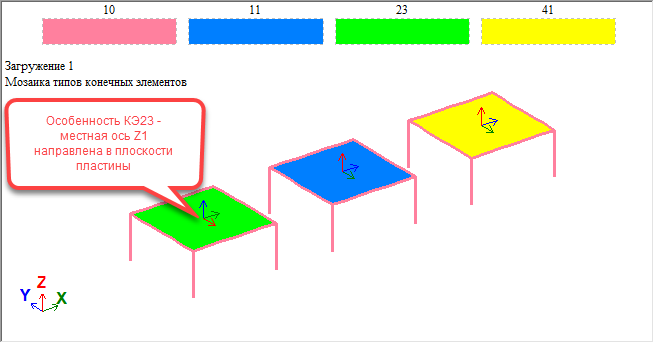
Особенности работа КЭ-плит
Плиты (КЭ 11…15, 19) имеют от двух до трёх степеней свободы в узле (Z, Ux, Uy), в зависимости от выбранного признака схемы и преимущественно предназначены для восприятия нагрузки, приложенной по нормали к их поверхности. В элементах плиты возникают, при этом, изгибающие моменты и поперечные силы. Нагрузки, направленные в плоскости плиты, данный тип КЭ воспринимать не может.
Особенности работы КЭ Балка-стенка
Балка стенка (КЭ 21…24, 27, 30) имеет три степени свободы в узле (X, Y, Z) и может воспринимать мембранные усилия, приложенные в плоскости данного элемента. Изгибающие моменты и поперечные силы в балке-стенке возникнуть не могут, а, следовательно, к данному типу КЭ невозможно приложить нагрузку, перпендикулярную или наклонную к его поверхности.
Особенности работы КЭ-оболочек
Данный тип КЭ имеет шесть степеней свободы в узле (X, Y, Z, Ux, Uy, Uz) и может воспринимать любые нагрузки, т.е. сочетает в себе признаки плиты и балки-стенки.
Применение разных типов КЭ при проектировании железобетонных конструкций
При выполнении расчётов зданий и сооружений пользователи, как правило, устанавливают пятый признак схемы при создании файла расчётной модели, а если в модели используются пластинчатые КЭ, то в большинстве случаев им по умолчанию присваивается тип КЭ-оболочка.
Разберём, как наиболее рационально применять признаки схемы и типы пластинчатых КЭ для расчётов зданий и сооружений.
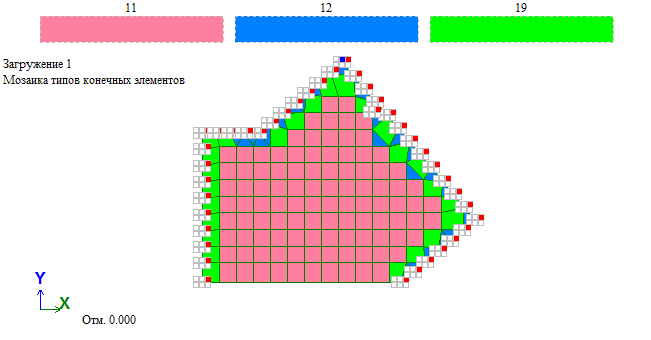
Применение КЭ-Плиты
Данный тип КЭ больше всего подходит для выполнения расчётов при проектировании плоских монолитных плит перекрытий, с опиранием на кирпичные стены. Его применение позволит сократить время выполнения расчёта компьютером.
Применение КЭ-Балки-стенки
Применение данного типа КЭ больше всего подходит для расчёта каркасов зданий, где применяются сборные плиты перекрытия, которые, при условии анкеровки плит между собой, образуют жёсткий диск. Такой подход позволяет избежать возникновения в ригелях продольных усилий и подобрать для них меньшее сечение или сэкономить арматуру.

Ригели могут быть стальными или железобетонными. Нагрузки следует прикладывать непосредственно к ригелям ввиду того, что для КЭ Балки-стенки невозможно приложить нагрузку перпендикулярно её поверхности.
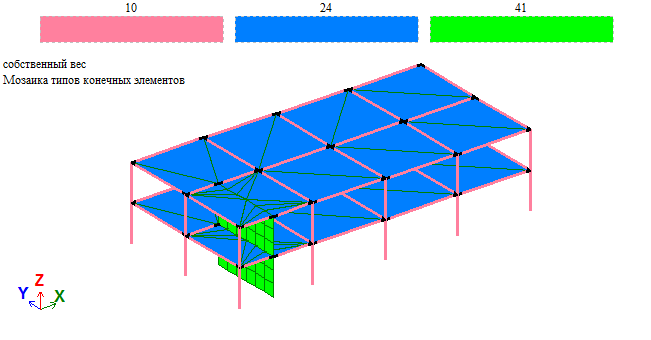
Важно: если в конструкции, которая по конструктивной схеме должна работать на изгиб, возникает продольное усилие, то его нельзя игнорировать. Следует разобраться в причинах его возникновения и либо откорректировать расчётную модель, чтобы его устранить, либо подбирать сечение или арматуру в ригеле с учётом продольного усилия.
Применение КЭ-оболочки
Данный тип КЭ применим при расчётах монолитных ребристых плит и кессонных перекрытий. В таких конструкциях изгибные и продольные усилия распределяются между стержневыми и пластинчатыми элементами пропорционально их жёсткостям. Нагрузки могут быть приложены непосредственно к поверхности оболочек.
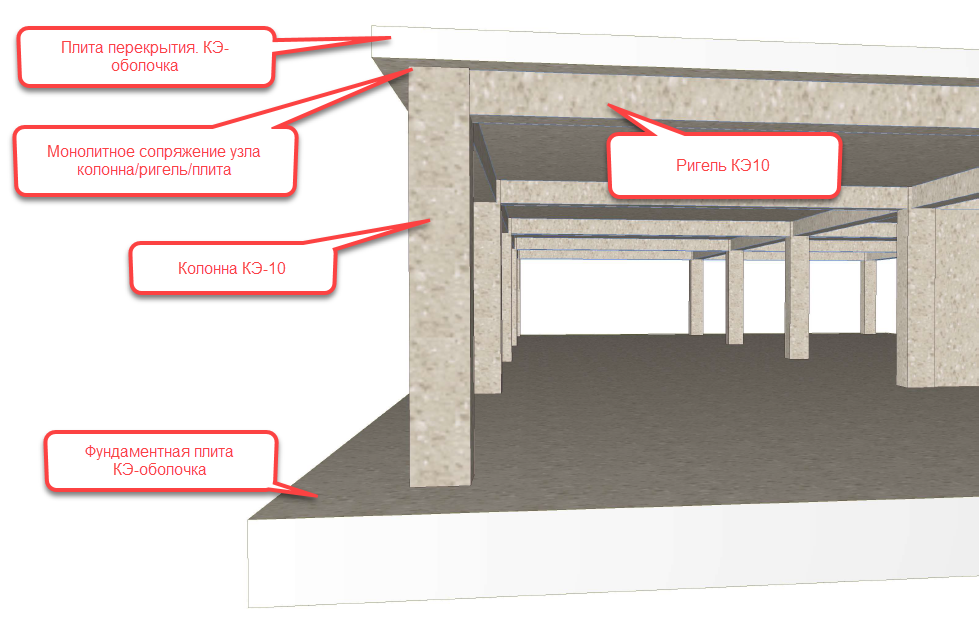
Сопряжение монолитного ребра с пластиной допускается выполнять разными способами. Один из способов представлен на рисунке.
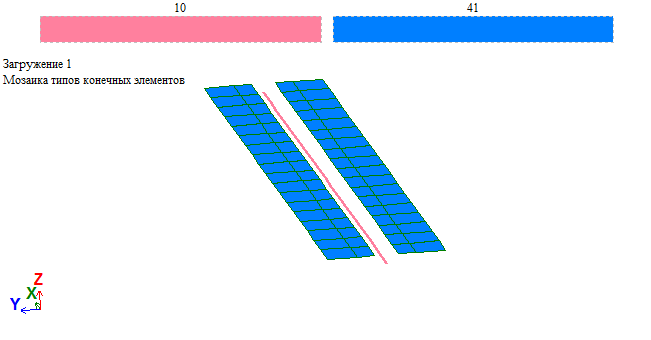
Модель монолитного ребристого перекрытия. Монолитная плита в месте сопряжения с ребром выполняется с вырезом.
Источник: liraserv.com