Цель моей курсовой работы — описать и усвоить, что, в общем, представляет собой сетевое планирование и управление (СПУ).
Можно выделить следующие задачи:
1) Рассмотреть понятие сетевого планирования.
2) Выделить основные понятия сетевого планирования.
3) Изучить правила построения сетевых моделей.
4) Определить направления применения сетевого планирования.
5) Рассмотрим основные методы сетевого планирования.
Содержание работы
Введение…………………………………………………………………. 3
Глава1Сетевое планирование…………………………………………. 5
1.1 Понятие сетевого планирования……………………………. 5
1.2 Основные понятия сетевого планирования………………………….8
1.3 Правила построения сетевых моделей……………………………. 10
1.4 Направления применения сетевого планирования………………. 12
1.5Методы сетевого планирования…………………………….. ……. 1
Содержимое работы — 1 файл
Глава1Сетевое планирование………… ………………………………. 5
1.1 Понятие сетевого планирования……………………… ……. 5
Методы сетевого планирования-1.
1.2 Основные понятия сетевого планирования… ……………………….8
1.3 Правила построения сетевых моделей……………………………. 10
1.4 Направления применения сетевого планирования………………. 12
1.5Методы сетевого планирования…………………………….. ……. 13
Тема моей курсовой работы – «Сетевое планирование в строительстве».
Планирование и управление комплексом работ по проекту представляет собой сложную и, как правило, противоречивую задачу. Оценка временных и стоимостных параметров функционирования системы, осуществляемая в рамках этой задачи, производится различными методами. Среди существующих большое значение имеет метод сетевого планирования.
Методы сетевого планирования могут широко и успешно применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, которые требуют участия большого числа исполнителей и затрат ограниченных ресурсов.
Следует отметить, что главной целью сетевого планирования является сокращение до минимума продолжительности проекта, таким образом, использование сетевых моделей обусловлено необходимостью грамотного управления крупными народнохозяйственными комплексами и проектами, научными исследованиями, конструкторской и технологической подготовкой производства, новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов и т.п.
С помощью сетевой модели руководитель работ или операции может системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
Цель моей курсовой работы — описать и усвоить, что, в общем, представляет собой сетевое планирование и управление (СПУ).
Можно выделить следующие задачи:
1) Рассмотреть понятие сетевого планирования.
2) Выделить основные понятия сетевого планирования.
3) Изучить правила построения сетевых моделей.
4) Определить направления применения сетевого планирования.
5) Рассмотрим основные методы сетевого планирования.
Сетевое планирование и управление
Следует отметить, что тема сетевое планирование в строительстве, недостаточно широко изучена и освещена как в учебной литературе по теории финансов, так и в работах, помещенных на страницах журналов и газет.
Глава 1 Сетевое планирование
1.1 Понятие сетевого планирования
Сетевое планирование — набор методов, который предназначен для управления расписанием проекта. Сетевое планирование позволяет определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.
Сетевое планирование основываются на разработанных практически одновременно и независимо методе критического пути МКП (СРМ — Critical Path Method) и методе оценки и пересмотра планов ПЕРТ (PERT — Program Evaluation and Review Technique).[13,с.303]
Методы сетевого планирования применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, требующими участия большого числа исполнителей и затрат ограниченных ресурсов.
Основная цель сетевого планирования — сокращение до минимума продолжительности проекта.
Задача сетевого планирования состоит в том, чтобы графически, наглядно и системно отобразить и оптимизировать последовательность и взаимозависимость работ, действий или мероприятий, обеспечивающих своевременное и планомерное достижение конечных целей. Для отображения и алгоритмизации тех или иных действий или ситуаций используются экономико-математические модели, которые принято называть сетевыми моделями, простейшие из них — сетевые графики. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
Важная особенность СПУ (сетевого планирования и управления) заключается в системном подходе к вопросам организации управления, согласно которому коллективы исполнителей, принимающие участие в комплексе работ и объединенные общностью поставленных перед ними задач, несмотря на разную ведомственную подчиненность, рассматриваются как звенья единой сложной организационной системы.
Использование методов сетевого планирования способствует сокращению сроков создания новых объектов на 15-20%, обеспечению рационального использования трудовых ресурсов и техники.
В основе сетевого планирования лежит построение сетевых диаграмм. Сетевая диаграмма (сеть, граф сети, PERT-диаграмма) — графическое отображение работ проекта и зависимостей между ними. В СПУ под термином «сеть» понимается полный комплекс работ и вех проекта с установленными между ними зависимостями.[15 с. 768]
Выделяют два типа сетевых диаграмм — сетевая модель типа «вершина-работа» и «вершина-событие» или «дуги-работы».
Сетевые диаграммы первого типа отображают сетевую модель в графическом виде как множество вершин, соответствующих работам, связанных линиями, представляющими взаимосвязи между работами. Так же этот тип диаграмм называют диаграммой предшествования-следования. Он является наиболее распространенным представлением сети.
Рисунок 1.1- Сетевая модель типа «работа-вершина».
Другой тип сетевой диаграммы — сеть типа «вершина-событие», на практике используется реже. При данном подходе работа представляется в виде линии между двумя событиями (узлами графа), которые, в свою очередь, отображают начало и конец данной работы. PERT-диаграммы являются примерами этого типа диаграмм.
Рисунок 2.1- Сетевая модель типа «работа-дуга».
Можно выделить следующие методы сетевого планирования:
- Детерминированные сетевые методы;
- Диаграмма Ганта;
- Метод критического пути (МКП);
- Вероятностные сетевые методы;
- Неальтернативные;
- Метод имитационного моделирования (метод Монте-Карло);
- Метод оценки и пересмотра планов (ПЕРТ, PERT);
- Альтернативные;
- Метод графической оценки и анализа (GERT).
1.2 Основные понятия сетевого планирования
Следует выделить следующие понятия, необходимые для сетевого планирования.
Работа — производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.
По своей физической природе работы можно рассматривать как действие (например, заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка), процесс (пример — старение отливок, выдерживание вина, травление плат) и ожидание (процесс, требующий только затраты времени и не потребляющий никаких ресурсов; является технологическим (твердение цементной стяжки) или организационным (ожидание сухой погоды) перерывом между работами, непосредственно выполняемым друг за другом.
По количеству затрачиваемого времени работа, может быть:
- действительной, то есть протяжённым во времени процессом, требующим затрат ресурсов;
- фиктивной (или зависимостью), не требующей затрат времени и представляющей связь между какими-либо работами: передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению.
Событие — это факт окончания одной или нескольких работ, необходимых и достаточных для начала следующих работ. События устанавливают технологическую и организационную последовательность работ. События ограничивают рассматриваемую работу и по отношению к ней могут быть начальными и конечными.
Начальное событие определяет начало работы и является конечным для предшествующих работ. Исходным считается событие, которое не имеет предшествующих работ в рамках рассматриваемого сетевого графика. Завершающее — событие, которое не имеет последующих работ в рамках рассматриваемого сетевого графика. Граничное событие — событие, являющееся общим для двух или нескольких первичных или частных сетей.
Путь — это любая последовательность работ в сети, в которой конечное событие каждой работы этой последовательности совпадает с начальным событием следующей за ней работы. Путь от исходного до завершающего события называется полным. Путь от исходного до данного промежуточного события называется путем, предшествующим этому событию. Путь, соединяющий какие-либо два события, из которых ни одно не является исходным или завершающим, называется путем между этими событиями.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим.
Для сетевой модели типа «работы-вершины» используются такие обозначения, как веха — некое ключевое событие, обозначающее окончание одного этапа и начало другого; дуга — связь между работами.
Различают различные типы связей в сетевой модели:
- — начальные работы;
- — конечные работы;
- — последовательные работы;
- — работы (операции) дробления;
- — работы (операции) слияния;
- — параллельные работы.
1.3 Правила построения сетевых моделей
Процесс разработки сетевой модели включает в себя определение списка работ проекта; оценку параметров работ; определение зависимостей между работами.
При построении сетевого графика необходимо соблюдать ряд правил:
1) Правило последовательности изображения работ: сетевые модели следует строить от начала к окончанию, т.е. слева направо.
2) Правило изображения стрелок. В сетевом графике стрелки, обозначающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны идти слева направо, не отклоняясь влево от оси ординат, и всегда направляться от предшествующего события к последующему, т.е. от события с меньшим порядковым номером к событию с большим порядковым номером.[16,с.281]
3) Правило пересечения стрелок. При построении сетевого графика следует избегать пересечения стрелок: чем меньше пересечений, тем нагляднее график.
4) Правило обозначения работ. В сетевом графике между обозначениями двух смежных событий может проходить только одна стрелка. Для правильного изображения работ можно ввести дополнительное событие и зависимость.
5) В сетевой модели не должно быть «тупиковых» событий, то есть событий, из которых не выходит ни одна работа, за исключением завершающего события. Здесь либо работа не нужна и её необходимо аннулировать, либо не замечена необходимость определённой работы, следующей за событием для свершения какого-либо последующего события.
6) Правило расчленения и запараллеливания работ. При построении сетевого графика можно начинать последующую работу, не ожидая полного завершения предшествующей. В этом случае нужно «расчленить» предшествующую работу на две, введя дополнительное событие в том месте предшествующей работы, где может начаться новая.
7) Правило запрещения замкнутых контуров (циклов, петель). В сетевой модели недопустимо строить замкнутые контуры — пути, соединяющие некоторые события с ними же самими, т.е. недопустимо, чтобы один и тот же путь возвращался в то же событие, из которого он вышел.
8) Правило запрещения тупиков. В сетевом графике не должно быть тупиков, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события (в многоцелевых графиках завершающих событий несколько, но это особый случай).
9) Правило запрещения хвостовых событий. В сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одна работа, за исключением начального события.
Источник: www.turboreferat.ru
Аленичева Е.В. и др. Метод сетевого планирования в строительстве
графическим и аналитическим спос обам и . И ссл едуют ся особ енн ости пост роени я сетев ог о графика в ма сшта бе времен и .
Прои зв одит ся опти ми заци я се те вых гра фик ов п о кр ите рию опти ма льн ого распре дел ени я т руд овых ре сурс ов . Мат ери алы
мет оди чески х указан ий могут быть испол ьзо ван ы в кур совом и дипл омн ом проек тиров ани и студен тов всех специа льн ос тей по
Лабораторные работы выполняются индивидуально на основании задан ия ( табл . П 1) . Вар иант задания опре деляется
Отчёт по лабор аторным работам о формляется на лист ах писчей бумаг и форм ата А 4 ( 2 10 × 2 97 мм ) на одн ой сторо не
лист а и должен содер жать назван ие работы , её цель и порядок вы полнения , необходимые расчёты и построен ия , выво д по
Цель ра боты : познаком иться с о сновными понятиями и определени ями сетево го мо делирования , изучи ть основны е
правила построе ния сетевых моделей , осво ить техник у постро ения сетевых моделе й на кон кретном пример е .
системного подхода для о тображен ия и алгор итмизаци и комплексо в взаимо связанных ра бот , дейс твий или мероприят ий для
Метод к ритическо го пути C PM (Critikal P ath Method ), разработанный под руководством Д . Кел ли и М . Уолкера с
участием математика Д . Ма лькольма , был о пробова н в 19 57 г . амер иканской ком панией » Дюпон де Нем ур » на строительс тве
завода химического во локна в г . Луисвилл , штат Кент укки . З атем в течение 1 957–1 958 гг . для р еализации В оенно — мо рским
ведомством США програм мы » Поларис » бы ла разработана и р еализована с истема сетевого планирования P ERT (Program
Evolution a nd Review T echni gue). Позд нее м етоды сетево го пла нирования и управления стали приме няться по в сему миру . В
• многоцелевые ( стр оительств о комплекса о бъектов с выд елением п усковых комп лексов и оче редей ).
• в ер оя т н ос т ны е ( п р ед у с ма т ри в аю т у ч ёт н е оп ре д ел ё нн о с т ей и рис к о в ).
На сетевых моделях схематическ и отображается по следователь ность выполнени я строительных процесс ов и их
– произво дственный процесс . На сетевы х м оделя х изображае тся сплош ной стрел кой с надписью на д ней
названия работы , а под ней – продолжительно сти выполнения рабо ты . Иногда указывается дополнительна я информ ация –
номером события вн утри . Номера начального и з авершающего событий работы , записанные через тире , явл яются шифром
( кодом ) данной ра боты . Все работы , входящие в данн ое событие , назы ваются предшествующ ими р аботам и , выходящие –
процессами , не требует затрат ресурсов , продолжительно сть фиктивной работы равна нулю . На сетев ом графике
– непр ерывная пос ледовательнос ть работ от исходного до з авершающего события се тевого гр афика . П уть ,
изображается двой ной ли нией . Критическ ие рабо ты определяю т общ ую про должитель ность с троительства ил и вы полнения
работ , поэтом у в процессе управле ния ходо м строительно го производс тва им уделяется максим альное внима ние , так ка к эти
Сетевая модель должна о тражать организац ионно — техно логическую пос ледовательно сть возведения зданий и
удовлетворять требованиям технологи и строите льного пр оизводства . При е ё построени и руководств уются следующ ими

• все стр елки м одели должны быть направле ны в о дну с торону развития ра бот о т ис ходного событ ия к
• сетевая модель должна име ть прос той и удоб ный для чтения в ид , след ует по воз можности избега ть пересе чения
• все события н умеруют , при этом каждое событие име ет номер больший , че м предше ствующее ем у событие ;
• при о бозначе нии двух или бо лее параллельно выполняе мых работ необходимо введение дополните льных собы тий и
зависимостей , так как в про тивном сл учае разные стро ительные процессы б удут име ть одинаковые ш ифры ( с м . рис . 1);
• на сетевом гра фике не долж но быть » тупиков «, » хвостов » и » замкнутых конт уров » ( см . рис . 2) .
Если для начала работы необходимо лишь частичное в ыполнение предшествующей работы , то она р азделяется на
соответствующ ие части со своими событ иями их завер шения , т . е . фактическ и разбивается на несколько работ .
Если на объ екте орган изу ет ся п оточ ный проц есс прои зво дс тва раб от , т о на сетев ой модел и он отр ажает ся в соо твет стви и с
при нят ой разби вк ой фронта рабо т на захватки ( ярус ы ). При этом на каж дой горизон тал ьной линии модел и могут опис ыват ься
либ о все ст роит ель ные п роцесс ы , происх одя щие на одной зах ватк е (» г ори зонт ал ь – з ахва тка «), ли бо отд ельн ый тех нол оги чес кий
про цес с , вып олн яе мый н а всех зах ватк ах данног о об ъект а (» гори зонт ал ь – пр оцес с «). Если сет ева я мод ель разра бат ывае тся по
сх еме » гориз онт аль – захв ат ка «, он а разв ива етс я преи муще ств енн о в гори зонта л ьном нап равл ен ии , что удобно с поз иц ии
гра фи ческ ой комп он овки черт еж а . Для многоэтажных зданий , п редусмат ривающих деление фронта р абот на
Если при р азработке сетевых м оделей предусматри ваются три или более за хваток ( я русов ), во зникает про блема ложны х
Как в идно из рис . 3, топология данной сетевой м одели является о шибочной , так как , например , работа по уст ройств у
фундаментов на III захват ке ( работ а 5–7) техно ло гич ески не зависит от монта жа карка са на I зах ватк е ( р абота 3–4) с учётом
того , что для производства монтажных работ нулевого цикла и надземной части использ уются р азные грузоподъёмные
механизмы . Аналогичная с итуация наблюдае тся и для р аботы 7 –8, ко торая техно логически зав исит л ишь от на личия фрон та
работ по захва тке ( дол жна быть за кончена ра бота 5– 7) и от загр уженности брига ды мо нтажников ( необходим о завершение
работы 5–6). Между тем на модели прослеживается завис имость начала р аботы 7–8 от окончани я р аботы 4–6 ( кровельные
Источник: www.studmed.ru
Сетевое планирование и управление
Сетевое планирование — это метод планирования работ, операции в которых, как правило, не повторяются (например, разработка новых продуктов, строительство зданий, ремонт оборудования, проектирование новых работ).
Для проведения сетевого планирования вначале необходимо расчленить проект на ряд отдельных работ и составить логическую схему (сетевой граф).
Работа — это любые действия, трудовые процессы, сопровождающиеся затратами ресурсов или времени и приводящие к определенным результатам. На сетевых графах работы обозначаются стрелками. Для указания того, что одна работа не может выполняться раньше другой, вводят фиктивные работы, которые изображаются пунктирными стрелками. Продолжительность фиктивной работы принимается равной нулю.
Событие — это факт окончания всех входящих в него работ. Считается, что оно происходит мгновенно. На сетевом графе события изображаются в виде вершин графа. Ни одна выходящая из данного события работа не может начаться до окончания всех работ, входящих в это событие.
С исходного события (которое не имеет предшествующих работ) начинается выполнение проекта. Завершающим событием (которое не имеет последующих работ) заканчивается выполнение проекта.
После построения сетевого графа необходимо оценить продолжительность выполнения каждой работы и выделить работы, которые определяют завершение проекта в целом. Нужно оценить потребность каждой работы в ресурсах и пересмотреть план с учетом обеспечения ресурсами.
Часто сетевой граф называют сетевым графиком.
Правила построения сетевых графиков.
1. Завершающее событие лишь одно.
2. Исходное событие лишь одно.
3. Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Если два события связаны более чем одной работой, рекомендуется ввести дополнительное событие и фиктивную работу:
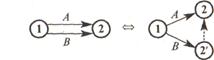
4. В сети не должно быть замкнутых циклов.
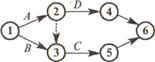
5. Если для выполнения одной из работ необходимо получить результаты всех работ, входящих в предшествующее для нее событие, а для другой работы достаточно получить результат нескольких из этих работ, то нужно ввести дополнительное событие, отражающее результаты только этих последних работ, и фиктивную работу, связывающую новое событие с прежним.
Например, для начала работы D достаточно окончания работы А. Для начала же работы С нужно окончание работ А и В.
Метод критического пути
Метод критического пути используется для управления проектами с фиксированным временем выполнения работ.
Он позволяет ответить на следующие вопросы:
1. Сколько времени потребуется на выполнение всего проекта?
2. В какое время должны начинаться и заканчиваться отдельные
работы?
3. Какие работы являются критическими и должны быть выполнены в точно определенное графиком время, чтобы не сорвать установленные сроки выполнения проекта в целом?
4. На какое время можно отложить выполнение некритических работ, чтобы они не повлияли на сроки выполнения проекта?
Самый продолжительный путь сетевого графика от исходного события к завершающему называется критическим. Все события и работы критического пути также называются критическими. Продолжительность критического пути и определяет срок выполнения проекта. Критических путей на сетевом графике может быть несколько.
Рассмотрим основные временные параметры сетевых графиков.
Обозначим t (i, j) – продолжительность работы с начальным событием i и конечным событием j.
Ранний срок tр (j) свершения события j – это самый ранний момент, к которому завершаются все работы, предшествующие этому событию. Правило вычисления:
где максимум берется по всем событиям i, непосредственно предшествующим событию j (соединены стрелками).
Поздний срок tn (i) свершения события i – это такой предельный момент, после которого остается ровно столько времени, сколько необходимо для выполнения всех работ, следующих за этим событием.
Правило вычисления:
где минимум берется по всем событиям j, непосредственно следующим за событием i.
Резерв R(i) события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:
Критические события резервов не имеют.
При расчетах сетевого графика каждый круг, изображающий событие, делим диаметрами на 4 сектора:
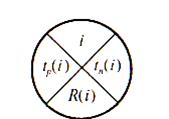
Управление проектами с неопределенным временем выполнения работ
В методе критического пути предполагалось, что время выполнения работ нам известно. На практике же эти сроки обычно не определены. Можно строить некоторые предположения о времени выполнения каждой работы, но нельзя предусмотреть все возможные трудности или задержки выполнения. Для управления проектами с неопределенным временем выполнения работ наиболее широкое применение получил метод оценки и пересмотра проектов, рассчитанный на использование вероятностных оценок времени выполнения работ, предусматриваемых проектом.
Для каждой работы вводят три оценки:
— оптимистическое время а – наименьшее возможное время выполнения работы;
— пессимистическое время b – наибольшее возможное время выполнения работы;
— наиболее вероятное время т – ожидаемое время выполнения работы в нормальных условиях.
По а, b и т находят ожидаемое время выполнения работы:
и дисперсию ожидаемой продолжительности t:
Используя значения t, находят критический путь сетевого графика.
Оптимизация сетевого графика
Стоимость выполнения каждой работы плюс дополнительные расходы определяют стоимость проекта. С помощью дополнительных ресурсов можно добиться сокращения времени выполнения критических работ. Тогда стоимость этих работ возрастет, но общее время выполнения проекта уменьшится, что может привести к снижению общей стоимости проекта. Предполагается, что работы можно выполнить либо в стандартные, либо в минимальные сроки, но не в промежутке между ними.
График Ганта
Иногда бывает полезным изобразить наглядно имеющийся в наличии резерв времени. Для этого используется график Ганта. На нем каждая работа (i, j) изображается горизонтальным отрезком, длина которого в соответствующем масштабе равна времени ее выполнения. Начало каждой работы совпадает с ранним сроком свершения ее начального события.
График Ганта очень полезен при составлении расписания работ. Он показывает рабочее время, время простоев и относительную загрузку системы. Ожидающие выполнения работы могут быть распределены по другим рабочим центрам.
График Ганта используется для управления работами в процессе. Он указывает, какая работа выполняется по расписанию, а какая опережает его или отстает. Существует много возможностей использования графика Ганта на практике.
Стоит заметить, что график Ганта не учитывает разнообразия производственных ситуаций (например, поломки или человеческие ошибки, которые требуют повторения работы). График Ганта должен регулярно пересчитываться при появлении новых работ и при пересмотре продолжительности работ.
График Ганта особенно полезен при работе над проектом с не связанными между собой работами. А вот при анализе проекта с тесно взаимосвязанными работами лучше воспользоваться методом критического пути.
Распределение ресурсов, графики ресурсов
До сих пор мы не обращали внимания на ограничения в ресурсах и считали, что все необходимые ресурсы (сырье, оборудование, рабочая сила, денежные средства, производственные площади и т. д.) имеются в достаточном количестве. Рассмотрим один из простейших методов решения проблемы распределения ресурсов – «метод проб и ошибок».
Пример. Произведем оптимизацию сетевого графика по ресурсам. Наличный ресурс равен 10 единицам.
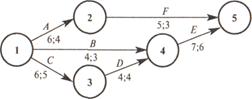
Первое число, приписанное дуге графика, означает время выполнения работы, а второе – требуемое количество ресурса для выполнения работы. Работы не допускают перерыва в их выполнении.

Находим критический путь. Строим график Ганта. В скобках для каждой работы укажем требуемое количество ресурса. По графику Ганта строим график ресурса. На оси абсцисс мы откладываем время, а на оси ординат – потребности в ресурсах.
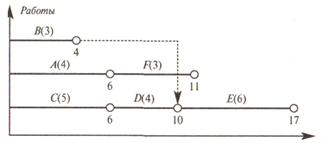
Считаем, что все работы начинаются в наиболее ранний срок их выполнения. Ресурсы складываются по всем работам, выполняемым одновременно. Также проведем ограничительную линию по ресурсу (в нашем примере это у = 10).

Из графика мы видим, что на отрезке от 0 до 4, когда одновременно выполняются работы В, А, С, суммарная потребность в ресурсах составляет 3 + 4 + 5 = 12, что превышает ограничение 10. Так как работа С критическая, то мы должны сдвинуть сроки выполнения или А, или В.
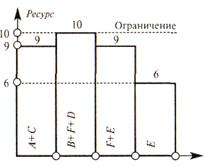
Запланируем выполнение работы В с 6-го по 10-й день. На сроках выполнения всего проекта это не скажется и даст возможность остаться в рамках ресурсных ограничений.
Параметры работ
Напомним обозначения: t (i, j) – продолжительность работы (i, j); tр (i) – ранний срок свершения события i; tn (i) – поздний срок свершения события /.
Если в сетевом графике лишь один критический путь, то его легко отыскать по критическим событиям (событиям с нулевыми резервами времени). Ситуация усложняется, если критических путей несколько. Ведь через критические события могут проходить как критические, так и некритические пути. В этом случае нужно использовать критические работы.
Ранний срок начала работы (i, j) совпадает с ранним сроком свершения события i: tpн (i, j) = tр (i).
Поздний срок начала работы (i, j) равен разности tn (j) (позднего срока свершения события j) и t (i, j): tпн (i, j) = tп (j) — t (i, j).
Полный резерв времени Rn(i, j) работы (i, j) – это максимальный запас времени, на которое можно задержать начало работы или увеличить ее продолжительность, при условии, что весь комплекс работ будет завершен в критический срок:
Свободный резерв времени Rс(i, j) работы (i, j) – это максимальный запас времени, на которое можно отсрочить или (если она началась в свой ранний срок) увеличить ее продолжительность при условии, что не нарушатся ранние сроки всех последующих работ: Rс(i, j)= tр (j) – tр (i) – t (i, j)= tр (j) – tpо (i, j).
Критические работы, как и критические события, резервов не имеют.
Пример. Посмотрим, каковы резервы работ для сетевого графика.

Находим tр (i), tn (i) и составляем таблицу. Значения первых пяти колонок берем из сетевого графика, а остальные колонки просчитаем по этим данным.
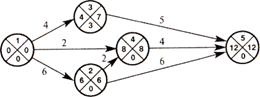
| Работа (i, j) | Продолжительность t (i, j) | tр (i) | tр (j) | tn (j) | Срок начала работы |
| tpн (i, j) = tр (i) | tпн (i, j) = tп (j) — t (i, j) | ||||
| (1,2) | 6-6 = 0 | ||||
| (1,3) | 7-4 = 3 | ||||
| (1,4) | 8-2 = 6 | ||||
| (2,4) | 8-2 = 6 | ||||
| (2,5) | 12-6 = 6 | ||||
| (3,5) | 12-5 = 7 | ||||
| (4,5) | 12-4 = 8 |
| Работа (i, j) | Срок окончания работы | Резервы времени работы | |
| tpо (i, j) = tр (i)+ t (i, j) | tпо (i, j) = tп (j) | Полный Rn(i, j)= = tпо (i, j) – tpо (i, j) | Свободный Rс(i, j)= = tр (j) – tpо (i, j) |
| (1,2) | 0 + 6 = 6 | 6-6 = 0 | 6-6 = 0 |
| (1,3) | 0 + 4 = 4 | 7-4 = 3 | 4-4 = 0 |
| (1,4) | 0 + 2 = 2 | 8-2 = 6 | 8-2 = 6 |
| (2,4) | 6 + 2 = 8 | 8-8 = 0 | 8-8 = 0 |
| (2,5) | 6 + 6= 12 | 12-12 = 0 | 12-12 = 0 |
| (3,5) | 4 + 5 = 9 | 12-9 = 3 | 12-9 = 3 |
| (4,5) | 8 + 4=12 | 12-12 = 0 | 12-12 = 0 |
Критические работы (работы с нулевыми резервами): (1, 2), (2,4), (2, 5), (4, 5). У нас два критических пути: 1 — 2 — 5 и 1 — 2 — 4 — 5.
Методы сетевого планирования и управления позволяют сосредоточиться на важнейших для выполнения проекта моментах. При этом требуется, чтобы работы были взаимно независимы, то есть в пределах определенной последовательности работ можно начинать, приостанавливать, исключать работы, а также выполнять одну работу независимо от другой работы. Все работы должны выполняться в определенной последовательности. Поэтому методы сетевого планирования и управления широко применяются в строительстве, самолетостроении и судостроении, а также в промышленных отраслях с быстро меняющимися тенденциями.
Скептическое отношение к методам сетевого планирования и управления часто основывается на их стоимости, которая может составлять около 5% общей стоимости проекта. Но эти расходы обычно полностью компенсируются экономией, достигаемой с помощью более точного и гибкого графика, а также сокращения сроков выполнения проекта.
Источник: studopedia.ru