Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения производных
Производная функции есть предел отношения приращения этой функции к приращению её аргумента при стремлении последнего к нулю, при условии существования данного предела.
Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.
Процесс нахождения производный называется дифференцированием.
– производная суммы (разницы).
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Примеры решений производных
Задача
Найти производную функции
Решение
Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:
Урок 323. Применение производной в задачах физики — 1
Ответ
Задание
Найти производную функции
Решение
Обозначим , где . Тогда, согласно правила вычисления производной сложной функции, получим:
Ответ
Задача
Найти производную функции при .
Решение
Ответ
Задача
Найти производную функции .
Решение
.
После приведения подобных членов получаем:
.
Ответ
Задача
Найти производную функции .
Решение
В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.
Ответ
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Применяя правила дифференцирования котангенса, получаем:
.
Учитывая, что и , после упрощения получим:
.
Ответ
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Ответ
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Ответ
Задача
Найти производную функции .
Решение
Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты:
.
Ответ
Задача
Найти производную функции .
Решение
По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.
Ответ
Средняя оценка 2.4 / 5. Количество оценок: 92
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Простое объяснение принципов решения частных производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Простое объяснение принципов решения сложных производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Простое объяснение принципов решения производных тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Простое объяснение принципов решения свойств производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Простое объяснение принципов решения частного дифференциала и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Анастасия на Как проанализировать и описать результаты практического исследования Добрый день! Я кандидат филологических наук, доцент. Специальность лингвистика. Если Вы студент или аспирант, и вам нужен отзыв или рецензия
Марина на Специалитет и бакалавриат – в чем разница, что выбрать, что лучше? Поступил на бакалавриат ( направление информационные технологии), можно ли работать потом преподавателем информатики, например в школе, если поступить потом на
Юлия на Специалитет и бакалавриат – в чем разница, что выбрать, что лучше? Добрый день, сын хочет поступать на специальность «Правовое обеспечение национальной безопасности» государственно-правовой профиль. Можно ли с таким образование работать за
Бахтиёр Махмудов на Примеры решения интегралов с ответами по определению , если икс в числителе в степени с минусом, то в числителе будет единица, а в знаменателе тот
Источник: nauchniestati.ru
Производная. Нестандартные прикладные задачи
1. ПРОИЗВОДНАЯ. НЕСТАНДАРТНЫЕ ПРИКЛАДНЫЕ ЗАДАЧИ.
Каждый
человек
время
от
времени
оказывается в ситуации, когда надо отыскать
наилучший способ решения какой-либо задачи,
и математика становится средством решения
проблем организации производства, поисков
оптимальных решений. Важным условием
повышения эффективности производства и
жизнедеятельности, улучшения качества жизни
является широкое внедрение математических
методов в технику и практику.
Российский математик 19
века Панфутий Львович
Чебышев
говорил,
что
«особенную важность имеют
те методы науки, которые
позволяют решать задачу,
общую
для
всей
практической деятельности
человека, например, как
располагать
своими
средствами для достижения
наибольшей выгоды».
Это задачи математического
анализа.
4. Одним из важнейших понятий математического анализа является производная функции.
ОДНИМ ИЗ ВАЖНЕЙШИХ ПОНЯТИЙ
МАТЕМАТИЧЕСКОГО АНАЛИЗА ЯВЛЯЕТСЯ
ПРОИЗВОДНАЯ ФУНКЦИИ.
Именно
с
помощью
дифференциального
счисления
эффективно
решаются
многие
практические задачи.
Производная характеризует
скорость
изменения
функции по отношению к
изменению
независимой
переменной.
Честь
открытия
основных
законов
математического
анализа
принадлежит
английскому физику и математику Исааку
Ньютону и немецкому математику, физику,
философу Лейбницу. Термин производная и
современные обозначения y’ , f ‘ ввёл
Ж.Лагранж в 1797г.
6. Объект исследования:
ОБЪЕКТ ИССЛЕДОВАНИЯ:
производная функции как модель, определяющая способы
и методы нахождения оптимального значения функции,
описывающей реальный процесс.
Ведущая цель — показать значимость производной не
только в математике, но и в других науках, её важность в
современной жизни и практической деятельности.
Методы исследования:
— сбор фактов (изучение литературы)
— качественный анализ, синтез, сравнение, обобщение
полученной информации.
— самостоятельное решение практических задач методами
дифференциального счисления, анализ и сравнение
результатов с реальной действительностью.
7. Задачи:
ЗАДАЧИ:
1) рассмотреть применение производной в
практической деятельности;
2) подбор задач на экстремум из различных
областей науки, техники и практики;
3) показать применение производной к
решению конкретных практических задач а
также продемонстрировать широкий спектр
возможностей её применения.
8. Дифференциальное исчисление
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
– это описание окружающего нас мира,
выполненное на математическом языке.
Производная помогает нам успешно решать не
только математические задачи, но и задачи
практического характера в разных областях
науки и техники
9. Произво́дная функции
ПРОИЗВО́ДНАЯ ФУНКЦИИ
—
понятие
дифференциального
исчисления,
характеризующее скорость изменения функции в
данной
точке.
Определяется
как предел отношения приращения функции к
приращению её аргумента при стремлении
приращения аргумента к нулю, если такой предел
существует.
Функцию,
имеющую
конечную
производную (в некоторой точке), называют
дифференцируемой (в данной точке).
Производная функции используется всюду, где
есть неравномерное протекание процесса: это
и неравномерное механическое движение, и
переменный ток, и химические реакции и
радиоактивный распад вещества и т.д.
Среди многих задач, решаемых с помощью
производной, наиболее важной является
задача нахождения экстремума функции и
связанная
с
ней
задача
нахождения
наибольшего
(наименьшего)
значения
соответствующих функций.
11. В геометрии
В ГЕОМЕТРИИ
производная позволяет решить огромный
класс задач, в которых требуется найти
наибольшее или наименьшее значение
функции.
В
качестве
функции
могут
рассматриваться периметр или площадь
фигуры или, например,
объем тела, а аргументом
функции служит какой-либо
параметр фигуры или тела −
длина стороны, угол между
сторонами и т.п.
12. В механике
В МЕХАНИКЕ
с помощью
производной
определяется скорость
неравномерного
прямолинейного
движения
v = S ΄(t),
и ускорение
как производная
скорости
a = v ΄(t),
13. В электротехнике
В ЭЛЕКТРОТЕХНИКЕ
Количественной характеристикой
электрического тока является сила тока.
В цепи электрического тока электрический
заряд меняется с течением времени по
закону q=q (t). Сила тока есть производная
заряда q по времени.
I=q´(t)
В электротехнике в основном используется А работа
переменного тока.
Получение переменного электрического тока основано
на законе электромагнитной индукции, формулировка
которого содержит производную магнитного потока.
Согласно закону электромагнитной индукции Фарадея :
ЭДС индукции в контуре, находящемся в переменном
магнитном поле, равна по величине и противоположна
по знаку скорости изменения магнитного потока через
поверхность, которую ограничивает данный контур:
Еинд=Ф´(t)
15. В химии
В ХИМИИ
Производную в химии используют для определения
скорости химической реакции, одного из
решающих факторов, который нужно учитывать во
многих
областях
научно-производственной
деятельности.
Если Q(t) – закон изменения количества
вещества, вступившего в химическую реакцию, то
скорость v(t) химической реакции в момент
времени t равна производной:
v(t)=Q`(t).
16. В биологии
В БИОЛОГИИ
Производная определяет скорость изменения
популяции (это совокупность особей данного вида,
занимающих определённый участок территории
внутри ареала вида, свободно скрещивающихся
между собой и частично или полностью
изолированных от других популяций).
Р = х´ (t) где, х(t) -численность в момент времени
t, Р(t) – скорость изменения популяции,
Р(t0) – относительный прирост
в данный момент.
17. В географии
В ГЕОГРАФИИ
Производная помогает рассчитать:
1. Некоторые значения в сейсмографии
2. Особенности электромагнитного поля земли
3. Радиоактивность ядерно-геоифзичексих
показателей
4. Многие значения в экономической географии
5. Вывести формулу для
вычисления численности
населения на территории
в момент времени t.
у’= к у
18. В экономике
В ЭКОНОМИКЕ
Дифференциальное исчисление – аппарат для экономического анализа.
Базовая задача экономического анализа – изучение связей экономических
величин в виде функций. Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении
налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличение цены на её
продукцию?
3. Отзывчивость производственной функции (выход продукта на единицу
затрат)
4. Скорость и темпы изменения различных экономических показателей.
Также с помощью экстремума функции
(производной) в экономике можно
найти наивысшую производительность
труда, максимальную прибыль,
максимальный выпуск и минимальные
издержки.
19. В СтроительствЕ
В СТРОИТЕЛЬСТВЕ
производная определяет
1)В строительстве мостов –
зависимость нагрузочного момента в
расчетной точке от расстояния до
ближайшей опоры моста, что является
залогом прочности и безопасности моста.
2) в архитектуре, строительстве и эксплуатации
зданий — распределение нагрузки для
устойчивости конструкции и оптимальное
использование строительных материалов.
20. Железнодорожный транспорт
ЖЕЛЕЗНОДОРОЖНЫЙ ТРАНСПОРТ
с помощью производной определяется
интенсивность нагрузки железнодорожного
пути от длины поезда и его загрузки.
21. Практическая часть
ПРАКТИЧЕСКАЯ ЧАСТЬ
Решение практических задач
методами дифференциального
счисления, анализ и сравнение
результатов с реальной
действительностью.
22. Строительство
СТРОИТЕЛЬСТВО
1. По одну сторону стены высотой 30 м по
горизонтальной площадке ездит кран. По другую
сторону стены на расстоянии 10 м от неё лежит
груз. Башня крана имеет высоту 20 м, а его
стрела, прикрепленная к верхней точке башни,
может быть расположена под любым углом к
горизонту. При какой наименьшей длине
стрелы кран может поднять груз через стену?
(длина троса не ограничена)
23. Решение: Очевидно, что необходимая длина стрелы зависит от расстояния между краном и стеной. Это показывает опыт:
РЕШЕНИЕ:
ОЧЕВИДНО, ЧТО НЕОБХОДИМАЯ ДЛИНА
СТРЕЛЫ ЗАВИСИТ ОТ РАССТОЯНИЯ МЕЖДУ
КРАНОМ И СТЕНОЙ. ЭТО ПОКАЗЫВАЕТ ОПЫТ:
24. Построим математическую модель задачи
ПОСТРОИМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ
ЗАДАЧИ
Пусть х м – расстояние от тележки крана до
стены,
10
f ( x) x 10 (1 )
Рассмотрим функцию
x
на промежутке 0; на наименьшее
значение.
2
2x
2
10
10
2
f ‘ ( x)
(1 ) x 100 ( 2 )
2
x
x
2 x 100
f ‘ ( x) 0 , если
x 3 1000
x2
x 2 100
0;
х=10 – стационарная точка функции.
Производная меняет знак с «минуса» на «плюс» в
точке х=10
Значит, х=10 — точка минимума
10
10 10 (1 ) 200 2 10 2 28,3
10
2
2
Ответ: 28,3 м
26. водоснабжение
ВОДОСНАБЖЕНИЕ
2. По трубе, сечение которой круг с радиусом R,
течет вода. При каком заполнении трубы водой
скорость течения (при неизменных других
условиях) будет наибольшей?
27. решение
РЕШЕНИЕ
Расчетным путём доказано, что скорость течения
пропорциональна так называемому гидравлическому радиусу
профиля сечения (заполненного водой).
28. Построим математическую модель задачи
ПОСТРОИМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ
ЗАДАЧИ
Гидравлическим радиусом профиля называется
отношение площади живого сечения к длине
смоченного (подводного) периметра профиля.
31. Архитектура
АРХИТЕКТУРА
3.
Архитектурное
бюро
проектирует
строительство
культурно-развлекательного
центра в виде конуса. Нижний ярус должен
иметь форму цилиндрического зала, а верхний форму правильной четырехугольной призмы.
Остальное – подсобные помещения. При какой
высоте цилиндрической части объем второго
яруса будет наибольшим?
Найти этот объем яруса в
форме призмы, если высота
всего комплекса – H,
радиус цилиндрического
яруса – R.
32. решение
РЕШЕНИЕ
Для устойчивости конструкции отношение
длины диагонали основания призмы к ее
высоте должно быть равно отношению длины
диаметра цилиндра к его высоте.
33. Построим математическую модель задачи
ПОСТРОИМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ
ЗАДАЧИ
Пусть высота цилиндрического яруса равна x.
Рассмотрим осевое сечение конуса – треугольник
SAT, содержащее диагональное сечение призмы –
прямоугольник MCLF.
35. Использование рек. Сплав леса.
ИСПОЛЬЗОВАНИЕ РЕК. СПЛАВ ЛЕСА.
4. Два канала шириной a и b соединяются
друг с другом под прямым углом.
Определить наибольшую длину бревен,
которые можно сплавлять по данной
системе каналов.
36. Решение:
37. Построим математическую модель задачи
ПОСТРОИМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ
ЗАДАЧИ
Пусть положение бревна описывается
углом α, как показано на
рисунке. Максимально возможная длина
бревна L зависит от угла α:
Источник: en.ppt-online.org
Решение прикладных задач с помощью производной функции
«Что значит владение математикой? Это есть умение решать задачи.
Причем не только стандартные, но и требующие известной независимости
мышления, здравого смысла, оригинальности, изобретательности».
Д. Пойа
Цели урока:
- Дидактические: рассмотреть применение метода поиска наибольших и наименьших значений функции к решению разнообразных прикладных задач, в первую очередь, задач на оптимизацию.
- Развивающие цели: развивать гибкость мышления, творческое отношение к изучаемому предмету, формировать независимость математического мышления в ходе решения задач.
- Воспитательные цели: на примере решения прикладных задач с простейшими жизненными ситуациями показать применение методов математического моделирования, поддержать этим интерес к предмету.
Вид занятия. Применение знаний, умений и навыков.
Оборудование. Интерактивная доска, карточки.
Методы – объяснительно-иллюстративное изложение, иллюстративный и демонстрационный.
План урока.
- Нахождение наибольшего и наименьшего значений функции на промежутке.
- Решение задач на нахождение наибольшего и наименьшего значений
Введение.
Современные требования к уроку предполагают использование новых подходов в преподавании математики. При подготовке к уроку преподаватель все чаще использует компьютерные технологии. Уроки с использованием презентаций становятся более насыщенными, эффективными и дают возможность развивать у студентов интерес к предмету, познавательную активность, творческий подход.
На данном уроке применение интерактивной доски должно наряду с самой темой привлечь внимание студентов к прикладной направленности математики. Одновременно текстовые задачи рассматриваются не только как прикладные, но и как умственные манипуляторы. Существует важное сходство между математикой и детской игрой: в обоих случаях исключительно важно творческое воображение. Потребность в умственных манипуляциях никогда не кончается, она присуща и профессиональным математикам на самом высоком уровне.
Решение любой задачи, особенно сложной, требует от ребят напряженного труда и упорства. А упорство проявляется, если задача интересна. Значит, нужно преподавателю подбирать такие задачи, которые студенты хотели бы решать. Чаще всего интерес вызывают задачи практического содержания.
Еще один метод применен на данном уроке для мотивации решения прикладных задач: в их тексты включаются фамилии студентов той группы, где идет занятие. Они становятся прорабами, предпринимателями, хозяевами предприятий и т.д.
Ход урока
1. Организационное начало
Приветствие студентов. Проверка присутствующих.
Сообщение темы занятия и плана работы, конкретизация задач и создание мотивации учебной деятельности. Прием – повествовательное изложение, форма – рассказ-вступление, Для быстрого включения студентов в работу на экран можно вывести слайд, содержащий информацию о плане урока, его целях и задачах.
2. Повторение опорных знаний студентов.
Провести дидактическую игру «Крестики- нолики» по теме «Производная функции». К доске приглашаются два студента. На доске подготовлено игровое поле. Первый, ответивший на вопрос преподавателя по данной теме, получает право выбрать знак («крестик» или «нолик») для себя и назвать первое окошко игрового поля.
Если он решает правильно выпавшее ему задание, то имеет право поставить в данное окошко свой знак. Если ему это не удается, то право решить его отдается второму игроку. В итоге побеждает тот, кто закрывает своими значками 3 клетки по диагонали, горизонтали, вертикали или больше, чем 4 клетки.
Задания.
3. Применение знаний при решении примеров и задач.
Сегодня на занятии мы вспомним задания на нахождение наибольшего, наименьшего значений функции на промежутке и применение этой темы для решения задач. На прошлом занятии мы записали алгоритм для этого. Повторим его (приглашается для ответа студент, а затем еще раз выводится на экран).
Нахождение наибольшего и наименьшего значений монотонной функции f(x) на отрезке (а;в) достигается на концах отрезка. Если же заданная функция не является монотонной, но известно, что она является непрерывной, то для нахождения наибольшего и наименьшего значений функции на отрезке применяется правило:
- Найти критические точки функции.
- Найти значения функции в критических точках, принадлежащих отрезку, и на концах отрезка. Наибольшее и наименьшее значения из этих чисел и будут соответственно наибольшим и наименьшим значениями функции на отрезке.
Теперь решаем задачи.
Задача 1. Молодой предприниматель Михайлов Юрий в свете экономического кризиса решил выкупить нерентабельное провинциальное перерабатывающее предприятие и пригласил экономиста Гульдерова Германа помочь с расчетами по оптимизации расходов. Одна из задач поставленных перед Германом была следующая: найти, при каких условиях расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет наименьшим.
Вспомним 3 этапа математического моделирования, применяемые при решении задач на оптимизацию (показ на экране):
- 1 этап. Составление математической модели.
- 2 этап. Работа с составленной моделью.
- 3 этап. Ответ на вопрос задачи.
1 этап. Составление математической модели.
Составление модели облегчается тем, что известна форма банки и оговорено, что она должна быть заданной емкости. Это существенно для составления модели. Существенным является также требование, чтобы расход жести на изготовление банки был минимальным. Это требование означает, что площадь полной поверхности банки, имеющей форму цилиндра, должна быть наименьшей; существенны и размеры банки. Несущественны для составления математической модели конкретное (численное) значение емкости банки и вид консервов (мясных, овощных), для которых банка предназначена.
Обозначив емкость банки через V см³, сформулируем задачу: Определить размеры цилиндра с объемом V см³ так, что бы площадь его полной поверхности была наименьшей.
Для решения задачи обозначим радиус основания цилиндра через х, а высоту его через h (все измерения в сантиметрах). Тогда объем цилиндра
Полная поверхность цилиндра:
S = 2x² + 2x h = 2x² + 2x = 2x² + = .
Так как переменная х может принимать только положительные значения, решение задачи сводится к нахождению наименьшего значения S(х) на (0;).
2 этап. Работа с составленной моделью.
Найдем производную S´(х):
Для нахождения критических точек решим уравнение S´(х) = 0.
Корень уравнения: х = .
Следовательно, в точке х = S(х) имеет минимум.
Следовательно, функция в этой точке достигает наименьшего значения.
Таким образом, площадь полной поверхности цилиндра, имеющего объем V, будет наименьшей при h = 2x = 2 = , т.е. когда цилиндр равносторонний.
3 этап. Ответ на вопрос задачи.
Наименьший расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой.
Полезно обратить внимание ребят на то, что в нашей стране выпускаются ежегодно сотни миллионов банок консервов в жестяной упаковке. Экономия 1% жести на изготовление каждой банки позволит за счет сэкономленного материала дополнительно изготовить несколько миллионов новых банок. Вместе с тем промышленность нередко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением минимизации отходов при изготовлении банок, соображениями торговой эстетики. Возможностями транспортировки и т.д.
Задача 2. Фрагмент рассказа Л.Н. Толстого «Много ли человеку земли нужно» о крестьянине Пахоме, покупавшем землю у башкир.
— А цена какая будет? – говорит Пахом.
— Цена у нас одна: 1000 рублей за день.
— Какая же это мера – день? Сколько в ней десятин будет?
— Мы этого, – говорит, — не умеем считать. А мы за день продаем; сколько обойдешь за день , то твое, а цена 1000 рублей.
— Да ведь это, — говорит, — в день обойти земли много будет.
— Вся твоя, — говорит. – Только один уговор: если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги.
Фигура, которая получилась у Пахома, изображена на рисунке( на экране).
Обежал он за день, например, прямоугольную трапецию периметром 40 км. С площадью S = 78 км².
Проверим, наибольшую ли площадь при этом получил бы Пахом (с учетом того, что участки обычно имеют форму прямоугольника)?
Р = 40 км. a – первая сторона, 20 – а – вторая сторона.
S = а (20 — а) = — а² + 20 а.
S´ = — 2а + 20 = 0, а = 10.
Следовательно, наибольший четырехугольник – квадрат, т.е. наибольшая площадь – 100 м².
Можно сделать вывод, что пахом вполне мог получить земли больше с меньшими усилиями.
Задача 3. Гарданов Марсель решил сделать своей маме подарок к 8 Марта и заказал другу юности Сабирову Денису шкатулку из драгоценного металла. В мастерскую он принес кусок листа из этого металла размером 80 Х 50 см. Требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и загибая оставшиеся кромки.
Обозначим через х длину стороны вырезаемого квадрата. Легко видеть, что
Объем при этом у коробки:
V = x (80-х) (50 – 2х) = 4х³ — 260х² + 4000х.
V´ = 12х² — 520х + 4000 = 0,
х = 100:3 = 33, х= 10.
х- посторонний корень по смыслу задачи.
х= 10 – единственное решение – высота, 80 – 20 = 60 – длина, 50 – 20 = 30 – ширина.
V = 10· 60 · 30 = 18000(см³).
Задачи для самостоятельного решения.
4. Требуется огородить прямоугольный участок земли площадью 294 м² и разделить этот земельный участок забором на 2 равные части. При каких линейных размерах участка длина всего забора окажется минимальной? (14 м, 21 м).
Задача 4. Из куска железа в форме прямоугольного треугольника с катетами 2 м и 4м необходимо вырезать прямоугольник наибольшей площади со сторонами, параллельными катетам треугольника.
S = x ( 4 – 2x) = 4x – 2x²,
S´ = 4 – 4x = 0, x =1,
S = 2 · 1 = 2(см²) – наибольшая площадь.
Соответствующие стороны прямоугольника: 1 см, 2 см.
Задача 5. Разрежьте отрезок длиной 18 см на две части так, чтобы приняв их за катеты, получить прямоугольный треугольник с наименьшей гипотенузой.
Задача 6. Окно имеет форму прямоугольника, периметр которого равен 8 м. Каковы должны быть размеры окна, чтобы оно пропускало наибольшее количество света?
Подведение итогов занятия.
Задание на дом.
Студентам предлагается решить дома задачи из задачника и составить по тексту одной из них задачу прикладного характера.
Источник: urok.1sept.ru
Разработка конференции по теме «Производная в народном хозяйстве»

В данной разработке представлен материал, позволяющий закрепить и развить знания учащихся по теме «Производная и ее применнение» в 11 классе.
Просмотр содержимого документа
«Разработка конференции по теме «Производная в народном хозяйстве»»
Муниципальное бюджетное общеобразовательное учреждение
«Отрадненская средняя общеобразовательная школа № 2»
ПРОЕКТНОЕ ЗАДАНИЕ
Внеклассная работа по математике.
Разработка конференции по теме «Производная в народном хозяйстве»
Работа выполнена слушателем годичных курсов
повышения квалификации — учителем математики
Голубовой Викторией Витальевной
Содержание работы
ПРЕДИСЛОВИЕ К ВЫПОЛНЕННОЙ РАБОТЕ 3
ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ 4
КОНФЕРЕНЦИЯ НА ТЕМУ «ПРОИЗВОДНАЯ В НАРОДНОМ ХОЗЯЙСТВЕ» 5
ПЛАН КОНФЕРЕНЦИИ 5
1. Вступительное слово 6
2. Задачи на оптимизацию. 7
3. Применение производной в строительстве. 8
4. Производная и транспорт. 8
5. Производная помогает мелиорации. 9
6. Космос и производная. 10
7. Случай в заповеднике. 12
Рекомендуемая литература 13
ПРЕДИСЛОВИЕ К ВЫПОЛНЕННОЙ РАБОТЕ
Современная педагогика видит три цели математического образования. Первая – общеобразовательная. Без математики невозможно понять ряд других предметов, нельзя продолжить образование в вузе по многим специальностям. Ядро математического знания давно стало общечеловеческой культурной ценностью.
Вторая цель – прикладная. Школьник, как правило, еще не знает, чем он будет заниматься, поэтому у учителя остается одна реальная возможность – научить детей принципам математического моделирования каких-либо реальных процессов.
Третья цель – воспитательная. Математика развивает логическое, пространственное и алгоритмическое мышление; формирует такие качества, как трудолюбие, настойчивость, усидчивость; учит ценить красоту мысли. Но еще важнее другое: математика – это мировоззрение. Человек, владеющий математическим методами исследования, иначе подходит к жизненным проблемам, иначе смотрит на мир.
Прикладная направленность преподавания математики связана со всеми тремя названными целями: с общеобразовательной (легче учить другие предметы), с прикладной ( будущий специалист еще в школе получает необходимые навыки прикладного математического исследования), с воспитательной ( мир един, и именно в содружестве с другими науками математика формирует у ребенка основы научной картины мира)
ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ
Чтобы достичь хороших результатов по математике, необходимо осуществлять хорошо спланированную внеклассную работу по предмету. При этом очень важно, чтобы работа, осуществляемая на уроках, и работа, проводимая во внеурочное время, представляли собой единое целое, были взаимосвязаны, имели логическое продолжение. Умело организованная, систематическая внеклассная работа даёт возможность развивать и углублять профессиональные интересы и склонности учащихся; значительно обогащать их знания о различных областях приложения математики, её роли в производстве; способствует развитию творческих способностей учащихся, усиливает их интерес к математике.
Для осуществления внеклассной работы можно использовать самые разнообразные формы. Со старшеклассниками можно готовить и проводить интересные вечера, конференции, посвящённые различным приложениям математики.
В качестве примера такого мероприятия предлагаю разработку конференции на тему «Производная в народном хозяйстве», которую можно провести при повторении темы «Производная и её применение». Особое внимание при подготовке основных понятий на смотре следует обратить на геометрический и механический смысл производной. В разработке конференции приводятся решения большинства встречающихся в ней задач. Чтобы не утомлять внимание учеников громоздкими выкладками во время конференции, при подготовке к ней можно подготовит презентации, таблицы с чертежами к задачам с обозначениями; функции, появляющиеся в результате решений, данные, полученные в ответах. Выступающие в ходе своих сообщений могут обращаться к этим презентациям и проводить по ним соответствующие объяснения.
КОНФЕРЕНЦИЯ НА ТЕМУ «ПРОИЗВОДНАЯ В НАРОДНОМ ХОЗЯЙСТВЕ»
Цель конференции: закрепить и развить знания учащихся по теме «Производная и её применение», продолжить формирование знаний о мире труда и мире профессий.
Оформление зала:
« Из истории дифференциального исчисления»
« Математика в народном хозяйстве»
Портреты: Исаак Ньютон, Готфрид Вильгельм Лейбниц, Леонид Витальевич Канторович
Алгоритм решения задач на оптимизацию:
Найти критические точки.
Вычислить значение функции в каждой критической точке.
Вычислить значение функции на концах отрезка.
Из полученных чисел выбрать наибольшее ( наименьшее).
Этапы решения прикладных задач:
Построение математической модели.
Решение внутри модели.
Интерпретация полученного результата.
Вступительное слово учителя.
Задачи на оптимизацию.
Применение производной в строительстве.
Производная и транспорт.
Производная помогает мелиорации.
Космос и производная.
Случай в заповеднике.
Ниже приводится некоторый материал к каждому пункту плана конференции, который может быть использован как учителем так и учащимися.
1. Вступительное слово
Сегодня на конференции мы с вами с некоторыми видами трудовой деятельности в которых используется важное понятие математики – производная.
Математика является одной из самых древних наук. Она зародилась на заре человеческой цивилизации пол влиянием потребностей практики. Когда-то была объявлена большая премия за книгу на тему: « Как человек без математике жил ». Премия осталась не выданной. По-видимому. Ни один писатель не сумел изобразить жизнь человека, лишенного всяких математических понятий.
Математические знания в далеком прошлом применялись для решения повседневных задач, и именно практика в значительной степени руководила всем дальнейшим развитием математики.
И в наше время, как и в далёком прошлом, практика выдвигает перед математикой сложные задачи. Именно в этом причина современного бурного развития математики, появление многих её новых областей, позволяющих глубоко изучать явления окружающего нас мира и решать конкретные практические задачи. В настоящее время математические методы становятся необходимым орудием расчета буквально всех важнейших процессов в народном хозяйстве. Без знаний математики невозможно представить себе работу многих специалистов: инженеров, экономистов, организаторов производства, агрономов, квалифицированных рабочих.
Когда-то королева Англии пригласила к себе великого Ньютона. Она попросила побывать на монетном дворе и подсчитать, сколько дополнительных помещений, станков и рабочих нужно добавить, чтобы выпускать в 1,5 раза больше монет. Ньютон, вникая в производство, провёл на монетном дворе полдня. Остальное время суток он просидел за письменным столом, занимаясь расчетами.
Утром он предложил королеве следующее решение: можно, не производя никаких добавлений, увеличить выпуск монет в два раза. Для этого достаточно произвести лишь некоторые изменения в организации производства: переставить станки, по-иному распределить рабочих, изменить последовательность операций.
2. Задачи на оптимизацию.
С задачами, подобной той, которую решал Ньютон, в настоящее время приходится встречаться представителям разных профессий: инженер-технолог стремится так организовать производство, чтобы на имеющимся станочном парке сделать как можно больше продукции; конструктор «ломает» голову, стремясь сделать наилегчайшим прибор на космическом корабле; экономист старается так спланировать прикрепление заводов к источникам сырья, чтобы транспортные расходы оказались наименьшими; рабочий-металлист старается из куска металла получить как можно больше деталей.
За разработку общих методов решения задач на наименьшее и наибольшее значение, или, как их еще называют, задач на оптимизацию, русский математик Леонид Витальевич Канторович в 1975 году стал лауреатом Нобелевской премии.
Следует различать два вида задач на оптимизацию. В задачах первого вида улучшение достигается за счет коренных качественных изменений (выбор новых конструктивных решений, переход на новую технологию изготовления данной продукции). В задачах второго рода качественная сторона дела остается неизменной, но меняются количественные показатели, например, размеры прибора, соотношение веществ, используемых для химической реакции, начальная скорость ракеты. С математической тоски зрения в этих задачах отыскивается наибольшее и наименьшее значения функций. Один из способов решения таких задач основан на применении производной.
3. Применение производной в строительстве.
При монтаже промышленных зданий небольшой высоты используется автомобильный кран. При выборе крана необходимо иметь сведения о сооружаемом объекте. В частности. Габаритные данные объекта позволяют заранее определить требуемую длину стрелы крана. Рассмотрим задачу: «Для строительства здания высоты Н и длины 2L с плоской крышей нужно выбрать автомобильный кран.
Вывести формулу для определения длины стрелы крана».
Пользуясь обозначениями, указанными на
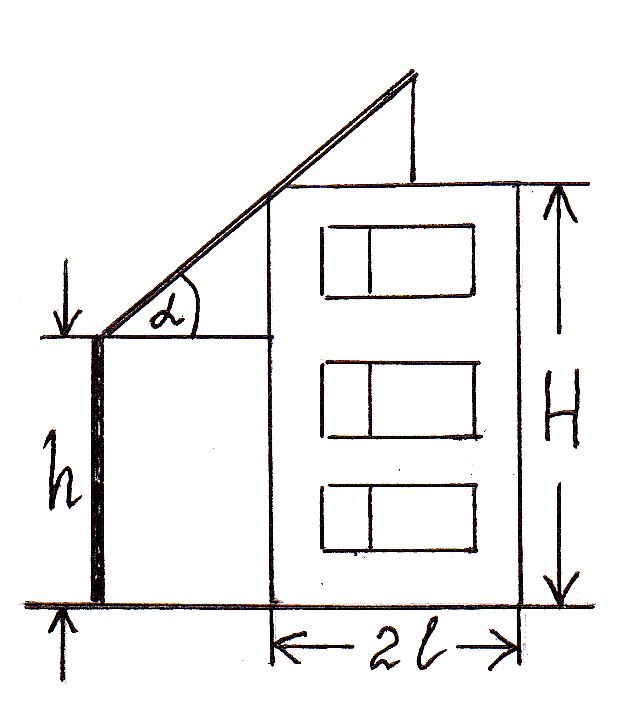
чертеже, получим формулу, выражающую длину
стрелы крана L=+, где α- угол наклона
стрелы. Из формулы видно, длина стрелы крана
зависит от угла α, который меняется изменением
положения крана. Выгодного положение
крана является такое место, с которого заданная
работа может быть выполнена краном с
наименьшей длиной стрелы.
В результате отыскание выгодного положения крана сводится к нахождению наименьшего значения функции L=+, на промежутке (0; ). С помощью производной установим, что наименьшее значение длины стрелы получается при α =
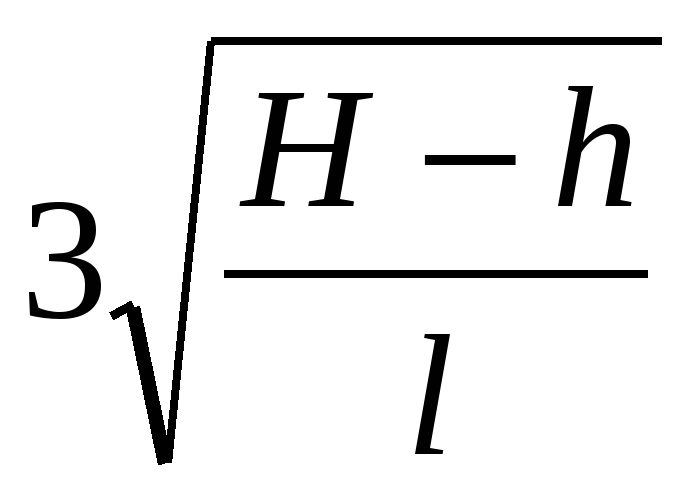
arctg. Эта формула используется на практике.
4. Производная и транспорт.
Производная находит применение и при проектировании мостов. Имеются мосты, профиль которых очерчен двумя прямыми, наклоненными к горизонту и сопряженными в заданных точках с дугой параболы (в целях создания благоприятных условий для водоотвода). Для нормальной эксплуатации моста необходимо, чтобы переход от прямолинейных участков к параболическому был плавным. Обеспечение этого условия способствует большей долговечности моста. В связи с этим можно рассмотреть следующую задачу: «Тангенс угла наклона прямых АМ и BN к горизонту равен m, стрела провеса моста равна С. Каким должно быть уравнение параболы АОВ, чтобы профиль моста не имел изломов?».
Выберем систему координат так, как показано на рисунке.
Уравнение параболы АОВ будем искать в виде у = ах, где х и у- координаты произвольной точки параболы, а — параметр. Рассмотрим точку А (х,С). Так как точка А лежит на параболе АОВ, то С = ах(1). По условию m = 2ах(2), где 2ах= у(х). Выразив х из уравнения (2) и подставив в равенство (1), получим выражение параметра а = m/4С. В результате уравнение параболы АОВ примет вид: у = x.
5. Производная помогает мелиорации.
В мелиоративной практике часто сооружаются каналы с поперечным сечением в форме прямоугольника, трапеции и сегмента круга. Рассмотрим некоторые характеристики канала: живое сечение, смоченный периметр, которые обозначаются соответственно через ω, λ. Положим для простоты, что канал полностью заполнен водой. Живое сечение – площадь поперечного сечения. Смоченный периметр – длина границы соприкосновения потока со стенками канала.
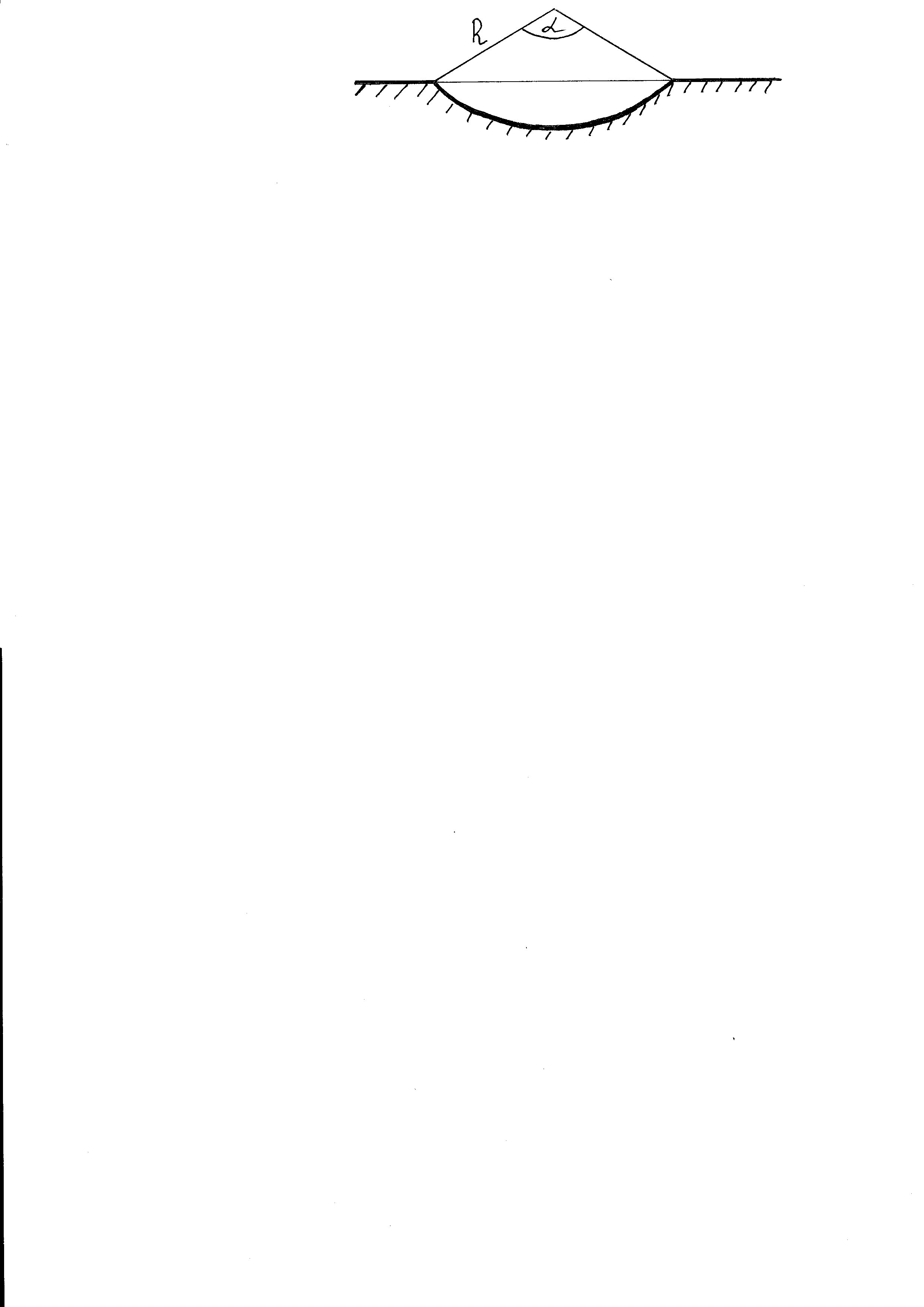
Пользуясь обозначениями, принятыми на чертеже, получим равенство λ=Rα, ω=(α-sinα ), где ω – задано. Поскольку λ зависит от двух переменных, то из второго равенства выразим R и подставим в первое, получим функцию, зависящую от α: λ = . С помощью производной установим, что функция λ принимает наименьшее значение при α = π, т. е. в сечении канала должен быть полукруг.
6. Космос и производная.
Дифференциальное и интегральное исчисления являются теоретическим базисом космонавтики. Без понятий производная, интеграл, решение дифференциального уравнения были бы невозможны расчеты прочности корпуса ракеты – носителя, тех скоростей, которые необходимо придавать космической станции, чтобы она могла выполнить порученное ей задание; невозможно осуществить управление ее полетом. Рассмотрим одну из задач такого рода: «Ракета – носитель движется прямолинейно по закону
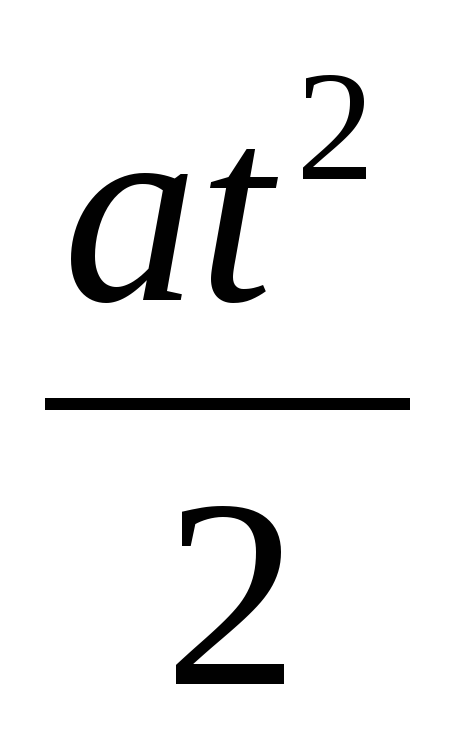
S = ν0t +

Через время t после начала движения от нее отделяется для выполнения задания пилотируемый аппарат, который продолжает двигаться по инерции.

В какой момент времени и какую постоянную скорость надо ему придать для того, чтобы, двигаясь дальше равномерно, он догнал ракету в момент t, имея при этом одинаковую с ней скорость?».

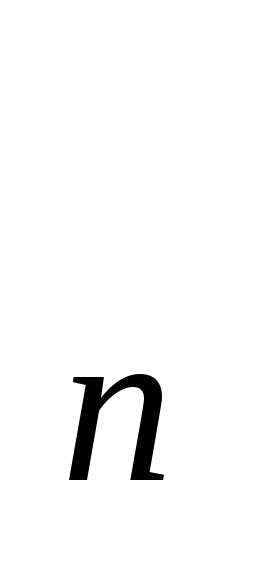
Рассмотрим геометрическую интерпретацию задачи (смотри рисунок). Обозначим скорость пилотируемого аппарата V. По условию задачи
V(t) = S´(t), с этой скоростью пилотируемый аппарат будет двигаться до момента ее изменения. В этом случаи графиком закона его движения является касательная, проведенная к параболе в точке (t, S(t)). В момент t V(t)=S´(t) . Поэтому в некоторый момент t t аппарату необходимо придать скорость S´(t) и, начиная с момента t до t момента, графиком его движения является касательная, проведенная к параболе в точке (t, S(t)). Легко видеть, что момент t будет найден, если будет найдена точка пересечения касательных. Найдем уравнения касательных, проведенных к параболе соответственно в точках: (t, S(t)), (t, S(t)).
S = S (t) + S´(t)(t — t) и S = S (t) + S´(t)(t — t), где S´(t) = V + at.
Найдем точку пересечения касательных:
S (t) + (V + at)( t — t) = S (t) +(V + at)(t — t) или
V t+ + (V + at)( t — t) = V t+ + +(V + at)(t — t).
Отсюда: t = (t+ t)/2. Таким образом, для того, чтобы пилотируемый аппарат догнал ракету – носитель, ему нужно придать скорость V= V + at в момент времени : t = (t+ t)/2.
7. Случай в заповеднике.
При обходе заповедника два егеря обнаружили тушу убитого дикого кабана. Осмотр показал, что кабан убит наповал точным выстрелом браконьера. Рассудив, далее, что браконьер обязательно вернется за добычей, егеря решили дождаться его, укрывшись неподалеку. Вскоре появились два человека, прямо направившиеся к убитому животному.
Задержанные всячески отрицали свою причастность к браконьерству. Однако у егерей уже были косвенные улики их виновности, но для ее полного доказательства следовало уточнить время, когда был убит кабан. Это удалось с помощью производной.
Согласно закону излучения тепла скорость охлаждения «тела» в воздухе пропорциональна разности между температурой «тела» и температурой воздуха, т. е. x´= -k( x – a ), где х – температура «тела» в момент времени t, а – температура воздуха, k – коэффициент пропорциональности. В момент задержания неизвестных температура воздуха составляла 21º С. Считая, что в момент выстрела в кабана его температура была равна 37ºС, полагая t = 0 временем задержания неизвестных, из уравнения, в которое входит производная, удалось определить время выстрела. Оказалось, что между моментом выстрела и моментом задержания неизвестных прошло 2 часа 6 минут. Найденное время и косвенные улики полностью доказали виновность задержанных.
Мы увидели сегодня как широко применяется производная. Какие профессии требуют хорошего знания математики. И поэтому, если вы хотите участвовать в большой жизни, то пополняйте свою голову математикой, пока есть к тому возможность.
Источник: kopilkaurokov.ru