Эпюра — это графическое изображение нагрузок и напряжений по всей длине бруса, используемое для визуального анализа напряженности, а также распределения нагрузок по всей длине бруса.
Эпюру можно построить на основании следующих параметров: внутренних сил (продольных и поперечных), крутящих и изгибающих моментов, напряжений (нормальных и касательных) и перемещений.
Процесс построения эпюр
Процесс построения эпюры стандартизирован и осуществляется по определенным правилам. Это сделано для общего понимания графиков всеми участниками производственного процесса.
Сначала строится нулевая линия. С левой стороны от линии пишется символическое название эпюры: $N$ — продольные силы, $Q$ — поперечные силы, $Mиз$ — изгибающие моменты, $T$ или $Mкр$ — вращающие момент, $σ$ и $τ$ — нормальное и касательное напряжения. Название сопровождается единицей измерения в соответствии с параметром (наименованием эпюры), например, $МПа$ — мегапаскаль.
Затем определяются границы силовых участков, то есть таких участков, где силовой фактор (деформация) остается постоянным или изменяется в рамках одной закономерности. Зачастую, границы силовых участков представляют собой сечения с приложенной внешней нагрузкой. Обозначение границ на эпюре реализуется в виде тонких вертикальных линий.
БАЛКА — 90% СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!
Если брус обладает сложной объемной формой, то границы определяют аналитически.
Далее эпюра масштабируется. Масштаб выбирается в соответствии с предварительным просчетом отображаемого фактора по всем контрольным сечениям (КС) бруса.
После выбора масштаба и построения внешнего контура эпюры КС присваиваются значения фактора без указания знака (“$+$” и “$–$”). Факторы с положительными значениями чертятся над нулевой линией, а с отрицательными под.
В области с положительными значениями на самом широком участке пишется знак “$+$” и обводится кружком, а с отрицательными выполняется также операция, но указывается знак “$–$”. Можно поставить знаки справа и слева от “$0$”, при этом кружками они обводится не будут.
Готовые работы на аналогичную тему
Определение знака фактора
Знак фактора определяется направлением внутренних силовых факторов и действием деформации. Например, нагрузке продольного типа, направленной на сжатие присваивается знак “$–$”, а на растяжение “$+$”.
Если вращение “отсеченной” части бруса осуществляется против часовой стрелки, то крутящий момент будет со знаком “$+$”, а по часовой стрелке знаком “$–$”. При рассмотрении поперечной силы $Q$, смотрим вертикальную плоскость, если она направлена вниз, то знак “$–$” (вверх “$+$”), а также учитываем поворот балки по часовой “$+$” и против часовой “$–$” .
Пример построения
Построим эпюры для простой двухоппорной балки с распределенной нагрузкой и действующей силой $F$=$10 кН$ и длиной $8$ $м$.
Начертим расчетную схему и укажем все нагрузки и значения:
Рисунок 1. Расчетная схема двухопорной балки. Автор24 — интернет-биржа студенческих работ
Вот для чего нужно строить эпюры в сопромате!
Определим реакции опор ($R$) в данном случае реакция для каждой точки будет равна половине приложенной, силы, так части балки равны по длине (нагрузка распределена).
Обозначаем границы участков балки.
Рисунок 3. Границы участков балки. Автор24 — интернет-биржа студенческих работ
На первом участке отметим произвольное сечение и назовем его буквой $D$. Оно расположено на расстоянии $z1$ от левого торца балки. Относительно этого сечения записываем законы, описывающие изменения поперечных сил и изгибающих моментов, в рамках участка.
Рисунок 4. Произвольное сечение D. Автор24 — интернет-биржа студенческих работ
Запишем уравнение для поперечной силы. Поворот реакции $Ra$ выполняется по часовой стрелке, поэтому уравнение имеет вид:
$Qy_1 = Ra = 10 кН$
Обозначим границы, указав значение поперечной силы на графике, и начертим эпюру.
Рисунок 5. Эпюра поперечной силы. Автор24 — интернет-биржа студенческих работ
Запишем уравнение для изгибающего момента. В данном случае момент силы направлен на растяжение, поэтому укажем знак “$+$”, поэтому уравнение имеет вид:
Из уравнения видно, что изменения изгибающего момента будут происходить, в соответствии с линейным законом, и зависеть от координаты $z_1$.
Изображение эпюров со стороны растянутых волокон (показано в примере) характерно для инженерно-строительной практики. В механике эпюра чертится со стороны сжатых волокон.
Рассчитаем эпюру этого участка, подставив в уравнение координаты $z_1 = 0$ (начало участка) и $z_2 = 4$ (конец участка), а затем построим ее.
$Mx_1(z_1 = 0) = Ra • z_1 = 5 • 0 = 0$
$Mx_1 (z_1 = 4) = Ra • z_1 = 5 • 4 = 20$
Рисунок 6. Эпюра изгибающего момента. Автор24 — интернет-биржа студенческих работ
Выполним расчеты для второго участка балки:
$Qy_2 = – Rb = –10 кН$
$Mx_2 (z_2 = 0) = Rb • z_2 = 5 • 0 = 0$
$Mx_2 (z_2 = 4) = Rb • z_2 = 5 • 4 = 20$
Начертим окончательную версию эпюры.
Рисунок 7. Полноценная эпюра рассматриваемой балки. Автор24 — интернет-биржа студенческих работ
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Виктория Валерьевна Колесникова
Эксперт по предмету «Сопротивление материалов»
Автор24 — это сообщество учителей и преподавателей, к которым можно обратиться за помощью с выполнением учебных работ.
Источник: spravochnick.ru
Правила построения эпюр поперечных сил и изгибающих моментов
Озвучим правила построения эпюр , вытекающие из метода сечений, и являющиеся следствием дифференциальных и интегральных зависимостей, некоторые из которых справедливы при обходе эпюр и слева направо. Зная правила построения эпюр, можно быстро найти грубую ошибку только по внешнему виду эпюр.
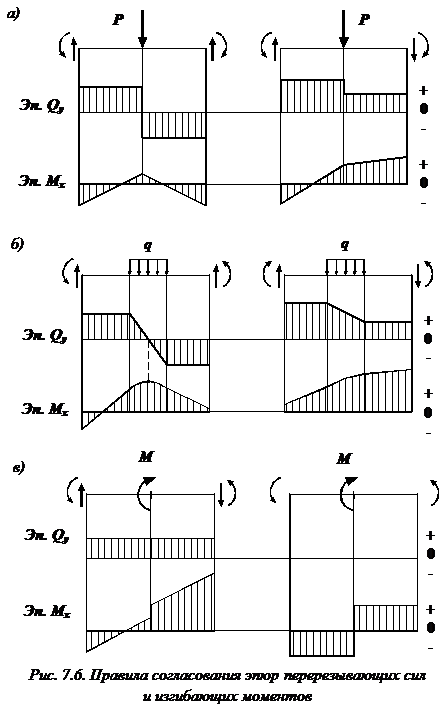
Правило построения эпюр – отсутствующая распределенная нагрузка
Если на участке балки отсутствует распределенная нагрузка (), то эпюра поперечных сил на этом участке представляет собой прямую, параллельную оси балки (рис. 7.6). По дифференциальной зависимости распределенной нагрузки и поперечной силы: поскольку , то и . Следовательно, .
Эпюра изгибающих моментов на участке, где , – прямая линия. Причем, если , то прямая идет вверх, а если , прямая идет вниз. Если , то изгибающий момент постоянен, поскольку .
Правило построение эпюр – скачки и изломы
Под сосредоточенной силой (P) на эпюре поперечных сил (рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре изгибающих моментов – излом, угол которого направлен навстречу нагрузке.
Правило построение эпюр – присутствует распределенная нагрузка
Если на участке балки имеется равномерно распределенная нагрузка: эпюра поперечных сил представляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка направлена вниз (и наоборот). Эпюра на этом участке, согласно третьей формуле дифференциальных зависимостей, изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.
Правило построение эпюр – экстремум
Если эпюра поперечной силы проходит через нулевое значение, то в этом сечении балки на эпюре изгибающих моментов имеется экстремум (последнее вытекает из дифференциальной зависимости ). В точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры переходят одна в другую плавно (без излома).
Правило построение эпюр – внешний момент
Сосредоточенный внешний момент M (рис. 7.6, в) никак не отражается на эпюре . На эпюре в месте приложения этого момента имеется скачок на его величину .
Заметим, что построение эпюр поперечных сил и изгибающих моментов ввел в практику расчета балок на изгиб французский ученый Жан Антуан Шарль Бресс (1822 – 1883 гг.) в 1859 г.
Источник: sopromato.ru