В механике твердого тела изгибающий момент представляет собой реакцию, возникающую внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента. Самым передовым, стандартным и простейшим элементом конструкции, подверженным изгибающим моментам, является балка. Если момент, приложенный к балке, пытается изогнуть балку в плоскости стержня, это называется изгибающим моментом. В случае простого изгиба, если изгибающий момент применяется к определенному поперечному сечению, возникающие напряжения называются изгибающим или изгибающим напряжением. Он изменяется линейно от нейтральной оси по поперечному сечению балки.
Уравнение изгибающего момента
Алгебраическая сумма моментов по конкретному поперечному сечению балки, возникающих из-за моментов по часовой или против часовой стрелки, называется изгибающим моментом в этой точке.
Пусть W — вектор силы, действующий в точке A тела. Момент этой силы относительно реперной точки (O) определяется как
Крутящий момент. Что это такое и зависит ли от мощности?
Где M = Момент вектор, р = вектор положения от опорной точки (О) до точки приложения силы А. символ обозначает векторное произведение. легко вычислить момент силы вокруг оси, которая проходит через опорную точку O. Если единичный вектор вдоль оси равен «i», момент силы вокруг оси определяется как
где [.]представляют собой точечное произведение вектора.
Математическая связь между интенсивностью нагрузки, поперечной силой и изгибающим моментом
Соотношения: Пусть f = интенсивность нагрузки
Q = поперечная сила
M = изгибающий момент

Скорость изменения поперечной силы даст интенсивность распределенной нагрузки.
Скорость изменения изгибающего момента даст силу сдвига только в этой точке.

Единица измерения изгибающего момента
Изгибающий момент имеет единицу, аналогичную паре как Нм.
Изгибающий момент балки
Предполагая, что балка AB определенной длины подвержена изгибающему моменту M, Если верхнее волокно балки, то есть выше нейтральной оси, находится в состоянии сжатия, это называется положительным изгибающим моментом или прогибающим изгибающим моментом. Точно так же, если верхнее волокно балки, то есть выше нейтральной оси, находится в напряжении, это называется отрицательным изгибающим моментом или изгибающим моментом изгиба.

Провисание и заедание балки
Соглашение о знаках изгибающего момента
При определении максимального изгибающего момента, вытяжки и BMD соблюдается соглашение о конкретных знаках.
- Если мы начнем вычислять изгибающий момент с правая сторона или правый конец луч, Момент по часовой стрелке принимается как отрицательныйи Противодействующий момент принимается как Положительно.
- Если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный, и Момент против часовой стрелки принимается как Negative.
- Если мы начнем вычислять поперечную силу с правая сторона или правый конец луч, Сила, действующая вверх принимается как Отрицательныйи Сила, действующая вниз принимается как Положительно.
- Если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Диаграмма усилия сдвига и изгибающего момента
Сдвигающая сила представляет собой алгебраическую сумму сил, параллельных поперечному сечению по конкретному поперечному сечению балки, возникающих из-за сил действия и противодействия. Сила сдвига пытается срезать поперечное сечение балки перпендикулярно оси балки, и из-за этого развитое распределение напряжения сдвига является параболическим по отношению к нейтральной оси балки. Изгибающий момент представляет собой сумму моментов в определенном поперечном сечении балки, обусловленных моментами по часовой стрелке и против часовой стрелки. Это пытается изогнуть балку в плоскости элемента, и из-за передачи его по поперечному сечению балки распределение развиваемого изгибающего напряжения является линейным относительно нейтральной оси балки.
Момент силы
Диаграмма усилия сдвига — это графическое изображение изменения поперечной силы в поперечном сечении по длине балки. С помощью диаграммы силы сдвига мы можем определить критические секции, подверженные сдвигу, и внести поправки в конструкцию, чтобы избежать разрушения.
Кроме того, Диаграмма изгибающего момента — графическое представление изменения изгибающего момента в поперечном сечении по длине балки. С помощью диаграммы B. M мы можем определить критические секции, подлежащие изгибу, и внести изменения в конструкцию, чтобы избежать отказа. При построении диаграммы поперечных сил [SFD], при построении диаграммы изгибающих моментов [BMD] происходит резкое повышение или резкое падение из-за точечной нагрузки, действующей на балку; происходит внезапный подъем или резкое падение из-за воздействия пар на балку.
Типы опор и нагрузок
Фиксированная поддержка: Он может предложить три реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция, 1 моментная реакция).
Поддержка контактов: Он может предложить две реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция).
Роликовая опора: Он может предложить только одну реакцию в плоскости члена (1 вертикальная реакция).
Концентрированная или точечная нагрузка: При этом вся интенсивность нагрузки ограничена конечной площадью или точкой.
Равномерно распределенная нагрузка [UDL]: При этом вся интенсивность нагрузки постоянна по длине балки.
Равномерно изменяющаяся нагрузка [UVL]: При этом вся интенсивность нагрузки изменяется линейно по длине балки.
Типы опор и нагрузок
Диаграмма усилия сдвига и диаграмма изгибающего момента только для балки, несущей точечную нагрузку.
Учитывайте только опорную балку, показанную на рисунке ниже, несущую только точечные нагрузки. В балке с простой опорой один конец опирается на штифт, а другой конец — на роликовую опору.
Схема свободного тела для балки с опорой, подверженной нагрузке F
Значение реакции в точках A и B можно рассчитать, применяя условия равновесия
[латекс]сумма F_y=0, сумма F_x=0 ,сумма M_A=0[/латекс]
Для вертикального равновесия
Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
Ставя ценность RB в [1] получаем
[латекс] Таким образом,; R_A=frac[/латекс]
Пусть XX — интересующий участок на расстоянии x от конца A.
В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сила сдвига в точке А
[latex]В;точке;Aстрелка вправо SF=R_A=frac[/latex]
Мы знаем, что поперечная сила остается постоянной между точками приложения точечных нагрузок.
Сила сдвига при C
Сдвигающая сила в области XX равна
Сила сдвига в точке B
- при A = 0
- при B = 0
- в C
Диаграмма поперечной силы и изгибающего момента для Просто поддерживаемый луч с точечной нагрузкой
Сдвигающая сила [SFD] и диаграмма изгибающего момента [BMD] только для консольной балки с равномерно распределенной нагрузкой (UDL).
Рассмотрим только консольную балку, показанную на рисунке ниже UDL. В консольной балке один конец зафиксирован, а другой конец может двигаться.
Консольная балка подвергается равномерно распределенной нагрузке
Результирующая нагрузка, действующая на балку из-за UDL, может быть определена как
W = Площадь прямоугольника
Эквивалентная точечная нагрузка wL будет действовать в центре луча. т.е. при L / 2
Диаграмма свободного тела луча становится

Схема свободного тела балки
Значение реакции в точке А можно рассчитать, применив условия равновесия.
[латекс]сумма F_y=0, сумма F_x=0 ,сумма M_A=0[/латекс]
Для горизонтального равновесия
Для вертикального равновесия
Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
Пусть XX — интересующий участок на расстоянии x от свободного конца.
В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сила сдвига в точке A составляет
Сила сдвига в точке B составляет
Значения силы сдвига в точках A и B показывают, что сила сдвига изменяется линейно от фиксированного конца к свободному концу.
Для BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.
Диаграмма SFD и BMD для консольная балка с равномерно распределенной нагрузкой
4-точечная диаграмма изгибающего момента и уравнения
Рассмотрим балку с простой опорой, у которой две равные нагрузки W действуют на расстоянии a от обоих концов.

FBD для 4-точечной диаграммы изгиба
Значение реакции в точках A и B можно рассчитать, применив условия равновесия.
[латекс]сумма F_y=0, сумма F_x=0 ,сумма M_A=0[/латекс]
Для вертикального равновесия
Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
Согласно описанному ранее соглашению о знаках, если мы начинаем вычислять поперечную силу с левой стороны или с левого конца балки, сила, действующая вверх, принимается как положительная, а сила, действующая вниз, принимается как отрицательная. Для построения диаграммы BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.
Сила сдвига в точке A составляет
Сила сдвига в C составляет
Сила сдвига в D составляет
Сила сдвига в точке B составляет
Для диаграммы изгибающего момента

Диаграммы SFD и BMD для 4-точечной диаграммы изгиба
Вопрос и ответ изгибающего момента
В.1) В чем разница между моментом и изгибающим моментом?
Ответ: Момент можно определить как произведение силы и длины линии, проходящей через точку опоры и перпендикулярной силе. Изгибающий момент — это реакция, возникающая внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента.
Q.2) Что такое определение диаграммы изгибающего момента?
Ответ: Диаграмма изгибающего момента — Графическое изображение изменения BM по поперечному сечению по длине балки. С помощью этой схемы мы можем определить критические участки, подлежащие изгибу, и внести изменения в конструкцию, чтобы избежать сбоев.
В.3) Какова формула напряжения изгиба?
Ответ: изгиб Напряжение можно определить как сопротивление, вызванное изгибающим моментом или двумя равными и противоположными парами в плоскости элемента. Его формула дается
[латекс] frac = frac = frac [/ латекс]
Где M = приложенный изгибающий момент по поперечному сечению балки.
I = Второй момент инерции площади
σ = изгибное напряжение, вызванное в стержне
y = расстояние по вертикали между нейтральной осью луча и желаемым волокном или элементом в мм
E = модуль Юнга в МПа
R = радиус кривизны в мм
Знать о прочности материала нажмите сюда
Я Хакимуддин Бавангаонвала, инженер-механик с опытом проектирования и разработки. Я получил степень магистра технических наук в области проектирования и 2.5 года исследовательского опыта. К настоящему времени опубликованы две исследовательские работы по твердой токарной обработке и конечноэлементному анализу приспособлений для термообработки. Сфера моих интересов — проектирование машин, прочность материалов, теплопередача, теплотехника и т. Д. Владею программным обеспечением CATIA и ANSYS для САПР и CAE. Помимо исследований. Подключитесь к LinkedIn — https://www.linkedin.com/in/hakimuddin-bawangaonwala
Последние посты
Гидроксид калия или едкий калий является неорганическим компонентом. Его молярная масса составляет 56.11 г/моль. Давайте резюмируем структуру КОН Льюиса и все факты в деталях. КОН представляет собой простой гидроксид щелочного металла.
Слово «еще» в основном служит в значении «до сих пор» или «тем не менее» в предложении. Проверим употребление слова «пока» в значении «союз». Слово «пока» можно обозначить как «координационное.
О НАС
Мы являемся группой профессионалов отрасли из различных областей образования, таких как наука, инженерия, английская литература, и создаем универсальное образовательное решение, основанное на знаниях.

report this ad
Источник: ru.lambdageeks.com
Что такое момент?
По совету пользователя Дима Богомолов и дабы избежать праведного гнева (и закидывания нас с ним томиками с Достоевским и Толстым) со стороны motor-serg открываю данную тему, начавшуюся в http://forum.dwg.ru/showthread.php?p=471397#post471397
Премного благодарен модератору Солидворкер за труд по переносу постов из вышеуказанной темы.
Кстати, я люблю подкалывать своих коллег подобными простыми вопросами. На вопрос «Что такое момент?» пока никто внятно не ответил, про поперечную силу я пока не спрашиваю. Хотя в изополях моментов в СКАДе людям всё понятно. 🙂
Кстати, обратился недавно друган с завода, ну и спрашивает: «Дай определение, что такое «покрытие». Оказывается, для какой-то бредовой бумажки, нужно было дать определение что такое «покрытие» и никто не может его сформулировать
Так вам всё сразу и расскажи. 🙂
Грунт — это горная порода с точки зрения инженера. Пойдёт?
Ну такое многие выдать способны. 🙂
Этими знаниями довольствуются люди, в задачи которых входит определять значение момента: они справедливо берут и умножают силу на плечо. Примерно так и поступали всю свою жизнь древние египтяне, но вот древних греков такое положение дел совершенно не устраивало. 🙂
Меня интересует определение самого понятия момент, в данном случае силы. Что же это есть такое, как его описать, увидеть, почувствовать, объяснить. Откуда он берётся и о чём говорит. Хочу, чтобы мне рассказали о его смысле (физическом, математическом, философском?).
То есть по указанному выше правилу можно определить значение момента, но сама суть и смысл понятия момент при этом, по-моему, останется «за кадром». Я так жить не могу. 🙂
Да, здесь моё упущение. Писал ночью, вокруг темно было. 🙂
Главным образом, речь идёт тех моментах, о которых иногда подолгу рассуждают проектировщики-конструкторы, глядя на изополя изгибающих моментов в плите перекрытия, рассчитанной в СКАДе (Mx, My). Т. е. это изгибающий момент в плите или балке, от действия внешних нагрузок и воздействий.
Но в любом случае, как только люди начинают отвечать что-то похожее на правду (отвечают многие), далее я неизбежно и, по-моему, справедливо спрашиваю: «А что такое момент, вообще?» Вот здесь и начинается негативная реакция. 🙂
Нет, я думаю не скатимся. Я не сторонник флуда и оффтопа.
К тому же, для люков есть отдельная тема. Очень, кстати, серьёзная тема. 🙂
Меня интересует определение самого понятия момент, в данном случае силы. Что же это есть такое, как его описать, увидеть, почувствовать, объяснить. Откуда он берётся и о чём говорит. Хочу, чтобы мне рассказали о его смысле (физическом, математическом, философском?).
Чей-то я не понял немного. объясните плиз в чем ошибка. И в строительной механике, и в сопромате момент силы сть произведение силы на плечо. или вы о другом? Представить себе данную величину не составляет труда, вот момент инерции (см^4) никак не получится.
Все понятия, здесь обсуждаемые, условны. Момент инерции (плоского(!) сечения) и момент сопротивления (плоского (!) сечения) — это интегралы по площади (этого самого сечения), которые сами по себе являются абстрактными величинами. Впрочем, как и всё в математике. Их не надо представлять, надо просто уметь с ними работать.
Попробуйте представить хотя бы число 2 безотносительно чего бы то ни было — не получится. На ум придут 2 яблока, 2 птицы, цифра 2, но никак не само число как понятие. И не надо!
Кстати, и момент как произведение величины (!) силы на величину (!) плеча есть число, т.е. понятие абстрактное, представить которое невозможно. (ИМХО)
Поэтому определение момента как произведения силы на плечо математически неверно. Нельзя складывать лампочки с апельсинами, и перемножение двух понятий (а не их величин) не имеет смысла.
Хорошо, предлагаю свой сугубо дилетантский взгляд, т.к. чертежник и расчетов касаюсь слабо:
Момент суть напряжение в изгибаемом элементе, которое увеличивается от центра к периферии сечения. Чем больше момент, тем больше разница напряжений: ноль в центре сечения (пусть будет без эксцентрисистетов симметричное сечение) и максимальное значение в удаленных от центра точках. Причем одна часть сечения растягивается, другая сжимается, что и отличает действие момента от поперечной силы.
Ну, как-то так?
внесу еще небольшое разнообразие, так называемый момент инерции, в чисто физическом смысле величина, которая зависит от массы, т. е. мера инертности тела, вращающегося вокруг произвольной оси. Это только строители понимают его всего лишь как геометрическую величину, независящюю от массы.
BM60, спасибо!
Момент суть напряжение в изгибаемом элементе, которое увеличивается от центра к периферии сечения. Ну, как-то так?
Pum-purum, что по сопромату было? Во-первых, какой момент? Из контекста ясно, что речь идёт об ИЗГИБАЮЩЕМ момент в отличие от момента инерции и момента сопротивления как геометрической характеристики плоского сечения стержня.
И изгибающий момент, и поперечная сила (так же, как и продольная) — это усилия (внутренние силовые факторы), возникающие в сечениях элементов конструкции. Их надо отличать от внешних сил — внешнего момента (как раз то «произведение силы на плечо»), сосредоточенной и распределённой нагрузок. Это также абстрактные понятия, физически это всего лишь дополнительные силы, возникающие между атомами (молекулами) материала элемента конструкции при приложении к этому элементу нагрузок.
Напряжение есть предел отношения вектора внутренних усилий к площади площадки, на которой он действует, когда последняя стремится к нулю.
http://sapr.mgsu.ru/biblio/mexanika/Section5.html
http://sapr.mgsu.ru/biblio/mexanika/Section4.html
И момент НИКАК не может быть напряжением.
Далее. Различают нормальные и касательные напряжения. Нормальные напряжения в изгибаемом элементе вызываются изгибающим моментом (сигма=М/W). Касательные — поперечной силой. В общем случае в сечениях балки действуют оба этих усилия.
Так вот, для двутавра, например, при изгибе касательные напряжения в конце стенки (близко к точке соединения с полкой) БОЛЬШЕ, чем касательные напряжения в начале полки (по высоте). тау=Q*S`/(J*b) — формула Журавского, где b — ширина (толщина) сечения.
Кстати, в общем случае внешний момент, приложенный к элементу, вызывает не только нормальные напряжения, но и касательные (сложное напряжённое состояние). Этот вопрос рассматривает теория упругости.
P.S. А я вот читаю теорию упругости Александрова-Потапова (МИИТовский) и последний учебник по сопромату (2009 года) — не помню, кто автор. Егоров, вроде бы. Ещё сказки на немецком языке Лёгкое чтени по методу Ильи Франка!:crazy:
P.P.S. rybin74, в сопромате рассматривают момент инерции ПЛОСКОГО СЕЧЕНИЯ как его (сечения) геометрическую характеристику. У него нет и не может быть никакой массы, потому как масса — это характеристика, присущая объемным телам.
Источник: forum.dwg.ru
Что такое момент в строительстве
Мы уже говорили о том, как вычислять нормальные напряжения. Однако мы не учитывали то, что материал может не только растягиваться и сжиматься, но и изгибаться. Интуиция подсказывает, что если мы что-то согнем слишком сильно, оно либо навсегда останется согнутым (т.е. произойдёт неупругая деформация), либо вообще сломается. Но как численно оценить, какие именно силы и напряжения в материале может создать изгибающий момент? В этой статье мы поговорим о том, что такое гипотеза плоских сечений, и как момент сопротивления изгибу помогает рассчитать прочность балки.
Робот-сгибальщик Бэндер решил сделать свой курс сопромата с блэкджеком и мемами. Фото в цвете.
Что такое изгибающий момент
В первой части цикла мы уже выяснили, что любые воздействия на материал и все виды сопротивления можно разложить по осям x, y, z на силы и моменты и получить шесть уравнений равновесия.
Тем не менее, если про силы мы уже поговорили достаточно подробно, то про моменты пока умолчали.
Момент – это количество «кручения». Для материальной точки он вычисляется произведением силы на плечо:

Момент — это произведение силы на плечо. [6]
Проводим из точки перпендикулярно силе линию, её длину умножаем на силу. Это и будет момент кручения данной точки.
Помимо прочего, момент может задаваться парой параллельных, но противоположных по направлению сил. Тогда равнодействующая сил не изменится, а тело будет стремиться к изгибу.

Момент Maz кручения задан парой сил. [6]
Эпюра моментов. Как распределяется изгибающий момент
Мы закрепили стержень в невесомости одной стороной. Взяли его за конец и начали крутить. Как следствие, в сечении около места кручения возникает противоположный момент, который сопротивляется изгибу.

Кусочек стержня. Mz — крутящий момент, M0 момент сопротивления. [6]
Если мы перейдем на следующее, находящееся дальше от места приложения момента, сечение, окажется, что в каждом следующем сечении возникает точно такой же момент сопротивления. Следовательно, от места закрепления стержня до конца балки будет действовать момент Mz=m. А эпюра момента (иными словами, график) будет выглядит вот так:

Момент противодействия изгибу возникающий в сечении. [6]
Гипотеза плоских сечений
Мы выяснили, что такое изгибающий момент. Но что такое изгиб, и какие изменения происходят в образце под его воздействием? Для этого мысленно разделим образец сеткой сечений и посмотрим, как будут меняться расстояния между узлами (местами пересечения продольных и поперечных сечений):

Смотря на картинку, можно сделать определенные выводы. Прямые поперечных сечений остались все такими же прямыми и не изменились в высоту, но перестали быть параллельными. Теперь они сходятся в определенную точку.
Продольные сечения же приняли форму дуги некоторой окружности. Называть их мы будем слоями. Ближе к верху слои сжались и стали короче, чем были изначально. Снизу же наоборот, растянулись и увеличились в длину. И где-то посредине (где именно, нам еще предстоит выяснить) располагается слой, который пусть и изогнулся, но не растянулся и не сжался.
Он называется нейтральным.
Данная модель укоренилась в сопромате под двумя именами. Первое имя она получила от создателя, Якоба Бернулли. А второе от своего содержания. Согласно допущению, на котором она основана, поперечные сечения до и после изгиба остаются плоскими. Отсюда и второе имя: гипотеза плоских сечений.
Еще одно допущение — это то, что эти сечения не деформируются. На самом деле, если вспомнить прошлый раздел, мы говорили, что по мере растяжения или сжатия стержня его ширина уменьшается или увеличивается. Однако влияние этого фактора в рамках дисциплины “сопротивление материалов” не учитывается, так как не может серьезно повлиять на точность вычислений.
Таким образом, единственные напряжения, которые возникают в плоском изгибе — это нормальные напряжения, которые изменяются по высоте сечения.
В прошлой части мы уже говорили, как именно вычислить растягивающие или сжимающие усилия в стержне. Вспомним, что относительная продольная деформация (ε=dl/l) определяется Законом Гука и равна нормальному напряжению деленному на модуль Юнга:
Модули Юнга для материалов уже давно вычислены и находятся в справочниках. Для нахождения нормальных напряжений остается только выяснить, какая продольная относительная деформация происходит под воздействием изгиба материала в каждом из слоев.
Вспомним немного геометрию и тригонометрию. В случае, если нам необходимо найти очень малую длину части окружности, она численно будет почти равна произведению синуса угла на радиус:

Для маленьких углов синус угла, тангенс угла и длина окружности на которую угол опирается численно равны. [7]
При этом, для малых углов синус численно равен углу (в радианах, т.е. равен длине дуги окружности с радиусом 1, на которую угол опирается).

Таким образом длина слоя находящегося на y дальше от центра окружности чем нейтральный слой будет равна произведению угла dφ и радиуса этого слоя (R+y):
В это время длина нейтрального слоя равна произведению угла dφ на радиус R:
А так как нейтральный слой не деформировался в длину, удлинение слоя будет равно его с нейтральным слоем разности:
А относительная продольная деформация будет равна отношению удлинения нашего слоя на нейтральный:
Таким образом, мы получили некоторое уточнение в формуле напряжения:
Примечание: прямо отсюда следует, что чем тоньше образец, тем меньше будет при изгибе возникать нормальных напряжений. За счет этого принципа и не разрушается оптоволокно. Стекло окна при небольшом изгибе разрушится. Волокна в оптоволокне же настолько тонкие, что при куда более существенных изгибах сохраняют свою структуру.Для желающих понастальгировать, старый выпуск Галилео про оптоволокно.
Оптоволоконный кабель [4]
Теперь для нахождения нормальных напряжений нам нужно либо найти радиус изгиба (или радиус кривизны) стержня и расположение нейтрального слоя, либо избавиться от них в формуле. Искать сложно, поэтому попробуем устранить кривизну.
Мы помним, что в нашем сечении сейчас действует только момент. Следовательно, не должно возникать никаких продольных сил:
N= ∑σdF=∫σdF=∫E*dy/RdF=E/R ∫ydF=0
Модуль Юнга не равен нулю, а радиус будет равен бесконечности только если изгибающий момент отсутствует. Следовательно нулю равен интеграл ∫ ydF. По-другому он называется статическим моментом инерции сечения по оси x и обозначается буквой S с индексом z.
Для того, чтобы найти координату y расположения геометрического центра сечения необходимо разделить статический момент на площадь сечения:
Статический момент и расположение нейтрального слоя для простейших фигур (параллелепипеда, круга, треугольника) довольно просто найти самостоятельно. Однако для более сложных фигур гораздо целесообразнее использовать сортаменты: справочники в которых собраны геометрические характеристики сечений.

Распределение нормальных напряжений в сечении при изгибе. [6]
Интеграл ∫y 2 dF— это осевой момент инерции тела, который обозначается буквой I.
Таким образом, момент внутренних будет равен:
И из этого мы уже сможем выразить радиус:
Подставляем все в формулу напряжения нейтрального слоя и навсегда забываем, что радиус когда-то использовался в вычислениях:
Момент инерции простейших фигур также можно рассчитать вручную, но для более сложных форм гораздо целесообразнее использовать сортамент.
Гипотеза плоских сечений дает возможность вычислить максимальное нормальное напряжение. Оно будет возникать на максимальном удалении от нейтрального слоя:
Момент сопротивления изгибу

Нахождение моментов инерции квадрата, прямоугольника, круга и кольца. [6]
Соотношение I/ymax характеризует то, как сильно сечение будет сопротивляться изгибу под действием момента. Его называют «момент сопротивления изгибу», а обозначается он как Wz. Эту величину также можно найти в сортаменте и, зная ее, максимальное напряжение в сечении найти можно в одно действие: σmax=Mz/Wz
То, что максимальные напряжения сконцентрированы на концах сечения, позволяет сэкономить на материале. Наибольшая ширина сечения нужна только на краях сечения балки, а в середине можно обойтись шириной похуже. Так мы задействуем меньше металла, а конструкция выдержит большую нагрузку.
Классический пример такой конструкции – это двутавр, на котором ближе к концам (где нормальные напряжения максимальны) ширина достаточно существенна, а в середине на порядок меньше:

Двутавр [5]
Чаще всего самые большие напряжения от изгиба — это именно нормальные. И для быстрого поверхностного расчета достаточно подобрать сечение под них. То есть разделить приложенный изгибающий момент на момент сопротивления изгибу. Однако нормальными напряжениями расчет не заканчивается, и для того, чтобы быть точно уверенными в том, что сечение выдержит нагрузки, необходимо также учесть и касательные напряжения. И этим мы займемся в следующих частях.
Над статьей работали:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Источник: stroikaveka.org
Изгибающий момент и поперечная сила
Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент.
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил.
На изгиб работают балки, оси, валы и другие детали конструкций. Если брус имеет хоть одну ось симметрии, и плоскость действия нагрузок совпадает с ней, то имеет место прямой изгиб, если же это условие не выполняется, то имеет место косой изгиб.
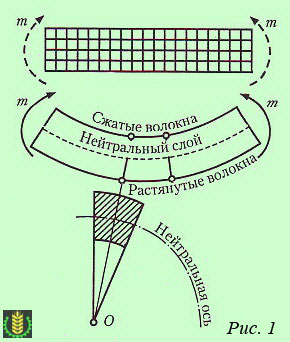
При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.
Подвергнув такой брус прямому изгибу, можно заметить, что (рис. 1):
— поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
— сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;
— продольные прямые линии искривятся.
Из этого опыта можно сделать вывод, что:
— при чистом изгибе справедлива гипотеза плоских сечений;
— волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.
Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью. Очевидно, что на нейтральной оси нормальные напряжения равны нулю.
Изгибающий момент и поперечная сила
Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).
Рассмотрим два случая:
1.К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент Ми, равный внешнему моменту. Таким образом, это случай чистого изгиба.

Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.
Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.
2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий моментМи и поперечная сила Q.
Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.
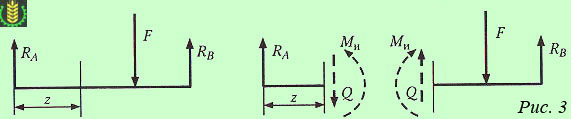
Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.
Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.
Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным.
У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих на балку справа или слева от сечения.
У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно сумма внешних сил, действующих на балку левее сечения, численно равна алгебраической сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.
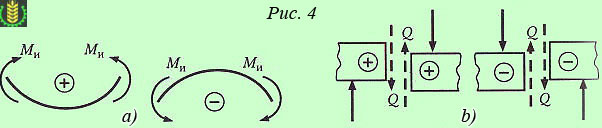
Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно: Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис 4a).
Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4b). Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями.
Еще раз отметим, что для определения реакций связей пользуются правилами знаков статики, а для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют «правилом дождя», имея в виду, что в случае выпуклости вниз образуется воронка, в которой задерживается дождевая вода (знак положительный), и наоборот – если под действием нагрузок балка выгибается дугой вверх, вода на ней не задерживается (знак изгибающих моментов отрицательный).
Эпюры внутренних усилий при прямом изгибе.
Прямым изгибом называется такой вид простого сопротивления, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствие с конфигурацией поперечного сечения балки.
Как известно, при прямом изгибе в поперечном сечении возникают два вида внутренних усилий: поперечная сила и внутренний изгибающий момент.
Рассмотрим пример расчетной схемы консольной балки с сосредоточенной силой Р, рис. 1 а., …
а) расчетная схема, б) левая часть, в) правая часть, г) эпюра поперечных сил, д) эпюра изгибающих моментов
Рис.1. Построение эпюр поперечных сил и внутренних изгибающих моментов при прямом изгибе:
Наиболее рациональным следует признать сечение, обладающее минимальной площадью при заданной нагрузке (изгибающем моменте) на балку. В этом случае расход материала на изготовление балки, будет минимальным. Для получения балки минимальной материалоемкости нужно стремиться к тому, чтобы по возможности наибольший объем материала работал при напряжениях, равных допускаемым или близким к ним. Прежде всего рациональное сечение балки при изгибе должно удовлетворять условию равнопрочности растянутой и сжатой зон балки.Иными словами необходимо, чтобы наибольшие напряжения растяжения (max ) н наибольшие напряжения сжатия (max ) одновременно достигали допускаемых напряжений и .
Поэтому для балки из пластичного материала (одинаково работающего на растяжение и сжатие: ), условие равнопрочности выполняется для сечений, симметричных относительно нейтральной оси. К таким сечениям относится, например, прямоугольное сечение (рис.
6, а), при котором обеспечено условие равенства . Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси.
Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричного двутавра (рис. 6): 2 горизонтальных массивных листа, соединенные стенкой (вертикальным листом), толщина которой назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости. К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение (рис. 6, в).
Рис.6. Распределение нормальных напряжений в симметричных сечениях
Рассуждая аналогично, приходим к выводу, что для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие (рис. 27):
которое вытекает из требования
Рис.7. Распределение напряжений несимметричного профиля сечения балки.
Идея рациональности поперечного сечения стержней при изгибе реализована в стандартных тонкостенных профилях, получаемых методами горячего прессования или прокатки из рядовых и легированных конструкционных высококачественных сталей, а также алюминия и алюминиевых сплавов, получивших широкое распространение в строительстве, машиностроении, авиационном машиностроении. Широко распространены показанные на рис. 7: а—двутавр, б— швеллер, в — неравнобокий уголок, г—равнобокий уголок. Реже встречаются тавр, таврошвеллер, зетовый профиль и др.
Рис.8. Используемые профили сечений: а) двутавр, б ) швеллер, в) неравнобокий уголок, г) равнобокий уголок
Формула осевого момента сопротивления при изгибе выводится просто. Когда поперечное сечение балки симметрично относительно нейтральной оси, нормальные напряжения в наиболее удаленных точках (при ) определяются по формуле:
Геометрическую характеристику поперечного сечения балки, равную называют осевым моментом сопротивления при изгибе. Осевой момент сопротивления при изгибе измеряется в единицах длины в кубе (как правило, в см3). Тогда .
формула осевого момент сопротивления при изгибе для прямоугольного поперечного сечения: ;
формула осевого момент сопротивления при изгибе для круглого поперечного сечения: .
| | | следующая лекция ==> | |
| ПРИМЕРЫ РАСЧЕТА ПРОЧНОСТИ СВАРНЫХ СОЕДИНЕНИЙ | | | Строительное производство в системе общественного производства. |
Дата добавления: 2016-05-28 ; просмотров: 23190 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник: poznayka.org