Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта (далее ФГОС) по специальности (специальностям)08.02.01 строительство и эксплуатация зданий и сооружений
1.2. Место учебной дисциплины в структуре программы подготовки специалистов среднего звена:
входит в профессиональный цикл, относится к общепрофессиональным дисциплинам.
1.3. Цели и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины:
В результате освоения учебной дисциплины обучающийся должен уметь :
— выполнять расчеты на прочность, жесткость, устойчивость элементов сооружений;
— определять аналитическими и графическими способами внутренние усилия и опорные реакции балок, ферм, рам;
— определять усилия в стержнях ферм;
— строить эпюры нормальных напряжений, изгибающих моментов и др.
В результате освоения дисциплины обучающийся должен знать:
-законы механики деформируемого твердого тела, виды деформаций, основные расчеты;
Строительная механика. Фермы основные понятия и гипотезы, Строймех для чайников.
-определения направлений реакций, связи;
-определение момента силы относительно точки и оси, его свойства;
-типы нагрузок и виды опорных балок, ферм, рам;
-напряжения и деформации, возникающие в строительных элементах при работе под нагрузкой;
-моменты инерции простых сечений и др.
Подготовка к освоению общих компетенций (ОК) и профессиональных компетенций (ПК):
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Быть готовым к смене технологий в профессиональной деятельности.
ПК 1.1. Подбирать строительные конструкции и разрабатывать несложные узлы и детали конструктивных элементов зданий
ПК 1.3. Выполнять несложные расчеты и конструирование строительных конструкций
ПК 4.1. Принимать участие в диагностике технического состояния конструктивных элементов эксплуатируемых зданий
ПК 4.4 Выполнять мероприятия по технической эксплуатации конструкций и инженерного оборудования зданий.
Техническая механика
1.4. Рекомендуемое количество часов на освоение программы учебной дисциплины:
максимальной учебной нагрузки обучающегося — 210 часов, в том числе:
обязательной аудиторной учебной нагрузки обучающегося — 140 часов;
Источник: xn--j1ahfl.xn--p1ai
Техническая механика: зачем она нужна и для чего необходимо решать задачи

Техническая механика – лишь одним из её разделов. В нём изучаются правила движения тел и их свойства. Также под технической механикой понимают учебную дисциплину, которая изучается многими студентами технических специальностей и включает в себя такие направления, как «Сопротивление материалов», «Детали и механизмы машин» и многие другие предметы.
Решение задач по технической механике – важная составляющая обучения, как и изучение теоретической базы. Очень важно, чтобы во время практических занятий студенты не просто изучали приёмы решения определённых задач, но и получали навыки самостоятельно решать даже незнакомые задачи.
Какими могут быть задачи
Существуют разные определения данного понятия. В целом можно обозначить его, как ситуацию, в которой человек должен целенаправленно приложить умственные усилия, чтобы найти заданное неизвестное, используя для этого те данные, которые есть в наличии. Их можно разделить на три вида:
• Стандартные. Студенты изучают способы решения таких задач и должны уметь их применять на практике.
• Нестандартные. У таких задач есть способы решения, но их либо мало изучают, либо их использование не очень очевидно. Такой тип задач также называется проблемным или творческим, поскольку для того, чтобы разобраться в том, как нужно решать задачу требуется приложить усилие.
• Оригинальные. На сегодняшний день для таких задач не существует решения.
Чаще всего на занятиях по технической механике решают именно стандартные задачи, которые помогают приобрести нужные навыки и закрепить пройденный теоретический материал. Но некоторые преподаватели могут советовать пытаться решать нестандартные задачи и даже оригинальные, чтобы существенно прокачать, как навыки, так и умственные способности.
Последовательность решения
Какой бы ни была задача, алгоритм её решения будет приблизительно одинаковым. Он выглядит следующим образом:
• Проведение анализа содержания задачи, во время которого кратко записываются её условия и то, что требуется найти.
• Выбор способа решения, а также составление плана, по которому оно будет происходить.
• Непосредственно осуществление решения. Когда задача решена нужно проверить правильность результата. А если её требуется сдавать преподавателю – ещё и правильно оформить.
• Анализ решения. Обычно это обсуждается вместе с преподавателем, но можно самостоятельно проанализировать проделанную работу и сделать выводы, которую могут помочь с последующим выполнением других заданий.
Если на каком-то из этапов возникают сложности, всегда можно использовать решение задач онлайн. Имея перед глазами пример – разобраться будет намного проще. Другой действенный метод, который подходит, когда у вас есть время – сходить на консультацию к своему университетскому преподавателю и попросить его объяснить.
Источник: volgasib.ru
Зачем нужна техническая механика
Механика — это наука о механическом движении и взаимодействии материальных тел.
Техническая механика является одним из разделов Механики, в котором изучаются законы движения тел и общие свойства этих движений.
На основе этих закономерностей разработаны методы и приемы технической механики, позволяющие конструировать сооружения, механизмы и машины, а также производить практические расчеты различных технических и строительных конструкций на прочность, устойчивость, жесткость, т. е. — на работоспособность в заданном интервале нагрузок.
Учебная дисциплина «Техническая механика», изучаемая студентами Каменского агротехнического техникума в пределах рабочих программ для технических специальностей, включает следующие разделы:
Изучение каждого последующего раздела Технической механики для техникумов предполагает знание обучающимся предыдущих разделов, а также базовые знания по общеобразовательным дисциплинам — математике, геометрии, физике.
Теоретическая механика
Раздел «Теоретическая механика» состоит из подразделов:

«Статика» является частью Теоретической механики, изучающей условия, при которых тело находится в равновесии. При этом равновесием считается такое состояние тела, когда оно находится в покое или движется прямолинейно и равномерно.
Методы и приемы, применяемые для решения задач Статики, позволяют определить внешние силовые факторы, благодаря которым тело находится в состоянии равновесия, т. е. по известным значениям внешних сил или моментов, приложенных к телу, осуществить расчет неизвестных силовых факторов (сил, моментов), воздействующих на данное тело.
Выполнение таких расчетов необходимо для осуществления оценки работоспособности конструкций различных сооружений или механизмов при помощи методов и приемов, применяемых в науке «Сопротивление материалов».
«Кинематика» является частью Теоретической механики, и изучает законы движения материальных тел без учета силовых факторов, вызывающих это движение, т. е. с геометрической точки зрения.
Задачи Кинематики сводятся к определению положения тела в пространстве относительно какой-либо системы отсчета в определенный момент времени или через временной промежуток.
Методы и приемы, применяемые при решении задач Кинематики, позволяют производить кинематические расчеты сложных механизмов машин, в которых отдельные детали и узлы совершают относительные перемещения при работе.
«Динамика», в отличие от Кинематики, изучает законы движения материальных тел с учетом силовых факторов, вызывающих это движение.
Методы и приемы, применяемые в Динамике, позволяют производить расчеты движения и перемещения деталей, узлов и механизмов машин, вызываемых приложенными нагрузками и реакциями.
Сопротивление материалов
«Сопротивление материалов» — наука о прочности и деформируемости материалов и элементов строительных и технических конструкций.
Применение методов и приемов Сопротивления материалов позволяет осуществлять расчет технических и строительных конструкций на прочность, жесткость и устойчивость в заданном рабочем режиме.
Изучение этого раздела Технической механики невозможно без знания основ раздела «Статика» курса Теоретической механики.
Детали и механизмы машин
Раздел «Детали и механизмы машин» является прикладным разделом Технической механики. Он изучает возможность практического применения методов и приемов Теоретической механики и Сопротивления материалов при конструировании и проектировании машин, механизмов, сооружений и других инженерных конструкций.
Структура раздела «Детали машин» складывается из составных частей, включающих основные понятия о надежности и работоспособности машин и механизмов, классификацию видов соединений деталей, их свойства и особенности с точки зрения сопротивления материалов, типы и виды механизмов (муфты, опоры, передачи, редукторы и т. п.), а также изучение методов расчета соединений и механизмов по основным критериям работоспособности.
В высших технических учебных заведениях разделы «Сопромат» и «Детали машин» выделены в отдельные предметы, изучаемые студентами по углубленным программам. Обучающимся техническим специальностям среднего профессионального образования (СПО) эти предметы обычно преподаются по упрощенным программам и объединяются в разделы общего курса Технической механики.
Билеты для проверки усвоения знаний при промежуточной аттестации по разделу «Детали машин» можно скачать здесь (документ в формате Word, 600 кБ)
Методические рекомендации и контрольные задания для студентов заочных отделений технических и машиностроительных специальностей:
Примечание: Документы размещены в формате Word, и могут быть сохранены на компьютере или распечатаны на принтере.
Экзаменационные вопросы по Технической механике для студентов:
Теоретическая механика является одновременно интересной и сложно дисциплиной. Главным объектом ее изучения является механическое движение, совершаемое материальными формами. Особенность материи заключается в том, что она должна беспрестанно пребывать в движении. Но говоря о движении, в данном случае имеется в виду не только непосредственное перемещение, но и разные процессы, такие как химические реакции, теплообмен, электрические процессы и пр. Таким образом механическим движением можно назвать даже перемещение самых мелких частиц, в то время когда само тело остается неподвижным и не меняет своего местоположения в пространстве.
Деформация, нагревание, охлаждение — это все примеры механического движения. Будет вполне справедливым предположение о том, что механическое движение — это одно из самых важных процессов, которые характеризуют материальное тело и именно движение должно стать фундаментом для изучения. Понимая всю глубину данного вопроса, учеными была расширены грани изучения механики, что привело к существованию и активному развитию научных отраслей механики. Специалисты производят изучение не только особенностей движения отдельных тел, но также осуществляют решение задач, касающихся проектирования механизмов, сооружений, приборов.
Основой изучения теоретической механики является движение, но то движение, которое не зависит от состава тела, его формы, размера. Науке интересны свойства, особенности механического движения, которое совершается капелькой росы или огромной планетой, микроскопической частичкой пара или огромным космическим кораблем. Для того, чтобы понять механическое движение, теоремехприбегает к приему выделения главного, основного, путем схематического изображения происходящего. При таком подходе удается сконцентрировать внимание на тех аспектах, факторах и процессах, которые провоцируют это движение. А те явления, которые не принимают непосредственного участия в процессе, автоматически отходят на второй план, не мешая этим самым сконцентрироваться на главном.
Такие сложные понятия как материя, пространство, время в теоретической механике присутствуют, но используются в более упрощенной форме. Решение теормех часто использует такое понятие, как материальная точка. Под данным словосочетанием следует подразумевать ничтожно малую частицу, но речь идет не о размерах, а о ее значимости.
Такой точкой может послужить наша планета, по отношению к Солнцу, когда идет процесс изучения особенностей движения Земли. Сама планета кажется ничтожно малой по сравнению с расстоянием к светилу, в таком случае, будет справедливым суждение о том, что все составляющие точки планеты совершают точно такое же самое движение, преодолевая одинаковые отрезки пути. Через понятие материальной точки можно вывести понятие абсолютно твердого тела. Это тело, которое не подвергается деформации, то есть расстояние между двумя соседними точками не меняется.
Теоретическая механика раскрывает много тайн природы, но это всего лишь не большая частица всего, что неизвестно человеку о жизни на Земле. Наука дает базовые знания ля дальнейшего изучения и является основой для других дисциплин. Значение предмета в современном мире постоянно растет, чему способствует стремительное развитие техники.
Перечень экзаменационных вопросов
- Техническая механика, ее определение. Механическое движение и механическое взаимодействие. Материальная точка, механическая система, абсолютно твердое тело.
Техническая механика – наука о механическом движении и взаимодействии материальных тел.
Механика является одной из самых древних наук. Термин «Механика» введен выдающимся философом древности Аристотелем.
Достижения ученых в области механики дают возможность решать сложные практические проблемы в области техники и по существу ни одно явление природы не может быть понято без уяснения его с механической стороны. И ни одно творение техники нельзя создать, не принимая в расчет те или иные механические закономерности.
Механическое движение – это изменение с течением времени взаимного положения в пространстве материальных тел или взаимного положения частей данного тела.
Механическое взаимодействие – это действия материальных тел друг на друга, в результате которых происходит изменение движения этих тел или изменение их формы (деформация).
Материальная точка – это тело, размерами которого в данных условиях можно пренебречь. Она обладает массой и способностью взаимодействовать с другими телами.
Механическая система – это совокупность материальных точек, положение и движение каждой из которых зависят от положения и движения других точек системы.
Абсолютно твердое тело (АТТ) – это тело, расстояние между любыми двумя точками которого всегда остается неизменным.
- Теоретическая механика и ее разделы. Задачи теоретической механики.
Теоретическая механика – это раздел механики, в котором изучаются законы движения тел и общие свойства этих движений.
Теоретическая механика состоит из трех разделов: статики, кинематики и динамики.
Статика рассматривает равновесие тел и их систем под действием сил.
Кинематика рассматривает общие геометрические свойства движения тел.
Динамика изучает движение тел под действием сил.
1. Преобразование систем сил, действующих на АТТ в системы им эквивалентные, т.е. приведение данной системы сил к простейшему виду.
2. Определение условий равновесия системы сил, действующих на АТТ.
Для решения этих задач используется два метода графический и аналитический.
- Равновесие. Сила, система сил. Равнодействующая сила, сосредоточенная сила и распределенные силы.
Равновесие – это состояние покоя тела по отношению к другим телам.
Сила – это основная мера механического взаимодействия материальных тел. Является векторной величиной, т.е. Сила характеризуется тремя элементами:
— линией действия (направлением);
— модулем (числовым значением).
Система сил – это совокупность всех сил действующих на рассматриваемое абсолютно твердое тело (АТТ)
Система сил называется сходящейся, если линии действия всех сил пересекаются в одной точке.
Система называется плоской, если линии действия всех сил лежат в одной плоскости, в противном случае пространственной.
Система сил называется параллельной, если линии действия всех сил параллельны друг другу.
Две системы сил называются эквивалентными, если одну систему сил действующих на абсолютно твердое тело можно заменить другой системой сил, не изменяя при этом состояния покоя или движения тела.
Уравновешенной или эквивалентной нулю называется система сил, под действием которой свободное АТТ может находится в покое.
Равнодействующей силой называется сила, действие которой на тело или материальную точку эквивалентно действию системы сил на это же тело.
Внешними силами называются силы, с которыми части данного тела действуют друг на друга.
Сила, проложенная к телу в какой-либо одной его точке называется сосредоточенной.
Силы, действующие на все точки некоторого объема или поверхности называются распределенными.
Тело, которому никакие другие тела не препятствуют перемещению в любом направлении называется свободным.
- Внешние и внутренние силы. Свободное и несвободное тело. Принцип освобождаемости от связей.
Внешними силами называются силы, с которыми части данного тела действуют друг на друга.
При решении большинства задач статики требуется несвободное тело представить как свободное, что осуществляется с помощью принципа освобождаем о с т и, который формулируется так:
всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их реакциями.
В результате применения этого принципа получается тело, свободное от связей и находящееся под действием некоторой системы активных и реактивных сил.
Условия, при которых тело может находиться в равновесии,выводятся из нескольких основных положений, принимаемых без доказательств, но подтвержденных опытами,и называемых аксиомами статики. Основные аксиомы статики сформулированы английским ученым Ньютоном (1642—1727), и поэтому они названы его именем.
Аксиома I (аксиома инерции или первый закон Ньютона).
Всякое тело сохраняет свое состояние покоя или прямолинейного равномерного движения, пока какие-нибудь Силыне выведут его из этого состояния.
Способность тела сохранять свое состояние покоя или прямолинейного равномерного движения называется инерцией. На основании этой аксиомы состоянием равновесия считаем такое состояние, когда тело находится в покое или движется прямолинейно и равномерно (т. е. ПО инерции).
Аксиома II (аксиома взаимодействия или третий закон Ньютона).
Если одно тело действует на второе с некоторой силой, то второе тело одновременно действует на первое с силой, равной по модулю, ко противоположной по направлению.
Совокупность сил, приложенных к данному телу (или системе тел), называется системой сил. Сила действия какого-либо тела на данное тело и сила противодействия данного тела не представляют собой систему сил, так как они приложены к различным телам.
Если какая-нибудь система сил обладает таким свойством, что после приложения к свободному телу она не изменяет его состояние равновесия, то такая система сил называется уравновешенной.
Аксиома III (условие равновесия двух сил).
Для равновесия свободного твердого тела, находящегося под действием двух сил, необходимо и достаточно, чтобы эти силы были равны по модулю и действовали по одной прямой в противоположные стороны.
Условие, сформулированное в этой аксиоме, является необходимым для равновесия двух сил. Это значит, что если система двух сил находится в равновесии, то эти силы должны быть равны по модулю и действовать по одной прямой в противоположные стороны.
Условие, сформулированное в этой аксиоме, является достаточным для равновесия двух сил. Это значит, что справедлива обратная формулировка аксиомы, а именно: если две силы равны по модулю и действуют по одной прямой в противоположные стороны, то такая система сил обязательно находится в равновесии.
В дальнейшем мы познакомимся с условием равновесия, которое будет необходимо, но не достаточно для равновесия.
Аксиома IV.
Равновесие твердого тела не нарушится, если к нему приложить или удалить систему уравновешенных сил.
Следствие из аксиом IIIи IV.
Равновесие твердого тела не нарушится от перенесения силы вдоль линии ее действия.
Аксиома параллелограмма. Эта аксиома формулируется так:
Равнодействующая двух сил, приложенных к телу в одной точке, равна по модулю и совпадает по направлению с диагональю параллелограмма, построенного на данных силах, и приложена в той же точке.
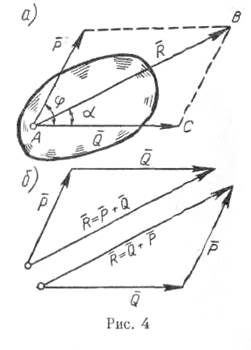
Связями называются тела, ограничивающие перемещение данного тела в пространстве. Сила, с которой тело действует на связь, называется давлением; сила, с которой связь действует на тело, называется реакцией. Согласно аксиоме взаимодействия реакция и давление по модулю равныи действуют по одной прямой в противоположные стороны.
Реакция и давление приложены к различным телам. Внешние силы, действующие на тело, делятся на активные и реактивные. Активные силы стремятся перемещать тело, к которому они приложены, а реактивные силыпосредством связей препятствуют этому перемещению. Принципиальное отличие активных сил от реактивных заключается в том, что величина реактивных сил, вообще говоря, зависит от величины активных сил, но не наоборот. Активные силы часто называют нагрузками.
Направление реакций определяется тем, в каком направлении данная связь препятствует, перемещению тела. Правило для определения направления реакций можно сформулировать так:
направление реакции связи противоположно направлению перемещения, уничтожаемого данной связью.
Если связи считать идеально гладкими, то во многих случаях можно сразу указать направление их реакций. Рассмотрим направление реакций основных видов связей, встречающихся в различных конструкциях.
1. Идеально гладкая плоскость
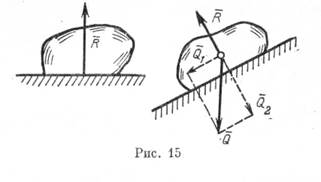
В этом случае реакция R направлена перпендикулярно опорной плоскости в сторону тела.
2. Идеально гладкая поверхность (рис. 16).
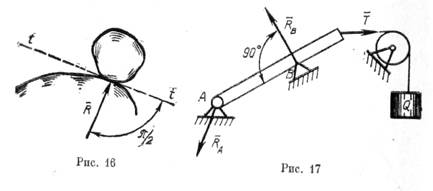
В этом случае реакция R направлена перпендикулярно к касательной плоскости t — t, т. е. по нормали к опорной поверхности в сторону тела.
3. Закрепленная точка или ребро угла (рис. 17, ребро В).
В этом случае реакция Rв направлена по нормали к поверхности идеально-гладкого тела в сторону тела.
4. Гибкая связь (рис. 17).
Реакция Т гибкой связи направлена вдоль с в я з и. Из рис. 17 видно, что гибкая связь, перекинутая через блок, изменяет направление передаваемого усилия.
5. Идеально гладкий цилиндрический шарнир (рис. 17, шарнир А; рис. 18, подшипник D).
В этом случае заранее известно только, что реакция R проходит через ось шарнира и перпендикулярна к этой оси.
6. Идеально гладкий подпятник (рис. 18, подпятник А).
Подпятник можно рассматривать как сочетание цилиндрического шарнира и опорной плоскости. Поэтому будем
считать реакцию подпятника состоящей из двух составляющих RA и YA. Полная реакция R подпятника будет равна векторной сумме этих составляющих.
7. Идеально гладкий шаровой шарнир (рис. 19).
В этом случае заранее известно только, что реакция R проходит через центр шарнира.
8. Стержень, закрепленный двумя концами в идеально гладких шарнирах и нагруженный только по концам (рис. 18, стержень ВС).
В этом случае реакция стержня направлена вдоль стержня, так как, согласно аксиоме III, реакции шарниров В и С при равновесии стержня могут быть направлены только по линии ВС, т. е. вдоль стержня.
- Система сходящихся сил. Сложение сил, приложенных в одной точке.
Сходящимисяназывают силы, линии действия которых пересекаются в одной точке.
В настоящей главе рассматриваются системы сходящихся сил, линии действия которых лежат в одной плоскости (плоские системы).
Представим, что на тело действует плоская система пяти сил, линии действия которых пересекаются в точке О (рис. 10, а). В § 2 было установлено, что сила—скользящий вектор. Поэтому все силы можно из точек их приложения перенести точку О пересечения линий их действия (рис. 10, б).
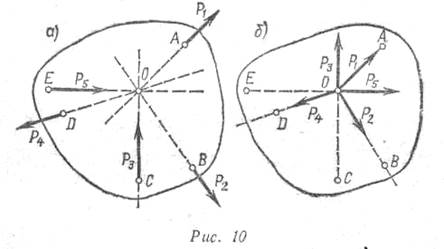
Таким образом, любую систему сходящихся сил, приложенных к различным точкам тела, можно заменить эквивалентной системой сил, приложенных к одной точке. Такую систему сил часто называют пучком сил.
Источник: govorun-otveti.ru
ПРЕДИСЛОВИЕ
Раздел первый КОНЦЕПЦИЯ СИЛ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ
Великое искусство научиться многому — это браться сразу за немногое. Джон Локк 1
ПРЕДИСЛОВИЕ
В предлагаемом курсе излагается инженерная теория сооружений в приложении к исследованию прочности строительных конструкций или «учение о жизни сооружений» 2 . В последнее время она стала называться строительной механикой. Мы считаем ее одной из самых значительных и чрезвычайно полезных для практики наук, являющейся в то же время изящной, увлекательной и действительно научной стороной деятельности строителей. Строительная механика дает возможность предсказывать прочность, устойчивость, долговечность и необходимую надежность проектируемых зданий и сооружений, вырабатывать новые, не существовавшие ранее в окружающем мире конструкции.
1 Джон Локк (D. Locke, 1642-1704) — английский философ, теоретик ассоцианизма — образования идей на базе законов механики.
«Назначение прочных размеров отдельных частей сооружений и механизмов, выявление экономически целесообразных форм сооружений, составление строительного проекта, научные приемы возведения мостов, зданий, покрытий и тому подобное — вот круг практических задач для широкого и благодарного использования законов и выводов строительной механики» 3 .
Инженерная деятельность все более нуждается в надежном инструменте оценки прочности, который дает теория сооружений. Тем не менее, большинство инженеров использует только малую долю знаний, полученных из курса строительной механики. По нашему мнению, существует потребность не столько в том, чтобы «дать больше строительной механики», сколько в том, чтобы лучше выяснить возможности её применения. Ценность теории сооружений для инженеров измеряется её практическим приложением. Она должна стать полезным орудием в руках инженеров и приблизить их к вершинам профессионализма.
Мы проанализировали степень использования знаний инженеров в области теории сооружений у нас в стране, включая доступные нам сведения об обучении и работе инженеров в дореволюционной России и за рубежом. В результате этого мы убедились, что практика требует специалистов с различным уровнем подготовки по строительной механике.
Наибольшая потребность существует в специалистах — инженерах, которые могут оценивать прочность и проектировать сооружения, используя готовые результаты расчетов. От них требуется глубоко понимать саму идею оценки прочности и грамотно, на профессиональном уровне, ею пользоваться. Инженеры этого уровня в своей деятельности опираются на справочники, нормативные материалы или вычислительные средства по расчету сооружений и могут не владеть в совершенстве методами нахождения внутренних усилий, но знать где и как их получить. Таким инженерам под силу решать широкий круг строительных задач — рассчитывать плоские и пространственные сооружения, сооружения, взаимодействующие с основанием и другими средами, стержневые и вантовые системы, мембраны, плиты, оболочки, массивы. Их деятельность ограничивается только полнотой справочной информации
Практика требует также инженеров более высокого уровня, которые умеют не только применять готовые результаты, но и владеют методами их получения и привязки к специфике эксплуатации сооружений. Такие инженеры должны уметь образовывать расчетные схемы реальных конструкций, выявлять их особенности, влияющие на расчет и его результаты, и владеть способами изменения конструктивных схем с целенаправленным изменением усилий. Хотя круг решаемых задач инженерами второго уровня несколько сужается, но значительно повышается глубина понимания работы конструкции, а следовательно, и проработки конструктивных вопросов. В меньшем объеме, но не менее остра потребность в специалистах, умеющих ставить и решать сложные инженерные задачи, больше относящиеся к научным вопросам.
Это такие задачи, как регулирование и оптимизация, разработка методов расчета новых конструктивных схем сооружений, в том числе и выполненных из новых материалов. Необходимы специалисты, которые умеют получать из практики сведения о расчетных свойствах материалов и конструкций, устанавливать критерии прочности, устойчивости, жесткости, Практика требует также инженеров более высокого уровня, которые умеют не только применять готовые результаты, но и владеют методами их получения и привязки к специфике эксплуатации сооружений.
Такие инженеры должны уметь образовывать расчетные схемы реальных конструкций, выявлять их особенности, влияющие на расчет и его результаты, и владеть способами изменения конструктивных схем с целенаправленным изменением усилий. Хотя круг решаемых задач инженерами второго уровня несколько сужается, но значительно повышается глубина понимания работы конструкции, а следовательно, и проработки конструктивных вопросов. В меньшем объеме, но не менее остра потребность в специалистах, умеющих ставить и решать сложные инженерные задачи, больше относящиеся к научным вопросам. Это такие задачи, как регулирование и оптимизация, разработка методов расчета новых конструктивных схем сооружений, в том числе и выполненных из новых материалов. Необходимы специалисты, которые умеют получать из практики сведения о расчетных свойствах материалов и конструкций, устанавливать критерии прочности, устойчивости, жесткости,
В курсе не затрагиваются все достижения строительной механики на настоящий период. В нем рассматриваются и тщательно разбираются вопросы, которые закладывают основу инженерной теории сооружений и дают возможность продолжить самостоятельную работу по профессиональному совершенствованию.
По приглашению частной фирмы «Skilling Ward Magnuson Barkshire Inc.» (SWMB, Сиэтл, США) – мирового лидера в области расчетов и проектирования сложных зданий и сооружений, авторы прошли в этой фирме стажировку. Познакомились с постановкой проектирования и использования методов расчета в работах американских инженеров — конструкторов. Мы убедились, что предлагаемый нами подход используется в реальном рациональном проектировании, но не нашел отражения в обучении.
Идея создания такого курса была принята и поддержана Сергеем Милентиевичем Рудченко (Сержем Рудченко) – вице-президентом фирмы SWMB, Тони Чензом – членом правления фирмы, специалистом в области воздействий на сооружения инерционной внешней среды (землетрясений и ветра). Они сделали ряд замечаний к рукописи и согласились стать соавторами учебника, передав нам свои идеи по методам расчета и оптимизации сооружений.
Авторы считают своим долгом выразить признательность и глубокую благодарность доценту, кандидату технических наук Л.К. Борисенко, первой прочитавшую нашу рукопись; отделу оснований и фундаментов ДальНИИС РААСН; профессору, доктору технических наук В.И. Фёдорову; доктору технических наук В.Е. Абрамову; кандидату технических наук А.А.
Ковалевскому; кафедре строительной механики и теории упругости Санкт-Петербургского технического университета; профессору И.А. Константинову; профессору, доктору технических наук В.Н. Слесаренко за их серьезные советы и замечания, данные при рецензировании рукописи, многие из которых были учтены при ее доработке. Мы будем очень признательны и с благодарностью примем любые другие замечания и предложения, которые поступят в наш адрес.
Главы 1, 5, 7, 8 (первая часть — ванты), 12 и часть приложений написаны А.А. Стоценко; главы 2 и 8 (вторая часть — мембраны) — Н.М. Мальковым; главы 3, 5, 6, 9, 11 и часть приложений — С.И. Доценко; глава 10 первой части учебника написана М.А. Белоконь; часть главы 2 и приложения – Тони Чензом и Сержем Рудченко.
Первая часть курса представлена двумя книгами. В первой помещен раздел, посвященный концепции сил, во второй излагаются особенности приложения концепции сил к конкретным сооружениям.
Источник: www.zimbelmann.ru