Создадим тему для фиксации практического опыта измерений в быту и на стройке.
А то нынче ЕГЭ да пандемия, сколько досок надо на стенку купить посчитать молодежь не может )))
Сначала о трёх красивых способах определения высоты объектов, которые находятся или рядом, или далеко от вас, но в пределах видимости и каждый из способов, если следовать правилам — дает довольно точный результат.
Итак, первый способ: Отражение
Первое: проливаем воду на землю! ..нужно вылить перед собой воду в любую ямку, создав небольшую лужицу — «зеркало». Кроме воды, можно использовать и другие подручные предметы: стекло, плоскую часть лезвия ножа, компакт-диск и пр.
В физике есть закон — закон преломления света, где в однородной среде, углы падения и отражения света равны. Поэтому, достаточно взглядом в зеркале воды поймать самую высокую точку объекта.
Вся суть определения высоты заключается в геометрических законах подобных треугольников и если два угла в них равны, то треугольники подобны, соответственно выполняется равенство коэффициента подобия соотношения сторон:
Теоретическая физика как геометрия XXI века — Андрей Лосев
Х/х = Y/y, поэтому высота объекта Y равна: Y = (X*y)/х, где:
Может возникнуть вопрос «Как зафиксировать точку О?». Ответ: любым камнем, палкой или монетой!
Второй способ: Тень
Суть этого способа та же — подобные треугольники, но создаваемые путем отбрасывания тени от предметов. Надеюсь, на фотографии факт о том, что треугольники подобны не вызывает вопросов — все углы равны
Здесь достаточно установить вертикально любой предмет, замерить высоту и длину его тени. Далее, по соотношению сторон получить искомую высоту:
Третий способ: Определение высоты по фото
Если у вас имеется с собой предмет, размер которого вы знаете, то можно установив его в непосредственной близости от объекта — сфотографировать.
Тогда, в фоторедакторе на телефоне можно отложить одинаковые отрезки до самой верхней точки объекта и высоту вашего предмета умножить на количество отрезков.
Берете линейку, общая длина которой — 31 см. Окладываем 9 целых отрезков и еще 1/3. Теперь, вычисляем: 31 * 9,3 = 288,3 см. или 2 м 88 см.
Предмет под рукой
Берем в руки любой вытянутый предмет, совмещаем его верхушку с верхней точкой объекта (пример — опора электропередач), а нижнюю точку — фиксируем ногтем большого пальца (эта точка в дальнейшем послужит точкой вращения).
Теперь, поворачиваем предмет на 90 град. и откладываем расстояние. Верхушка предмета укажет на точку, которая является проекцией высоты на горизонтальную плоскость. Всё что остается — измерить.
Как узнать глубину колодца? Или, — дерева, на котором сидите
Достаем телефон, открываем приложение «секундомер», нажимаем «Старт» и одновременно выпускаем из рук камушек или какой-нибудь предмет, который в свободном падении не унесет ветром.
Пройденный телом путь равен:
Принимая ускорение свободного падения за 9,8 м/кв.с, получим упрощенную формулу:
Зачем нужны синусы и косинусы?
Источник: imhodom.ru
Проект по математике на тему «Геометрия в архитектуре»

Геометрия в архитектуре Выполнила: ученица 7 «а» класса

Геометрия в архитектуре
Выполнила: ученица 7 «а» класса
Бедюх Вероника
Учитель: Грибачева Юлия Геннадьевна
Прошли века, но роль геометрии не изменилась

«Прошли века, но роль геометрии
не изменилась. Она по-прежнему
остается грамматикой архитектора»
Цель: Изучение геометрических фигур встречающихся в архитектурных сооружениях

Цель:
Изучение геометрических фигур встречающихся в архитектурных сооружениях.
Задачи:
Изучить связь геометрии и архитектуры
Найти геометрические фигуры в зданиях
Создать свое здание из геометрических фигур
ВОПРОСЫ: 1.Что такое архитектура? 2

1.Что такое архитектура?
2.Есть ли взаимосвязь математики и архитектуры?
3.Какие геометрические фигуры чаще всего используют
в архитектуре?
ГИПОТЕЗА: Геометрия является основополагающей наукой в архитектуре

Геометрия является основополагающей наукой в
архитектуре.
Основные понятия: Архитекту́ра (лат

Архитекту́ра (лат. architectura от др.-греч. αρχι — старший, главный и др.-греч. τέκτων — строитель, плотник) — искусство проектировать и строить здания и другие сооружения (также их комплексы), создающие материально организованную среду, необходимую людям для их жизни и деятельности, в соответствии с назначением, современными техническими возможностями и эстетическими воззрениями общества.
Гео» означает «Земля», «метр» — это единица измерения длины (от греческого слова «метрео» — «измеряю»)
«Гео» означает «Земля», «метр» — это единица измерения длины (от греческого слова «метрео» — «измеряю»). Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».
Пирамида» — многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину
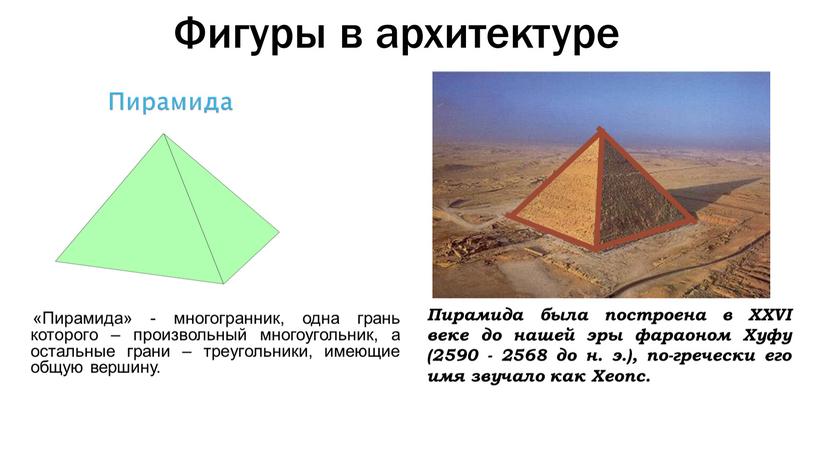
«Пирамида» — многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Пирамида была построена в XXVI веке до нашей эры фараоном Хуфу (2590 — 2568 до н. э.), по-гречески его имя звучало как Хеопс.
Фигуры в архитектуре
Параллелепипед — это призма, в основании которой лежит параллелограмм

Параллелепипед — это призма, в основании которой лежит параллелограмм. Все грани параллелепипеда — параллелограммы. Противоположные грани параллелепипеда равны и параллельны.
Гостиница Мариотт, г.Алма-Ата, Казахстан
Фигуры в архитектуре
Цилиндр — это тело, полученное при вращении прямоугольника вокруг прямой, содержащей его сторону

Цилиндр — это тело, полученное при вращении прямоугольника вокруг прямой, содержащей его сторону.
Фигуры в архитектуре
Сфера — геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки

Сфера — геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки.
Фигуры в архитектуре
Кафе «Sphere» в г.Новосибирск
Три основы архитектуры Произведение архитектуры — это такое сооружение, в котором заложен определенный замысел — идея его создателя

Три основы архитектуры
Произведение архитектуры — это такое сооружение, в котором заложен определенный замысел — идея его создателя. Архитектор вкладывает в свое творение не только научные и технические знания, но и свои мысли, чувства. Древнеримский теоретик искусства Витрувий назвал три основы, на которых держится архитектура:
«Прочность, Польза, Красота»
В Греции возникли основные жанры художественной литературы, искусство театра, складываются предпосылки для блестящего расцвета архитектуры

В Греции возникли основные жанры художественной литературы, искусство театра, складываются предпосылки для блестящего расцвета архитектуры. Используются колонны цилиндрической формы, расположенные параллельно друг другу, крыши формы равнобедренного треугольника.
Восприняв от греков рационально организованную, строгую планировку, римляне усовершенствовали ее и воплотили в городах большего масштаба

Восприняв от греков рационально организованную, строгую планировку, римляне усовершенствовали ее и воплотили в городах большего масштаба.
Готика

Анализируя архитектуру начала XXI века, можно увидеть, что она выходит из рамок элементарной геометрии и развивается в сторону усложнения, прекращения использования стандартных фигур

Анализируя архитектуру начала XXI века, можно увидеть, что она выходит из рамок элементарной геометрии и развивается в сторону усложнения, прекращения использования стандартных фигур.
Начало ХХI века
Проект по математике на тему «Геометрия в архитектуре»

Г.Петропавловск-Камчатский

Проект по математике на тему «Геометрия в архитектуре»

Вывод При постройке, как современных зданий, так и зданий прошлых веков необходимы знания математики

При постройке, как современных зданий, так и зданий прошлых веков необходимы знания математики. Архитектурное формообразование с помощью геометрических построений сохраняется во всех случаях. Эта проблема стояла перед архитекторами прошлых веков, не исчезла она и сегодня.
Архитектура и математика на протяжении веков активно влияют друг на друга. Каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой.
Источник: znanio.ru