Разницу в работе гибких и жестких стержней под воздействием нагрузки люди заметили достаточно давно. Так один из мастеров восточных единоборств, гуляя по зимнему саду, сделал примерно следующий вывод: жесткая сухая ветка под тяжестью налипшего снега ломается, а гибкая ветка прогибается и, сбросив налипший снег, возвращается в прежнее положение с минимумом повреждений.
Если перевести это гибкую поэтическую аллегорию, помогавшую мастеру восточных единоборств привлекать новых учеников, на современный жесткий язык теории сопротивления материалов, то звучать это будет примерно так: если напряжения в рассматриваемом поперечном сечении жесткого элемента конструкции превышают значение нормативного сопротивления, то это приведет сначала к значительным пластическим деформациям, а затем, при увеличении напряжений, и к разрушению жесткого элемента (будет это разрушение хрупким или вязким, принципиального значения не имеет). В то же время гибкий элемент конструкции под действием такой же нагрузки, не разрушится, но потеряет устойчивость.
Гибкость — разбираем физическое качество
Конечно же мне, как и любому другому обычному человеку, гораздо ближе и понятнее определение жесткости и гибкости, данное средневековым мастером восточных единоборств. Но справедливости ради следует отметить, что этот мастер сильно перегнул палку (точнее ветку или, выражаясь языком строительной механики, стержень). Дело в том, что гибкий стержень потеряет устойчивость задолго до того, как значение нагрузки в переводе на напряжения в рассматриваемом сечении достигнет уровня нормативного сопротивления.
Чтобы было более понятно, о чем идет речь, приведу еще один пример.
Если взять достаточно ровный человеческий волос со среднестатистического человека длиной 10 см и попробовать его разорвать руками, то это будет не так уж и просто, для этого следует приложить достаточно большую физическую силу, или выражаясь по-научному, создать достаточно большие растягивающие напряжения в волосе или растягивающую силу около 5 кг (может больше, может меньше, не в этом суть).
А вот если мы попробуем поставить этот волос в вертикальное положение, например, на стол, то волос стоять не будет, а будет сгибаться под действием своего собственного веса, вряд ли превышающего несколько миллиграмм, даже если мы обеспечим ему такое закрепление на верхней опоре, при котором верх волоса не сможет смещаться в горизонтальном направлении, но сможет смещаться в вертикальном направлении.
Вот такое, условно говоря, сгибание и означает потерю устойчивости. Таким образом использовать очень гибкие стержни в качестве сжатых элементов строительных конструкций не имеет никакого смысла.
Между тем, если мы отрежем от этого же волоса кусок длиной 1 см, то этот кусок уже будет сгибаться не так сильно под действием собственного веса и будет обладать некоторой устойчивостью, а если это будет волос длиной 2-5 мм, то об него уже можно сильно уколоться, а волос при этом даже и не согнется.
Как, надеюсь, понятно из вышеприведенного примера, даже для стержня с постоянными геометрическими характеристиками поперечного сечения (радиусом инерции и моментом инерции) его устойчивость зависит от расчетной длины стержня. Другими словами один и тот же стержень может быть и гибким и жестким в зависимости от его расчетной длины.
Гибкая кувалда. #строительство
Абсолютно жестких и абсолютно гибких стержней, пластин и объемных тел не существует, хотя подобные понятия и могут использоваться для упрощения некоторых расчетов. А для того, чтобы оценить жесткость рассматриваемого элемента используется понятие — гибкость элемента. Как правило гибкость элемента обозначается литерой λ.
Для того, чтобы определить гибкость элемента, достаточно расчетную длину элемента lo разделить на радиус инерции i поперечного сечения (при условии, что параметры поперечных сечений постоянны по всей длине элемента):
Примечание: в различных нормативных документах указанные характеристики могут иметь и другие обозначения, но принципиального значения это не имеет.
Таким образом чем меньше гибкость элемента, тем он более жесткий, соответственно чем больше гибкость элемента, тем более он гибкий. А чтобы определить, не является ли такая гибкость чрезмерной для рассматриваемого элемента конструкции, используются таблицы из соответствующих нормативных документов.
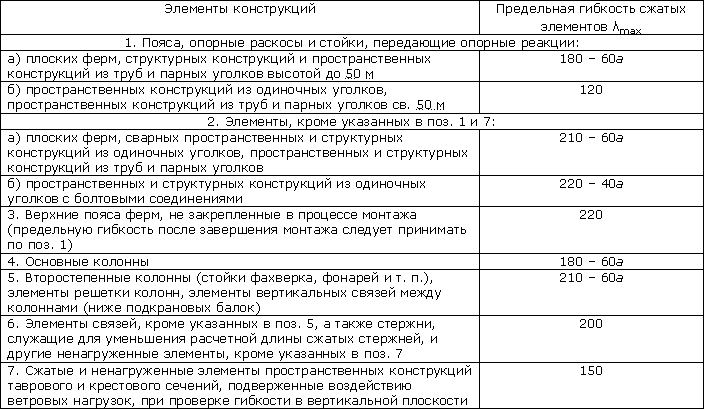
Например, при расчете сжатых элементов стальных конструкций используется такая таблица:
Таблица 19* (согласно СНиП II-23-81 (1990))
А при расчете деревянных конструкций, такая:
Таблица 251.1. Предельные значения гибкости (согласно СНиП II-25-80 (1988))

На значение гибкости влияет и модуль упругости материала. Чем меньше значение модуля упругости, тем больше может быть гибкость. В связи с этим предельно допустимые значения гибкости могут быть разные для элементов из различных материалов, что и отражено в указанных таблицах.
А еще, если приглядеться к таблице 251.1 повнимательнее, то окажется, что предельные значения гибкости устанавливаются не только для сжатых, но для растянутых элементов, для которых гибкость вроде бе не должна иметь значения как в примере с растягиваемым волосом. Впрочем, расчет растягиваемых элементов конструкций — это отдельная тема.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)).
Источник doctorlom.comПредельные гибкости стержней
Элементы конструкций должны проектироваться из жестких стержней. Особенно существенное значение имеет гибкость “” для сжатых стержней теряющих устойчивость при продольном изгибе.
Даже при незначительных сжимающих усилиях гибкость сжатых стержней не должна быть слишком большой, так как гибкие стержни легко искривляются от случайных воздействий, провисают, вибрируют при динамических нагрузках. Поэтому для сжатых стержней устанавливается предельная гибкость, зависящая от назначения стержня и степени его нагружения
, где — расчетное усилие, — несущая способность стержня:
сжатые пояса, а также опорные стойки и раскосы,
передающие опорные реакции……………………………………………… 180-60
прочие сжатые стержни фермы………………………………………………… 210-60
При этом принимается не менее 0,5.
Растянутые стержни конструкций так же не должны быть слишком гибкими, так как могут прогнуться при транспортировании и монтаже.
Стержни должны иметь достаточную жесткость особенно в конструкциях подверженных динамическим воздействиям.
Для растянутых стержней ферм, подвергающихся действию динамической нагрузки, установлены следующие значения предельной гибкости:
растянутые пояса и опорные раскосы………………………………………250
прочие растянутые стержни ферм………………………………………….350
растянутые стержни связей………………………………………………….400
В конструкциях, не подвергающихся динамическим воздействиям, гибкость растянутых стержней ограничивают только в вертикальной плоскости (чтобы предотвратить чрезмерное провисание), установив для всех растянутых стержней предельную гибкость .
Источник studopedia.ruГибкость стержня


Схемы деформирования и коэффициенты при различных условиях закрепления и способе приложения нагрузки
Гибкость стержня — отношение расчетной длины стержня к наименьшему радиусу инерции его поперечного сечения.


Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба . Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.

Расчетная длина вычисляется по формуле:

, где
— коэффициент, зависящий от условий закрепления стрежня, а — геометрическая длина. Расчетная длина, также называется привиденной или свободной.
Понятие приведенная длина впервые ввел Ясинский, для обобщения формулы критической силы Эйлера, которую тот выводил для стержня с шарнирно-опертыми концами. Соответственно коэффициент равен при шарнирных концах(основной случай) одному, при одном шарнирном, другом защемленным , при обоих защемленных концах . Схемы деформирования и коэффициенты при различных условиях закрепления и способе приложения нагрузки, изображены на рисунке. Также, стоит отметить, что формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка и выше.
При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования.
В расчетах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов(длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу.
Источник dic.academic.ru