Метод проектных горизонталей является наиболее наглядным способом решения вопросов проектирования вертикальной планировки улиц и проездов.
Этот метод заключается в том, что на топографическом плане наносят проектные горизонтали нового рельефа, который образуется после изменения естественного рельефа путем планируемых срезок и подсыпок грунта. Он позволяет наглядно изобразить на чертеже характер проектируемой поверхности и степень изменения существующего рельефа для отдельных объектов застройки (улиц, зданий, парков, площадей и др.).
Составление проекта вертикальной планировки территории методом проектных горизонталей начинают с определения высотного положения осей улиц, тротуаров и других элементов застройки.
Проектирование вертикальной планировки территорий улиц выполняют после разработки схемы вертикальной планировки квартала микрорайона, (раздел 6.4 настоящего учебного пособия), принятия общего принципиального высотного решения территории города и определения проектных продольных уклонов по улицам. Это позволяет перейти к более детальной проработке изменения существующего рельефа.
Построение горизонталей на топоплане. Аналитический и графический способ. Инженерная геодезия.
Такую детальную проработку вертикальной планировки осуществляют методом проектных (красных) горизонталей. Их наносят на геоподоснову с показанными на ней улицами, зданиями, площадками и другими элементами застройки. Вертикальная планировка, разработанная в красных (проектных) горизонталях, дает возможность определить не только проектные отметки любой точки территории, но и рабочие отметки. Они в свою очередь позволяют определить участки срезки и подсыпки грунта и объемы земляных работ.
Красные горизонтали в отличие от черных отображают новый проектируемый рельеф застраиваемой территории, новую поверхность, преобразованную в целях решения задач планировки, застройки и благоустройства. Исходя из этого красные горизонтали представляют собой линии проекций на горизонтальную плоскость следа от пересечения рельефа горизонтальными плоскостями с определенным шагом.
Красные горизонтали проектируют на плане территорий масштабов 1:500 и 1:1000. Их наносят на чертеж с интервалом по высоте через каждые 0,1; 0,2; 0,25 или 0,5 м, который называют шагом горизонталей и обозначают /гш.
Проектирование вертикальной планировки городских территорий в красных горизонталях начинают, как правило, с проработки улиц. Перед началом формирования проектных горизонталей оценивают элементы поперечного профиля улицы, например, приведенного на рис. 11.

Рис. 11. Поперечный профиль улицы:
1 — красная линия или линия застройки; 2 — линия кромки проезжей части (верхняя линия бордюрного камня-офаждения); 3 — ось улицы; 4 — лоток; /„, — поперечный уклон тротуара; г„ — поперечный уклон проезжей части; а — ширина полосы проезжей части; b — ширина тротуара; /г, — превышение оси улицы над лотком; /ь — высота бордюра (превышение верха бордюрного камня над лотком); h3 — превышение отметки красной линии над бордюром
Тема 9. Изображения Рельефа (Горизонтали)
Как видно из рис. 11, превышение оси улицы над лотком ht возникает за счет устройства поперечного уклона проезжей части. Его определяют по формуле

где а — ширина полосы проезжей части, м; /„ — поперечный уклон проезжей части, доли единицы.
Превышение линии кромки верха бордюрного камня над лотком hj обосновывают расчетом или принимают по проекту в пределах до 45 см [9, 15].
Превышение красной линии над верхом бордюра h3 определяют по формуле

где b — ширина тротуара, м; — поперечный уклон тротуара, доли единицы.
Фрагмент вертикальной планировки улицы методом проектных горизонталей приведен на рис. 12.

Рис. 12. Фрагмент вертикальной планировки улицы методом проектных горизонталей:
а) — план улицы в горизонталях; б) — поперечный профиль; / — проектные горизонтали; 2 — красные линии; 3 — линии лотков; 4 — ось улицы; 5 — тротуары; 6 — проезжая часть улицы; 7 — отметка бордюрного камня; i — продольный уклон улицы; /, — сдвиг проектной горизонтали на дорожном покрытии от оси 4 к лотку 3; /2 — сдвиг проектной горизонтали по боковой поверхности бордюра за счет возвышения бордюра над лотком; /3 — сдвиг проектной горизонтали на тротуаре от кромки проезжей части к красной линии 2; / -расстояние между проекгными горизонталями на плане
При симметричном поперечном профиле улицы относительно ее оси каждая точка на поверхности покрытия, равноудаленная в ту или иную сторону от нее, будет иметь определенную и одинаковую высотную отметку. Последующие точки на горизонтали равноудаленные от оси улицы, также будут иметь одинаковые отметки.
Таким образом, проектные горизонтали, лежащие на плоскости улицы, будут иметь сдвиги в характерных точках поперечного профиля. Места сдвигов проектных горизонталей находятся на линиях лотков, кромок проезжей части, красных линиях и других, например, краевых границах тротуарных дорожек, линиях отмостков зданий, подошв откосов насыпей и выемок, подпорных стенок.
Величина сдвига проектной горизонтали от оси к лотку /ь скачок горизонтали за счет высоты бордюрного камня /2 и сдвиг ее к красной линии /3 зависят от принятых значений поперечных и продольных уклонов улицы. Расчетную величину вышеупомянутых сдвигов проектных горизонталей на плане улицы определяют по формулам:

где i — продольный уклон улицы, %; hi — превышение оси улицы над лотком, м; h2 — высота бордюра, м; h3 — превышение отметки красной линии над бордюром, м.
Величину сдвига горизонтали 1 откладывают на чертеже вертикальной планировки улицы по линии лотка в сторону, противоположную направлению уклона улицы.
Величину сдвига /2 откладывают на чертеже плана также по линии лотка, но в сторону, совпадающую с направлением уклона улицы.
Величину сдвига /3 откладывают на чертеже плана по красной линии в сторону, также совпадающую с направлением уклона улицы.
Так, например, на участке улицы длиной 400 м между перекрестками Д и Б, см. рис. 8 поперечный профиль представлен двускатной проезжей частью с двумя полосами для встречного движения и тротуарами, см. рис. 11. Применительно к данному рисунку, ширина проезжей части будет равна 7 м, ширина полосы движения — 3,5 м (поперечный профиль симметричен относительно оси), ширина тротуаров — 3,0 м. Поперечные уклоны полос движения равны 20 %о, а тротуаров 30 %о и они направлены к лотку. Продольный уклон улицы равен 0,013 %о и направлен от перекрестка Д к перекрестку Б.
В этом случае превышение оси улицы над лотком /ц, определенное по формуле (21), составит h=a-i„= 3,5×0,020 = 0,07,и, высота камня бордюрного ограждения И2 = 0,20 м, а высота /г3 превышения красной линии над линией верха бордюра, определенная по формуле (22), составит

Тогда сдвиг горизонтали относительно оси улицы на плане полосы проезжей части произойдет по линии лотка в сторону противоположную направлению уклона улицы, то есть в сторону перекрестка Д.
Пример 7. Расчет сдвига проектных горизонталей на плане улицы.

Величину сдвига горизонтали определяют по формуле (23). Она составит

Сдвиг этой горизонтали по вертикальной стенке бордюра, определенный по формуле (24) произойдет в сторону перекрестка Б и составит
Далее сдвиг этой горизонтали произойдет уже по плоскости тротуара, к красной линии 2 (см. рис. 12) в сторону уклона улицы к перекрестку Б, определенный по формуле (25), составит

Соединив на плане точки сдвига (см. рис. 12), получим ломанную симметричную оси улицы проектную горизонталь, подлежащую выносу в натуру при разбивочных работах в строительстве.
Расстояние / между смежными проектными горизонталями зависит от продольного уклона улицы и от шага горизонталей /?ш Его определяют по формуле

где /?ш — шаг горизонталей, м; i — продольный уклон улицы.
Это расстояние между проектными горизонталями на чертеже вертикальной планировки будет одинаковым для всех плановых элементов улицы, в том числе проезжей части, тротуаров, газонов, площадок, имеющих на протяжении улицы неизменную величину продольного уклона. В таком случае все линии проектных горизонталей на фрагментах плана улицы будут параллельны друг другу, см. рис. 12.
Таким образом, линии проектных горизонталей, расходящиеся на чертеже вертикальной планировки под углом в противоположные стороны от оси проезжей части, образуют условные стрелки. Направление этих стрелок из горизонталей совпадает с направлением уклона улицы и водостока.
Так, при шаге горизонталей, равном 0,20 м и продольном уклоне улицы 0,005 расстояние между проектными горизонталями на плане улицы составит

С этим интервалом наносят горизонтали на план улицы в соответствующем масштабе.
Пример 8. Определение расстояния (интервала) между проектными горизонталями в масштабе плана чертежа.
Для участка улицы Г-Д, приведенного на рис. 8, имеющего продольный уклон 0,010 при шаге горизонталей 0,20, расстояние между проектными горизонталями будет равным

Таким образом, убеждаемся, что чем круче продольный уклон улицы, тем чаще располагаются проектные горизонтали с одинаковым шагом проектирования на чертеже вертикальной планировки.
При проектировании вертикальной планировки улиц методом проектных (красных) горизонталей, их отметки должны быть кратны принятому шагу горизонталей. Так, например, при шаге горизонталей 0,20 м проектные горизонтали будут иметь отметки 100,00; 100,20; 100,40; 100,60; 100,80 и т. д. Однако на плане вертикальной планировки улиц полное значение высотных отметок указывают только для главных (базовых) горизонталей (они приводятся кратными одному метру), например, 100,00 или 101,00, а на промежуточных горизонталях указывают только лишь высотные значения кратные величинам шага горизонталей после запятой, например, . 20; . 40; . 60; . 80; 101,00.
В большинстве случаев проектирования высотные отметки перекрестков, как опорных точек топоплана городского квартала, устанавливают без учета величины шага проектных горизонталей. Поэтому на практике проектирования возникает необходимость устанавливать место положения проектных горизонталей на осях улиц с учетом шага проектных горизонталей.
Расстояние от точки пересечения осей улиц перекрестка до ближайшей горизонтали определяют как частное от деления превышения перекрестка над ближайшей к ней проектной горизонталью к величине продольного уклона улицы.
Пример 9. Градуирование проектных горизонталей.
Градуирование проектных горизонталей на плане улицы Д-Г, применительно к фрагменту рис. 8, приведено на рис. 13.

Рис. 13. Пример градуирования проектных горизонталей на чертеже плана улицы Д-Г:
1 — ось улицы; 2 — красные линии; «Д» и «Г» — перекрестки. 99,80 — вертикальная отметка проектной горизонтали; 0,010 — продольный уклон улицы; 10 — расстояние от точки пересечения осей улиц на перекрестке до ближайшей проектной горизонтали, м; 20 — расстояние между проектными горизонталями с шагом 0,20 м.
На рис. 13 проектная отметка на перекрестке улиц Д, см. рис. 8 составляет 99,90, продольный уклон » улицы Д-Г равен 0,010, принятый шаг горизонталей — 0,20. Ближайшая проектная горизонталь на оси улицы у перекрестка в сторону падения рельефа будет иметь отметку 99,80. Разница высот между отметками составит Л’= 99,90-99,80 = 0,10 М
Тогда расстояние по направлению уклона улицы от перекрестка до ближайшей проектной горизонтали составит


На плане улицы смежные проектные горизонтали с шагом 0,20 будут одинаково располагаться друг от друга на расстоянии равном
Таким образом, определив расчетом места расположения проектных горизонталей, их наносят на план улиц.
Пример 10. Варианты вертикальной планировки перекрестков.
Варианты вертикальной планировки участков улиц, приведены на рис. 14-20. Пример решения вертикальной планировки участка многополосной улицы в красных (проектных) горизонталях приведён на рис. 14 [24].

Рис. 14. Пример решения вертикальной планировки многополосной улицы на участке Е-Г, (см. рис. 8):
1 — проектные горизонтали; 2 — горизонтали естественного рельефа; цифры над горизонталями показывают высотное значение горизонталей 3 — красная линия; 4 — ось улицы; 5 — кромка проезжей части; 6 — направление уклона
На участках улиц могут быть понижения и водоразделы. Расположение красных горизонталей в этих случаях проектируют индивидуально для каждого перекрестка. Примеры вертикальной планировки участков улиц в области вогнутого и выпуклого переломов продольного профиля приведены соответственно на рис. 15 и рис. 16.
В пониженных местах лотка улицы в обязательном порядке устанавливают дождеприемные колодцы водосточной сети. Если на участках улиц между перекрестками расположение красных горизонталей зависит от поперечного профиля и продольного уклона, то решение вертикальной планировки территорий определяют особенностями рельефа.

Рис. 15. Вертикальная планировка улицы в точках вогнутого перелома продольного профиля:
1 — дождеприемник; 2 — красная линия; 3 — ось улицы; 4 — направление уклона; 5 — горизонталь; 6 — точка перелома продольного уклона. Цифры над горизонталями — значение их высотных отметок

Рис. 16. Вертикальная планировка участка улицы в точках выпуклого перелома проектной линии (водораздела). Применительно к перекрестку на улице В-Г (см. рис. 8).
Обозначения — приведены в соответствии с рис. 15
Они могут быть разнообразными и поэтому напрямую связаны с организацией поверхностного водоотвода, созданием удобного водостока, движением транспорта и категориями пересекающихся улиц. Из всего многообразия случаев вертикальной планировки перекрестков наиболее характерными и основными решениями могут быть следующие:
1. Перекресток расположен на косогоре рис. 17.

Рис. 17 Вертикальная планировка перекрестка, расположенного на косогоре (применительно к перекресткам Б и В (см. рис. 8)): а) — пересечение равнозначных улиц; б) — пересечение главной и второстепенной улиц; 1 — красная линия; 2 — линия проектной горизонтали; 3 — оси улиц; 4 — направление уклона; 5 — дождеприемник.
В этом случае возможны два основных варианта — пересечение улиц, одинаковых по категории и пересечение неравнозначных улиц, например, магистральной и жилой. В первом случае перекресток может быть односкатным с уклоном, направленным в сторону понижения рельефа, причем переход от двухскатного поперечного профиля улицы к односкатному происходит постепенно. Во втором случае при пересечении неравнозначных по категории улиц основное внимание уделяют главной из них. Вертикальную планировку такого перекрестка проектируют как главный элемент планировки с привязкой к нему элементов второстепенной улицы. При таком решении вертикальной планировки на проезжей части главной улицы создается лоток, пересекающий второстепенную улицу со стороны притока воды к перекрестку.
- 2. Довольно часто встречается расположение перекрестка, когда улица запроектирована по водоразделу (рис. 18, а) или по тальвегу (рис. 18, б). При расположении перекрестка на холме или на бугре (рис. 19, а) поверхностный водоотвод с него будет полностью обеспечен, поскольку уклоны по всем улицам направлены от перекрестка.
- 3. Наиболее неудобным следует считать размещение перекрестка в низине (рис. 19, б), когда к нему поступает вода со всех улиц. Отвод поверхностных вод с такого перекрестка может быть обеспечен лишь закрытой водосточной системой с устройством дождеприемных колодцев по лоткам всех улиц. При этом для обеспечения стока к решеткам колодцев середину перекрестка приподнимают.
Рис. 18. Вертикальная планировка перекрестка расположенного па: а) водоразделе; б) на тальвеге (применительно к перекресткам БиД, см. рис. 8): 1 — дождеприемник; 2 — лоток; 3 — красная линия

Рис. 19. Вертикальная планировка перекрестка, расположенного: а) — на бугре; б) — в низине; 1 — ось улицы; 2 — красная линия; 3 — горизонталь проектная; 4 — дождеприемник; 5 — направление уклонов улиц; 6 — берпнтрихи
В случае, когда перекресток находится в седловине, уклон по двум улицам направлен к перекрестку, а по двум другим — от него (рис. 20).

Рис. 20. Вертикальная планировка перекрестка, расположенного в седловине:
I — ось улицы; 2 — красная линия; 3 — направление уклона улиц; 4 — возвышенная центральная часть площади перекрестка; 5 — бергштрих возвышения; 6 — дождеприемник; 7 — лоток
Для отведения поступающего к нему стока на другие улицы, вертикальную планировку решают путем возвышения середины перекрестка.
Источник: studme.org
Горизонтали
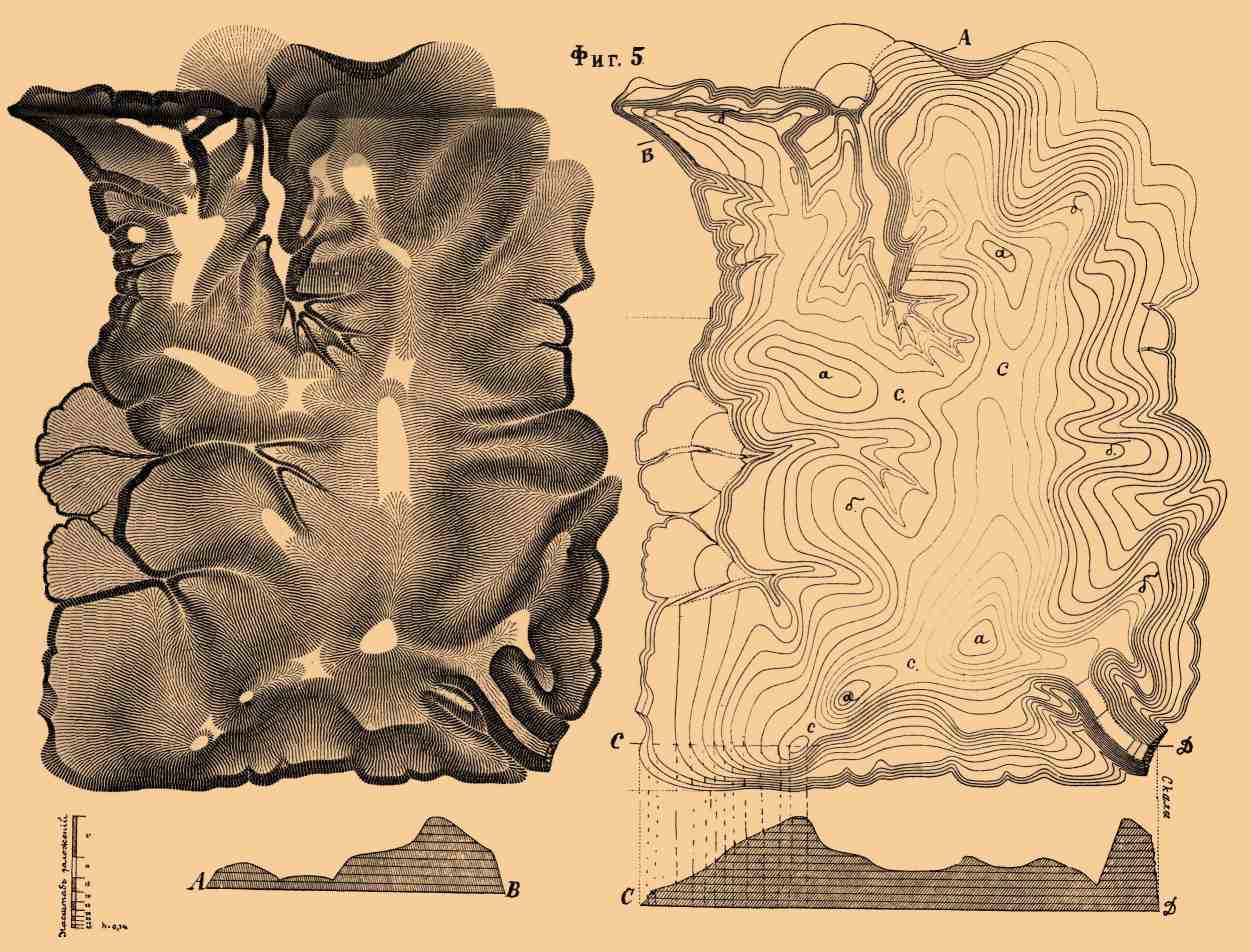
(изогипсы) — линии, соединяющие на местности точки, лежащие на одной высоте над уровнем моря или какой-нибудь основной плоскости, принятой за основание. Для изображения неровностей горизонталями обыкновенно предполагают секущие горизонтальные плоскости одну над другой, на одинаковом вертикальном расстоянии, причем линии пересечения этих мысленно проводимых плоскостей с поверхностью неровностей и образуют именно то, что называется горизонталями. На местности горизонтали обозначаются посредством кипрегеля и мензулы или нивелира.
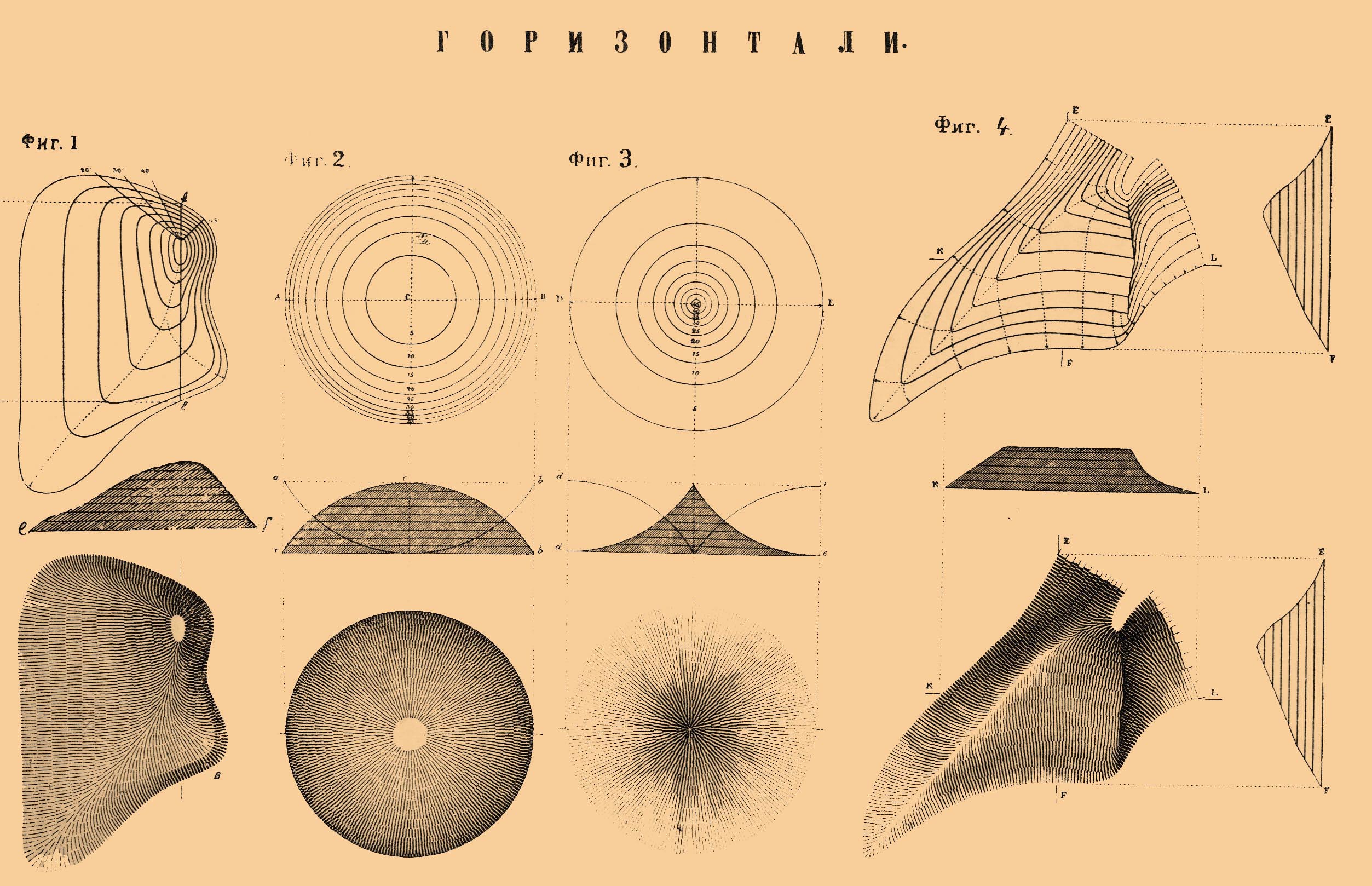
Рельеф местности выражается горизонталями очень точно, и хотя по нему прямо трудно отличить возвышенности от углублений, что, впрочем, становится ясным при ориентировке на планах по болотам, рекам, озерам и пр., все же этот способ выражения неровностей является самым понятным и наглядным. Вершина или дно изображаются наименьшими сомкнутыми объемлемыми горизонталями (фиг.
1, 2 и 3 и на фиг. 5 a.a. ). Отроги гор и лощины — частями горизонталей, растянутыми в виде языков (фиг. 4 и на фиг. 5. б.б. ), а седловины — части рельефа, где сходятся 2 отрога и 2 лощины, — обозначаются четырехугольником, ограниченным кривыми линиями, обращенными внутрь выпуклостями (фиг. 5 сс.).
Равноудаленность по вертикали горизонталей и расстояние между ними дают возможность судить о крутизна скатов. Обозначая эту крутизну через i, через h равноудаленность горизонталей и через b заложение рассматриваемой части ската (расстояние на плане между горизонталями), зависимость выразится уравнением tang i = h/b, так как для каждого плана h известна, b может быть взятым по масштабу, при помощи циркуля, то из уравнения легко определить и i.
Чтобы не делать вычисления, обыкновенно вычерчивается графический масштаб крутостей. Наглядное представление о характере рельефа по желаемому направлению можно получить построением профилей, данными для которых служат самые горизонтали и расстояние между ними.
Очевидно, чем удаленность горизонталей между собой будет меньше, тем точнее будет представлен рельеф, но предел уменьшения зависит от масштаба съемки и характера рельефа. При 100-саженном масшт. равноудаленность равна 1 сажени, при верстовом — 5 и т. д. На наших военно-топографических съемках 1/2 верстового масшт. равноудаленность горизонталей равна 2 саженям, причем для выражения отлогостей скатов допускаются вспомогательные горизонтали.
При определенном масштабе, горизонтали вполне характеризуют местность; чем расстояние между ними ближе, тем круче скаты. На прилагаемом листе чертежей свойства горизонталей вырисовываются очень ярко. Для составления профили (напр. по направлению CD, фиг.
5) поступают так: если масштаб высот и расстояний один и тот же, то окладывают на горизонтальной линии все точки пересечения прямой, по которой желаем составить профиль, с горизонталями, и в каждой точке восстанавливают перпендикуляры, на которых и откладывают соответственное число частей вертикального масштаба, после чего остается только соединить все отмеченные точки; если же масштаб высот увеличен в 10 раз, что иногда нарочно делается ввиду небольших возвышений или углублений сравнительно с их горизонтальными размерами, то прежде чем откладывать высоты, надо или увеличить расстояние между горизонталями в 10 раз, тогда местность будет выражена в масштабе высот, или наоборот, уменьшить в 10 раз высоты — тогда все будет выражено в масштабе горизонталей. Иногда для большей рельефности горизонтали покрываются штрихами (см. Штрихи).
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон . 1890—1907 .
Полезное
Смотреть что такое «Горизонтали» в других словарях:
Горизонтали — линии, соединяющие точки одинаковой высоты над ур. м. С помощью Г. на топографических картах отображают особенности рельефа поверхности разл. участков земной коры. Син.: изогипсы. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н … Геологическая энциклопедия
ГОРИЗОНТАЛИ — (изогипсы) линии на карте, соединяющие точки земной поверхности с одинаковой абсолютной высотой и в совокупности передающие формы рельефа … Большой Энциклопедический словарь
ГОРИЗОНТАЛИ — линии на карте или плане местности, получающиеся от пересечения земной поверхности горизонтальными плоскостями, отстоящими друг от друга на одинаковых расстояниях. Г., соединяя между собой на плане или карте все точки поверхности, имеющие одну и… … Технический железнодорожный словарь
горизонтали — Линии на плоскости или поверхности, параллельные горизонтальной плоскости проекций. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика
Горизонтали — ГОРИЗОНТАЛИ, линіи, соединяющія точки мѣстности съ равными высотами надъ ур. м., при чемъ берегъ моря представляетъ Г. съ высотою ноль, или, иначе, линіи, получающіяся отъ пересѣченія мѣстности гориз ными плоскостями на опред. равныхъ между собою … Военная энциклопедия
Горизонтали* — (изогипсы) линии, соединяющие на местности точки, лежащие на одной высоте над уровнем моря или какой нибудь основной плоскости, принятой за основание. Для изображения неровностей горизонталями обыкновенно предполагают секущие горизонтальные… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
горизонтали — (изогипсы), линии на карте, соединяющие точки земной поверхности с одинаковой абсолютной высотой и в совокупности передающие формы рельефа. * * * ГОРИЗОНТАЛИ ГОРИЗОНТАЛИ (изогипсы), линии на карте, соединяющие точки земной поверхности с… … Энциклопедический словарь
ГОРИЗОНТАЛИ, ИЗОГИПСЫ — (Horizontal) линии, соединяющие на плане точки местности, имеющие одинаковые высоты. Служат для изображения на плане рельефа местности. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
Горизонтали — изогипсы (от греч. ísos paвный и hýpsos высота), линии на географической карте, соединяющие точки местности с одной и той же высотой относительно уровня моря (Мирового океана) и дающие представление о рельефе земной поверхности. Г.… … Большая советская энциклопедия
ГОРИЗОНТАЛИ — изогипсы, линии, соединяющие на топографическом плане местности точки, имеющие одинаковые высоты над принятым условным горизонтом уровнем. Г. дают изображение рельефа местности и наносятся по данным геодезической съемки … Сельскохозяйственный словарь-справочник
Источник: dic.academic.ru
Проектные горизонтали
Проектные горизонтали – это линии, которые графически отображают форму проектируемого рельефа или преобразованную поверхность площадки.
Схемы вертикальной планировки
Вертикальная планировка строительной площадки – это планировка естественных или искусственных грунтовых масс для создания проектного рельефа местности под проектируемое здание или сооружение.
Вертикальная планировка площадок выполняется для подготовки территории строительства и является начальным этапом работ нулевого цикла.
Составление схемы вертикальной планировки является завершающим этапом проектирования площадок. Данная схема отличается от схемы анализа рельефа тем, что на ней показываются исключительно конечные результаты анализа, а при каждой опорной точке записываются рабочие и проектные отметки, даже если они совпадают по своему значению. Все условные обозначения и надписи на таких чертежах выполняются черным цветом.
Метод профилей является одним из самых распространенных методов вертикальной планировки. Он применяется при проектировании поперечных и продольных профилей для отдельных линейных городских объектов (например, автомобильных и железных дорог). В садово-парковом проектировании метод профилей используется для разработки трасс улиц и дорог.
Продольный профиль определяет высотные положения улицы. Его проектирование основывается на вычерчивании проектной линии и определении продольных уклонов.
Порядок работ систематизирован и состоит из нескольких этапов. Сначала методом интерполяции координат естественных горизонталей определяются отметки существующих поверхностей (черные отметки). Затем проводится линия, соединяющая все эти отметки. Данная линия называется черной линией и отражает существующий рельеф площадки.
Вторым шагом наносятся проектные отметки (красные отметки) точек проектируемой поверхности. Линия, соединяющая красные отметки, называется красной линией.
В последнюю очередь определяются рабочие отметки. Они представляют собой разность черных и красных значений. Рабочие отметки записываются со стороны красной линии. В случае насыпи их записывают сверху, при выемке грунта – снизу.
Готовые работы на аналогичную тему
Поперечный профиль проектируется по разрезам перпендикулярно оси улицы или дорожной сети. Чаще всего горизонтальный масштаб для подобных чертежей выбирают 1:200, вертикальный – 1:10 (1:20).
В поперечном профиле дорог и улиц из соображений обеспечения стока вод предусматривается поперечный уклон, который обычно направлен к лоткам проезжих частей. Различают двускатные и односкатные поперечные профили. При этом последние применяются для ширины проезжей части до 10,5 метров и одностороннем движении транспорта.
Метод проектных горизонталей
Данный метод является этапом более детальной проработки рельефа. Он осуществляется путем изображения горизонталей, которые с графической точки зрения отображают форму проектируемого рельефа или преобразованную поверхность площадки.
Красные горизонтали представляют собой проекции линий пересечения проектируемых поверхностей и горизонтальных секущих на горизонтальную плоскость. Такие горизонтали проводятся через 0,1, 0,2 или 0,5 метра. Данное расстояние принимается единым и называется шагом горизонталей.
На основании разработанной вертикальной планировки, а также генерального плана участка разрабатывается вертикальная планировка отдельных участков территории. Данный метод предполагает совмещение на одном листе план и профиль, что дает полное представление о сечении проектируемого рельефа в любом направлении.
Что касается горизонталей, то их расположение относительно друг друга может дать представление о характере изменения рельефа после проведения вертикальной планировки. Если проектная горизонталь расположена ниже одноименной черной горизонтали в сторону падения уклона, необходима подсыпка грунта, выше – срезка.
Следует заметить, что основными параметрами, определяющими взаиморасположение горизонталей, являются уклон и шаг горизонталей (характеристика, выражающая превышение одной горизонтали над другой).
Для того, чтобы в полной мере отобразить планировку рельефа улицы в красных горизонталях, необходимо располагать информацией о поперечном профиле улицы на участке между красными линиями, а также задаться шагом горизонталей. Продольный уклон улиц на участке между двумя опорными точками принимается по схеме вертикальной планировки, которая выполняется по методу проектных отметок.
Также метод красных горизонталей применяется для проработки улицы бордюрного поперечного профиля, который состоит, например, из полосы зеленых насаждений, проезжей части и тротуара.
При проектировании вертикальных планировок с помощью красных горизонталей необходимо следить за тем, чтобы отметки этих горизонталей были кратны принятому шагу. Так, при шаге горизонталей 0,2 метра проектные горизонтали должны иметь отметки 100,00, 100,20 и т.д. Исходные отметки для проектирования вертикальных планировок чаще всего выражаются числами не кратными принятому шагу.
В связи с тем, что исходные отметки чаще всего не кратны принятому шагу горизонталей, в первую очередь необходимо определить точку расположения ближайшей проектной горизонтали. Процесс определения положения вершин красных горизонталей называют градуированием.
Источник: spravochnick.ru
Горизонтали и их свойства. Способы построения горизонталей
Рельефом называют совокупность неровностей земной поверхности. Знание рельефа местности необходимо при проектировании и строительстве железных и автомобильных дорог, осушительных и оросительных систем, промышленных предприятий и т. д. Существует несколько способов изображения рельефа на топографических картах и планах. Наиболее старый способ – это изображение рельефа штрихами, наносимым на карту по особой шкале.
Рельеф местности может быть также изображен подписями отметок ряда точек или отмывкой красками различного тона. Однако наилучшим способом оказалось изображать рельеф горизонталями в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами.
Чтобы правильно изобразить рельеф, необходимо знать его основные формы.
Существует пять основных форм рельефа (рисунок 3.5):
— возвышенность (рисунок 3.5, а);
— котловина (рисунок 3.5, б);
— хребет (рисунок 3.5, в);
— лощина (рисунок 3.5, г);
— седловина (рисунок 3.5, д).
На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами.
Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности.
Для наглядности некоторые горизонтали подписывают, кроме того у них ставят черточки-бергштрихи, показывающие направление ската местности.
Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м.
Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
i = h / d = tg υ. (3.6)
Уклон и угол наклона линии местности являются основными характеристиками крутизны скатов. Чем больше угол наклона, тем круче скат местности. Из формулы (3.6) следует, что чем меньше заложение d или чем чаще горизонтали на плане, тем скат местности круче.
Изображение горизонталями котловины, лощины, хребта и седловины показано на рисунке 3.5. Котловина (впадина) – замкнутое углубление поверхности (см. рисунок 3.5, б). Самую низкую часть впадины называют дном, боковые поверхности – скатами, а линию слияния с окружающей местностью – бровкой.
| а) | б) |
| в) | г) |
| д) |
Рисунок 3.5 – Основные формы рельефа
Хребет – вытянутая в одном направлении возвышенность с двумя скатами (см. рисунок 3.5, в). Линию встречи скатов в верхней части называют водоразделом (водораздельной линией).
Лощина – вытянутое в одном направлении понижение с двумя скатами (рисунок 3.5 г). Линию встречи скатов в нижней их части называют водосливом или тальвегом (водосливной линией).
Седловина – понижение между двумя возвышенностями (см. рисунок 3.5 д). Наиболее низкую точку между возвышенностями называют перевалом.
Бергштрихи на картах и планах обычно показывают по водораздельным и водосливным линиям. Подписи на горизонталях делают так, чтобы основание числа показывало направление ската. Горизонтали вычерчивают коричневым цветом. Каждую десятую или пятую из них вычерчивают утолщенной линией.
Из сущности горизонталей вытекают их свойства:
— горизонталь – это замкнутая кривая линия, все точки на которой имеют одинаковую высоту, кратную высоте сечения рельефа;
— горизонтали на плане не могут раздваиваться и обрываться; если горизонталь не замыкается в пределах плана, она замыкается за его пределом;
— горизонтали не должны пересекаться между собой, так как они получаются пересечением земной поверхности плоскостями, лежащими на разных высотах;
— чем чаще горизонтали на плане, тем уклон местности больше, или чем меньше заложение, тем скат круче;
— водораздельные и водосливные линии и направления максимального уклона горизонтали пересекают под прямым углом.
Высота сечения рельефа устанавливается в зависимости от масштаба плана и характера рельефа местности так, чтобы горизонтали не сливались между собой. В Республике Беларусь приняты следующие высоты сечения рельефа при масштабах съемки:
| 1:500 – h = 0,25; 0,5 м; 1:1000 – h = 0,25; 0,5; 1 м; 1:2000 – h = 0,5; 1; 2 м; | 1:5000 – h = 0,5; 1; 2; 5 м; 1:10000 – h = 1; 2,5; 5 м. |
Для более полного изображения и удобства чтения рельефа на картах и планах подписывают отметки характерных точек рельефа (вершин холмов, дна котловин, перевалов и т. д.). Например, на рисунке 3.5, б подписана отметка дна котловины 98,7 м.
Способы построения горизонталей по отметкам точек.
Для проведения горизонталей на плане нужно нанести характерные точки, снятые на местности, и выписать их высоты. Те точки, между которыми земная поверхность не имеет переломов, т. е. имеет постоянный уклон, соединить линиями. Далее на каждой линии интерполированием находят точки пересечения ее горизонталями и отмечают высоты этих горизонталей.
Соединив затем плавными кривыми линиями точки с одинаковыми высотами, получают изображение рельефа местности на плане. Таким образом, задача построения горизонталей на плане в основном сводится к умению находить проекции точек пересечения горизонталями линий, отметки концов которых известны, при этом высота сечения рельефа должна быть уже установлена. Эта задача называется интерполированием горизонталей, т. е. нахождением промежуточных значений высот горизонталей по отметкам точек. Интерполирование можно производить аналитическим или графическим способом.
Аналитический способ. По известным высотам точек А и В и расстоянию d между ними (рисунок 3.6, а) необходимо найти величины расстояний d1 и d2 от точки А до точек М0 и N0 c отметками Нм и HN, равными отметкам горизонталей.
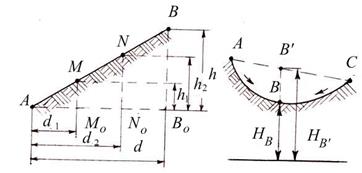
Рисунок 3.6 – Аналитический способ интерполирования
Из подобия треугольников АВВО, АММО и ANNO находим:
На плане откладывают отрезки d1 и d2 и получают точки MO и NO, у которых подписывают их отметки. Следует отметить, что интерполирование горизонталей проводят только по линиям с равномерным скатом. На рисунке 3.6, б показан случай неправильной интерполяции между точками А и С с неравномерным скатом местности. Как видно из рисунка, вместо действительного положения точки В будет получена точка В ‘ и соответственно вместо НВ будет получена неверная высота НВ ‘ .
Графический способ. Интерполирование этим способом выполняют с помощью миллиметровой или прозрачной бумаги. При наличии миллиметровой бумаги ее прикладывают к линии плана АВ. По отметкам концов АВ строят профиль этой линии. Проектируя затем на линию плана точки пересечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N.
При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.
Решение инженерных задач по планам и картам
Современные топографические карты и планы дают богатый и разносторонний материал о той местности, которая на них изображена условными знаками. Зная условные знаки, при изучении карты можно получить необходимые данные о населенных пунктах, гидрографии, растительности, дорожной сети, рельефе и других объектах. Кроме того, при помощи карты можно решать ряд инженерных задач: определять географические и прямоугольные координаты точек, измерять дирекционные углы и азимуты направлений, определять высоты точек, уклоны заданных линий, водосборные площади бассейнов, строить профили земной поверхности, производить трассирование и т. д.
Рассмотрим решение этих задач более подробно .
1. Прямоугольные координаты точек на карте определяют от линии координатной (километровой) сетки, абсциссы и ординаты которых подписываются в общегосударственной системе координат.
2. На картах подписываются также широты и долготы точек пересечения параллелей и меридианов, ограничивающих данный лист. Кроме того, на обрамляющих карту рамках вычерчиваются одноминутные деления широты и долготы. Соединяя точки одноименных делений северной и южной сторон рамок, а также западной и восточной, получим на карте сетку меридианов и параллелей, пользуясь которой, можно определить широту и долготу любой точки карты.
3. Дирекционный угол или азимут линии можно измерить транспортиром непосредственно на карте, как угол между направлением линии километровой сетки или истинного меридиана и направлением заданной линии. Обычно на полях карты всегда дается для данного листа сближение меридианов и склонение магнитной стрелки, используя которые, по формулам (2.3) – (2.4) можно вычислить все углы ориентирования.
4. Высоту (отметку) любой точки, например С (рисунок 3.8, а), можно определить, если через нее провести линию ab по кратчайшему расстоянию между горизонталями.
Из подобия треугольников abb1 и acc1, учитывая, что h – высота сечения рельефа, d – заложение (рисунок 3.8, б), получим cc1 = ac bb1 / ab или Δh = Δd h /d. (3.7)
Отметка точки НС будет равна отметки точки a плюс величина Δh:
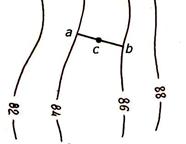 |
Рисунок 3.8 – Определение отметки точки
В формуле (3.7) величины d и Δd измеряют на плане, а высота сечения рельефа известна на плане или карте.
5. Определяют уклон линии. Уклоном линии называется тангенс угла наклона этой линии или отношение высоты сечения рельефа к заложению (рисунок 3.8, б):
i = tg υ = h / d. (3.8)
Для определения уклона можно воспользоваться формулой (3.6) или (3.8). Из формул следует, что уклон – безразмерная величина. Его выражают в процентах (% – сотых долях) или в промилях (‰ – тысячных долях). Для определения угла наклона линии (крутизны ската) υ из формулы (3.8) можно получить:
υ = arctg i = arctg (h / d). (3.9)
Угол наклона можно также определить графически с помощью графика заложений, который обычно приведен под южной рамкой карты. При отсутствии графика заложений его можно построить. Для этого на горизонтальной прямой АВ от точки А откладывают равные отрезки произвольной величины (рисунок 3.9). Из точек отложения к прямой АВ восстанавливают перпендикуляры. Используя формулу (3.8), определяют заложение:
d = h / tg υ = h / i, (3.10)
где h – высота сечения рельефа
Подставляя в формулу (3.10) величины υ, равные 1, 2, 3 о и т. д., последовательно получают заложение для каждого из углов наклона υ и откладывают их на перпендикулярах в масштабе плана или карты. Полученные на перпендикулярах точки соединяют плавной кривой линией, а внизу подписывают углы наклона.
Для определения угла наклона по графику заложений с помощью циркуля-измерителя измеряют величину заложения на плане (ab) и прикладывают раствор измерителя к графику заложений так, чтобы одна игла измерителя находилась на основании графика, а вторая располагалась параллельно вертикальным линиям графика, и перемещают измеритель по горизонтальной линии основания вправо или влево до совпадения верхней иглы с кривой графика. По росписи графика заложений отсчитывают крутизну ската. Например, на рисунке 3.9 при заложении ab крутизна ската υ = 1,4 о . По графику заложений можно решать и обратную задачу, т. е. по заданной крутизне ската определять величину заложения на плане.
6. Для построения по заданному направлению АВ на плане профиля линии местности при помощи полоски бумаги линия с плана переносится на миллиметровую бумагу с отметками всех точек пересечения линии с горизонталями. Далее в заданном вертикальном масштабе по вертикальным линиям откладывают отметки точек, и все вершины перпендикуляров соединяют прямыми линиями. Получают профиль местности по заданному направлению (рисунок 3.10).
7. Для проведения на карте или плане линии заданного уклона по графику заложений или, исходя из формулы (3.10), определяют величину заложения соответствующего уклона. Затем циркулем-измерителем откладывают это заложение в масштабе плана и, начиная от первой горизонтали, пересекающей линию, последовательно засекают смежные горизонтали. Полученная ломаная линия будет иметь заданный уклон (рисунок 3.11).
 |
Рисунок 3.10 – Продольный профиль
8. Водосборные площади по картам и планам определяют для вычисления расхода воды с бассейнов при строительстве плотин, мостов, труб и т. п. Водосборной площадью или бассейном водотока называют ту площадь, с которой поверхностные воды после дождя или таяния снега по условиям рельефа местности и его геологического строения стекают в данный водоток. Границами водосборной площади служат водораздельные линии и линии наибольшего ската. На карте или плане сначала намечают границы водосборной площади до створа строящегося сооружения, а затем при помощи планиметра или палетки определяют площадь в пределах установленной границы (рисунок 3.12).
Решение практических задач на планах и картах подробно изложено в учебно-методических пособиях по выполнению расчетно-графических и лабораторных работ по геодезии.
Определение площадей по картам и планам
При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам.
Существует три основных способа определения площадей:
— графический, когда площадь вычисляется по данным, взятым графически с плана или карты;
— аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям – координатам вершин участка;
— механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.
Часто эти способы применяются комбинированно. Например, общая площадь участка определяется аналитическим способом, а площадь внутренних контуров – графическим или механическим. Рассмотрим каждый из вышеуказанных способов более подробно.
Графический способ определения площадей. Сущность этого способа состоит в том, что данный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже – прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры.
Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка. Ошибка определения площади графическим способом равна примерно 1:100 – 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.
Площади криволинейных контуров удобно определять при помощи палеток. Палетка (рисунок 3.13) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Пользование палеткой видно из рисунка 3.13. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура.
Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Точность определения площадей палеткой несколько ниже, описанного выше графического способа. Главная ошибка при этом происходит от оценки частей неполных квадратов на глаз. Более высокую точность дают палетки с меньшей стороной квадрата.
Аналитический способ определения площадей. Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.
Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 3.14), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 3.14 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:
Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:
или в общем виде для n-угольника можно записать
Подобным образом из уравнения (3.11) после преобразований можно получить:
Согласно формулам (3.12) и (3.13) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.
Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (3.12) и (3.13). Погрешность вычисления площадей аналитическим способом не превышает 1:1000 вычисляемой площади.
Механический способ определения площадей. Определение площадей механическим способом производится при помощи планиметров. Наибольшее распространение получил полярный планиметр (рисунок 3.15), состоящий из полюсного и обводного рычагов.
Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом – штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3.15), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.
Червячная передача устроена так, что одному обороту колеса соответствует поворот циферблата на одно деление. Рядом с колесом находится верньер, по которому отсчитывают десятые доли делений колеса или тысячные доли его оборота.
Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья – по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3.15 составит 3215.
При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Р при полюсе вне фигуры вычисляют по формуле
а при полюсе внутри фигуры –
где С – цена деления планиметра;
g – постоянное число планиметра.
Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число.
При проверке планиметра должны быть проверено выполнение следующих условий:
— счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний. Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.
— плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага. Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.
Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры.
Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:
После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры.
Постоянное число планиметра:
При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.
При определении площадей планиметром необходимо соблюдать следующие правила:
— план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;
— положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;
— обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;
— для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.
Точность определения площадей планиметром зависит от формы и размера обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10–30 см 2 ) ошибка определения площади планиметром не превышает 1:200 величины площади.
Источник: studopedia.ru
Горизонтали топографические

Горизонтали являются одним из способов отображения рельефа. Таких способов много, но на плоской поверхности наглядно изобразить высоту местности лучше всего при помощи них.
Что такое горизонтали?
Горизонтали -это линии на плане или карте, соединяющие все точки на местности с установленной высотой. В зависимости от масштаба и задач карты или плана выбирается промежуток высоты, через который пускается горизонталь. Чем более мелкий масштаб, тем больше промежуток.
Более мелкий масштаб, это когда на карте видно бОльшую площадь, чем при более крупном. Карта всей России имеет более мелкий масштаб, чем карта любого ее города. Масштаб 1:1000 крупнее масштаба 1:100.
Для чего нужны?
С помощью горизонталей наглядно изображают рельеф местности на плоских (двумерных) планах. Обычно они имеют коричневый цвет или его вариации. Выглядит горизонталь плавной изогнутой линией, проходящей по всему чертежу, за исключением домов и других объектов техногенного происхождения. То есть горизонтали передают информацию о высотах только для незастроенной земной поверхности. На застроенной ее не проводят, так как план будет слишком переполнен линиями и горизонтали как бы будут перечеркивать весь чертеж.

Для более точного понимания сути горизонталей ниже отображено яблоко. Представим, что наша земля, это оно. И горизонтали режут его на ровные части по высоте — сверху вниз. И если вынуть любой кусок из яблока, то мы увидим контур какой-то конкретной горизонтали.
Какие бывают?
Бывают основные и утолщенные. При топографической съемке масштаба 1:500 горизонтали проводятся через каждые 0.5 м высоты. Каждая четвертая горизонталь, с высотой кратной 2 метрам, является утолщенной. Остальные- более тонкие основные.
Где применяются?
Горизонтали применяются на планах масштабом от 1:100 (крупномасштабные планы) до 1:50000 (зачастую обзорные, например топоплан для Роснедра). Как говорилось выше в городах горизонтали не применяются. Вместо этого пишется высота в принятой системе координат в разных точках на плане — на бордюре, около углов строений и т.д.
Чтобы выразить рельеф на плоскости еще прибегают к цветовому решению. То есть раскрашивают карту в цвета с оттенками от синего до красного. Чем более насыщенный красный — это выше, чем синее синий — тем ниже. Но это очень приблизительная градация, поэтому используется для обзорных карт мелких масштабов.
Источник: domzem.su