Теорема Пифагора — пожалуй, одна из самых известных теорем в математике вообще и геометрии в частности. На самом деле несмотря на то, что она названа именем Пифагора, она была известна еще за тысячу лет до него.
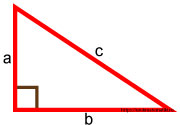
Терема Пифагора гласит следующее: если у нас есть прямоугольный треугольник с катетами a, b и гипотенузой c , то сумма квадратов катетов равна квадрату гипотенузы.
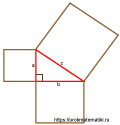
Мы знаем, что величина a 2 описывает площадь квадрата со стороной a . То есть, если мы на катете a построим квадрат, на катете b построим квадрат и на гипотенузе c построим квадрат, мы получим, что площадь квадрата со стороной a + площадь квадрата со стороной b равняется площади квадрата со стороной c . Это, так называемое, геометрическое объяснение теоремы Пифагора: сумма площадей квадратов, построенных на катетах, равняется площади квадрата построенного на гипотенузе.
Теорема Пифагора для чайников)))
Если вы построите вместо квадратов любые подобные фигуры, допустим полуокружности, то сумма этих площадей, построенных на катетах, все равно будет равняться площади фигуры, построенной на гипотенузе.
Доказательство теоремы Пифагора
На сегодняшний день известно более 200 различных доказательств теоремы Пифагора. Мы воспользуемся одним из них.

Для того, чтобы доказать теорему Пифагора, мы рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c .
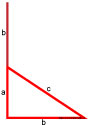
Достроим прямоугольный треугольник со сторонами a, b, c до квадрата следующим образом: катет длиной a мы достраиваем на расстояние b .
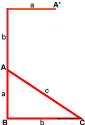
Из конца получившегося отрезка a+b проводим перпендикуляр на расстояние a .
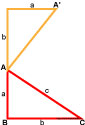
Объединив точки A и A’ , получаем исходный треугольник, только перевёрнутый.
8 класс, 16 урок, Теорема Пифагора
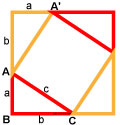
Аналогично достраиваем с других сторон. Получается квадрат со стороной a+b .
- Площадь квадрата со стороной a+b равна квадрату стороны (a+b) .
- Квадрат состоит их четырех одинаковых прямоугольных треугольников и внутренней фигуры — квадрата. Площадь каждого прямоугольного треугольника — половина произведения его катетов.
- Внутренняя фигура — квадрат имеет стороны c .
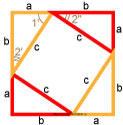
Докажем, что внутренняя фигура — это квадрат .
У фигуры все стороны равны — значит это ромб. Если доказать, что один угол является прямым, то все остальные углы будут прямыми.
Из свойств прямоугольного треугольника мы знаем, что острые углы прямоугольного треугольника равны 90°.
∡1′ + ∡2′ = 90°
Т.к. все показанные треугольники равны, то ∡2′ = ∡2″ и ∡1′ + ∡2″ = 90°
Отсюда следует, что 180° — ∡1′ + ∡2″ = 90° — это угол между сторонами внутренней фигуры — ромба.
В нашем случае было доказано, что этот ромб является квадратом.
Преобразовав описанное выше в формулу, получаем:
a + b 2 = 4 · 1 2 a b + c 2
Раскроем формулу квадрата суммы:
a 2 + b 2 + 2 a b = 2 a b + c 2
a 2 + b 2 + 2 a b = 2 a b + c 2
Мы доказали теорему Пифагора.
Задачи на тему «Теорема Пифагора»
Египетский треугольник
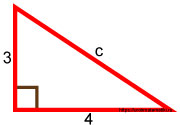
Дано:
Прямоугольный треугольник с катетами 3 и 4 .
Требуется найти его гипотенузу.
Решение:
Обозначим гипотенузу как c и воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
3 2 + 4 2 = c 2
9 + 16 = c 2
25 = c 2
c = 5
Ответ: гипотенуза прямоугольного треугольника с катетами с катетами 3 и 4 равна 5 .
Прямоугольный треугольник со сторонами 3 , 4 и 5 называется египетским.
Пифагорова тройка
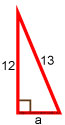
Дано:
Гипотенуза равна 13 , а один из катетов равен 12 .
Требуется найти второй катет.
Решение:
Обозначим второй катет как a и снова воспользуемся теоремой Пифагора: сумма квадратов катетов равняется квадрату гипотенузы:
12 2 + a 2 = 13 2
144 + a 2 = 169
a 2 = 169 — 144
a 2 = 25
a = 5
Ответ: второй катет a прямоугольного треугольника с гипотенузой 13 и одним из катетов 12 равен 5 .
Обратите внимание, что в первом и втором примерах стороны треугольников получились целыми числами. Такие числа, которые удовлетворяют теореме Пифагора, называются пифагоровыми тройками.
Равнобедренная трапеция
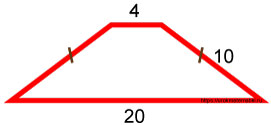
Дано:
Равнобедренная трапеция. Верхнее основание равно 4 , боковая сторона равна 10 , нижнее основание равно 20 .
Требуется найти площадь трапеции S .
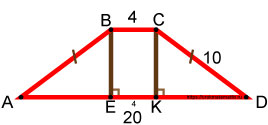
Обозначим углы трапеции точками A, B, C, D . Из точек B и C опустим перпендикуляры на сторону AD в точки E и K соответственно.
Рассмотрим четырёхугольник BCKE . Этот четырёхугольник является прямоугольником. Стороны BC и EK взаимно параллельны, и стороны BE и CK тоже взаимно параллельны, причём один из углов прямоугольника BCKE имеет 90°. Это доказывает, что прямоугольник BCKE является прямоугольником.
В прямоугольнике противоположные стороны равны. Если отрезок BC равен 4 , то EK тоже равен 4 .
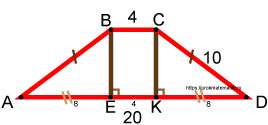
Так как наша трапеция равнобокая, то левый и правый треугольники равны между собой, т.к. имеют одинаковые катеты и одинаковые гипотенузы. По признакам равенства прямоугольных треугольников они равны. Это означает, что отрезки AE и KD равны между собой.
Отрезок AD равен 20, отрезок EK равен 4 . Значит, на отрезки ( AE + KD ) остаётся 20 — 4 = 16 . Значит, каждый из них равен 8 .
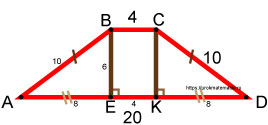
Рассмотрим любой из треугольников, например, ABE . Он является прямоугольным. Один из катетов равен 8 , а гипотенуза равна 10 .
По теореме Пифагора можем найти BE . Сумма квадратов катетов равна квадрату гипотенузы:
BE 2 + 8 2 = 10 2
BE 2 + 64 = 100
BE 2 = 100 — 64
BE 2 = 36
BE = 6
Таким образом мы нашли высоту трапеции.
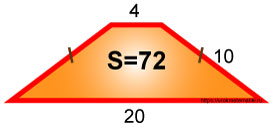
Теперь можно найти площадь трапеции S .
Площадь трапеции равна полусумме оснований умноженной на высоту трапеции.
Ответ: площадь трапеции S равна 72 .
Применение теоремы Пифагора
Наиболее частое применение теоремы Пифагора можно увидеть в строительстве. В современные дальномеры встраивается функция, косвенно определяющая размеры стороны (треугольника) при измерении двух других сторон.
Рассмотрим два теоретических примера, когда необходимо произвести расчёт конструкции крыши, а в другом примере научимся позиционировать стены дома относительно друг друга под углом 90°.
Расчет стропильной системы крыши
Задача крайне упрощённая для точных расчётов стропильной системы крыши, но достаточно понятная, чтобы донести принципы расчёта по теореме Пифагора.
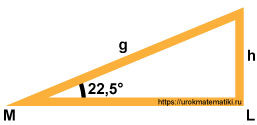
Дано:
Расстояние между мауэрлатом ( M ) и лежнем ( L ) (они лежат на стенах) известно и равно 5 метрам.
Крыша покрыта металлочерепицей, минимальный рекомендуемый угол наклона которой является 22,5° .
Стойка ( h ) расположена строго перпендикулярно лежню ( L )
Требуется найти длину стропила ( g ) и высоту стойки ( h ).
Чтобы найти высоту стойки ( h ) можно применить теорему синусов. Для этого необходимо найти угол, который лежит против известной стороны. Зная, что сумма углов треугольника равна 180° вычисляем угол, лежащий против известной стороны ML
180° — 90° — 22,5° = 67,5°
Теперь подставляем в формулу известные значения для определения высоты стойки ( h ) по теореме синусов:
sin 22,5° h = sin 67,5° ML
h = 5 · sin 22,5° sin 67,5° = 2.0710678118655
Также по теореме синусов можно найти и длину ( g ), но нас интересует теорема Пифагора.
Поэтому зная, что квадрат гипотенузы (в нашем случае это g ) равен сумме квадратов катетов (в нашем случае это h и расстояние между точками ML ), получаем:
Подставляя в формулу ранее вычисленные и известные значения, получаем:
Ответ: полученные значения исчисляются в метрах. В строительстве округление до миллиметров таких деталей — более чем точно. Поэтому округляя значения стропилы g и стойки h , получаем:
Египетский треугольник
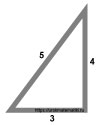
Ещё одним примером практического применения теоремы Пифагора в строительстве может служить использование египетского треугольника.
Чтобы на плоской поверхности вывести угол 90°, необходимо взять верёвку и отложить на ней три расстояния: 3, 4, 5 . И не важно в каких единицах измерения будут отрезки, возможно эти единицы измерения будут выдуманными вами.
Соедините верёвку в треугольник, как показано на изображении, и натяните стороны полученного треугольника.
Угол между сторонами 3, 4 всегда будет равен 90°. По нему можно разметить стены или фундамент будущего дома.
Источник: urokmatematiki.ru
Презентация «Применение теоремы Пифагора в строительстве» по математике – проект, доклад

Слайд 1

Слайд 2

Слайд 3

Слайд 4
Слайд 5

Слайд 6
Слайд 7

Слайд 8
Презентацию на тему «Применение теоремы Пифагора в строительстве» можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на соответствующий текст под плеером. Презентация содержит 8 слайд(ов).
Слайды презентации

Выполнили: Я.В.Востриков, Н.В.Зарековская МБОУ СОШ № 3 г.Канска учащиеся 9 класса Руководитель: Г.Г. Мухометзянова учитель математики
Применение теоремы Пифагора в строительстве ( исследование)

Актуальность данного исследования.
существует около 500 различных доказательств этой теорем (геометрических, алгебраических, механических), которые свидетельствуют о числе ее конкретных реализаций. В 2011-2012 учебном году на ГИА включены задания по геометрии, в решение которых применяется теорема Пифагора. Объект исследования: теорема Пифагора. Предмет исследования: применение теоремы Пифагора при расчетах в строительстве

выявить кто открыл теорему Пифагора, познакомиться с различными доказательствами теоремы Пифагора, применить ее при строительстве крыш домов, сооружений на даче. Задачи: 1.Познакомиться с биографией Пифагора и деятельностью пифагорейского союза. 2. Обосновать название «теоремы Невесты». 3. Уточнить историю открытия теоремы Пифагора.
4. Систематизировать наиболее интересные доказательства теоремы Пифагора. 5. Оформить результаты своего исследования в виде таблиц. 6. Показать применение теоремы Пифагора в строительстве.

Великий древнегреческий ученый Пифагор родился на острове Самос в VI веке до нашей эры. В молодости побывал в Египте, где учился у жрецов. Посетил халдейских мудрецов и персидских магов, познакомился с восточной математикой. В Древней Греции, он основал пифагорейский союз,где была доказана «теорема Пифагора».

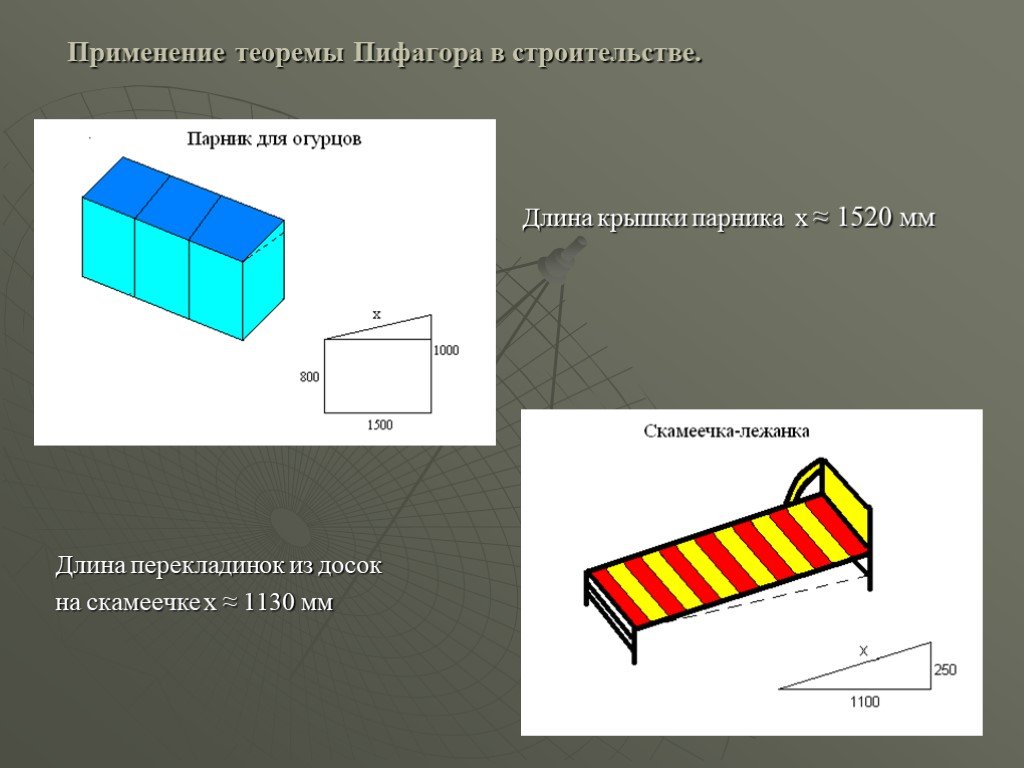
Длина крышки парника х ≈ 1520 мм
Применение теоремы Пифагора в строительстве.
Длина перекладинок из досок на скамеечке х ≈ 1130 мм

Двускатная крыша (в разрезе)
В доме задумано построить двускатную крышу (форма в сечении). Применяя теорему Пифагора можно рассчитать длины стропил АВ и АD, если часть балки СВ = 1м, высота стены АС = 1,5м. При длине стропил 1,8м и 1,7м угол наклона между крышей и стеной 60۫ ۫ .

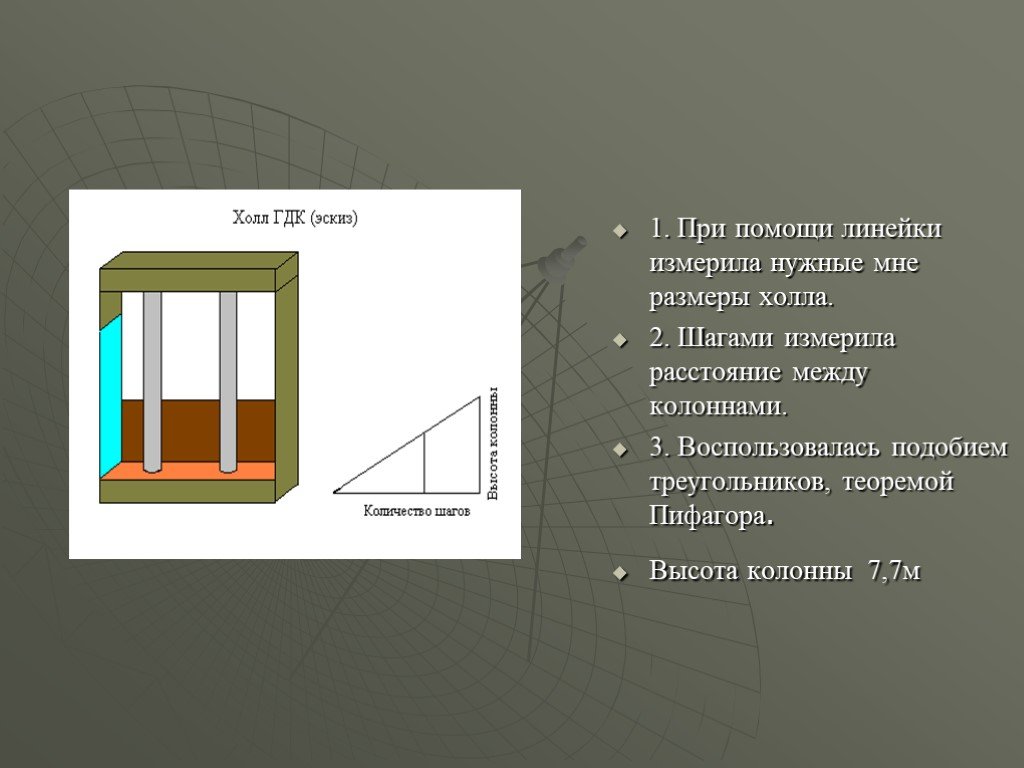
1. При помощи линейки измерила нужные мне размеры холла. 2. Шагами измерила расстояние между колоннами. 3. Воспользовалась подобием треугольников, теоремой Пифагора. Высота колонны 7,7м

Теорема Пифагора позволяет находить длину отрезка (гипотенузы), не измеряя его, она открывает путь с прямой на плоскость, с плоскости в пространство. Этим определяется ее важность для геометрии и математики. Вычисление стороны прямоугольных треугольников по двум известным сторонам; построение прямых углов; нахождение высоты объекта и определение до недоступного предмета применяются в строительстве и машиностроении.
Список похожих презентаций

Cпособы доказательства теоремы Пифагора
a2+b2=c2 c a b П. Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым .

Алгебраические кривые в полярной системе координат и их применение в природе и технике
Цель: познакомиться с кривыми, не изучаемыми в школьном курсе алгебры, найти для них примеры в природе и технике. Локон Аньези. плоская кривая, геометрическое .

Арифметические действия в двоичной системе счисления
ЗАДАНИЕ «ТЕЗИСЫ». Верно ли каждое из следующих утверждений? Если «Да», то записывайте 1. Если «Нет», то записывайте 0. В результате должно получиться .

Арифметические операции в позиционных системах счисления
Ответьте на вопросы:. Какие системы называются НЕПОЗИЦИОННЫМИ? Какие системы называются ПОЗИЦИОННЫМИ? Какое число называют – ОСНОВАНИЕ позиционной .

Арифметическая прогрессия в древности
Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э., содержат примеры задач на арифметическую прогрессию. Каких-либо .

Арифметические действия в двоичной системе счисления
Самостоятельная работа. Вариант I Вариант II. Выполнить действия в двоичной системе счисления:. 1) 101012 + 1012 2) 101012 + 10102 3) 1000012 – 1102 .

«Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. .

Арифметическая и геометрическая прогрессии в заданиях ГИА
Цели урока: Обобщить и систематизировать знания учащихся по данной теме. Разобрать типичные задания встречающихся в сборниках для подготовки к ГИА. .

Биография М.В. Ломоносова в цифрах
=2 =0,3 =3,6 =0,04 =1 =0,8 =0,42 =21,2 М И Ш А Н С К О Е. Ломоносов Родился в с. Мишанинском Архангельской губернии. 8 ноября 1711. Длина = 15,5 м .

Больше в несколько раз, меньше в несколько раз
ЦЕЛЬ УРОКА. раскрытие смысла слов “больше (меньше) в несколько раз”. Расположите числа в порядке возрастания. 18, 9, 45, 27, 36, 72, 54, 63, 9, 18, .

5.Уравнение в полных дифференциалах. Интегрирующий множитель
Теорема:. Для того чтобы дифференцировать выражение , где и определены и непрерывны в области плоскости и имеют в ней непрерывные частные производные .

Без математики, друзья, в жизни нам никак нельзя
Актуальность. Математика находится в тесной связи со всеми естественными, гуманитарными, точными науками и др., математические знания применяются .

«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной .

«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной .

«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План .
«Смешанные дроби. Представление смешанного числа в виде неправильной дроби».
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. .

«Симметрия в архитектуре Старого Оскола»
Остановка 1. Главная улица города – улица Ленина. Мы находимся в центре нашего города у здания администрации. Какие приемы использовал архитектор, .

Бийская крепость в цифрах и фактах
Бийская крепость в цифрах и фактах. Цели урока:. Познакомиться с историей возникновения родного города Научиться определять временные промежутки и .

Алгебра в 9 классе.
Функция их свойства и графики. Сформулируйте определение чётной функции, определение нечётной функции. Не является ни чётной, ни нечётной. чётная .

Биссектриса угла в треугольнике
Задачи УЧЕБНИК А О В С D 80º ? 180º- 80º= 100º 100º Ответ:155º, 25º, 155º. Задача №535 биссектриса ? Определение. Биссектриса угла – это луч с началом .
Конспекты
Web -разработка. Применение производной.10 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА КОНСТРУИРОВАНИЯ УРОКА С ИСПОЛЬЗОВАНИЕ СРЕДСТВ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ. Учитель Беломестнова Наталья Петровна. Предмет, .
Виды углов в планиметрии
Лабораторно-практические занятия по геометрии в 7 классе. Лабораторно-практические занятия имеют важное значение, особенно при обучении детей с .
Видеть и слышать, или как не потеряться в мире информации
Конспект – сценарий урока, разработанного учителями МОУ Брызгаловская СОШ Ивановой Е.Б. и Колпаковой Л.В. Тема: «Видеть и слышать, или как не потеряться .
Введение в теорию вероятностей
9 класс. Тема: Введение в теорию вероятностей.(90 мин.). Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, .
Бородинское сражение в математических задачах
Открытый урок «Бородинское сражение в математических задачах». Карташова Ирина Викторовна , учитель математики МБОУ «Бирюковская СОШ». Техническое .
Большие и малые числа в химии
МКОУ «Средняя общеобразовательная школва №5. . города Ершова Саратовской области». . Бинарный урок. Большие и малые числа в химии. Провели .
Арифметический способ отбора корней в тригонометрических уравнениях
Конспект урока для 11 класса на тему «Арифметический способ отбора корней в тригонометрических уравнениях». Цели и задачи урока:. . . повторение .
I признак равенства треугольников в задачах
ТЕМА УРОКА:. I. признак равенства треугольников в задачах. ТИП УРОКА. : закрепление изученного материала. КОНТИНГЕНТ УЧАЩИХСЯ:. 7 класс. .
+ двухзначных и однозначных чисел в пределах 100
УРОК МАТЕМАТИКИ. Тема:. + двухзначных и однозначных чисел в пределах 100 (урок обобщения). Цель:. Создание условий для формирования УУД при .
Источник: prezentacii.org