Кэ что это такое в строительстве

Оптимальная расчетная конечно-элементная модель. Способы соединения частей КЭ-модели

Скачать статью в формате PDF — 4.15 Мбайт

Главная » CADmaster №1(95) 2021 » Машиностроение Оптимальная расчетная конечно-элементная модель. Способы соединения частей КЭ-модели

«Оптимальная расчетная конечно-элементная модель — какая она?» — такой чаще всего не проговоренный вслух, а порою даже и неосознанный вопрос непременно рождается (как минимум в подсознании) у каждого инженера-расчетчика при получении ТЗ на решение задачи методом конечных элементов (рис. 1). Каковы критерии этой самой расчетной модели-мечты? Пожалуй, здесь стоит отталкиваться от известного философского принципа «Всё следует упрощать до тех пор, пока это возможно, но не более того». Вот только как применить этот принцип к нашим научным и инженерным задачам?

Критерии оптимальной расчетной конечно-элементной модели

Поразмыслив, проанализировав свой практический опыт, я выделил три основных критерия оптимальной расчетной конечно-элементной модели:

Строительные Лайфхаки и Хитрости. Ты обязан это увидеть

1. физические допущения, адекватные целям расчета;
2. упрощения детализации геометрии, правильный выбор видов конечных элементов и способов их соединения;
3. качественная сетка КЭ.

Эта статья является продолжением моего доклада «Особенности использования различных видов конечных элементов в Femap с NX Nastran», прочитанного на Femap Symposium 2020. В докладе я обзорно рассказывал о применении этих трех критериев на примере конкретных проектов, а здесь подробнее остановлюсь на втором критерии.

Чтобы определиться с концепцией рациональной расчетной схемы, в которую мы будем преобразовывать (чаще упрощать) исходную геометрическую модель, нужно в первую очередь хорошо понимать физику моделируемого процесса; знать, изменение каких факторов и параметров более всего влияет на результат. Необходимо разбираться в видах конечных элементов (линейные, поверхностные, объемные), способах соединения частей модели и в особенностях их совместного применения. Причем части модели могут состоять из конечных элементов разных видов. Да, и конечно же нужно знать возможности используемого вами расчетного комплекса. Расчетный комплекс Femap с NX Nastran поддерживает все виды конечных элементов и позволяет соединять области, состоящие из конечных элементов разных видов, всеми основными способами.

Способы соединения частей КЭ-модели

Существует три основных способа соединения (в более широком смысле слова — взаимодействия) частей конечно-элементной модели, передачи нагрузки и внутренних усилий между частями модели. Эта классификация носит условный характер, и я ввел ее для удобства восприятия информации расчетчиками-практиками.

Первый способ — соединение конечных элементов разных частей модели «узел в узел» (рис. 2). Это самый классический способ. При его использовании граница перехода между частями модели не оказывает никакого собственного влияния. Фактически решатель работает с единой сплошной моделью, а части модели существуют только для удобства работы пользователя в пре- и постпроцессоре.

Информационное моделирование при строительстве зданий

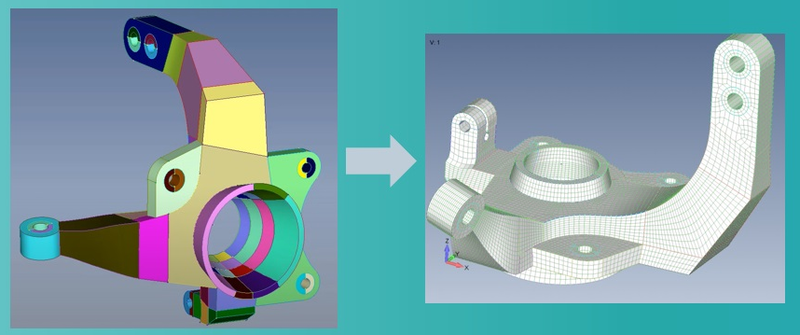
Рис. 2

Второй способ — это применение MPC-связей (multiple point constraint). MPC соединяют узел с узлом (тогда это скорее SPC — single point constraint) или узел с группой узлов с помощью жестких или интерполяционных элементов (рис. 3).

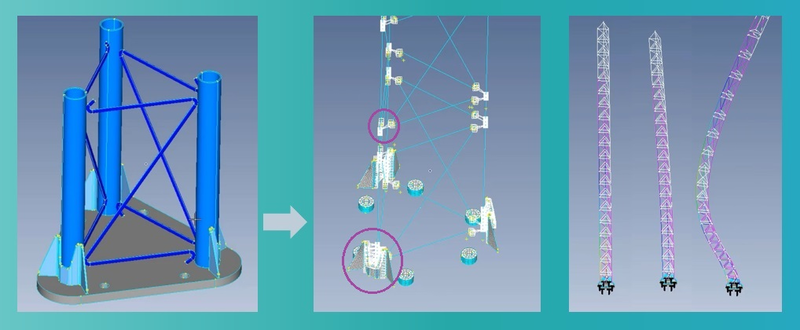
Рис. 3

Третий способ — применение контактных поверхностей различных типов (например, «склейка» или «с трением»). При использовании этого способа пользователь выбирает контактирующие поверхности, а препроцессор автоматически определяет взаимодействующие узлы (рис. 4).

Эти три способа соединения (взаимодействия) даже более чем различны. Например, целые классы задач (штамповка, соударение тел) просто невозможно решить без применения контактных поверхностей. При решении же более простых задач (линейная статика, модальный анализ), как правило, есть возможность выбрать, как именно упрощать геометрию и какой способ соединения частей модели применить.

Практические примеры

Разберем и проанализируем по вышеописанным критериям модель радиобашни, изображенную на рис. 3. Расчетная модель радиобашни используется для определения собственных форм и частот колебаний металлоконструкции башни, потому точный учет жесткости силовых элементов исключительно важен. Это очень ответственная задача — собственные частоты колебаний необходимы для определения динамической составляющей ветровой нагрузки (см. Руководство по расчету зданий и сооружений на действие ветра к СП 20.13330.2010 «Нагрузки и воздействия»).

Модель радиобашни состоит из конечных элементов трех видов:

• несущие вертикальные круглые трубы и связи соединяющих (также из круглых труб) смоделированы балочными конечными элементами;
• ребра жесткости, соединяющие трубы и опорную плиту, смоделированы поверхностными КЭ;
• опорная плита смоделирована солидами (объемными КЭ).

В модели также применены три основных способа соединения частей конечно-элементной модели:

• узел в узел соединены части модели (линейные), между которыми нет зазоров;
• с помощью MPC-связей соединены линейные элементы (имитирующие трубы), между которыми есть зазоры. Кроме того, посредством MPC-связей соединены элементы ребер жесткости и вертикальных труб;
• контакты заданы между нижней гранью ребер жесткости и поверхностью опорной плиты.

Я считаю эту расчетную модель очень грамотным результатом преобразования геометрической модели в расчетную, так как модель достаточно проста, но при этом в ней учтены основные конструктивные элементы, определяющие жесткость конструкции. Как правило, в простых строительных САПР отсутствуют инструменты, позволяющие соединять конечные элементы различных видов (в случае радиобашни не было бы возможности смоделировать опорные элементы). То есть в простой строительной САПР конструкцию радиобашни удалось бы смоделировать лишь из одних труб, разбив их балочными конечными элементами. В этом случае податливость основания не учитывается и собственные частоты колебаний конструкции оказываются завышены.

Элементы RROD, RBAR, RBE1, RBE2 и RTRPLT — это жесткие элементы. Элементы RBE3 и RSPLINE — интерполяционные, они не являются жесткими (рис. 5).

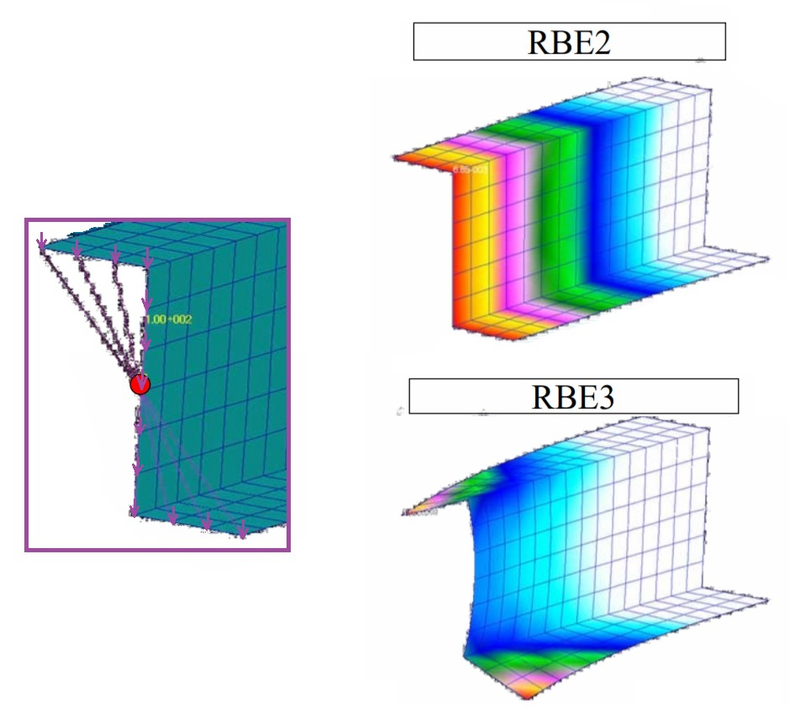
Рис. 5

Элемент RBE2 использует уравнения связи, чтобы связывать степени свободы зависимых узлов со степенями свободы независимого узла. Относительные деформации между зависимыми узлами отсутствуют, то есть соответствующие элементы не деформируются. Варьируя настройки степеней свободы RBE2 в поле Dependent (Зависимый), можно получить WELD — сварное соединение (активируя шесть степеней свободы TX, TY, TZ, RX, RY, RZ) или BOLT — болтовое соединение (активируя TX, TY, TZ, вращения остаются свободными).

В отличие от элементов RBE2, элемент RBE3 не добавляет конструкции дополнительную жесткость, то есть RBE3 — это интерполяционный элемент. RBE3 можно использовать как инструмент распределения нагрузки и массы в КЭ-модели, аналогичный «грузовым площадям» в строительных системах автоматизированного проектирования. Нагрузки в виде сил и моментов, приложенные к зависимому узлу, распределяются в независимые узлы пропорционально весовым коэффициентам (рис. 6).

Для большинства случаев в настройках степеней свободы RBE3 в поле Independent (Независимый) не рекомендуется активировать вращательные степени свободы (рис. 7).

Подробнее специфика применения RBE2 и RBE3 представлена в статье наших партнеров из компании «КАДИС»: «RBE2 в сравнении с RBE3 в Femap c NX Nastran».

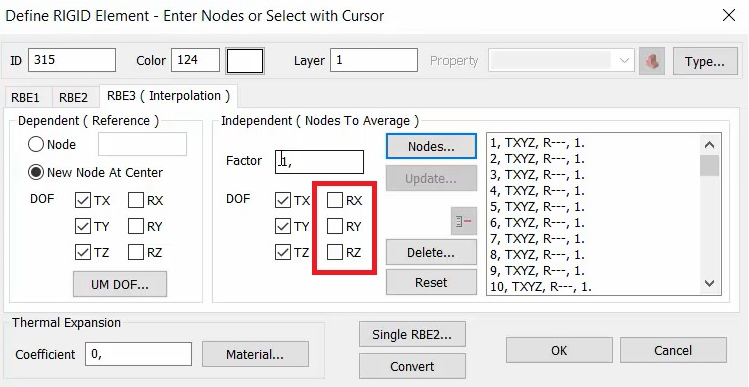
Рис. 7

Но вернемся от теории к практике и разберем типовую задачу расчета кронштейна, на примере которой отлично видно, что, неправильно задав способ соединения частей модели, мы получим принципиально неверное решение. Кронштейн закреплен на П-образной пластине с помощью двух болтов. К отверстиям кронштейна приложена сила с направлением вдоль пластины.

П-образная пластина разбита поверхностными конечными элементами, а кронштейн — объемными КЭ. С учетом толщины пластины пластина и кронштейн соприкасаются (рис. 8).

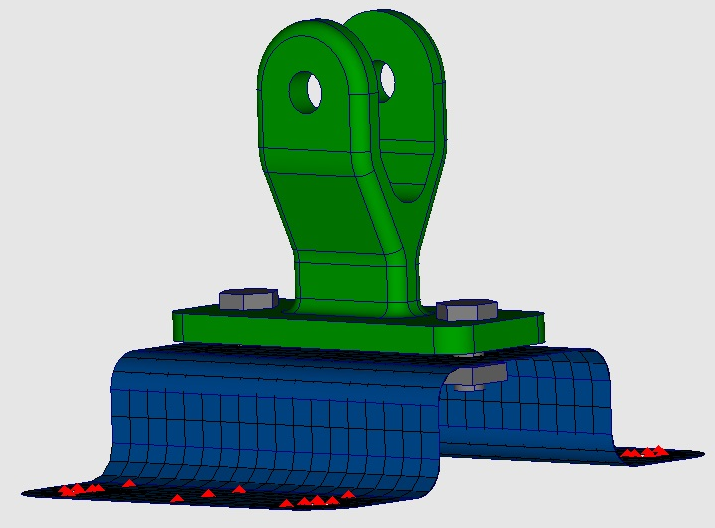
Рис. 8

Чтобы результат расчета был адекватен, способ соединения кронштейна с П-пластиной (модель передачи нагрузки) должен соответствовать реальной физике работы болтового соединения. Гайки закручены с некоторым усилием (моментом). Этот момент вызывает силу, прижимающую кронштейн к поверхности пластины. Силу трения в свою очередь определяют коэффициент трения и сила реакции. При приложении нагрузки к кронштейну часть его основания прижимается к пластине, а некоторая часть, напротив, стремится от него оторваться, вследствие чего при превышении определенной нагрузки происходит частичное раскрытие стыка.

С точки зрения математического моделирования нам необходимо: а) задать непосредственное соединение болтов и гаек с кронштейном и пластиной и б) задать взаимодействие изначально прижатых друг к другу поверхностей. На рис. 9 показаны напряженно-деформированные состояния кронштейна с пластиной при двух вариантах задания соединений. Составляющая а — назовем ее «имитация болтов» — в обоих вариантах задана одинаково: два «паучка» из RBE-элементов и болт из балочных конечных элементов созданы с помощью встроенной API-команды Hole to Hole Fastener.

Первый и второй варианты различаются настройками свойств контактной пары поверхностей — составляющей б. В первом варианте настройки контакта соответствуют «склейке» двух поверхностей, что не отвечает физике работы болтового соединения. Этот вариант можно было бы использовать, если бы кронштейн был соединен с пластиной при помощи сварных швов — по периметру и внутри.

Адекватное решение (второй вариант расчета) получается при задании контакта с трением. Такой вид взаимодействия поверхностей позволяет учесть эффект частичного раскрытия стыка. Задача при этом становится нелинейной и требует гораздо больше времени в связи с необходимостью обеспечить сходимость решения. Подробнее о нелинейном анализе и обеспечении сходимости можно прочитать в моей статье «Просто о нелинейном анализе методом конечных элементов. На примере кронштейна».

Существует несколько способов моделирования болтового соединения. Представленный выше способ (балочный элемент + RBE + контакт с трением) относительно прост, однако он позволяет учесть передачу сдвиговых усилий. Есть более точный, но и гораздо более трудоемкий способ моделирования болтового соединения: непосредственное моделирование болтов, гаек, шайб объемными конечными элементами (рис. 10). Этот способ позволяет учесть все тонкости работы болтового соединения (даже контакт в резьбе) и в том числе производить нелинейный анализ с учетом пластичности.

Глобально-локальный анализ

Проанализируем теперь сложную конечно-элементную модель марсохода «Кьюриосити» («Curiosity»). На примере марсохода я хочу познакомить читателя с понятием глобально-локального анализа (ГЛА). Глобально-локальный анализ — это процесс изолированного рассмотрения отдельных частей конструкции, при котором выполняется условие равенства силовых факторов и перемещений, соответствующих поведению этой части в составе конструкции. Возможность применения ГЛА обоснована принципом Сен-Венана: в частях конструкции, достаточно удаленных от места приложения нагрузки, напряжения и деформации мало зависят от способа приложения нагрузки. Потому часть модели можно вырезать и выполнить анализ только для этой части — при условии, что значения силовых факторов на границах выреза заданы правильно.

Но вернемся к марсоходу и его модели. Весит марсоход около тонны, его габариты: длина — 4,5 метра, ширина — 2,5 метра, высота — 2,1 метра. В процессе проектирования было проведено множество расчетов средствами Simcenter Femap , в том числе линейный статический анализ, анализ потери устойчивости, нелинейный анализ; рассчитаны отклики на воздействие случайной вибрации, выполнен анализ переходных процессов.

Конечно-элементная модель марсохода, изображенная на рис. 11, — это глобальная конечно-элементная модель (ГКЭМ). С ее помощью можно подобрать сечения труб и толщины оболочек, вычислить нагрузки — реакции в узлах конструкции. В модели применены линейные, поверхностные и объемные КЭ, части модели соединяются как «узел в узел», так и посредством MPC-связей и контактов.

Для такой сложной конструкции, как марсоход, рационально использовать глобальную модель как нагрузочную, а узлы считать отдельно с помощью подробных локальных конечно-элементных моделей (ЛКЭМ) — то есть применять алгоритм глобально-локального анализа (рис. 12).

Для расчета узлов в ЛКЭМ очень важно правильно задать граничные условия, силовые факторы. Существует три способа переноса граничных условий из ГКЭМ в локальную конечно-элементную модель: перенос перемещений, перенос силовых факторов, комбинированный способ. Для осуществления этих операций в Femap есть удобный инструмент FreeBody. Чтобы более подробно узнать о ГЛА и о применении FreeBody, рекомендую ознакомиться с докладом Алексея Патая из компании «Центр Технических Проектов»: «Возможности Femap для глобально-локального анализа авиационных конструкций».

Заключение

Подведем итоги, опираясь на вышеприведенные результаты анализа трех расчетных моделей: радиобашни, кронштейна и марсохода. Какая она все-таки — оптимальная расчетная конечно-элементная модель, и насколько простой модель может быть? Ответ для каждой конкретной задачи индивидуален, но есть общие критерии.

Что касается понимания физики процесса: например, нам не нужно моделировать каждый крепежный элемент радиобашни, чтобы определить собственные формы и частоты колебаний конструкции, — требуется учитывать лишь элементы, в целом определяющие распределение масс и жесткость конструкции.

Для подбора сечений в строительных расчетах (металлоконструкции, деревянные конструкции и даже часть железобетонных), где чаще всего можно ограничиться использованием только линейных конечных элементов, достаточно понимать, является ли узел условно «жестким» или условно «шарнирным». Условно — потому как в любом «шарнирном» узле есть трение, а любой «жесткий» узел все равно имеет некоторую податливость. Для моделирования течений жидкости или газа, с точки зрения геометрической модели, и вовсе достаточно задать поверхность обтекаемого объекта. Так, например, геометрическая модель для определения буксировочного сопротивления судна — это прямоугольный параллелепипед, из которого вычтен объем корпуса судна.

На примере расчета кронштейна, соединенного болтами с П-образной пластиной, мы увидели, что очень важно правильно задать способ передачи нагрузки, граничные условия. В противном случае мы получим результат, не соответствующий действительности. Да, в соответствии с принципом Сен-Венана, напряженно-деформированное состояние (НДС) конструкции в глобальной модели на достаточном удалении от неточно смоделированного узла практически не изменится. Но НДС элементов узла будет определено неверно, что может быть критичным, если это ответственный узел и он сильно нагружен. Особенно важно — как для точности решения, так и для сходимости — правильно задавать нелинейные контакты.

Для сложных же конструкций, таких как марсоход «Кьюриосити», делать одну сложную и подробную конечно-элементную модель чаще всего нерационально. Целесообразнее использовать алгоритм глобально-локального анализа, то есть формировать глобальную нагрузочную конечно-элементную модель и локальные конечно-элементные модели для расчета ответственных узлов. Затем, после расчета узлов, при необходимости можно внести изменения-уточнения в ГКЭМ.

Конечно, тема оптимальной расчетной конечно-элементной модели не может быть исчерпана в рамках одной статьи. Но я надеюсь, что мой обобщенный практический опыт и теоретические знания будут полезны, и в следующий раз вы сможете быстрее найти свое оптимальное решение. При этом расчетная модель будет проще, а точность выше!

Бесплатную пробную версию Simcenter Femap с NX Nastran можно скачать по адресу solidrules.ru/simcenter-femap.

Источник: www.cadmaster.ru

Назначение размеров/формы/типа конечного элемента при расчете различных конструкций (сбор информации).

К сожалению, в нашей нормативной литературе отсутствуют требования к назначению размеров и типа КЭ в зависимости от вида моделируемой конструкции.

В данной теме имею цель собрать в одном месте рекомендации по назначению размеров/формы/типа КЭ (соответственно и сетки КЭ) при моделировании различных конструкций и узлов.

Просьба указывать источник информации и к какому программному комплексу относится.

Из того, что на данный момент найдено:
А.О. Шимановский, А.В. Путято «Применение метода конечных элементов в решении задач прикладной механики» 2008

. … … Расчет и моделирование выполнялись по программному комплексу «Лира-Windows» версии 9.0 и 9.2. . … … На точность определения прогибов в плитах с учетом физической нелинейности значительное влияние оказывает шаг конечно-элементной сетки. Показано, что шаг КЭ должен быть не менее 1/20 пролета плиты.

геометрия конечных элементов – если стороны элементов сильно различаются по длине, то это приведет к плохой обусловленности матрицы накопленных уравнений и также к потере точности;

Рекомендуемые ограничения: 1. Углы пластинчатых элементов не менее 30 и не более 150 градусов; 2. Отношение сторон не более 1:10; 3. В случае, когда вершины четырехугольника не лежат в одной плоскости предпочтительнее использование двух треугольных элементов. Обязательные ограничения: 1. Четырехугольный пластинчатый элемент не должен иметь самопересечений; 2. Четырехугольный пластинчатый элемент должен быть выпуклым; 3. Грани объемных элементов должны подчиняться 1-му и 2-му ограничениям.

— КЭ в плитах перекрытия принимается размером в 2 толщины и более (т.е. для плиты толщиной 200 мм – размер КЭ 400х400 мм); — размер КЭ плиты перекрытия не более 1/6 пролета плиты; — размер КЭ плиты перекрытия не менее 1/15 пролета плиты; — 10 элементов на пролет — во многих случаях довольно оптимальная сетка; — не рекомендуется использовать треугольные элементы в которых присутствует угол меньше 15 градусов; — не рекомендуется использовать прямоугольные КЭ с соотношением сторон a/b > 5; — для строительных расчетов годится такое разбиение на КЭ, когда последующий расчет выдает результат, отличающийся от предыдущего не более 5%; — в лире КЭ с углом менее 5 градусов являются явно вырожденными и портят матрицу жесткости.

Под «непроверенными» источниками подразумеваю то, что слышал на курсах по обучению, встречал в темах и пр. без ссылки на источник.

Ответ Юрия Гензерского на форуме (администратор тех. поддержки http://www.liraland.ru).

На этот вопрос нет однозначного ответа. Размеры элементов принимаются в зависимости от ряда требований. У каждого расчета их перечень быть разный. Какие же это требования: -Соотношение размеров сторон и толщины. В идеале элемент должен быть равносторонний. Неблагоприятное соотношение сторон более чем 1:10. Соотношение меньшей стороны к толщине (идеальное) в пределах 1 – 30. -Количество элементов на пролет. Идеально не мене 6. -Учет особенностей расчетной схемы. Необходимые точки для вычисления перемещений, усилий, места приложения нагрузок, места опираний, …… -Виды расчетов (линейный, линейный динамический, физнелинейный, геомнелинейный). -Может что то еще.

Перельмутер А.В. «Беседы о строительной механике». Научное издание.— М: Издательство SCAD Soft, издательство ассоциации строительных вузов, 2014.— 250 с.

С точки зрения конечно-элементного анализа можно смело говорить о том, что оптимальным является разбиение на элементы имеющие форму простейших равносторонних фигур (равносторонний треугольник, квадрат, равносторонний тетраэдр, куб). Практически это требование достигается очень редко и получаемое разбиение на конечные элементы отлично от оптимального. Поэтому возникает задача оценки качества полученного сеточного разбиения, для чего строятся различные измерители (см. табл. 2.4). Одним из таких измерителей является коэффициент формы, который вычисляется следующим образом. Для каждой стороны элемента Li определяется площадь идеального элемента такой величины (для равностороннего треугольника она равна 0,433(Li)^2, а для квадрата — (Li)^2), и затем эти площади осредняются. Отношение этой осредненной «идеализированной» площади к реальной площади элемента принимается в качестве меры качества. Для четырехугольных элементов следует ограничить их стремление к «игольчатой форме», для чего используется такой измеритель, как вытянутость. Используются и другие измерители, данные о которых приведены в таблице 2.4, где также указаны рекомендуемые и оптимальные значения соответствующих мер качества.

Вопрос на данную тему было не мало. Вразумительных ответов — не много.
По слухам, есть некоторые рекомендации по назначению КЭ в Eurocode 2 и в документации к программному комплексу Ing+2011.

А О Шимановский АВ Путято = Применение метода конечных элементов в решении задач прикладной механики (881.2 Кб, 16648 просмотров)

__________________
«Точно знают, только когда мало знают. Вместе со знанием растет сомнение». Иоганн Вольфганг Гете

Работаю в APM Civil Engineering.
Ограничения углов пластин и объёмных элементов существуют и даже более жёсткие.
Имеется инструмент «Проверка углов пластин».

Его использование позволяет выявить пластины, углы которых не принадлежат диапазону 30. 150 градусов. Такие пластины потенциально могут служить источниками дополнительной погрешности. Замечание: указанный диапазон углов охватывает подавляющее большинство случаев, но при необходимости его можно изменить- например, с целью отыскания в созданной модели грубых ошибок»

Замрий А. А. «Проектирование и расчёт методом конечных элементов в среде APM Civil Engineering», APM, Москва, 2010

На соотношение сторон прямоугольных пластин также имеется ограничение и составляет не более 1:10

см. рис. (скриншот справки APM Structure3D)

до кучи. Галлагер Р. Метод конечных элементов. Основы.
9.2.2 Вопросы выбора треугольной сети. стр. 274

Вложения

Галлагер Метод конечных элементов.rar (3.00 Мб, 627 просмотров)

После долгих поисков в лит-ре, после многократных споров и обсуждений с коллегами, после многочисленных консультаций с людьми, стоящими у истоков МКЭ, после многократных численных экспериментов пришли к тому что нет идеальной «формулы» для определения подробности расчетной схемы.
Проверено в Скаде на себе на нескольких десятках расчетов различных расчетных схемах из оболочечных КЭ:
Для строительных расчетов годится такое разбиение на КЭ, когда последующий расчет выдает результат, отличающийся от предыдущего не более 5%.
ИМХО особенно это важно при расчетах жб конструкций, т.к. в Скаде армирование оболочки рассчитывается не по максимальным напряжениям в элементе, а по средним.
В этой книге кое что есть

А.В.Перельмутер, В.И.Сливкер, Расчетные модели сооружений и возможность их анализа (издание 4-е переработанное и дополненное).- Москва: Изд-во СКАД СОФТ

Проектирование зданий и частей зданий

После долгих поисков в лит-ре, после многократных споров и обсуждений с коллегами, после многочисленных консультаций с людьми, стоящими у истоков МКЭ, после многократных численных экспериментов пришли к тому что нет идеальной «формулы» для определения подробности расчетной схемы.

Это как раз таки понятно. Тоже много споров, обсуждений, перерытой литературы за плечами.

Тем не менее. Про угол не менее 15 (30) градусов слышал не раз.
Про соотношение сторон не более 5 (10) раз тоже не раз слышал.

__________________
«Точно знают, только когда мало знают. Вместе со знанием растет сомнение». Иоганн Вольфганг Гете

Про углы и соотношение верно все — просто нам об этом сказали еще на 2-м курсе ВУЗа. Поэтому даже вопросов никогда не возникало. Вру — на 3-м крусе )))

См. вложение.
Вольный перевод: определяется индивидуально. Начальный размер для поиска не больше 1/10 пролета и не больше 1000 мм.
Источник: How-to-Design-rc-Flat-Slabs-Using-Finite-Element-Analysis

Проектирование зданий и частей зданий

См. вложение.
Вольный перевод: определяется индивидуально. Начальный размер для поиска не больше 1/10 пролета и не больше 1000 мм.
Источник: How-to-Design-rc-Flat-Slabs-Using-Finite-Element-Analysis

Нарыл электронную версию
За неимением другого, перевёл с помощью google-переводчика.
Перевод конечно кривой, но смысл понятен.
У кого есть Promt с профессиональными словарями, просьба помочь с переводом.

How to design reinforced concrete flat slabs using Finite Element Analysis
Как проектировать железобетонные плоские плиты с использованием анализа методом конечных элементов

The importance of selecting the correct mesh size is illustrated in Figure 5. The same model was analysed three times with the only change being the maximum mesh size. Where a very coarse mesh was used (up to 5000 mm) it took just 30 seconds to analyse; although it is analytically correct it does not give sufficient detail. Conversely, when a much finer mesh was used (up to 500 mm) it took 15 minutes to analyse and gives the shape of bending moment diagram that would be expected. However, a mesh up to 1000 mm took just four minutes to analyse; it gave very similar results and is considered to be sufficiently accurate for the purpose of structural design.

As the processing speed of computers increases there will be less need to be concerned about optimising the mesh size; but it is worth noting that, although the 500 mm mesh gave notionally more accurate results, the reinforcement provision would have been identical for both the 500 and 1000 mm mesh spacings. The 500 mm mesh has produced a higher peak moment; this is due to ‘singularities’ or infinite stresses and internal forces that occur at the location of high point loads. This is due to assumptions that have been made in the model. In flat slabs the concrete will crack and the reinforcement yield locally and thus distribute the forces to adjacent areas.

Definitive advice cannot be given as to the ideal size mesh size, but a good starting point is for elements to be not greater than span/10 or 1000 mm, whichever is the smallest. For large models it is worth running the initial analysis with a coarse mesh, which can then be refined when the model has been proved to be free of errors or warnings and gives reasonable results. With most software packages the meshing is carried out automatically and the software can even reduce the element size at critical locations to obtain more data where it is most needed. This will give more detailed results without a significant increase in analysis time.

Elements should be ‘well conditioned’, i.e. the ratio of maximum to minimum length of the sides should not exceed 2 to 1 (See Figure 6). Again this is because the results are accurately calculated only at the node positions. It is important to ensure that there are more nodes included in the model where the forces change rapidly because it is only at node locations that results are obtained directly; in between the nodes the results given are based on interpolation

Важность выбора правильного размера сетки показан на рисунке 5. Эта же модель была проанализирована в три раза с единственным изменением является максимальный размер сетки. Если очень грубая сетка была использована (до 5000 мм) понадобилось всего 30 секунд, чтобы проанализировать, хотя она аналитически исправить это не дает достаточно подробно.

И наоборот, когда много тонкой сетки была использована (до 500 мм) она занимает 15 минут, чтобы проанализировать и дает форму эпюра изгибающих моментов, которые можно было бы ожидать. Тем не менее, сетки до 1000 мм потребовалось всего четыре минуты, чтобы проанализировать, он дал схожие результаты и считается достаточно точным для конструкции.

Поскольку скорость обработки компьютеров увеличивает будет меньше необходимости беспокоиться об оптимизации сетки, но стоит отметить, что, несмотря на 500 мм сетка дали условно более точные результаты, укрепление положения были бы одинаковы для обоих 500 и 1000 мм, расстояние между сеткой. 500 мм сетка выпустил более пиковый момент, это связано с «особенностями» или бесконечные стрессы и внутренние силы, которые происходят на месте высоких нагрузках точки.

Это связано с предположениями, которые были внесены в модель. В плоских плит бетон трескается и укрепление выход на местном уровне и таким образом распределить силы в прилегающих районах.

Окончательная рекомендация не может быть предоставлена как на идеальный размер сетки, но хорошая отправная точка для элементов, которые будут не больше, чем диапазон 10 или 1000 мм, в зависимости от самых маленьких. Для больших моделей стоит запустить первоначальный анализ с грубой сеткой, которая затем может быть усовершенствован, если модель оказалась свободна от ошибок и предупреждений и дает неплохие результаты. В большинстве программных пакетов, сетки осуществляется автоматически, а программное обеспечение может даже уменьшить размер элемента в критических местах, чтобы получить больше данных, где она наиболее необходима. Это даст более подробные результаты без значительного увеличения времени анализа.

Элементы должны быть «хорошо условным, т.е. отношение максимальной к минимальной длины сторон не должна превышать 2 к 1 (см. рисунок 6). Опять же, это происходит потому, что результаты были точно рассчитаны только на узле позиции. Важно, чтобы есть больше узлов, включенных в модель, в которой силы быстро меняться, потому что только на узел местах, что результаты, полученные непосредственно, между узлами результаты, приведенные на основе интерполяции

__________________
«Точно знают, только когда мало знают. Вместе со знанием растет сомнение». Иоганн Вольфганг Гете

Источник: forum.dwg.ru

53. Выбор размеров конечных элементов

Авторы: Канев Данил, Таралов Рустам

Данная заметка нацелена прежде всего на начинающих расчётчиков, у которых часто возникают вопросы, как выбрать размер сетки конечных элементов, в каких случаях она является качественной, а в каких нет и т.д. Но, возможно, и более опытные пользователи ПК ЛИРА 10 найдут в ней полезные вещи.

Процесс разбиения модели на конечные элементы (КЭ) называется триангуляцией. Совокупность КЭ, на которые разбита конструкция, называется, конечно, элементной сеткой. Триангуляция является одним из ключевых этапов создания расчетной схемы в ПК ЛИРА 10. От корректности разбиения на КЭ зависит точность результатов расчета. К основным видам КЭ относят:

• одноузловые;
• стержневые;
• пластинчатые;
• объемные.

К двум основным типам сетки КЭ относятся регулярные и нерегулярные.

Регулярные сетки представляют собой совокупность КЭ правильной геометрии (рис. 1).

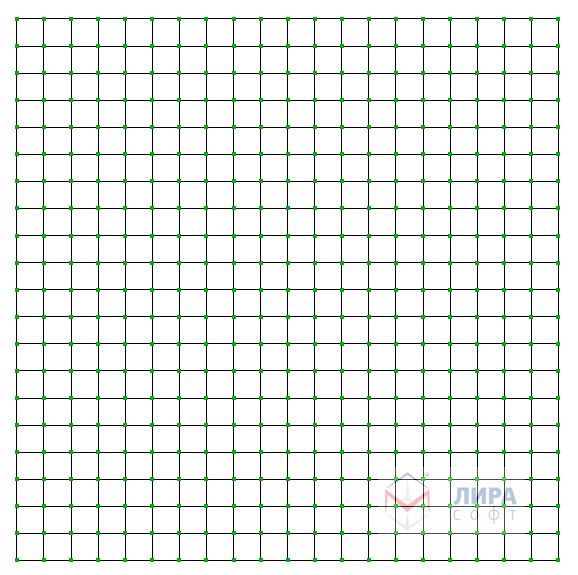
Рис. 1. Упорядоченная сетка КЭ

Для нерегулярной сетки размеры соседних элементов (h) могут существенно различаться, и сетка не имеет четкой структуры (рис. 2).

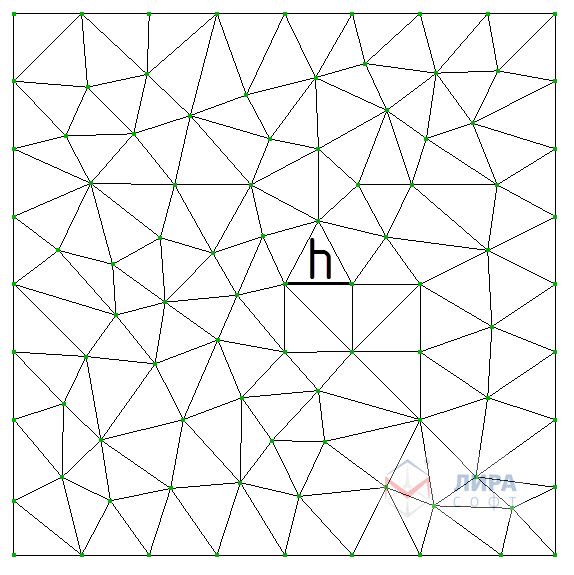
Рис. 2. Произвольная сеть КЭ

При выборе типа и размера сетки конечных элементов рекомендуем руководствоваться следующими принципами, которые помогут получить максимально близкие к реальности результаты:

• регулярная сетка дает более точные результаты, чем нерегулярная;
• прямоугольные 4-узловые КЭ дают более точные результаты, чем треугольные;
• треугольные элементы с промежуточными узлами имеют точность, близкую к сетке прямоугольных 4-х узловых элементов;
• прямоугольная сетка с промежуточными узлами дает более точные результаты, чем треугольная сетка с промежуточными узлами, несмотря на большую площадь;
• промежутки между КЭ не допускаются;
• допускается комбинация треугольных и четырехугольных элементов в одной модели;
• строить 4-узловые элементы с тупым (>180°) внутренним углом запрещается.

Количество элементов в расчётной модели обратно пропорционально размеру конечных элементов h, при этом, время расчета увеличивается по экспоненте с уменьшением размеров КЭ (рис. 3).

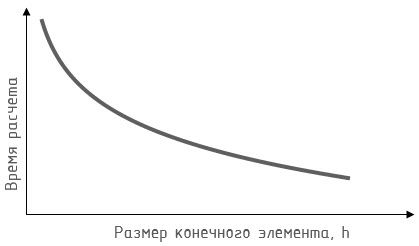
Рис. 3. График зависимости времени расчёта от размеров КЭ

При выборе размеров сетки конечных элементов необходимо всегда помнить, что сам метод конечных элементов – это метод числового приближения, и абсолютной точности он дать не может. Да, погрешность вычислений снижается при уменьшении размеров КЭ, но полностью она не устраниться, и, зачастую, дальнейшее уменьшение сети не будет приводить к ощутимому увеличению точности, но время расчёта будет возрастать, этот момент нужно держать в голове и не стремиться к слишком мелкой сетке.

Для примера рассмотрим модель прямоугольной консольной плиты (рис. 4).

Геометрия:

Рис. 4. Пример

Исходные данные:

; ;

Характеристики материала:

Изотропный упругий: ,

Граничные условия:

Контур плиты вдоль оси Y жёстко заделан.

Распределённая нагрузка по площади плиты:

Описание задачи:

Плита моделировалась КЭ 42,44 – тонкой оболочки.

На рисунке 5 и в таблице демонстрируются изменения величины перемещения по Z в зависимости от размера КЭ. Одну и ту же модель прямоугольной консольной плиты рассчитали трижды, меняя лишь максимальный размер КЭ. Сравнивая результаты, полученные при аналитическом расчете с результатами расчета в ПК ЛИРА 10.8, видим, что наиболее точные значения получаются при расчете с меньшим шагом сетки.

Результаты расчёта:

Результаты расчёта ЛИРА 10.8

, м

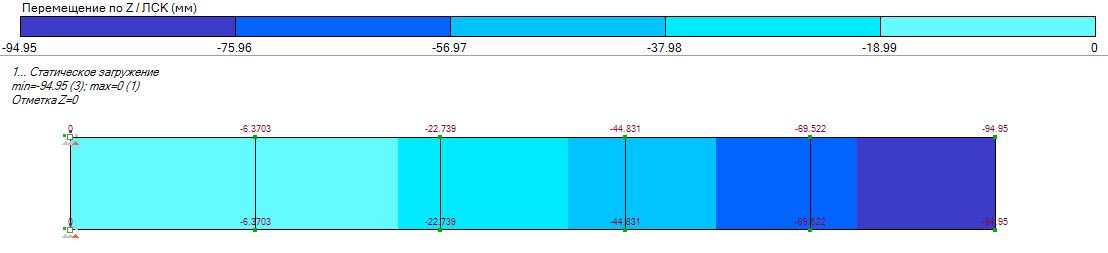
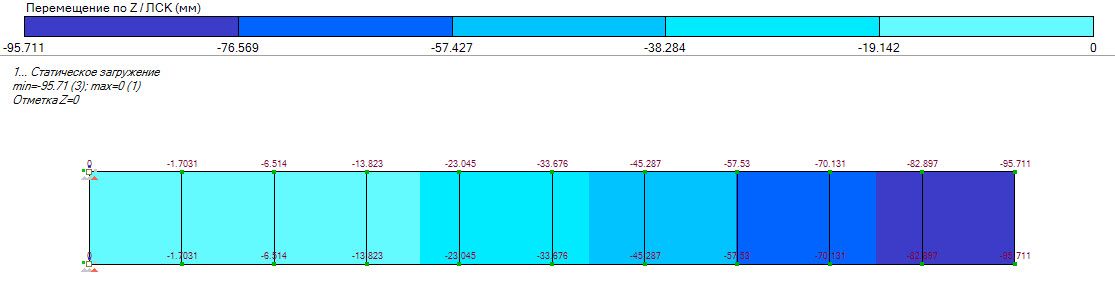
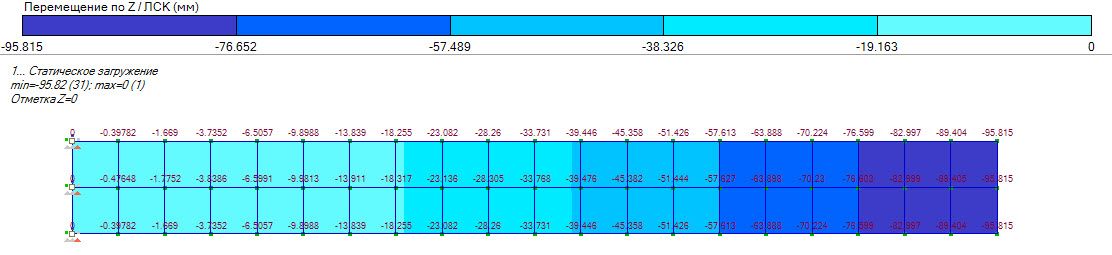
Рис. 5. Результаты расчётов

Более мелкая сетка особенно важна там, где есть изменения напряжений и деформаций (изменяются на порядок). Крупная сетка КЭ может использоваться в областях постоянного напряжения или зонах, которые не интересуют пользователя. При этом расчётчик должен четко понимать, где какая зона находится. Более мелкая сетка может потребоваться в местах стыка нескольких несущих элементов, у отверстий, в углах, зонах контакта и в областях с высоким напряжением (рис. 6).

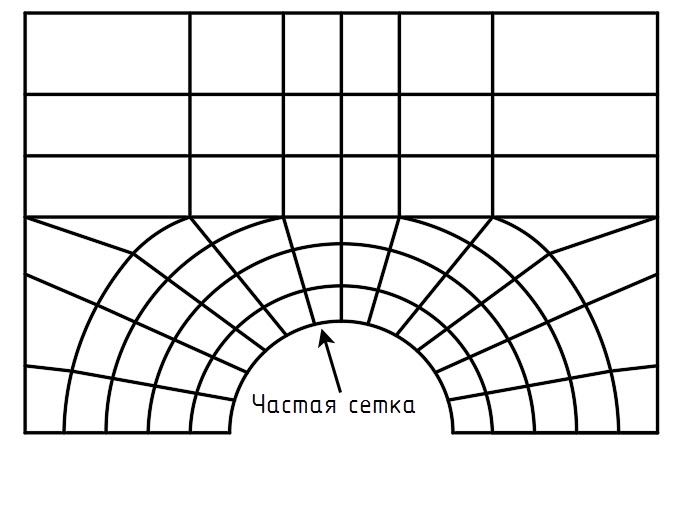
Рис. 6. Область сгущения сетки КЭ

В то же время, необходимо учитывать тот факт, что точность уменьшается, если размеры соседних элементов около концентраторов напряжений сильно различаются. Это связано с тем, что матрица жесткостей становится плохо обусловленной. Ко всему вышесказанному следует добавить следующее: отношение максимального размера элемента к минимальному не должно превышать 2, или угол не должен быть меньше 30° (рис.7).

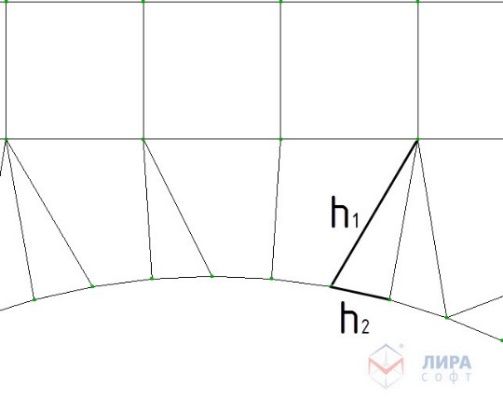
≤2

Рис. 7. Выбор формы КЭ

Форма конечных элементов значительно влияет на точность. При создании расчётных моделей рекомендуется избегать появление острых углов в КЭ, наибольшую точность дают элементы с одинаковыми сторонами или близкими к одинаковым (рис. 8).

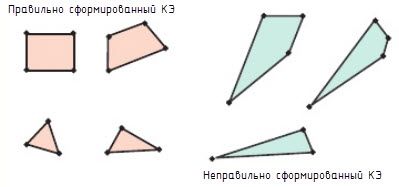
Рис. 8. Выбор формы КЭ

Точных рекомендаций относительно идеального размера пластинчатых КЭ не существует, но отталкиваться следует от размеров 1:10 пролета и не превышать размера в 1000 мм.

При отношении толщины КЭ к его длине и ширине более 1:5 следует использовать объёмные элементы.

Источник: lira-soft.com

Оптимальная расчетная конечно-элементная модель. Способы соединения частей КЭ модели

«Оптимальная расчетная конечно-элементная модель – какая она?» – такой чаще всего не проговоренный вслух, а порою даже и неосознанный вопрос непременно рождается (как минимум в подсознании) у каждого инженера-расчетчика при получении ТЗ на решение задачи методом конечных элементов. Каковы критерии этой самой расчетной модели-мечты? Пожалуй, здесь стоит отталкиваться от известного философского принципа «Всё следует упрощать до тех пор, пока это возможно, но не более того». Вот только как применить этот принцип к нашим научным и инженерным задачам?

Рисунок 1

Критерии оптимальной расчетной конечно-элементной модели

Поразмыслив, проанализировав свой практический опыт, я выделил три основных критерия оптимальной расчетной конечно-элементной модели: 1) физические допущения, адекватные целям расчета; 2) упрощения детализации геометрии, правильный выбор видов конечных элементов и способов их соединения; 3) качественная сетка КЭ. Эта статья является продолжением моего доклада «Особенности использования различных видов конечных элементов в Femap с NX Nastran», прочитанного на Femap Symposium 2020. В докладе я обзорно рассказывал о применении этих трех критериев на примере конкретных проектов, а здесь я подробнее расскажу подробнее о втором критерии.

Чтобы определиться с концепцией рациональной расчетной схемы, в которую мы будем преобразовывать (чаще упрощать) исходную геометрическую модель, нужно в первую очередь хорошо понимать физику моделируемого процесса, осознавать факторы и параметры, изменение которых более всего влияет на результат. Необходимо разбираться в видах конечных элементов (линейные, поверхностные, объемные), способах соединения частей модели и в особенностях их совместного применения. Причем части модели могут состоять из конечных элементов разных видов. Да, и конечно же нужно знать возможности используемого вами расчетного комплекса. Расчетный комплекс Femap с NX Nastran поддерживает все виды конечных элементов и позволяет соединять области, состоящие из конечных элементов разных видов, всеми основными способами.

Способы соединения частей КЭ-модели

Существует три основных способа соединения (в более широком смысле слова – взаимодействия) частей конечно-элементной модели, передачи нагрузки и внутренних усилий между частями модели. Эта классификация носит условный характер, и я ввел ее для удобства восприятия информации расчетчиками-практиками.

Первый способ – соединение конечных элементов разных частей модели «узел в узел». Это самый классический способ. При его использовании граница перехода между частями модели не оказывает никакого собственного влияния. Фактически решатель работает с единой сплошной моделью, а части модели существуют только для удобства работы пользователя в пре- и постпроцессоре.

Рисунок 2

Второй способ – это применение MPC-связей (multiple point constraint). MPC соединяют узел с узлом (тогда это скорее SPC – single point constraint) или узел с группой узлов с помощью жестких или интерполяционных элементов.

Рисунок 3

Третий способ – применение контактных поверхностей различных типов (например, «склейка» или «с трением»). При использовании этого способа пользователь выбирает контактирующие поверхности, а препроцессор автоматически определяет взаимодействующие узлы.

Рисунок 4

Эти три способа соединения (взаимодействия) даже более чем различны. Например, целые классы задач (штамповка, соударение тел) просто невозможно решить без применения контактных поверхностей. При решении же более простых задач (линейная статика, модальный анализ), как правило, есть возможность выбрать, как именно упрощать геометрию и какой способ соединения частей модели применить.

Практические примеры

Разберем и проанализируем по вышеописанным критериям модель радиобашни, изображенную на рис.3. Расчетная модель радиобашни используется для определения собственных форм и частот колебаний металлоконструкции башни, потому точный учет жесткости силовых элементов исключительно важен. Это очень ответственная задача – собственные частоты колебаний необходимы для определения динамической составляющей ветровой нагрузки (см. Руководство по расчету зданий и сооружений на действие ветра к СП 20.13330.2010 «Нагрузки и воздействия»).

Модель радиобашни состоит из конечных элементов трех видов: 1) несущие вертикальные круглые трубы и связи соединяющих их (также из круглых труб) смоделированы балочными конечными элементами; 2) ребра жесткости, соединяющие трубы и опорную плиту, смоделированы поверхностными КЭ; 3) опорная плита смоделирована солидами (объемными КЭ).

В модели также применены три основных способа соединения частей конечно-элементной модели:

а) узел в узел соединены части модели (линейные), между которыми нет зазоров;
б) с помощью MPC-связей соединены линейные элементы (имитирующие трубы), между которыми есть зазоры. Кроме того, посредством MPC-связей соединены элементы ребер жесткости и вертикальных труб;
в) контакты заданы между нижней гранью ребер жесткости и поверхностью опорной плиты.

Я считаю эту расчётную модель очень грамотным результатом преобразования геометрической модели в расчетную, так как модель достаточно проста, но при этом в ней учтены основные конструктивные элементы, определяющие жесткость конструкции. Как правило, в простых строительных САПР отсутствуют инструменты, позволяющие соединять конечные элементы различных видов (в случае радиобашни не было бы возможности смоделировать опорные элементы). То есть в простой строительной САПР конструкцию радиобашни удалось бы смоделировать лишь из одних труб, разбив их балочными конечными элементами. В этом случае податливость основания не учитывается и собственные частоты колебаний конструкции оказываются завышены.

Далее на примере расчетного комплекса Simcenter Femap c NX Nastran я подробнее расскажу о втором способе соединения частей модели, а точнее о применении MPC-связей. Элементы типа R математически эквивалентны многоточечному уравнению связи (Multipoint Constraints Equations, MPC). Они накладывают постоянные ограничения на компоненты перемещения соединяемых узлов. Каждое уравнение связи выражает зависимую степень свободы как функцию независимой степени свободы.

Элементы RROD, RBAR, RBE1, RBE2 и RTRPLT – это жесткие элементы. Элементы RBE3 и RSPLINE – интерполяционные элементы, они не являются жесткими.

Рисунок 5

Элемент RBE2 использует уравнения связи, чтобы связывать степени свободы зависимых узлов со степенями свободы независимого узла. Относительные деформации между зависимыми узлами отсутствуют, то есть соответствующие элементы не деформируются. Варьируя настройки степеней свободы RBE2 в поле DEPENDENT (Зависимый), можно получить WELD – сварное соединение (активируя шесть степеней свободы TX, TY, TZ, RX, RY, RZ) или BOLT – болтовое соединение (активируя TX, TY, TZ, вращения остаются свободными).

В отличие от элементов RBE2, элемент RBE3 не добавляет конструкции дополнительную жесткость, то есть RBE3 – это интерполяционный элемент. RBE3 можно использовать как инструмент распределения нагрузки и массы в КЭ-модели, аналогичный «грузовым площадям» в строительных системах автоматизированного проектирования. Нагрузки в виде сил и моментов, приложенные к зависимому узлу, распределяются в независимые узлы пропорционально весовым коэффициентам.

Рисунок 6

В большинстве случаев в настройках степеней свободы RBE3 в поле INDEPENDENT (Независимый) не рекомендуется активировать вращательные степени свободы.

Подробнее специфика применения RBE2 и RBE3 представлена в статье наших партнеров из компании «КАДИС»: «RBE2 в сравнении с RBE3 в Femap c NX Nastran».

Рисунок 7

Но вернемся от теории к практике и разберем типовую задачу расчета кронштейна, на примере которой отлично видно, что, неправильно задав способ соединения частей модели, мы получим принципиально неверное решение. Кронштейн закреплен на П-образной пластине с помощью двух болтов. К отверстиям кронштейна приложена сила с направлением вдоль пластины. П-образная пластина разбита поверхностными конечными элементами, а кронштейн – объемными КЭ. С учетом толщины пластины пластина и кронштейн соприкасаются.

Рисунок 8

Чтобы результат расчета был адекватен, способ соединения кронштейна с П-пластиной (модель передачи нагрузки) должен соответствовать реальной физике работы болтового соединения. Гайки закручены с некоторым усилием (моментом). Этот момент вызывает силу, прижимающую кронштейн к поверхности пластины. Силу трения в свою очередь определяют коэффициент трения и сила реакции. При приложении нагрузки к кронштейну часть его основания прижимается к пластине, а некоторая часть основания, напротив, стремится от него оторваться, вследствие чего при превышении определенной нагрузки происходит частичное раскрытие стыка.

С точки зрения математического моделирования нам необходимо: а) задать непосредственное соединение болтов и гаек с кронштейном и пластиной и б) задать взаимодействие изначально прижатых друг к другу поверхностей. На рис. 9 показаны напряженно-деформированные состояния кронштейна с пластиной при двух вариантах задания соединений. Составляющая а – назовем ее «имитация болтов» – в обоих вариантах задана одинаково: два «паучка» из RBE-элементов и болт из балочных конечных элементов созданы с помощью встроенной API-команды Hole to Hole Fastener.

Первый и второй варианты различаются настройками свойств контактной пары поверхностей – составляющей б. В первом варианте настройки контакта соответствуют «склейке» двух поверхностей, что не отвечает физике работы болтового соединения. Этот вариант можно было бы использовать, если бы кронштейн был соединен с пластиной при помощи сварных швов – по периметру и внутри.

Адекватное решение (второй вариант расчета) получается при задании контакта с трением. Такой вид взаимодействия поверхностей позволяет учесть эффект частичного раскрытия стыка. Задача при этом становится нелинейной и решение занимает гораздо больше времени в связи с необходимостью обеспечить сходимость решения. Подробнее о нелинейном анализе и обеспечении сходимости можно прочитать в моей статье «Просто о нелинейном анализе методом конечных элементов. На примере кронштейна».

Рисунок 9

Существует несколько способов моделирования болтового соединения. Представленный выше способ (балочный элемент + RBE + контакт с трением) относительно прост, однако он позволяет учесть передачу сдвиговых усилий. Есть более точный, но и гораздо более трудоемкий способ моделирования болтового соединения: непосредственное моделирование болтов, гаек, шайб объемными конечными элементами (рис. 10). Этот способ позволяет учесть все тонкости работы болтового соединения (даже контакт в резьбе) и в том числе производить нелинейный анализ с учетом пластичности.

Рисунок 10

Глобально-локальный анализ

Проанализируем теперь сложную конечно-элементную модель марсохода «Кьюриосити» («Curiosity»). На примере марсохода я хочу познакомить читателя с понятием глобально-локального анализа (ГЛА). Глобально-локальный анализ – это процесс изолированного рассмотрения отдельных частей конструкции, при котором выполняется условие равенства силовых факторов и перемещений, соответствующих поведению этой части в составе конструкции. Возможность применения ГЛА обоснована принципом Сен-Венана: в частях конструкции, достаточно удаленных от места приложения нагрузки, напряжения и деформации мало зависят от способа приложения нагрузки. Потому часть модели можно вырезать и выполнить анализ только для этой части – при условии, что значения силовых факторов на границах выреза заданы правильно.

Рисунок 11

Но вернемся к марсоходу и его модели. Весит марсоход около тонны, его габариты: длина – 4,5 метра, ширина – 2,5 метра, высота – 2,1 метра. В процессе проектирования было проведено множество расчетов средствами Simcenter Femap, в том числе линейный статический анализ, анализ потери устойчивости, нелинейный анализ; рассчитаны отклики на воздействие случайной вибрации, выполнен анализ переходных процессов.

Конечно-элементная модель марсохода, изображенная на рис. 11, – это глобальная конечно-элементная модель (ГКЭМ). С ее помощью можно подобрать сечения труб и толщины оболочек, вычислить нагрузки – реакции в узлах конструкции. В модели применены линейные, поверхностные и объемные КЭ, части модели соединяются как «узел в узел», так и посредством MPC-связей и контактов.

Для такой сложной конструкции как марсоход рационально использовать глобальную модель как нагрузочную, а узлы считать отдельно с помощью подробных локальных конечно-элементных моделей (ЛКЭМ) – то есть применять алгоритм глобально-локального анализа (рис. 12).

Для расчета узлов в ЛКЭМ очень важно правильно задать граничные условия, силовые факторы. Существует три способа переноса граничных условий из ГКЭМ в локальную конечно-элементную модель: перенос перемещений, перенос силовых факторов, комбинированный способ. Для осуществления этих операций в Femap есть удобный инструмент FreeBody. Чтобы более подробно узнать о ГЛА и о применении FreeBody, рекомендую ознакомиться с докладом Алексея Патая из компании «Центр Технических Проектов»: «Возможности Femap для глобально-локального анализа авиационных конструкций».

Рисунок 12

Подведем итоги, опираясь на вышеприведенные результаты анализа трех расчетных моделей: радиобашни, кронштейна и марсохода. Какая она все-таки – оптимальная расчетная конечно-элементная модель, и насколько простой модель может быть? Ответ для каждой конкретной задачи индивидуален, но есть общие критерии.

Что касается понимания физики процесса: например, нам не нужно моделировать каждый крепежный элемент радиобашни, чтобы определить собственные формы и частоты колебаний конструкции, – требуется учитывать лишь элементы, в целом определяющие распределение масс и жесткость конструкции.

Для подбора сечений в строительных расчетах (металлоконструкции, деревянные конструкции и даже часть железобетонных), где чаще всего можно ограничиться использованием только линейных конечных элементов, достаточно понимать, является ли узел условно «жестким» или условно «шарнирным». Условно – потому как в любом «шарнирном» узле есть трение, а любой «жесткий» узел все равно имеет некоторую податливость. Для моделирования течений жидкости или газа, с точки зрения геометрической модели, и вовсе достаточно задать поверхность обтекаемого объекта. Так, например, геометрическая модель для определения буксировочного сопротивления судна – это прямоугольный параллелепипед, из которого вычтен объем корпуса судна.

На примере расчета кронштейна, соединенного болтами с П-образной пластиной, мы увидели, что очень важно правильно задать способ передачи нагрузки, граничные условия. В противном случае мы получим результат, не соответствующий действительности. Да, в соответствии с принципом Сен-Венана, напряженно-деформированное состояние (НДС) конструкции в глобальной модели на достаточном удалении от неточно смоделированного узла практически не изменится. Но НДС элементов узла будет определено неверно, что может быть критичным, если это ответственный узел и он сильно нагружен. Особенно важно – как для точности решения, так и для сходимости – правильно задавать нелинейные контакты.

Для сложных же конструкций, таких как марсоход «Кьюриосити», делать одну сложную и подробную конечно-элементную модель чаще всего нерационально. Целесообразнее использовать алгоритм глобально-локального анализа, то есть формировать глобальную нагрузочную конечно-элементную модель и локальные конечно-элементные модели для расчета ответственных узлов. Затем, после расчета узлов, при необходимости можно внести изменения-уточнения в ГКЭМ.

Конечно, тема оптимальной расчетной конечно-элементной модели не может быть исчерпана в рамках одной статьи. Но я надеюсь, что мой обобщенный практический опыт и теоретические знания будут полезны, и в следующий раз вы сможете быстрее найти свое оптимальное решение. При этом расчетная модель будет проще, а точность выше!

Уважаемые читатели, приглашаю вас на бесплатный «Профессиональный курс по расчетам методом конечных элементов» (март-апрель 2021 г.). Чтобы зарегистрироваться на курс и ознакомиться с его программой, пройдите, пожалуйста, по ссылке здесь или щелкните на рисунок выше.

Профессиональный курс по расчетам МКЭ от АО «Нанософт» включает в себя как ценные теоретические знания и инженерные методики, ориентированные на прикладное применение, так и практические демонстрации, вокршопы по решению типовых инженерных задач в расчетном комплексе конечно-элементного моделирования Simcenter Femap c NX Nastran.

Курс состоит из трех вебинаров и предназначен для инженеров, технических работников и студентов, работающих в областях, где требуется проведение физических расчетов. В заключительной части каждого вебинара вы сможете задать вопрос ведущему, Филиппу Титаренко, и получить консультации по интересующим вас вопросам.

Источник: habr.com