Факультативное занятие в 6 классе по теме «Основные правила построения сетевого графика»
Цель
познакомиться с основными правилами построения сетевых графиков.
Оборудование
— раздаточный материал(карточки с упражнениями);
— электронная презентация с готовыми рисунками графов.
Ход занятия:
Орг. момент. Сообщение темы занятия.
Изучение нового материала.
Прежде чем непосредственно приступать к построению сетевого графика, составляют список всех работ, необходимых для выполнения заданного комплекса работ. Далее выясняют технологическую последовательность их выполнения; строят отдельные фрагменты сетевого графика; по возможности их упрощают. После этого из отдельных фрагментов строят общий сетевой график. В таких случаях принять говорить о «сшивании сетевого графика».
Познакомимся с основными правилами построения сетевых графиков:
1. Каждую стрелку в сетевом графике по возможности рисуют так, чтобы её конец находился правее начала, по возможности горизонтально.
Сетевой график или календарный план. Что выбрать?
2. Для удобства сетевой график строят без лишних пересечений стрелок. ( Вместе с тем при составлении чернового варианта не следует увлекаться внешним видом сети).
3. Следят за тем, чтобы во все вершины, кроме той, которая соответствует исходному событию, входила по меньшей мере одна стрелка, так как все события, кроме исходного, имеют предшествующую работу.
4. Следят за тем, чтобы из всех вершин сети, кроме той, которая соответствует завершающему событию, выходили стрелки, так как все события, кроме завершающего, имеют последующую работу.
5. Следят за тем, чтобы в сетевом графике не образовывалось циклов.
6. Если одно событие служит началом для двух или более работ, после завершения которых начинается выполнение следующей работы, то вводится штриховая стрелка (условная зависимость) и дополнительное событие со своим номером.
На рисунке 1 приведены неправильное и правильное изображения двух работ а и b, начинающихся после события 1; после завершения а и b начинается работа с.
На рисунке 2 приведены неправильное и правильное изображения трёх работ а, b, с, начинающихся после события 1; после их завершения начинается работа d.
Правило 6 важно для расчётов сетевых графиков на компьютере, так как работы кодируются начальными и конечными событиями. При нарушении этого правила в памяти компьютера окажутся две или более одинаково закодированных работ.
7. Если какие – то работы могут начаться до полного завершения предыдущей работы, то её следует разбить на части и считать каждую из них самостоятельной.
На рисунке 3 изображена часть сетевого графика. Здесь работа а разбита на 3 части а1, а2 и а3, причём после выполнения а1 начинается работа b1, после а2 – b2, после а3 – b3.
Такая ситуация может возникнуть, например, при проведении труб (водопроводных или газовых). Укладку труб можно производить по частям, не дожидаясь, когда будет готова траншея на всём участке.
Календарно-сетевой график строительного проекта
8. На сетевом графике следует чётко отражать последовательность выполнения отдельных работ и их взаимосвязи. В помощь вводятся штриховые стрелки (условные зависимости) и дополнительные вершины (события).
Рассмотрим примеры построения отдельных фрагментов сетевых графиков.
1) Четыре работы (а, b, с, d) связаны между собой следующей зависимостью: b начинается после завершения работ а и с; d — после завершения работы с.
2) Пять работ (а, b, с, d, е) связаны между собой следующей зависимостью: с начинается после завершения а и b; е – после окончания b и d.
3) Пять работ (а, b, с, d, е) связаны между собой так: работы а и b начинаются после завершения каких – то одних и тех же работ; работу d можно начинать по окончании работ а и с; работу е – после завершения работ b и с.
Коллективное выполнение упражнений.
Упражнение 1. Ниже перечислены отдельные работы, которые выполняются при подготовке к туристическому походу.
а) Разработка маршрута похода.
b) Получение снаряжения.
с) Заготовка продуктов.
d) Формирование группы.
е) Утверждение руководителя группы и маршрута в совете по туризму.
f) Выбор руководителя группы и его помощников.
h) Получения разрешения на выход.
g) Сбор денег и получение дотации.
l) Проверка пригодности снаряжения и ремонт его.
m) Выход на маршрут.
Составьте сетевой график подготовки туристического похода. Используйте буквы, которыми обозначены отдельные работы в списке.
Упражнение 2. Ниже перечислены отдельные работы, которые выполняют при ремонте квартиры.
а) Шпаклёвка потолков и стен.
b) Побелка потолков.
c) Замена внешней электропроводки на внутреннюю.
d) Принятие решения о ремонте квартиры.
e) Договор с малярами.
f) Покупка материалов, необходимых для малярных работ.
h) Договор с электромонтёрами.
g) Оклеивание стен обоями.
l) краска дверей и оконных рам.
m) Покрытие полов лаком.
n) Уборка после завершения малярных работ.
o) Шпаклёвка дверей и оконных рам.
Составьте сетевой график ремонта квартиры. Используйте буквы, которыми обозначены отдельные работы в списке.
Итог занятия.
Итак, познакомившись с основными правилами построения сетевых графиков, мы сумели самостоятельно составить их наглядные примеры.
Источник: wiki.tgl.net.ru
Кто составляет сетевой график строительства
Эффективное планирование и управление работами и ресурсами проекта (оборудование, производственные мощности, денежные средства, трудовые ресурсы) заключается в системном подходе к вопросам организации управления, согласно которому коллективы исполнителей, принимающие участие в комплексе работ и объединенные общностью поставленных перед ними задач, несмотря на разную ведомственную подчиненность, рассматриваются как звенья единой сложной организационной системы. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами.
Методы сетевого планирования широко применяются в строительстве для оптимизации планирования и управления сложными разветвленными комплексами работ, требующими участия большого числа исполнителей и затрат ограниченных ресурсов. Основная цель сетевого планирования – сокращение до минимума продолжительности проекта.
Научная новизна работы заключается в предложении авторов автоматизировать построение сетевых графиков в строительстве скважин. Анализ рынка прикладных программ построения сетевых графиков показал, что существующие программы ограничиваются 2D-моделированием, и наряду с простотой интерфейса имеют ограниченные возможности, не отвечающие решению заявленных недостатков текущей методики моделирования графиков.
В ПАО «Татнефть» сегодня успешно используется программный комплекс – Технико-экономический тренажер «Энергоэффективная нефтедобыча». Использование данного тренажера позволяет повысить знания специалистов как в направлении основ процесса разработки, эксплуатации скважин и процесса нефтедобычи, так и в направлении стратегического управления нефтяным бизнесом. Опыт разработки данного приложения может быть взят за основу при создании программы для моделирования сетевых графиков строительства скважин. Экономический эффект от внедрения автоматизированного программного комплекса построения сетевых графиков строительства скважин заключается, во-первых, в возможности осуществлять экономически целесообразный выбор бурового блока при планировании строительства нефтяных скважин, во-вторых, сократить время на составление сетевых графиков, в-третьих, оперативно реагировать на изменения сроков строительства текущих скважин (при отклонении от плановых сроков) и с помощью программы моделировать оптимальные варианты дальнейших действий.

2. Цифровая экономика [Электронный ресурс] // Цифровая экономика. – URL: http://www.proprof.ru/stati/careera/vybor-professii/o-professiyah/cifrovaya-ekonomika (дата обращения: 19.10.2018).
3. Гарифуллина З.А. Определение критериев успеха реализации IT-проектов на предприятиях нефтяной отрасли с позиций теории функциональных систем // Нефть, газ и бизнес. – 2013. – №?6. – С. 27–34.
4. Карпов В.Г. Экономическая оценка инвестиционных проектов: учеб. пособие / В.Г. Карпов, Р.А. Нугайбеков. – Уфа: Изд-во УГНТУ, 2007. – 159 с.
5. Разработка и построение сетевого графика [Электронный ресурс] // Разработка и построение сетевого графика. – URL: https://studbooks.net/1436743/menedzhment/razrabotka_postroenie_setevogo_grafika (дата обращения: 06.11.2018).
6. Иванов А.Ф. Технико-экономический тренажер «Энергоэффективная нефтедобыча» // Информационно-коммуникационные технологии в реальном и виртуальном образовательном пространстве: материалы Международной научно-практической видеоконференции. – 2015. – С. 40–42.
7. Андреев А.Ф. Основы менеджмента (нефтяная и газовая промышленность): учебник / А.Ф. Андреев и др.; под ред. А.Ф. Андреева. – М.: ФГУП Изд-во «Нефть и газ» РГУ нефти и газа им.
И.М. Губкина, 2007. – 264 с.
Основными принципами управления, как на уровне промышленных предприятий, так и на уровне государства становятся следующие[2]:
- Получение данных в реальном времени.
- Управление экономическими процессами, основанное на автоматизированном анализе больших данных.
- Высокая скорость принятия решений, изменение правил в реальном времени – мгновенное реагирование на изменения и интерактивность среды.
- Решения в одно касание.
Многие организационные и технические мероприятия представляют собой сложную совокупность взаимосвязанных работ. Примером таких мероприятий являются проекты строительства нефтяных скважин. При реализации таких проектов возникает ряд проблем: определение рациональных сроков начала и окончания этапов строительства, обеспечивающих выполнение всего срока строительства скважины за минимальное время; распределение ресурсов между работами, минимизирующее суммарные затраты. В частности, отдельные работы, например, плановые ремонты, могут оказаться «узким местом», сдерживать проведение остальных мероприятий. Их следует выявить и выполнять заблаговременно или выделить на них дополнительные средства [3].
Сетевой график позволяет получить наглядное представление о порядке выполнения отдельных операций, а также о взаимосвязях между ними. Он является моделью реализации мероприятия, на которой можно изучать последствия тех или иных решений с целью выбора наилучшей стратегии управления [4].
На сетевом графике каждая работа изображается стрелкой, а факт ее окончания, называемый событием, обозначается кружком.
Предположим теперь, что некоторая работа а2 может начаться только после окончания работы а1. В таком случае говорят, что работа а2 опирается на работу а1.
Если же одна работа опирается на несколько других, то естественно, что она может начаться не ранее, чем закончится последняя из предшествующих. Логическая же связь со всеми остальными изображается в виде фиктивных работ, не требующих затрат времени и изображаемых пунктирными стрелками, идущими к началу данной работы. На рис. 1 работа а4 опирается на а1, а2 и а3, но позже всех заканчивается а2.
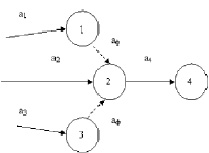
Рис. 1. Фрагмент сетевого графика с фиктивными работами
Построение сетевого графика начинается с простого перечисления всех необходимых работ (графа 2 в табл. 1).
Пример организации исходных данных задачи сетевого планирования
Опирается на работу
Затем на основании простого логического анализа заполняется второй столбец таблицы и определяется ранг каждой работы. Работы первого ранга не опираются на другие. Работы второго ранга опираются только на работы первого ранга. Работы третьего ранга могут опираться на работы второго и первого рангов и т. д.
После этого производится перенумерация работ и заполняется последний столбец таблицы. При этом безразлично, в каком порядке присваивать номера работам одного и того же ранга.
После этого составляется новая таблица, в которой указывается продолжительность выполнения каждой работы (табл. 2).
Существует несколько методов решения задач сетевого планирования. По-видимому, наиболее наглядным и простым является графоаналитический метод. При этом методе сначала проводится ось времени. В начале оси располагается исходный узел 0. Величина стрелки и угол ее наклона для любой работы выбираются, чтобы ее проекция на ось времени была равна ее продолжительности. Очевидно, что в этом случае есть множество вариантов изображения каждой работы.
Упорядоченные исходные данные
Опирается на работу
Если же одна работа опирается на несколько других, то изображающая ее стрелка должна начинаться из самого правого кружка, а логическая связь с другими работами изображается пунктирными стрелками (фиктивные работы).
Пример построения сетевого графика приведен на рис. 2.
На графике двойными стрелками выделены критические работы. Критическая дуга составляется только из сплошных стрелок. Из графика, построенного графоаналитическим методом, сразу видна общая продолжительность производственного процесса. В данном случае Тобщ = 31 день.
Фиктивные работы характеризуют резервы времени соответствующих реальных работ. Эти резервы определяются проекцией соответствующей фиктивной работы на ось времени. В данном случае работа а4 имеет резерв времени в 2 дня, а5 – 5 дней, а7 – 9 дней, а1 и а6 – 18 дней и а9 – 2 дня.
Знание этих резервов позволяет изменить сроки начала некритических работ и дать рекомендации о перераспределении имеющихся ресурсов в пользу критических работ с целью сокращения общей продолжительности выполнения всего комплекса. Например, если а6 – завоз оборудования, то его можно осуществить не сразу после завершения работы а1, а на 12 дней позже. При этом не будет излишне загромождаться территория и само оборудование будет более сохранным. Если же, например, работы а2, а7 и а8 выполняются за счет трудовых ресурсов, с а2 и а7 вполне можно снять половину рабочих и перевести их на выполнение критических работ а2 и а8.
На многих предприятиях построение сетевых графиков выполняется с помощью программы MicrosoftExcel, пример представлен на рис. 3.
Недостатками текущей методики построения сетевых графиков являются:
1. Отсутствие возможности отследить продолжительность строительства скважины по этапам строительства.
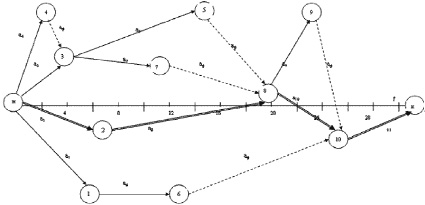
Рис. 2. Сетевой график комплекса работ, построенный графоаналитическим методом

Рис. 3. Пример сетевого графика строительства скважин
2. Отсутствие информации об экономически оптимальном варианте работы буровых установок или возможных вариантах.
3. Оперативное изменение графика в таком формате является трудоемкой работой и, как правило, сконцентрировано на знаниях 1–2 специалистов.
4. Отсутствие наглядной информации о расположении на местности с реальными географическими координатами.
Анализ рынка прикладных программ построения сетевых графиков показал, что существующие программы ограничиваются 2D-моделированием, и наряду с простотой интерфейса имеют ограниченные возможности (рис. 4), не отвечающие решению заявленных недостатков текущей методики моделирования графиков [5].
В ПАО «Татнефть» сегодня успешно используется программный комплекс – Технико-экономический тренажер «Энергоэффективная нефтедобыча», который представляет собой обучающую систему, охватывающую технологическую цепочку процесса разработки нефтяного месторождения, построенную на основе технологий 3D-визуализации, специализированного интегрированного программного комплекса для создания и сопровождения трехмерных постоянно действующих гидродинамических моделей месторождений [6]. Использование данного тренажера позволяет повысить знания специалистов как в направлении основ процесса разработки, эксплуатации скважин и процесса нефтедобычи, так и в направлении стратегического управления нефтяным бизнесом. Опыт разработки данного приложения может быть взят за основу при создании программы для моделирования сетевых графиков строительства скважин.
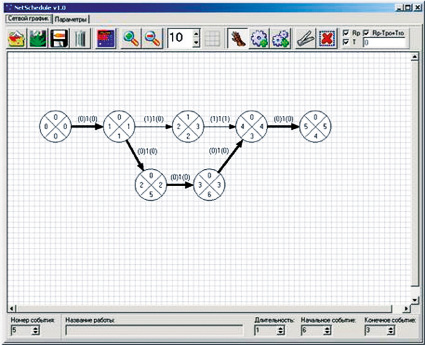
Рис. 4. Интерфейс программы NetSchedule для построения сетевых графиков
Скриншот из программы представлен на рис. 5, для наглядности предлагаемого решения на рисунке добавлены данные бурения скважин.
Программу предлагается реализовать в двух версиях: веб-приложении, доступном через веб-браузер и мобильной iPad-версии для доступа с iPad-устройств.
Таким образом, предлагаемое приложение позволит в режиме реального времени руководству отслеживать не только планируемые работы, но и текущие работы на буровых.

Рис. 5. Скриншот из программы «Технико-экономический тренажер «Эффективная нефтедобыча»
Основная цель разработки программного обеспечения – это автоматизация процесса формирования сетевых графиков. В систему должны вноситься исходные параметры – географические данные забоя скважины, плановые сроки и длительность работ, данные буровых установок, сведения о плановых ремонтах, исходные расположения буровых блоков.
В программу должна быть заложена логистика сетевого планирования, описанная выше. Задача программы смоделировать сетевой график или возможные варианты сетевых графиков. Должна быть предусмотрена возможность сохранения нескольких проектов сетевых графиков. В приложении должна быть возможность оперативно перестраивать графики при изменении условий строительства скважины – возникновение внепланового ремонта, увеличение срока строительства скважины, например, в связи с ремонтом или авариями, осложнениями, и предупреждать пользователей системы об отклонении от плановых сроков.
Экономический эффект от внедрения автоматизированного программного комплекса построения сетевых графиков строительства скважин заключается, во-первых, в возможности осуществлять экономически целесообразный выбор бурового блока при планировании строительства нефтяных скважин, находящихся на оптимальном расстоянии от будущей скважины с учетом географических условий местности [7]. При этом программа позволит увидеть альтернативные варианты действий для возможности принятия экономически правильных решений специалистами и руководством компании. Во-вторых, сократить время на составление сетевых графиков. В-третьих, оперативно реагировать на изменения сроков строительства текущих скважин (при отклонении от плановых сроков) и с помощью программы моделировать оптимальные варианты дальнейших действий. Предлагаемое решение будет интересно также и Заказчику строительства скважин.
Источник: vaael.ru
Проследим этапы составления сетевого графика.
Наиболее распространенным и практичным инструментом планирования операций является график (диаграмма) Гаита ( Gantt Chart ). На диаграмме операции представлены отрезками, соответствующими определенному периоду времени, а также отражена их последовательность и взаимосвязь.
В случае большого количества операций целесообразно использовать при планировании структуру работ проекта (см. проектироване операций). При этом график Ганга может детализироваться посредством построения дополнительных диаграмм, соответствующих уровням работ проекта
График строится следующим образом.
Вначале имеет смысл определить состав операций и дать описание каждой операции, используя приведенную ниже форму.
| Обозначение операции | Описание операции |
Затем стоит установить очередность их выполнения. Операции, как правило, взаимосвязаны между собой (окончание одной операции связано с началом другой), полому следует определить последовательность операций.
Далее необходимо оценить продолжительность каждой операции, определить взаимосвязь операций, используя следующую форму.
Затем стоит установить очередность их выполнения. Операции, как правило, взаимосвязаны между собой (окончание одной операции связано с началом другой), полому следует определить последовательность операций.
Далее необходимо оценить продолжительность каждой операции, определить взаимосвязь операций, используя следующую форму.
| Обозначение операции | Описание операции | Продолжительность (дни) | Непосредственно предшествующие операции |
Обратите внимание на то, что в данном пособии мы будем рассматривать последовательность операций с использованием однозначной, т. е. наиболее вероятной оценки — наиболее точное предположение периода времени, необходимого для выполнения конкретной операции.
В реальной практике, если однозначная оценка времени, необходимого для выполнения операции, является ненадежным показателем, то для оценки продолжительности операций используется три оценки (оптимистическая — минимальный период времени выполнения операции, наиболее вероятная оценка и пессимистическая оценка — максимальный период времени выполнения операции).
Рассмотрим один из фрагментов графика (или диаграммы) Ганта на примере проекта проведения студенческой научно-технической конференции. Вероятно, на этапе подготовки потребуется отдельный график для получения заявок от выпускающих кафедр на определенное количество докладов, количество участников — студентов и преподавателей, количество научных секций, количество членов организационного комитета и т. п.
Цепью построения графика является обеспечение контроля над ходом выполнения двенадцати взаимосвязанных операций проекта. Данные для построения графика приведены в табл. 1
Таблица 1 — Перечень операций фрагмента проекта по проведению студенческой научно-технической конференции
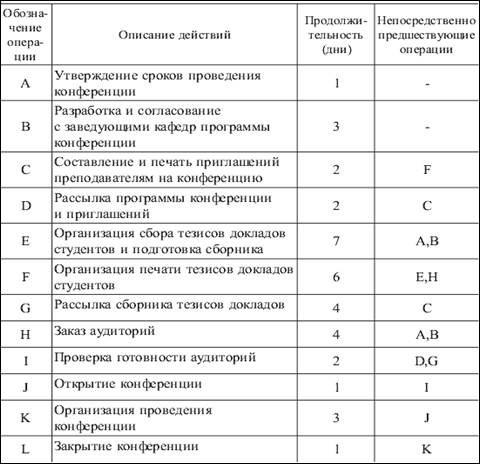
Сформированный на основании данных таблицы график Ганта будет выглядеть следующим образом (рис. 1).

Рис. 1. График Ганта проекта проведения студенческой научно-технической
Таким образом, график Ганга позволяет «привязать» операции ко времени, а также выявить операции, которые можно выполнять параллельно. Это важно знать менеджеру, чтобы при выполнении плана можно было эффективно управлять перераспределением ресурсов в случае непредвиденных обстоятельств.
Однако в проектах с числом операций 25-30 график оказывается слишком громоздким для визуального восприятия. Кроме того, график Ганга не располагает прямой процедурой для определения критического пути, но, несмотря на ряд таких недостатков, он имеет огромное практическое значение.
Сетевой график
Сетевые методы планирования известны как методы составления графика критического пути и были разработаны для планирования и отслеживания факторов (время, затраты или издержки, наличие ресурсов) как но отдельности, так и в различных комбинациях.
Рассмотрим построение сетевого графика на примере создания новой модели портативного компьютера весом до 0,5 кг (оптимальный размер — не больше 12x24x2,5 см). Модель имеет складную клавиатуру, оснащена дисплеем на жидких кристаллах дисплеем, микродисководом и портом для работы в глобальных сетях. Компьютер предназначен для бизнесменов, однако может применяться и более широким кругом потребителей, например, студентами, поэтому цена на него не должна превышать 175-200 условных единиц.
Таким образом, в задачи проекта входит конструирование, разработка и создание опытного образца такого компьютера. В быстро меняющейся отрасли производства компьютерной техники чрезвычайно важно освоить новую модель и вывести ее на рынок не позже, чем через год. При этом проектная группа имеет в своем распоряжении около восьми месяцев (35 недель).
Проследим этапы составления сетевого графика.
1. Идентификация операции
Узловыми событиями проекта должны стать следующие операции: конструирование компьютера, изготовление опытного образца (прототипа), его тестирование, разработка технологии изготовления, подбор, приобретение и монтаж оборудования, а также составление итогового отчета, обобщающего все аспекты конструирования, технологии и производства.
2. Определение последовательности операций и построение сетевого графика
На основе обсуждения, проведенного в группе, менеджер проекта составляет таблицу с перечнем работ с указанием последовательности их выполнения (табл. 2).
Таблица 2 — Операции по созданию повой модели компьютера
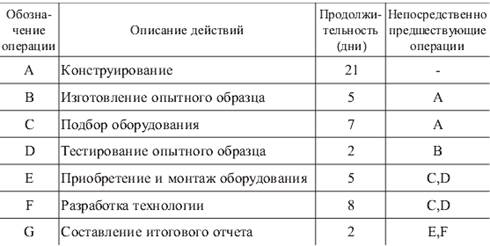
Тогда сетевой график, который предлагает менеджер проекта, будет выглядеть как показано на рис. 2.
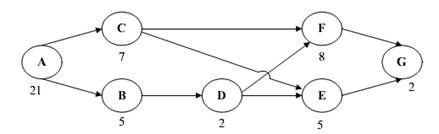
Рис. 2.Сетевой график проекта создания новой модели компьютера
Полученные данные позволят приступить к определению критического пути и построению сетевого графика.
3. Определение критического пути
Критическим путем называют цепочку последовательно связанных операций в сетевом графике с наибольшей продолжительностью. Он характеризуется как путь с нулевым резервом времени.
Резерв времени поочередно вычисляется отдельно для каждой операции. Он представляет собой разницу между поздним и ранним ожидаемыми сроками завершения работ. Резерв также описывается как время, на которое можно задержать выполнение отдельной операции, не увеличивая при этом срок окончания всего проекта.
Для правильного составления графика необходимо вычислить для каждой операции четыре временных параметра:
— ранний срок начала операции от начала проекта (Late Start Time — ES);
— ранний срок окончания операции от начала проекта (Late Finish Time — EF);
— поздний срок окончания операции (Late Finish Time- LF),t. е. крайний срок, когда операцию можно завершить, не задерживая окончания всего проекта;
— поздний срок начала операции (Late Start Time- LS), т. е. поздний срок окончания, минус время, необходимое для выполнения операции.
Процедуру вычисления этих показателей, определения резерва времени и критического пути легче всего объяснить на простом сетевом графике, изображенном на рис. 3. Буквами обозначены операции, а цифрами — их средняя продолжительность.
а. Определим срок ES.
В качестве даты начала проекта принимается «нулевой» день, и он же будет ранним сроком начала операции А. Чтобы получить ES для операции В, прибавляем продолжительность операции А и получаем значение 2. Точно так же ES для операции С будет 0+2=2.
Чтобы вычислить ES для операции D, берем большее значение ES и продолжительность времени для каждой из предшествующих операций. Поскольку путь через операцию В=2+5=7 больше нуги через операцию С = 2 + 4 = 6, ES для D =7. Эти значения указываются на сетевом графике (см. рис. 2.7, этап а). Наибольшее значение выбирается потому, что операцию D нельзя начать прежде, чем будет завершена самая продолжительная из предшествующих ей операции.
б. Теперь вычислим срок EF для операции А равен ее сроку ES (т е. 0) плюс ее продолжительность 2. EF операции В равен ее сроку ES (т. е. 2), плюс продолжительность 5, т е. 7. EF для операции С будет 2+4=6, а для операции D : 7 + 3 = 10. На практике ES и EF вычисляются вместе, по мере построения соевого графика Поскольку ES плюс время продолжительности операции равняется EF, то EF предшествующей операции является ES для следующей, и т. д.
в.Затем вычисляются поздние сроки начала и завершения операций (LF и LS). Процедуру этих вычислений можно выразить в математической форме, однако ее проще объяснить и освоить, представив ее на чисто понятийном уровне. Расчет LS и LF начинают с конца проекта, т.е. с какого-то определенного предполагаемого или желательного срока его завершения.
Двигаясь потом от конца к началу и анализируя все операции по очереди, определим, насколько можно задержать начало каждой операции, не задерживая при этом начала следующей за ней операции.
Предположим, что поздний срок завершения проекта совпадает с ранним сроком окончания операции D,t. е. равен 10. В таком случае поздний срок начала операции D будет 10 — 3=7. Самый поздний срок, когда может быть выполнена операция С, не задерживая LS для D. равен 7, что означает, что LS для операции С будет 7 — 4=3.
Наиболее поздний срок, когда можно завершить операцию В, не задерживая LS операции D , также равен 7, что означает, что LS для операции В составляет 7 — 5=2. Поскольку операция А предшествует двум операциям, выбор значений LS и LF зависит оттого, какая из этих операций должна начинаться первой.
Очевидно, что в данном примере показатель LF для операции А должен определяться на основе операции В, поскольку ее значение LS равно 2, в то время как выполнение операции С можно отложить только на один день, в противном случае это повлечет за собой задержку окончания проекта. И, наконец, поскольку операция А должна быть завершена ко второму дню, она не может начаться позже, чем в исходный день, следовательно, значение LS для этой операции равно 0.
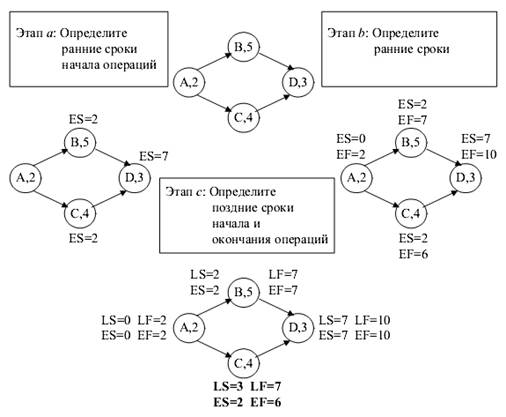
Рис. 3. Этапы расчета параметров сетевого графика
г.Наконец определяется резерв времени для каждой операции. Он определяется либо разницей LS — ES, либо LF — EF . В рассматриваемом нами примере резерв времени существует только для операции С (один день), следовательно, критический путь проходит через операции А, В и D .
Выполнив все описанные выше процедуры для рассматриваемого примера создания новой модели компьютера, мы определили критический путь, а также поздние и ранние сроки начала операций для проекта.
Полученные результаты приведены на рис. 4.
Используя рисунок, рассмотрим, как построен сетевой график: На сетевом графике операции обозначены узлами, а стрелки указывают последовательность выполнения операций.
Каждая стрелка исходит из непосредственно предшествующей операции. Например, операции Е непосредственно предшествуют операции Си D. В каждом узле приведено описание операции и указана ее продолжительность в днях.
Обратите внимание, что в данном случае мы получили сетевой график, в котором два критических пути.
Первый проходит через операции А, С, F , D и С, а второй — через А, В, D , F и С Следовательно, вне критического пути находится только одна операция Е. Это означает, что реализовать данный проект в минимальные сроки будет довольно сложно.
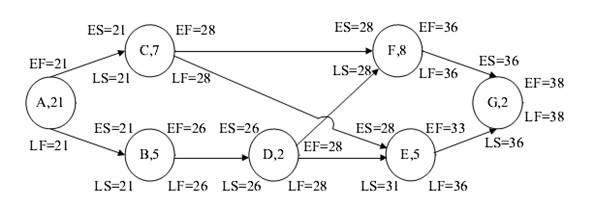
Рис. 4. Параметры ceтевого графика проекта создания новой модели компьютера
Таблица 3 — Параметры ceтевого графика проекта создания новой модели компьютера

Чтобы методы сетевого планирования можно было применить с наибольшей эффективностью, проект должен обладать следующими характеристиками:
— в нем должны быть точно определены операции или задания, которые обозначают начало и окончание проекта;
— задания или операции должны быть взаимно независимы. Необходимо, чтобы в пределах определенной последовательности их можно было начинать, приостанавливать, исключать и выполнять независимо один от другого;
— необходимо наметить точный порядок выполнения операций и заданий; они должны выполняться в определенной последовательности.
Задачи для решения
Задача 1. Подготовьте проект проведения олимпиады по физике, математике, литературе и русскому языку среди абитуриентов, поступающих в вузы в формате графика (диаграммы) Ганта.
Подготовьте проект проведения олимпиады по физике, математике, литературе и русскому языку среди абитуриентов, поступающих в вузы.
Олимпиада будет проводиться в период с 10 по 24 марта в нашем университете. Предполагается, что будет шесть потоков абитуриентов, в каждом из которых будет по тридцать человек.
Предлагаемый вами проект должен содержать не менее десяти операций по подготовке и проведению олимпиады.
Перед тем, как вы начнете решать задачу, целесообразно посмотреть пример построения графика Ганта.
1. Дополните, при необходимости, описание ситуации, определите состав и дайте краткое описание операций, необходимых для реализации проекта проведения олимпиады среди абитуриентов.
2. Определите последовательность операций для каждой группы отдельно, используя представленную ниже форму.
| Обозначение операции | Последовательность операци |
3. Самостоятельно определите длительность и взаимосвязь операций, используя следующий формат представления результата.
| Обозначение операции | Продолжительность (дни) | Непосредственно предшествующие операции |
4. Постройте план действий по проведению олимпиады среди абитуриентов в формате графика (диаграммы) Ганта.
Задача 2. Построение сетевого графика.
Ниже приводится перечень операций, входящих в проект разработки нового авиационного прибора, с указанием времени, необходимого для выполнения каждой операции.
| Обозначение операции | Продолжительность (дни) | Непосредственно предшествующие операции |
| A | 1 | — |
| В | 4 | A |
| С | 3 | A |
| D | 7 | A |
| E | 6 | B |
| F | 2 | C,D |
| G | 7 | E,F |
| H | 9 | D |
| I | 4 | G,H |
Задание
1. Составьте сетевой график проекта.
2. Укажите ранние сроки начала и окончания операций.
3. Определите критический путь.
4. Что произойдет, если продолжительность выполнения операции F будет увеличена с двух дней до четырех?
Задача 3. Построение сетевого графика.
Ниже приводится перечень операций, входящих в проект разработки новой радиоаппаратуры, с указанием времени, необходимого для выполнения каждой операции.
| Обозначение операции | Продолжительность (дни) | Непосредственно предшествующие операции |
| A | 1 | — |
| В | 4 | A |
| С | 3 | A |
| D | 2 | B |
| E | 5 | C,D |
| F | 2 | D |
| G | 2 | F |
| H | 3 | E,G |
Задание
1. Начертите сетевой график выполнения операций.
2. Укажите конкретные операции, которые образуют критический путь.
3. Предположим, что необходимо максимально сократить время выполнения проекта и у вас есть возможность ускорить выполнение операций B, C, D и G (все или выборочно) на две недели. Какие операции Вы бы сократили?
4. Какими будут новый критический путь и наиболее раннее время завершения проекта?
Задача 4 . Построение сетевого графика.
Исходные данные. Таблица 4
Построить сетевой график выполнения работ и рассчитать продолжительность критического пути при следующих данных:
Таблица 4 — Очередность событий и продолжительность работ
| Номер предшествующего события | 1 | 1 | 2 | 3 | 3 | 4 | 5 |
| Номер последующего события | 2 | 3 | 5 | 4 | 6 | 6 | 6 |
| Продолжительность работы, дни | 5 | 4 | 3 | 6 | 8 | 1 | 2 |
Задача 5. Построение сетевого графика.
Исходные данные. Таблица 5.
Построить сетевой график постройки гаража и обеспечить снижение продолжительности строительных работ на 1 день по сравнению c первоначально рассчитанным критическим путем. На каждой работе задействовано 3 рабочих.
Таблица 5 — Содержание и продолжительность работ
Как вы ведете себя при стрессе?: Вы можете самостоятельно управлять стрессом! Каждый из нас имеет право и возможность уменьшить его воздействие на нас.
Как выбрать специалиста по управлению гостиницей: Понятно, что управление гостиницей невозможно без специальных знаний. Соответственно, важна квалификация.

Источник: megaobuchalka.ru
Лекция 6. Параметры сетевого графика и их расчет
Работы и события сетевого графика обладают временными параметрами, знание которых необходимо как в процессе планирования, так и в ходе оперативного управления строительством. Рассмотрим сущность этих параметров и методы их расчета.
Расчет сетевых графиков сводится к численному определению его параметров. Поэтому сначала перечислим их.
При расчете сетевых графиков определяются следующие параметры:
- — ранние начала и окончания работ;
- — поздние начала и окончания работ;
- — продолжительность критического пути;
- — общие и частные резервы работ.
За расчетную схему (рис. 6.1) выберем расположение работ, закодированных буквами: (/г-z) — предшествующая работа; (i-y) -рассматриваемая работа; (j-k) — последующая работа.

Рис. 6.1. Расчетная модель
Кодирование расчетных параметров сетевых графиков: i-j — код данной работы;
i — код начального события данной работы;
j — код конечного события данной работы;
h-i — код работы, предшествующей данной работе;
h — код событий, предшествующих начальному событию данной работы;
j-k — код работ, последующих за конечным событием данной работы;
к — код событий, последующих конечному событию данной работы;
L — путь;
LKp — критический путь;
TL — продолжительность пути;
Т1хр . продолжительность критического пути и критический срок;
T^j — продолжительность работы;
Т,_] — раннее начало работы z-j;
Т,-црО) — раннее окончание работы i-j;
Ti-jim,) — позднее начало i-j;
— позднее окончание работы i-j;
Т^) — ранний срок совершения события j;
7п) — поздний срок совершения события j;
R,.j — общий (полный) резерв времени i-j;
r,_t — частный (свободный) резерв времени i-j.
Раннее начало работы — самый ранний из возможных сроков начала работы, который обуславливается выполнением всех предшествующих работ.
Раннее начало работы (рис. 6.2) равно продолжительности максимального пути от исходного события графика до начального события данной работы:

Рис. 6.2. Модель расчета ранних начал

Раннее окончание работы — самый ранний из возможных сроков окончания работы. Оно равно сумме раннего начала работы и ее продолжительности:
Для начальных (исходных) работ:
- — раннее начало принимается равным 0;
- — раннее окончание численно равно продолжительности работы.
Максимальное раннее окончание одной из завершающих работ определяет продолжительность критического пути.
Позднее начало работы — самый поздний допустимый срок начала работы, при котором планируемый срок достижения конечной цели не меняется.
Позднее окончание работы определяется разностью между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события графика.
Позднее окончание любой работы (рис. 6.3) равно наименьшему из поздних начал последующих работ:

Рис. 6.3. Модель расчета поздних окончаний
Позднее начало работы равно разности между величинами ее позднего окончания и продолжительности.
Для завершающих работ сетевого графика:
— позднее окончание равно величине продолжительности критического пути: t»». = Т = max ;
— позднее начало завершающей работы равно разности между продолжительностью критического пути и продолжительностью данной работы:
= Т -t. .
Общий (или полный) резерв времени работы (рис. 6.4) -это максимальное время, на которое можно увеличить продолжительность данной работы или перенести ее начало без увеличения продолжительности критического пути. Он равен разности между одноименными поздними и ранними параметрами этой работы:

Рис. 6.4. Модель расчета общих резервов
Частный резерв времени (рис. 6.5) — это максимальное время, на которое можно увеличить продолжительность данной работы или перенести ее начало без изменения ранних сроков начала последующих работ. Он равен разности между ранним началом последующей работы и ранним окончанием данной работы:
Рис. 6.5. Модель расчета частных резервов
Частный резерв времени отличается от нуля, если в конечное событие работы входят две и более работы.
6.2. Методы расчета сетевых графиков
Сетевые графики можно рассчитывать с помощью компьютерной техники и вручную. В настоящее время известно несколько методов расчета сетевых графиков вручную: табличный метод; расчет на графике — четырехсекторный метод; метод дроби; метод потенциалов и др.
6.2.1. Табличный метод
Классическим методом, положившим начало теории расчета сетевых графиков, является табличный метод, или, как говорят, алгоритм расчета сетевого графика по таблице.
Пример графика для расчета табличным методом приведен на рис. 6.6. В этом случае определение параметров сетевого графика выполняется в таблице.

Рис. 6.6. Пример графика для расчета табличным методом и методом потенциалов
Заполнение таблицы ведется в следующем порядке:
- 1. В первые три графы заносят исходные данные по каждой работе. Необходимо последовательно записывать все работы, выходящие из первого события (по часовой стрелке), затем — все работы, выходящие из второго события, и т.д.
- 2. Производят расчет ранних параметров работ построчно сверху вниз.
- 3. Определяют продолжительность критического пути, равную максимальному из ранних окончаний завершающих работ.
- 4. Рассчитывают поздние параметры работ. Расчет ведется построчно снизу вверх, от завершающих работ до исходных.
- 5. Определяют общие и частные резервы времени (их можно определить по каждой работе вразбивку).
Определяют перечень работ, составляющих критический путь, т.е. работ, не имеющих резервов времени.
При расчете сетевых графиков табличным методом заполняют следующую таблицу (табл. 6.1).
Расчет сетевого графика
Номер предшествующего события
В графу 3 заносят шифр (код) каждой работы, запись ведут последовательно, начиная с первого события. Когда из события выходит несколько работ, запись ведут в порядке возрастания номеров их конечных событий. После этой процедуры в графу 2 записывают номера событий, предшествующих каждой работе.
Следующей заполняют графу 4. Напротив каждой работы, записанной в графе 3 из сетевого графика, проставляют ее продолжительность t.
Графы 5 (раннее начало работы 7*’») и 6 (раннее окончание работы Т 1 ’») заполняются одновременно. У работ 1-2 и 1-3 предшествующих событий нет, следовательно, их раннее начало равно нулю. Раннее окончание работы равно сумме его раннего начала и продолжительности.
Таким образом, в графу 6 вносят сумму цифр граф 4 и 5. Для работы 2-4 раннее начало равно раннему окончанию предшествующей работы, т.е. работы 1-2 (в графе 2 записано предшествующее событие 7); следовательно, раннее начало работ, начинающихся с события 2 (2-3, 2-4), также равно 5 дням. Прибавляя к ранним началам работ их продолжительности, получим их раннее окончание. Если у работы есть два и более предшествующих события (например, работа 4-6), то в этом случае выбирают максимальное значение раннего окончания этих работ и заносят в графу 5, на ее основе определяют раннее окончание.
Максимальное раннее окончание последней работы равно величине критического пути.
Дальше заполняют графы 7 и 8. Позднее начало Т'» и окончание 7″» записываем в табл. 6.1, начиная с конца графы.
Критический путь, а следовательно, и позднее окончание завершающей работы, равен 16 дням. Вносим эту цифру в строку 8 графы 8. Позднее начало работы равно разности его позднего окончания и продолжительности.
Общий резерв R (графа 9) определяют как разность между числами в графах 8 и 6 или 7 и 5.
Частный резерв г (графа 10) подсчитывают как разность между ранним началом последующей работы и ранним началом данной. При заполнении данной графы необходимо учитывать что, если в конечное событие данной работы входит только одна стрелка, то частный резерв ее равен нулю. Для работ, не лежащих на критическом пути, но входящих в события, лежащие на нем, общие и частные резервы численно равны. Частные и общие резервы работ, лежащих на критическом пути, равны нулю.
Правильность расчета сетевого графика подтверждают проверкой:
- — ранние параметры никогда не превосходят по численному значению поздние параметры;
- — критический путь должен представлять собой непрерывную последовательность работ от исходного события до завершающего;
- — величина частного резерва времени работ не должна превосходить величину общего резерва времени;
- — позднее начало одной из исходных работ обязательно должно быть нулевым.
- 6.2.2. Секторный метод расчета
При этом методе каждое событие (рис. 6.7) графиком делится на 4 сектора, в которых указываются необходимые расчетные данные.
Раннее начало работы Б—-
Номер события, через которое к данному приходит путь наибольшей

Позднее окончание работы А
продолжительности, считая от исходного события в сети
Рис. 6.7. Условные обозначения при секторном методе расчета
Исходным графиком для расчета четырехсекторным методом служит график, приведенный на рис. 6.8.

Рис. 6.8. Исходный график для расчета четырехсекторным методом
Вначале от исходного события до завершающего определяют все ранние начала работ. Для завершающего события графика значения в левом и правом секторах равны, поскольку максимальное из ранних окончаний завершающей работы равно позднему окончанию этой работы.
Затем рассчитывают поздние окончания работ от завершающего к начальному событию. Рассчитанный график будет иметь вид, показанный на рис. 6.9.

R | г fj-j ~tjk * (h-j + ^/.у 7 (Частный резерв времени)
~ (Общий резерв времени)
Рис. 6.9. График, рассчитанный четырехсекторным методом
Дополнительным требованием к критическим работам является требование по соблюдению условия
l j-k ‘i-j — Ч-r
20 — 12 = 8; 25 — 5 = 20; 25 — 11 12. Следовательно, работы нижнего пути некритические.
Резервы времени работ графика можно отметить на самом графике в виде R || г, а рассчитать их следует по формулам
Я,-, = С; — (*? + Ь-j); + . ?) .
Четырехсекторный способ расчета сетевых графиков позволяет быстрее осуществить расчет и определить продолжительность критического пути (иногда требуется прикидочный расчет), но при повторном расчете требуется перебирать данные па графике. Этого не требуется при табличном способе, где пересчитывается сама таблица. Кроме того, в таблице наглядно прослеживаются все без исключения параметры сетевого графика (включая резервы времени).
6.3. Сетевой график в масштабе времени и линейный график работ
До сих пор мы рассматривали безмасштабиые сетевые графики, в которых длина стрелки не имеет значения. Однако на практике для наглядности нередко сетевые графики строят в масштабе времени. Для этого работы наносятся на график в определенном масштабе, а длина каждой стрелки при этом соответствует количеству делений, равному числу дней выполнения работы, т.е. ее продолжительности .
Изобразим в масштабе времени сетевой график, показанный па рис. 6.10 и рассчитанный непосредственно па графике.

Для этого построим временную сетку в масштабе, например, 1 день = 1 см (рис. 6.11). Затем последовательно нанесем на сетку каждое событие, устанавливая его в ранний срок совершения. Событие / ставим в нулевой момент, т.к. ранний срок его совершения равен нулю. Далее наносим событие 2, отступив на 2 дня от начала, и показываем работу 1-2.
При этом длина стрелки берется между центрами событий. Если работа изображена в виде ломаной стрелки (как работа 1-2), то длина стрелки принимается равной ее горизонтальной проекции. Двойной линией изображается продолжительность работы, а одинарной — частный резерв времени, если он у работы есть.
Далее наносим событие 3 и изображаем работу 1-3, затем событие 4 и критическую работу 1-4, ит.д. Связи 3-4 и 5-6, не имеющие продолжительностей, показаны с учетом того, что у них условно есть частные резервы времени.
На сетевом графике в масштабе времени наглядно видны ранние сроки выполнения всех работ, а также их частные резервы времени. Это значительно повышает оперативность использования сетевого графика. При этом обычно дни по порядку (показанные на рис. 6.11) привязывают к месяцам и календарным датам.

Однако сетевой график, построенный в масштабе времени, имеет и серьезный недостаток. Он состоит в том, что при внесении в график различных корректив, связанных с изменением сроков выполнения работ, изменяются сроки свершения событий, а следовательно, и точки нахождения их на графике, что приводит к необходимости перестройки графика.
При использовании безмас-штабного сетевого графика, как показано на рис. 6.12, такой необходимости не возникает, поскольку длина стрелок и местонахождения событий на таком графике не имеют значения. Например, если работу 1-2 по каким-либо причинам мы выполним вместо планируемых 2 дней через 4 дня, то на рис. 6.12 событие 2 необходимо будет сдвинуть вправо на 2 дня, а это, в свою очередь, вызовет сдвиг на 2 дня событий 3, 5 и 6, что практически приведет к необходимости перестроить график или отдельные его фрагменты.
о 1 2 3 4 5 6 7 8 9 10 II 12 13 14
То Т1 То ТЭ То Ts Т» То Т.
Рис. 6.12. Линейный график работ сетевого графика
Линейный график работ строится так же, как сетевой график в масштабе времени, с той лишь разницей, что на линейном графике нс вычерчиваются события (кружочки). Кроме того, на линейный график вместо частных резервов обычно наносят полные резервы времени работ. Работы показывают в ранние сроки в виде сплошных горизонтальных отрезков, а полные резервы — в виде пунктирных отрезков.
У начала работы ставят помер ее начального события, а у конца — номер конечного события. На рис. 6.12 показан линейный график работ сетевого графика, изображенного на рисунках. Буквой г обозначены точки на горизонтальной оси, совпадающие по времени с началами и концами работ. При этом каждая смежная пара точек [г„ г, ] образует промежуток времени, в пределах которого не начинается и не заканчивается ни одна работа (например, промежуток [r(), ]).
Линейный график, как и сетевой график в масштабе времени, нагляден и удобен в использовании (вместе с безмасштабным сетевым графиком). Кроме того, он необходим при оптимизации сетевого графика, о которой речь пойдет в следующей главе.
- 6.4. Оптимизация сетевого графика
- 6.4.1. Общие понятия
После расчета сетевого графика необходимо проверить, согласуются ли найденные параметры с теми ограничениями, которые всегда имеются у строительной организации.
Во-первых, следует выяснить, не превышает ли продолжительность критического пути того срока сдачи объекта в эксплуатацию, который установлен в генеральном договоре с заказчиком.
Во-вторых, необходимо определить, выполнимы ли параметры сетевого графика при тех людских, материально-технических и финансовых ресурсах, которыми располагает или будет располагать в ходе строительства строительная организация.
Другими словами, параметры сетевого графика нужно привести в соответствие с теми временными и ресурсными ограничениями, которые имеются у строительной организации.
Процесс улучшения сетевого графика и приведения его параметров в соответствие с заданными или имеющимися ограничениями называют оптимизацией сетевого графика.
Оптимизация сетевого графика обычно производится в два этапа: на первом этапе сетевой график оптимизируют по времени, на втором — по ресурсам.
Следует отметить, что термин «оптимизация» в строго математическом смысле означает нахождение максимума некоторой функции, чего в нашем случае пет. Применение этого термина к сетевым графикам имеет несколько условных характер, поэтому иногда вместо этого термина используют «корректировку сетевого графика».
6.4.2. Оптимизация сетевого графика по времени
Если критический путь окажется больше договорных сроков, предусмотренных договором с заказчиком, то необходимо уменьшить продолжительность пути, т.е. оптимизировать сетевой график по времени.
При этом следует стремиться к тому, чтобы сокращение продолжительности критического пути потребовало минимального количества дополнительных ресурсов или вовсе их не потребовало. Для этого оптимизацию проводят поэтапно: вначале применяют способы оптимизации, позволяющие сократить продолжительность критического пути без привлечения дополнительных ресурсов, и если этими способами не удается решить задачу до конца, тогда прибегают к способам, требующим дополнительных ресурсов.
Рассмотрим подробнее эти способы.
- 1. Внесение изменений в структуру сетевой модели. Суть этого способа состоит в том, что анализируется организационнотехнологическая последовательность выполнения критических работ с целью выявления возможностей большего совмещения их выполнения во времени, то есть возможностей начать некоторые из этих работ раньше, чем это предусмотрено сетевым графиком.
- 2. Внутреннее перераспределение ресурсов. При этом способе часть трудовых ресурсов и техники снимается с некритических работ и перебрасывается на критические. В результате продолжительность критических работ сокращается, а некритических увеличивается. Разумеется, рабочие, перебрасываемые на критические работы, должны иметь ту профессию и ту квалификацию, которые необходимы для выполнения этих работ.
- 3. Привлечение дополнительных ресурсов. Привлечение дополнительных ресурсов (рабочих и машин) обычно наталкивается на трудности: во-первых, не так просто изыскать дополнительные ресурсы, во-вторых, их привлечение, как правило, вызывает удорожание работ. Поэтому следует стремиться к тому, чтобы процесс сокращения продолжительности критических работ путем привлечения дополнительных ресурсов протекал менее «болезненно» и с минимальным удорожанием работ.
- 6.5. Расчет и корректировка КУСГ
Расчет графика может быть выполнен вручную или на компьютерной технике после построения топологии сети и определения продолжительности всех работ в карточке-определителе.
Корректировка КУСГ проводится после привязки работ к календарю и осуществляется со следующими целями:
- — обеспечение нормативного, директивного или расчетного срока строительства при ограничениях на ресурсы;
- — обеспечение непрерывной поточной работы всех бригад подрядных организаций на объектах комплекса;
- — улучшение распределения капитальных вложений во времени при строительстве комплекса путем максимально возможного смещения их центра тяжести на завершающих этапах строи тельства, если нет ограничений на распределение капитальных вложений и других ресурсов по плановым периодам;
- — соблюдение других заданных ограничений.
Если после КУСГ величина критического пути превышает нормативную (директивную или расчетную) продолжительность строительства, то производится его корректировка посредством изменения топологии сети, насыщения отдельных видов работ трудовыми и машинными ресурсами, применения более эффективных организационно-технологических решений.
После корректировки сетевого графика по ранним началам работ его привязывают к календарю и строят линейный график работ с указанием на нем числа рабочих на всех работах.
Источник: ozlib.com