Математика в строительстве проект для 3 класса

Жизненные потребности заставили человека измерять уже в древности расстояния, а также площадь. Человек хотел знать измерения своего земельного участка, жилища и т. д. Из этой потребности возникла наука «геометрия» («гео» – земля, «метрио» – мерить). «Измерялись площади земельных участков, емкость сосудов и амбаров, объем вынутой при земельных работах земли. Из сохранившихся клинописных записей вавилонян известно, что единицы измерения площади и объема, были при своем возникновении связаны с материальными потребностями общества. Оказывается, иероглиф понятия «площадь» тождественен с иероглифом «количество зерна» (нужного для посева на ней), иероглиф понятия «объем» – с иероглифом «куча земли» (вынутой при выполнении оросительных работ). Русская мера объема «ведро» также указывает на конкретный практический характер происхождения пространственных мер.

Зарождение геометрических знаний, связанных с измерением площадей, теряется в глубине тысячелетий. Имеются вполне достоверные сведения о значительном развитии измерений в Египте более чем за две тысячи лет до нашей эры.

Математика 3 класс (Урок№1 — Повторение: устные и письменные приёмы сложения и вычитания.)

Узкая плодородная полоса земли между пустыней и рекой Нилом ежегодно подвергалась затоплению, и каждый раз разлив смывал границы участков, принадлежавших отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко. Это заставило египтян заниматься вопросами измерения, то есть землемерием.

В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, их называли «натягивателями веревки» – гарпетонаптами.

Они брали длинную веревку, делили ее узелками (расстояние между ними равно одному локтю фараона) на 12 равных частей, концы ее связывали и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Получался прямоугольный треугольник (сейчас его называют египетским треугольником), площадь которого принимали за эталон, если пользовались одной и той же веревкой. Угол между сторонами, равными 3 и 4, был прямым, поэтому этот метод использовали для построения прямых углов. Но египетские строители не осознавали, что их метод нуждался в каком-либо обосновании.

Египтяне правильно вычисляли площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция. Около 4 000 лет назад египтяне определяли площадь прямоугольника, теми же приемами, как и мы, т.е. умножали длину на ширину. Единицей измерения площади издревле использовали квадрат.

Таким образом, уже древним египтянам были известны многие математические знания, которые они с большим успехом использовали в строительстве, например вычисление площадей и пропорций зданий, а также углов наклона стен пирамид и насыпей, по которым на эти стены доставлялись необходимые материалы. Математическое мышление египтян с древних времен способствовало созданию таких шедевров в строительстве, которые до сих пор считаются чудесами света.

Школьные проекты. Математическая сказка.

1.2. Математика и современное строительство

В своё время известный философ Иммануил Кант сказал: « В каждой науке ровно столько истины, сколько в ней математики». В современном строительстве роль этой науки непрерывно возрастает. Строительные задачи отличаются по степени сложности расчётов. Например, расчёты на прочность определяют степень выносливости несущих конструкций и относятся к сложнейшим вычислениям. Кроме того, неотъемлемой частью математических знаний, используемых в строительстве, являются нахождение части от числа, пропорции, проценты, площади фигур, объёмы многогранников.

До начала какого-либо строительства составляется смета, в которой просчитываются затраты на строительные материалы, виды работ и количество рабочей силы. Это доказывает, что точек соприкосновения математики со строительством достаточно много.

Важно отметить и обратную историческую взаимосвязь: потребности зарождающегося строительства и, возникшей вслед за ним архитектуры, явились одним из стимулов, благодаря которым возникла и сделала первые шаги математика. Это, в частности, нашло отражение в названии одного из старейших разделов математики — геометрии, что означает землемерие.

Действительно, с задач измерения расстояний, площадей земельных участков, нахождения закономерностей между линейными размерами и площадями различных фигур и начиналась геометрия — важный и самый наглядный раздел математики.

Таким образом, можно говорить об исторической взаимосвязи математики и строительства, а так же об огромной актуальности математических знаний в современном строительстве.

2. Задачи, связанные со строительством и ремонтом

Вот строительство большое

Прежде, чем его начать,

Нужно все еще подробно

Начертить и рассчитать.

Каждая семья, так или иначе, обязательно сталкивается с проблемой строительства или ремонта. Изучив литературу и интернет-источники я подобрала задачи на различные темы, связанные со строительством и ремонтом. Это задачи на нахождение площади, объема, периметра, цены и стоимости и другие.

Задача 1. Постройка дома начинается с котлована. Требуется выкопать котлован размером 10х11 метров и глубиной 2 метра. Сколько нужно вывезти машин грунта, если грузоподъёмность одной машины 10м³?
Решение:
1) 10 · 11 · 2= 220(м³) – объем котлована.
2) 220: 10=22 (машины)

Ответ: 22 машины потребуется.

Задача 2.Вычислите количество блоков, необходимых для строительства фундамента с перегородкой. Длина блока 2,4м. Сколько стоят все блоки, если цена одного блока 1200 рублей?
Решение:
1) (11+10) · 2 + 10 = 52(м) – периметр дома с перегородкой.
2) 52 : 2,4 = 21,66… ≈ 22 (б.) – потребуется.
3) 22 · 1200 = 26400(руб.)

Ответ: 22 фундаментных блока стоят 26400 рублей.

Задача 3. Вычислите объем бетона, который потребуется, чтобы залить пол в подвале, если его толщина 10 см.
Решение:

1000 · 1100 · 10 = 11000000(см 3 ) = 11(м 3 )

Ответ: 11 м 3 бетона потребуется, чтобы залить пол в подвале.

Задача 4.Вычислите оптимальное количество плит, чтобы перекрыть подвал. Длина плиты 5,5м, имеются плиты шириной 1,2м, 1м и 1,5м. Сколько нужно заплатить за кран, если один подъем крана стоит 200 рублей?
Решение:
2 плиты шириной 1м и 12 плит шириной 1,5м
14 · 200= 2800 (руб.) – нужно заплатить за кран

Ответ: понадобится 2 плиты шириной 1м и 12 плит шириной 1,5м,
2800 рублей нужно заплатить за кран.

Задача 5. Один каменщик выкладывает за 6 рабочих дней 13 м 3 кирпича, а двое учеников на 1 м 3 меньше. Найти производительность одного ученика. За какое время 5 учеников построят дом, если нужно выложить 75 кубов?

Решение:

1) (13-1):2= 6(м 3 ) –1 ученик за 6 дней.
2) 6 : 6=1(м 3 ) – производительность 1 ученика.
3) 1 · 5= 5(м 3 ) – 5 учеников за 1 день.
4) 75 : 5 = 15 (дней)

Ответ: за 15 дней 5 учеников построят дом.

Задача 6.Поместятся ли комнаты с такими площадями в дом размером 10х11м, если хозяин хочет иметь кабинет площадью 9м², его сын комнату площадью 12м², хозяйка кухню площадью 10м², дочь комнату площадью 12м², зал площадью 25м², ванная и туалет 10м², спальня площадью 16м².
Решение:
1) 10 · 11= 110 (м 2 ) – площадь дома.
2) 9+12+10+12+25+10+16 = 94(м 2 )

Задача 7.Какой площади должна быть котельная, если ее минимальный объем 12 м³, а высота комнаты 3м?
Решение:

Ответ: 4 м 2 должна быть площадь котельной.

Задача 8. Вычислите площадь стен дома снаружи. Высота дома 3м. Размер дома 10х11м. Сколько нужно облицовочного кирпича, если для того, чтобы выложить 1м² требуется 52 кирпича? В одном поддоне 400 штук кирпича.

Сколько стоит кирпич, если один поддон стоит 4000 рублей?
Решение:
1) (10 + 11) · 2= 42 (м) – периметр дома.
2) 42 · 3 = 126 (м 2 ) – площадь стен.
3) 126 · 52 = 6552 (шт.) – кирпича потребуется.
4) 4000 : 400 = 10(руб.) – стоит 1 кирпич.
5) 6552 · 10= 65520(руб.) – стоит кирпич.

Ответ: 126 м 2 , 65520 рублей.

Задача 9.Нужно приготовить 10 м³ цементного раствора. Сколько нужно килограмм цемента, если на 1 м³ раствора уходит 4 мешка цемента по 50 кг?
Решение:
10 · 4 · 50 =2000(кг)

Ответ: 2000 кг цемента потребуется.

Задача 10.Вычислите площадь огорода, если дом имеет размеры 10м х 11м, баня – 4м х 5м, гараж – 6м х 4м. Площадь всего участка 10 соток.
Решение:
1) 10 · 11= 110 (м 2 ) – площадь дома.
2) 4 · 5 = 20 (м 2 ) – площадь бани.
3) 6 · 4 = 24 (м 2 ) – площадь гаража.
4) 10 соток = 1000 м 2 – площадь участка.
5) 1000-110-20-24 = 846 (м 2 ) – площадь огорода.

Ответ: площадь огорода примерно 8 соток.

Итак, в данной работе представлено 10 задач, связанных со строительством и ремонтом. Эти задачи помогли мне убедиться в том, что темы: «Действия с десятичными дробями», «Периметр», «Площадь», «Объем», изученные нами на уроках математики, используются постоянно.

Ученики 9 и 11 классов проходят государственную итоговую аттестацию, т.е. сдают экзамены. Моя мама работает учителем математики. Из любопытства я иногда просматриваю у нее пособия, по которым выпускники готовятся к экзаменам. Я обнаружила, что в тренировочных вариантах содержатся задачи прикладного характера.

В прошлом году, делая подборку таких задач, я заметила, что среди них много задач так или иначе связанных с ремонтом, строительством и обустройством территории. Изучив сборники и интернет-ресурсы для подготовки к ОГЭ и ЕГЭ, я сделала подборку таких задач (Приложение 3) и оформила их в виде брошюры.

Мне стало интересно, во сколько она мне обошлась, и я сделала расчеты ее себестоимости (Приложение 4). По затратам на бумагу и краску она обошлась мне в 5 рублей 50 копеек.

3. Практическая часть

Когда семья сталкивается с проблемой строительства или ремонта, возникает ряд вопросов: какой выбрать дизайн, сколько и где надо закупить необходимого материала, где это можно сделать дешевле и т.д.

Мои родители, как и многие другие, чаще отдают предпочтение строительству «своими руками». Поэтому мне часто приходится слышать их разговоры о том, сколько нужно закупить какого-либо материала и сколько за него нужно заплатить. В этом году родители строили баню, и я нередко помогала маме выполнять расчеты.

В этой части своей работы я приведу примеры практического применения формул математики в строительстве.

Вычисление объема. В жизни нередко приходится вычислять объем каких-либо помещений (дом, комната, баня и т.д.), которые, как правило, имеют форму прямоугольного параллелепипеда. Например, вычислить объем бетона, который потребуется, чтобы залить пол в подвале, гараже, бане — площадь пола умножить на его толщину (высоту). При покупке печи для бани в специализированном магазине, продавец спрашивает объем бани, для которой она приобретается, потом предлагает те модели печей, которые подходят для данного объема. Чтобы построить дом или баню из бруса необходимо рассчитать, какое его количество необходимо купить: зная размеры бруса (четырехугольной балки), вычисляется объем одной балки, а затем, зная размеры строения, вычисляется общий объем бруса (в м 3 ) путем умножения объема одной балки на их количество.

Вычисление периметра.Чтобы вычислить количество вагонки, необходимое для обшивки стен в бане, необходимо вычислить периметр соответствующего помещения (сумму длин стен) и разделить на ширину вагонки (одной доски). Этот способ применим в том случае, когда вагонка располагается вертикально.

Количество вагонки можно рассчитать и иначе: вычисляется площадь стены (или сумма площадей стен) и делится на площадь одной доски.

Самым непонятным для меня было вычисление длины листа кровельного материала для крыши. Я понимала, что длина листа d больше длины основания a , но как определить, на сколько, я поняла не сразу. Мама сказала, что она для этого применяет теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Длина листа d = b + c для двухскатной крыши (рис.1), d = b + c + e для односкатной крыши (рис.2), где b – длина листа по ширине здания, c и e –длина свеса.

Длина b вычисляется по формуле b 2 = h 2 + a 2 (теорема Пифагора), где h — высота подъема крыши, а- ширина здания (фронтона).

При решении всех этих задач приходится выполнять действия с десятичными дробями и результаты вычислений округлять (чаще с избытком). В любой из приведенных задач вычисление количества строительного материала – это только начало расчетов, т.к. далее, зная цену за единицу товара, необходимо вычислить стоимость необходимых строительных материалов.

Заключение

В работе была рассмотрена значимость математики в практической деятельности людей в области строительства. Закончив свою работу, я могу сказать точно: математика — наука не только для ученых. Она нужна всем. Я убедилась, что без знания математики никакого ремонта не сделать, ничего не построить.

На уроках математики мы много решали различных задач на нахождение периметров, площадей комнат, залов, полей. Огромное число задач на использование величин цена, количество, стоимость, но это для меня были пустые, абстрактные числа, которые не имели для меня определенного смысла. Вот теперь я точно знаю, что математика не сухая наука, без знания которой, невозможно решить простейшие житейские вопросы. А сколько для этого надо знать!

В результате работы гипотеза подтвердилась.

Математические знания, полученные в школе, применимы в строительстве.

Теоретическая значимость нашей работы заключается в том, что, познакомившись с нашим исследованием, многие ученики, на вопрос о необходимости изучать математику, ответят положительно.

Практическая значимость ее в том, что она может быть использована школьниками для повышения своего образовательного уровня, а также научить применять полученные в школе знания на практике, что сегодня очень актуально.

Таким образом, задачи исследовательской работы решены, поставленная цель достигнута, выдвинутая проблема выяснена.

И теперь на вопрос «Что нам стоит дом построить?», поставленный в начале работы, я могу сказать, что для этого нужно немало знаний, вычислительных навыков, сил и денежных средств. Т.е. эта фраза имеет как прямой, так и переносный смысл.

1. Энциклопедический словарь юного математика /Сост. Э-68 А . П . Савин . – М.: Педагогика, 1989. — 352 с.

«Математика в школе» №8, 2003г. «Расчётно-экспериментальные работы при изучении математики».

3. Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику. – М.: Наука. Гл. ред. физ.-мат. Лит., 1989. – 240с.

4. Бурбаки Н. Очерки по истории математики / Пер. И. Г. Башмаковой под ред. К. А. Рыбникова. – М.: КомКнига, 2007.

5. Древний Египет. Энциклопедия. С-Птб., 2008.

6. Решу ОГЭ. Образовательный портал для подготовки к экзаменам. https://oge.sdamgia.ru/

7. Решу ЕГЭ. Образовательный портал для подготовки к экзаменам. https://ege.sdamgia.ru/

Приложение 1.

Пользуетесь ли Вы математикой в повседневной жизни?

Приложение 2.

В каких сферах жизни Вам может пригодиться математика?

Приложение 3.

Практические задачи из ОГЭ и ЕГЭ

1.Пол ком­на­ты, име­ю­щей форму пря­мо­уголь­ни­ка со сто­ро­на­ми 4 м и 9м, тре­бу­ет­ся по­крыть пар­ке­том из пря­мо­уголь­ных до­ще­чек со сто­ро­на­ми 10см и 25 см. Сколь­ко по­тре­бу­ет­ся таких до­ще­чек?

2.Сколь­ко по­тре­бу­ет­ся ка­фель­ных пли­ток квад­рат­ной формы со сто­ро­ной 20 см, чтобы об­ли­це­вать ими стену, име­ю­щую форму пря­мо­уголь­ни­ка со сто­ро­на­ми 3 м и 4,4 м?

3.Сколь­ко досок дли­ной 4 м, ши­ри­ной 20 см и тол­щи­ной 30 мм вый­дет из бруса дли­ной 80 дм, име­ю­ще­го в се­че­нии пря­мо­уголь­ник раз­ме­ром 30 см × 40 см?

4.Сколько досок дли­ной 3,5 м, ши­ри­ной 20 см и тол­щи­ной 20 мм вый­дет из че­ты­рех­уголь­ной балки дли­ной 105 дм, име­ю­щей в се­че­нии прямоугольник раз­ме­ром 30 см 40 см?

5.Керамическая плит­ка одной и той же тор­го­вой марки вы­пус­ка­ет­ся трёх раз­ных размеров. Плит­ки упакованы в пачки. Тре­бу­ет­ся купить плитку, чтобы об­ли­це­вать пол квад­рат­ной комнаты со сто­ро­ной 3 м. Раз­ме­ры плитки, ко­ли­че­ство плиток в пачке и сто­и­мость пачки при­ве­де­ны в таблице

Размер плитки
(см х см)

Количество
пли­ток в пачке

6.При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1 600 рублей, щебень стоит 780 рублей за тонну, а мешок цемента стоит 230 рублей.

Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?

7. Участок земли для стро­и­тель­ства са­на­то­рия имеет форму прямоугольника, сто­ро­ны ко­то­ро­го равны 900 м и 400 м. Одна из бóльших сто­рон участ­ка идёт вдоль моря, а три осталь­ные сто­ро­ны нужно от­го­ро­дить забором. Най­ди­те длину этого забора. Ответ дайте в метрах.

8 .Два садовода, име­ю­щие пря­мо­уголь­ные участ­ки раз­ме­ра­ми 35 м на 40 м с общей границей, до­го­во­ри­лись и сде­ла­ли общий пря­мо­уголь­ный пруд раз­ме­ром 20 м на 14 м (см. чертёж), причём гра­ни­ца участ­ков про­хо­дит точно через центр. Ка­ко­ва пло­щадь (в квад­рат­ных метрах) остав­шей­ся части участ­ка каж­до­го садовода?

9 .Дачный уча­сток имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 20 мет­ров и 30 метров. Хо­зя­ин пла­ни­ру­ет об­не­сти его за­бо­ром и раз­де­лить таким же за­бо­ром на две части, одна из ко­то­рых имеет форму квадрата. Най­ди­те общую длину за­бо­ра в метрах.

1 0. Дачный уча­сток имеет форму квадрата, сто­ро­ны ко­то­ро­го равны 30 м. Раз­ме­ры дома, рас­по­ло­жен­но­го на участ­ке и име­ю­ще­го форму прямоугольника, — 8 м × 5 м. Най­ди­те пло­щадь остав­шей­ся части участка. Ответ дайте в квад­рат­ных метрах.

11. Садовод решил разбить на своём дачном участке 4 квадратные клумбы и 8 клумб в виде правильных треугольников, огородив каждую из них небольшим заборчиком. Длина каждой стороны у любой клумбы равна одному метру. Найдите общую длину всех заборчиков в метрах.

1 2. Определите, сколь­ко необходимо за­ку­пить пленки (в м 2 ) для гид­ро­изо­ля­ции садовой дорожки, изоб­ра­жен­ной на рисунке, если её ши­ри­на везде одинакова.

13. Рыболовное хо­зяй­ство строит бас­сейн для раз­ве­де­ния рыбы. Бас­сейн имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 4 м и 12 м. В цен­тре бас­сей­на находится тех­ни­че­ская постройка, ко­то­рая имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 2 м и 3 м. Най­ди­те площадь остав­шей­ся части бассейна.

1 4. Два садовода, име­ю­щие пря­мо­уголь­ные участ­ки раз­ме­ра­ми 20 м на 30 м с общей границей, до­го­во­ри­лись и сде­ла­ли общий круг­лый пруд пло­ща­дью 140 квад­рат­ных мет­ров (см. чертёж), причём гра­ни­ца участ­ков про­хо­дит точно через центр пруда. Ка­ко­ва пло­щадь (в квад­рат­ных метрах) остав­шей­ся части участ­ка каж­до­го садовода?

1 5.Участок земли под стро­и­тель­ство са­на­то­рия имеет форму прямоугольника, сто­ро­ны ко­то­ро­го равны 1000 м и 500 м. Одна из боль­ших сто­рон участ­ка идёт вдоль моря, а три осталь­ные сто­ро­ны нужно огра­дить забором. Най­ди­те длину этого забора. Ответ дайте в метрах.

16.Для стро­и­тель­ства гаража можно ис­поль­зо­вать один из двух типов фундамента: бе­тон­ный или фун­да­мент из пеноблоков. Для фун­да­мен­та из пе­нобло­ков необходимо 2 кубометра пе­нобло­ков и 4 мешка цемента. Для бе­тон­но­го фундамента необходимо 2 тонны щебня и 20 мешков цемента.

Ку­бо­метр пеноблоков стоит 2450 рублей, ще­бень стоит 620 рублей за тонну, а мешок це­мен­та стоит 230 рублей. Сколь­ко рублей будет сто­ить материал, если вы­брать наиболее де­ше­вый вариант?

17.Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 2 кубометра пеноблоков и 4 мешка цемента. Для бетонного фундамента необходимо 2 тонны щебня и 20 мешков цемента. Кубометр пеноблоков стоит 2450 рублей, щебень стоит 620 рублей за тонну, а мешок цемента стоит 230 рублей.

Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант?

18.Керамическая плит­ка одной и той же тор­го­вой марки вы­пус­ка­ет­ся трёх раз­ных размеров. Плит­ки упакованы в пачки. Тре­бу­ет­ся купить плитку, чтобы об­ли­це­вать пол квад­рат­ной комнаты со сто­ро­ной 3 м. Раз­ме­ры плитки, ко­ли­че­ство плиток в пачке и сто­и­мость пачки при­ве­де­ны в таблице

Источник: school-science.ru

Математика в строительстве

В проекте путем изучения памятников архитектуры отражено применение математических знаний в строительстве. Обоснованы способы укладки паркета из различных фигур, созданы свои варианты паркета.

Порядок знакомства:

1) Документ Microsoft Word
2) Документ Microsoft Power Point

Контактная информация:

* Для распаковки архива вы можете воспользоваться бесплатной программой 7-Zip или любой другой программой, поддерживающей архивы 7z и Zip.

Источник: project.1sept.ru

Презентация на тему Математика вокруг нас. Математика в строительстве

Презентация на тему Презентация на тему Математика вокруг нас. Математика в строительстве из раздела Математика. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 25 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!

• Главная
• Математика
• Математика вокруг нас. Математика в строительстве

Слайды и текст этой презентации

Математика вокруг нас

Презентация
ученицы 7 класса «Д»
МАОУ СОШ №211
Тишиной Златы

В истории мы черпаем мудрость, в поэзии остроумие, а в математике – проницательность.

Слово «математика» произошло от др.-греч. μάθημα, что означает изучение, знание, наука, и др.-греч. μαθηματικός, первоначально означающего восприимчивый, успевающий, позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη, на латыни ars mathematica, означает искусство математики. Термин др.-греч. μᾰθημᾰτικά в современном значении этого слова «математика» встречается уже в трудах Аристотеля (IV век до н. э.). По мнению Фасмера в русский язык слово пришло либо через польск. matematyka, либо через лат. mathematica.

Математика вокруг нас

Математика окружает нас везде. Благодаря ней мы решаем множество вопросов в повседневной жизни. Мало кто задумывался , что математика окружает нас с первых дней жизни. Любой ребенок, даже не изучавший еще математику, сталкивался с цифрами. В поликлинике узнают наш вес, рост с первых дней жизни.

И дальше, всю жизнь мы сталкиваемся с математикой, абсолютно везде.

А где нужна нам математика?

а может быть везде?!

Математика нужна не только в определенных профессиях, но и в повседневной жизни

В нашей повседневной жизни мы настолько привыкли к математике, что даже не замечаем, что пользуемся ею постоянно. А ведь до сих пор ученики задают вопрос «А зачем нам нужна математика? Только в магазин сходить?». Так для чего же мы изучаем дроби, площадь, периметр, объем? Для чего нужны геометрические сведения? Где каждому человеку математика необходима в повседневной жизни?

А что будет, если математику совсем не знать? Необходимо рассмотреть все виды своей деятельности и доказать, что без математики не обойтись в быту.

Математика в жизни человека

Многие известные математики говорят, что главное в математике — научить человека мыслить, ставя порою перед ним очень сложные задания. «Математика развивает логическое мышление, умение самостоятельно решать проблемы, способность быстро уловить суть и найти к жизненной задаче наиболее подходящий и простой подход»- говорят нам взрослые. Математика тесно связана с нашей повседневной жизнью. Математика встречается в нашей жизни практически на каждом шагу и не такая уж она серая и скучная, а разноцветная и веселая.

Математика вокруг нас

Например, наш распорядок дня — режим, не что иное как определение времени и его планирование в течение дня при помощи несложных математических вычислений.
Мы весь день следим за временем по часам и учимся правильно его распределять, чтобы не опаздывать и не прибегать раньше, чем нужно.
Математика используется и в медицине.
Без математики не обойдутся химические опыты.
Математика используется и для приготовления пищи.
Математика используется в строительстве.
Математика используется практически во всех направлениях.

МАТЕМАТИКА В СТРОИТЕЛЬСТВЕ

Без знания математики не обойтись при строительстве или планировании дома, подсчете затрат на материалы.

Ещё в древности, людям, во время строительства часто приходилось прибегать к помощи математики.

ЗАДАЧА: Один каменщик выкладывает за 6 рабочих дней 13 м3 кирпича, а двое учеников(с одинаковой производительностью) на 1 м3 меньше. Найти производительность одного ученика, если их производительность одинакова. За какое время 5 учеников выложат 75 кубов?

РЕШЕНИЕ:
1) (13-1):2= 6(м3) –выкладывает 1 ученик за 6 дней.
2) 6 : 6=1(м3) –производительность 1 ученика.
3) 1 · 5= 5(м3) – 5 учеников за 1 день.
4) 75 : 5 = 15 (дней)

Ответ: за 15 дней 5 учеников выложат 75 кубов кирпича.

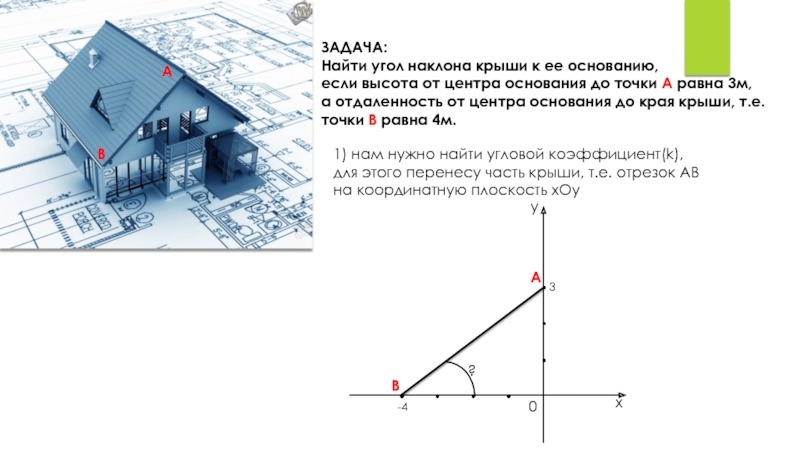
ЗАДАЧА:
Найти угол наклона крыши к ее основанию,
если высота от центра основания до точки А равна 3м,
а отдаленность от центра основания до края крыши, т.е. точки В равна 4м.

1) нам нужно найти угловой коэффициент(k),
для этого перенесу часть крыши, т.е. отрезок АВ на координатную плоскость хОу

2) теперь мы знаем координаты двух точек: А и В, от сюда следует, что мы можем составить систему двух линейных уравнений с двумя переменными, учитывая линейную функцию: y=kx+m.
Т.к. А(0;3) и В(-4;0), то получу следующую систему уравнений:

решу систему методом подстановки:

m = 3 (1) — подставлю в (2),
0 = -4k+m (2);

В строительстве очень часто возникает потребность в определении прямого угла, которую можно решить двумя способами. Первый состоит в использовании специального инструмента — угольника. Однако габариты этого инструмента накладывают ограничение на область применения этого метода.

Второй метод можно использовать для определения перпендикулярности поверхностей любой протяженности. Он состоит в использовании следующего правила — соотношение катетов и гипотенузы в прямоугольном треугольнике соответствует числовому ряду 3-4-5. Следовательно, для проверки перпендикулярности поверхностей достаточно отметить на сопрягаемых участках расстояние в 3 (или 30) и 4 (или 40) метров и соединить их 5-ти (или 50-ти) метровой гипотенузой. История утверждает, что этот метод был известен еще строителям Древнего Египта. Однако современные инженеры и прорабы рассматривают этот способ, как частный случай общеизвестной теоремы Пифагора.

Строителю заказали покрасить помещение. Для этого ему нужна краска, но тут сколько же краски нужно купить, чтобы излишне не потратиться и купить чересчур много краски или купить мало краски и не доделать работу? Он знает, сколько краски расходуется на 1 квадратный метр (допустим, что на 1 квадратный метр понадобиться 2 литра). Строителю остается рассчитать площадь стен и потолка.

Он знает, что высота одной стены 3 метра, а длина 4 метра. При помощи формулы (S = ab) строитель узнает, что площадь одной стены равна 12 метров в квадрате и узнает, что ему понадобиться 24 литра на одну стену. Те же вычисления он проводит с потолком и другими стенами и едет в магазин.

Необходимо поменять пол для последующей укладки паркета. Это требует заливки пола раствором на высоту 10 см. Для этого ему нужно знать объем заливаемого раствора. Длина пола 6 метров, ширина 4 метра. При помощи формулы (S = ab) он узнает, что площадь пола равна 24 квадратных метра. (Формула вычисления объема V=Sh). Он знает, что пол ему надо поднять ровно на 10 сантиметров.

За высоту он принимает то расстояние, на которое ему надо поднять пол, то есть на 10 сантиметров. Он узнает, что объем пола составляет 2,4 кубометра.

С определением площади нестандартной фигуры сталкиваются в основном мастера отделочники. Большинство комнат в квартирах и домах современной планировки имеют сложную форму пола, основанную на соединении нескольких геометрических фигур: трапеции и окружности, прямоугольника и треугольника. Просчитать потребность в расходном материале для такой площади очень сложно. Однако, используя принцип деления сложной геометрической фигуры на несколько простых, можно быстро добиться нужных результатов. Для этого достаточно вычислить площадь простой геометрической фигуры, а затем добавить или отнять от нее площадь другой фигуры, которая исказила стандартные формы при сопряжении.

Следует отметить, что потребности зарождающегося строительства и, возникшей вслед за ним архитектуры явились одним из стимулов, благодаря которым возникла и сделала первые шаги математика. Это, в частности, нашло отражение в названии одного из старейших разделов математики — геометрии, что означает землемерие. Действительно, с задач измерения расстояний, площадей земельных участков, нахождения закономерностей между линейными размерами и площадями различных фигур, на предметном уровне, и начиналась геометрия — важный и самый наглядный раздел математики.

Несомненно, и то, что математика, в своем развитии, оказала определенное влияние на архитектуру.

С другой стороны, можно проследить и влияние архитектуры на развитие математики в целом. Действительно, для осуществления все более сложных и в то же время экономичных построек всегда требовалось предварительное планирование, разработка более тонких математических приемов и моделей, использование более совершенных точных вычислительных методов. Все это, в ответ на запросы архитектурной практики разрабатывала теоретическая и прикладная математика.

Рассмотрев некоторые аспекты применения математики в строительстве, видно, как математика очень эффективно решает любые строительные задачи, связанные с разметкой и обмером. В общем, не зря все-таки говорят, что математика — это царица наук. При грамотном применении решает почти любую задачу.

ЗАКЛЮЧЕНИЕ Современная жизнь в отсутствии математики маловероятна. Ибо, если мы не очень хорошо разбираемся в языке цифр, нам будет трудно достичь важных решений в выполнении повседневных задач. Будь то поход в магазин или приготовление пищи, или ремонт дома, — знание математики является ключевым, и, следовательно, необходимо.

Математика присутствует везде, она помогает нам в жизни, делает ее понятнее. Нужно только ее старательно учить и вникать в каждую теорему и в каждый закон. Развивать свое мышление и тогда математика будет помогать во всем на протяжении всей жизни.

Источник: theslide.ru

Презентация «Математика вокруг нас. Математика в строительстве» (7 класс) – проект, доклад

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25

Презентацию на тему «Математика вокруг нас. Математика в строительстве» (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию.

Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на соответствующий текст под плеером. Презентация содержит 25 слайд(ов).

Слайды презентации

Математика вокруг нас

Презентация ученицы 7 класса «Д» МАОУ СОШ №211 Тишиной Златы

В истории мы черпаем мудрость, в поэзии остроумие, а в математике – проницательность.

Слово «математика» произошло от др.-греч. μάθημα, что означает изучение, знание, наука, и др.-греч. μαθηματικός, первоначально означающего восприимчивый, успевающий, позднее относящийся к изучению, впоследствии относящийся к математике. В частности, μαθηματικὴ τέχνη, на латыни ars mathematica, означает искусство математики. Термин др.-греч. μᾰθημᾰτικά в современном значении этого слова «математика» встречается уже в трудах Аристотеля (IV век до н. э.). По мнению Фасмера в русский язык слово пришло либо через польск. matematyka, либо через лат. mathematica.

Математика окружает нас везде. Благодаря ней мы решаем множество вопросов в повседневной жизни. Мало кто задумывался , что математика окружает нас с первых дней жизни. Любой ребенок, даже не изучавший еще математику, сталкивался с цифрами. В поликлинике узнают наш вес, рост с первых дней жизни.

И дальше, всю жизнь мы сталкиваемся с математикой, абсолютно везде.

А где нужна нам математика?

МАТЕМАТИКА в торговле в строительстве в играх в школе в авиации в кулинарии в спорте в библиотеке в литературе

а может быть везде?!

Математика нужна не только в определенных профессиях, но и в повседневной жизни

В нашей повседневной жизни мы настолько привыкли к математике, что даже не замечаем, что пользуемся ею постоянно. А ведь до сих пор ученики задают вопрос «А зачем нам нужна математика? Только в магазин сходить?». Так для чего же мы изучаем дроби, площадь, периметр, объем? Для чего нужны геометрические сведения? Где каждому человеку математика необходима в повседневной жизни?

А что будет, если математику совсем не знать? Необходимо рассмотреть все виды своей деятельности и доказать, что без математики не обойтись в быту.

Математика в жизни человека

Многие известные математики говорят, что главное в математике — научить человека мыслить, ставя порою перед ним очень сложные задания. «Математика развивает логическое мышление, умение самостоятельно решать проблемы, способность быстро уловить суть и найти к жизненной задаче наиболее подходящий и простой подход»- говорят нам взрослые. Математика тесно связана с нашей повседневной жизнью. Математика встречается в нашей жизни практически на каждом шагу и не такая уж она серая и скучная, а разноцветная и веселая.

Например, наш распорядок дня — режим, не что иное как определение времени и его планирование в течение дня при помощи несложных математических вычислений. Мы весь день следим за временем по часам и учимся правильно его распределять, чтобы не опаздывать и не прибегать раньше, чем нужно. Математика используется и в медицине. Без математики не обойдутся химические опыты.

Математика используется и для приготовления пищи. Математика используется в строительстве. Математика используется практически во всех направлениях.

МАТЕМАТИКА В СТРОИТЕЛЬСТВЕ

Без знания математики не обойтись при строительстве или планировании дома, подсчете затрат на материалы.

Ещё в древности, людям, во время строительства часто приходилось прибегать к помощи математики.

ЗАДАЧА: Один каменщик выкладывает за 6 рабочих дней 13 м3 кирпича, а двое учеников(с одинаковой производительностью) на 1 м3 меньше. Найти производительность одного ученика, если их производительность одинакова. За какое время 5 учеников выложат 75 кубов?

РЕШЕНИЕ: 1) (13-1):2= 6(м3) –выкладывает 1 ученик за 6 дней. 2) 6 : 6=1(м3) –производительность 1 ученика. 3) 1 · 5= 5(м3) – 5 учеников за 1 день. 4) 75 : 5 = 15 (дней)

Ответ: за 15 дней 5 учеников выложат 75 кубов кирпича.

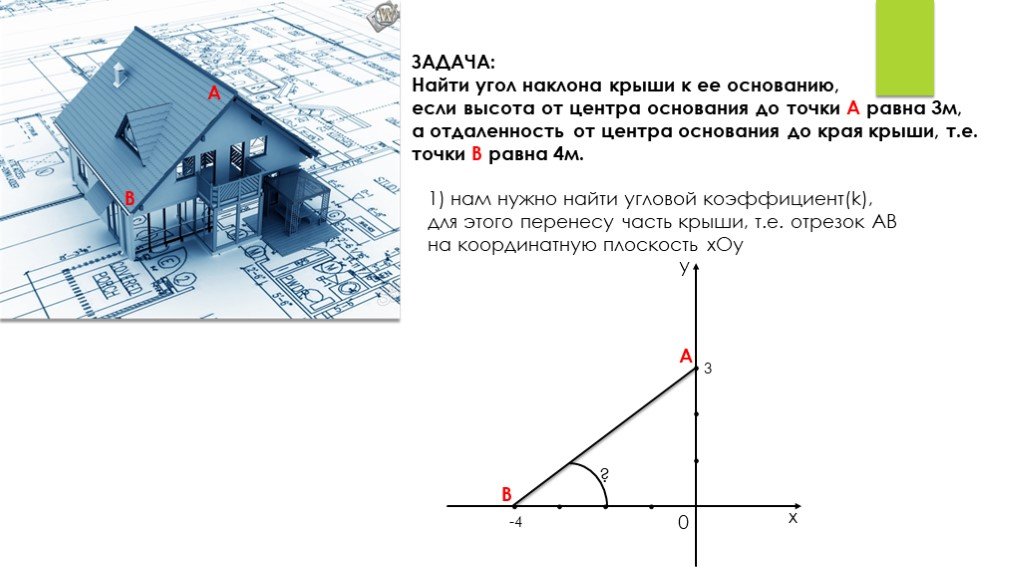
ЗАДАЧА: Найти угол наклона крыши к ее основанию, если высота от центра основания до точки А равна 3м, а отдаленность от центра основания до края крыши, т.е. точки В равна 4м.

1) нам нужно найти угловой коэффициент(k), для этого перенесу часть крыши, т.е. отрезок АВ на координатную плоскость хОу

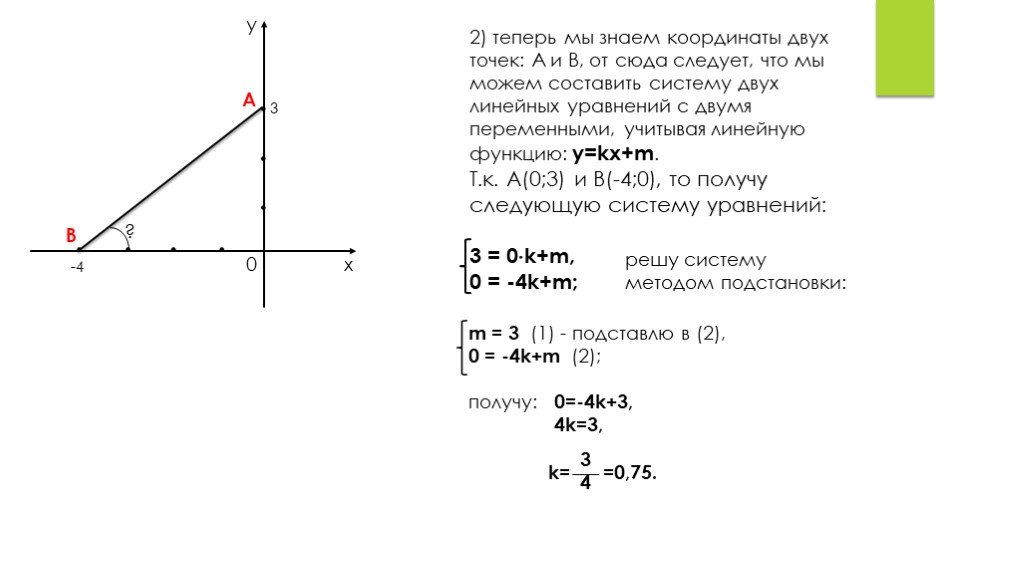
2) теперь мы знаем координаты двух точек: А и В, от сюда следует, что мы можем составить систему двух линейных уравнений с двумя переменными, учитывая линейную функцию: y=kx+m. Т.к. А(0;3) и В(-4;0), то получу следующую систему уравнений: 3 = 0 k+m, 0 = -4k+m;

решу систему методом подстановки:

m = 3 (1) — подставлю в (2), 0 = -4k+m (2); получу: 0=-4k+3, 4k=3, k= =0,75.

В строительстве очень часто возникает потребность в определении прямого угла, которую можно решить двумя способами. Первый состоит в использовании специального инструмента — угольника. Однако габариты этого инструмента накладывают ограничение на область применения этого метода.

Второй метод можно использовать для определения перпендикулярности поверхностей любой протяженности. Он состоит в использовании следующего правила — соотношение катетов и гипотенузы в прямоугольном треугольнике соответствует числовому ряду 3-4-5. Следовательно, для проверки перпендикулярности поверхностей достаточно отметить на сопрягаемых участках расстояние в 3 (или 30) и 4 (или 40) метров и соединить их 5-ти (или 50-ти) метровой гипотенузой. История утверждает, что этот метод был известен еще строителям Древнего Египта. Однако современные инженеры и прорабы рассматривают этот способ, как частный случай общеизвестной теоремы Пифагора.

Строителю заказали покрасить помещение. Для этого ему нужна краска, но тут сколько же краски нужно купить, чтобы излишне не потратиться и купить чересчур много краски или купить мало краски и не доделать работу? Он знает, сколько краски расходуется на 1 квадратный метр (допустим, что на 1 квадратный метр понадобиться 2 литра). Строителю остается рассчитать площадь стен и потолка.

Он знает, что высота одной стены 3 метра, а длина 4 метра. При помощи формулы (S = ab) строитель узнает, что площадь одной стены равна 12 метров в квадрате и узнает, что ему понадобиться 24 литра на одну стену. Те же вычисления он проводит с потолком и другими стенами и едет в магазин.

Необходимо поменять пол для последующей укладки паркета. Это требует заливки пола раствором на высоту 10 см. Для этого ему нужно знать объем заливаемого раствора. Длина пола 6 метров, ширина 4 метра. При помощи формулы (S = ab) он узнает, что площадь пола равна 24 квадратных метра. (Формула вычисления объема V=Sh).

Он знает, что пол ему надо поднять ровно на 10 сантиметров. За высоту он принимает то расстояние, на которое ему надо поднять пол, то есть на 10 сантиметров. Он узнает, что объем пола составляет 2,4 кубометра.

С определением площади нестандартной фигуры сталкиваются в основном мастера отделочники. Большинство комнат в квартирах и домах современной планировки имеют сложную форму пола, основанную на соединении нескольких геометрических фигур: трапеции и окружности, прямоугольника и треугольника. Просчитать потребность в расходном материале для такой площади очень сложно. Однако, используя принцип деления сложной геометрической фигуры на несколько простых, можно быстро добиться нужных результатов. Для этого достаточно вычислить площадь простой геометрической фигуры, а затем добавить или отнять от нее площадь другой фигуры, которая исказила стандартные формы при сопряжении.

Следует отметить, что потребности зарождающегося строительства и, возникшей вслед за ним архитектуры явились одним из стимулов, благодаря которым возникла и сделала первые шаги математика. Это, в частности, нашло отражение в названии одного из старейших разделов математики — геометрии, что означает землемерие. Действительно, с задач измерения расстояний, площадей земельных участков, нахождения закономерностей между линейными размерами и площадями различных фигур, на предметном уровне, и начиналась геометрия — важный и самый наглядный раздел математики.

Несомненно, и то, что математика, в своем развитии, оказала определенное влияние на архитектуру.

С другой стороны, можно проследить и влияние архитектуры на развитие математики в целом. Действительно, для осуществления все более сложных и в то же время экономичных построек всегда требовалось предварительное планирование, разработка более тонких математических приемов и моделей, использование более совершенных точных вычислительных методов. Все это, в ответ на запросы архитектурной практики разрабатывала теоретическая и прикладная математика.

Рассмотрев некоторые аспекты применения математики в строительстве, видно, как математика очень эффективно решает любые строительные задачи, связанные с разметкой и обмером. В общем, не зря все-таки говорят, что математика — это царица наук. При грамотном применении решает почти любую задачу.

ЗАКЛЮЧЕНИЕ Современная жизнь в отсутствии математики маловероятна. Ибо, если мы не очень хорошо разбираемся в языке цифр, нам будет трудно достичь важных решений в выполнении повседневных задач. Будь то поход в магазин или приготовление пищи, или ремонт дома, — знание математики является ключевым, и, следовательно, необходимо.

Математика присутствует везде, она помогает нам в жизни, делает ее понятнее. Нужно только ее старательно учить и вникать в каждую теорему и в каждый закон. Развивать свое мышление и тогда математика будет помогать во всем на протяжении всей жизни.

Источник: prezentacii.org