Всем доброго времени, принимайте новенького и сразу вопрос:
Как определяют напряжения и усилия в загруженных конструкциях?
Вопрос по предмету Обследование и испытание сооружений. Завтра госэкзамен, а внятного ответа так и не нашел. Заранее большое спасибо.
ETCartman- болбшое спасибо. Если не трудно дайте ссылку на СНиП/статью/учебник. Ответ в общих чертах уже есть, но хотелось бы еще дополнить.
— чтоб препод офигел еще сошлись кроме ETCartman, еще на это СНиП 2.02.01-84* “Бетонные и железобетонные конструкции” СНиП II-23-81* “Стальные конструкции” СНиП II-22-81* “Каменные и армокаменные конструкции”
небольшой начальник в большой местной конторе
— чтоб препод офигел еще сошлись кроме ETCartman, еще на это СНиП 2.02.01-84* “Бетонные и железобетонные конструкции” СНиП II-23-81* “Стальные конструкции” СНиП II-22-81* “Каменные и армокаменные конструкции”
А также СНиП 52-01-2003 “Бетонные и железобетонные конструкции”, СНиП 2.02.01-84* “Бетонные и железобетонные конструкции” отменен на него не стоит ссылаться,а то 2 балла поставят
Сопромат. Напряжения. Доступным языком.
Наехали.
На саомом деле вопрос для студентов. Отвечать можно, например, так: — Определить дополнительное перемещение (удлинение) при приложении дополнительной нагрузки, далее — как сказали выше. Сопромат и строймех.
Во флудеров понабежало.
При этом вопрос внимательно прочесть даже никто и не попытался.
Товарищ на самом деле спрашивает про напряжения в уже построенных конструкциях — так что флудить надо на тему всяких тензодатчиков , а не поминать всуе строительную механику и СНиП 2.02.01-84.
Достаточно трудно представить как это можно делать в балках, колоннах плитах и т.д. Может быть какие-то ультразвуковые методы? Знаю, что можно определять натяжение в канатах с помощью устройства, которое устанавливается на канат и с затем с помощью винта пытается оттянуть его поперек. Что-то слышал про то что, натяжение в арматуре можно проверить аналогичным способом. Посмотрите учебник Землянского (где-то есть в интернете) когда у меня была такая дисциплина он мне показался достаточно полезным.
Знаю, что можно определять натяжение в канатах с помощью устройства, которое устанавливается на канат и с затем с помощью винта пытается оттянуть его поперек.
Товарищ на самом деле спрашивает про напряжения в уже построенных конструкциях — так что флудить надо на тему всяких тензодатчиков , а не поминать всуе строительную механику и СНиП 2.02.01-84.
Вы возможно будете смеяться, но надо собрать нагрузки с использованием СНиП 2.01.07-85*, а дальше таки методами сопромата и строительной механики
Вы возможно будете смеяться, но надо собрать нагрузки с использованием СНиП 2.01.07-85*, а дальше таки методами сопромата и строительной механики
Смеяться не буду. Нет ничего смешного в том, что кто-то не понимает в чем разница между проектированием и обследованием сооружений.
Поприкалываться можно в специальных темах.
zx-constr
Что такое НАПРЯЖЕНИЕ и в чем разница с током?
Интересно, насколько близки ваши усилия/напряжения при сборе нагрузок по 2.01.07-85* к действующим в конструкции?
Навешав тензодатчиков, прогибомеров и проч. и пригрузив конструкцию, конечно можно воспользоваться методами строит. механики для определения приращения, а усилия/напряжения, которые были до этого? На самом деле интересно было бы узнать о существовании методов, о которых спрашивал автор?
Vavan Metallist
Такая хреновина типа куска двутавра со стрелочным индикатором?
Нет ничего смешного в том, что кто-то не понимает в чем разница между проектированием и обследованием сооружений.
При обследовании методы те же самые, о которых я сказал ранее.
| На самом деле интересно было бы узнать о существовании методов, о которых спрашивал автор? |
Нет таких методов. Пример с канатами и частотомером (не тензометром) — это приятное исключение. Тензодатчики вообще не в тему. Они нужны для другого. Только сбор нагрузок и поверочные расчеты.
Исключение — когда система инструментального мониторинга была установлена в здание, как правило на этапе строительства.
Таких приборов, чтобы к примеру подойти к кирпичной стене и замерить действующее в ней напряжение — не существует.
ТЕНЗОДАТЧИК,
прибор для измерения механической ДЕФОРМАЦИИ,
например, вызванной движением моста или ледника. Электрические
тензодатчики используют явление (впервые замеченное лордом
КЕЛЬВИНОМ в 1856 г.), заключающееся в следующем: если трос
растягивается, то меняется его электрическое сопротивление.
Электрический тензодатчик обычно состоит из сетки, сделанной из
проволочной нити, оттиснутой на металлической фольге. Прибор
приклеивается на поверхность конструкции, деформацию которой
необходимо измерить. Когда конструкция деформируется, тензодатчик
также испытывает деформацию, при этом изменяя свое электрическое
сопротивление, которое можно измерить.
проектировщик ж/б, ОиФ
Исключение — когда система инструментального мониторинга была установлена в здание, как правило на этапе строительства.
Такие системы проектируются индивидуально для каждого объекта. Чаще всего это комплекс из тензо- и термодатчиков, подключенных к компьютеру. Французы (Фрейсине) мутили с акустической эмиссией. Энергетики делали системы для контроля величины натяжения канатной арматуры. Такие системы могут быть полезны при эксплуатации зданий и сооружений.
Только к обсуждаемой теме всё это имеет очень слабое отношение.
Констукцию можно разгрузить, или нет? Если можно, то в стальных конструкциях при помощи тензодатчиков при повторных нагружениях, можно определить напряжения.
Если разгрузить нельзя, то только по деформациям и теоретически. Марку стали можно определить специальным оборудованием.
1. Если фундамент свайный — при помощи гидравлических домкратов и прогибомеров можно выяснить реальную несущую способность свайного основания. Я это делал много раз. У нас в г. Новокузнецке было много заброшенных свайных ростверков.
2. Для фундаменов на естественном основании — теоретически.
Реально для Вас есть небольшой нормативный документ, почитаете и сдадите на пять — СП 13-102-2003. «Правила обследования несущих строительных конструкций зданий и сооружений». ФГУП КТБ ЖБ. Москва, 2003 г.
Источник: forum.dwg.ru
Прочность и напряжение в строительстве
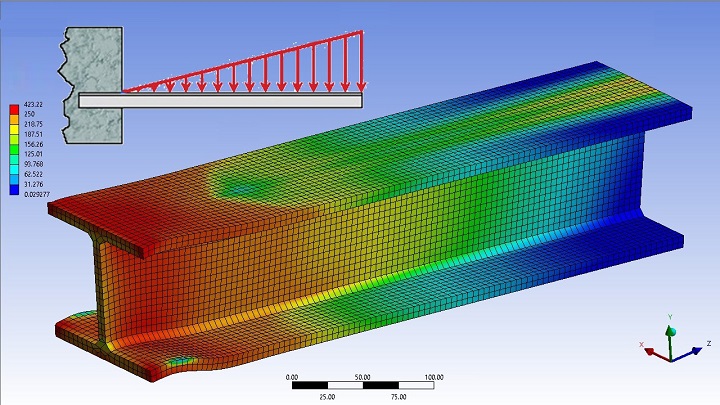
Если сила действует на какое-либо тело, то это тело нагружено. Силы сцепления молекул внутри нагруженного тела (когезия) сопротивляются внешней силе. Чтобы все строительные конструкции могли выдержать действие на них внешних сил, они должны иметь соответствующую прочность.
Под ПРОЧНОСТЬЮ понимают силу тела, которая противодействует изменению формы и разрушению этого тела внешней силой.
При действии внешней силы, например силы растяжения стального каната, тело будет находиться в напряженном состоянии, т.е. в состоянии внутреннего сопротивления разрыву. Оно тем больше, чем меньше нагружаемая площадь. В случае, например, сжатия или растяжения это называется напряжением σ (произносится «сигма»).
Под НАПРЯЖЕНИЕМ понимают силу внутреннего сопротивления тела, отнесенную к площади его сечения.
Напряжение = сила/площадь поперечного сечения:
А — в мм 2 или в м 2 ;
σ — в Н/мм 2 или в МН/м 2 .
Напряжение в теле увеличивается с увеличением внешней нагрузки. Если нагрузка на тело, а следовательно, и напряжение в нем будут слишком велики, то тело разрушится. Достигнутое при разрушении тела напряжение называют разрушающим напряжением.
Строительные материалы можно нагружать только до определенного напряжения. Его называют допустимым напряжением — σдоп. ПО СООБРАЖЕНИЯМ БЕЗОПАСНОСТИ СУЩЕСТВУЮЩЕЕ НАПРЯЖЕНИЕ В МАТЕРИАЛЕ (σсущ) ДОЛЖНО БЫТЬ МЕНЬШЕ ИЛИ РАВНО ДОПУСТИМОМУ НАПРЯЖЕНИЮ (σдоп), т.е. σсущ ≤ σдоп .
По виду нагрузки различают напряжения сжатия, растяжения, изгиба, среза, сдвига и кручения.
Сжатие в строительстве
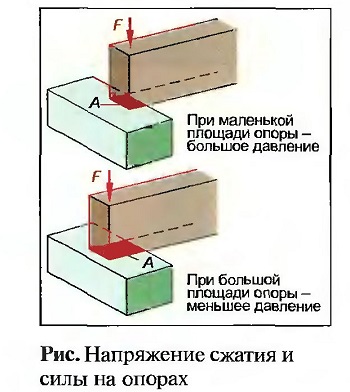
Если фундамент нагружен, например, весом стены дома, то он должен воспринимать силы сжатия. В фундаменте возникают напряжения сжатия. Прочность на сжатие у различных материалов различна. Она увеличивается при увеличении плотности и вязкости материала. Для восприятия сжимающих усилий подходят такие материалы, как сталь, бетон, природный камень, стеновые камни и дерево.
Высокую прочность на сжатие должны иметь в основном фундаменты, несущие стены, опоры и колонны. Напряжения сжатия, которые должны восприниматься основанием (грунтом), называют напряжением в грунте (рис. «Напряжение сжатия и силы на опорах»).
Источник: www.ocenin.ru
Напряжения и деформации. Закон Гука
Для осуществления деформаций растяжения или сжатия необходимо в концевых сечениях стержня приложить сплошную по площади равномерно распределенную нагрузку, направленную параллельно оси стержня (рис. 5.4). Однако, применяя принцип Сен-Венана, нетрудно показать, что аналогичный результат мы получим и в том случае, когда к концам стержня приложены любые нагрузки, равнодействующая которых действует по оси стержня.

Продольная сила N, возникающая в поперечном сечении стержня, представляет собой равнодействующую внутренних нормальных к поперечному сечению сил, распределенных по его площади, и связана с возникающими в этом сечении нормальными напряжениями зависимостью (4.5):

На основании гипотезы плоских сечений, гак как все продольные волокна стержня при растяжении или сжатии деформируются одинаково, нормальные напряжения, вызывающие эти деформации, также должны быть одинаковы по всему поперечному сечению, т.е. ст = const.

Тогда на основании формулы (4.5) получим
откуда нормальные напряжения могут быть определены как

Правило знаков для нормальных напряжений принимается таким же, как и для продольных сил: растягивающие напряжения считаются положительными, а сжимающие — отрицательными.
Для наглядного представления характера изменения нормальных напряжений по длине стержня при растяжении или сжатии строят их графики, называемые эпюрами напряжений.
При действии растягивающих сил стержень претерпевает деформацию растяжения, которая проявляется в изменении длины и поперечных размеров стержня. Его первоначальная длина / увеличивается на величину Д/, называемую абсолютным удлинением (рис. 5.5, а), и становится равной 1Л, т.е. Д/ = /,-/.
При действии сжимающих сил стержень претерпевает деформацию сжатия. В этом случае величину Д/ называют абсолютным укорочением стержня (рис. 5.5, 6), так как при сжатии длина стержня уменьшается.

Абсолютное удлинение или укорочение стержня называют абсолютной продольной деформацией.
Отношение абсолютной продольной деформации к первоначальной длине стержня называется относительной продольной деформацией:

Поперечные размеры стержня при растяжении (сжатии) также изменяются: при растяжении поперечное сечение стержня сужается, при сжатии — расширяется (см. рис. 5.5). Изменение поперечных размеров стержня называется поперечной деформацией, которая также может быть охарактеризована либо абсолютной поперечной деформацией Ab = bi — Ь, либо относительной поперечной деформацией:

На основании экспериментов Р. Гук в XVII в. пришел к заключению, которое можно сформулировать следующим образом: в упругих телах деформации усилия пропорциональны усилиям. Последующие исследования показали, что утверждение Гука справедливо только в определенной области работы материала и лишь при малых деформациях.
Для подавляющего большинства строительных материалов с достаточной для практики точностью можно считать, что в известных пределах нагружения между относительной продольной деформацией и соответствующим нормальным напряжением существует прямая пропорциональная зависимость

которая носит название закона Гука. Его графическая интерпретация показана на рис. 5.6, где Е = tga.

Коэффициент пропорциональности Е называется модулем упругости материала и, как видно из (5.6), имеет ту же размерность, что и напряжения.
Абсолютное значение отношения относительной поперечной деформации к относительной продольной деформации при растяжении и сжатии в области действия закона Гука называется коэффициентом поперечной деформации или коэффициентом Пуассона:


Коэффициент Пуассона р и модуль упругости Е характеризуют упругие свойства материала и устанавливаются экспериментально. Значения модулей упругости и коэффициентов Пуассона для основных строительных материалов приведены в прил. 1.
Подставив в формулу (5.7) выражения (5.4) и (5.5), получим
Произведение ЕА принято называть жесткостью стержня при растяжении или сжатии.
В том случае, когда по длине стержня на его оси действуют несколько внешних сил, стержень по длине имеет ступенчатое изменение поперечного сечения или изготовлен из разных материалов, определяются удлинения (укорочения) на каждом участке, и полное перемещение перемещаемого конца стержня получают путем алгебраического суммирования удлинений (укорочений) по участкам:

где п — число рассматриваемых участков стержня.
При продольной нагрузке q(x), распределенной по оси стержня (см. рис. 5.3, а), и переменной по длине жесткости стержня ЕЛ необходимо рассмотреть совокупность бесчисленного множества бесконечно малых участков длиной dr. Продольная деформация каждого такого участка определяется на основании закона Гука выражением

а полная деформация любого участка стержня длиной /

В случае действия собственного веса стержня постоянного сечения нормальные напряжения с учетом (5.3) и (5.4) определяются по формуле

а полная деформация стержня на основании (5.11) с подстановкой (5.3)

Умножая числитель и знаменатель результата (5.13) на Л и учитывая, что уЛ/ = G — вес всего стержня, получим

Эпюра напряжений в стержне постоянного сечения от действия собственного веса показана на рис. 5.3, в.
Рассмотрим несколько примеров построения эпюр напряжений и определения перемещений в стержнях, работающих на растяжение (сжатие).
Требуется определить напряжения в поперечных сечениях и полное перемещение свободного конца бруса при действии продольных сил (см. пример 5.1, рис. 5.1). Материал бруса — сосна (?=0,1 • 10 5 МПа), диаметр бруса d = 8 см.
Решение. 1. Площадь поперечного сечения бруса А = к ? г [1] [2] = л ? 0,04 [2] = 0,005 м [4] .
Эпюра нормальных напряжений показана на рис. 5.1, е.
5. Полное перемещение свободного конца бруса согласно (5.10):
Д/ = Д/| + Д/2 + Д/3 = 1,5 — 0,9 + 0,9 = 1,5 мм.
Требуется определить напряжения в поперечных сечениях и перемещение среднего сечения бруса (точка В) при действии продольных сил (см. пример 5.2, рис. 5.2). Материал бруса — сталь (Е = 2,06 • 10> МПа), поперечное сечение бруса — 2×2 см. Решение. 1. Площадь поперечного сечения бруса А = 0,02 [2] = 0,0004 м [4] .
- 2. Жесткость стержня ЕА = 2.06 • 10> • 10 :! • 0,0004 = 8,24 • ИИ кН.
- 3. Определим напряжения по участкам бруса согласно рис. 5.2, е и (5.2). Участок 1. а, = Nx/A = 80/0,0004 = 20 • 10> кН/м [2] = 200 МПа.
Эпюра нормальных напряжений показана на рис. 5.2, ж.
Участок 4. оА = N a/Aa = 120/10 • 10~ 4 = 12 • 10 4 kH/m 2 = 120 МПа.
Участок 5. a5 = N5/A5 = 120/20 • 10 4 =6 10 4 kH/m 2 = 60 МПа.
Эпюра напряжений a, построенная по полученным данным, показана на рис. 5.7, г.



6. Определим продольные деформации бруса по каждому расчетному участку. Участок 1. А/, = NJi/EAi = 360 • 1/(515 • 10 3 ) = 0,699 • 10 3 м.
Участок 3. Д/3 = N3l3/EA3 =-120 • 1/(206 • 10 3 ) = -0,583 • КИ м.
Участок 4. Мл = NJ a/EAa = 120 • 1/(206 ? 10 3 ) = 0,583 ? КИ м.
Участок 5. М5= N5l5/EA5= 120 • 1/(412 • 10 3 ) = 0,291 • КИ м.
7. Полное перемещение свободного конца бруса
М= Д/,+ Д/,+ Д/3+ Д/4+ Д/5= (0,699 — 0,233 — 0,583 + 0,583 + 0,291) • 1(Н = 0,757 х х 10 3 м.
8. Построение эпюры перемещений.
Для построения эпюры перемещений определяем перемещения граничных точек на оси бруса.
ил = 0 (опора неподвижна).
M oi = и л + Д/i = 0,699 • 10 3 м = 0,699 мм.
и в = и01 + Д/2= (0,699 — 0,233) • 10-3 ы = 0,466 • 1(Н м = 0,466 мм. и02 = ив + Д/3= (0,466 — 0,583) • 10 3 м = -0,117 • 10 3 м = -0,117 мм. ис = и02 + Д/4 = (-0,117 + 0,583) • Ю-з м = 0,466 • 1(Н м = 0,466 мм. ип = Д/ = 0,757 ? 10 -3 м = 0,757 мм.
Эпюра перемещений точек оси бруса, построенная по полученным данным, показана на рис. 5.7, Э.
Источник: studme.org
Напряжение в строительстве это
Для расчета строительных конструкций в настоящее время используют техническую систему единиц, в которой силу, нагрузку, вес, так же как и массу тела, выражают в килограммах или тоннах. Между тем вес тела при одной и той же массе зависит от ускорения свободного падения g и потому зависит от географического района.
Для того чтобы различать единицы силы и массы, килограмм-силу обозначают «кгс», тонну-силу — «тс», а массу — «кг», «т».
Так как величина g изменяется незначительно, разница между массой и весом невелика и в практических расчетах строительных конструкций принимают, что кгс и кг, тс и т численно равны между собой. При таких единицах линейная нагрузка (нагрузка на единицу длины элемента) составляет кгс/см, кгс/м, тс/м, а поверхностная нагрузка (давление) — кгс/см2, кгс/м2, тс/м2.
Напряжения в материалах, модули деформации измеряют в единицах: кгс/см2, кгс/мм2, тс/м2; моменты сил — как произведение силы на плечо: кгс-м, кгссм, т-м и т.д. Эти единицы применены в нормативных документах для расчета строительных конструкций: СНиП II-6-74 «Нагрузки и воздействия»; СНиП II-B.3-72 «Нормы проектирования. Стальные конструкции»; СНиП П-21-75 Нормы проектирования. Бетонные и железобетонные конструкции» и др.
В тех отраслях науки и техники, где требуется высокая точность вычислений, нельзя принимать одинаковыми численные значения силы и массы, т.е. не учитывать изменение g в различных географических районах, отождествлять единицы напряжения и поверхностной нагрузки и т.д., поэтому там применяют единицы международной системы СИ (Система интернациональная).
В этой системе единицы кг и т предусмотрены только для обозначения- массы. Для силы, нагрузки, веса введена единица ньютон (Н); для давления, напряжения, модуля деформаций — паскаль (Па) . Соответственно линейная нагрузка выражается в Н/м (ньютон на метр); поверхностная нагрузка —в Н/м2 (ньютон на~ квадратный метр); момент силы — в Н • м (ныо- тон-метр), Проект ГОСТа «Единицы физических величин» предусматривает распространить систему СИ на все виды инженерных расчетов.
Для перехода от технической системы единиц к системе единиц СИ следует учитывать величину g= =9,8 м/с2 (при этом получаются неудобные для практических расчетов числа). Если число 9,8 округлить до 10, легче перейти от одной системы единиц к другой
В тексте учебника используются единицы, соответствующие единицам, принятым в Строительных нормах и правилах. Перевод этих единиц в систему СИ проиллю* стрирован в ряде числовых примеров.
Смотрите также:
Глава 4. ТЕПЛОИЗОЛЯЦИОННЫЕ КОНСТРУКЦИИ. Строительные конструкции с применением эффективных утеплителей.
Монтаж строительных конструкций — комплексно-механизированный процесс сборки зданий, сооружений или их частей из заранее изготовленных элементов или узлов.
Наиболее распространенные строительные конструкции — бетонные и железобетонные. При строительстве зданий и сооружений черной и цветной металлургии.
Монтаж строительных конструкций — это комплексный процесс механизированной сборки здания или сооружения из готовых элементов.
Укрупнительная сборка конструкций на строительной площадке. Железобетонные конструкции с местных заводов-изготовителей обычно привозят полностью собранными.
Строительные элементы, в которых неправильно подобраны слои или пароизоляция
Паронепроницаемый слой укладывают с внутренней стороны ограждающей конструкции ( 7.2).
Монтаж строительных конструкций — это специализированный поток, в состав которого включаются частные потоки по отдельным видам работ.
Строительные технологии. Технология строительного производства.
§ 1. Усиление конструкций. Многие конструкции объекта нуждаются в усилении при его реконструкции.
Монтаж строительных конструкций ведут под руководством прораба или мастера по ППР, где содержатся указания по охране труда.
Технологический процесс монтажа строительных конструкций состоит из комплекса взаимосвязанных операций: приемки, перевозки.
Источник: www.bibliotekar.ru