Ответы на решение задач по строительству

Средняя плотность солнца (p) — 1400 кг/м3 m = p * V, где m — масса, V — объём. Умножаем плотность на объём: 1400 * 2 = 2800 кг Ответ: ёмкость 2 м3, заполненная солнечным веществом, будет. Читать далее

Если я смогу решить задачку, то мне исправят оценку. Помогите, пожалуйста.

Окружность разбита точками на 3k дуг: по k дуг длины 1, 2 и 3. Докажите, что найдутся две. Развернуть

Длина первых двух дуг равна длине третьей. А их всегда одинаковое количество. Поэтому, как ты их не комбинируй, половину окружности покроют дуги величиной 3,а половину сумма дуг. Читать далее

Источник: yandex.ru

Студланс — биржа заказчиков
и авторов студенческих работ

Исполнитель работает над заказом —
задаёт уточняющие вопросы и

строительные кострукции с элементами статики (решение задач на расчетную нагрузку)

отправляет выполненную работу
на проверку.

От 100 рублей

от 15 минут

Бесплатные доработки

У нас можно заказать работы любого типа!

Где заказать решение задач?

Если ваш допуск к сессии зависит от решения блока задач, а у вас нет ни времени, ни желания садиться за расчёты – используйте возможности Студланса. Заказ задач на нашем портале – дело нескольких минут. Специалисты по высшей математике, экономике, физике, химии, логики и другим дисциплинам, где требуется решение задач, обязательно помогут вам получить допуск к экзамену или зачёту.

Размещая заказ на решение задач, вы находитесь под защитой администрации Студланса. Мы гарантируем, что ваши деньги будут перечислены исполнителю только после того, как вы подтвердите получение качественной работы – правильно решённых задач.

Решаем задачи по любым предметам

Точное решение задач – с гарантией!

Задачи – обязательный атрибут обучения на факультетах точных, технических, естественных наук. Кто-то решает задачи по высшей математике, кто-то – по физике, кто-то – по генетике, статистике, экономике. С необходимостью решения задач сталкиваются даже студенты гуманитарных факультетов. Философы мучаются над задачами по логике, историки – над задачами по матстатистике.

Ваш гуманитарный мозг не воспринимает цифры? Попалась слишком сложная задача? Или у вас просто острый дефицит времени? Студлансеры готовы вам помочь. На Студлансе можно заказать решение задач по любым дисциплинам – и по доступным студенчеству ценам!

Используя функционал Студланса, вы получаете:

• доступ к интеллектуальным ресурсам человечества (в лице старшекурсников-отличников ведущих вузов, победителей олимпиад, аспирантов и даже преподавателей);
• возможность самостоятельного выбора исполнителя и назначения цены;
• поддержку администрации в решении спорных вопросов;
• гарантию перечисления гонорара исполнителю только после качественного решения задач.

Задачи бывает трудно решить, но заказать их на Студлансе – очень просто. Интуитивно понятный интерфейс позволяет оформить заказ на решение задач по любому предмету за пару минут. А результат вы сможете получить уже через сутки – на Студлансе оперативно выполняют даже самые строчные заказы!

Источник: studlance.ru

Решение задач на заказ

Гарантийный срок на нашем сервисе 20 дней. В период работы над заданием и гарантии деньги заморожены на ресурсе. В течение гарантийного срока ты можешь дать свои замечания для дальнейших правок или запросить перерасчет, если работа выполнена некорректно и ты хочешь вернуть деньги назад. После истечения гарантийного срока заказ считается выполненным и оплата автоматически переводится исполнителю.

Сколько стоит помощь с решением задач?

На сервисе не существует установленных цен, они зависят от сложности работы, срока сдачи и опыта эксперта. Ты всегда можешь предложить свою цену и обсудить варианты с исполнителем.

Как оплатить в рассрочку?

Предоплата доступна при ставке от 500 до 7000 рублей. Чтобы использовать предоплату, зайди на страницу заказа и рядом со ставкой эксперта нажми кнопку «нанять», выбери пункт «по частям», выбери способ оплаты и нажми кнопку «перейти к оплате».

Какая комиссия для заказчика?

Комиссия заказчика фиксированная и составляет 35% от ставки автора.

Как выбрать эксперта по решению задач?

Чтобы выбрать эксперта, зайди на страницу заказа и рядом с интересующей ставкой нажимай кнопку «нанять». Далее выбери способ и тип оплаты и нажми кнопку «перейти к оплате». После этого останется ввести данные карты, с которой планируется оплата и ввести код из смс на странице банка.

Как заказать работу у определенного автора?

Если хочешь заказать работу у знакомого эксперта, нужно зайти в завершенный заказ, и нажать на аватар эксперта. Ты попадешь на страницу профиля, где под аватаром можно будет нажать кнопку ‘заказать у автора’. Размещай задание и жди реакции эксперта – он получит уведомление оставит свое предложение, если будет заинтересован в работе.

Как изменить срок сдачи?

Чтобы изменить срок сдачи работы, тебе нужно зайти в заказ с полной версии сайта. После этого нажми на кнопку «детали заказа» и выбери «срок сдачи». Откроется календарь, и ты сможешь выбрать подходящую дату. Учти, что если заказ уже в работе, то изменить срок можно только на более поздний.

Топ экспертов

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Киевский государственный университет им. Т.Г.Шевченко 1994, механико-математический факультет, преподаватель

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Экперт входит в ТОП-10 по своему предмету Эксперт проверен администрацией Автор24 Эксперт — зарекомендовал себя и выполнил более 100 работ с хорошим рейтингом

Отзывы студентов

Заказываю второй раз! Все отлично! Быстро и качественно! Побольше таких исполнителей ) А исполнителю — побольше клиентов) Спасибо!

Всё сделано качественно, спасибо большое, всё в срок, автор быстро отвечает, всё супер, буду ещё заказывать у него работы обязательно. И цена приятная очень.

Автор сделал заказ ранее уставновленного срока. Работа соответствует всем требованием. Ответы на задачи четкие и аргументированные

Заказ по технической механике было выполнено в срок. Все было очень подробно расписано и начерчено. Спасибо огромное

Видео-отзывы

Готовые работы, которые можно купить

Хотите заказать решение задач – сделайте это на Автор24! Решение задач на заказ по любым предметам

Помните, как в школе у вас «отлетали от зубов» задачки вроде «У Пети 2 яблока, а у Коли на 2 больше» или «х2 = 4»? Совсем другое дело – задачи в колледжах и вузах. Решение задач необходимо для закрепления практических навыков и умений студентов по данной теме и дисциплине. Подобные задания дают преподаватели и гуманитарных, и точных наук. Например, в математике необходимо решить задачу при помощи определенного набора формул, в юриспруденции – разобрать тот или иной казус, в филологии – дать анализ слову, предложению, тексту согласно имеющемуся алгоритму и т.д.

Конечно, студентам-очникам, посещающим все лекции и практические занятия и, что немаловажно, хорошо вникающим в предмет, легче справляться с решением задач. Многое зависит и от преподавателя – насколько доходчиво он объясняет механизм решения.

У студентов-заочников чаще всего не хватает времени для того, чтобы сесть за учебники, справочники и конспекты и освоить алгоритм самостоятельно. А сдавать работу все-таки нужно. Что делать в таком случае? – Заказать решение задач профессионалу своего дела! Именно такие исполнители ждут вас на этом сайте.

В этом разделе вы можете оставить заявку на решение задач на заказ, и в кратчайшие сроки с вами свяжутся для уточнения всех необходимых деталей:

• какова дисциплина и тема;
• в каком количестве требуется решить задачи на заказ;
• есть ли особые пожелания относительно алгоритма решения, есть ли примеры и предпочтительные варианты для ориентира;
• нужно ли выполнять задание от руки или предоставлять в печатном виде;
• насколько подробное должно быть приведено решение;
• каковы требования к оформлению работы;
• требуется ли оглавление и список литературы и т.д.

Решение задач на заказ нашими исполнителями проводится всегда качественно, но от того, насколько точные указания вы дадите, будет зависеть уровень соответствия работы требования конкретно вашего руководителя, а значит, и итоговый балл (зачет/незачет).

Почему заказать решение задач стоит именно здесь?

• Наши авторы – профессионалы своего дела, опытные преподаватели колледжей и вузов, имеющие как минимум одно высшее образование, как максимум – ученые степени. Они точно знают, как правильно решить и оформить даже самые сложные и нестандартные задачи, и даже не одним, а несколькими способами, если это возможно.
• Наши сроки – самые сжатые. Чаще всего для студентов принципиальное значение имеет не только правильность решения, но и срочность: что называется, сдать работу нужно было «еще вчера». Кроме того, наши авторы всегда четко соблюдают обозначенные временные рамки.
• Наши цены – вполне адекватные и совершенно оправданные. Решение задач на заказ, цена которого зависит и от объема работы, и от сложности, и от сроков, предлагается нами на оптимальных условиях, ведь в большинстве своем студенты – народ не слишком обеспеченный финансово.
• Наш сервис – на высшем уровне. Диалог между заказчиком и тем, кому доверено решение задач на заказ, идет в режиме онлайн. При необходимости вы получите не просто решенные задачи, но и подробные пояснения к алгоритму решения, что поможет вникнуть и самому понять весь механизм. Вдруг придется давать такие же пояснения своему преподавателю!

Итак, если вы решили заказать решение задач на этом сайте, просто оставьте заявку. Мы поможем вам получить желанный «зачет» или высокий балл и при этом сэкономить время на более приятные занятия, чем перелопачивание учебников и конспектов!

Источник: author24.ru

Решаем проверочные задачи по статистике

1. Задача на определение средней арифметической

Рассчитать средний возраст студентов в группе из 20 человек:

Если сгруппировать данные, то получим ряд распределения:

2. Задача на нахождение средней арифметической взвешенной

Распределение рабочих по выработке деталей

Выработка деталей за смену одним рабочим, шт., Х i

Число рабочих, fi

20

3. Задача на в ычисление средней по групповым средним или по частным средним.

Распределение рабочих по среднему стажу работы

Средний стаж работы, лет.

Число рабочих, чел.,

4. Задача на в ычисление средних в рядах распределения (интервальный ряд).

Распределение рабочих АО по уровню ежемесячной оплаты труда

Группы рабочих по оплате труда у.е.

Число рабочих, чел.

Середина интервала, х i

=(450*5+550*15+650*20+750*30+850*16+950*14)/100= 729 у.е.

Задача 5 . Вычисление средних в интервальных рядах методом моментов

Распределение малых предприятий региона по стоимости основных производственных фондов

Группы предприятий по стоимости ОПФ, у.е.

Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.

Один из вариантов, обладающий наибольшей частотой принимают за А, i — величина интервала.

А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I , получим новый вариационный ряд распределения новых вариантов х i . Средняя арифметическая их новых вариантов- момент первого порядка m i = = 0/25=0

Задача 6 на определение Средней гармонической.

Заработная плата предприятий АО

Численность промышленно- производственного персонала, чел

Месячный фонд заработной платы, тыс руб.

Средняя заработная плата, руб.

Определить среднюю з/п по всем предприятиям.

Составим логическую формулу средней: средняя з/п по всем предприятиям =

1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.

Искомая средняя величина определяется по средней агрегатной: = =

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.

3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:

Все ответы верны.

Задача 7. Определить среднюю цену моркови по всем магазинам.

Цена и выручка от реализации по трем коммерческим магазинам.

Цена моркови., руб за кг.

Выручка от реализации, руб.

Решение.

Логическая формула средней: средняя цена моркови =;

нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.

Искомая средняя определяется по средней гармонической взвешенной:

Задача 8 по статистике с решением: средние величины.

Информация о вкладах в банке

Число вкладов, тыс., f

Средний размер вклада, руб., x

Сумма вкладов, млн. руб., F

Средний размер вклада, x

Определить средний размер вклада по двум видам.

1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:

2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:

Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.

1) Решение задачи по средней арифметической простой:

2) решение по средней арифметической взвешенной

Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.

Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная

Источник: www.goodstudents.ru

Решение задач на расчет концентрации растворов по химии

Смесь, состоящая из частиц растворителя, растворяемого вещества и продуктов их взаимодействия, называется раствором. Это гомогенные структуры однородной консистенции, состоящие из двух либо нескольких компонентов. Решение задач на растворы – определение их концентрации, степени растворимости веществ, условий протекания растворообразующих процессов.

Задачи на растворы по химии

Чистое вещество либо смесь нескольких компонентов, попадая в растворитель, могут проявлять свойства:

• хорошей растворимости;
• малой растворимости;
• быть нерастворимыми.

При растворении в воде образуются многочисленные атомно-молекулярные связи. Их количество зависит от коэффициента растворимости – химической величины, которая рассчитывается путем деления массы растворяемого вещества на массу растворителя.

Кроме этого, в задачах могут присутствовать массовая доля вещества, растворенного в соответствующем растворителе.

Как решать задачи с процентными растворами

Растворы, о которых идет речь в задачах по химии, обладают общими свойствами:

• они однородны;
• смешивание компонентов происходит за малый отрезок времени, как и изменение их концентрации;
• в результате смешивания двух (или более) растворов с различной концентрацией, происходит не только увеличение общей массы и объема раствора, но и усреднение процентного содержания растворенного вещества.

Поэтому существуют общие принципы их решения. Так, увеличение концентрации происходит в результате упаривания (испарения растворителя), а уменьшение – разбавления. В результате смешения может наблюдаться как увеличение, так и уменьшение, в зависимости от конкретных условий задачи.

В любом случае характеристики начального и конечного продуктов будут различаться, поэтому важно, данные в условии сведения не перепутать. Для этого применяется их нумерация.

Чтобы грамотно составить алгоритм решения, часто бывает полезно использовать уравнение химической реакции относительно активного вещества либо кислоты.

Концентрация растворов и способы ее выражения

На бытовом уровне понятие концентрации раствора выражается в отношении массы растворенного вещества к массе раствора, выраженном в процентах. Однако правомерно более широкое определение, охватывающее различные способы выражения концентрации.

Концентрация раствора – количественный показатель состава активного вещества в растворе, выраженное в определенных единицах и заключенное в единице массы или объема. Выражается в долях, процентах, массовых долях, молярности, мольных долях, титрах. Из них чаще применяются молярность и мольная доля.

1. О массовой доле ( (omega) ) идет речь в задачах, когда можно составить соотношение масс растворенного компонента и всего раствора. Для ее выражения существует формула:

Выражается она в процентах либо долевых частях единицы.

2. Молярность (по-другому – молярная концентрация) или (С) показывает сколько молей растворяемого компонента содержится в литре раствора. Ее формула имеет вид:

где (n) – это растворенное вещество в молях. Исходя из его значения, раствор может быть одномолярным (содержит 1 моль в 1 литре), децимолярным (0,1 моля в 1 л), сантимолярным (0,01 моль) и т.д.

3. Концентрация моляльная (обозначается (С_х) ) – моляльность – показатель количества (n) молей растворенного компонента в 1 кг растворителя ( (M_) ).

4. Для определения содержания (в граммах) вещества в 1 л раствора применяется понятие «титр» ( (Т) ).

5. Под растворимостью ( (S) ) понимают максимальную массу растворяемого вещества, способного раствориться в 100 г растворителя:

6. Коэффициент растворимости ( (K_s) ) – показатель, который определяется отношением массы вещества к массе растворителя при условии получения насыщенного раствора при обозначенной температуре:

Решение задач на упаривание растворов

Выпаривание раствора происходит в результате испарения воды, что ведет за собой уменьшение общего объема и массы. В то же время масса растворенного вещества остается без изменений. Существуют случаи, когда, кроме растворителя, испаряется растворенное вещество, если оно обладает повышенной летучестью.

Пример. Водный раствор аммиака

Рассмотрим пример решения задачи на упаривание.

Условие: В наличии 800 г раствора с 15%-ной концентрацией определенного вещества. Нужно увеличить его массовую долю на 5%. Сколько г воды должно испариться?

1. Какова масса вещества в первичном растворе?

(M_в=omega_вtimes M_р=0,15×800=120) г, где (M_в) — масса вещества, (M_р) — масса раствора

Найденное значение останется постоянным, поскольку при выпаривании изменения массы растворенного вещества не происходит. Значит M’=120г

2. (M_р=M_вdivomega_в= 120÷0.2=600) г

3. Теперь можно найти массу испаренной воды:

Решение задач на разбавление растворов

В результате процесса разбавления масса того вещества, которое растворено, не меняется в отличие от массы всего раствора и растворителя.

Задача

Масса имеющегося раствора NaCl 200г, его концентрация – 15%. К раствору добавлено 40г воды. Определить массовую долю NaCl в конце реакции.

Решение

1. Определение массы раствора в конце процесса:

2. Определение массы NaCl в начале процесса:

(M_=(omega_times M_р)div100%=15%times200гdiv100%=30 <>) г

В конечном растворе (M’_ =M_)

3. Определение массовой доли NaCl в конце процесса:

Решение задач на концентрирование растворов

Повышение концентрации происходит при добавлении вещества в раствор. При этом конечная масса растворенного вещества равна сумме первоначального содержимого и того, который добавлен.

Задача. Имеется 180 г раствора с 8%-ной концентрацией соли (формула NaCl). В этот раствор всыпали еще 20 г поваренной соли. Какая массовая доля NaCl получилась в конце реакции?

Решение

1. Определение окончательной массы раствора:

2. Определение конечной массы NaCl:

Следовательно, нужно найти (M) – массу в начале процесса.

(M=(omega_times M_р)÷100%=14,4) г

Тогда (M’=14,4г+20г=34,4) г

3. Определение массовой доли NaCl в конечном продукте:

Решение задач на смешение растворов

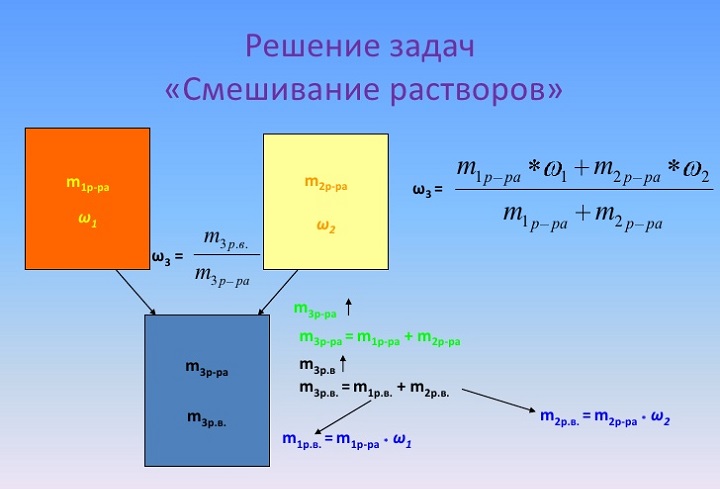
Смешение растворов с различной концентрацией растворенного вещества происходит с соблюдением «конверта Пирсона». Это – диагональная модель, при которой нельзя складывать массовые доли, а можно – лишь массы растворенных компонентов и растворов.

Задача

Дано два раствора с массами (M) и (M_1) . Массовые доли растворенного вещества обозначим соответственно (ω) и (ω_1) . В конечном продукте аналогичная величина – (ω_3) . Необходимо приготовить третий раствор с отличной от имеющихся концентраций.

Решение

1. Определение общей массы растворенного вещества:

2. Математические действия:

Следовательно, согласно этому математическому выражению, и нужно взять соотношение растворов.

Задачи на определение процентной концентрации раствора

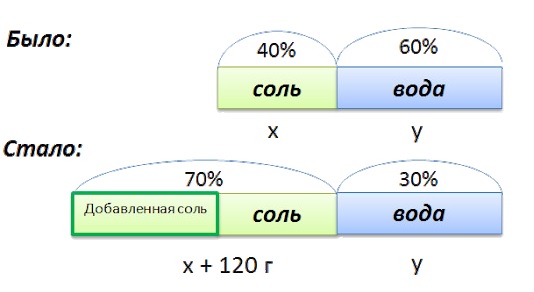
Задача 1

Какая процентная концентрация раствора (KNO_3) , если нормальная равна (0,2) моль/л. Плотность равна (1) г/мл.

1. Определение массы раствора объемом (1000) мл:

(M=rhotimes V=1times1000=1000) г

2. Составление и решение следующей пропорции:

(20,0) г (KNO_3) — (1000) г раствора

(Х_г) — (100) г раствора

Задача 2

Нужно приготовить (300) г 25%-ного раствора соли, имея 60%-ный и 10%-ный. Сколько нужно взять таких компонентов (m1 и m2)?

Для решения применим правило Креста:

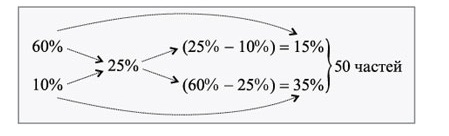
1. Определение веса одной из 50-ти частей образуемого раствора:

2. Определение массы каждой части (m_1) и (m_2) :

Задача 3

Используя 250г 45%-ного раствора соли, нужно понизить его концентрацию до 10%. Сколько воды необходимо использовать?

Концентрация соли в воде, используемой в качестве добавки, равна 0.

По методу креста образуется 45 частей раствора:

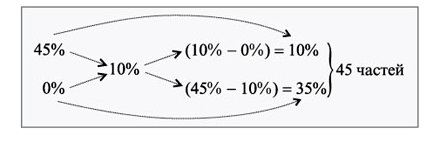
Решение

1. Масса одной части первичного раствора равна: (250div10=25) г

2. Определение массы воды, что необходима: (25times35=875) г

С целью проверки можно выполнить следующие действия:

1. Определение массы конечного продукта-раствора:

2. Для исходного раствора действует пропорция:

В 250г 40%-ного р-ра содержится Хг соли

Отсюда Х=112,5 г соли

3. Определение конечной концентрации раствора:

1125 г раствора – 112,5 соли

Следовательно, нужно взять 875 г воды.

Решать задачи на растворы – интересное занятие! Знание основных закономерностей будет полезно с теоретической и практической точек зрения. Однако бывают случаи, когда нужно быстро сдать контрольную либо перепроверить собственные решения. Тогда можно обратиться на сайт ФениксХелп.

Источник: blog.fenix.help