При построении сетевых графиков необходимо соблюдать следующие основные правила:
а) никакая работа не может быть начата до тех пор, пока все предшествующие ей работы не будут завершены;
б) в сетевых графиках с ориентацией на события — работы в каждое событие должна входить и из каждого события выходить не менее чем одна работа;
в) в сетевом графике не должно быть замкнутых контуров, т. е. ни один путь сетевого графика не должен дважды проходить через одно и то же событие;
г) для построения параллельных, одновременно выполняемых работ в сетевых графиках с ориентацией на события — работы следует вводить дополнительные события и фиктивную работу;
д) для изображения двух дифференцированно зависимых работ, т. е. работ, начало одной из которых зависит от выполнения всех предшествующих работ, а начало другой — только от выполнения одной из этих работ, необходимо в сетях с ориентацией на события работы расчленить данные работы путем ввода дополнительного события и указать их точную зависимость от предшествующей дополнительной фиктивной работы;
Расчет (построение) сетевого графика
е) в случае сложной работы, когда выполнение какой-то ее части позволяет начать одну или несколько работ, следует данную работу расчленить на последовательно выполняемые работы, от которых начинаются другие работы.
При планировании выполнения большого комплекса работ на шахте сетевые графики могут составляться на различные периоды времени (смену, сутки, месяц, квартал, год, пятилетку и т. д.).
В связи с этим, а также в зависимости от уровня управления сетевые графики приходится иногда детализировать, укрупнять или объединять в общий.
Источник: sv-barrisol.ru
Порядок и правила построения сетевых графиков.
Nbsp; Министерство просвещения РФ Поморский государственный университет им. М. В. Ломоносова КУРСОВАЯ РАБОТА на тему: «Программирование на сетях: модель сетевого планирования и управления; транспортная задача в сетевой постановке» Выполнила студентка 3 курса (33 группа) математического факультета дневного отделения Лебедева Юлия Владимировна Научный руководитель: Самбурская Е. В.
Архангельск, 2005
Оглавление.
1. Сетевая модель и ее основные элементы…………………………………………………..4
2. Порядок и правила построения сетевых графиков…………………………………………5
3. Упорядочение сетевого графика. Понятие о пути………………………………………….7
4. Временные параметры сетевых графиков………………………………………………….11
5. Сетевое планирование в условиях неопределенности…………………………………….17
6. Коэффициент напряженности работы. Анализ и оптимизация сетевого графика………20
7. Оптимизация сетевого графика методом «время — стоимость»…………………………23
Поиски более эффективных способов планирования сложных процессов привели к созданию принципиально новых методов сетевого планирования и управления (СПУ).
Методы сетевого планирования-2.
Система методов СПУ — система методов планирования и управления разработкой крупных народнохозяйственных комплексов, научными исследованиями, конструкторской и технологической подготовкой производства, новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов путем применения сетевых графиков.
Первые системы, использующие сетевые графики, были применены в США в конце 50-х годов и получили названия СРМ (английская аббревиатура, означающая метод критического пути) и РЕКТ (метод оценки и обзора программы). Система СРМ была впервые применена при управлении строительными работами, система РЕКТ — при разработке систем «Поларис».
В России работы по сетевому планированию начались в 60-х годах. Тогда методы СПУ нашли применение в строительстве научных разработках. В дальнейшем сетевые методы стали широко применяться и в других областях народного хозяйства.
СПУ основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.
· формировать календарный план реализации некоторого комплекса работ;
· выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;
· осуществлять управление комплексом работ по принципу ведущего звена с прогнозированием и предупреждением возможных срывов в ходе работ;
· повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.
Диапазон применения СПУ весьма широк: от задач, касающихся деятельности отдельных лиц, до проектов, в которых участвуют сотни организаций и десятки тысяч людей (например, разработка и создание крупного территориально-промышленного комплекса).
Под комплексом работ (комплексом операций, или проектом) мы будем понимать всякую задачу, для выполнения которой необходимо осуществить достаточно большое количество разнообразных работ. Это может быть и строительство некоторого здания, корабля, самолета или любого другого сложного объекта, и разработка проекта этого сооружения, и даже процесс построения планов реализации проекта.
Для того чтобы составить план работ по осуществлению больших и сложных проектов, состоящих из тысяч отдельных исследований и операций, необходимо описать его с помощью некоторой математической модели. Таким средством описания проектов (комплексов) является сетевая модель.
В данной курсовой работе поставлены задачи: изложить основные теоретические факты по данной теме, рассмотреть типовые примеры и задачи, разобраться в сетевой постановке и научиться оптимизировать данные на приведенных примерах.
Сетевая модель и ее основные элементы.
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.
Главными элементами сетевой модели являются событиями и работы
Термин работа используется в СПУ в широком смысле.
Во-первых, это действительная работа — протяженный во времени
процесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответственного исполнителя.
Во-вторых, это ожидание — протяженный во времени процесс,
не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).
В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.
Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится.
Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним — начальным. При этом предполагается, что событие не имеет про должительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.
Среди событий сетевой модели выделяют исходное и завершающее события. Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.
События на сетевом графике (или, как еще говорят, на графе)
изображаются кружками (вершинами графа), а работы — стрелками
(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:
На рис. 2, а приведен сетевой график задачи моделирования и построения оптимального плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — математическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построитьи отладить программу для ЭВМ; Е — рассчитать оптимальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.
Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.
В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки продолжительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствующими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.
Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики состояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определенные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения.
В качестве примера сетевой график «события — работы» задачи моделирования и построения оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, представлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см.
правило 3 в разд. 3).
Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — работы» обладает известными преимуществами: не содержит фиктивных работ, имеет более простую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (показатель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления комплексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами представления сети) в настоящее время наибольшее распространение получили сетевые графики «события — работы».
Порядок и правила построения сетевых графиков.
Сетевые графики составляются на начальном этапе планирования. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, продумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями. С их помощью оценивается длительность каждой работы.
Затем составляется (сшивается) сетевой график. После упорядочения сетевого графика рассчитываются параметры событий и работ, определяются резервы времени и критический путь. Наконец, проводятся анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ.
При построении сетевого графика необходимо соблюдать ряд правил.
1. В сетевой модели не должно быть «тупиковых» событий, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события (рис. 3 а). Здесь либо работа (2, 3)не нужна и ее необходимо аннулировать, либо не замечена необходимость определенной работы, следующей за событием 3 для свершения какого-либо последующего события. В таких случаях необходимо тщательное изучение взаимосвязей событий и работ для исправления возникшего недоразумения.
2. В сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа (событие 3 — на рис. 14.3 б). Здесь работы, предшествующие событию 3, не предусмотрены. Поэтому событие 3 не может свершиться, а следовательно, не может быть выполнена и следующая за ним работа (3, 5).
Обнаружив в сети такие события, необходимо определить исполнителей предшествующих им работ и включить эти работы в сеть.
3. В сети не должно быть замкнутых контуров и петель, т.е. путей, соединяющих некоторые события с ними же самими (рис. 3 в, г).

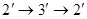
Представим себе, что в сетевом графике, изображенном на рис 2 а работы Б (построение математической модели) и Д (построение и отладка программы для ЭВМ) при формулировании первоначального списка работ мы объединили бы в одну работу Б’. Тогда получили бы сетевой график, представленный на рис 2 в Событие 2′ означает, что можно переходить к работе Б’,которую нельзя выполнить до выбора метода расчета (работа Г), а выбор метода расчета нельзя начинать до окончания построения модели (событие З’). Другими словами, в сети образовался простейший контур: .
При возникновении контура (а в сложных сетях, т.е. в сетях с высоким показателем сложности, это встречается довольно часто и обнаруживается лишь при помощи ЭВМ) необходимо вернуться к исходным данным и путем пересмотра состава работ добиться его устранения. Так, в нашем примере потребовалось бы разделение работы Б’ на Б и Д.
4. Любые два события должны быть непосредственно связаны не более чем одной работой — стрелкой.
В этом случае рекомендуется ввести фиктивное событие (событие 2′ на рис. 3 е) и фиктивную работу (работа 2′, 2), при этом одна из параллельных работ (1, 2’) замыкается на это фиктивное событие. Фиктивные работы изображаются на графике пунктирными линиями.
5. В сети рекомендуется иметь одно исходное и одно завершающее событие. Если в составленной сети это не так (см. рис. 3 ж), то добиться желаемого можно путем введения фиктивных событий и работ, как это показано на рис.
3 з.
Фиктивные работы и события необходимо вводить и в ряде других случаев. Один из них — отражение зависимости событий, не связанных с реальными работами. Например, работы А и Б (рис. 3 и) могут выполняться независимо друг от друга, но по условиям производства работа Б не может начаться раньше, чем окончится работа А. Это обстоятельство требует введения фиктивной работы С.
Другой случай — неполная зависимость работ. Например, работа С требует для своего начала завершения работ А и Б, но работа Д связана только с работой Б, а от работы А не зависит. Тогда требуется введение фиктивной работы Ф ификтивного события З’, как показано на рис. 3 к.
Кроме того, фиктивные работы могут вводиться для отражения реальных отсрочек и отражения. В отличие от предыдущих случаев здесь фиктивная работа характеризуется протяженностью во времени.
Дата добавления: 2018-09-22 ; просмотров: 529 ; Мы поможем в написании вашей работы!
Источник: studopedia.net
Порядок построения сетевых графиков.
Сетевой график представляет собой схему, на которой наглядно показаны все работы по созданию сначала промежуточной продукции определенной степени готовности, а под конец — полное возведение объекта строительства.
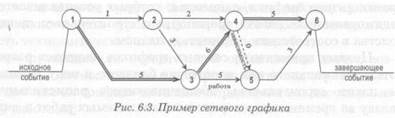
По внешнему виду сетевой график представляет собой сеть, состоящую из стрелок и кружков, отражающих логическую и технологическую взаимосвязь и взаимообусловленность всех операций, входящих в общий комплекс работ строящегося объекта (рис. 6.3). В этом способе стрелками обозначают работы, а кружками с цифрами-индексами (кодами) — события. Образуемая из сочетания работ и событий сеть представляет собой весь процесс создания объекта.
Для построения сети используются такие элементы сетевого графика, как работа, зависимость, событие, продолжительность и путь.
Работа, обозначаемая в сетевом графике стрелкой, может выражать:
- действительную работу, т. е. производственный процесс, требующий затрат труда, времени и ресурсов (например, отрывка котлована, монтаж фундаментов и т. д.). На сетевых графиках работу принято изображать сплошной стрелкой с надписью над ней названия или шифра работы, а под ней — продолжительности выполнения работы;
- ожидание, которое представляет собой тоже работу, но требующую только затрат времени и не требующую затрат каких-либо ресурсов. Как правило, к ожиданиям относятся технологические и организационные перерывы. Ожидание, как и действительная работа, обозначается сплошной стрелкой;
- зависимость или фиктивная работа отражает технологическую или организационную взаимосвязь работ и не требует ни времени, ни ресурсов. В сетевом графике зависимость обозначается пунктирной стрелкой (см. рис. 6.3), указывающей что выполнение последующих за ней работ возможно только при условии предварительного выполнения предшествующих работ.
Факт окончания одной или нескольких работ, необходимых и достаточных для начала следующих работ, называют событием. Всякая работа сетевого графика ограничена двумя событиями. Подразумевается, что событие совершается мгновенно, и поэтому оно не требует ни времени, ни ресурсов. Событие на сетевом графике обычно изображается кружком. Внутри кружка указывают код события, который только определяет события, но не указывает их последовательность.
В сетевой график всегда входят особые события: исходное и завершающее. Исходное событие не имеет предшествующих работ. Этим событием начинается развитие сетевого графика. Завершающее событие не имеет последующих работ и завершает работы в сетевом графике.
Каждая работа в сетевом графике имеет свою продолжительность, которая на сетевом графике указывается над стрелкой. Пройдя от исходного события к завершающему, последовательно по цепочке зависимостей можно подсчитать общую продолжительность всех работ.
Взаимосвязанные между собой работы и события образуют пути сетевого графика. Путем называется такая последовательность работ в сети, у которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы.
В сетевом графике различают несколько видов путей. Путь от исходного до завершающего события сетевого графика называют полным путем.
Самый длинный из всех полных путей (их может быть несколько) имеет особое значение — его временная длина определяет срок выполнения работ по сетевому графику, поэтому на графике он выделяется двойной или жирной линией и называется критическим путем. В сетевом графике может быть несколько критических путей. Работы, которые лежат на критическом пути, называют критическими. Путь, длина которого несколько меньше критического, называют подкритическим.
Совокупность критических и подкритических путей образует критическую зону.
Выявление в сетевом графике критической зоны позволяет выявить работы, на которые нужно обращать внимание при необходимости сокращения сроков строительства при проектировании сетевого графика или при контроле за ходом строительства.
Каждая работа и ее результат должны иметь четкое определение. Последовательность выполнения работ устанавливается в соответствии с требованиями технологии строительства объекта. При этом осуществляют работы, выполняемые последовательно, т. е. начало следующей работы после окончания предшествующей, и работы, выполняемые параллельно. Схематическое изображение этой последовательности и взаимосвязей работ на графике называют топологией сетевой модели.
Сетевой моделью необходимо отразить правильную зависимость работ, соответствующую принятым методам организации и производства работ. Для этого надо соблюдать следующие правила построения сетевого графика:
Фиктивные работы и события необходимо вводить и в ряде других случаев. Один из них — отражение зависимости событий, не связанных с реальными работами. Например, работы А и Б (рис. 6.4, а) могут выполняться независимо друг от друга, но по условиям производства работа Б не может начаться раньше, чем окончится работа А. Это обстоятельство требует введения фиктивной работы Ф и фиктивного события 3’.
Другой случай — неполная зависимость работ. Например, работа В требует для своего начала завершения работ А и Б, а работа Г связана только с работой Б и от работы А не зависит. Тогда требуется введение фиктивной работы Ф и фиктивного события 3’, как показано на рис. 6.4, б.
Кроме того, если последующая работа зависит от части предшествующей, то последнюю следует изобразить двумя стрелками, вводя между ними промежуточное (дополнительной) событие. Например, работа В (рис. 6.4, в) может начаться после полного окончания работы А и частичного окончания работы Б. Это требует введения между частями работы Б фиктивного события 3’.
Источник: infopedia.su