Задача 2. Рассчитать расход материалов (цемента и заполнителей), нужных для бетонирования массивных фундаментов общим объемом 200 м3.
Бетон класса В10 (М150), Для приготовления бетонной смеси использованы: шлакопортландцемент активностью 340 кгс/м2, песок речной, известняковый щебень наибольшей крупностью 40 мм и с пустотностью 44%.
Файлы: 1 файл
Задача 2. Рассчитать расход материалов (цемента и заполнителей), нужных для бетонирования массивных фундаментов общим объемом 200 м3.
Бетон класса В10 (М150), Для приготовления бетонной смеси использованы: шлакопортландцемент активностью 340 кгс/м2, песок речной, известняковый щебень наибольшей крупностью 40 мм и с пустотностью 44%.
Решение задачи 2
Расчет состава бетона заключается в установлении наиболее рационального соотношения между составляющими бетон материалами.
Для расчета состава бетона необходимы следующие данные:
Класса бетона В10 (марка 150) Rб,
активность портландцемента Rц — 340 кг/см2
7 класс, 23 урок, Примеры задач на построение
насыпная плотность цемента сн.ц.=1,0 г/см3
истинная плотность цемента сц.=3,0 г/см3,
насыпная плотность песка сн.п.=1,5 г/см3
истинная плотность песка сп.=2,6 г/см3,
насыпная плотность щебня сн.щ.=1,4 г/см3
истинная плотность щебня сщ.=2,5 г/см3,
наибольшая крупность заполнителя (гранитный щебень) — Vп.щ =40 мм.
пустотность щебня — 44%
влажность щебня — 4%
пустотность песка — 42%
влажность песка — 5%
Вычисляем водоцементное отношение по формуле:
Rб=А Rц(Ц/В-0,5), после преобразования
Коэффициент А=0,65 выбираем как для высококачественных материалов по таблице 9.2 [1].
Расход воды на 1 м3 бетонной смеси определяем по таблице 9.3 [1], учитывая крупность гравия В=145 л.
Расход цемента на 1 м3 бетонной смеси вычисляем
Ц= В/(В/Ц)=145/0,73=198 кг
Расход щебня в сухом состоянии на 1 м3 бетонной смеси составляет:
Значение коэффициента раздвижки зерен б =1,6 выбираем согласно рекомендациям справочников, как для малоподвижной смеси.
Расход песка в сухом состоянии на 1 м3 бетона определяем по формуле:
В результате получаем следующий ориентировочный номинальный (лабораторный) состав бетона, кг/м3:
Производственный (полевой) состав бетона вычисляем, принимая во внимание влажность заполнителей (в данном примере влажность песка 5%, щебня 2 %), — уменьшаем необходимое количество воды:
145 — (5•587/100+4•1408/100)=145 — (29,35+56,32)=86,33 кг, соответственно увеличиваем и количество заполнителей:
Песок (кг)- 587(1+5/100)=616,35кг;
Щебень (кг)- 1408(1+4/100)=1464,3кг.
На 200м3 необходимо:
Песок (кг)- 616,35•200= 123270кг=123,27т;
Щебень (кг)- 1464,3•200= 292860кг=293т.
Вода 86,33•200= 17266кг=17,3т
1.Что представляет собой стеклянная вата, каковы ее свойства и какие изделия из нее изготавливают?
Ответ: Стеклянная вата представляет собой минеральное волокно, которое по технологии изготовления и свойствам имеет много общего с минеральной ватой.
Решение геотехнических задач в транспортном строительстве. Пример расчёта
Для получения стеклянного волокна используют то же самое сырье, что и для производства обычного стекла, или отходы стекольной промышленности.
Изготавливают стекловату из стеклянного боя или из тех же компонентов, что и оконное стекло (кварцевый песок, известняк или мел, сода или сульфат натрия).
Тонкое стеклянное волокно для текстильных материалов получают с помощью вытягивания из расплавленной стекломассы (фильерный или штабиковый способ). Более грубое волокно изготавливают способом дутья.
Маты и полосы из стеклянной ваты получают путем прошивки стеклянных волокон асбестовыми или скрученными из того же стекловолокна нитями.
Стекловата имеет повышенную химическую стойкость, не горит и не тлеет, а ее плотность в рыхлом состоянии не превышает 130 кг/м 3 .
Стеклянная вата почти не дает усадки в процессе эксплуатации, а ее волокна не разрушаются даже при длительной вибрации.
Она хорошо поглощает звук, малогигроскопична, морозостойка.
Слой стеклянной ваты толщиной 5 см соответствует термическому сопротивлению кирпичной стены толщиной 1 м.
Следует отметить, что прочность волокон стеклянной ваты выше, чем у минеральной, а температуростойкостьстекловаты обычного состава составляет — 450°С, что ниже, чем у минеральной.
Применяют стеклянную вату из непрерывного стекловолокна для изготовления термоизоляционных материалов и изделий, а также для теплоизоляции конструкций при температуре поверхности от -200°С до 450°С.
Комовую стеклянную вату для тепловой изоляции применяют реже, чаще всего ее перерабатывают в изделия.Стекловату применяют также в качестве акустического материала.
Кроме того, для нужд специальной теплоизоляции используются следующие виды ваты:
Эти разновидности ваты обладают повышенной температуростойко
2.Описать свойства и области применения вспученных вермикулита и перлита.
Ответ: Вспученный перлит — продукт измельчения и термической обработки кислого вулканического стекла перлита. Получение
По внешнему виду представляет собой песок или щебень (в зависимости от степени предварительного измельчения), окраски от снежно-белой до серо-белой, без запаха. Вспученный перлит производится различного фракционного состава: от перлитовой пудры (менее 0,14 мм) до перлитового щебня (10-20 мм). Насыпная плотность перлитового песка колеблется от 45 до 200 кг/м 3 , щебня — 500 кг/м 3 .
В зависимости от размера зерен и области применения выделяют строительный перлит (фракция 0,16-1,25 мм), агроперлит (1-5 мм) и фильтроперлит (0-0,16 мм). В строительстве перлит применяется для теплоизоляционных засыпок, как наполнитель длялёгких бетонов и теплоизоляционных ст роительных растворов, для фильтрации в различных областях промышленности.
Вермикулит представляет собой минерал из группы гидрослюд, желтовато-палевого цвета, с характерным для продуктов слюды блестящим отсветом, вспучивающийся при температуре град. с увеличением объема в 7-10 раз. Насыпная масса вспученного вермикулита составляет 75-200 кг/куб.м..
Вспученный вермикулит, экологически чистый пористый материал, получаемый обжигом природного слюдистого минерала, в форме продолговатых червеобразных столбиков и нитей материал, за что и получил название –«вермикулит» (в переводе с английского vermiculus- червячок). За рубежом вермикулит называют- минералом урожайности, японцы- лечебным минералом. Выпускается заданный фракционированный гранулированный состав от 0,25 до10 мм.
Данный материал отличается хорошими тепло и звукоизоляционными свойствами, термической и биологический стойкостью, химической инертностью, способностью к избирательному ионному обмену. Этот комплекс свойств объясняет широкое использование вспученного вермикулита в различных отраслях промышленности, включая строительство, машиностроение, сельское хозяйство, металлургию, химию и т.д.
Первое место по запасам и качеству залежей вермикулитового сырья принадлежит ЮАР, второе Ковдорскому месторождению в Мурманской области. Основная масса вермикулитового концентрата за рубежом производится в США и ЮАР. За последние годы выпуск концентрата за рубежом постоянно увеличивается, достигнув в США в 2000 году 760 тыс. тонн в год.
Однако, несмотря на развитую вермикулитовую промышленность, можно констатировать, что сырьевая база вермикулита в зарубежных странах территориально ограничена, но даже в условии увеличения объема трансатлантических перевозок руды применение вермикулита остается весьма рентабельным.
В настоящее время вспученный вермикулит за рубежом используется в производстве более 100 наименований продукции. Продолжаются дальнейшие поиски целесообразных областей применения вермикулита. В нашей стране вермикулит стал применяться в промышленных масштабах в 60-ых годах.
На территории бывшего СССР открыто более 22 месторождений вермикулита (из них 17 в России) с прогнозным запасом еще 200 млн. тонн, которые расположены по всей стране. В т.ч. на Урале, в Сибири, на севере Европейской части страны и т.п. Россия располагает крупнейшей в мире сырьевой базой вермикулита.
3.Перечислите способы зимнего бетонирования и дать краткую характеристику каждого способа.
Ответ: В зависимости от характера выдерживания бетона способы зимнего бетонирования подразделяют на две группы: безобогревные и обогревные. К безобогревным способам относится бетонирование в тепляках, метод термоса, применение бетонов с противоморозными добавками и «холодных» бетонов. К обогревным относят методы искусственного подогрева бетона с применением электричества, пара или горячего воздуха. Способ бетонирования для конкретного объекта выбирают после технико-экономического сравнения вариантов с учетом темпа бетонирования, местных ресурсов и возможностей.
Необходимую для твердения бетона тепловлажностную среду можно обеспечить в тепляках или шатрах. Шатры в отличие от тепляков применяют при возведении высотных сооружений, перемещая их вверх по мере бетонирования. Основным условием является создание над железобетонной конструкцией замкнутого пространства с достаточной термоизоляцией его от внешней среды.
Укладку бетона в тепляках производят в исключительных случаях при наличии технико- экономического обоснования. Тепляки возводят при строительстве подземных коллекторов, тоннелей, опор мостов и подпорных стенок из инвентарных легких элементов или в виде пневматических сооружений над участком укладки бетона. В закрытом замкнутом пространстве под тепляком нагревается воздух различными источниками теплоты до заданной величины. Когда бетон при положительной температуре в тепляке (не ниже 5°С) наберет прочность, предусмотренную проектом, тепляк демонтируют или на колесах перекрывают на новую позицию.
Если котлован или траншею ленточных фундаментов заглубляют в талый грунт на 1/3 максимальной глубины промерзания, то твердение бетона может происходить за счет использования теплоты, которая накоплена грунтом в период летнего времени. Бетон в такие траншеи или котлован необходимо укладывать с температурой не ниже 10 °С. Для уменьшения тепловых потерь в атмосферу траншеи сверху перекрывают утепленными щитами.
Твердение бетона при использовании метода термоса происходит с использованием того количества теплоты, которую он получил в период приготовления (от подогрева воды и инертных материалов), и теплоты, выделяемой цементом в период его гидратации (экзотермии). Суммарного количества теплоты должно быть достаточно, чтобы в определенной среде при остывании бетона до 0°С он набрал бы необходимую прочность. Это условие определяют уравнением теплового баланса, предложенным проф. В. Г. Скрамтаевым.
Продолжительность остывания бетона зависит не только от объема конструкции, но. и от ее формы, т. е. величины поверхности охлаждения.
Зная, какую прочность должен иметь бетон к моменту его замерзания при средней температуре, находим срок выдерживания в сутках (по таблицам). Задаваясь расходом цемента с определенным тепловыделением, значением коэффициента, определяем требуемый коэффициент теплопередачи, а по нему и толщину слоя утеплителя.
При укладке бетонной смеси по способу термоса на ранее уложенный и замерзший бетон поверхность последнего должна быть отогрета на глубину, предусмотренную проектом. При температуре воздуха ниже —10 °С арматура диаметром более 25 мм, а также арматура из жестких прокатных профилей и крупные металлические закладные части должны быть перед укладкой бетонной смеси отогреты до положительной температуры.
Бетоны с противоморозными добавками приготовляют с применением нитрита натрия NaN02 и поташа K2CO3. Для изготовления конструкций неармированных или с нерасчетной арматурой с защитным слоем бетона не менее 50 мм бетон формуют с добавками солей хлористого натрия (NaCl) в сочетании с хлористым кальцием (СаС12). Роль противоморозных добавок состоит в том, чтобы снизить температуру замерзания воды и тем самым продлить срок гидратации цемента.
Противоморозные добавки применять нельзя: при устройстве пролетных строений мостов; изготовлении предварительно напряженных конструкций; в конструкциях, подвергающихся динамическим нагрузкам, расположенных в зоне переменного уровня воды, находящихся в непосредственной близости (до 100 м) к источникам постоянного тока высокого напряжения, эксплуатируемых при относительной влажности воздуха более 60 % (если в зернах заполнителей размером более 0,12 мм имеется реакционноспособный кремнезем); при возведении монолитных дымовых и вентиляционных труб.
Нарастание прочности бетона с добавками хлористых солей при отрицательных температурах происходит относительно медленно: за 7 сут — до 30%, за 28 сут — до 50—60% и за 90 сут — до 90—100% от проектной марки бетона.
Соли вводят в бетонную смесь в виде водных растворов, концентрация которых определяется по таблицам. Раствор СаС1 допускается к применению с концентрацией не более 6%, так как СаО2 вызывает быстрое загустевание бетонной смеси.
Холодную бетонную смесь изготовляют и укладывают только при отрицательной температуре (однако не ниже —20°С) вследствие быстрого загустевания ее при положительной температуре. Уложенная и уплотненная смесь должна быть защищена способом термоса. Изготовление густоармированных железобетонных конструкций с применением холодного бетона не рекомендуется, так как хлористые соли вызывают коррозию стальной арматуры.
Свойства холодного бетона несколько хуже по сравнению с бетонами, твердеющими в обычных условиях. При равной прочности холодные бетоны обладают меньшей долговечностью, морозостойкостью, повышенной усадкой и хрупкостью.
Источник: www.yaneuch.ru
Примеры решения задач оптимального проектирования строительных конструкций
Характеристики исследуемого элемента: длина ℓ =3 м, продольное усилие N = 190 кН, расчетное сопротивление стали Ry = 240 МПа, коэффициент условия работы γс = 1,0; сечение постоянно по длине элемента ЕА = const.
Первый этап решения задачи – анализ центрально растянутого элемента.
1 шаг — определить границы элемента. Границы элемента представлены на рис. 4.

2 шаг – выбрать критерий оптимальности.
За критерий оптимальности принимаем массу (М) центрально растянутого элемента.
3 шаг – определить общее число независимых параметров, влияющих на величину критерия оптимальности, провести их ранжирование по степени влияния на величину критерия оптимальности.
Масса элемента определяется произведением длины элемента, площади сечения и удельного веса
В выражении (27) длина элемента ℓ и удельный вес стали ρ величины постоянные, то есть ℓ=3 м = const (по условию задачи), ρ =7850 кГ/м 3 = const. Поэтому независимой переменной (или управляемым параметром) является площадь поперечного сечения элемента А.
Таким образом, уравнение (27) имеет один независимый параметр А.
4 шаг – составить уравнение целевой функции.
Сначала представим описание некоторой основной величины F в ее зависимости от управляемых и неуправляемых параметров:
где управляемый параметр (независимый параметр) х1→площадь поперечного сечения растянутого элемента А; неуправляемые параметры (параметры, значения которых не подлежат изменению в рамках задачи):
с1→расчетное сопротивление стали Ry=240 МПа,
с2→коэффициент условия работы γc =1,0
с3→длина элемента ℓ=3 м,
с4→удельный вес стали ρ =7850 кГ/м 3 ,
с5→предельная гибкость [λ] =400,
с6→усилие в стержне N=190 кН.
Для данной простейшей задачи, учитывая выражения (27) и (28), можно легко записать уравнение целевой функции
F=М = А*ℓ*ρ = А*3*78,5 = 235,5*А →min (29)
5 шаг – составить неравенства – ограничения.
λ = ℓ / imin ≤ [λ] ≤ 400 (31)
6 шаг – составить уравнения состояния.
Уравнения состояния составлять не нужно, так как задача статически определима.
Второй этап решения задачи.
7 шаг -провести анализ целевой функции и неравенств-ограничений
Целевая функция (29) представляет собой уравнение с одним неизвестным (А). Условие прочности (30) представлено неравенством с одним неизвестным (А). Условие жесткости (31) представлено неравенством с одним неизвестным (imin) .
Задача относится к линейному программированию.
8 шаг –выбор метода решения задачи линейного программирования. Так как задача с одним неизвестным, то решение задачи сводится к решению линейного уравнения (29) с одним неизвестным.
Проведем некоторые упрощения. Из условий прочности (30) и жесткости (31) определяем требуемые величины площади поперечного сечения и минимального радиуса инерции сечения стержня
Атр ≥ 190/24 ≥ 7,92 см 2 (32)
imin ≥ 300/400 ≥ 0,75 см. (33)
Решение задачи (29) лежит на пересечении двух прямых (32) и (33), что представлено на рис. 5 (т. М с координатами Атр = 7,92 см 2 и imin= 0,75 см.)

Так как подразумевается, что мы имеем в базе данных сокращенный сортамент стальных элементов, то выбираем профиль с наименьшим поперечным сечением. Однако, учитывая большую величину коэффициента градации сортамента, почти невозможно найти сечение стержня с характеристиками А = 7,92 см 2 и imin = 0,75 см (фактический экстремум в практических задачах чаще всего не совпадает с математическим).
Поэтому решение задачи (минимум целевой функции) для разных видов поперечных сечений стержня минимальной массы будет находиться в области допустимых решений (в закрашенной области рис. 4). За окончательное решение принимаем сечение с характеристиками приближенными по величине к требуемым (т. М [А = 7,92 см 2 и imin = 0,75 см], рис.5).
По сортаменту подбираем профиль, площадь которого (Аф) и минимальный радиус инерции удовлетворяют условиям (32), (33). При этом для каждого профиля необходимо определить то сечение, которое удовлетворяет требованию минимальной массы элемента, т.е. удовлетворяет уравнению целевой функции (29). Для этого необходимо создать базу данных (сортамент) и провести расчет, например, в программе Exel.
Результаты по приведенному выше примеру представлены в табл. 2 и на рис 5.
Результаты решения задачи оптимизации
| Профиль Параметры сечения | Равнобок. уголок | Швеллер | Двутавр | Круглая труба | Квадратная труба | Парные равнобок.уголки |
| Сечение, мм | 70*6 | №8 | №10 | 76*3,5 | 80*3 | 50*5, δ=10 |
| Аф , см 2 | 8,15 | 8,98 | 7,97 | 8,85 | 9,6 | |
| imin, см | 2,15 | 1,19 | 1,22 | 2,57 | 3,1 | 2,45 |
| F, кг | 6,39 | 7,05 | 9,46 | 6,26 | 6.95 | 7,54 |
| Fmin, кГ | 6,26 |
Вывод.Для требуемого элемента оптимальным сечением из условия минимальной массы будет сечение из круглой трубы размерами 76*3,5 мм (т. М1 с координатами А = 7,97 см 2 и imin = 2,57 см на рис. 4).
Задача № 2. Определение оптимального сечения центрально растянутого стального элемента (по СНиП П-23-81. Стальные конструкции)
Усложним задачу оптимизации центрально растянутого элемента. Характеристики исследуемого элемента: длина ℓ =3 м, продольное усилие N = 190 кН, коэффициент условия работы γс =1,0; сечение постоянно по длине элемента ЕА=const; 240 МПа≤Ry≤360 МПа.
Первый этап решения задачи – анализ центрально растянутого элемента.
1 шаг — определить границы элемента. Границы элемента представлены на рис. 4.
2 шаг – выбрать критерий оптимальности.
За критерий оптимальности принимаем массу центрально растянутого элемента.
3 шаг – определить общее число независимых параметров, влияющих на величину критерия оптимальности, провести их ранжирование по степени влияния на величину критерия оптимальности.
Масса элемента определяется произведением длины элемента, площади сечения и удельного веса (1) В этом выражении независимым параметром является площадь поперечного сечения элемента А, которая зависит от марки стали, то есть от величины расчетного сопротивления Ry. Мы имеем два независимых параметра
Произведем ранжирование независимых параметров.
1. Величина площади сечения (А) при N=const зависит от расчетного сопротивления стали (марки стали). Чем выше расчетное сопротивление, тем меньше площадь поперечного сечения растянутого элемента (4).
Таким образом, для центрально растянутого элемента основным неизвестным является расчетное сопротивление стали. За первый неизвестный параметр принимаем расчетное сопротивление стали, за второй – площадь поперечного сечения:
Учитывая (10), мы получаем задачу с двумя независимыми параметрами.
4 шаг – составить уравнение целевой функции.
Сначала представим описание некоторой основной величины F в ее зависимости от управляемых и неуправляемых параметров:
где управляемые параметры (независимые параметры) х1→расчетное сопротивление стали; х2→площадь поперечного сечения растянутого элемента; неуправляемые параметры (параметры, значения которых не подлежат изменению в рамках задачи)
с1→ коэффициент условия работы γc =1,0
с2→ длина элемента ℓ=3 м,
с3→ удельный вес стали ρ =7850 кГ/м 3 ,
с4→предельная гибкость [λ] =400
Для данной задачи, учитывая выражения (27) и (28), можно легко записать уравнение целевой функции
F=М = А*ℓ*ρ →min (36)
5 шаг – составить неравенства – ограничения.
Условие прочности (37)
Условие жесткости λ= ℓ / imin ≤ [λ] = 400 (38)
Расчетное сопротивление 240 МПа ≤Ry ≤360 МПа (39)
6 шаг – составить уравнения состояния.
Уравнения состояния составлять не нужно, так как задача статически определима.
Второй этап решения задачи. Для решения математической задачи оптимизации необходимо выполнить
7 шаг -провести анализ целевой функции и неравенств-ограничений
Целевая функция (36) представляет собой уравнение с одним неизвестным (А). Условие прочности (37) представлено неравенством с двумя неизвестными (А, Ry). Условие жесткости (38) представлено неравенством с одним неизвестным (imin).
Проведем некоторые упрощения в уравнении функции цели (36) с учетом ограничения (37)
F=М = *ℓ*ρ = *3*7,85 = 447,45* →min (40)
Неизвестный параметр в уравнении функции цели находится в знаменателе, поэтому задача относится к нелинейному программированию.
8 шаг –выбор метода решения задачи линейного программирования. Так как в 7 шаге мы выявили зависимость переменных А Ry , то получили уравнение функции цели с одним неизвестным. Поэтому решение задачи сводится к решению линейного уравнения (40) с одним неизвестным, но в нелинейной постановке.
Представим ограничения (37) и (39) графически (рис. 6). При этом с учетом ограничений (39) определим минимальные значения площади сечения растянутого элемента
Аmin =190/36=5,3 см 2 (41)
Таким образом, мы получили область допустимых решений, ограниченную прямыми
Аmin = 190/36=5,3 см 2 ; Ry ≤ 360 МПа; Ry ≥ 240 МПа
и кривой (на рис. 6 область допустимых решений закрашена).
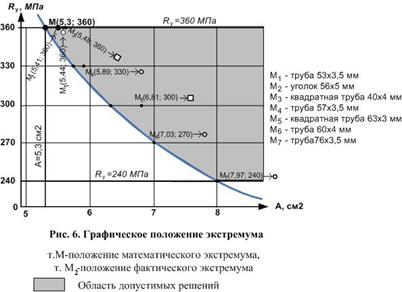
По сортаменту подбираем профиль, площадь которого (А) и минимальный радиус инерции удовлетворяют условиям (37), (38). При этом для каждого профиля необходимо определить то сечение, которое удовлетворяет требованию минимальной массы элемента, т.е. удовлетворяет уравнению целевой функции (36). Для этого необходимо создать базу данных (сортамент) и провести расчет, например, в программе Exel.
На рис. 6 представлены значения стержней с минимальной массы из различных профилей. Оптимальным решением (с учетом существующего сортамента) является стержень из равностороннего уголка 56х5 мм с площадью сечения А = 5, 41 см 2 , выполненным из стали с расчетным сопротивлением Ry = 360 МПа (т. М2 на рис. 6).
Таким образом, задачи оптимального проектирования строительных конструкций это задачи, цель которых состоит в достижении наилучшего проектного решения при учете противоречивых требований проектирования: эффективности, надежности, долговечности, технологичности, эстетичности, экономичности. Поэтому они представляют собой сложные комплексные задачи, решаемые большой группой специалистов, в которую должны войти архитекторы, инженеры, технологи, экономисты, математики и др.
Все задачи оптимального проектирования строительных конструкций можно разделить на два этапа. 1 этап – формирование математического описания задачи (статический или динамический расчет конструкций, составление уравнения целевой функции, ограничений – неравенств, уравнений состояния). 2 этап – решение математической задачи оптимизации методами линейного или нелинейного программирования (рис. 7).
Тема 3. МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ ЗАДАЧ ОПТИМАЛЬНОГО
ПРОЕКТИРОВАНИЯ
В этой главе рассматриваются методы решения задач оптимизации, как задач линейного программирования. При этом будем считать, что математическое описание задачи выполнено, то есть, решена первая часть задачи оптимального проектирования строительных конструкций.
К задачам линейного программирования относятся задачи, в которых все переменные имеют степень, равную единице, разделены и все коэффициенты при этих переменных постоянны. Математически задача линейного программирования имеет такой вид:
минимизировать значение функции
В выражении (42) всего m ограничений, часть из которых являются ограничениями – равенствами, остальные могут быть неравенствами со знаком ≥ или ≤.
При m ≥ n возможны три варианта решений: система имеет только одно решение; система имеет множество решений; система не имеет решения. При m ≤ n система имеет или множество решений, или несовместима.
Для решения задач линейного программирования используются графический метод, симплекс-метод, метод наискорейшего спуска, целочисленное программирование и др. Рассмотрим некоторые методы, наиболее предпочтительные для решения задач оптимизации строительных конструкций.
Графический метод
Графические методы решения линейных задач оптимального проектирования применяются в самых простейших случаях – при двух независимых переменных.
Тогда математическая задача имеет следующий вид:
минимизировать значение функции
3.2. Симплекс – метод
Впервые работа по линейному программированию была опубликована Канторовичем в 1939 году. В 1947 году Данциг разработал симплекс-метод, который привлек исследователей к задачам линейного программирования. Особенность этого метода состоит в возможности использования аналитического решения.
Порядок решения задач линейного программирования симплекс – методом
Обычно в реальных задачах ограничения представлены в виде неравенств
Поэтому для возможности использования симплекс – метода необходимо ограничения — неравенства (63) превратить в равенства, представить их в каноническом виде (43). Для этого вводятся дополнительные переменные параметры у1 , у2 ,…,уm , количество которых определяется количеством ограничений
При этом дополнительные переменные параметры у1 , у2 ,…,уmв уравнение функции цели не вводятся.
Итак, с учетом вышесказанного, функция цели имеет линейный вид с разделенными переменными (65), а ограничения представлена системой канонических переменных (64), в которых неизвестные параметры положительны
х1 ≥ 0, х2 ≥ 0, … , хn ≥ 0, у1 ≥ 0, у2 ≥ 0,…,уm ≥ 0 (66)
Методы исследования в анатомии и физиологии: Гиппократ около 460- около 370гг. до н.э. ученый изучал.
Основные идеи славянофильства: Славянофилы в своей трактовке русской истории исходили из православия как начала.
Источник: poisk-ru.ru
Примеры задач в строительстве
Важной задачей при решении транспортной и складской задач является систематизация знаний о процессах и явлениях, возникающих при хранении, распределении и передаче материалов и средств производства, о закономерностях функционирования комплектов и комплексов машин при различных формах организации механизированного процесса и включает совокупность методов, позволяющих реализовать с наибольшим эффектом потенциальные возможности машин, комплектов и комплексов машин для распределения материалов и их подготовки. Однако возникают затруднения при слиянии транспортной и складской задач и одновременном использовании существующих методик для различных технологических операций, решение этой проблемы возможно за счет создания методики решения транспортно-складских задач в неразрывной взаимосвязи друг с другом.

4. Ельдештейн Ю.М., Смирнова Л.П. Задачи моделирования и оптимизации производственных процессов. – Красноярск, ФГОУ ВПО КрасГАУ, 2003. – 126 с.
Транспортная задача, как и задача линейного программирования была впервые поставлена советским экономистом А.Н. Толстым в 1930 году. Разработка общих методов решения задачи линейного программирования и их математическое исследование связано с именем советского ученого Л.В. Канторовича.
В 1939 году методам решения задачи линейного программирования посвящено также большое число работ зарубежных ученых. Основной метод решения задачи линейного программирования – симплекс метод – был опубликован в 1949 году Дандигом. Симплекс метод дает решение любой задачи линейного программирования, но если переменных очень много, то решение весьма затруднительно и для более сложных задач симплекс метод стали модифицировать [1].
Цель исследования. Целью работы является установление методики решения транспортно-складской задачи для механизации строительного производства и организации технологических процессов протяженного объекта.
Идея работы заключается в создании комплекса, позволяющего произвести расчет эффективной организации строительного производства по различным критериям (себестоимость работ, производительность и т.д.) на базе существующих методик решения транспортной и складской задач.
Материалы и методы исследования
Транспортная задача делится на два вида: транспортная задача по критерию стоимости – определение плана перевозок, при котором стоимость груза была бы минимальна; транспортная задача по критерию времени – более важным является выигрыш по времени [2].
Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления – объем потребления. Известна стоимость перевозки из каждого пункта производства в каждый пункт потребления единицы продукта. Требуется составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной.
Пусть имеется n поставщиков – строительные материалы разной продукции (присвоим им имена – ai) и m потребители – строительные бригады этой продукции (bj). Каждый поставщик может поставлять свою продукцию любому из потребителей. Известны затраты Cij на перевозку единицы продукции от каждого поставщика к каждому потребителю.
Необходимо так распределить перевозки, чтобы суммарные затраты были минимальными. Элементы решения – Хij количество продукции, перевозимой от каждого поставщика к каждому потребителю [3]. Требуется составить план перевозок груза, в котором все пункты потребления были бы обеспечены необходимыми строительными материалами, ни из какого пункта производства не вывозилось бы грузов больше, чем там производится, а стоимость перевозки была бы минимальной.
Структурная схема транспортной задачи при строительстве автомобильных дорог приведена в графической постановке на рис. 1.
При этом будем иметь в виду, что строительные бригады – потребителм материалов, не закреплены в пространстве, а постоянно перемещаются вдоль объекта строительства.
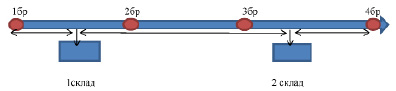
Рис. 1. Пример структурной схемы транспортной задачи
Обозначим через Ai возможности поставщиков, основных складов и через Bj строительные бригады потребности которых является строительные материалы.
Составим математическую модель задачи.
Ограничения по производственным мощностям поставщиков:
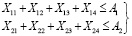
(1.1)
Ограничения по производственным мощностям потребителей, строительных бригад:
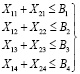
(1.2)
Целевая функция – требование минимизации суммарных затрат на перевозки:
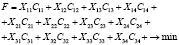
. (1.3)
В краткой форме записи эта модель для связи потребителей и поставщиков имеет вид:
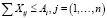
(1.4)
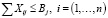
; (1.5)
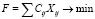
. (1.6)
Закрытой моделью транспортной задачи называется такая задача, в которой суммарные потребности потребителей равны суммарным возможностям поставщиков, то есть
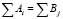
. (1.7)
Построим исходный опорный план. Опорный план является основой для оптимизации процесса. Существует несколько способов его построения. Здесь описано два из них. Один из них – метод северо-западного угла – наиболее простой, но и наименее эффективен, второй – метод наименьшего элемента несколько сложнее, но значительно ближе к оптимальному [4].
Метод северо-западного угла. Существует несколько методов составления исходного опорного плана. Самый простой из них – метод «северо-западного угла». Исходные данные примера (затраты на перевозку единицы продукции от каждого поставщика к каждому потребителю) приведены в верхних правых углах табл. 1.
Опорный план решения транспортной задачи, составленный методом «северо-западного угла»
Источник: applied-research.ru
Примеры, задачи и загадки по ТРИЗ с ответами

Говоря о разработанном Г. С. Альтшуллером алгоритме, мы отмечаем не только стройность научной теории, но и её способность без перебора многочисленных вариантов приводить к сильному решению. В этом несомненное преимущество ТРИЗ, ведь она располагает большим количеством практических инструментов для решения творческих задач и производственных кейсов любой сложности.
Чтобы наглядно это продемонстрировать, мы собрали задачи и упражнения и объяснили их решение, применяя методику ТРИЗ. Несмотря на то, что теория предназначена для работы с техническими задачами, примеры подобраны так, что даже человек без специального образования сможет по достоинству оценить её эффективность.
На этой странице приведены некоторые задачи и упражнения, которые Г. Альтов (псевдоним, под которым Г. С. Альтшуллер писал научную фантастику) публиковал в газете «Пионерская правда» для юных изобретателей. И, как часто бывает в таких случаях, не каждый взрослый мог справиться с этими задачами, в чём вы сможете убедиться самостоятельно. Подобраны и кейсы – описания реальных ситуаций, когда возникшие противоречия были решены при помощи ТРИЗ. Они более сложные для решения, но позволяют завершить представление о теории, как практическом инструменте.
Содержание:
Марсоход
Условие. Во время научной экспедиции на Марс, космический корабль произвёл посадку в долине. Астронавты снарядили марсоход для лучшего изучения планеты, но как только покинули корабль, столкнулись с проблемой. Дело в том, что по поверхности было сложно передвигаться – этому мешали многочисленные холмы, ямы, большие камни.
На первом же склоне колёсный вездеход с надувными шинами перевернулся на бок. С этой проблемой астронавты справились – они прицепили снизу груз, что усилило устойчивость машины, но стало причиной новой проблемы – груз задевал неровности, что усложняло движение. Итак, что нужно сделать, чтобы повысить проходимость марсохода? При этом у космонавтов нет возможности изменять его конструкцию.
Решение. Техническое противоречие сформулировано в условии задачи. Идеальный конечный результат – достичь абсолютной проходимости. При этом космонавты действуют в условиях Марса, у них нет возможности изменять конструкцию марсохода. Исходя из этого, ресурсом выступает груз.
Не стоит также забывать и о законах развития технических систем, и следить за тем, чтобы изменение одной части не влияло на функционирование других элементов. Памятуя об этом, становится очевидным, что поднять груз в кабину или на крышу невозможно, так как произойдёт смещение центра тяжести и проблему решить не удастся. Спустить воздух из шин также нельзя – устойчивость немного повысится, но пострадает проходимость, усилится тряска.
Чтобы понять, как поступить с грузом, и получить сильное решение, нужно вспомнить, как мы обычно поступаем в условиях нехватки места? Стараемся разместить всё максимально компактно: объединить, сложить одно в другое. В ТРИЗ такой приём получил название «матрёшка». С её помощью задача про марсоход легко решаема: груз (металлические шарики, тяжёлая жидкость) нужно поместить внутрь шин. Этот способ имеет применение на практике, его предложил использовать японский изобретатель П. Шохо, для повышения устойчивости и проходимости кранов и погрузчиков.
Вода в трубе
Условие. Достаточно простая и известная задача. Есть металлическая труба, проложенная под землёй, по которой течёт вода. Для устранения неполадок в работе системы, часть трубы раскопали и столкнулись с необходимостью определить, в какую сторону движется вода. Попытки выяснить это путём простукивания, на слух, завершились неудачей.
Вопрос: как понять в какую сторону течёт вода в трубе? Нарушать герметичность трубы (сверлить, резать) нельзя.
Решение. Эта задача решается очень просто. ТРИЗ предусматривает не только строгий алгоритм решения, но и чёткую проработку условий задания. Г. С. Альтшуллер всегда советовал перед началом работы попробовать сформулировать условия задачи другими словами. В нашем случае есть труба и вода, которая по ней движется.
Воздействовать на трубу нельзя, значит нужно воздействовать на воду. Отсюда самое простое решение – нагреть трубу в одном месте, и по тому в какую сторону будет течь подогретая жидкость, нагревая и трубу, определить направление.
Безопасный бассейн
Условие. Это скорее не задача, а упражнение на способность находить эффективные творческие решения. Цель – предложить максимально безопасный бассейн для людей, которые не умеют плавать.
Решение. Используя метод системного анализа, можно найти ряд приемлемых решений, поскольку условия задачи не ограничивают нас в выборе средств. Так, можно построить бассейн уникальной конструкции (с небольшой глубиной, верёвочными ограждениями для каждой дорожки, выталкивающими фонтанами).
Также можно снабжать пловцов вспомогательными плавсредствами, к примеру, спасательными жилетами. С точки зрения идеальности наиболее удачным вариантом можно считать предложение наполнить бассейн раствором концентрированной поваренной соли. В нём тело будет выталкиваться на поверхность без дополнительных усилий. Кстати, на эту тему существует загадка: «В каком море невозможно утонуть?». Поскольку физическую составляющую необходимого условия вы уже знаете, в качестве дополнения к упражнению подумайте над географической.
Лекарства для космонавтов
Условие. Не многим известно, что «морской болезнью» страдают не только моряки и путешествующие по морю, но и космонавты. Лекарства от данного недуга существуют, но есть оговорки по его применению в условиях космоса. Так, малые дозы нужно принимать часто, что неудобно, а большие – вредно. Как решить эту проблему?
Решение. Противоречие заключается в необходимости подачи в организм нужного количества лекарства без постоянного отвлечения на этот процесс космонавта. Для его решения был применён метод маленьких человечков. Лекарство представили как толпу людей, желающих попасть в нужное место.
Очевидно, что для совершенствования этого процесса нужна определённая организация – очередь, постепенное продвижение. Эту идею реализовали в препарате, придя к выводу, что он должен усваиваться по частям, а не сразу. По этому принципу и были изобретены таблетки со скополамином, помогающие космонавтам справиться с «морской болезнью». Они имеют форму плоского диска, который, как пластырь, крепится за ухом. При этом активное вещество вследствие диффузии нормировано попадает в организм.
Одуванчики
Условие. Одуванчики имеют набор хромосом очень качественно близкий к человеческому. Как это можно использовать при контроле работы атомной электростанции?
Решение. Здесь, как видим, не совсем традиционная задача. Тем не менее, решается она достаточно просто, всё что нужно – применить один из законов развития ТС – закон согласования ритмики частей системы. И одуванчик, и человек – системы, а тот факт, что их хромосомы похожи, даёт возможность судить о достоверности результатов экспериментов на растениях и в случае с людьми. Но ритмика у одуванчика чаще (смена поколений раз в год), что за достаточно короткий период времени позволяет проследить генетические изменения экземпляров, растущих рядом с АЭС, и сделать соответствующие выводы и о влиянии на человека.
Корм для рыбок
Условие. У вас есть аквариум с рыбками, которые питаются циклопами. Вам нужно уехать на несколько дней и решить проблему с кормлением. Попросить помочь вы никого не можете. Запустить много циклопов за один раз нельзя – рыбки их съедят, и всё равно будут голодать.
Как поступить в этом случае?
Решение. Бытовая ситуация, с которой (с возможными вариациями – кошки, попугаи и т.д. вместо рыбок) сталкивался каждый. По аналогии с предыдущей задачей становится очевидным, что приток корма в аквариум должен быть постоянным. Другими словами, в данном случае ИКР – независимое статическое поступление корма. Как это сделать?
Знакомые с физикой, и в частности, с термодинамикой, должны найти решение достаточно быстро, используя описание мыслительного эксперимента Дж. Максвелла, известного как «Демон Максвелла». В переносе на наш случай решением может служить перегородка аквариума стенкой из органического стекла с небольшими отверстиями – достаточными для движения циклопов сквозь них и, в то же время, ограничивающие движения рыбок на «сторону циклопов».
Лёд на проводах
Условие. Напоследок сложная задача, с которой справляются очень немногие. В наших климатических условиях зимой существует опасность нарастания льда на проводах линии электропередач. Со временем образовавшаяся глыба может оборвать своей тяжестью провода, да ещё и повредить то, что находится на земле под ними. Какими методами бороться с обледенением?
Решение. Как и было анонсировано, решение данного кейса потребовало от изобретателей значительных усилий. Сначала высказывались предложения очищать провода внешними способами, например, с помощью человека. Но такие методы были откинуты в силу своей нецелесообразности. Появилась идея нагревать провода, пуская по них ток под сильным напряжением.
Но это рождало новое противоречие, ведь в такое время пользователи не смогли бы пользоваться энергией. В данном случае сам ресурс (ток) был выбран правильно и учёные начали развивать идею нагрева проводов его посредством. Вскоре решение нашли – по всей линии на расстоянии в 5-6 м на провода надели специальные кольца из материала, обладающего магнитными свойствами – феррита. Под воздействием переменного тока магнит нагревался, что исключало обледенение.
Но и это решение не оказалось оптимальным. Дело в том, что провода продолжали греться и в тёплую пору, что было ненужным. Изобретение было усовершенствовано – кольца начали делать из магнита с точкой Кюри (П. Кюри первым заметил, что разные магниты сохраняют свои свойства до разных температур) равной нулю градусов. Такие магниты не грелись, когда температура воздуха поднималась выше 0°.
Больше интересных задач и кейсов по ТРИЗ ищите на официальном сайте фонда Г. С. Альтшуллера, на сайте «Креативный мир», в книге Н. и А. Нарбут «Учебник и сборник задач по ТРИЗ». Желаем вам успехов в практике решения изобретательских задач!
А также предлагаем сыграть в нашу игру на развитие нестандартного подхода в решении задач.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Далее вы найдете ссылки на полезные статьи и другие материалы, так или иначе относящиеся к теме.
Источник: 4brain.ru