Проецированием называется процесс получения изображения предмета на плоскости.
Получившееся при этом изображение называют проекцией. Проекция – в переводе с латинского – «бросать (отбрасывать) вперёд».
В черчении изображения получают по так называемому методу проекций.
Чтобы построить изображение предмета по методу проекций, нужно через точки на предмете провести воображаемые лучи до встречи их с плоскостью. Эти лучи называются проецирующими. Плоскость, на которой получается изображение предмета, называется плоскостью проекций.
Если проецирующие лучи расходятся из одной точки, проецирование называется центральным (рис. 60а). Точка, из которой выходят лучи, называется центром проецирования.
Полученное при этом изображение называется центральной проекцией. Пример: тени, отброшенные от предмета лучами электрической лампочки.
Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным (рис. 60б), а полученное изображение – параллельной проекцией. Пример: солнечные тени.
Построение проекции вектора на ось

Рис. 60
При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же углом. Если это любой острый угол, то проецирование называется косоугольным (рис. 61а). В косоугольной проекции, как и в центральной, форма и величина предмета искажаются.
Когда проецирующие лучи перпендикулярны к плоскости проекций, проецирование называют прямоугольным (рис. 61б), а полученное изображение – прямоугольной проекцией.

Рис. 61
Способ прямоугольного проецирования является основным в черчении.
Проецирование на одну, две и три взаимно перпендикулярные плоскости проекций
Расположим предмет перед плоскостью проекций так, чтобы на получившемся изображении были видны три его стороны (рис. 62).

Рис. 62
По такому изображению легко представить пространственный образ предмета.
Такое проецирование в черчении используют для построения наглядных изображений, однако, на наглядных изображениях предметы получают большие искажения и по ним трудно определить истинные размеры предмета.
Теперь расположим предмет перед плоскостью проекций так, чтобы на изображении была видна только одна его сторона, и построим его прямоугольную проекцию (рис. 63а).
На данном изображении проекции рёбер предмета, которые параллельны двум его измерениям (например: длина и ширина), равны натуральным размерам. Но на таком изображении нет третьего измерения предмета (высоты), поэтому оно не наглядно. Такие изображения используют в случаях, когда высота (толщина) детали одинакова во всех её точках (например, чертежи прокладок).
Тогда на чертеже такой детали делают запись, указывающую её толщину (высоту). Пример приведен на рис. 63б (S4).
Иногда на одной плоскости изображают предметы, не имеющие одинаковой высоты во всех его точках. Тогда рядом с изображением точки числом указывают её высоту. Такие изображения называют проекциями с числовыми отметками (рис. 63в).

Рис. 63
Чтобы судить о трёх измерениях предмета, его необходимо спроецировать ещё на одну плоскость проекций (П2), которая параллельна другой паре измерений предмета. Тогда вторая плоскость будет расположена перпендикулярно первой плоскости проекций (рис. 64).

Рис. 64
Теперь по двум прямоугольным проекциям можно судить о размерах и форме предмета. Хотя форма не всегда ясно выражается двумя проекциями. Поэтому при изображении предметов сложной формы необходимо строить три (а иногда и более) прямоугольных проекции.
Возьмём три взаимно перпендикулярные плоскости проекций (рис. 65).
Одна из них занимает горизонтальное положение, её называют горизонтальной плоскостью проекций и обозначают П1. Две другие плоскости — вертикальные. Одну называют фронтальной плоскостью проекций (от французского слова «фронталь» – «лицом к зрителю»), другую – профильной плоскостью проекций (от французского слова «профиль» – «вид сбоку») и обозначают соответственно П2 и П3.
Линии пересечения плоскостей проекций называют осями проекций и обозначают буквами x, y, z. Точку пересечения осей проекций обозначают буквой О.

Рис. 65
В трёхгранный угол, образованный плоскостями проекций, поместим параллелепипед и, проведя проецирующие лучи перпендикулярно плоскостям проекций, получим его проекции. Изображение на плоскости П1 – горизонтальная проекция, на плоскости П2 и П3 – соответственно фронтальная и профильная проекции.
Для получения плоского чертежа трёхгранный угол «разрезают» по оси у, а плоскости П1 и П 3 поворачивают соответственно вокруг осей х и z по направлению, указанному на рис. 65а стрелками, до совмещения с плоскостью П 2 .
Совмещённые плоскости с построенными на них изображениями предмета показаны на рис. 65б. Линии, соединяющие между собой проекции, называют линиями связи. Линии связи всегда перпендикулярны осям проекций.
На чертежах плоскости проекций не ограничивают и не обозначают. Кроме того, на чертеже при изображении предмета можно не наносить и оси проекций, так как при параллельном проецировании расстояние от плоскости проекций до изображаемого предмета не влияет на очертание его проекций (рис. 66а).

Рис. 66
Это даёт возможность устанавливать произвольное расстояние между проекциями, сохраняя между ними проекционную связь даже при отсутствии линий связи (рис. 66б). Такой чертёж называется безосным. При построении проекций здесь пользуются осями симметрии предмета, центровыми линиями или характерными его плоскостями (рис. 67).

Рис. 67
Метод прямоугольного проецирования на две и три взаимно перпендикулярные плоскости был разработан французским учёным-геометром Гаспаром Монжем в конце XVIII века. Поэтому его называют ещё методом Монжа.
Г. Монж положил начало развитию новой науки об изображении предметов – начертательной геометрии.
Способы построения третьей проекции
Проекционную связь между горизонтальной и профильной проекциями можно установить несколькими графическими приёмами:
- дугой окружности (рис. 68а);
- с помощью прямой под углом 45° (рис. 68б);
- с помощью постоянной прямой чертежа (рис. 68в).
На рис. 68а,б,в эти приёмы показаны на примере построения третьей проекции точки.

Рис. 68
Удобнее всего пользоваться третьим способом, т.к. при наименьшем количестве графических операций достигается большая точность построения.
Если три вида уже построены, то место постоянной прямой чертежа произвольно выбирать нельзя. Нужно найти точку, через которую она пройдет. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии предмета. Через полученную точку К под углом 45° проводят отрезок прямой.
Если осей симметрии на чертеже нет, то продолжают до пересечения в точке К1 горизонтальную и профильную проекции любой грани, проецирующейся в виде отрезков прямой (рис. 69).

Рис. 69
Источник: hspline.com
Проекции на чертеже
Проекция – это способ изображения объемной фигуры на проекционной полости.
Виды проекций на чертеже по ГОСТу
Согласно ГОСТ 2.305-2008 и правилам аксонометрии предусматривается использование нескольких видов проекций на чертеже:
- ортогональная проекция или прямоугольная проекция, предполагает перенос изображения на плоскость, перпендикулярную направлению лучей предмета или его части;
- параллельная проекция получается путем проецирования предмета или его части параллельным пучком лучей на плоскость.
Как расположены проекции на чертеже
При выполнении чертежей используется метод прямоугольного проецирования и предполагается, что некий предмет, элемент или деталь располагаются между наблюдателем и плоскостью проекции. В качестве плоскостей проекции используются шесть граней куба. Фронтальная проекция считается главным видом, поэтому расположение предмета должно быть таким, чтобы на этой проекция было отражено полное представление о форме и размерах.
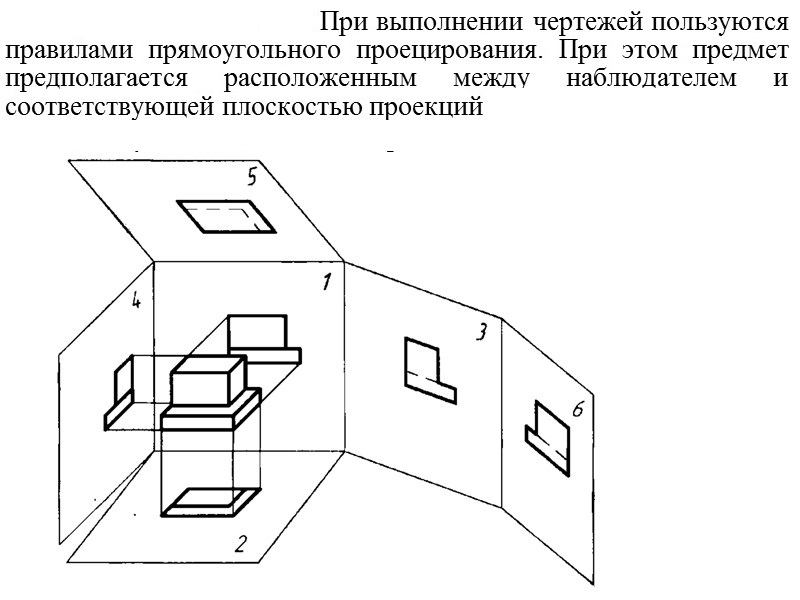
Рисунок 1. Шесть плоскостей проекций
Аксонометрические проекции на чертеже
Работа по выполнению аксонометрических проекций начинается с построения осей. Оси необходимо построить в трех направлениях: горизонтальная ось Х, вертикальная ось Y и ось, идущая под углом – Z.В изометрической проекции вертикальная и горизонтальная ось располагаются под углом в тридцать градусов к горизонтальной линии.
В аксонометрической проекции масштабы по всем осям равны.
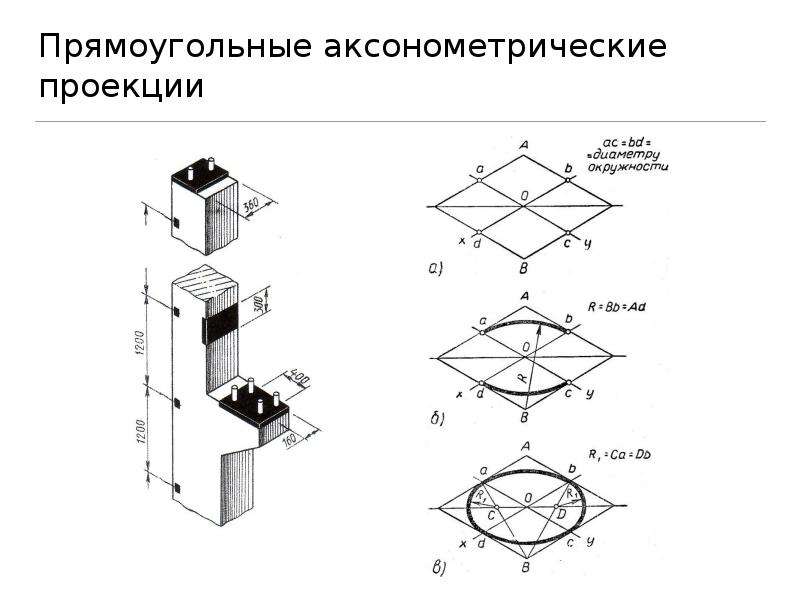
Рисунок 2. Аксонометрическая проекция
Аксонометрическая проекция по чертежу в Компас
При выполнении аксонометрической проекции в программе Компас работа сводятся к построению проекций точек и их соединению в определённой последовательности.
Рассмотрим порядок действий на примере прямоугольника. Вначале в меню «Создать» выбираем «Деталь», в «Дерево модели» раскрываем меню «Начало координат» и выбираем плоскость ХY, затем переходим в двухмерное построение, нажимаем инструмент «Прямоугольник» вводим соответствующие размеры. Закрыв двухмерный эскиз переходим, в трехмерный режим создания детали. С помощью инструмента «Выдавливание» создаем объект.
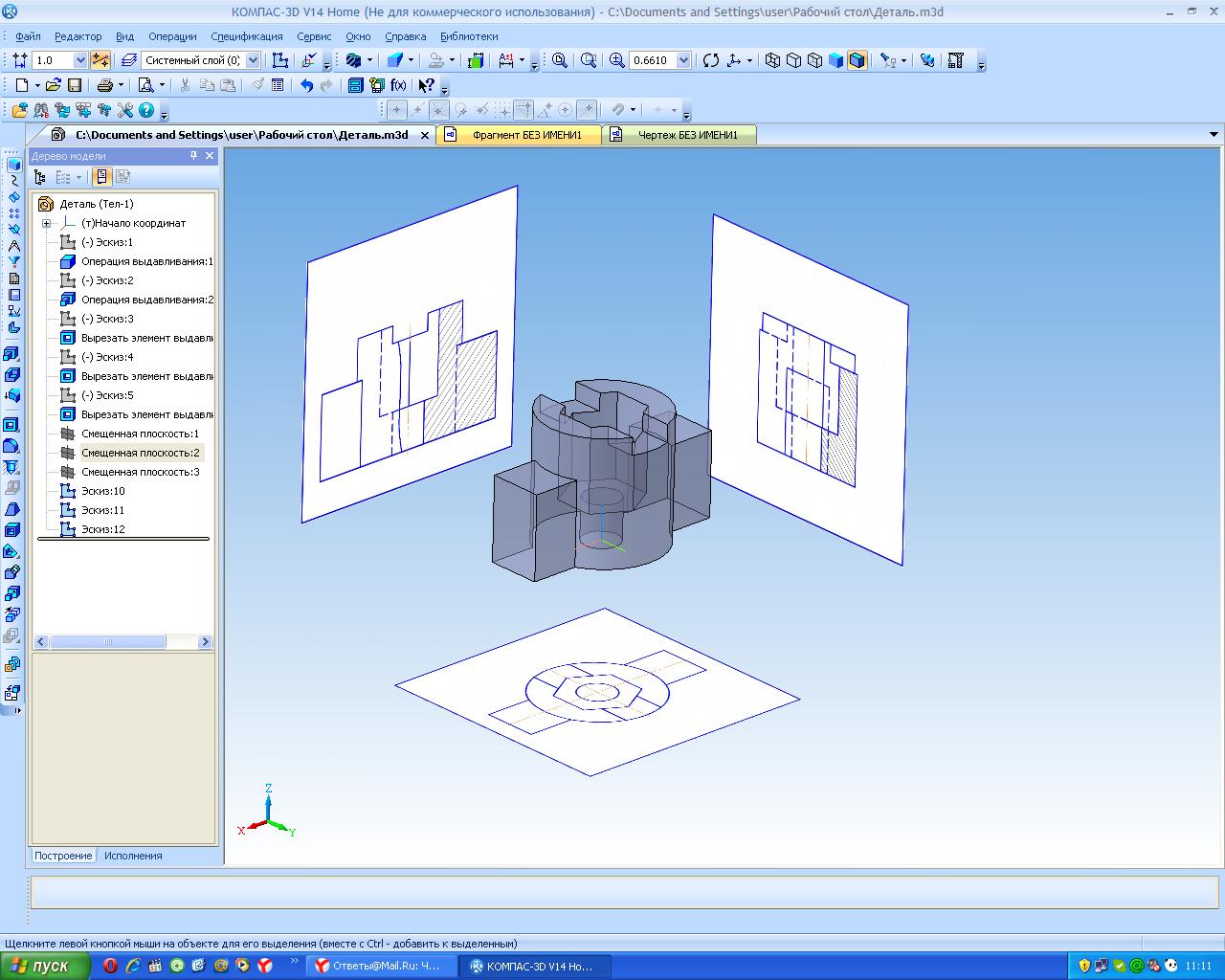
Рисунок 3. Аксонометрическая проекция в Компас
Горизонтальные проекции на чертеже
Построение горизонтальных и вертикальных проекций выполняется достаточно легко, для этого необходимо перенести изображение предмета с помощью проекционных лучей. Профильная плоскость называется так, поскольку дает полное представление о детали. Профильная плоскость располагается вертикально, справа от детали. Комплексный чертеж содержит все три проекции.
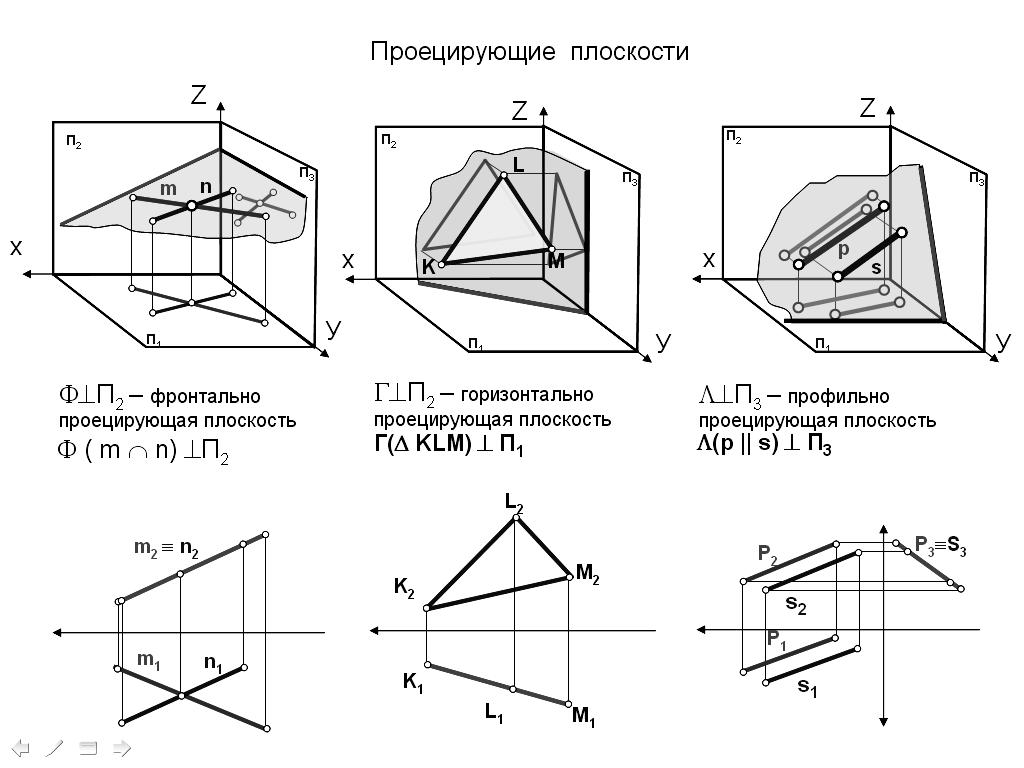
Рисунок 4. Горизонтальная, вертикальная и профильная проекции
Изометрические проекции на чертеже
Изометрическая проекция является разновидностью аксонометрической, которая позволяет отобразить трехмерный объект с одинаковым коэффициентом искажения по всем осям. Изометрическая проекция может быть прямоугольной, косоугольной фронтальной и косоугольной горизонтальной.
Дальнейший порядок построения предполагает построение передней грани детали, откладывая фактические размеры высоты вдоль оси Z, а длины вдоль горизонтальной оси X. Затем строят ребра, они идут параллельно оси Y, их длина соответствует толщине детали. В изометрическом изображении откладывается действительная длина, в диметрической проекции построены меньше в два раза. Затем полученные точки соединяют прямыми, параллельными передней фронтальной плоскости и удаляют невидимый контур.
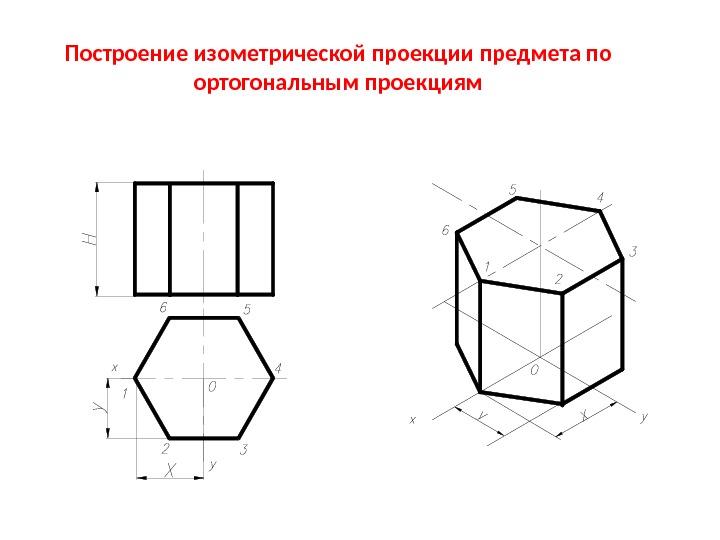
Рисунок 5. Изометрические проекции
Проекции пересекающихся прямых на комплексном чертеже
Существует несколько способов задания плоскости, в том числе с помощью пересекающихся линий. На комплексном чертеже проекции плоскости задаются проекциями элементов. Проекции точки пересечения прямых всегда находятся на одной линии связи.
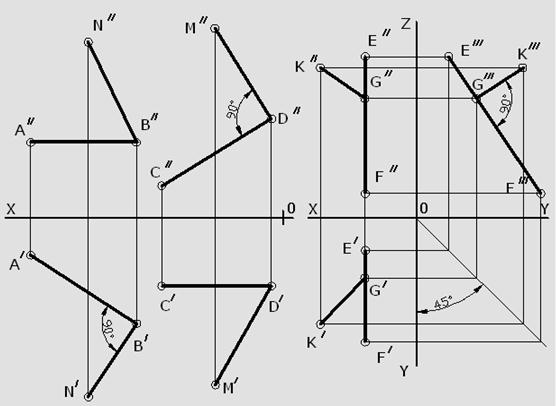
Рисунок 6. Пересекающиеся прямые на плоскости проекции
Чертеж в трех проекциях
Для выполнения чертежа используется метод ортогонального проецирования, который позволяет начертить любое техническое изделие. В ортогональном проецировании лучи параллельны друг другу и перпендикулярны плоскости, но на каждой проекции видны лишь два измерения (высота и длина). Поэтому лишь три проекции дают полное представление о трехмерном предмете. В совмещенных на одном листе чертежах можно найти точные сведения о всех геометрических характеристиках детали.
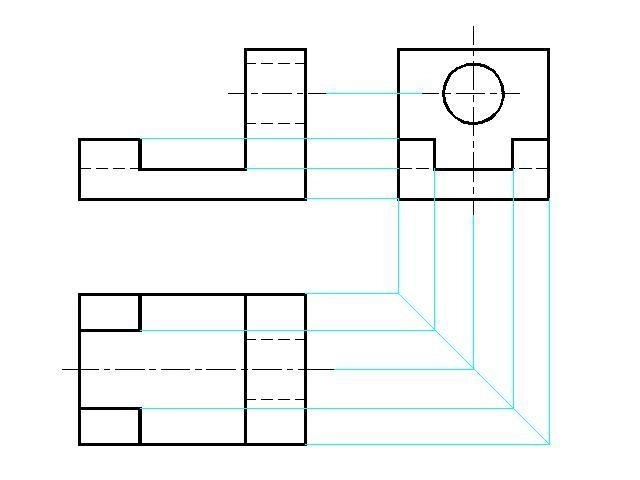
Рисунок 7. Чертеж в трех проекциях
Чертежи в системе прямоугольных проекций
Согласно названию используют ортогональное проецирование на одну, две или три плоскости. Если плоскость расположена перед наблюдающим, то она называется фронтальной, проекция на нее строится первой. Предмет располагается так, чтобы его поверхности были параллельными плоскости проекции. Выполнив построение в двух плоскостях проекции, можно получить основные данные о высоте, ширине и длине детали и мысленно представить себе ее в объеме. Но этой информации недостаточно для выявление характерных особенностей, к примеру формы выемки в детали, поэтому требуется третья проекция.
Как сделать чертеж в трех проекциях в Компас
Чтобы выполнить чертеж и совместить на одном листе три проекции, вначале нужно воспользоваться командой «Новый чертеж». Затем выберите формат листа, чтобы разместить все 3 изображения, приведенные в модели (потребуется формат А3 или А4). Затем выбираем виды и то, как они будут расположены на чертеже, через команду «Вид» основного меню.
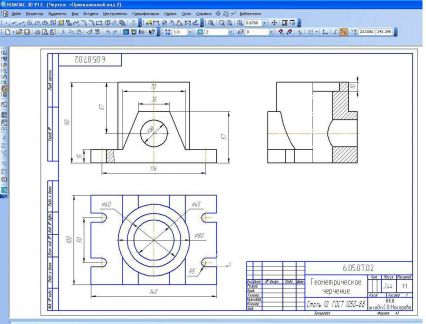
Рисунок 8. Чертеж в трех проекциях в Компасе
Ответы на вопросы
Как обозначаются изометрические проекции?
Чтобы показать изометрическую проекцию используют обозначение осей, также показывают углы между осями.
Как найти проекцию точек по заданному положению на поверхности предмета?
Построение начинается с построения проекции поверхности, на которой расположена отдельная заданная точка, а затем проводят линию связи к проекции, где поверхность изображена линией и находят вторую проекцию точки, третья проекция будет лежат на пересечении линий связи.
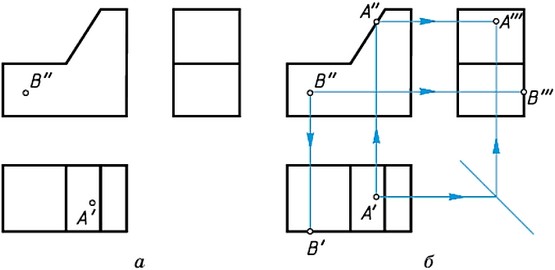
Рисунок 9. Построение проекций точек, заданных на поверхности предмета
Как расположить проекции на чертеже?
Виды располагаются в проекционной связи. Главный вид располагается в левом верхнем углу, вид сверху располагается под ним, справа от главного вида расположен вид слева (сбоку).
Источник: spravochnick.ru
Проекция в строительстве это
Плоскостью называется поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной направляющей прямой .
Проекции плоскости на комплексном чертеже будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей вне этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.

На комплексном чертеже (рис. 99) проекции плоскости также задаются проекциями этих элементов, например, на рис 99, а — проекциями трех точек А, , и С, не лежащих на одной прямой; на рис. 99, б — проекциями прямой ВС и точки А у не лежащей на этой прямой; на рис. 99, в — проекциями двух пересекающихся прямых; на рис. 99, г проекциями двух параллельных прямых линий АВ и CD.
На рис. 100 плоскость задана прямыми линиями, по которым эта плоскость пересекает плоскости проекций. Такие линии называются следами плоскости.
Линия пересечения данной плоскости Р с горизонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Рн.
Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Рv.
Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается Pw.

Следы плоскости пересекаются на осях проекций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Рx, Рy и Рz.
Расположение следов плоскости Р на комплексном чертеже по отношению к осям проекций определяет положение самой плоскости по отношению к плоскостям проекций. Например, если плоскость Р имеет фронтальный и профильный следы Pv и Pw, параллельные осям Ох и Оу то такая плоскость параллельна плоскости Н и называется горизонтальной (рис. 101, и).
Плоскость Р со следами Рн и Pw , параллельными осям проекций Ох и Oz (рис. 101, называется фронтальной, а плоскость Р со следами Pv и Pн параллельными осям проекций Оу и Oz, — профильной (рис. 101, в).

Горизонтальная, фронтальная и профильная плоскости, перпендикулярные к двум плоскостям проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например, треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проекций эта фигура проецируется без искажения, а на две другие плоскости проекций — в виде отрезков прямых.
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость, перпендикулярная к плоскости Н (рис. 102, а),называется горизонтально-проецирующей плоскостью. Фронтальный след Pv этой плоскости перпендикулярен оси Ох, а горизонтальный след Рн расположен под углом к оси Ох (комплексный чертеж на рис. 102, а)
Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, например треугольником АВС (рис. 102, 6), то горизонтальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профильная проекции — искаженный вид треугольника АВС.

Фронтально-проецирующей плоскостью называется плоскость, перпендикулярная к фронтальной плоскости проекций (рис. 102, в).
Горизонтальный след этой плоскости перпендикулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).
При задании фронтально-проецирующей плоскости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости представляет собой прямую линию (рис. 102, г), а на горизонтальную и профильную плоскости проекций параллелограмм проецируется с искажением.
Профильно-проецирующей плоскостью называется плоскость, перпендикулярная к плоскости W (рис. 102, д). Следы Pv и Рн этой плоскости параллельны оси Ох.
При задании профильно-проецирующей плоскости не следами, а, например, треугольником АВС (рис. 102, е) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоскостям проекций, как было сказано, называются плоскостями уровня.
Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего положения. Все три

следа Pv, Рн и Pw плоскости Р наклонены к осям проекций.
Если плоскость общего положения задана не следами, а, например, треугольником АВС (рис. 102, з), то этот треугольник проецируется на плоскости H, V и W в искаженном виде.
ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ
Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут быть взяты на следах плоскости — одна на горизонтальном, а другая на фронтальном. Так как следы прямой и плоскости находятся на плоскостях проекций и то следы прямой, принадлежащей плоскости, должны быть расположены на одноименных следах этой плоскости (рис. 103, а);например, горизонтальный след Н прямой — на горизонтальном следе плоскости, фронтальный след V прямой — на фронтальном следе Рv плоскости (рис. 103, б).

Для того чтобы на комплексном чертеже плоскости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v’ или считать их следами искомой прямой (точнее, v’ — фронтальной проекцией горизонтального следа прямой).
Опустив перпендикуляры из v’ и на ось проекций х, находим на ней вторые проекции следов прямой: v — горизонтальную проекцию фронтального следа прямой и h’ — фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т. е. v’c h и v c h прямыми, получим две проекции прямой линии, расположенной в плоскости общего положения Р.
Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются главными линиями плоскости или линиями уровня. Главные линии помогают решать многие задачи проекционного черчения.
Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например, горизонталь имеет только фронтальный след). Поэтому, зная один след главной линии, проекцию главной линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Таким образом, чтобы на комплексном чертеже плоскости Р провести в этой плоскости какую-либо горизонталь, нужно наметить на следе Рv плоскости точку v’ (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v’ параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.
Опустив перпендикуляр из точки v’ на ось x , получают точку v, которая будет горизонтальной проекцией фронтального следа горизонтали. Прямая, проведенная из точки v параллельно следу PH плоскости, представляет собой горизонтальную проекцию искомой горизонтали. Построение проекции фронтали показано на рис. 104, в и г.
11 с редко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмотрим, например, построение горизонтали на фронтально-проецирующей плоскости (рис. 105). На следе плоскости Рv намечаем фронтальную проекцию фронтального следа горизонтали и на оси находим его горизонтальную проекцию v (рис. 105, а).
Затем через точку проводим параллельно Рн горизонтальную проекцию горизонтали; фронтальная проекция горизонтали совпадает с точкой v’.

Если плоскость задана не следами, а пересекающимися или параллельными прямыми, то построение проекций горизонтали или фронтали, расположенных в этой плоскости, выполняется следующим образом.
Пусть плоскость задана двумя параллельными прямыми AВ и СD (рис. 105, 6). Для построения горизонтали, лежащей в этой плоскости, проводим параллельно оси х фронтальную проекцию горизонтали и отмечаем точки е’и f’ пересечения фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е’и f’ проводим вертикальные линии связи до пересечения с ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.
Если требуется найти следы плоскости, заданной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.
Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, a),который задает некоторую плоскость X. Отрезок DC расположен в плоскости H, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости (точнее — горизонтальной проекцией горизонтального следа плоскости).
Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью х в точке Рх, через которую должен пройти искомый фронтальный след плоскости.

Второй точкой v’, через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекцию фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восставленном из точки v к оси х, в точке v’ его пересечения с продолжением фронтальной проекции а’в’ прямой АB. Соединив точки Px с v’, находим фронтальный след Pv плоскости.
Пример решения подобной задачи приведен на рис 106, б.
Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проекций точки, расположенной на заданной плоскости, определить две другие проекции точки. Ход решения задачи следующий.
Через заданную проекцию точки, например фронтальную проекцию n’ точки N, расположенной на плоскости треугольника АВС (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например m’к’.

Горизонталью плоскости называется прямая, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций Н.
Строим другую проекцию mк вспомогательной прямой. Для этого проводим вертикальные линии связи через точки m’ и к’ до пересечения с линиями ас и вс. Из точки n’ проводим линию связи до пересечения с проекцией mк в искомой точке n.
Профильную проекцию n» находим по общим правилам проецирования.
В качестве вспомогательной прямой для упрощения построения чаще используются горизонталь или фронталь.
Чтобы найти какую-либо точку на плоскости Р, например точку А (рис. 108, а и б) надо найти ее проекции а’и а, которые располагаются на одноименных проекциях горизонтали, проходящей через эту точку. Через точку А проведена горизонталь Av’ .

Проводим проекции горизонтали: фронтальную — через v’ параллельно оси х, горизонтальную — через v параллельно следу Рн плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а’ искомой точки и, проводя вертикальную линию связи, определяем горизонтальную проекцию а точки А.
Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположена на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проекции горизонтального следа плоскости (рис. 108, в и г)
При заданной фронтальной проекции a’ точки А, лежащей на горизонтально-проецирующей плоскости , найти вторую проекцию этой точки (горизонтальную) можно без вспомогательной прямой, посредством проведения линии связи через а’ до пересечения со следом РН.
Если точка расположена на фронтально-проецирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а’ находится на фронтальном следе Хv плоскости Р.
ПРОЕКЦИИ ПЛОСКИХ ФИГУР
Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, прямоугольника, треугольника, круга.
Как известно, каждая плоская фигура ограничена отрезками прямых или кривых линий, которые могут быть построены по точкам.
Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные проекции вершин соединяют прямыми линиями и получают проекции фигур.
Проекции круга или другой криволинейной фигуры строят при помощи нескольких точек, которые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.
Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций и Наиболее просто построить проекции фигуры, расположенной параллельно плоскостям Н и V; сложнее — при расположении фигуры на проецирующей плоскости или на плоскости общего положения.
Рассмотрим несколько примеров.
Если треугольник АВС расположен на плоскости, параллельной плоскости H (рис. 109, a), то горизонтальная проекция этого треугольника будет его действительным видом, а фронтальная проекция — отрезком прямой, параллельным оси х. Комплексный чертеж треугольника АВС показан на рис. 109, 6. Такой треугольник можно видеть на изображении резьбового резца (рис. 109, в),передняя грань которого треугольная.

Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальная проекция трапеции представляет собой отрезок прямой линии, а горизонтальная — трапецию (рис. 110, б)
Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.
Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.
Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111), то фронтальная проекция круга совпадает с фронтальным следом Pv плоскости Р. Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру 37.

На рис. 111,6 показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Две плоскости могут быть взаимно параллельными или пересекающимися.
Из стереометрии известно, что если две параллельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого положения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.

Если даны две профильно-проецирующие плоскости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на комплексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо построить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и K будут параллельны только в том случае, если параллельны их профильные следы Pw и Kw.
Одноименные следы пересекающихся плоскостей Р и Q (рис. 112, в) пересекаются в точках V и H, которые принадлежат обеим плоскостям, т. е. линии их пересечения. Так как эти точки расположены на плоскостях проекций, то, следовательно, они являются также следами линии пересечения плоскостей.
Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами Pv, Рн и Qv,Qh, необходимо отметить точки пересечения одноименных следов плоскостей, т. е. точки v’ и h (рис. 112, г); точка v’ — фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h — горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v’ и h на ось х, находим точки v и h’. Соединив прямыми одноименные проекции следов, т. е. точки v’ и h’, v и h’ получим проекции линии пересечения плоскостей Р и Q.
ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ
Дана плоскость, заданная треугольником АВС, и прямая, заданная отрезком MN. На рис. 113, а треугольник АВС и отрезок MN заданы горизонтальными и фронтальными проекциями. Требуется определить, лежит ли прямая в плоскости данного треугольника.

Для этого фронтальную проекцию отрезка m’n’ продолжаем до пересечения с отрезками a’b’ и c’d’ (проекциями сторон треугольника АВС), получаем точки (рис. 113, б).
Из точек е’к’ проводим линии связи на горизонтальную проекцию до пересечения с отрезками ab и ca , получаем точки еk. Продолжим горизонтальную проекцию mn отрезка прямой MN до пересечения с проекциями сторон bа и са, если точки пересечения совпадут с ранее полученными точками e и k то прямая MN принадлежит плоскости треугольника.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
Если прямая АВ пересекается с плоскостью Р, то на комплексном чертеже точка их пересечения определяется следующим образом.
Через прямую А В проводят любую вспомогательную плоскость Q. Для упрощения построений плоскость Q обычно берется проецирующей (рис. 114, a). В данном случае проведена вспомогательная горизонтально-проецирующая плоскость Q. Через горизонтальную проекцию аb прямой АВ проводят горизонтальный след QH плоскости Q и продолжают его до пересечения с осью x в точке Qx . Из точки Qx к оси х восставляют перпендикуляр QxQy , который будет фронтальным следом Qv вспомогательной плоскости Q.

Вспомогательная плоскость Q пересекает данную плоскость Р по прямой VH, следы которой лежат на пересечении следов плоскостей Р и Q. Заметив точки пересечения следов Pv и Qv — точку v’ и следов Qн и PH — точку h,опускают из этих точек на ось х перпендикуляры, основания которых — точки v’ и h’ — будут вторыми проекциями следов прямой VH. Соединяя точки v’и h’, v и h, получают фронтальную и горизонтальную проекции линии пересечения плоскостей.
Точка пересечения М заданной прямой AB и найденной прямой VH и будет искомой точкой пересечения прямой АВ с плоскостью Р. Фронтальная проекция m’ этой точки расположена на пересечении проекций a’b’ и v’h’. Горизонтальную проекцию m точки М находят, проводя вертикальную линию связи из точки m’ до пересечения с ab.
Если плоскость задана не следами, а плоской фигурой, например, треугольником (рис. 114, 6), то точку пересечения прямой MN с плоскостью треугольника АВС находят следующим образом.
Через прямую МN проводят вспомогательную фронтально-проецирующую плоскость . Для этого через точки m’ и n’ проводят фронтальный след плоскости Ру продолжают его до оси x и из точки пересечения следа плоскости Ру с осью х опускают перпендикуляр Рн, который будет горизонтальным следом плоскости Р.
Затем находят линию ED пересечения плоскости Р с плоскостью данного треугольника ABC. Фронтальная проекция e’d’ линии ED совпадает с m’n’. Горизонтальную проекцию ed находят, проводя вертикальные линии связи из точек е’и d’ до встречи с проекциями ab и ас сторон треугольника АВС. Точки e и d соединяют прямой. На пересечении горизонтальной проекции ed линии ED с горизонтальной проекцией прямой MN находят горизонтальную проекцию k искомой точки К. Проведя из точки k вертикальную линяю связи, на ходят фронтальную проекцию k’ Точка К — искомая точка пересечения прямой МК с плоскостью треугольника АВС.

В частном случае прямая может быть перпендикулярна плоскости Р.Из условия перпендикулярности прямой к плоскости следует, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим на этой плоскости (в частности, этими прямыми могут быть следы плоскости). Тогда проекции прямой АВ будут перпендикулярны одноименным следам этой плоскости (рис 115, а) Фронтальная проекция а’b’ перпендикулярна фронтальному следу Ру, а горизонтальная проекция ab перпендикулярна горизонтальному следу Рн плоскости Р.
Если плоскость задана параллельными или пересекающимися прямыми, то проекции прямой, перпендикулярной этой плоскости, будут перпендикулярны горизонтальной проекции горизонтали и фронтальной проекции фронтали, лежащих на плоскости.
Таким образом, если, например, на плоскость, заданную треугольником АВС необходимо опустить перпендикуляр, то построение выполняется следующим образом (рис. 115, б).
На плоскости проводят горизонталь СЕ и фронталь FA. Затем из заданных проекций d и d’ точки D опускают перпендикуляры соответственно на ce и f’a’. Прямая, проведенная из точки D будет перпендикулярна плоскости треугольника АВС.
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Задачи на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение плоскости с прямыми линиями. На рис. 116 показано построение линии пересечения плоскостей, заданных треугольниками АВС и DEF. Прямая MN построена по найденным точкам пересечения сторон DE и EF треугольника DEF с плоскостью треугольника АВС.

Например, чтобы найти точку M, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника АВС по прямой 12. Через полученные точки 1′ и 2′ проводят вертикальные линии связи до пересечения их с горизонтальными проекциями ав и ас сторон треугольника АВС в точках 1 и 2. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М, которая будет точкой пересечения прямой DF с плоскостью АВС. Затем находят фронтальную проекцию m’ точки M. Точку N пересечения прямой EF с плоскостью АВС находят так же, как и точку М.
Соединив попарно точки m’ и n’, m и n, получают проекции линий пересечения MN плоскостей АВС и DEF.
Источник: forkettle.ru
Проецирование. Основные виды и их расположение на чертеже
Основным методом изображения предметов на чертеже является проекция (от латинского projectio – бросание вперёд, вдаль).
Основные элементы и сущность метода проецирования рассмотрим на примере точки (рисунок 31):
· плоскость проекций П’– плоскость, на которую производится проецирование;
· центр проецирования S–точка из которой производится проецирование;
· точки А, В -объекты проецирования;

· проецирующие лучи SA и SB–воображаемые прямые, при помощи которых производится проецирование.
Рисунок 31. Метод проецирования.

Проведя через центр проекций S и точку А прямую линию до пересечения с плоскостью П’ получим точку А’. Точка А’ – проекция точки А на плоскость П’. Символически это .

Проведя через центр проекций S и точку В прямую линию до пересечения с плоскостью П’ получим точку В’. Точка В’ – проекция точки В на плоскость П’. Символически это .
Если центр проекций S находится на конечном расстоянии (т.е. все лучи проекций выходят из неё), то проецирование называется центральным.
Если центр проекций S бесконечно удалённая точка, то в обозримом пространстве проецирующие лучи будут параллельны. В этом случае проецирование называется параллельным(рисунок 32).
Если проецирующие прямые перпендикулярны плоскости проекций, то проецирование называют ортогональным или прямоугольным(рисунок 33).
Если проецирующие лучи не перпендикулярны к плоскости проекций, то проецирование называют косоугольным.
В процессе проецирования происходит изменение фигуры, которую проецируют, она теряет свои свойства и приобретает новые. Некоторые свойства остаются неизменными:
1. Проекция точки есть точка.
2. Если одна фигура принадлежит другой фигуре, то проекция первой фигуры принадлежит проекции второй фигуры.


Рисунок 32. Параллельное Рисунок 33. Ортогональное
3. Если фигура принадлежит плоскости, параллельной плоскости проекций, то проекция фигуры на эту плоскость проекций равна самой фигуре, т.е. в натуральную величину.
Чертёж, состоящий из проекций объекта, называют комплексным чертежом.Для получения комплексного чертежа пользуются следующим алгоритмом:
1. Объект проецируют ортогонально на три взаимно перпендикулярные плоскости (рисунок 34).
2. Эти плоскости совмещают в одну путём поворота вокруг линии пересечения этих плоскостей (рисунок 35).
Для построения третьей проекции по двум данным необходимо выполнить следующее:
1. Через фронтальную проекцию А2 провести перпендикуляр к оси z.
2. На проведённом перпендикуляре от оси z отложить отрезок равный расстоянию от горизонтальной проекции А1 до оси х.

Рисунок 34. Проецирование точки на три плоскости проекций.

Рисунок 35. Комплексный чертёж точки.
При выполнении машиностроительных чертежей пользуются правилами прямоугольного проецирования. Предмет проецируют на 6 граней пустотелого куба, располагая его между наблюдателем и соответствующей гранью куба. Грани куба принимаются за основные плоскости проекций. Следовательно, имеется 6 основных плоскостей проекций (рисунок 36). Эти плоскости совмещаются разворотом в одну плоскость вместе с полученными на них изображениями.
Изображение на фронтальной плоскости проекций на чертеже принимается за главное. Предмет располагают так, чтобы изображение на фронтальной плоскости давало наиболее полное представление о форме и размерах предмета.
В инженерной графике изображения предметов называют видами.
Вид – изображение, обращённой к наблюдателю видимой части поверхности предмета.
В целях уменьшения количества изображений допускается показывать на видах невидимые контуры предмета штриховыми линиями.
Все виды на чертеже должны располагаться в проекционной связи. Это облегчает чтение чертежей. В этом случае не наносятся какие-либо надписи, разъясняющие наименование видов. Количество видов на чертеже должно быть наименьшим, но обеспечивающим полное представление о предмете.

Рисунок 36. Образование основных видов.
По ГОСТ 2.305 – 68 устанавливаются следующие названия видов (рисунок 36):
1- Вид спереди (главный вид);

Рисунок 37. Расположение основных видов на чертеже.
Аксонометрические проекции.
Кроме прямоугольных (ортогональных) проекций для изображения предмета на чертеже используют аксонометрические проекции.
Чертёж даёт чёткое представление о форме и размерах объекта, но в некоторых случаях требуется наглядное представление предмета.

В этих случаях дают дополнительно изображение этого предмета в аксонометрической проекции.
Способ аксонометрического проецирования заключается в том, что данный предмет вместе с осями координат, к которым этот предмет отнесен в пространстве, параллельно проецируется на некоторую плоскость (рисунок 38). Следовательно, аксонометрическая проекция – это проекция только на одну плоскость.
В зависимости от направления проецирования аксонометрические проекции делят на два вида:
Косоугольное проецирование – проецирование не перпендикулярно плоскости аксонометрических проекций;
Прямоугольное проецирование – проецирование перпендикулярное к плоскости аксонометрических проекций.

Рисунок 38. Аксонометрическое проецирование.
Отношения расстояний по осям в пространстве к полученным аксонометрическим проекциям этих расстояний: ex/e = k; ey/e = m; ez/e = n.
k, m, n называют коэффициентами искажения по осям.
В зависимости от величины коэффициентов аксонометрию делят на три вида:
Изометрия: k = m = n;
Триметрия: k ≠ m ≠ n.
Триметрия применяется очень редко.
ГОСТ 2.317 – 69 устанавливает правила построения аксонометрических проекций, применяемых на чертежах всех отраслей промышленности и строительства.
Диметрическая проекция.
Коэффициент искажения по оси у составляет 0,47, а по осям x и z – 0,94.
Принято диметрическую проекцию выполнять без искажения по осям x и z, т.е. равным 1, а по оси у — 0,5 (меньше в 2 раза).
Окружности в аксонометрии проецируются в эллипс. Большая ось эллипсов будет составлять 1,06d, d — диаметр окружности, а малая ось эллипса в плоскости xz – 0,95d, эллипсов в плоскостях xy и zy – 0,35d.


Рисунок 39. Диметрическая проекция.
Изометрическая проекция.
Коэффициенты искажения по всем осям равны 1. Большая ось эллипсов – 1,22d, меньшая ось эллипсов – 0, 71d, где d – диаметр окружности.

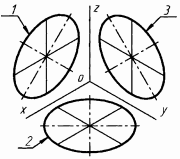
Рисунок 40. Изометрическая проекция.
ПРИЛОЖЕНИЕ
ГБПОУ «Курганский государственный колледж»
КОНТРОЛЬНАЯ РАБОТА
Специальность 08.02.01 Строительство и эксплуатация зданий и сооружений (заочное отделение)
Ф.И.О. студента Иванов И.И.
По предмету: Инженерная графика
Преподаватель: Белошевская М.А.
Дата регистрации работы:
| 2016 |
| Белошевская М.А. |
Рисунок 1. Пример выполнения задания №1 «Титульный лист»
| Белошевская М.А. |
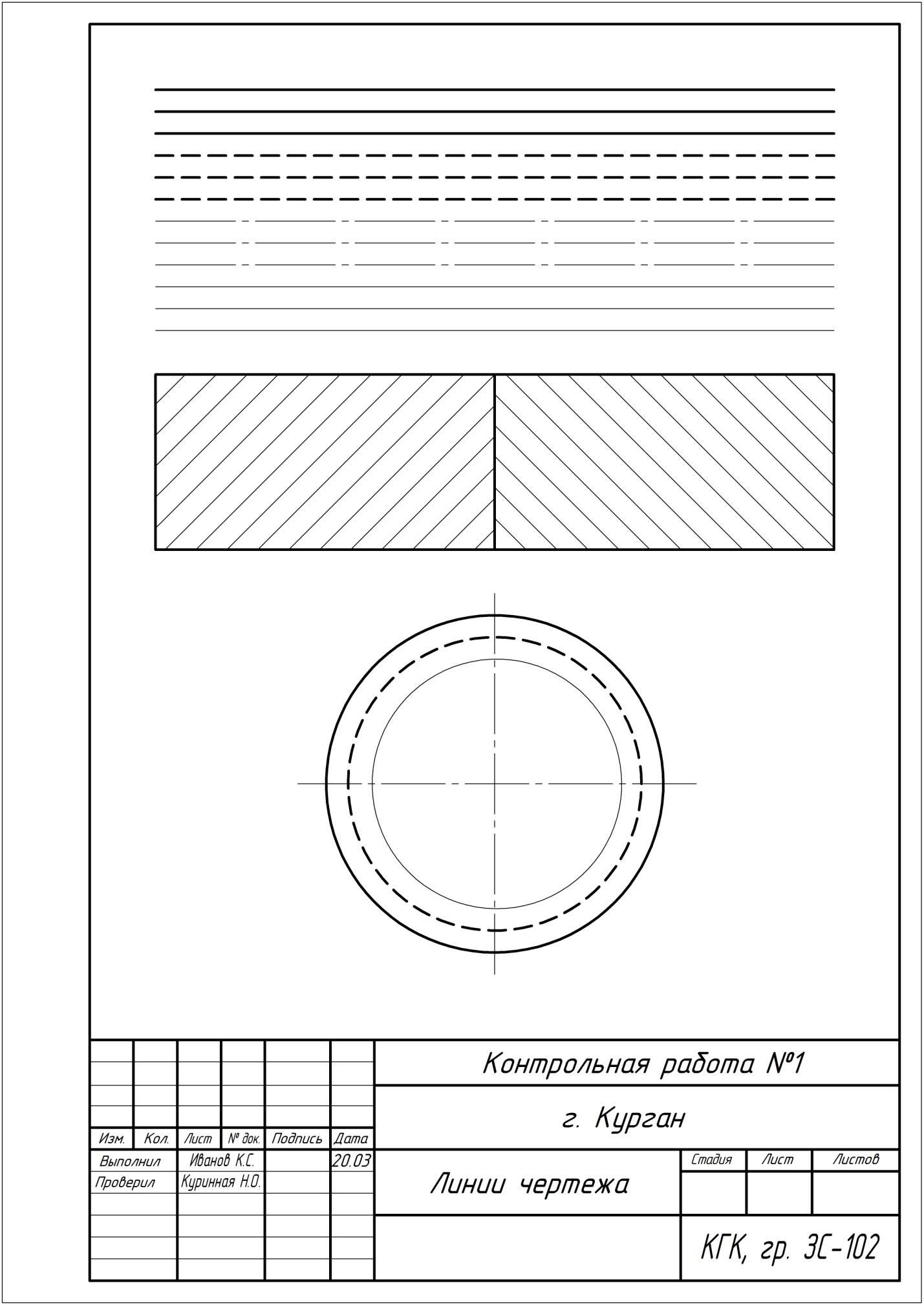
Рисунок 2. Пример выполнения задания №2 «Линии чертежа»
| Белошевская М.А. |

Рисунок 3. Пример выполнения задания №3 «Геометрические построения»
| Белошевская М.А. |

Рисунок 4. Пример выполнения задания 4 «Проекции детали», лист 1
| Белошевская М.А. |
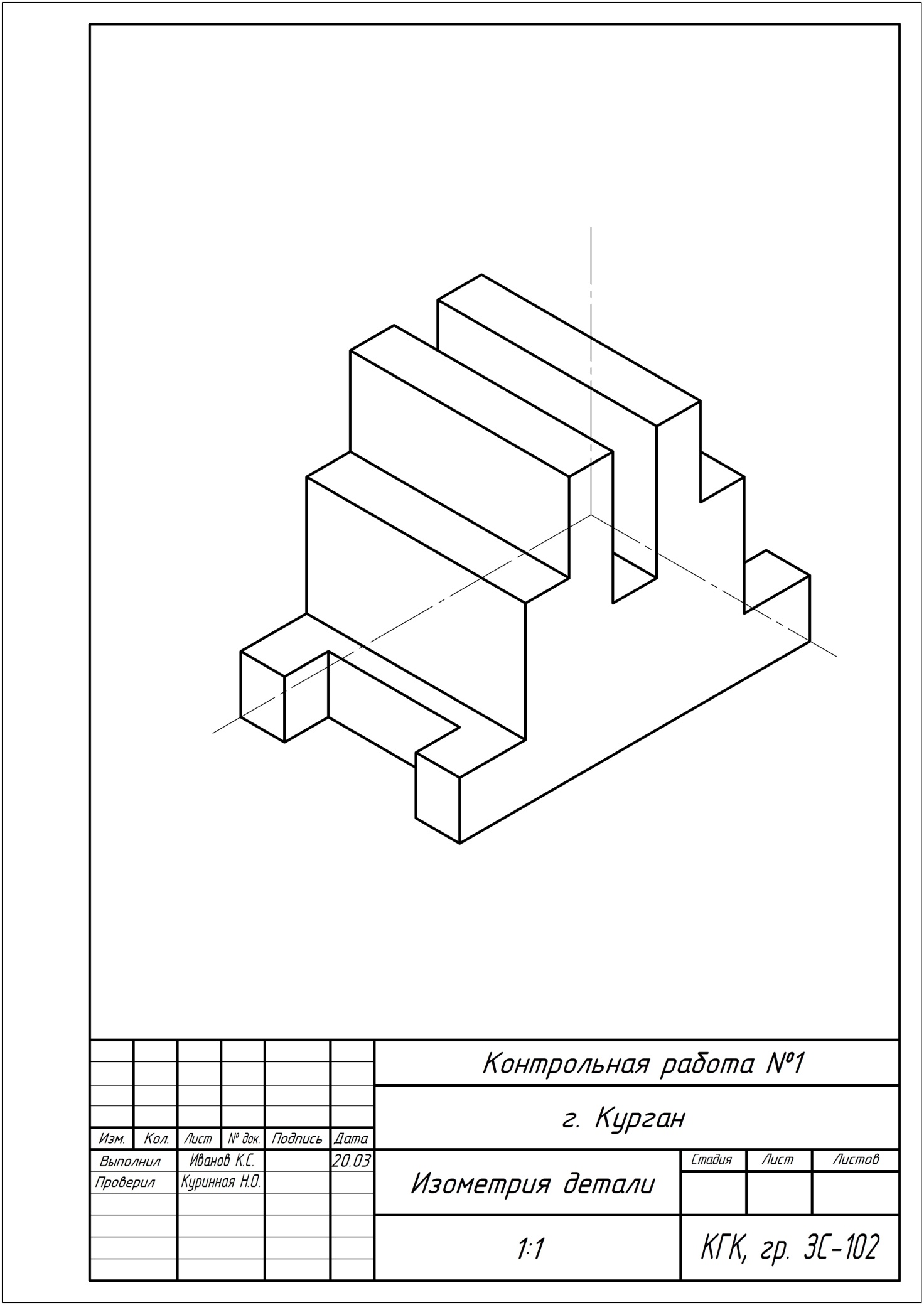
Рисунок 5. Пример выполнения задания 4 «Проекции детали», лист 2.
Список литературы:
1. Боголюбов С.К. Инженерная графика. – М.: Машиностроение, 2000.
2. Куликов В.П., Кузин А.В. Инженерная графика: учебник – 3-е издание, испр. – М.:ФОРУМ, 2009.-368 с.- (Профессиональное образование).
3. Чекмарёв, А.А., Осипов В.К. Справочник по машиностроительному черчению — М.: Высшая школа, 2001г- 360с.
4. Чумаченко Г.В. Техническое черчение: учеб. пособ. для профессиональных училищ и технических лицеев / Г.В. Чумаченко, канд. тех. наук. –Изд. 6-е, стер. – Ростов н/Д : Феникс, 2013. -349 с. – (НПО).
5. alldrawings. ru.
7. Боголюбов С.К. Инженерная графика. – М.: Машиностроение, 2000.
8. Белягин, С.Н. Черчение: справ. пособие/ С.Н. Белягин. – 4-е изд., доп. – М.: ООО « Издательство АСТ»: ООО «Издательство Астрель», 2002-424с.
9. Государственные стандарты. Единая система конструкторской документации.
10. Вышнепольский, И.С. Техническое черчение: учеб. для студ. среднего проф. Образования / И.С. Вышнепольский. – М.: Высшая школа, 2001. – 392 с.
11. Миронов Б.Г., Сборник заданий по инженерной графике с примерами выполнения чережей на компьютере: Учеб. пособие / Б.Г Миронов, Р.С. Миронова, Д.А. Пятника, А.А. Пузиков – 3-е изд., испр. и доп. – М.: Высш. шк., 2003.-355с.
12. Степакова В.В., Гордиенко Н.А. Черчение. – М.: ООО «Издательство Астрель», 2004 – 272 с.
13. Чекмарёв А.А., Осипов В.К., Справочник по машиностроительному черчению – М.: Высшая школа, 2001г – 360с.
Источник: lektsia.com