Композиция в интерьере или в целом архитектурном объекте состоит из частей, взаимосвязанных друг с другом и с целым. При этом,части как правило, имеют различную величину. Эта взаимосвязь выражается через пропорциональные отношения частей между собой и их отношение к целому.
Пропорции — один из важнейших методов достижения выразительности и гармонии.Пропорции в архитектуре часто привязываются к параметрам человека. Все сооружения служат человеку и должны быть ему соразмерны.
В древние времена части человеческого тела стали естественной основой всех единиц измерения. И сейчас все размеры мы сравниваем с человеческим ростом, это важно и с точки зрения эргономики и психологии.
Один из самых известных способов пропорционирования это правило Золотого сечения
Правило Золотого сечения
Золотое сечение- это гармоническая пропорция, которая удовлетворяет следующему соотношению:

Пропорция. Основное свойство пропорции. 6 класс.
Деления отрезка на части по принципу Золотого сечения
Малая часть отрезка А, так относится к средней части Б, как Б относится к сумме А+Б
Если приравнять С к 1, то получим такое соотношение
(0,382:0,618)=0,618:(0,382+0,618) и (0,382+0,618)=1
Отношение между числами 0,382 и 0,618 соответствует Золотому сечению
Только это отношение 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или умньшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему .
Чтобы создавать наиболее гармоничные отношения между частями композиции желательно приводить их пропорциональные размеры к золотому сечению. Для этого необходимо использовать коэффициенты 0,618 и 1,618.
Например, в декоративных целях необходимо разделить стену высотой 2,7 метра по правилу золотого сечения на 2 части.
Для этого 2,7 умножим на 0,618 получим 1,6686 теперь из общей высоты 2,7 вычтем 1,6686 получим 1,0314. Таким образом стену высотой 2,7 метра делим на части 1,6686 м. и 1,0314 м.
Ряд Фибоначчи
С историей золотого сечения связано и имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи).
Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами.
В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится».
Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:, который удовлетворяет Золотому сечению
0 — 0 — 1 — 2 — 3 — 5 — 8 — 13 — 21 — 34 и т.д.
Сумма двух предшествующих чисел равна последующему в ряду числу. Отношение соседних чисел в ряду приближено к Золотому сечению.
Этот ряд чисел называют рядом Фибоначчи. Воспользовавшись рядом Фибоначчи мы можем получить пропорцию для деления.предмета на гармоничные части.
Например, для отрезка длиной 5 идеальной пропорцией будет деление его на части равные 2 и 3, для отрезка 8 это 3 и 5 и т.д.
Золотой прямоугольник
Прямоугольник, стороны которого находятся в золотом отношении, называют золотым прямоугольником. Из определения золотых прямоугольников следует, что все они подобны. Если от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник меньших размеров
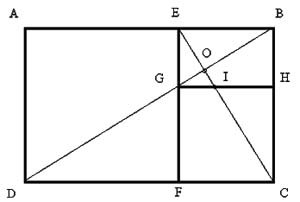
Примеры золотого сечения в архитектуре
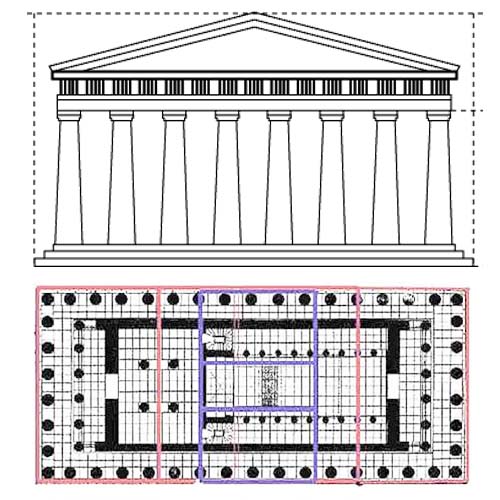
Парфенон в Афинах (V в. до н.э.) имеет 8 колонн по коротким сторонам и 17 по длинным..Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.

Известный русский архитектор М.Ф. Казаков тоже широко использовал в своем творчестве золотое сечение. Его можно обнаружить, например, в архитектуре здания бывшего Сената в Кремле.

По проекту М.Ф.Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей им. Н.И.Пирогова (Ленинский просп., д. 8).

Как использовать пропорциональность в интерьере
Возникает вопрос- а что дает на практике знание закона золотого сечения и гармоничной пропорции. Вот некоторые приемы, использующие эти знания.
Например, для отделки стен мы хотим использовать деревянные панели. При этом будем обшивать стену не на всю высоту, а частично. Чтобы панели смотрелись гармонично, можно использовать два варианта обшивки стены.
- Вначале замеряйте высоту стены и умножьте её значение на 0,618 ( «золотое число»).
- Запишите полученное значение.
- Теперь из общей высоты стены вычтите его..
- В результате мы имеем два значения высот для обшивки панелями стены.
- Первое = высота стены умноженная на 0,618, а второе равно высота стены минус высота, умноженная на 0,618.

Этот же прием можно использовать и при оклеивании стен обоями. Разделив стену по высоте на бордюр,фриз и основное полотно обоев.

Пропорциональность можно использовать при зонировании пространства. Для этого можно разбить стену вертикалью на части по правилу золотого сечения и отделывать полученные сегменты стены разными материалами или разным цветом.

.Пропорциональность можно использовать при выборе мебели в интерьер.
например высота шкафа и стоящего рядом рядом дивана будут смотреться гармонично если соотношение их размеров будут приближены к «магическому числу» 0,618. То есть высота дивана должна быть приблизительно равна высоте шкафа умноженной на 0,618
По пропорции можно подбирать размер декоративных элементов на плоскости. Например панно или гобелен на стене или ковер на полу.
Ну и так далее, проявляйте творчество и все получится!
Кроме этого приема композиции в интерьере, вы можете ознакомиться с видеосюжетом Правила Дизайна Баланс и Порядок в котором автор рассказывает о многих композиционных приемах, применяемых в современном дизайне интерьера
Источник: interior-in.ru
VIII Международная студенческая научная конференция Студенческий научный форум — 2016

Проблема пропорций в архитектурной композиции с настойчивостью и увлечением рассматривается теоретиками и практиками не одно столетие. В каждой эпохе находятся архитекторы, строители, исследователи, которые с неиссякаемой энергией устремляются к новым открытиям в области художественного воздействия архитектуры на человека и разрешению проблемы пропорций в практической деятельности. В связи с эволюцией вкусов происходит низвержение старого идеала и его замена новым каноном.
Следует заметить, что архитектура очень тесно связана с числами и мерами, математическими расчетами и геометрическими схемами. Специалисты сталкиваются в своей работе с дилеммой – или слишком суровое подчинение математическим принципам, или полное их отрицание. Актуальность проблемы и желание выяснить, где же кроется тайна между абсолютными законами чисел и свободным чутьем интуиции архитектора, обусловили выбор темы исследования «Приемы нахождения точных пропорций в архитектуре».
Под понятием «пропорция» в архитектуре мы понимаем согласование отдельных частей здания между собой и в отношении к целому.
В ходе исследования было выявлено, что в построении пропорций возможны два основных метода:
1. Арифметические системы, где пропорции вычисляются абстрактным методом (по числам). Разновидностью этого способа является модульная система, при которой какая-либо часть здания (например, длина его или диаметр колонны) принимается за единицу (модуль), и по отношению к ней все остальные размеры выражаются в простых числах. Римский теоретик Витрувий ещё I в. до н. э на основе этой системы объяснил пропорции греческой архитектуры. А французский ученный Шуази исследовал арифметическую систему нового времени.
2. Геометрические системы пропорций, где все три проекции сооружения определяются путем геометрических построений (чаще всего на основе квадрата или круга). В этой системе основополагающим является принцип подобия частей.
Рисунок 1. Золотое сечение в архитектуре Кремля.
Частым случаем геометрических построений является «золотое сечение» — отрезок так относится к большей своей части, как большая часть относится к меньшей, т. е. деление отрезка производится в среднем и крайнем отношении. Постоянная пропорция этой системы, образуя убывающую или возрастающую прогрессию, связывает воедино все элементы здания, от больших до самых малых величин (рис. 1).
Золотым сечением наиболее часто занимались теоретики, исходя из квадрата, точнее, из двух квадратов или из деления окружности на части.
Так, немецким архитектором Месселем были приведены общие законы построений, объясняющие все схемы геометрических пропорций. Ученый осуществил построение геометрических фигур путем деления окружности на различное число частей (рис. 2). Например, на основании выводов Месселя, были определены пропорции храма Хонсу в Карнаке путем вписывания его в круг (описанный веревкой на земле), разделенный на 8 частей.
Рисунок 2. Построение геометрических фигур, путем деления окружности на различное число частей.
Как показали исследования система пропорций, применявшаяся еще в архитектуре Древнего Египта, построена на квадрате и его «производных» (рис. 3). Если отложить диагональ квадрата, равную √2, на продолжении одной из сторон его и восстановить к этой стороне в конце ее перпендикуляр, то получится прямоугольник с отношением сторон квадрата и его диагонали.
Если далее построить новую фигуру, отложив диагональ полученного прямоугольника, равную √3 на продолжении той же стороны квадрата, то мы получим второй прямоугольник с отношением сторон 1 : √ 3. Дальнейшее повторение того же построения дает новый прямоугольник с отношением сторон 1: √4. Диагональ последнего прямоугольника равна √5. Эта система носит название Система диагоналей. И она связывает между собой шесть величин:
2) его диагональ;
3) прямоугольный треугольник с углом в 60°;
4) прямоугольник, состоящий из двух квадратов;
5) и 6) отношения его диагонали к сторонам √5/2 и √5/1, которые лежат в основе пропорций большинства сооружений Древнего царства.
Рисунок 3. Система построения путем построения квадрата и его «производных»
В литературных источниках понятие «симметрия» означает соразмерность художественных форм и частей художественного произведения. Симметрия обычно подразделяют на: симметрию отражения; центральную и осевую симметрии; бордюр; лента; симметрию переноса.
Симметрия отражения (рис. 4). Если на плоскости проведена прямая mm’ и вне ее дана точка А, то симметричной ей точкой относительно этой прямой будет точка А’, лежащая на перпендикулярной mm’ прямой Аа, по другую сторону от прямой на равном ей расстоянии: ВА’=BA. Прямая mm’ называется осью симметрии точек А и А’. Симметрия на плоскости относительно прямой линии называется осевой симметрией, а также отражением от прямой: точка А’ является как бы зеркальным отражением точки А. На рисунке справа – плоские фигуры с одной, двумя и тремя осями симметрии.
Рисунок 4. Симметрия отражения
Аналогичной является симметрия отражения пространственной фигуры: например, если предмет состоит из двух зеркальных половин, то каждую из этих половин можно рассматривать как бы зеркальным отражением другой от воображаемой плоскости (зеркала); эта плоскость называется плоскостью симметрии. Симметрия относительно плоскости носит также название отражения в плоскости.
Симметрия центральная (рис. 5). Точка A’ называется симметричной точке А относительно точки О, если О есть середина отрезка AA’; точка О называется центром симметрии. Два параллельных и равных между собой отрезка AB и A’B’, но направленные в противоположные стороны называются обратно параллельными. Обратная параллельность есть одно из характерных свойств фигур, обладающих центром симметрии.
Рисунок 5. Примеры центральной симметрии
Симметрия осевая (рис. 6). Ось симметрии n-го порядка – это линия при полном обороте вокруг которой плоская или пространственная фигура несколько раз приходит в совмещение сама с собой (ось проходит через центр фигуры перпендикулярно плоскости изображения, т.е. на бумаге ось есть точка – проекция оси на плоскость – бумагу).
Число совмещений при полном обороте называется порядком оси, а наименьший угол поворота, при котором фигура совмещается сама с собой, – элементарным углом поворота. На рисунке представлены изображения с осями симметрии следующих порядков: 2, 3, 4, 5, 6, 7 и соответственно элементарными углами поворота – 180, 120, 90, 72 градуса и т.д. Наряду с осью симметрии n-го порядка в каждом из приведенных изображений имеется несколько пересекающихся осей симметрии. Справа помещены два изображения, из которых верхнее можно рассматривать как имеющее ось симметрии 1-го порядка, нижнее – как имеющее ось симметрии 5-го порядка и не имеющие осей симметрии.
Рисунок 6. Примеры осевой симметрии:
а) Московский кремль; б) Мавзолей-мечеть Тадж-махал.
Композиция осевой симметрии и нетождественного переноса параллельно оси симметрии называется переносной симметрией плоскости.
Однако понятие переносной симметрии применяют и в случае фигур конечных размеров, имея в виду наблюдаемое при переносе частичное совмещение фигуры (рис. 7).
Рисунок 7. Симметрия переноса.
Дефиниция «бордюр» – означает совокупность равных фигур, повторяющихся последовательно одна за другой вдоль прямой линии переноса (рис 8).
Проведенные исследования дали возможность заключить, что общее число всех возможных видов симметрии бордюров – семь:
1. Перенос — фигура приходит в совмещение сама с собой после переноса на расстояние а; создается впечатление поступательного движения.
2. Симметрия линии скользящего отражения — фигура переносится на расстояние а/2 и отражается; создается впечатление волнообразного движения.
3. Комбинация оси переноса с осями симметрии 2-го порядка (обозначены точками). Эту комбинацию можно рассматривать как перенос двойных фигур; создающих впечатление взаимообратного движения.
4. Комбинация оси переноса с поперечными осями симметрии (обозначены пунктиром), что создает впечатление горизонтальности.
5. Комбинация оси переноса с продольной осью симметрии для создания впечатления вертикальности.
6. Комбинация линии скользящего отражения с осями симметрии 2-го порядка. При этом возникают поперечные оси симметрии и создается впечатление последовательного перевертывания.
7. Комбинация линии переноса с продольной и поперечными осями симметрии, где создается впечатление статичности.
Рисунок 8. Бордюр.
Лента (рис 9). Определение этого термина повлекло бы за собой введение новых терминов и понятий, излишних в нашей теме, а поэтому ограничимся приведением схем лент и вида их симметрии. Треугольники на рисунке как бы сделаны из картона, лицевая сторона которых черная, а обратная белая; треугольники с точкой имеют одинаковые поверхности. На рисунке снизу даны примеры лент. На следующем рисунке показаны варианты получения симметрии лент при помощи вырезания из бумаги:
1. Бумагу перед вырезанием перегибают поперек один, два, три раза и т.д., благодаря чему образуются две, четыре, восемь и т.д. долей; линии перегиба соответствуют осям симметрии.
2. Бумагу перегибают несколько раз поперек, как и в предыдущем способе, и кроме того один раз вдоль, в связи с чем возникает еще и продольная ось симметрии.
3. Бумагу сворачивают трубочкой, благодаря чему образуются многослойные витки.
Рисунок 9. Лента.
Таким образом, в ходе исследования были рассмотрены современные возможности нахождения точных пропорций в архитектуре и сделан вывод, что индустриальные и гражданские строительные элементы имеют как стандартные унифицированные размеры, отвечающие требованиям их массового производства и применения, так и необходимую гармоничность и соразмерность для придания архитектурным сооружениям высоких эстетических качеств.
Проведенное исследование не претендует на окончательное решение проблемы. В дальнейшем основы построения пропорций будут использованы при разработке дипломного проекта «Водный дворец спорта».
Список использованных источников:
Власов, В. Г. Архитектура. Классика и современность. Учебно-методическое пособие / В.Г. Власов. – СПбГУ, 2014. – 180 с.
Георгиевский, О.В. Художественно-графическое оформление архитектурно-строительных чертежей : учебное пособие / О.В. Георгиевский. – М.: Архитектура-С, 2004. – 80 с.
Источник: scienceforum.ru
Золотое сечение в строительстве
В оформлении интерьера также используют золотое сечение; если пропорции в строительстве заданы верно, закон гармонии (пропорциональных отрезков) поможет решить вопросы зонирования и композиции. Закон применяют следующим образом:
- Пусть комната имеет ширину 3 м (300 см).
- Используют последовательность чисел Фибоначчи: 300х0,618=185,4 см.

Золотое сечение в современном дизайнеИсточник artstation.com
Полученные отрезки 185,4 и 114,58 см используют для разных целей. Например, с их помощью расставляют мебель, предметы декора или цветы.
На практике точные расчеты применяются редко. Для того, чтобы правильно зонировать пространство и красиво расставить мебель, в большинстве случаев можно использовать приближенную пропорцию 2:3. Тогда поступают следующим образом:
- Комнату делят на две части в отношении 1 к 2.
- Часть комнаты, занимающая большую площадь (2/3) – функциональная зона, предназначенная для расстановки мебели. Внутри этой зоны также действует ЗС: наибольшее количество предметов входит в 2/3 площади, оставшийся участок стараются не заполнять полностью.
- Меньшую часть комнаты (1/3) оставляют свободной от мебели или используют для декоративных целей.

Расстановка мебели в загородном домеИсточник shopify.com
Принцип ЗС хорошо работает при выборе цветового оформления; цвета подбирают следующим образом:
- На доминирующий (фоновый) оттенок приходится 60% площади покрытия.
- Сопровождающий (дополнительный) оттенок занимает 30% отделки.
- Аккомпанирующий (близкий или, наоборот, контрастный) оттенок – 10%.
Правило 1/1,618 в интерьере можно использовать и для других целей, например, подбирать площадь отделки или мебель по высоте.
Видео описание
Об интерьере по золотому сечению в следующем видео:
Почему сегодня ценность ЗС снижается
Столетиями принцип золотого сечения задавал пропорции в строительстве домов, а формула служила гарантией получения строения с правильными, естественными пропорциями. Однако, ЗС – лишь одна из многих закономерностей, используемых в проектировании.
Многие современные архитекторы вообще никогда не пользуются числами Фибоначчи, и это не мешает им создавать восхитительные или величественные проекты. Они не считают ЗС универсальным правилом, единственной формулой, ответственной за эстетическую красоту.
Часто золотую пропорцию добавляют в проект в качестве изюминки, но весь дизайн, как в прошлые века, на ней не выстраивают. Использование только одной закономерности многими дизайнерами считается упрощенным, лишенным индивидуальности подходом.

Золотое сечение в архитектуре современного жилого домаИсточник artfasad.com
Видео описание
О том, как создать гармоничный интерьер с помощью золотой пропорции, в следующем видео:
Коротко о главном
Золотое сечение – правило, которое используется в архитектуре не одно тысячелетие. Оно определяет закономерности развития живых существ и природных процессов, поэтому многие считают его универсальным гармоническим законом.
Естественные пропорции, существующие в природе, человек переносит не только в архитектуру, но и в дизайн внутренних помещений. Численно их выражают в виде ряда Фибоначчи, последовательности чисел с особыми свойствами.
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
Из формулы (7) найдем ( small b ) и подставим в (6):
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
Вычислим дискриминант квадратного уравнения (10):
Сторона прямоугольника вычисляется из следующих формул:
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( b=frac>>0 ) | (*) |
| ( frac< P>>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 < 0 ) |
| ( sqrt=sqrt= ) ( small sqrt < sqrt=2d ) |
Имеем ( small sqrt 2d .) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):
Подставляя значения и в первую формулу (12), получим:
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62.
Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
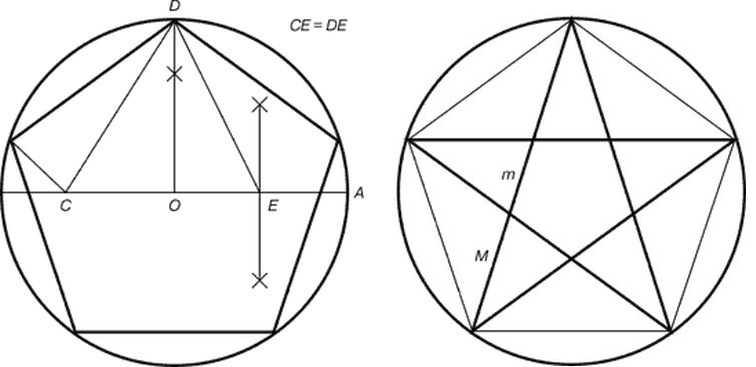
Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Как получили золотое сечение
Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.
Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.
На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.
Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:
- Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
- Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
- В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.
К сведению! В отличие от классического золотого соотношения, архитектурная версия подразумевает соотношение сторон отрезка в пропорции 44:56.
Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.
Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.
Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.
Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.
Съемка людей и неживых объектов
В композиции натюрморта, основная сложность заключается в расположении объектов по пространству кадра. При этом нужно оценивать высоту и форму предметов. Для произведения на зрителя положительного эффекта вещи должны находиться в активных точках, о которых уже говорилось выше. Использование двух — трех точек вполне достаточно, не нужно перегружать изображение массой элементов.
Большее внимание, мы уделим фотографии человека и группы людей. Для начала определите масштаб портрета и дальше вспомните про правило третей:
- В головном портрете обычно выделяют глаза или губы (чаще глаза), поэтому логично усилить впечатление, расположив их в точках пересечения упомянутых линий, составляющих правило.
- В бюстовом и поясном портрете значимость приобретает не только положение головы человека, его эмоции, но и туловище. Кроме того, руки могут стать важным моментом всей фотографии. Почему бы их не поместить как раз на линию сечения? Давайте попробуем!
- При съемке по колено и в рост самого человека можно слегка сместить в кадре вправо или влево, таким образом он будет четко располагаться с правилом трех третей.
- Если вы хотите не просто сфотографировать по центру нескольких человек, а сделать художественную фотографию, то поставьте людей так, чтобы они точно попали на две линии или точки золотого сечения. Примером может быть семейное фото: дети, стоящие впереди на первой линии, и родители, расположенные чуть дальше – на второй.

Особенность золотого сечения для человека
Старинная архитектура зданий и домов средневековья остается притягательной и интересной для современного человека по многим причинам:
- Индивидуальный художественный стиль в оформлении фасадов позволяет избежать современного штампа и серости, каждое здание представляет собой произведение искусства;
- Массовое использование для декорирования и украшения статуй, скульптур, лепнины, необычных сочетаний строительных решений разных эпох;
- Пропорции и композиции здания притягивают взор к наиболее важным элементам постройки.
Важно! При проектировании дома и разработке внешнего вида средневековые архитекторы применяли правило золотого сечения, неосознанно используя особенности восприятия подсознания человека. Современные психологи экспериментально доказали, что золотое сечение является проявлением неосознанного желания или реакции человека на гармоничное сочетание или пропорцию в размерах, формах и даже цветах
Был проведен эксперимент, в ходе которого группе людей, незнакомых между собой, не имеющих общих интересов, разных профессий и возрастных категорий, предложили ряд тестов, среди которых была задача согнуть лист бумаги в наиболее оптимальной пропорции сторон. По результатам тестирования было установлено, что в 85 случаях из 100 лист сгибался испытуемыми практически точно по золотому сечению
Современные психологи экспериментально доказали, что золотое сечение является проявлением неосознанного желания или реакции человека на гармоничное сочетание или пропорцию в размерах, формах и даже цветах. Был проведен эксперимент, в ходе которого группе людей, незнакомых между собой, не имеющих общих интересов, разных профессий и возрастных категорий, предложили ряд тестов, среди которых была задача согнуть лист бумаги в наиболее оптимальной пропорции сторон. По результатам тестирования было установлено, что в 85 случаях из 100 лист сгибался испытуемыми практически точно по золотому сечению.
Поэтому современная наука считает, что феномен универсальной пропорции является психологическим явлением, а не действием каких-либо метафизических сил.
Осями в саду являются прямые линии, намечаемые дорожками, поверхностями или руслом ручья
Если линия завершается некоторой точкой, которая особым образом подчеркивается каким-либо объектом, то он явно представляет собой оптический акцент, рассчитанный на то, чтобы привлечь к себе внимание. Если оси специально выделяются, то тем самым они создают в саду определенное настроение и подчеркивают перспективу
Зачастую такие оси уже имеются, если, например, главный вход расположен по центру здания и к нему ведет прямолинейная дорожка.
С осями сада связано понятие симметрии. Если здание или сад построены по этому принципу, то общее впечатление гармонии может быть усилено симметричным расположением растений, дорожек и объектов. На этом фоне особенно выделяются доминантные точки. Но иногда этот порядок осознанно нарушается асимметричностью расположения.

Без арочных конструкций для вьющихся растений и без скамейки в конце мощеной дорожки обзорная ось производила бы впечатление слишком длинной
Золотое сечение и симметрия
Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863…1925) считал золотое сечение одним из проявлений симметрии.
Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост.
Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.
ПРОДОЛЖЕНИЕ СТАТЬИ ЧИТАЙТЕ ВОТ ТУТ
Вспомните и посмотрите, что такое Капля «принца Руперта», а так же освежите в памяти Рекорды ХИМИИ
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
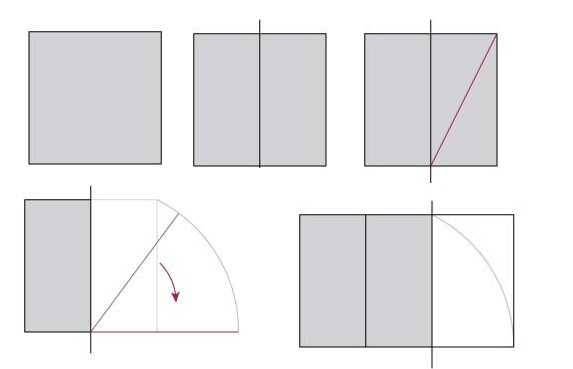
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
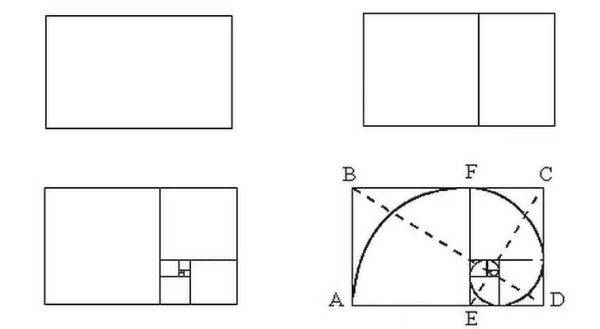
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Принцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
- 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
- если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.
Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.
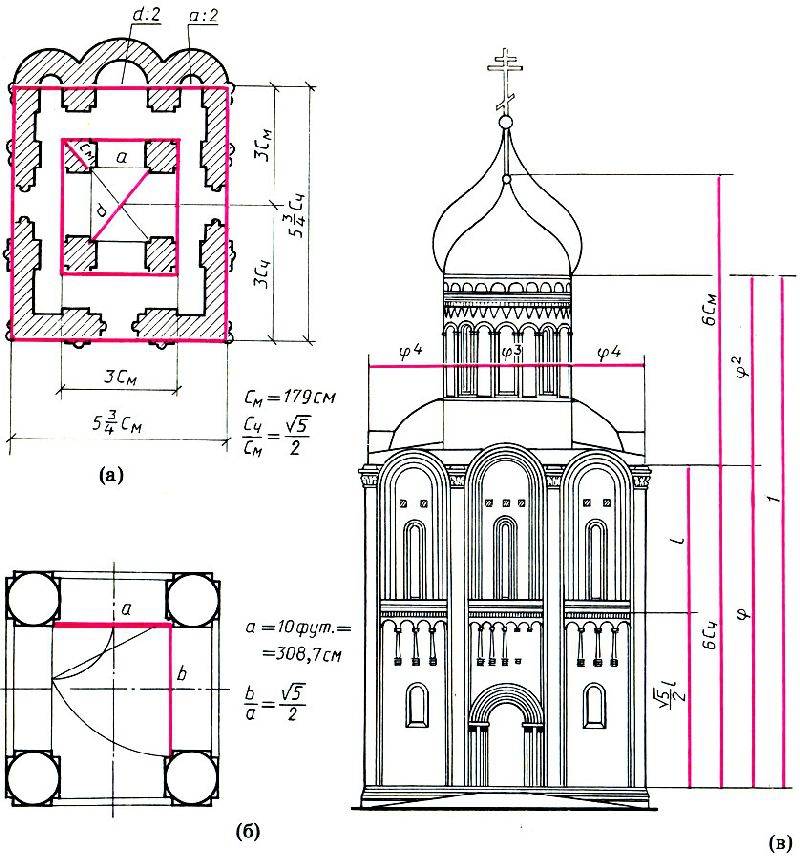
Ряд Фибоначчи в церкви Покрова на Нерли
Как рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.

Простой пример золотого сечения в курином яйце
Как построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
- нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
- над ними разместить квадрат со стороной 2;
- слева гармонично помещается квадрат с гранью 3;
- ниже – квадрат со стороной 5;
- справа пространство займет квадрат с гранью 8;
- площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
- если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
- если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.
Принцип золотого сечения в прямоугольникеПостроение золотой спирали из прямоугольника
На видео можно более подробно узнать про магию чисел Фибоначчи:
Watch this video on YouTube
Гармония
Гармония в саду предполагает дополнение отдельных его участков различными растениями и иными элементами в рамках единого общего. Зачастую необходимый эффект благоустройства сада достигается путем создания цветовой гармонии. Это может означать, что стилистические особенности дома повторяются в саду путем использования аналогичных строительных материалов. Единство форм, материалов и растений, a также построек создает впечатление гармонии. В качестве примера можно привести круглую мощенную камнями площадку с родезией (Rodgersia), имеющей круглые листья.
Столь же гармонично выглядят симметричные размещения растений и построек
Для этого весьма важно соблюдение пропорций
Правило золотого сечения
Золотое сечение — пропорция, которую заметили еще древние египтяне. Чтобы её получить, нужно разделить линию на две части так, чтобы длинная часть соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной. Оказывается, эта пропорция всегда равняется 1,618. Это число еще называют числом «фи».
Сохранившиеся постройки древности тоже подчинены правилу золотого сечения
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.
Принцип и формула золотого сечения
На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
Последовательность Фибоначчи — не только математическая формула
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Пропорции в задачах
Итак, мы обсудили:
- Когда появляется пропорция.
- Какие арифметические действия мы можем с ней выполнять.
Осталось обсудить последний вопрос: как пропорция помогает нам решать задачи?
У пропорции члена. Если три известны, а один нет, то мы можем его найти. Причем нет большой разницы, какой именно член неизвестен: , или , или , или .
Пример 1. Найти неизвестный член пропорции .
1. Первый способ.
2. Второй способ
После того как мы сократили правую дробь, поменять местами средние члены:
И сразу получаем ответ:
Пример 2. Найти неизвестный член пропорции: .
Перемножим крайние и средние члены:
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно
Важно соотношение. А «на глаз» даже в приближении смотрится гармонично
Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов
Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно
Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.
Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.
Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Источник: dipplast.ru
Архитектурные приёмы: как правильно рассчитать масштаб и пропорции дома

Ещё один инструмент в арсенале архитектора – это масштаб и пропорции. Они относится к тому, как отдельные части здания связаны друг с другом и с тем, как в целом необычный дом гармонирует с окружающим ландшафтом.
Обратите внимание, что масштаб необязательно означает размер. Апартаменты могут быть довольно большими, но иметь комфортную и интимную для человека обстановку. И наоборот. В маленьком домике можно жить вполне прекрасно с использованием маленьких элементов и других конструктивных особенностей.
Некоторые дизайнеры и архитекторы интуитивно проектируют строения с великолепными пропорциями, другие применяют такие системы, как золотое сечение. Сегодня мы вас познакомим с тем, как использовать эти инструменты при разработке собственного творческого шедевра.
1. Сформируйте уголки в большом доме
Этот особняк был разделён на отдельные области, каждая из который с собственной крышей, придающей ему визуально меньший облик. Материалы, палитра и пропорций связывают различные части вместе, а также резиденцию с окружающими холмами и зелёными насаждениями.
 3. Изменение масштаба по мере приближения к дому
3. Изменение масштаба по мере приближения к дому
Уменьшите размер архитектурных деталей, поскольку существует прямая зависимость между человеческим телом и габаритами сооружения.

Проект от Bud Dietrich, AIA
4. Используйте пропорциональную систему, чтобы установить оптимальные размеры помещений
Высоту и ширину комнаты определите с использованием золотого сечения – техники, которая была разработана ещё тысячу лет назад.
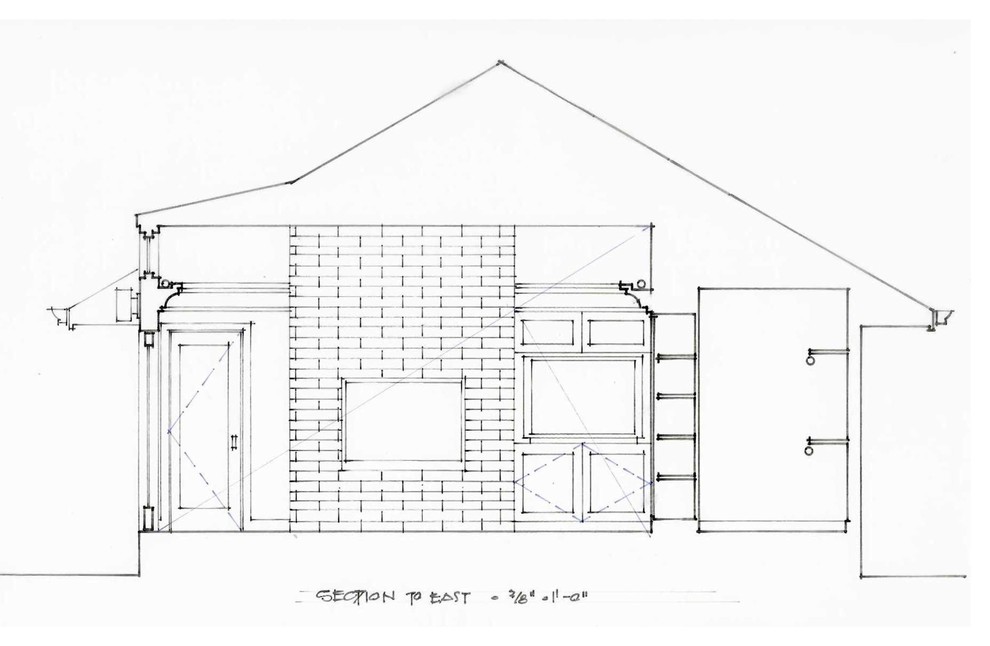
Эскиз от Bud Dietrich, AIA
В этой комнате высота потолка и расположение декоративных панелей на кирпичной кладке стены было определено специалистом на основе мерных правил.

Спальня от Bud Dietrich, AIA
5. Стильные аксессуары и отделка
Подбирайте стильную мебель, аксессуары и варианты отделки, чтобы сохранить человеческий масштаб. Камин, мягкий уголок и ковёр создают интимную обстановку в довольно большом зале с высоким потолком.

Гостиная от Christopher A Rose AIA, ASID
6. Сформируйте грандиозный размах в помещении с помощью маленьких элементов
В этой крошечной комнатке ощущение простора и объёма создаётся благодаря сводчатому потолку, камину и балюстрадам.

Гостиная от Eck | MacNeely Architects inc.
7. Используйте обивку для потолка, чтобы уменьшить его воспринимаемую высоту
К тому же этот архитектурный элемент позволяет сформировать более комфортную атмосферу в комнате.

Дизайн от Lisa Henderson — Harvest Architecture
8. Сохраните существующие габариты здания при добавлении новых инженерных элементов
Обратите внимание на следующую фотографию, выступ из крыши гармонично сочетается с общей конструкцией благодаря использованию аналогичной черепицы и оконных блоков.

Фасад от One Room at a Time, Inc.
А, ведь и, правда! Что может быть лучше наличия высоких потолков в жилище, но такое явление, к сожалению, присутствует далеко не в каждом доме. Я уверена, что, благодаря толковым дизайнерским решениям, можно сформировать и в помещении с меньшими высотами! Но всё же, насколько гармонично смотрится гостиная от Christopher A Rose AIA, ASID?
Какую уютную атмосферу можно создать, благодаря ковру и мягко мебели? Немаловажно в этой композиции даже освещение!
Когда-то у моей семьи была стройка века, понадеявшись на «а у меня есть знакомый архитектор» родители доверили расчет строения этому как оказалось самоучке. Коттедж построили по «100% правильным расчетам» и через год дом треснул. Огромная глубокая трещина через всю стену свела на нет все старания, стройка до сих пор стоит замороженная. Очень важно правильно и точно произвести расчеты будущего строения, что бы избежать неприятных неожиданностей и чтобы дом простоял не одно десятилетие.
Смотри видео о сайте
Приветствуем вас на нашем сайте Красивые дома. здесь вас ждет собрание ярких и неординарных интерьеров загородных домов и примеров ландшафтного дизайна.
Источник: designerdreamhomes.ru