Угол измеряется в градусах (°) и радианах. Он образуется между двумя соседними сторонами многоугольника. Каждый многоугольник имеет разные стороны и разное количество углов. Формула для нахождения углов в градусах полезна в геометрии и тригонометрии. Важно понимать и другие понятия математики, такие как дуга, центральный угол окружности и т. д.
- Полный круг = 360°
- Прямая линия = 180°
- Полукруг = 180°
- Четверть окружности = 90°
Вычисление углов в градусах
Существует три различных метода нахождения углов в градусах:
- Использование протектора D
- Использование теоремы Пифагора и тригонометрической функции в прямоугольном треугольнике
- Используя формулу суммы углов
- Центральный угол окружности
Использование протектора D
Протектор — это разновидность линейки или шкалы, которая используется для измерения расстояния в сантиметрах или миллиметрах. Протектор, используемый для измерения углов, имеет форму буквы «D» со значением угла, отмеченным от 0 до 180 ° в любом направлении (вправо или влево). Нам нужно выровнять ось с линией на D, чтобы измерить угол. Средняя окружность протектора совмещена с вершиной измеряемого угла. Лучи, проходящие через вершину угла, помогут найти угол в градусах.
Как отмерить прямой угол в помещении или на местности без угольника
Использование теоремы Пифагора и функции тригонометрии в прямоугольном треугольнике
В тригонометрии есть шесть функций: синус, кос, косек, тангенс, кот и сек. Прямоугольный треугольник имеет три стороны, основание, перпендикуляр и гипотенузу.
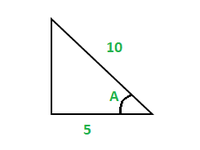
- Основание: это сторона, примыкающая к углу 90°.
- Перпендикуляр: это также сторона, примыкающая к углу 90°.
- Гипотенуза: Сторона, противоположная углу 90°.
Прямоугольный треугольник представлен углом 90 ° как один из углов. Сумма всех углов треугольника равна 180°.
- Cosecθ: Гипотенуза делится на перпендикуляр.
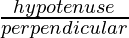
Cosecθ =
- Cotθ: представляет собой основание, разделенное перпендикуляром.
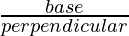
Cotθ =
Остальные тригонометрические функции представлены в виде:
sinθ =
Cosθ =
tanθ =
secθ =
Cosecθ can also be represented as 1/ sinθ
secθ can also be represented as 1/ cosθ
Cotθ can also be represented as 1/ tanθ
Where,
Θ is the angle
Теорема Пифагора
Если известны две стороны прямого угла, мы можем легко вычислить третью сторону прямоугольного треугольника. В прямоугольном треугольнике теорема Пифагора дается формулой:
(Hypotenuse) 2 = (Base) 2 + (perpendicular) 2
Формула суммы углов
Сумма углов относится к общей сумме внутренних углов многоугольника, образующегося между двумя сторонами. Если у многоугольника шесть сторон, то и углов примерно шесть. Это помогает найти угол, если известны другие углы и сумма углов многоугольника.
Строим прямой угол
Формула для нахождения суммы углов многоугольника выглядит следующим образом:
Total sum of angles = 180 (n – 2)
Where,
n is the number of sides of a polygon
Пример:
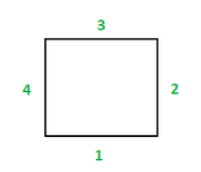
Total sum of angles = 180 (4 – 2)
= 180 (2)
= 360 °
If n = 5,
Total sum of angles = 180 (5 – 2)
= 180 (3)
= 540 °
- Если п = 6

Центральный угол окружности
Окружность – это фигура круглой формы, граница которой равноудалена от ее центра. Расстояние между центральной точкой и границей называется радиусом окружности. Угол, образованный двумя радиусами окружности, называется центральным углом. Значение центрального угла окружности лежит в пределах от 0 до 360 градусов.
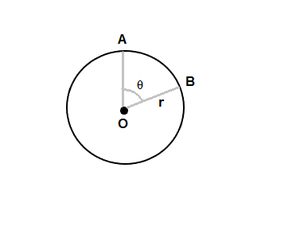
Формула для расчета центрального угла окружности:
Length of arc = 2πr × (θ/360)
Θ = 360L/2πr
Where,
r is the radius of the circle
AB is the arc
Theta is the angle in degrees.
L = Arc length
Примеры проблем
Вопрос 1: Найдите центральный угол окружности радиусом 2 м с длиной дуги 4 м?
Решение :
The formula to calculate the center angle of a circle is given by:
Θ = 360L/2πr
Where,
r is the radius of the circle
Theta is the angle in degrees.
L = Arc length
Θ = Angle in degrees
r = 2m
L = 4m
Θ = 360 × 4 /2× π × 2
Θ = 114.6°
Thus the central angle of the circle is 114.6°.
Вопрос 2: Найдите центральный угол окружности радиусом 10 см с длиной дуги 18 см?
Решение :
The formula to calculate the center angle of a circle is given by:
Θ = 360L/2πr
Where,
r is the radius of the circle
Theta is the angle in degrees.
L = Arc length
r = 10cm
L = 18cm
Θ = Angle in degrees
Θ = 360 × 18 /2 × π × 10
Θ = 103.13°
Thus the central angle of the circle is 103.13°.
Вопрос 3: Найдите угол параллелограмма, если три других угла равны 80°, 95° и 105°?
Решение :
There are four sides in a parallelogram with the total sum of angles 360°.
Formula to find the sum of angles = 180 (n – 2)
Where,
n is the number of sides of a polygon
Here, n = 4,
The total sum of angles = 180 (4 – 2)
= 180 (2)
= 360 °
Total sum = Angle 1 + Angle 2 + Angle 3 + Angle 4
360 = 80+ 95+ 105+ Angle 4
360 = 280 + Angle 4
Angle 4 = 360 – 280
Angle 4 = 80°
Вопрос 4: Найдите угол А на данном рисунке.

Решение :
Given: Hypotenuse = 12
Perpendicular = 6
The trigonometry function to calculate the angle is given by:
sinA = 6/12
A = 30°
Вопрос 5: Найдите угол А на данном рисунке.

Решение :
Given: Hypotenuse = 10
Base= 5
The trigonometry function to calculate the angle is given by:
CosA = 5/10
A = 60°
Вопрос 6: Найдите угол пятиугольника, если остальные четыре угла равны 115°, 100°, 105° и 100°?
Решение :
There are five sides in a pentagon with the total sum of angles 540°.
Formula to find the sum of angles = 180 (n – 2)
Where,
n is the number of sides of a polygon
Here, n = 5,
Total sum of angles = 180 (5 – 2)
= 180 (3)
= 540°
Total sum = Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5
540 = 115° + 100° + 105°+100° + Angle 5
540 = 420 + Angle 5
Angle 5 = 540 – 420
Angle 5 = 120°
Вопрос 7: Найдите угол А на данном рисунке.

Решение :
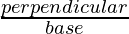
Given: Base = √3
Perpendicular= 1
The trigonometry function to calculate the angle is given by:
tanθ =
tanθ = 1/√3
A = 30°
Вопрос 8: Найдите угол параллелограмма, если три других угла равны 100°, 70° и 80°?
Решение :
There are four sides in a parallelogram with the total sum of angles 360°.
Formula to find the sum of angles = 180 (n – 2)
Where,
n is the number of sides of a polygon
Here, n = 4,
Total sum of angles = 180 (4 – 2)
= 180 (2)
= 360°
Total sum = Angle 1 + Angle 2 + Angle 3 + Angle 4
360 = 100 + 70 + 80 + Angle 4
360 = 250 + Angle 4
Angle 4 = 360 – 250
Angle 4 = 110°
Thus, the other angle is 110°.
Вопрос 9: Найдите угол шестиугольника, если остальные пять углов равны 120°, 115°, 110°, 125° и 105°?
Решение :
There are six sides in a hexagon with the total sum of angles 720°.
Formula to find the sum of angles = 180 (6 – 2)
Where,
n is the number of sides of a polygon
Here, n = 6,
Total sum of angles = 180 (6 – 2)
= 180 (4)
= 720°
Total sum = Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5 + Angle 6
720 = 120 + 115 + 110 + 125 + 105 + Angle 6
720 = 575 + Angle 6
Angle 6 = 720 – 575
Angle 6 = 145°
Thus, the sixth angle of hexagon is 145°.
Источник: progler.ru
Как найти прямой угол
Интересует, как найти прямой угол при помощи рулетки? Необходима Ваша помощь!
Спасибо!
Часто в быту необходимо найти прямой угол или же определить – острый угол или тупой (другими словами меньше или больше 90 градусов).
Все это изучается на уроках геометрии в школе, но мы рассмотрим метод, который может быть использован любым из нас без воспоминания о школьных правилах и теоремах.
Используем следующий рисунок.
На стороне a угла отмерим 60 см, а на стороне b – 80 см. Если от получившихся точек расстояние с будет составлять 1 метр (100 см), то имеющийся угол – прямой (равен 90 градусов). Если же расстояние окажется большим, то угол является тупым, а в случае меньшего от 1 метра расстояния – угол является острым.
Кто хочет более глубоко разобраться в вопросе почему именно такие цифры были взяты (60 и 80 см), то необходимо вспомнить теорему Пифагора, согласно которой нужно найти сумму квадратов катетов и найти квадратный корень из получившегося числа:
60 * 60 + 80 * 80 = 3 600 + 6 400 = 10 000
Корень из 10 000 равен 100.
Таким образом, получаем прямоугольный треугольник с катетами, равными по 60 см и 80 см и гипотенузой 100 см.
По представленной выше схеме можно также самому сконструировать угольник. Для этого нужно соединить две ровные деревянные планки под прямым углом и сбить их, например, гвоздём.
Далее измерить катеты по представленной выше схеме.
Соединить деревянной планкой первую и вторую метку.
Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
Выберите язык:
- Онлайн калькуляторы
- Справочник
- Примеры решений
- Заказать решение
- Учебные статьи
- О проекте
- Задать вопрос
- Контакты
- Карта сайта
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб на первый заказ.
Источник: ru.solverbook.com
Как сделать прямой угол без угольника. Как с помощью циркуля и линейки построить прямой угол
1й способ. — С помощью «золотого», или «египетского», треугольника . Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град . Этим качеством широко пользовались древние египтяне и другие пракультуры.
Илл.1. Построение Золотого, или египетского треугольника
- Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров . Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок ».
- Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
- Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
- В момент натяжения на линии границы – точка А, вбиваем колышек.
- Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
- После этого натягиваем мерку R5 – от А до В.
- В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника , со сторонами 3;4;5 и с прямым углом в точке О .
2й способ. С помощью циркуля .
Циркуль может быть веревочный или в виде шагомера . См:
Наш циркуль-шагомер имеет шаг в 1 метр.

Илл.2. Циркуль-шагомер
Построение – также по Илл.1.
- От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
- Ставим ногу циркуля в точку О.
- Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
- Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль .
- Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
- Проводим прямую (отрезок) через точки С и D.
- Все! Полученный отрезок, или прямая, — есть точное направление на север:). Простите, — на прямой угол .
- На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
- Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.

Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля
Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного . Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.
- Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.

Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки
- Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..
Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.
Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.
Угол 90 градусов.
Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол (90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.
А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.
Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.
Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т.д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.
Угол 45 градусов.
Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.
Угол 30 и 60 градусов.
Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.
Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.
Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов.
Можете проверить на транспортире — все точно!
Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.
Прямоугольность заготовки.
При разметке заготовок или построений на деталях кроме самих углов весьма важно и их соотношение. Особенно это важно при изготовлении прямоугольных деталей или например при разметке фундамента, раскрое больших листов материала. Неправильное построение или разметка приносит впоследствии много лишней работы или к появлению большого числа отходов.
К сожалению, даже весьма точные разметочные инструменты, даже профессиональные, всегда имеют определенную погрешность.
Между тем, существует весьма простой метод определения прямоугольности детали или построения. В прямоугольнике диагонали абсолютно равны! Значит, после построения необходимо измерить длины диагоналей прямоугольника. Если они равны, все в порядке, это действительно прямоугольник. А если нет — вы построили параллелограмм или ромб.
В этом случае следует немного «поиграть» смежными сторонами, что бы добиться точного (для данного случая) равенства диагоналей размечаемого прямоугольника.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).

Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)

В самом угольнике уже есть прямой угол. (Рис. 4)

Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).

1.

2.

3.

4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.

Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).

Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)

Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)

Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Общие правила для любого фундамента
Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.
Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен одной из сторон забора. Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.
Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.
Способ 1. Правило золотого треугольника
Для построения прямого угла будем применять теорему Пифагора.

Чтобы не углубляться в геометрию попробуем описать проще. Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки. Очень просто расчет сделать с помощью калькулятора.
Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.
Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21
Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.
Калькулятор
Также стоит отметить, что измерения можно производить в любых системах измерения длины главное использовать известное нам соотношение сторон: 3х4х5 метра, 3х4х5 сантиметра и т.п. То есть, если даже у вас нет инструмента для измерения длины, то можно взять, например, рейку (длина рейки не имеет значения) и померить ей (3 рейки х 4 рейки х 5 реек).
Теперь давайте посмотрим как это применить на практике.
Инструкция по разметке прямоугольного фундамента
Способ 1. Правила золотого треугольника (т.Пифагора)
Рассмотрим на примере построение прямоугольного фундамента с размерами 6х8м с помощью золотого треугольника (т.Пифагора).
1. Размечаем первую сторону фундамента. Это самая простая часть в построении нашего прямоугольника. Главное, что нужно помнить. Если хотим чтобы наш фундамент (дом) был параллелен одной из сторон забора либо другого объекта на участке или за его пределами, то первую линию нашего фундамента делаем равноудаленной от выбранного нами объекта. Данную процедуру мы описывали выше.
Для размещения первой бечевки можно использовать колушки, прочно закрепленные в грунте, но в идеальном варианте для данной цели использовать обноску. Ее и будем использовать. Расстояние между обносками для данной стороны сделаем 14м: между обносками и будущими углами по 3м и 8м под фундамент.
2. Натягиваем вторую бечевку максимально перпендикулярно первой. Идеально перпендикулярно на практике натянуть сложно, поэтому на рисунке мы также отобразили ее не много отклоненной.

3. Скрепляем обе бечевки в точке пересечения. Скрепить можно скобкой либо скотчем. Главное чтобы надежно.
4. Приступаем к формированию прямого угла с применением теоремы Пифагора. Будем строить прямоугольный треугольник с катетами 3 на 4 метра и гипотенузой 5 метров. Для начала отмеряем на первой бечевке 4 метра от места пересечения бечевок, а на второй 3 метра. Ставим отметки на шнурке с помощью скотча (прищепка и т.п.).

5. Соединяем рулеткой обе отметки. Один конец рулетки фиксируем у отметки в 4 метра и ведем в сторону отметки в 3 метра на другой бечевке.
6. Если у нас прямоугольный треугольник, то обе отметки должны сойтись при расстоянии в 5 метров. В нашем случае отметки не сошлись. Поэтому перемещаем бечевку в нашем случае вправо до того момента когда отметка на 3 м совпадет с делением рулетки на 5 м.

7. В итоге у нас получился прямоугольный треугольник с углом в 90⁰ между двумя бечевками.
8. Больше отметки нам не нужны и их можно убрать.

9. Приступаем к построению прямоугольника. Отмеряем на обеих бечевках длины сторон нашего фундамента 6 и 8 метров соответственно. Ставим отметки на бечевках.
10. Натягиваем третью бечевку максимально перпендикулярно к первой бечевке. Скрепляем обе бечевки на отметке в 8 м.

11. Натягиваем четвертую бечевку максимально перпендикулярно ко второй бечевке. Скрепляем обе бечевки на отметки в 6 метров.
12. Делаем отметки на третьей бечевке 6 метров и на четвертой 8 метров.

13. Чтобы получить четырехугольник с прямыми углами в нашем случае необходимо, чтобы обе отметки на третьей и четвертой бечевках совпали. Для этого перемещаем обе бечевки до момента соединения отметок.
14. В итоге, если все правильно измерили, то у нас должен получиться правильный прямоугольник. Давайте проверим, получился ли он с помощью измерения диагоналей.

15. Измеряем длины диагоналей. Если они одинаковые, как в нашем случае, мы имеем правильный прямоугольник. Диагонали имеют одинаковую длину и в равнобедренной трапеции. Но у нас известен один угол в 90⁰, а в равнобедренной трапеции таких углов нет.

Способ 2. Паутина
Очень простой способ сделать разметку в виде прямоугольника с углами в 90⁰. Самое главное что нам понадобится — это бечевка, которая не растягивается, и точность ваших измерений с помощью рулетки.
1. Нарезаем куски бечевки, которые нам понадобятся для формирования разметки. В данном примере мы строим фундамент со сторонами 6 на 8 метров. Также для правильного построения прямоугольника нам понадобятся равные диагонали, которые для прямоугольника 6 на 8 метров будут равны 10 метрам (т.Пифагора описана выше). Также нужно взять запас длины бечевок на крепление.
2. Соединяем нашу «паутину» как на рисунке. Скрепляем стороны с диагоналями в 4 местах по углам. Сами диагонали в точке пересечения скреплять не нужно.

3. Натягиваем первую бечевку (точки 1,2). Крепить ее будем с помощью колышков. Главное чтобы колышки крепко держались в земле и при натяжении нашей конструкции их не увело. Этот важный момент нужно учесть.
4. Натягиваем угол 3. Главное условие чтобы бечевка 1-3 и диагональ 2-3 не провисали и были максимально натянуты. После фиксации с помощь колышка в точке 3 мы имеем угол в точке 1 в 90⁰.

5. Натягиваем угол 4 и устанавливаем колышек. Следим, чтобы бечевка в точках 2-4, 3-4 и диагональ 1-4 не провисали и были максимально натянуты.
6. Если соблюдены все условия, то в результате у нас должен получиться прямоугольник с углами максимально близкими 90⁰.

Разметка под фундамент дома
Делаем двухъярусную обноску. Нижний ярус – это уровень столбов.

Верхний ярус обноски – уровень ростверка.

Создаем прямоугольник для внешнего контура применяя т.Пифагора. Затем отступаем на величину, равную ширине ленты и делаем внутренний контур.


От автора
В данной статье мы рассмотрели, как произвести разметку под фундамент своими руками с построением прямоугольника с углами в 90⁰. В целом ничего сложно в разметке нет. Цена вопроса – это стоимость бечевки, доски для обноски (эконом вариант — колышки) и умение пользоваться рулеткой.
Люди, которые впервые строят загородный дом самостоятельно, часто теряются при разметке участка. Действительно, отложить на местности угол или провести прямую линию ощутимо сложнее, чем на бумаге — масштабы иные. Осложняется дело тем, что природный участок никогда не бывает идеально ровным и всегда находятся особенности ландшафта, мешающие измерению. Тем не менее, проблема решаема.
В основе разметки лежат принципы геометрии, которая изначально служила именно этой цели: само слово в переводе с греческого означает “измерение земли”. Так что откладывать углы на местности — не новое дело, похожее на черчение в школьной тетради. Тем не менее, разница существенна: для построения фигуры на бумаге используются линейка и циркуль, а на реальном участке их не применишь.
Как построить прямой угол на местности
Выручит в этой ситуации длинная армированная нить или подходящий шпагат (”бельевая” веревка).
С помощью нити строят прямые линии и отрезки. Для этого в начальной точке в землю вбивают колышек, к которому привязывают один конец нити. Затем нить натягивают в нужном направлении, в случае построения отрезка — на заданную длину, заранее отмеченную на нити. В полученной точке вбивают второй колышек и, туго натянув, привязывают к нему нить.
Если шпагат используется только для измерения, то имеет смысл предварительно нанести на него метражную шкалу. Для этого каждый второй метр покрывают черной краской, желательно водостойкой, а каждый пятый — яркой (например, красной). Такая “зебра” упрощает разметку, позволяя быстрее отмерять длинные отрезки. Иногда имеет смысл сделать шкалу более мелкой, раскрасив каждые 50 или даже 20 см шпагата.
Если рельеф очень неровный, то лучше использовать “подвесную” разметку, вбивая разные по высоте колышки (рис. 1, а). Если разница по высоте между начальной и конечной точкой слишком велика (участок расположен на крутом склоне), то задача немного усложняется. Можно использовать несколько колышков, суммируя расстояние между ними.
Правда, выполняя разметку “ступеньками”, нужно следить за тем, чтобы угол между колышком и веревкой оставался прямым. (Рис. 1, б).
Для того чтобы отложить на местности прямой угол, можно использовать принцип треугольника, где стороны относятся как 3:4:5 (так называемая “пифагорова тройка”). В этом случае треугольник является прямоугольным, с углами в 90, 60 и 30 градусов. Меньшие стороны — катеты, угол между ними — прямой.
На практике метод применяется следующим образом. На местности, из начальной точки “0″ (см. рис. 2), отмеченной колышком, проводится прямая линия, на которой откладывается отрезок длиной 4 метра — сторона будущего угла (”а”). Конец отрезка (точка “1″) отмечается колышком.
Затем, к начальному колышку привязывается нить, с отметкой на расстоянии ровно 3 метров от колышка, и на глаз укладывается на земле, приблизительно по направлению второй стороны угла (”b”). Из точки 1 к концу нити b аналогично прокладывается нить с отметкой на 5 метрах (”c”). Затем нити b и c нужно взять в разные руки, максимально натянуть и в таком состоянии свести их вместе, точно совместив отметки (точка “2″). В результате получится треугольник, где “нулевой” угол окажется прямым. Для наглядности приведен схематичный рисунок.
Длины направляющих нитей могут быть большими или меньшими, но обязательно должны соотноситься как 4:3:5. Очевидно, что прямой угол будет всегда лежать напротив большей стороны треугольника.
Этим же способом можно легко отложить практически любой угол, кратный 30 градусам, подбирая длину направляющих нитей. Вот соотношение длин для некоторых углов: 90 градусов (а = 4; b = 3; с = 5), 60 градусов (а = 3; b = 5; с = 4 или а = 5; b = 5; с = 6), 30 градусов (а = 5; b = 4; с = 3), 120 градусов (а = 5; b = 5; с = 8)
Как правильно рассчитать прямой угол
Как найти прямой угол 90 градусов
Как найти угол 90 градусов с помощью строительной рулетки и карандаша?
Многие строители сталкивались с такой проблемой — как найти угол 90 градусов или, как узнать — угол тупой (больше 90 градусов) или острый (меньше 90 градусов).
Не будем, возвращается к школьной геометрии, и изучать хитроумные слова, а рассмотрим на практике, где каждый человек, буквально за одну минуту, сможете определить, сколько градусов имеет тот или другой угол. А за 5 минут, вы сможете сделать точный угольник с прямым углом, то есть 90°.
Возьмем к примеру.
На одной стороне (на катете “ a ”) отмеряем 60 см. Затем на другой стороне (катет “ b ”) отмеряем 80 см. Если от точки “ a ” к точки “ b ” перпендикуляр “ c ” будет составлять 100 см (1 метр) значит, угол имеет 90 градусов. Если больше, например 1.1 м угол тупой, а когда 0.9 м, угол острый. Таким образом, с помощью строительной рулетки и карандаша мы смогли получить прямой угол.

Теперь разуберём цифры 60 и 80 и почему перпендикуляр должен иметь 1 м. Берем комбинацию чисел “3,4,5” и каждую цифру умножаем на свое придуманное число – например “5”.
3(умножаем)5=15 катет
4*5=20 катет
5*5=25 гипотенуза
В выше представленном примере, мы взяли числа “30, 40, 50” и каждое число умножили на “2”, таким способом, у нас получилась такая комбинация:
30*2=60 катет
40*2=80 катет
50*2=100 гипотенуза
Как сделать угол 45 градусов с помощью строительной рулетки и карандаша?
Перед тем, чтобы получить угол 45 градусов, по выше изложенной системе сделайте прямой угол. Затем, на катете “ а ” и ” b ” измеряем одинаковые размера и проводим гипотенузу. Измеряем гипотенузу и разделяем на два (/2). Затем проводим линию к прямому углу. Таким способом мы разделили 90 градусов на 45 – две одинаковые части по 45°.

Как сделать самому угольник с прямым углом за 5 минут?
1 Соединяем между собой две ровные деревянные рейки, так чтобы одна из них была перпендикулярная другой.

2 Затем измеряем два катета по выше изложенной системе.

3 Прибываем деревянную рейку к первой метке

4 Измеряем гипотенузу и фиксируем на втором катете.

5 Проверяем все размеры и во всех местах дополнительно фиксируем.

6 Затем лишние части обрезаем.

Как найти прямой угол 90 градусов видео
Как сделать прямой угол между стенами.
Древнегреческие геометры и, в частности Евклид, старались зря, их знания до советских строителей так и не дошли. В том смысле, что прямоугольных помещений в советских домах не бывает. А бывают в лучшем случае в виде параллелограмма, усеченной трапеции или ромба, а в худшем и наиболее распространенном в виде неправильного четырехугольника.
Это довольно часто затрудняет качественную отделку помещений. Приходится искать прямой угол самому. Сделать это в общем-то несложно.
Разметку проще всего производить на полу. Для этого Вам понадобятся:
- Маркер, мел или карандаш
- Строительный уровень, суровая нитка или строительный шнур.
- Рулетка.
С помощью строительного уровня или отвеса (проще — с помощью уровня, точнее — с помощью отвеса) определите выпирающие участки стен. В этих местах перенесите вертикальные отметки на пол. Проведите через 2 отметки вдоль каждой стены прямые линии так, чтобы остальные отметки (если они у Вас есть) остались между линией и стеной.

Если стены перпендикулярные это расстояние должно равняться
1.414 м более точно 1.41421356 м, но такая точность вам не понадобится.
Если расстояние (гипотенуза треугольника) больше, то у Вас вместо прямого угла между стенами тупой. Для того, чтобы получить прямой угол, приложите начало рулетки к точке пересечения линий в углу и нарисуйте небольшую дугу радиусом 1 м. Затем приложите начало рулетки к отметке на линии вдоль стены принятой за основу и нарисуйте небольшую дугу радиусом 1.414 м. Проведите через точку пересечения дуг и точку пересечения линий в углу прямую линию.
Эта новая линия и будет контуром стены. Если это для Вас слишком сложно, то просто отмерьте на гипотенузе 1.414 м от отметки у той стены которую вы приняли за основу. Проведите прямую линию через полученную отметку и точку пересечения линий в углу. В этом случае Вы получите не прямой угол, но все же намного ближе к прямому, чем тот который был.

Как вычислить прямой угол
Если линии, образующие угол, начерчены на бумаге, то определить, что угол является прямым можно, например, с помощью транспортира. Приложите его параллельно любой из сторон таким образом, чтобы нулевая отметка совпала с вершиной угла. Если другая сторона угла соответствует девяностоградусному делению транспортира, то вас можно поздравить — вы определили, что именно этот угол и является прямым. Это же самое можно проделать и с помощью угольника, а если абсолютной точности не требуется, то даже с использованием других имеющихся под рукой предметов — спичечного коробка, дискеты, пластиковой коробки CD/DVD-диска и любого другого прямоугольного предмета.
Если в условиях задачи даны длины сторон треугольника, то вам следует определить ту из них, которая является гипотенузой — угол, лежащий напротив нее, будет прямым. Гипотенуза — это всегда самая длинная сторона прямоугольного треугольника, поэтому с предварительным определением ее проблем не будет.
Разметка фундамента под дом. Рассказывают форумчане
Если таких окажется две, то треугольник не является прямоугольным и нужного вам угла в нем нет вообще. В противном случае произведите дополнительную проверку — квадрат длины гипотенузы должен быть равен сумме квадратов длин двух коротких сторон (катетов). Если это так, то лежащий напротив длинной стороны угол (его обычно обозначают буквой γ) является прямым.
Если вам нужно рассчитать построение прямого угла, то проделайте операцию, обратную описанной в предыдущем шаге. Сначала определите длины двух сторон, которые будут этот угол образовывать. Проще работать с правильным равнобедренным треугольником, поэтому лучше взять одинаковые длины катетов.
Если результат надо отобразить на бумаге, то отложите на циркуле нужную длину, поставьте точку в вершине будущего угла и обозначьте ее буквой А. Начертите круг с центром в этой точке и проведите радиус, обозначив точку его касания с окружностью буквой В. Затем рассчитайте длину гипотенузы — умножьте длину катета на квадратный корень из двойки. Полученное значение отложите на циркуле и начертите второй круг с центром в точке В. Затем соедините точку пересечения двух окружностей (точка С) с центром первого круга (точка А). Это и будет прямой угол ВАС.
Комментариев пока нет!
Видеоурок «Построение прямых углов на местности» — видеоматериал, который может быть использован учителем на уроке геометрии для ознакомления с методами построения углов на местности. Данный материал содержит информацию об устройстве измерительного инструмента — экера, а также подробное описание способа измерения данным прибором углов на местности. Материал выявляет практическое применение предмета, связывает геометрию со сферами жизни человека.
Выполняем точную разметку фундамента самостоятельно
Данная информация вызывает большую увлеченность предметом изучения, помогает лучше усвоить учебный материал.
Использование видеосредств дает возможность ознакомиться с устройством прибора, не прибегая к дополнительному оборудованию для демонстрации прибора, его устройства и принципа действия. При изучении одноименной темы видеоматериал может стать помощником учителя, заменяя его рассказ об устройстве и действии прибора наглядным подробным описанием с голосовым объяснением. Также данный материал может быть рекомендован для самостоятельного изучения при углубленном изучении материала, а также просто дополнить урок геометрии или внеклассные занятия по математике познавательной информацией.
Видеоурок начинается с объявления названия темы «Построение прямых углов на местности». Ученик информируется о том, что для построения углов на местности используются специальные приборы. Среди таких приборов рассматривается простейший измерительный прибор экер.
На экране отображается нарисованный экер, который представляет собой два бруска, угол между которыми составляет 90°. Данный прибор укрепляется на треножнике, для принятия им устойчивого положения. Прибор дополнен вбитыми в его бруски гвоздями так, что угол между прямыми, проведенными через них, будет прямым, то есть эти прямые перпендикулярны между собой.
Построение прямых, угол ∠АОВ между которыми составит 90°, начинается с правильного расположения прибора. Экер устанавливается таким образом, что находящийся в его центре отвес располагается непосредственно над точкой, являющейся вершиной угла. Направление одного из брусков следует за направлением одной стороны угла.
Закрепить данное направление можно при помощи установки вехи, фиксирующей прохождение стороны ОА. Чтобы построить прямой угол, в направлении второго бруска также проставляется веха, фиксирующая направление прямой. Таким образом получается прямой угол, построение которого обусловливается установленными вехами.
Данный прибор несовершенен, это простейший инструмент для построения углов на местности, поэтому ученикам демонстрируется специальный прибор, применение которого широко распространено в строительстве и архитектуре — это теодолит.
Видеоурок «Построение прямых углов на местности» рекомендуется как наглядное пособие для проведения урока по одноименной теме. Также его можно использовать в качестве дополнения к внеклассной работе по математике, для дистанционного обучения, для самостоятельного освоения материала.

Обычно прямая линия вдоль одной из 2 самых широких стен принимается за основу, если нет каких либо других точек отсчета. В этом случае площадь помещения при дальнейшей отделке будет уменьшена минимально.
Отмерьте от одного из углов с помощью рулетки 1 м и поставьте отметку на линии. Сделайте то же самое на перпендикулярной (возможно, не совсем) линии.
Соедините полученные отметки так, чтобы получился треугольник.
Измерьте расстояние между полученными отметками.
Если стены перпендикулярные это расстояние должно равняться ~ 1.414 м более точно 1.41421356 м, но такая точность вам не понадобится.
Если расстояние (гипотенуза треугольника) больше, то у Вас вместо прямого угла между стенами тупой.
Как построить прямой угол?
Для того, чтобы получить прямой угол, приложите начало рулетки к точке пересечения линий в углу и нарисуйте небольшую дугу радиусом 1 м. Затем приложите начало рулетки к отметке на линии вдоль стены принятой за основу и нарисуйте небольшую дугу радиусом 1.414 м. Проведите через точку пересечения дуг и точку пересечения линий в углу прямую линию. Эта новая линия и будет контуром стены. Если это для Вас слишком сложно, то просто отмерьте на гипотенузе 1.414 м от отметки у той стены которую вы приняли за основу. Проведите прямую линию через полученную отметку и точку пересечения линий в углу. В этом случае Вы получите не прямой угол, но все же намного ближе к прямому, чем тот который был.
Если расстояние (гипотенуза треугольника) меньше, то у Вас вместо прямого угла между стенами острый. Для того, чтобы получить прямой угол, отступите от отметки на линии вдоль стены, принятой за основу, несколько сантиметров. Нарисуйте на полу небольшие дуги по принципу, изложенному в предыдущем пункте. Полученную линию можно перенести ближе к стене. Главное условие — отметки выпирающих участков стены должны остаться между новой линией и стеной.
Если Вы не совсем поняли этот текст, то рисунок поможет Вам лучше разобраться:

От полученных 2 сторон прямоугольника методом параллельного переноса определяются оставшиеся 2 стороны.
 |
Какой угол образуют стены. Первый способ — измерение.
Для проектирования мебели мы не только должны измерять длину и высоту стен в квартире или доме, но и необходимо измерить угол в который будет установлена мебель.
Для чего это нужно делать? — чтобы не возникали проблемы с монтажем, чтобы избежать огромные боковые щели, и для того чтобы еще на производстве можно было проводить необходимые корректировки.
К примеру развернутый угол не позволит смонтировать угловую кухню без дополнительных подрезов внутренних угловых модулей и столешницы. Острый угол может потянуть выход корпуса мебели за габариты установочных размеров, потому что в влотную в угол невозможно установить мебельный модуль.
Собственно, когда причины выяснили и необходимость измерения угла очевидна — дело за малым — измерить угол.
Если у Вас имеется в домашнем арсенале угломер — тогда без проблем, а если нет, то нижеописанный способ всегда прийдет на помощь.
Первое что необходимо сделать — это отметить две точки на стенах в одном уровне (на высоте где будет установлен мебельный модуль) следующим образом:
- От угла рулеткой отмеряете по левой и правой стене размер к примеру 500мм. и ставите точки.
- Далее измеряете диагональ — т.е. расстояние между точками.
Итак например у нас есть три размера — катет 500мм., 500мм. и диагональ 700мм.
Следующий этап -это построение угла на шаблоне из любого материала. В нашем случае я покажу как это сделать в программе autоcad, но тоже можно сделать имея циркуль, линейку, транспортир и материал для шаблона.
- Чертим горизонтально отрезок 500мм. с точками «АБ». (см. чертеж ниже.)
- Чертим окружность с радиусом 500мм. с центром в точке «В».
- Чертим вторую окружность с радиусом 700мм. с центром в точке «А».
- В точке пересечения окружностей ставим точку «С».
- Соединяем точки «В» и «С» отрезком и получаем наш угол.
- Далее остается измерить угол транспортиром на шаблоне или специальным инструментом в программе autоcad. и уже имеющийся чертеж применить для проектирования.



Когда чертеж построен, мы можем в заключении сделать вывод — измеряемый угол 89градусов, угол острый и негативно повлиять на установку мебели он не сможет, т.к.
Как точно разметить прямой угол на местности, не имея транспортира?
1 градус величина довольно малая.
Какой угол образуют стены. Второй способ — расчёт.
- От угла отмеряем 1000 мм (чем больше, тем лучше — погрешность меньше… конечно если вы для полочки 400*400 мм, то больше чем 400 мм отмерять не надо) на обеих стенах, и ставим отметки (если обои то можно иголками);
- Замеряем расстояние между отметками (лучше делать это вдвоем, опять же из соображений точности), допустим у нас получилось 1500 мм.
Т.е. по примеру это: (10002+ 10002– 15002) / (2 1000 1000) = -0.125 отсюда arccos (-0.125)= 97.18 градусов.
Пользователь Настя Галкина задал вопрос в категории Прочее образование и получил на него 11 ответов.
Как построить прямой угол?
Существует метод построения прямого угла с помощью циркуля и линейки. Сначала нужно циркулем обрисовать окружность и начертить ее диаметр. Затем отметить на окружности произвольную точку и соединить ее с концами диаметра: получится треугольник, вписанный в окружность. Его угол (с вершиной в точке на окружности) будет прямым.
Второй способ – нарисовать две любые пересекающиеся окружности. Две точки пересечения соединить одной линией, другую – провести через центры окружностей. Два этих отрезка пересекутся под углом 90 градусов. Если нет чертежных инструментов, можно воспользоваться любыми прямоугольными предметами. Это может быть лист картона, любая упаковка (от лекарства, пачка от сигарет, коробка конфет и т. д.), книжка, рамка для фото и др.
Как с помощью циркуля и линейки построить прямой угол
Как построить прямой угол?
Прежде, чем узнать, как построить прямой угол, нужно вспомнить его определение. Прямым называется угол в девяносто градусов, образованный двумя перпендикулярными прямыми. Можно также сказать, что это половина развернутого угла. Существует несколько способов построения прямого угла.
Способы построения прямого угла
Самое простое – построение прямого угла при помощи чертежного угольника. Его прикладывают к бумаге и проводят линии вдоль перпендикулярных сторон: получается прямой угол. Также можно использовать транспортир. К проведенной карандашом линии приложить транспортир, отметить на бумаге угол девяносто градусов. Затем соединить линией (по линейке) эту отметку с линией на бумаге.
Существует метод построения прямого угла с помощью циркуля и линейки. Сначала нужно циркулем обрисовать окружность и начертить ее диаметр. Затем отметить на окружности произвольную точку и соединить ее с концами диаметра: получится треугольник, вписанный в окружность.
Как разметить фундамент. Строительный лайфхак своими руками
Его угол (с вершиной в точке на окружности) будет прямым. Второй способ – нарисовать две любые пересекающиеся окружности. Две точки пересечения соединить одной линией, другую – провести через центры окружностей. Два этих отрезка пересекутся под углом 90 градусов. Если нет чертежных инструментов, можно воспользоваться любыми прямоугольными предметами.
Это может быть лист картона, любая упаковка (от лекарства, пачка от сигарет, коробка конфет и т. д.), книжка, рамка для фото и др.
Построение прямых углов на местности
Вообще, построение прямых углов на местности необходимо в строительстве, при разделе участков земли и т. д. Для этого используются специальные приборы – экер, астролябия, теодолит. Но, вряд ли эти инструменты окажутся, к примеру, на дачном участке. Тогда можно воспользоваться методом, применяемым с давних времен. Понадобятся три колышка и веревки по 3, 4 и 5 метров.
Воткнуть в землю колышек, к нему привязать веревки 3 и 4 метра, а к их концам – остальные колья. Последние два колышка соединить 5-метровой веревкой, натянуть получившийся треугольник, и забить эти колья в землю. Угол треугольника с первым колышком будет прямым.
Как видите, существует масса несложных способов построения прямого угла.
Как с помощью циркуля и линейки построить прямой угол
Как с помощью циркуля и линейки построить угол, зная тангенс этого угла?
Для начала вспомним, что такое тангенс
С помощью циркуля и обычной линейки (без делений) построим две перпендикулярные прямые
Построим угол, тангенс которого равен 2/3.
Отмерим циркулем произвольный отрезок и от точки пересечения отложим вверх два раза, затем влево три раза. Проведем через эти точки луч, как показано на рисунке. Угол построен.
Построим угол, тангенс которого равен корню кубическому из трех.
С помощью калькулятора найдем это число
Округлим до удобного нам значения 1,25 и запишем в виде неправильной дроби 5/4. Аналогично с предыдущим способом с Помощью циркуля отложим пять одинаковых отрезков вверх и четыре влево. С Помощью линейки проведем через них луч. Угол построен.
Построим угол, тангенс которого равен Π .
И все также, как в предыдущих примерах — 19 отрезков вверх и шесть влево, соединили — и угол построен.
Хочу добавить — в связи с тем, что я немного менял значения, в результат построения углов заложилась Маленькая погрешность , но невооруженным глазом и даже с помощью транспортира она будет незаметна.
Можно легко проверить — берем калькулятор
И насчет правильности построения угла по способу, который я указал — с помощью компьютерной программы строим углы по заданным параметрам, затем строим по моему способу — сравниваем и убеждаемся — кто прав, а кто не прав. — более месяца назад
Как известно, по соотношению сторон прямоугольного треугольника можно найти все эти тригонометрические величины. В частности, тангенс угла определяется как соотношение длины катета (стороны), лежащей напротив данного угла, и стороны, примыкающей к данному углу. Следовательно, порядок действия будет следующий:
1) проводим любую прямую линию;
2) проводим другую линию под прямым углом к ней — для этого циркулем проводим окружность любого радиуса с центром, расположенным на первой прямой, а затем еще одну окружность того же радиуса с центром, расположенным в точке пересечения первой окружности и первой прямой; прямая, проведенная через две точки пересечения данных окружностей, будет перпендикулярна первой;
3) из точки пересечения первой и второй прямой — вершины прямого угла — отмеряем отрезок любой подходящей длины на первой прямой, считаем, что это прилежащий катет;
4) зная соотношение — тангенс, вычисляем длину второго отрезка-катета — противолежащего, (умножаем тангенс на длину первого отрезка), и отмеряем его из той же точки / вершины на второй прямой;
5) соединяем все вершины получившегося прямоугольного треугольника, один из углов которого, со стороной на первой прямой, является искомым.
FEBUS , я понял, кажется, что вы имеете ввиду — при tgA = π угол получается близким к 90 градусов, а если тангенс угла стремится к бесконечности — так вообще, длина линейки для построения такого треугольника тоже должна быть бесконечной. Ну и что, собственно? Длина одного катета будет в 3,14 раз больше, чем длина другого — такой треугольник вполне можно построить указанным методом. Что не так-то? — более месяца назад
Тангенс это отношение катета, противолежащего углу к катету, прилежащему к углу.
Тангенс надо представить в виде дроби числителя(это величина противолежащего катета) и знаменателя (величина прилежащего катета)
Чертим прямую и проводим к ней перпендикуляр точка пересечения это вершина прямого угла (точка А)
Из точки пересечения (вершины прямого угла — точка А) на прямой надо отложить отрезок, равный величине противолежащего катета (точка В).
На прямой надо отложить отрезок, равный величине прилежащего катета (точка С)
Соединяем точки В и С получился треугольник АВС
Тангенс угла АСВ равен известному тангенсу.
Представьте в виде дроби tgA = π. — более месяца назад
Чтобы построить угол с заданным значением тангенса угла, циркуль не нужен, достаточно одной линейки.
В системе координат откладываем по оси абсцисс (Х) единицу, по оси ординат (У) откладывает значение тангенса угла. Точку с такими координатами соединяем с началом системы координат. Угол между осью Х и построенной линией — искомый угол.
Тангенс = отношение противоположного катета к прилежащему, т. е. tg (a) = У/Х.
Источник: ik-ptz.ru
Как проверить прямой угол между стенами

Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
Как сделать самому угольник с прямым углом за 5 минут?
1. Соединяем между собой две ровные деревянные рейки, так чтобы одна из них была перпендикулярна другой.
2. Измеряем два катета по выше изложенной системе.
3. Прибиваем деревянную рейку к первой метке.
4. Измеряем гипотенузу и фиксируем на втором катете.
Прямой угол между стенами необходим довольно часто. Например, чтобы грамотно установить ванну, кухонную мойку или стол. Но большинство людей просто не берут в расчет такую необходимость, а потом жалеют, когда между ванной и стеной возникает сантиметровая щель. Также непрямой угол выявляется по напольной плитке, когда подрезка по бокам получается разной.
А бывают ситуации и еще хуже. Поэтому отнеситесь к данному материалу со всей серьезностью.
Строители, возводящие современные дома, вопреки мнению большинства, не заботятся о близости углов в квартирах к 90 градусам. Им важен только объем работы, а часто им даже не дают никакого измерительного . Только мастерок, да полутерок. «Ваяй, Ровшан!»
Как сделать прямой угол между стенами после такой халтуры? Здесь есть два варианта: либо мы штукатурим по маякам, либо выравниваем стены гипсокартоном. И если во втором случае никаких сложностей возникнуть не должно – просто крутим профили по угольнику, то с все немного сложнее. Кстати, вариант «да я плиткой все выровняю» тоже не прокатит.
Практика показывает, что все те, кто пытается сделать прямой угол путем плавного наращивания слоя плиточного клея, неизменно косячат. Причем и угол у них прямой не получается, и плитка лежит криво. Если вы нашли в себе силы и смелость штукатурить по маякам, то без проблем сможете сделать идеальный прямой угол. На который совершенно спокойно уложите плитку «под гребенку».
Первый основополагающий принцип штукатурки под прямой угол – сначала штукатурим одну стену обычным образом.
Обычно самую длинную. Целиком. Гораздо проще и быстрее строить угол уже от готовой плоскости.
Что дальше? Вам понадобятся два штукатурных правила. Желательно длиной во всю стену. Часто ванные имеют размеры в районе 175х175, так что, в таком случае, берете две «двушки» и болгаркой или ножовкой укорачиваете их.
Предположим, что одну стену вы уже оштукатурили в идеале. А смежная имеет размеры 175х275 см. В этом случае понадобятся два маяка. Размечаем их. Все как положено, на расстоянии 30 см от стен. Но здесь есть один важный нюанс. Пара нижних саморезов должна находиться строго в одном уровне. Соответственно, пара верхних – тоже. Немного позже узнаете, почему.
И еще рекомендуется отбить на оштукатуренной стене линию, лежащую в одном уровне с нижней парой саморезов.
Дальше бурятся отверстия, в них загоняются дюбели и саморезы. Что теперь? С простым полуметровым угольником ничего вы, понятное дело, не сделаете. Решение лежит на поверхности – нужен угольник побольше. Он делается из двух правил. Но как сделать так, что бы они образовали строго угол в 90 градусов? Не по маленькому же угольнику, в этом ведь никакого смысла.
Все гораздо проще.
Есть теорема Пифагора. Которая однозначно устанавливает соотношения сторон прямоугольного треугольника. Корень из суммы квадратов катетов равен гипотенузе. Вспоминайте школьный курс геометрии. Это все значит, что, если вы сможете построить на полу треугольник, стороны которого будут соотноситься таким же образом, один из его углов будет абсолютно точно равен 90 градусам.
Самый простой случай – это т.н. Египетский треугольник, у которого стороны соотносятся как 3:4:5. Обычно удобно взять на практике 120:160:200 см.
Итак, на полу рисуется линия карандашом. Маркером — нежелательно, здесь же важна точность. На ней ставятся две точки: одна с краю, вторая – на удалении 120 см от первой. Затем берется отрезок маяка, либо можно воспользоваться рулеткой. Нужно будет отложить от первой точки 160 см, а от второй – 200 см.
Точнее построить фрагменты окружностей указанных радиусов. Точка пересечения этих фигур и будет являться третьей вершиной треугольника. Остается только соединить вершины. Все, вы построили прямоугольный треугольник с высокой точностью.
Следующий шаг – положить на пол два правила в точности по линиям. Так как они будут лежать скошенными гранями наружу, это будет не так просто. Придется воспользоваться угольником. Итак, правила совмещаются с линиями:
Теперь необходимо надежно скрепить их между собой. Это обычно делается саморезами с прессшайбой или черными саморезами по металлу. Главное при этом – не допустить смещения правил относительно линий под воздействием вибрации от шуруповерта или дрели. Достаточно скрепить правила в двух точках:
Но, в целом, этого недостаточно. Нужно применить дополнительную планку из защитного уголка Кнауф, например. Крепим ее, как показано на рисунке:
Теперь у вас есть огромный, жесткий, а главное, точный угольник. Вы возвращаетесь в помещение, где у вас будут маяки. Там уже намечена линия, по которой вы и будете прикладывать угольник. Да, нужно располагать его строго в горизонтальной плоскости, иначе получится погрешность.
Вы уже предварительно должны были оценить степень отклонения угла от 90 градусов, поэтому знаете, какой саморез из нижней пары взять за основу. Предположим, что угол был тупой, поэтому выкручивается на минимум (7-8 мм) ближний к уже оштукатуренной стене саморез. А дальний уже будет выкручиваться по угольнику.
Прикладываете его к линии на уже готовой стене и к выставленному саморезу нижней пары на размечаемой. Смотрите. Допустим, дальний саморез не достает до угольника примерно 4 мм. Выкручиваете его примерно на это расстояние и снова оцениваете ситуацию угольником.
Возможно, придется прикладывать его несколько раз, но, в целом, процесс установки самореза займет у вас не более пары минут. Если же изначально угол был острый – первым выставляйте дальний саморез. А ближний – по угольнику.
Верхнюю же пару саморезов выставлять этим же угольником неудобно – он тяжелый, поднимать его сложно, он постоянно соскальзывает со шляпок. Поэтому проще будет выставить их просто вертикально относительно нижней пары. По отвесу или пузырьковому уровню. В любом случае, если первая стена у вас выровнена в идеале, получится идеально прямой угол и сверху, и снизу, автоматически.
Если вам нужно выставить прямой угол и на противоположной стене – то нет проблем, делаете все точно так же. Такое бывает необходимо, например, если ванна по габаритам встает впритык к стенам. Заодно и подрезка плитки на полу получится в идеале. Рекомендуется не выставлять заранее все маяки, а потом штукатурить.
Гораздо лучше, хоть и дольше, будет поочередная разметка и штукатурка каждой стены. Зато вы будете точно знать, что нигде не ошиблись.
Теперь вы знаете, как сделать прямой угол между стенами при штукатурке. Потратив пару часов на разметку, вы сэкономите больше на укладке плитки, и получить профессиональное качество будет гораздо проще.
Июн 6, 2014 ADMIN
Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Математика. Это страшное для многих слово
, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке
, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Решение задачи
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру

Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис.
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
Итоговые рекомендации
Что бы принять штукатурные работы и проверить их качество вы должны знать как проверить ровность стен, вам необходим новый строительный уровень, рулетка и новое правило высотой 2 2.5 метра.
1.Проверяем отклонения по вертикали и горизонтали Допускаются перепады плоскости стен от вертикали на 1 метр их длины на 1 миллиметр. На всю высоту помещения не больше 5 миллиметров. Плоскости стен от горизонтали, на 1 метр их длины 1 миллиметр. Совет! Обязательно проверяйте каждые два метра поверхности стены.
2. Проверяем ровность стен Поверхность может иметь не более двух неровностей плавных очертаний на 4 квадратных метра глубиной или высотой не более 2 миллиметров. Проверить это можно с помощью правила. Внимание! Проверяйте помимо видимых зон и в местах труднодоступных.
3. Проверяем прочность отштукатуренной поверхности Трещин быть не должно. Ударьте раскрытой ладонью по поверхности в нескольких местах по вашему усмотрению, если услышите гулкий звук от удара и ощутите отслоение, то работы необходимо переделывать. Внимание: Проконтролируйте, чтобы все металлические маяки были удалены из стен.
4. Проверяем углы Углы под 90 градусов, особенно это актуальны в местах установки мебели и оборудования, в частности на кухне, в коридоре и спальне. Прямые углы стен можно проверять с помощью длинного строительного угольника не менее 50 см длинной, проверяйте весь угол от пола до потолка.
5. Проверяем параллельность стен при необходимости, с помощью рулетки замеряем расстояние между стенами, в начале и в конце, они должны быть одинаковое.
6. Проверяем зоны особого контроля
Внимание! Дверные наличники, потолочные и половые плинтусы ровные, поэтому зоны примыканий плинтусов и наличников должны быть идеально ровными, чтобы не получить в этом месте щель.
Внимание! Проверьте, чтобы стены были оштукатурены до самого края дверного проема, так как наличники могут не скрыть оставшуюся поверхность.
Внимание! Проверьте, что бы штукатурка на оконных откосах не мешала свободному ходу оконных створок. Для этого надо открыть окно до упора и посмотреть открывается ли окно полностью.
Внимание! Проконтролируйте, чтобы все металлические уголки, особенно над дверными проемами были предварительно загрунтованы, что бы в последствии при окраске не проступали пятна от коррозии металла.
Угольники плоские УП
| Поверочные слесарные угольники типа УП, имеют две плоских рабочих стороны, образующие наружный и внутренний угол. Основным назначением УП являются слесарно-сборочные работы связанные с градусной разметкой деталей. В отличие от других угловых инструментов, все сторону угольника УП плоские. Основные характеристики поверочных угольников УП приведены в таблице. Информация касающаяся правил приемки, маркировки, упаковки и хранения содержится в ГОСТ 3749-77. |
| Тип угольника | Классы точности | Регламентирующий документ | Допуск перпендикулярности мкм, для класса точности | ||
| 0 | 1 | 2 | |||
| УП 60х40 | 1, 2 | ГОСТ 3749-77 | 2,5 | 5 | — |
| УП 100х60 | 2,5 | 5 | 13 | ||
| УП 160х100 | 3 | 6 | 15 | ||
| УП 250х160 | 3,5 | 7 | 18 | ||
| УП 400х250 | 4,5 | 9 | 22 | ||
| УП 630х400 | 6 | 12 | 30 | ||
Симметрия прямоугольника
Как было отмечено, центр его симметрии — это точка C, образованная пересекающимися диагоналями. Рассматривая фигуру на плоскости, можно сказать, что ось, через эту точку проходящая и параллельная двум сторонам прямоугольника, является осью симметрии второго порядка, то есть поворот вокруг нее на 180o переведет прямоугольник сам в себя. Поскольку рассматриваемый четырехугольник имеет две пары параллельных сторон, то очевидно, что он обладает двумя указанными осями симметрии.
Ось симметрии делит фигуру на два одинаковых прямоугольника со сторонами:
Источник: pressadv.ru