Решение технических задач в строительстве

Сборник задач по курсу начертательной геометрии для студентов 1-го курса в ВУЗах. Данный решебник по начертательной геометрии позволит студентам, обучающимся по программе курса начертательной геометрии, поупражняться с задачками различной сложности и более эффективнее пройти курс обучения. В данном задачнике подробно расписаны примеры решения задач с ответами для «чайников». Данный сборник задач соответствует программе обучения машиностроительных, приборостроительных и механико-технологических специальностей в высших технических учебных заведений.

Автор Гордон В.О., Иванов Ю.Б., Солнцева Т.Е. Издательство «Наука», главная редакция физико-математической литературы. Москва 1977 г.

Данный сборник задач и упражнений соответствует программа курса начертательной геометрии для машиностроительных, приборостроительных и механико-технологических специальностей высших технических учебных заведений.

Сборник составлен в соответствии и применительно к учебнику «Курс начертательной геометрии» В. О. Гордона и М. А. Семенцова-Огиевского, из которого в данный сборник перенесен ряд примеров и задач.

CADLib для решения задач цифровизации строительства

Авторы стремились помочь изучающим курс в их самостоятельной работе. Этим определился характер пособия, а именно показ процесса решения ряда типовых задач, относящихся к основным вопросам курса. Вместе с тем даны и условия задач для самостоятельного их решения. Условия большинства задач подобны условиям решенных задач, но имеются также задачи и без решенных прототипов, что требует от учащегося проявления большей самостоятельности и творческой инициативы.

Ограничение курса начертательной геометрии в часах и его преимущественно одно семестровое прохождение обусловливают и программное ограничение круга рассматриваемых вопросов. Очевидно, это предельный минимум; авторы исходили из него при составлении сборника.

В основном задачи, решенные 1 ) и предлагаемые для решения, относятся к взаимному сочетанию геометрических элементов и их расположению в пространстве и к применению способов преобразования чертежа вращением и введением дополнительных плоскостей проекций. Объектами рассмотрения являются точки, прямые и кривые линии, плоские и некоторые другие поверхности — отдельно и в их взаимном расположении. Рассматриваются задачи на определение расстояний и углов, на построение аксонометрических проекций — прямоугольных — изометрических (с сокращением по оси y вдвое).

Чертежи в большинстве случаев даны в поэтапном их выполнении. Это облегчит чтение чертежей и рассмотрение последовательности их построений. Для лучшего понимания сущности вопроса и представле-

1 ) Их номера отмечаются звездочкой вверху.

ния пространственной картины в некоторых из решенных задач даны наглядные изображения. Даны также примеры составления планов решения задач и анализа полученных решений.

Такие сборники задач по начертательной геометрии с их решениями уже издавались, например, в 1928 г. «Сборник задач по ортогональным проекциям с подробными решениями» С. К. Руженцова и Б. А. Иванова. Опыт показывает их полезность.

ГЕНИАЛЬНЫЕ ИНЖЕНЕРНЫЕ РЕШЕНИЯ В СТРОИТЕЛЬНОЙ ИНДУСТРИИ

Особенностью данного сборника является наличие ответов к задачам, предложенным для самостоятельного решения. Правильно ли решена задача? Этот вопрос при самостоятельном решении по большей части является открытым, что затрудняет работу учащегося. Для того чтобы он сам мог убедиться в правильности полученного им решения, в сборнике помещены ответы.

Они даны в текстовой или графической форме в зависимости от поставленных в задаче вопросов. Ответ к задаче в форме чертежа содержит положение искомых элементов на фоне задания.

В сборнике даны преимущественно чертежи с указанием оси x как базы для отсчета размеров при построениях и для удобства при перечерчивании заданий. Наличие оси x как направляющей линии облегчает введение в чертеж любой информации и построение чертежей-ответов.

Если же ось не показана (как это сделано в некоторых задачах), то ее роль для отсчета размеров может быть присвоена какой-либо из прямых на данном чертеже. Все это находится в логической связи с техническими чертежами, где всегда имеет место база отсчета, хотя и не обозначаемая так, как на чертежах в начертательной геометрии. Однако ось x сохраняет и присущее ей знaчениe линии nepeceчeния плоcкоcтeй пpоeкций V и H, что имеет значение для представления пространственной картины рассматриваемого положения. Но и вне этого значения (определяемого названием «ось проекций») такая прямая является неотъемлемой составляющей каждого чертежа для построения его по заданным размерам. При этом выбор положения оси не является ограниченным и определяется исходя из необходимости и целесообразности.

Авторы придерживаются в основном обозначений, примененных еще в XIX столетии отечественными учеными Н И. Макаровым и В. И. Курдюмовым и в настоящее время используемых в учебной литературе и в практике кафедр без каких-либо осложнений. Эти обозначения, в отличие от всех других, в достаточной степени просты, выразительны, легко читаемы и не загромождают чертежи.

В сборнике применен термин пpoeциpoвaть (от латинск. projicere) взамен пpoeктиpoвaть, так как последнее имеет и другое значение, а именно «разрабатывать, составлять проект» (например, сооружения, механизма, перевозок и т. д.). Переход на слово пpoeциpoвaть вызвал также такие названия, как пpoeциpующaя пpямaя, гopизoнтaльнo-пpoециpующaя плоскость и т. п.

В том же смысле, в каком в некоторых курсах начертательной геометрии применено слово «эпюр» (а иногда «эпюра»), в данном сборнике взято слово «чертеж» (что, вообще, не является новым).

Для лучшего понимания решенных в сборнике задач и усвоения построений рекомендуется перечерчивать исходный чертеж и выполнять на нем все описанные построения.

Следует обратить особое внимание на то, что для сравнимости полученного учащимся чертежа-ответа предложенной для самостоятельного решения задачи с приведенным в сборнике ответом необходимо как можно точнее воспроизвести чертеж-задание, пользуясь осью x как базой отсчета. При желании можно чертеж-задание увеличить> что должно быть учтено при сравнении полученного ответа с ответом в сборнике.

При решении задач, для которых нет решенных прототипов, можно использовать помещенные в конце сборника краткие указания.

Выражение изoбpaзить наглядно, дать наглядное изображение, означает построить изображение в косоугольной фронтальной диметрической проекции (хотя бы в известной под названием «кабинетная»).

Рекомендуется при самостоятельном решении задач предварительно дать рисунок требуемого построения и составить план решения, как это сделано в сборнике для некоторых решенных задач, а лишь затем выполнять построение.

Согласованность данного сборника задач с учебником «Курс начертательной геометрии» В. О. Гордона и М. А. Семенцова-Огиевского не исключает возможности пользоваться другими учебниками, так как для понимания и решения задач по данному сборнику требуется знание тех основных положений, которые должны содержаться в любом учебнике. При этом, если имеется различие в некоторых обозначениях, можно сопоставить обозначения при помощи таблицы, которую можно найти в учебнике.

Для линий связи применена штрих-пунктирная линия с одной точкой между смежными штрихами. Но если линия связи проведена лишь для проверки правильности построения, то использована линия с двумя точками.

Номера решенных задач отмечены звездочками. Ответы на нерешенные задачи помещены в конце сборника.

Некоторые сокращения слов и условные обозначения в сборнике: пл.— плоскость;

горизонт. — горизонтальный, -ая, -ое; фронт.—фронтальный, -ая, -ое; X — перпендикулярно;

Источник: nachert.ru

Основные этапы решения и виды технических задач

Интерес к вопросам психологии и теории техническо­го творчества возник к концу XIX — началу XX века, когда из различных видов производственной деятельности начал выделяться как самостоятельный изобретательский и конс­трукторский труд.

В то время в литературе, как правило, обсуждались про­блемы творчества в искусстве (художественном, поэтичес­ком, музыкальном и др.)* Техническое творчество при этом почти не анализировалось и не изучалось ни психологами, ни теоретиками творчества. Таким образом, обширная об­ласть творческой деятельности оказалась за пределами на­уки о творчестве. Это было вызвано двумя причинами:

— во-первых, считалось, что творить могут только люди искусства, а технические новинки создаются грязным, низким трудом ремесленников и не могут быть отнесе­ны к сфере творчества;

— во-вторых, если представители искусства раскрывали свои творческие секреты, свою «творческую лабора­торию», то изобретатели и создатели новой техники старались держать в секрете свои приемы, методы и принципы, применяемые при создании технических новинок.

Начало изучения природы технического и научного твор­чества в России своими трудами положили ее ученые и ин­женеры. К числу наиболее известных относятся такие ра­боты, как: «Теория творчества» инженера П. Энгельмейера (1910 г.); «Философия изобретения и изобретение в филосо­фии» философа И. Лапшина (1922 г.); «Процесс творческой работы изобретателя» П.М. Якобсона (1934 г.) и др.

Среди зарубежных работ наиболее известны: «Математи­ческое творчество» Анри Пуанкаре (русский перевод 1919 г.); «Изобретатели и исследователи» (1909 г.) и «Великие люди» (1910 г.) В. Оствальда; «Творческое воображение» Т. Рибо (1901 г.); «Психология изобретения» И. Россмана (1931 г.) и др.

На этом этапе авторам указанных работ приходилось от­стаивать тезис о том, что творчество в технике и науке есть такое же творчество, как и творчество в искусстве, и что за­рождение творческой идеи как у художника, так и у изобре­тателя происходит совершенно одинаково, отличаясь лишь целями и условиями проявления [21].

В этих первых работах о техническом и научном творчес­тве была выполнена классификация этапов творческого про­цесса, что явилось дисциплинирующим работу изобретателя моментом. Выдающийся русский исследователь творчества Петр Энгельмейер (1855-1942) творческий процесс предста­вил состоящим из трех актов:

— первый акт — акт интуиции и желания. Происхождение замысла, появление идеи, гипотезы, принципа изобре­тения, цели того, над чем следует работать;

— второй акт — акт знания и рассуждения. Выработка схе­мы и плана. Ставятся мысленные опыты, проводятся эксперименты и логический анализ, определяется но­визна;

— третий акт — акт умения. Конструктивное выполнение изобретения. Решение задачи применения, эксплуата­ции.

П.М. Якобсон процесс работы изобретателя подразделял на семь стадий:

1. Интеллектуальной готовности.

2. Усмотрение проблемы.

3. Зарождение идеи — формулировка задачи.

4. Поиск решения.

5. Разработка принципа решения.

6. Превращение принципа в схему.

7. Техническое оформление и развитие изобретения.

Вот, например, как П.М. Якобсон представляет себе ин­теллектуальную готовность и усмотрение проблемы изоб­ретателем [21]: «У него появляется желание изобретать, он чувствует беспокойство, ему не по себе от сознания, что он ничего в этом направлении не делает. Вместе с тем он чувс­твует известную активность мысли, чувствует себя готовым к какой-то новой работе.

Он читает различные книги. Иног­да даже без всякого специального подбора и вместе с тем он читает так, что вбирает в себя определенный ряд вещей с со­знанием, что это сможет ему пригодиться. Изобретатель на­капливает известные технические впечатления, он проявля­ет повышенный интерес к машинам, механизмам, которые его окружают. Он сознает, что над этой машиной работать не будет, а все-таки его занимает, как она действует, как сочле­нены одна часть с другой, какая техническая задача разре­шена таким устройством ».

Постепенно изобретатель выявляет наиболее интересую­щие его вопросы и проблемы, над которыми он начинает бо­лее целенаправленно работать. Так происходит усмотрение проблемы, которая чаще всего вызвана текущими потреб­ностями общества.

Эти схемы творческих процессов не претерпели серь­езных изменений до настоящего времени. Так, в работе [6] предложена схема решения для любой технической задачи, состоящая из следующих главнейших этапов:

1. Постановка задачи.

2. Поиск вариантов решения.

3. Анализ вариантов.

4. Оценка вариантов и выбор решения.

Под постановкой задачи понимается усмотрение обще­ственной потребности или трудности, определение цели, ограничений и критерия выбора решения.

Возникшая общественная потребность в создании техни­ческой системы (ТС), выполняющей требуемую функцию, оп­ределяет цель. Цель — это то, к чему мы стремимся и что будем иметь в результате решения. При формулировке цели обычно указывается начальное и конечное состояние ТС. Например, создать машину, преобразующую электрическую энергию (начальное состояние) в механическую (конечное состояние).

Ограничения — условия создания ТС, нарушение которых приведет к неприемлемому решению по работоспособности, экономической целесообразности, размещению и т.п. ТС. Кри­терий выбора — наиболее важный признак или комплекс таких признаков решения, по которым можно качественно или ко­личественно оценить оптимальность принимаемого решения.

После выполнения этапа постановки задачи приступа­ют к процессу поиска вариантов решений, которые должны быть:

-физически осуществимыми (соответствовать законам природы);

— технически реализуемыми (соответствовать ресурсам и уровню научно-технического развития общества);

Решить задачу, начиная с конца, однозначно, т.е. от цели и требуемых характеристик к техническим средс­твам, возможно лишь для простых, тривиальных задач. Для сложных задач неопределенность решения может быть преодолена за счет перебора вариантов. Вначале намеча­ются и определяются характеристики как можно больше­го количества вариантов, а затем отбрасываются наименее подходящие по выбранному критерию качества (минимум массы, наименьшие габариты, надежность работы, высо­кий КПД и т.п.).

Чаще всего на практике решаются технические задачи, связанные с усовершенствованием существующего прототи­па. Эти задачи возникают после выявления в эксплуатации недостатков ТС. Устранение недостатков зачастую приводит к ухудшению других свойств ТС, т.е. возникает задача по ус­транению технического противоречия, иначе — задача-про- тиворечие [6].

Кроме таких, наиболее часто возникающих задач, имеет­ся целый класс задач по синтезу структуры. Задача синтеза может возникнуть при необходимости достройки недостаю­щих подсистем в ТС или построения ТС с нуля, т.е. синтез многофункциональной технической системы, обеспечиваю­щей выполнение требуемых функций. Эти задачи наиболее сложны и трудоемки.

Сложной является взаимная увязка подсистем, зачастую приводящая к возникновению целого ряда дополнительных задач, причем эти задачи могут быть как задачами-противоречиями, так и задачами простого синтеза. Задачи-противоречия в процессе совершенствова­ния ТС возникают более часто. Однако оба типа задач могут переходить одна в другую при поиске решения.

Например, при синтезе ТС возникают противоречия. Некоторые из них могут оказаться довольно обостренными, что потребует ре­шения задачи-противоречия. С другой стороны, разрешение противоречия может потребовать разрушения системы или ее части и решения новой задачи синтеза.

Простая задача синтеза — это построение одной подсис­темы с одной элементарной функцией. Сложная задача син­теза — построение нескольких взаимосвязанных подсистем или построение многофункциональной ТС. Также и задача- противоречие может быть простой, имеющей одно техничес­кое противоречие, и сложной с несколькими противоречия­ми, т.е. иметь несколько взаимосвязанных положительных и отрицательных эффектов.

Решение сложных задач может быть облегчено за счет ранжирования простых задач, из которых состоит сложная.

Синтез ТС может выполняться на основе структурного или функционального подхода [22]. При поиске структуры ТС, соответствующей условиям задачи, согласно первого подхода выполняют следующее:

— анализ условия задачи;

— предварительный синтез структуры на основе выпол­ненного анализа;

— сравнение предварительной структуры с другими из­вестными структурами;

— выделение нужной структуры и ее перекомбинирова­ние.

При формировании структуры на основе функциональ­ного подхода процесс идет несколько иначе, в основу его по­ложены:

— анализ условия задачи;

— выделение основной функции будущей конструкции;

— поиск механизма с нужной функцией;

— перенос выбранного механизма в новые условия;

— переконструирование механизма с целью применения найденной функции.

В настоящее время стал применяться смешанный при­нцип поиска структуры, включающий как наиболее извес­тный структурный принцип, так и менее разработанный — функциональный.

§ 2.3. Законы диалектики в технике и закономерности развития технических объектови систем

Исследование описаний изобретений [2, 17] позволило сформулировать следующие идеи, легшие в основу разработ­ки теории решения технических (инженерных) задач:

1. Наиболее целесообразно при разработке теории учитывать не столько закономерности мышления, сколько законо­мерности развития ТС;

2. Так как главный предмет исследования — развитие ТС, то теория должна строиться на основе науки о развитии

— диалектики и важнейшего в ней учения — о противоре­чиях [17]. Закономерности развития ТС являются частны­ми проявлениями всеобщих законов диалектики:

— единства и борьбы противоположностей (закон противо­речий);

— перехода количественных изменений в качественные;

— о всеобщей связи и взаимозависимости явлений. Реализуются эти законы соответствующими изменения­ми материи (деление, объединение, переходы из одного аг­регатного состояния в другое и т.п.). Способы изменения яв­ляются как бы своеобразными операторами преобразования материи. В неживой природе преобразования происходят без участия человека или живых существ (разрушение гор, таяние льда, замерзание воды, испарение и образование об­лаков и т.п.). Там, где есть живые существа, они интенсивно влияют на процессы в природе.

В технике изменения целенаправленно производит сам человек.

Закономерности развития ТС могут быть разделены на законы статики (ТС рассматриваются в неподвижном состо­янии), динамики (ТС рассматриваются в движении) и кине­тики (фиксируются изменения ТС во времени).

В работах [2, 23] выделены три следующих закона, опре­деляющих условия возникновения и жизнеспособности ТС:

— закон полноты частей ТС, требующий обязательного минимума компонентов (двигатель, трансмиссия, ра­бочий орган и средства управления) и их минимальную работоспособность;

— закон энергетической проводимости ТС9 согласно ко­торому необходимо обеспечение сквозного прохода энергии через систему;

— закон согласования ритмики частей ТС, предусматри­вающий согласование периодичности действия, частот колебаний и т.п.

Кроме этих законов выявлены законы развития ТС:

— закон увеличения степени идеальности ТС, означаю­щий, что его развитие идет в направлении максималь­ного приближения к идеальной машине, т.е. к маши­не, создающей полезный результат при наименьших затратах;

— закон неравномерности развития частей ТС, согласно которому отдельные части ТС развиваются по-разному, усиливая технические противоречия между ними, осо­бенно у сложных ТС;

— закон перехода ТС в подсистему, означающий, что сис­тема может развиваться до определенного предела, пос­ле которого для обеспечения дальнейшего развития она должна быть включена в надсистему в качестве ее части;

— закон динамизации ТС, согласно которому для разви­тия системы ТС необходим ее переход от жесткой, пос­тоянной структуры к гибкой, управляемой структуре. Например, в авиации переход к убирающимся шасси, к крылу самолета с изменяющейся геометрией: на транс­порте- автобус с выдвигаемой ступенькой; складной велосипед, пантограф на электровозе и др.;

-закон перехода рабочих органов системы с макроуров­ня на микроуровень. Например, обработка твердых материалов режущими инструментами заменяется

воздействием лазера, плазменной струи, электроис­кровым методом.

Наряду с перечисленными законами, имеющими при­кладной практический характер, А.И. Половинкиным вы­полнены работы по выявлению законов развития теорети­ческого направления [3]:

— закон прогрессивной эволюции техники, описываю­щий этапы жизненного цикла ТС и изменение главных показателей критериев развития системы во времени. Главные показатели ТС изменяются в соответствии с функцией вида:

K=L/(a+e be» fit ), (2.1)

где L, afb,fi- коэффициенты, определяемые статистически­ми данными; t — время. Функция (2.1), называемая S-функ- цией, имеет вид, представленный на рис. 2.1. На начальном участке (до точки А) ТС развивается медленно, затем, когда начинается ее массовое применение, идет бурное развитие (до точки Б). После этого темпы развития начинают спадать. Законы прогрессивной эволюции наиболее целесообразно использовать при выполнении работ по анализу истории тех­ники и прогнозированию развития техники:

— закон соответствия между функцией и структурой объекта, заключающийся в том, что в правильно спро­ектированной ТС каждый элемент имеет свою опреде­ленную функцию (назначение). У правильно спроекти­рованной ТС нет «лишних деталей». Любая функция может быть реализована множеством различных конс­трукций (структур);

— закон симметрии, учитывающий то обстоятельство, что если по условиям работы ТС должна иметь какой- либо тип симметрии, то он должен найти отражение в конструкции. Например, железнодорожный путь сим­метричен относительно оси движения, поэтому теле­жки электровоза, тепловоза, трамвая и др. выполняют­ся с симметричным расположением колес относительно этой оси;

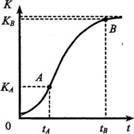Рис. 2.1. Закономерность изменения главных показателей ТС при неизменном принципе действия

— закон стадийного развития отражает четыре основ­ные стадии развития ТС: первая стадия — реализу­ется технологическая функция (обработки); вторая стадия — реализуется технологическая , а также энер­гетическая функция (обеспечение энергией процесса обработки предмета труда); третья стадия — ТС реали­зует еще функцию управления процессом труда; чет­вертая стадия — ТС реализует для себя еще функцию планирования объема труда.

Источник: studopedia.ru

Помощь по технической механике

Техническая механика, наряду с математикой и физикой, является областью, имеющей большое образовательное значение. Она способствует развитию логического мышления и приводит к пониманию очень широкого круга явлений, связанных с механическим движением, простейшей формой перемещения материи. Область «техномеханики» является основополагающей для разработки надежных и экономичных конструкций как на стадии проектирования, так и в процессе производства и эксплуатации.

Если у вас нет времени на выполнение заданий по технической механике , вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней .

Ответы на вопросы по заказу заданий по технической механике:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете «Техническая механика», если у вас есть желание и много свободного времени!

Содержание:

Механика одна из древнейших наук. Она развивалась вместе с семимильной поступью человечества, своевременно отвечая на многочисленные запросы практики. В древности не существовало деления науки по отраслям знаний, поэтому механика, как и философия, естествознание, являлась составной частью науки о природе и обществе. И только после Аристотеля (384-322 до н.э.) начинается отделение частных наук из общего естествознания.

• В древнем Египте при строительстве пирамид уже пользовались рычагами, наклонными плоскостями, блоками. Эмпирические знания, накопленные человечеством, помогли установить законы механики.

Основоположником механики как науки считают Архимеда (ок. 287212 гт. до н.э.); он дал точное решение задач о равновесии сил, приложенных к рычагу, об определении центра тяжести тел.

В эпоху Возрождения (XIV-XVI вв.) большой вклад в развитие механики сделал знаменитый итальянский художник, ученый и инженер Леонардо да Винчи (1452-1519). Он изучал трение скольжения, движение падающего тела, впервые ввел понятие момента силы.

Современное развитие машиностроения требует решения специальных задач. Бурно развивается наука о прочности и деформируемости элементов сооружений и деталей машин сопротивление материалов. В отличие от теоретической механики сопротивление материалов рассматривает задачи, в которых наиболее существенными являются свойства деформируемых тел. Законы движения абсолютно твердого тела отступают на второй план. В то же время вследствие общности основных положений сопротивление материалов может рассматриваться как раздел механики, который можно назвать механикой деформируемых тел.

Теоретическая механика это наука, в которой изучается механическое движение тел и устанавливаются общие законы этого движения. Теоретическая механика разделяется на статику, кинематику и динамику.

Возможно, вас также заинтересует эта ссылка:

Помощь с заданием 1.

Определить модули скорости, тангенциального, нормального и полного ускорений для точки находящейся на ободе колеса, которое равномерно катится без скольжения по прямой линии (рис. 9.7).

Закон движения для точки М найдем в предыдущем примере:

где — скорость движения оси колеса; —диаметр колеса.

Модуль скорости точки но формуле (9.16)

Найдем модуль тангенциального ускорения. В соответствии с формулой (9.28) имеем

Для модуля нормального ускорения (9.30) получим

Модуль полного ускорения (9.33)

Возможно, вас также заинтересует эта ссылка:

Помощь с заданием 2.

Тело брошено вертикально снизу вверх со скоростью 19,6 м/с. На какую высоту оно поднимается и за какое время? Построить графики движения, скорости и ускорения (сопротивлением воздуха пренебречь, тело считать за точку).

Будем считать движение тела прямолинейным и равнопеременным. За положительное направление отсчета удобно принять вертикальное направление снизу вверх.

При таких условиях можно написать где — ускорение силы тяжести (направлено всегда к центру Земли).

Применяя формулу (10.8), находим откуда Тогда по формуле (10.10) находим закон движения тела

Отсюда высота, на которую поднимается тело

Графически закон экзамен движения тела показан на рис. 10.6, а. График скорости дан на рис. 10.6,6. Так как ускорение постоянное и всегда направлено вниз, т. е. положительного направления отсчета, то его график будет прямая, параллельная оси абсцисс и лежащая ниже оси (рис. 10.6, в).

Из графиков видно, что в первые две секунды полета тело двигалось равнозамедленио, а в следующие две секунды — равноускоренно.

Возможно, вас также заинтересует эта ссылка:

Помощь с заданием 3.

После отключения электродвигателя его вал вращался равпозамедленно до полной остановки Ю секунд. За это время он сделал 60 оборотов. Определить угловое ускорение и угловую скорость вала в момент отключения двигателя.

Определим угол поворота вала за время остановки двигателя

Примем, что Тогда в соответствии с формулой (11.11) получим

(11.13)

Из соотношения (11.12), учитывая, что со имеем

Подставляя это выражение в уравнение (11.13), получим угловое ускорение

Тогда угловая скорость в момент отключения двигателя

Число оборотов вала в минуту

Возможно, вас также заинтересует эта ссылка:

Помощь с заданием 4.

Шестерня находящаяся в зацеплении с шестерней 2 (рис. 11.7), из состояния покоя начинает вращаться равноускоренно с угловым ускорением Найти закон вращения шестерни 2, если радиус первой шестерни равен 0,3 м, а радиус второй — 0,2 м. Найти линейные скорости и ускорение точки лежащей на расстоянии 0,1 м от оси вращения второй шестерни.

Начальная угловая скорость первой шестерни равна ну. лю, поэтому

Закон равнопеременного вращения первой шестерни будет

Так как шестерни находятся в зацеплении, то при вращении точка контакта этих шестерен будет иметь одинаковую линейную скорость v. Если рассмотреть первую шестерню, то линейная скорость точки

Эту же линейную скорость будет иметь точка, принадлежащая второй шестерне, поэтому откуда

Учитывая, что будем иметь Если проинтегрировать правую и левую части последнего равенства, считая, что в начальный момент времени то мы получим закон вращения шестерни

Вращение второй шестерни, как видно из закона движения, будет равноускоренным. При этом касательное ускорение = 0,075-

Находим линейную скорость точки

Модуль полного ускорения точки

• Необходимо отметить, что в точке касания М только линейные ускорения колес будут одинаковы, а линейные нормальное и полное ускорения будут различными (рис. 11.8). Так в нашем случае значения касательных ускорений будут равны:

Так как линейные нормальные ускорения зависят от расстояния точки до осп вращения, то имеем атм

Нормальные ускорения имеют не только разные значения, но и направления — нормальное ускорение точки первой шестерни направлено к центру а нормальное ускорение направлено к центру

Модули ускорений вычисляются по формуле (12.18):

Помощь с заданием 4.

Панель стены весом поднимается краном прямолинейно и равноускоренно с ускорением (рис. 13.5). Определить натяжение троса.

Так как панель движется поступательно, то все точки имеют одинаковые скорости и ускорения. Поэтому ее можно считать материальной точкой. Заменим действие троса реакцией Теперь панель будет свободной. Согласно принципа Даламбера, на панель будет действовать сила инерции Составим уравнение равновесия на ось

Помощь с заданием 5.

Материальная точка имеющая массу равномерно вращается вокруг точки (рис. 13.6). Сила натяжения нити, с помощью которой точка связана с центром вращения, равна Найти ускорение материальной точки и ее скорость (силу тяжести не учитывать).

Так как материальная точка совершает равномерное вращательное движение, то касательное ускорение будет равно нулю, а нормальное ускорение по модулю Таким образом, если рассматривать материальную точку как свободную, то на нее будут действовать реакции нити и, согласно принципу Даламбера, сила инерции

Из уравнения равновесия на ось, проходящую через центр вращения и материальную точку получим или откуда

Скорость вращения

Возможно, вас также заинтересует эта ссылка:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.

Источник: natalibrilenova.ru