Инструкция . Выберите количество предприятий и количество строк (количество вариантов эффективного вложения), нажмите Далее (см. Пример заполнения). Если доход и остатки предприятий задан в виде функций f(x) и g(x) , задача решается через этот калькулятор.
Пример №1 . Определите оптимальный план расширения производства трех предприятий, если известна их прибыль в год при отсутствии вложений и при инвестировании 1, 2, 3 или 4 млн. Определите, при каком инвестировании будет максимальный процент прироста прибыли.
| f1 | f2 | f3 | xi |
| 40 | 30 | 35 | 0 |
| 90 | 110 | 95 | 1 |
| 395 | 385 | 270 | 2 |
| 440 | 470 | 630 | 3 |
| 620 | 740 | 700 | 4 |
Решение задачи №631 на Vipreshebnik ru
I этап. Условная оптимизация.
1-ый шаг. k = 3.
| e 2 | u 3 | e 3 = e 2 — u 3 | f3(u 3 ) | F*3(e 3 ) | u3(e 3 ) |
| 1 | 0 | 1 | 35 | ||
| 1 | 0 | 95 | 95 | 1 | |
| 2 | 0 | 2 | 35 | ||
| 1 | 1 | 95 | |||
| 2 | 0 | 270 | 270 | 2 | |
| 3 | 0 | 3 | 35 | ||
| 1 | 2 | 95 | |||
| 2 | 1 | 270 | |||
| 3 | 0 | 630 | 630 | 3 | |
| 4 | 0 | 4 | 35 | ||
| 1 | 3 | 95 | |||
| 2 | 2 | 270 | |||
| 3 | 1 | 630 | |||
| 4 | 0 | 700 | 700 | 4 |
Финансовая грамотность. Разбор задач по теме инвестиции.
2-ый шаг. k = 2.
| e 1 | u 2 | e 2 = e 1 — u 2 | f2(u 2 ) | F*2(e 1 ) | F1(u 2 ,e 1 ) | F*2(e 2 ) | u2(e 2 ) |
| 1 | 0 | 1 | 30 | 95 | 125 | 125 | 0 |
| 1 | 0 | 110 | 0 | 110 | |||
| 2 | 0 | 2 | 30 | 270 | 300 | ||
| 1 | 1 | 110 | 95 | 205 | |||
| 2 | 0 | 385 | 0 | 385 | 385 | 2 | |
| 3 | 0 | 3 | 30 | 630 | 660 | 660 | 0 |
| 1 | 2 | 110 | 270 | 380 | |||
| 2 | 1 | 385 | 95 | 480 | |||
| 3 | 0 | 470 | 0 | 470 | |||
| 4 | 0 | 4 | 30 | 700 | 730 | ||
| 1 | 3 | 110 | 630 | 740 | 740 | 1 | |
| 2 | 2 | 385 | 270 | 655 | |||
| 3 | 1 | 470 | 95 | 565 | |||
| 4 | 0 | 740 | 0 | 740 |
3-ый шаг. k = 1.
| e 0 | u 1 | e 1 = e 0 — u 1 | f1(u 1 ) | F*1(e 0 ) | F0(u 1 ,e 0 ) | F*1(e 1 ) | u1(e 1 ) |
| 1 | 0 | 1 | 40 | 125 | 165 | 165 | 0 |
| 1 | 0 | 90 | 0 | 90 | |||
| 2 | 0 | 2 | 40 | 385 | 425 | 425 | 0 |
| 1 | 1 | 90 | 125 | 215 | |||
| 2 | 0 | 395 | 0 | 395 | |||
| 3 | 0 | 3 | 40 | 660 | 700 | 700 | 0 |
| 1 | 2 | 90 | 385 | 475 | |||
| 2 | 1 | 395 | 125 | 520 | |||
| 3 | 0 | 440 | 0 | 440 | |||
| 4 | 0 | 4 | 40 | 740 | 780 | 780 | 0 |
| 1 | 3 | 90 | 660 | 750 | |||
| 2 | 2 | 395 | 385 | 780 | |||
| 3 | 1 | 440 | 125 | 565 | |||
| 4 | 0 | 620 | 0 | 620 |
Примечание: Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 3-го шага столбцы 5 и 6 отсутствуют).
В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.
Этап II. Безусловная оптимизация.
Из таблицы 3-го шага имеем F*1(e 0 = 4 млн.руб.) = 780 тыс.руб., то есть максимальная прибыль от инвестирования e 0 = 4 млн.руб. равна 780 тыс.руб.
Из этой же таблицы получаем, что первому предприятию следует выделить u*1(e 0 = 4 млн.руб.) = 0 млн.руб.
При этом остаток средств составит: e 1 = e 0 — u 1 , e 1 = 4 — 0 = 4 млн.руб.
Из таблицы 2-го шага имеем F*2(e 1 = 4 млн.руб.) = 740 тыс.руб., т.е. максимальная прибыль при e 1 = 4 млн.руб. равна 740 тыс.руб.
Из этой же таблицы получаем, что второму предприятию следует выделить u*2(e 1 = 4 млн.руб.) = 1 млн.руб.
При этом остаток средств составит: e 2 = e 1 — u 2 , e 2 = 4 — 1 = 3 млн.руб.
Последнему предприятию достается 3 млн.руб. Итак, инвестиции в размере 4 млн.руб. необходимо распределить следующим образом: первому предприятию ничего не выделять, второму предприятию выделить 1 млн.руб., третьему предприятию выделить 3 млн.руб., что обеспечит максимальную прибыль, равную 780 тыс.руб.
Пример №2 . Имеются 4 предприятия, между которыми необходимо распределить 100 тыс. усл. ед. средств. Значения прироста выпуска продукции на предприятии в зависимости от выделенных средств Х представлены в таблице. Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.
Источник: math.semestr.ru
Задачи по инвестициям

Если у вас нет времени на выполнение заданий по инвестициям , вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней .

 Ответы на вопросы по заказу заданий по инвестициям:
Ответы на вопросы по заказу заданий по инвестициям:


Сколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?
- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?
- Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости бесплатна.

Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?
- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время! Я стараюсь быть всегда онлайн.


Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете «Инвестиции», если у вас есть желание и много свободного времени!

Содержание:
Инвестиции (от лат. investire — облачать, одевать) — это вложения капитала в отрасли экономики внутри страны и за ее пределами, осуществление определенных экономических проектов в настоящем с расчетом получить доходы в будущем.
В эпоху феодализма инвеститурой называли ввод вассала во владение феодом и назначение епископов, получавших в управление церковные земли с их населением. Введение в должность сопровождалось церемонией облачения и наделения полномочиями. Инвеститура позволяла инвеститору (инвестору) брать новые территории для получения доступа к их ресурсам, управлять ими и насаждать свою идеологию, которая позволяла увеличивать получаемый с этих территорий доход, но и являлась развивающим фактором.
В широком смысле инвестиции — это денежные средства, имущественные и интеллектуальные ценности государства, юридических и физических лиц, направляемые на создание новых предприятий, расширение, реконструкцию, приобретение акций, активов с целью получения прибыли.
Инвестиционные решения — это решения о текущих затратах с целью получения доходов в будущем. Краткосрочные решения принимаются на относительно короткий период времени (например, от вложения денежных средств до получения прибыли от них пройдет один год). Долгосрочные инвестиционные проекты рассчитаны на более длительный период времени.
В этой главе мы проанализируем обоснованность долгосрочных инвестиционных решений для предприятий, целиком финансируемых за счет акционерного капитала (или выпуск простых акций, или за счет нераспределенной прибыли). Будем считать, что денежные потоки точно определены и нет необходимости делать поправку на риск. Денежные притоки или оттоки происходят в начале или конце каждого периода. Хотя вычисления в этом случае не совсем точны, но для большинства решений они достаточно приемлемы.
Возможно, вас также заинтересует эта ссылка:
Альтернативные издержки по инвестициям
При выработке долгосрочных инвестиционных решений необходимо знать, какую отдачу принесут инвестиции, и сопоставить прибыль от инвестирования в различные проекты.
Тот, кто не любит рисковать, может вложить деньги в безрисковые ценные бумаги (такими считаются особо надежные государственные ценные бумаги), которые будут приносить постоянный доход. Доходность по инвестициям в такие ценные бумаги представляет собой альтернативные издержки по инвестициям, так как инвестированные в особо надежные государственные ценные бумаги средства не могут быть инвестированы еще куда-то.
Альтернативные издержки по инвестициям также называют стоимостью капитала, минимально необходимой нормой прибылиу ставкой дисконтирования и процентной ставкой. Предприятие должно рассматривать только такие инвестиционные проекты, прибыль от которых выше альтернативных издержек по инвестициям.
При рассмотрении инвестиционных проектов мы должны решить, будет ли инвестирование капитала более прибыльным, чем простое помещение средств в безрисковые ценные бумаги или в банк под проценты при данной банковской процентной ставке. Кроме того, необходимо выбрать тот инвестиционный проект, который принесет максимальную выгоду.
Возможно, вас также заинтересует эта ссылка:
Метод чистой приведенной стоимости
В методе чистой приведенной стоимости учитывается временная стоимость денег.
Предположим, что нам известен будущий денежный поток и его распределение по времени. Дисконтируем денежные потоки до их текущей стоимости (на нулевой момент времени, то есть на начало реализации проекта), используя минимально необходимую норму прибыли. Суммировав полученные результаты, найдем чистую приведенную стоимость (NPV) проекта.
Если полученное значение положительно, то реализация инвестиционного проекта более выгодна, чем помещение средств в безрисковые ценные бумаги. Если полученное значение отрицательно, то реализация инвестиционного проекта менее выгодна, чем помещение средств в безрисковые ценные бумаги. Нулевое значение чистой приведенной стоимости говорит о том, что предприятию безразлично, принять проект или отвергнуть его.
При принятии решений по инвестициям при оценке потоков денежных средств в них не включается амортизация, так как она не является расходом в форме наличных денежных средств. Затраты капитала на амортизируемые активы учитываются как расход наличных денежных средств в начале реализации инвестиционного проекта. Амортизационные отчисления — это просто метод бухгалтерского учета для соответствующего распределения вложений в активы по анализируемым отчетным периодам. Любое включение амортизационных отчислений в потоки денежных средств приводит к повторному счету.
Метод чистой приведенной стоимости особенно полезен, когда необходимо выбрать один из нескольких возможных инвестиционных проектов, имеющих различные размеры требуемых инвестиций, различную продолжительность реализации, различные денежные доходы.
Мы определяем чистую приведенную стоимость каждого инвестиционного проекта на основе альтернативных издержек по инвестициям. Положительность чистой приведенной стоимости говорит о прибыльности инвестиций. Затем выбираем, в рамках какого инвестиционного проекта положительная чистая приведенная стоимость наибольшая, так как именно это при прочих равных условиях и является индикатором самого рентабельного проекта.
Возможно, вас также заинтересует эта ссылка:
Задача 1 (44)

Предприятие анализирует два инвестиционных проекта в 2 млн. руб. Оценка чистых денежных поступлений приведена в таблице.
Альтернативные издержки по инвестициям равны 12%. Определим чистую приведенную стоимость каждого проекта.

Чистая приведенная стоимость проекта равна:


Чистая приведенная стоимость проекта равна:

Так как то проект предпочтительнее.
Положительная чистая приведенная стоимость инвестиций свидетельствует об увеличении рыночной стоимости средств акционеров, которое должно произойти, когда на фондовой бирже станет известно о принятии данного проекта. Она также показывает потенциальное увеличение текущего потребления для владельцев обыкновенных акций, которое возможно благодаря реализации проекта после возвращения использованных средств.
Возможно, вас также заинтересует эта ссылка:
Задача 2

Предприятие анализирует два инвестиционных проекта в 2,5 млн. руб. Оценка чистых денежных поступлений приведена в таблице.
Альтернативные издержки по инвестициям равны 11%.

Определить чистую приведенную стоимость каждого проекта. Какой проект предпочтительнее? Замечание. Мастер функций пакета Excel содержит финансовую функцию ЧПС, которая возвращает величину чистой приведенной стоимости инвестиций, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).

Появляется диалоговое окно, которое нужно заполнить. Ставка — это альтернативны издержки по инвестициям. Значения — это выплаты (со знаком «-») и поступления (со знаком «+»). ОК.
В примере 44 для проекта (из-за ошибок округления этот результат отличается от результата примера 44) и для проекта
Возможно, вас также заинтересует эта ссылка:
Метод внутренней нормы доходности
В методе внутренней нормы доходности учитывается временная стоимость денег.

Внутренняя норма доходности (дисконтированная норма прибыли) — это ставка дисконтирования, при которой чистая приведенная стоимость инвестиций равна нулю.
Значение внутренней нормы доходности можно найти приближенно методом линейной интерполяции. Подбираем значение ставки дисконтирования при которой чистая приведенная стоимость инвестиций Подбираем значение ставки дисконтирования при которой чистая приведенная стоимость инвестиций Тогда внутренняя норма доходности
Задача 3

Определим внутреннюю норму доходности инвестиционного проекта из примера 44.
Чистая приведенная стоимость проекта при ставке дисконтирования равна:

При чистая приведенная стоимость
При чистая приведенная стоимость

Тогда внутренняя норма доходности равна:

Задача 4

Определить внутреннюю норму доходности инвестиционного проекта из задачи 44.
Замечание. Мастер функций пакета Excel содержит финансовую функцию которая возвращает значение внутренней нормы доходности для потока денежных средств. Значение функции вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции не сходятся с точностью 0,0000001 после 20 итераций, то возвращает сообщение об ошибке #число!.
Появляется диалоговое окно, которое нужно заполнить. В графе Предположение указывается предполагаемая величина процентной ставки (если значение не указано, то по умолчанию оно равно 10%). ОК. В примере
Для определения целесообразности реализации инвестиционного проекта нужно сопоставить внутреннюю норму доходности с альтернативными издержками по инвестициям, или с принятой на данном предприятии минимальной нормой прибыли на инвестиции.
Сравнение методов чистой приведенной стоимости и внутренней нормы доходности
Во многих ситуациях метод внутренней нормы доходности склоняется к тому же решению, что и метод чистой приведенной стоимости. Но бывают ситуации, когда метод внутренней нормы доходности приводит к ошибочным решениям.
При анализе взаимоисключающих проектов (принятие одного из них исключает принятие другого) рекомендуется метод чистой приведенной стоимости.
- В методе внутренней нормы доходности подразумевается, что все поступления от инвестиционного проекта реинвестируются по собственно проектной норме доходности. Но это не обязательно фактическая альтернативная стоимость капитала.
- В методе внутренней нормы доходности результат показывается в виде процентной ставки, а не абсолютного денежного значения. Поэтому этот метод отдаст предпочтение инвестированию 10 тыс. руб. под 100%, а не инвестированию 200 млн. руб. под 20%.
В нестандартных денежных потоках (выплаты и поступления чередуются) возможно получение нескольких значений внутренней нормы доходности.
С учетом вышеперечисленного инвестиционные проекты нужно оценивать на основе чистой приведенной стоимости.
Метод окупаемости
Достоинство метода окупаемости — его простота. На практике этот метод применяется довольно часто, хотя при этом не учитывается временная стоимость денег.
Нужно определить период окупаемостиу который показывает, сколько времени понадобится для того, чтобы инвестиционный проект окупил первоначально инвестированную сумму (то есть до превышения наличным доходом первоначальных инвестиций). Чем короче период окупаемости, тем инвестиционный проект лучше.
Задача 5
Определим период окупаемости каждого инвестиционного проекта в примере 44.
В проекте для окупаемости первоначальных инвестиций в сумме 2 млн. руб. необходимо поступление 0,9 млн. руб. в первый год и (2 — 0,9) — 1,1 млн. руб. (из 1,6 млн. руб.) во второй год. Поэтому период окупаемости проекта равен 1 + 1,1/1,6 * 1,7 лет.
В проекте для окупаемости первоначальных инвестиций в сумме 2 млн. руб. необходимо поступление 0,8 млн. руб. в первый год, 1,1 млн. руб. во второй год и 2 — (0,8 + 1,1) — 0,1 млн. руб. (из 0,6 млн. руб.) в третий год. Поэтому период окупаемости проекта равен 1 + 1 + + 0,1/0,6 = 2,2 лет.
Так как то проект предпочтительнее.
Задача 6
Определить период окупаемости каждого инвестиционного проекта в задаче 44.
Недостатки метода окупаемости:
1) не учитываются потоки денежных средств после завершения срока окупаемости;
2) не учитывается временная разница поступлений денежных средств (поэтому возможно одобрение инвестиционного проекта с отрицательной чистой приведенной стоимостью).
Учитывая приведенные недостатки, применение метода окупаемости не обязательно приведет к максимизации рыночной цены обыкновенных акций.
Одна из модификаций метода окупаемости — дисконтированный метод расчета периода окупаемости, когда все потоки денежных средств дисконтированы до их приведенной стоимости, а период окупаемости определяется на основании дисконтированных потоков.
Дисконтированный метод расчета периода окупаемости также не учитывает все потоки денежных средств после завершения срока окупаемости. Но из-за того, что в дисконтированном методе расчета периода окупаемости полученная величина периода окупаемости больше, чем в методе окупаемости, исключается меньшее количество денежных потоков. Поэтому переход от метода окупаемости к дисконтированному методу расчета периода окупаемости — это шаг в правильном направлении.
На практике метод окупаемости очень часто используется для грубой оценки инвестиционных проектов.
Учетный коэффициент окупаемости инвестиций
В этом методе не учитывается временная стоимость денег. Для расчетов используются данные о прибыли, а не о поступлениях денежных средств.
Учетный коэффициент окупаемости инвестиций (прибыль на инвестированный капитал, прибыль на используемый капитал) вычисляется по следующей формуле:

Средняя стоимость инвестиций зависит от метода начисления износа. При равномерном начисления износа средняя стоимость инвестиций вычисляется по следующей формуле:

Задача 7
Пусть в примере 44 остаточная стоимость каждого проекта равна нулю. Определим их учетные коэффициенты окупаемости инвестиций.

Для проекта среднегодовая прибыль = (суммарные доходы — первоначальные инвестиции)/(срок реализации проекта) = а учетный коэффициент окупаемости инвестиций = (среднегодовая прибыль)/(средняя стоимость инвестиций) =
Для проекта среднегодовая прибыль = (суммарные доходы — первоначальные инвестиции)/(срок реализации проекта) а учетный коэффициент окупаемости инвестиций — (среднегодовая прибыль)/(средняя стоимость инвестиций)
Задача 8
Пусть в задаче 44 остаточная стоимость каждого проекта равна нулю. Определить их учетные коэффициенты окупаемости инвестиций.
Как и период окупаемости, учетный коэффициент окупаемости инвестиций имеет свои недостатки. Он использует балансовую прибыль (а не денежные потоки) в качестве оценки прибыльности проектов. Существует множество путей вычисления балансовой прибыли, что дает возможность манипулировать учетным коэффициентом окупаемости инвестиций. Несоответствия в вычислении прибыли приводят к существенно различающимся значениям учетного коэффициента окупаемости инвестиций.
- Балансовая прибыль страдает от таких «искажений», как затраты на амортизацию, прибыли или убытки от продажи основных активов, которые не являются настоящими денежными потоками, и поэтому не оказывают влияния на благосостояние акционеров.
Применение средних величин искажает относящуюся к делу информацию о сроках получения дохода.
Первоначальные инвестиции и остаточная стоимость усреднены для отражения стоимости активов, связанных между собой в течение всего срока реализации инвестиционного проекта. Наблюдается парадокс остаточной стоимости: чем больше остаточная стоимость, тем меньше учетный коэффициент окупаемости инвестиций. Это может привести к принятию неправильного решения.
Хотя применение учетного коэффициента окупаемости инвестиций иногда приводит к принятию ошибочных инвестиционных решений, на практике он очень часто используется для обоснования инвестиционных проектов. Возможно, это связано с тем, что лица, принимающие решения, часто предпочитают анализировать инвестиции через прибыль, так как деятельность самих менеджеров часто оценивается именно по этому критерию.
Возможно, вас также заинтересует эта ссылка:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
В случае копирования материалов, указание web-ссылки на сайт natalibrilenova.ru обязательно.
Источник: natalibrilenova.ru
Задание №2
Предприятие собирается приобрести оборудование, чтобы самостоятельно производить детали, которые раньше покупали от поставщиков. Стоимость оборудования — 500000. Эксплуатационные расходы в первый год составляют100000 и ежегодно возрастают на 10000. За поставку деталей ежегодно платили поставщикам по 250000. Срок эксплуатации оборудования – 5 лет.
Ликвидационная стоимость – 30000 (чистый доход от продажи оборудования в конце 5-го года). Ставка по альтернативным проектам- 8% годовых. Эффективна ли данная инвестиция ( NPV , PI , IRR , MIRR , PP , PPD )? Дайте письменное заключение о целесообразности реализации проекта.
Дисконтированный поток платежей
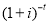
Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:
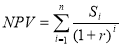
, где S i – поступления в i -ый период времени, r — норма пр и были альтернативных проектов.
Определим индекс прибыльности.
ИД определим по формуле:
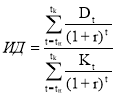
PI = 1018595/972995 = 1,047
Внутренняя норма доходности ( IRR ) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.
Определим внутреннюю норму доходности для каждого из проектов.
Для первого проекта решим уравнение:
∑ CF k / ( 1 + IRR ) k = ∑ INV t / (1 + IRR) t
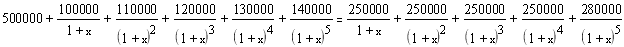
Решим уравнение аналитически, методом подбора.
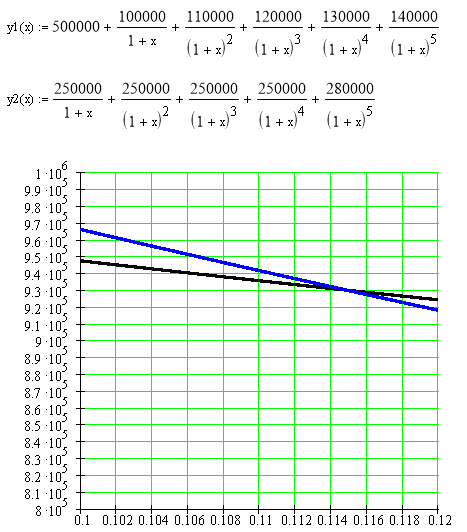
Следовательно, IRR = 0, 115 .
Опр еделим срок окупаемости для проекта с учетом дисконтирования .
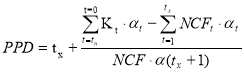
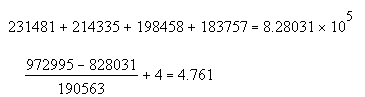
При ставке сравнения 8% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход , индекс доходности 104,7%. Однако при увеличении инфляции свыше 11 ,5 % не имеет смысла инвестировать средства в данный проект ( IRR =0,115), так же срок окупаемости проекта достаточно высокий и составляет 4,761 года, и близок к эксплуатационному сроку работы оборудования.
Фирма «Смирнов и Андрианов» покупает завод по производству глиняной посуды за 100 млн.рублей. Кроме того расчёты показывают, что для модернизации этого предприятия в первый же год потребуются дополнительные затраты в 50 млн. рублей. Однако, при этом предполагается, что в последующие 9 лет этот завод будет обеспечивать ежегодные денежные поступления по 25 млн. рублей. Затем, через 10 лет, предполагается, что фирма продаст завод по остаточной стоимости, которая составит согласно расчётам 80 млн. рублей. Средняя ставка доходности 10% . Эффективна ли данная инвестиция ( NPV , PI , IRR , MIRR , PP , PPD )? Дайте письменное заключение о целесообразности реализации проекта
Источник: easyhelp.su