Пример №1 . Требуется принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.
Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.
Полная замена оборудования экономически оправдана при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.
В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.
Предполагается, что спрос может оказаться высоким, средним и низким.
Дерево решений имеет два типа вершин: «решающие» и «случайные» (рис.).
Рис. Дерево решений
Строительство дома в условиях повышенной сейсмики. часть 1 из 2х
Начиная с «решающей» вершины 1, необходимо принять решение о полной замене оборудования или его ремонте.
Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 «случайные».
Допускается, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют соответственно 0,6, 0,3 и 0,1. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого – в 0,8 млн р.
Затраты на частичную замену оборудования более совершенным оцениваются в 1,5 млн р., а повторный ремонт старого – в 0,8 млн р.
Ежегодные доходы для каждой стратегии фирмы следующие.
1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт соответственно 0,95, 0,7 и 0,45 млн р.
2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается соответственно в 0,3, 0,15 и 0,1 млн р.
3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит соответственно 0,9, 0,6 и 0,4 млн р.
4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3, 0,2 и 0,1 млн р. соответственно.
Определим оптимальную стратегию фирмы в замене оборудования.
Решение.
Оценим результаты каждой стратегии и определим, какие решения следует принимать в «решающих» вершинах 1 и 4.
Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:
ДЧЗ = (0,9 × 0,6 + 0,6 × 0,3 + 0,4 × 0,1) × 4 – 1,5 = 1,54 млн р.,
Как решиться на строительство дома, не имея опыта? // FORUMHOUSE
ДДР = (0,3 × 0,6 + 0,2 × 0,3 + 0,1 × 0,1) × 4 – 0,8 = 0,2 млн р.,
где ДЧЗ – доход от частичной замены оборудования на более совершенное; ДДР – доход от замены оборудования, прошедшего дважды ремонт.
Так как ДЧЗ > ДДР , то в вершине 4 выгоднее частично заменить оборудование на более совершенное, при этом доход составит 1,54 млн р.
Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.
Вычислим доходы на 1-м этапе для «решающей» вершины 1:
ДЗН = (0,95 × 0,6 + 0,7 × 0,3 + 0,45 × 0,1) × 5 – 2,5 = 1,625 млн р.,
ДЗО = 0,3 × 0,6 × 1 + 0,15 × 0,3 × 5 + 0,1 × 0,1 × 5 +1,54 – 0,8 = 1,195 млн р.,
где ДЗН – доход от замены старого оборудования на новое того же вида; ДЗО— доход от отремонтированного оборудования и дальнейшей замены на более совершенное.
Так как ДЗН > ДЗО , то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.
Итак, оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.
- среднее предприятие при высоком (низком) спросе – F=1,4 (K=0,38) млн. руб.;
- малое предприятие при низком спросе – L=0,25 млн. руб.;
- малое предприятие при высоком спросе – М=0,27 млн. руб.;
- расширенное предприятие при высоком (низком) спросе дает N=1,6 (P=0,24) млн. руб.;
- малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R=0,2 млн. руб. за остальные восемь лет.
Решение:
Данная задача является многоэтапной, так как если фирма решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о размере предприятия и решение о необходимости его расширения, принимаемое через два года.
На следующем рисунке задача представлена в виде «дерева» решений. Предполагается, что спрос может оказаться высоким и низким. Дерево имеет два типа вершин: «решающие» вершины, обозначенные квадратными узлами, и «случайные» вершины, обозначенные круглыми узлами.
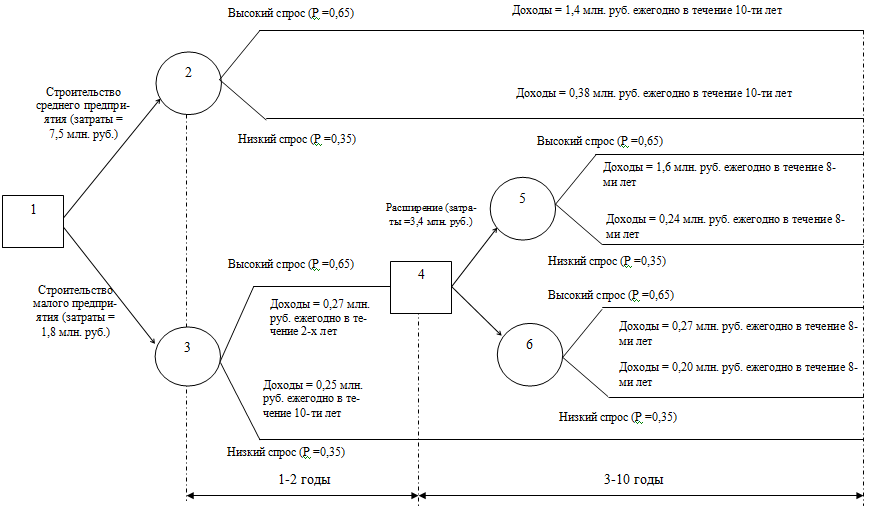
Начиная с вершины 1, являющейся «решающей», необходимо принять решение относительно размера предприятия. Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или не расширении предприятия. Вершины 5 и 6 будут «случайными».
Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются так:
— доход малого предприятия с последующим расширением:
ДР = (1,6*0,65 + 0,24*0,35)*8 – 3,4 = 5,592 млн. руб.
— доход малого предприятия без расширения
ДБР = (0,27*0,65 + 0,2*0,35)*8 = 1,964 млн. руб.
Таким образом, в вершине 4 выгоднее провести расширение, при этом доход составит 5,592 млн. руб.
Перейдем к вычислениям 1-го этапа. Для вершины 1:
— доход среднего предприятия:
ДС = (1,4*0,65 + 0,38*0,35)*10 – 7,5 = 2,93 млн. руб.
— доход малого предприятия с последующим расширением через 2 года:
ДМ = 5,592 + 0,27*0,65*2 + 0,25*0,35*10 – 1,8 = 5,018 млн. руб.
Сравнивая получаемые в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства малого предприятия с последующим расширением через 2 года.
Источник: math.semestr.ru
Решение логических задач табличным способом
Главным в предлагаемых задачах является способ решения — построение таблицы, строки которой соответствуют элементам одного из рассматриваемых в условии задачи множеств, столбцы — элементам другого, пересечение строки и столбца — комбинации двух элементов разных множеств. С помощью такой таблицы анализируются условия задачи, делаются выводы, проверяется избыточность, полнота и правильность выводов.
Задача 1. После соревнований бегунов на табло появилась надпись:
• Рустам не был вторым.
• Эдуард отстатл от Рустама на два места.
• Яков не был первым.
• Галина не была не первой ни последней.
• Карина финишировала сразу за Яковом.
Кто же победил в этих соревнованиях? Каково было распределение бегунов на финише?
Решение:
Рисуем таблицу, где столбцы –имена детей, а строки – номера мест. Читаем задачу, пошагово анализируем условие и ставим в таблицу «+», если соответствие установлено и «–», если точно соответствия нет.
Так как Рустам не был вторым и Эдуард отстал от Рустама на два места, то Эдуард не может быть ни первым, ни вторым, ни четвёртым.
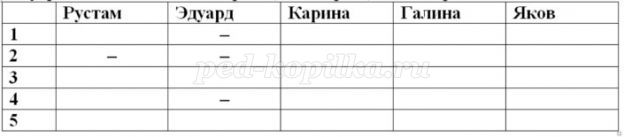
Яков не был первым и Галина не была не первой ни последней и так как Карина финишировала сразу за Яковом то она не могла быть ни первой ни второй.
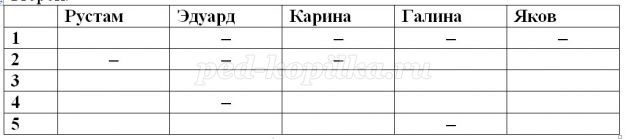

Так как Карина финишировала сразу за Яковом, то очевидно, что Яков был четвёртым, а Карина последней и тогда Галина была второй.
Итак, можно выделить
Пять простых шагов на пути поиска решения логических задач.
1. Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты.
2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов.
3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок.
4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия.
5. Решение можно найти простым методом последовательных исключений.
Чем больше будете тренироваться, тем лучше у вас это будет получаться. А теперь за дело.
Задача 2.
В субботний вечер Семен, Коля и Витя решили развлечься. У них был выбор: кино, рок-концерт или танцы.
• Семён любит кино, но к танцам менее нетерпим, чем к рок-музыке.
• Коля любит танцевать, но готов пойти в кино скорее, чем на рок концерт.
• Витя любит рок-музыку меньше чем танцы, но кино ему всё-таки не так неприятно, как танцы или концерт.
Поскольку вопрос решатся большинством голосов, то куда, на ваш взгляд отправились эти ребята?
Задача 3.
Трое мальчиков Костя, Фома и Марат дружили с тремя девочками – Женей, Светой и Мариной. Но вскоре компания разделилась на пары, потому, что оказалось:
• Света ненавидит ходить на лыжах.
• Костя, Женин брат часто катается со своей подружкой на лыжах
• А Фома теперь бежит на свидание к Костиной сестре.
С кем же проводит время Марат?
Задача 4.
Шестеро друзей в ожидании электрички заскочили в буфет.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад.
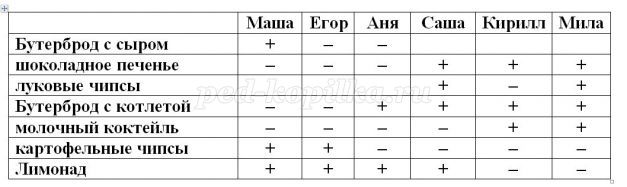
Из чего состоял завтрак каждого из друзей?
Решение: Так как
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром;
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье;
• Кирилл ел то же, что и Мила, но без луковых чипсов;
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы;
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то:
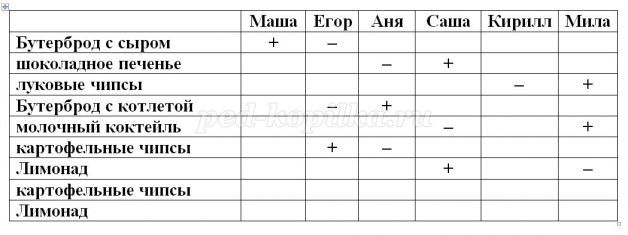
Второй раз проанализируем условия.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы и Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то и Кирилл ел то же, что и Мила, но без луковых чипсов.
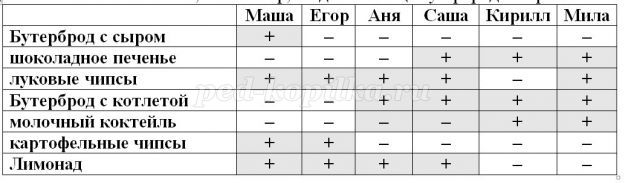
Третий раз проанализируем условия.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то и Кирилл ел то же, что и Мила, но без луковых чипсов.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром
Задача 5.
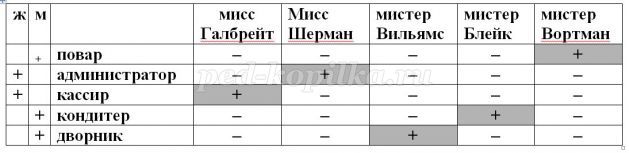
В одном небольшом кафе в смене одновременно работали 5 человек: администратор, повар, кондитер, кассир, дворник. Одновременно на работу выходили мисс Галбрейт, мисс Шерман, мистер Вильямс, мистер Вортман и мистер Блейк. При этом известно, что:
1. Повар – холостяк.
2. Кассир и администратор жили в одной комнате, когда учились в колледже.
3. Мистер Блейк и мисс Шерман встречаются только на работе.
4. Миссис Вильямс расстроилась, когда муж сказал ей, что администратор отказал ему в отгуле.
5. Вортман собирается быть шафером на свадьбе у кассира и кондитера.
Кто на какой должности в этом кафе?
Естественно, что на уроке я не использую все предложенные задачи, а подбираю для каждого класса индивидуально, в зависимости от их подготовленности и способностей.
Можно разделить учащихся на группы и каждой группе дать индивидуальное задание или подобрать задачи для каждого ученика.
Задача 1.
Коля, Боря, Вова и Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они ответили:
1) «Коля не занял ни первое, ни четвертое места».
2) “Боря занял второе место”.
3) “Вова не был последним”.
Какое место занял каждый мальчик?
Задача 2.
Три одноклассника — Влад, Тимур и Юра встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой — физиком, а третий — юристом. Один увлекся туризмом, другой — бегом, третий — регби.
1. Юра сказал, что, на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист.
2. Врач сказал, что он разделяет увлечение коллеги.
3. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Кто чем любит заниматься в свободное время и у кого какая профессия?
Задача 3.
Три друга — Иван, Дмитрий, Степан преподают различные предметы (химию, литературу, физику) в школах Москвы, Калининграда и Перми. Известно:
1) Иван работает не в Москве, а Дмитрий не в Калининграде;
2) москвич преподает не физику;
3) тот, кто работает в Калининграде, преподает химию;
4) Дмитрий преподает не литературу.
Какой предмет и в каком городе преподает каждый из товарищей?
Задача 4.
Четыре девочки Маша, Таня, София и Полина взяли в кафе сок. Каждая из них покупал только один сок, причем две из них купили сок яблочный, одна виноградный, и одна – грушевый. Известно, что у Маши и Тани разные вкусы. Разные соки взяли Маша с Софией, Полина с Софией, Полина с Машей и Таня с Софией. Кроме того известно, что Маша купила не грушевый сок.
Определить, какой сок пила каждая из них.
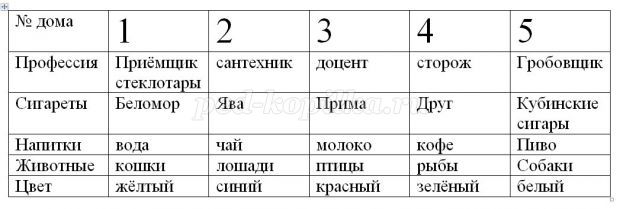
Задача 6. (Один из вариантов «Задачи Эйнштейна»)
Пять домов стоят вдоль дороги, один за другим.
1. Доцент живёт в красном доме.
2. Гробовщик держит собак.
3. Сантехник пьёт чай.
4. Зелёный дом слева от белого.
5. Хозяин зелёного дома пьёт кофе.
6. Любитель «Примы» держит птицу.
7. Хозяин жёлтого дома курит «Беломор канал».
8. В центральном доме любят молоко.
9. Приёмщик стеклотары живёт в первом доме.
10. Курящий «Яву» сосед хозяина кошек.
11. Хозяин лошадей – сосед курящего «Беломор».
12. Любитель пива курит «Кубинские» сигары.
13. Ночной сторож предпочитает сигареты «Друг».
14. Приёмщик стеклотары живёт рядом с синим домом.
15. Курящий «Яву» сосед пьющего воду.
Кто держит рыб? (номер дома, цвет профессия, напитки)
Решение:
Составить логическую задачу самостоятельно.
Удачи вам!
Задачи, составленные моими учениками.
Иванова Светлана, 7«Б» кл.
На дискотеку пошли 4 девочки: Маша, Оля, Рита. На медленный танец их приглашали Сергей, Рома, Саша, Паша. Кто с кем танцевал, если:
1) Оля не танцевала с Пашей;
2) Таня не танцевала с Пашей и Романом;
3) Рита танцевала с Ромой;
4) Оле понравился Сергей, но она не танцевала с ним.
Маякова Оксана, 9«А» кл.
Бизнесмены Боря Вова Гриша и Гена зарабатывают сумасшедшие деньги, их фамилии засекречены, но удалось их узнать, правда непонятно какая кому принадлежит. Их фамилии: Иванов, Енин, Сидоров, Петров. Так же наши шпионы выяснили:
1) Боря и Петров не имеют личные самолёты.
2) Гриша и Иванов вообще ничего личного не имеют, кроме счетов в швейцарском банке.
3) Гена теперь важнее Енина, хотя Енин и имеет личный самолёт.
4) Петров важнее Енина.
У кого какая фамилия?
Конева Ксения, 9«А» кл.
Четыре подружки: Даша, Маша, Ольга и Таня ходили в магазин покупать подарки. И все подарки разные. Блокнот, альбом, брелок, и книга. На вопрос кто какие подарки купил, они ответили так:
1) Даша и Оля не знали кто купил блокнот;
2) Оля сказала, что Даша и Маша вместе с ней посещали магазин, где продают брелки.
3) Даша не покупала альбом.
Кто какой подарок купил?
Источник: ped-kopilka.ru