Индексами в статистике называются относительные величины, характеризующие соотношение показателей во времени, в пространстве или фактических с плановыми.
При всем их разнообразии, индексы можно разделить на два класса:
- 1. Индивидуальные, элементарные, простые (i).
- 2. Сводные, сложные, общие (I).
Под элементарными индексами понимаются относительные величины, характеризующие изменение во времени показателей, относящихся к одному объекту, или сравнивающие размеры показателей для одновременно существующих однородных объектов.
i = — или 1 = —-, 1 = —, (93)
то есть соотносятся величины простого явления (объекта), характеризуемые одним показателем (например, цена или себестоимость по одному конкретному виду продукции),
При этом обязательным условием для его вычисления является максимальная однородность объекта, для которого он вычисляется.
Однако в экономике существуют в основном сложные явления, составные части которых нельзя непосредственно сложить. Относительные показатели, характеризующие изменение сложного явления в целом, характеризуемого двумя и более показателями, называются сводными, общими индексами.
Индекс качества воздуха: чем мы дышим
X P, xq, X р1хЧ|
; IPq=JT——> (95)
Х р » х Ч> ЁРоХЧо
где Р], Ро — цена изделия соответственно в отчетном и базисном периодах;
qb qo — объем произведенной продукции соответственно в отчетном и базисном периодах.
Исходными величинами для их построения служат индивидуальные индексы, размеры явлений, специальные расчетные показатели. Выражаются индексы в коэффициентах или процентах.
Виды сложных индексов
Сложные индексы, в свою очередь, можно разделить на основные два вида:
- 1) агрегатные;
- 2) средние.
Агрегатным называется сложный индекс, полученный путем сопоставления итогов, выражающих величину сложного явления в отчетном (базисном) периодах при помощи соизмери-телей, а способ их получения — агрегатным. Отличительной особенностью любого агрегатного индекса является то, что в числителе и знаменателе этого индекса фигурирует сумма произведений двух и более показателей, один может меняться, то есть индексируется, другой же выступает в роли соизмерителя, то есть остается неизменным.
Например, на основе агрегатного способа построим общий индекс товарооборота (Т):
Z Ti Е pixqi
I _ 1=1____ Дн1________
Е То Е РохЯо
Данный индекс зависит от двух величин, то есть изменение величины товарооборота зависит от изменения цен (Р) на продаваемые товары и объема продаж (q) этих товаров, поэтому можно построить два индекса, каждый из которых характеризует влияние лишь одного фактора:
1. Индекс цен (I/O характеризует изменение товарооборота за счет изменения цен (то есть во сколько раз изменится товарооборот за счет изменения цен).
Разность числителя и знаменателя данного индекса характеризует абсолютную величину такого изменения (в руб.).
В индексе цен цена изменяется, так как ее влияние определяется, объем фиксируется на уровне отчетного периода, так как это количественный фактор и его влияние устраняется.
Лекция 24: Статистические индексы
2. Индекс физического объема (1Д характеризует изменение товарооборота за счет изменения объема (то есть во сколько раз изменится товарооборот за счет изменения объема).
Разность числителя и знаменателя данного индекса характеризует абсолютную величину такого изменения (в руб.).
В индексе физического объема объем изменяется, так как его влияние устанавливается, цена фиксируется на уровне базисного периода, так как это качественный фактор и его влияние устраняется.
При построении этих индексов используется правило фиксации Г. Пааше: в индексе, характеризующем влияние качественного показателя (р, z, w), данный показатель индексируется, (то есть изменяется), тогда как другой количественный показатель, влияние которого устраняется, фиксируется (то есть остается неизменным), причем на уровне отчетного периода (qb Т[).
Если же характеризуем влияние количественного фактора, то он индексируется, другой же — качественный — фиксируется на уровне базисного периода (Zo, Ро, Wo) (то есть на уровне базисного периода «О» фиксируется качественный показатель, а на уровне отчетного «1» — количественный).
Средние индексы. Агрегатный способ исчисления общих индексов является основным, но не единственным. Другой способ состоит в том, что по отдельным видам показателей рассчитываются индивидуальные индексы, а затем из них рассчитывается средний. При построении среднего индекса возникает вопрос о форме средней величины, используемой для его вычисления, и о весах. В практике статистики средний индекс рассчитывается как средние арифметические или гармонические величины, обязательно взвешенные.
где i — индивидуальный индекс;
Для того чтобы правильно выбрать веса и форму среднего индекса, следует руководствоваться тем, что средний индекс должен быть тождественен агрегатной форме, которая является основной.
Исходя из этого все индексы можно свести в две группы:
1) агрегатные индексы с базисными весами, им соответствуют средние арифметические с базисными весами.
Е Ч1 хр о Е iqXqoXPo
Для того чтобы перейти к среднему индексу, показатель qi (в числителе индекса) выражают через индивидуальный индекс:
Данное выражение подставляем в агрегатную форму (в числитель) и получаем среднеарифметический индекс;
2) агрегатные индексы с текущими весами, им соответствуют средние гармонические с текущими весами.
Для того чтобы перейти к среднему индексу, показатель Ро (в знаменателе индекса) выражают через индивидуальный индекс:
Данное выражение подставляем в агрегатную форму (в знаменатель индекса) и получаем среднегармонический индекс.
В этом смысле общий индекс изучаемого явления рассматривается как результат изменения уровня данного явления у отдельных единиц совокупности. В процессе осреднения индивидуальных индексов веса подбираются так, чтобы был возможен переход от общего индекса в форме средней величины к общему индексу в агрегатной форме.
Источник: ozlib.com
Сущность статистических индексов
Методы статистики — это особые приемы и способы изучения массовых общественных явлений. Каждый метод ориентирован на особые представления изучаемого объекта, на его особую модель. Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или в пространстве две совокупности, элементы которых являются несоизмеримыми величинами. И поскольку объекты изучения индексов весьма разнообразны, то они широко применяются в экономической практике.
Целью работы является изучение методологии вычисления среднегармонических индексов.
Задачами работы являются: изучение среднегармонических индексов, решение задач по основам статистики и проведение статистического анализа конкретного явления.
В ходе выполнения работы применялись следующие методы исследования: монографический (использование специальной литературы), аналитический, расчётный, сравнение.
В теоретической части рассмотрены понятие о индексах и понятие среднегармонических индексов. В расчетной части решены практические задания.
Использование среднегармонических индексов в статистическом анализе деятельности торгового предприятия
Сущность статистических индексов
В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана.
Многие общественные явления состоят из непосредственно несопоставимых явлений, поэтому основной вопрос — это вопрос сопоставимости сравниваемых явлений.
К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения.
Индексы классифицируют по трем признакам: по характеру изучаемых объектов; степени охвата элементов совокупности; методам расчета общих индексов. По содержанию индексируемых величин индексы разделяют на индексы количественных (объемных) и индексы качественных показателей — эти индексы будут рассматриваться нами ниже в полном объеме. Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.
Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами. Индивидуальные индексы обозначаются i и снабжаются подстрочным знаком индексируемого показателя. Индивидуальные индексы относятся к одному элементу и не требуют суммирования данных.
Они представляют собой относительные величины динамики, выполнения обязательств, сравнения. Выбор базы сравнения определяется целью исследования. Название индекс получает по названию индексируемой величины. В большинстве случаев в числителе стоит текущий уровень, а в знаменателе — базисный уровень. Исключением является индекс покупательной способности рубля.
Индексы измеряются либо в виде процентов, либо в виде коэффициентов.
Общие индексы отражают изменение всех элементов сложного явления. При этом под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объем продукции, включающей разноименные товары цены на разные группы продуктов и т.д.). Общие индексы обозначаются буквой I и также сопровождаются подстрочным знаком индексируемого показателя. Методика расчета общих индексов сложнее, чем индивидуальных, и различна в зависимости от характера индексируемых показателей, наличия исходных данных и целей исследования.
Сложные явления, для которых рассчитывается сводный индекс, отличаются той особенностью, что элементы, их составляющие, неоднородны и, как правило, несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов невозможно. Сопоставимость может быть достигнута различными способами:
) сложные явления могут быть разбиты на такие простые элементы, которые в известной степени являются однородными;
) сравнение по стоимости, без разбиения на отдельные элементы.
Цель теории индексов — изучение способов получения относительных величин, используемых для расчета общего изменения ряда разнородных явлений.
Сводные индексы в агрегатной форме позволяют нам измерить не только относительное изменение отдельных элементов изучаемого явления и явления в целом в текущем периоде по сравнению с базисным, но и абсолютное изменение.[4, c.161]
Почему человек чувствует себя несчастным?: Для начала определим, что такое несчастье. Несчастьем мы будем считать психологическое состояние.
Как вы ведете себя при стрессе?: Вы можете самостоятельно управлять стрессом! Каждый из нас имеет право и возможность уменьшить его воздействие на нас.
Генезис конфликтологии как науки в древней Греции: Для уяснения предыстории конфликтологии существенное значение имеет обращение к античной.
Как выбрать специалиста по управлению гостиницей: Понятно, что управление гостиницей невозможно без специальных знаний. Соответственно, важна квалификация.

Источник: megaobuchalka.ru
Понятие об индексах.
В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей, анализируются результаты производственно-хозяйственной деятельности предприятий и организаций, исследуется роль отдельных факторов в формировании важнейших экономических показателей, выявляются резервы производства. Индексы используются также в международных сопоставлениях экономических показателей, определении уровня жизни, мониторинга деловой активности в экономике и т.д.
Статистический индекс – это относительная величина сравнения сложных совокупностей и их отдельных единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не могут быть просуммированы.
Например, ассортимент продовольственных товаров состоит из продуктов, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, яйцо – в штуках, консервы – в условных банках и т.п. Для определения общего объема производства и реализации продовольственных товаров суммировать данные учета разнородных товарных масс в натуральных измерителях нельзя. То же относится и к непродовольственным товарам, к продукции крупных промышленных предприятий и т.д.
Для получения в сложных статистических совокупностях обобщающих, суммарных величин прибегают к индексному методу. Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.
В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности индексы подразделяются на индивидуальные и общие.
Индивидуальные индексы характеризуют изменения отдельных единиц изучаемой совокупности. Например, при изучении оптовой реализации продовольственных товаров изменения в продаже отдельных товаров дают индивидуальные (однотоварные) индексы.
Общие или сводные или агрегатные индексы выражают обобщающие результаты совместного изменения всех единиц, образующих статистическую совокупность. Например, показатель изменения объема реализации товарной массы продуктов питания в отдельные периоды будет общим индексом физического объема товарооборота. Из общих индексов выделяют иногда групповые индексы (субиндексы), охватывающие только часть (группу) единиц в изучаемой статистической совокупности.
Важной особенностью общих индексов является то, что они обладают синтетическими и аналитическими свойствами.
Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агрегирование) в целое разнородных единиц статистической совокупности.
Аналитические свойства индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. На основе изучения состава и роли факторов, выявления силы их действия осуществляются возможности квалифицированного управления развитием экономических процессов не только в нужном направлении, но и с заранее заданными параметрами.
Для определения индекса надо произвести сопоставление не менее двух величин. При изучении динамики социально-экономических явлений сравниваемая величина (числитель индексного отношения) принимается за текущий (или отчетный) период, а величина, с которой производится сравнение, – за базисный период. Если в индексном отношении сравнивается величина фактического уровня развития с величиной планового задания, то основание сравнения называют плановым уровнем. Кроме того, при сравнении текущих величин с предшествующими получают цепные индексы (при сравнении с базисными величинами – базисные индексы).
Индивидуальные индексы обозначают i, а общие – I.
Индивидуальные индексы физического объема реализации товаров определяют по формуле
где q1 и q0 – количество продажи отдельной товарной разновидности в текущем и базисном периодах в натуральных измерителях.
Индивидуальные индексы цен определяются по формуле
где p1 и p0 – цены за единицу товара в текущем и базисном периодах.
Результаты расчета индексных отношений могут выражаться в коэффициентах или в процентах.
Источник: moodle.kstu.ru
Индексы в статистике
где q1 — количество товара в текущем периоде; q0 — количество товара в базисном (предшествующем) периоде.
Изменение стоимостного объёма товарооборота по данному товару отражается в значении индивидуального индекса товарооборота. Для его расчёта товарооборот текущего периода (произведение цены на количество проданного товара) сравнивается с товарооборотом предшествующего периода:
Данный индекс также может быть получен как произведение индивидуального индекса цены и индивидуального индекса физического объёма реализации.
В отличие от индивидуальных индексов, сводные индексы позволяют обобщить показатели по нескольким видам товаров, нескольким видам продукции, по ценным бумагам нескольких эмитентов и т. д. Исходной формой сводного индекса является агрегатная форма. Сводные индексы также могут исчисляться в среднеарифметической и среднегармонической формах.
Сводный индекс товарооборота в агрегатной форме показывает изменение стоимостного объёма товарооборота по товарной группе. При этом определяется совокупный объём товарооборота по n товарам в текущем периоде:
Аналогично определяют совокупный объём товарооборота для базисного периода:
Сводный индекс товарооборота получают как отношение данных агрегатов:
Величина индекса товарооборота формируется под воздействием двух факторов — на неё оказывают влияние как изменение цен на товары, так и изменение объёмов их реализации. Для того, чтобы оценить изменение только цен (индексируемой величины), количество проданных товаров (веса индексы) фиксируют на каком-либо постоянном уровне. Таким способом получают сводные индексы цен (смотри Индексы цен).
Сводный индекс физического объёма реализации характеризует изменение количества проданных товаров по той или иной товарной группе; при этом входящие в группу товары могут быть непосредственно несоизмеримы, существенно отличаться по своим характеристикам, в том числе и по единицам измерения (предположим, часть товаров измеряется в кг, часть — в штуках, часть — в литрах). Весами в данном случае выступают цены, которые фиксируются на уровне базисного или текущего периода, например:
Знаменатель данного индекса отражает фактический стоимостной объём товарооборота в базисном периоде. Числитель же — условная величина, показывающая, каким бы был стоимостной объём товарооборота в текущем периоде при условии сохранения цен на уровне базисного периода. В итоге данный индекс отражает изменение физического объёма реализации по группе товаров, объёмы которых непосредственно в натуральном выражении суммировать нельзя.
Между индексами товарооборота, цен и физического объёма реализации существует следующая взаимосвязь:
Аналогично приведённым выше индексам рассчитываются и другие сводные индексы в агрегатной форме (себестоимости, урожайности и пр.).
Индексы позволяют получать сводную оценку изменения наблюдаемых показателей постоянно — месяц за месяцем, год за годом. При этом для достижения сопоставимости они рассчитываются по единой методологии. Такая методология, или схема расчёта индекса за n последовательных временных периодов, называется системой индексов.
В зависимости от информационной базы и целей исследования индексная система может включать индексы цепные или базисные, с переменными или постоянными весами. Например, при расчёте индекса цен, если сравнивать цены каждого периода с ценами периода предшествующего, получаемая индексная система будет включать цепные индексы, отражающие изменение цен за каждый из периодов рассматриваемого временного интервала. При этом в качестве весов используют объёмы реализации каждого конкретного периода или же постоянные объёмы какого-либо периода, принятого в качестве базисного. В первом случае индексная система включает цепные индексы с переменными весами:
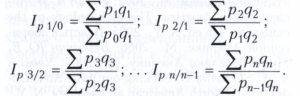
При использовании весов базисного периода получают цепные индексы цен с постоянными весами:
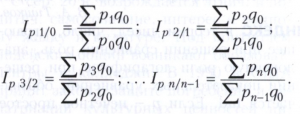
Использование постоянных весов более предпочтительно, поскольку рассчитываемые таким образом индексы мультипликативны, т. е. их можно последовательно перемножать и получать величину показателя за более продолжительный период. Так, например, располагая индексы цен за 3 последовательных месяца, можно получить сводную оценку изменения цены в целом за квартал и т.п. Индексы с переменными весами такой возможности не предоставляют.
При сравнении цен каждого периода с ценами какого-либо базисного периода (как правило, начального) получаемая индексная система включает базисные индексы, отражающие изменение цен накопленным итогом, то есть с начала рассматриваемого временного интервала (например, изменение цен в январе по сравнению с декабрём предшествующего года, в феврале — по сравнению с тем же декабрём и т.д.). При этом в качестве весов также можно использовать объёмы реализации каждого конкретного периода или же постоянные объёмы периода, принятого за базисный. Система базисных индексов с переменными весами имеет следующий вид:
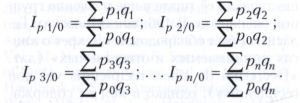
Базисные индексы цен с постоянными весами рассчитываются по формулам:
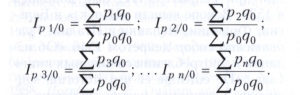
При расчёте индексов используют не только агрегатную, но и средние их формы — среднеарифметическую и среднегармоническую, т.к. любой сводный индекс можно представить как среднюю взвешенную из индексов индивидуальных. Использование средних форм связано с тем, что часть необходимой для расчёта индекса информации в ряде случаев отсутствует или данные базируются на результатах выборочных обследований, которые приобретают всё большее значение в статистической практике. Например, при расчёте сводного индекса цен по методу Пааше используют следующую замену:
Тогда сводный индекс цен будет выражен в форме средней гармонической:
Данный сводный индекс цен в среднегармонической форме соответствует сводному индексу Пааше в агрегатной форме. Для получения среднего индекса цен, соответствующего индексу Ласпейреса, в формуле последнего используется следующая замена:
С учётом этой замены сводный индекс цен в среднеарифметической форме имеет вид:
Среднеарифметическая и среднегармоническая формы также используются при расчёте сводного индекса физического объёма товарооборота и других индексов.
Индексы используются не только для оценки динамики показателей, характеризующих разнородные в качественном отношении совокупности (товарные группы). Даже если рассматриваемая совокупность однородна (товар одного вида), на величине результативного показателя — средней цены данного товара — отражается влияние структурных изменений, например изменений в структуре его реализации по территориям. В этом случае в индексном анализе используются индексы переменного и фиксированного состава, а также индексы структурных сдвигов.
Индекс цен переменного состава представляет собой соотношение средних значений цены данного товара за 2 рассматриваемых периода:
Значение индекса отражает изменение средней цены как за счёт изменения региональных уровней цен, так и за счёт изменений в структуре реализации товара по регионам. Воздействие структурного фактора оценивают на основе индекса структурных сдвигов, зафиксировав цены на уровне базисного периода:
Индекс цен фиксированного состава не учитывает структурные сдвиги, а характеризует изменение средней цены товара, обусловленное лишь изменением региональных цен:
Взаимодействие учитываемых в данных И. факторов отражается следующей взаимосвязью:
В отличие от представленных выше динамических индексов, территориальные индексы служат для сравнения показателей в пространстве, то есть по городам, районам, областям и т. п. Важную роль играют территориальные индексы цен, являющиеся незаменимым инструментом исследования в практике международных сравнений уровней цен, в том числе между странами СНГ.
Построение территориальных индексов имеет определённые особенности, связанные с выбором базы сравнения и весов, или уровня, на котором фиксируются веса. Один из вариантов расчёта территориальных индексов цен заключается в том, что в качестве весов принимаются объёмы проданных товаров i-го вида (i = 1,2. n) по двум территориям, вместе взятым:
где qia — количество i-го товара, проданного на территории А; qib — количество i-го товара, проданного на территории В.
Территориальный индекс цен в этом случае рассчитывается по формуле:
где pib — цена i-го товара на территории В; рia — цена i-го товара на территории А.
При расчёте территориальных индексов данным способом в их формуле вместо суммарных весов могут использоваться некоторые теоретические или стандартизованные веса; в качестве таких весов также может выступать структура продажи данных товаров по более крупному территориальному образованию.
Лит.: Гусаров В. М. Теория статистики. М., 1998; Статистика. Курс лекций. М., 1998; Общая теория статистики. 5-е изд.
М., 2007; Теория статистики. 4-е изд. М., 2007.
Источник: knowledge.su