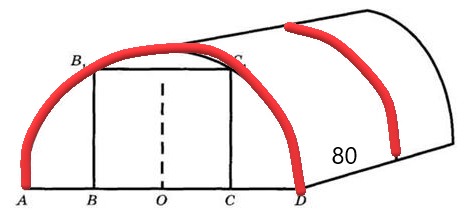
Виктор Николаевич решил построить на дачном участке теплицу длиной 6 метров. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы он заказал металлические дуги в форме полуокружности длиной 5 метров каждая, а также покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется сделать вход, который показан на рисунке прямоугольником ВВ1С1С, где точки В,О и С делят отрезок АД на равные части.
Внутри теплицы Виктор Николаевич планирует сделать три грядки по длине теплицы – одну центральную широкую и две по узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых нужно купить тротуарную плитку размером 25 см 25 см.
Теория для решения:
Задание №1. Какое наименьшее количество дуг надо заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение
На рисунке дуги выделены красным цветом и показано, что расстояние между ними не более 80 см.
ОГЭ-2022. ДЕМОВЕРСИЯ. ЧАСТЬ-1.
Зная, что длина теплицы 6 метров, переведем её в сантиметры: 6м=600 см. Теперь разделим 600 см на 80 см, получим 7,5. Округлим до целого числа и получим 8, но это не количество дуг, а количество расстояний (отрезков) между ними. Далее нужно прибавить единицу, чтобы получить точное количество: 8+1=9 дуг.
Если способ с рисунком теплицы не совсем понятен, то можно изобразить дуги точками на отрезке вот таким образом.

Задание №2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение
По условию задачи знаем, что в теплице будет три грядки, следовательно, будет две дорожки, ширина которых по условию 50 см. Длина каждой дорожки равна длине теплицы, т.е. 600 см.
Зная длину и ширину дорожки, можно найти её площадь: 600 × 50=30000 см 2 . Таких дорожек у нас две, значит 30000 × 2=60000 см 2 .
По условию задачи известно, что тротуарная плитка имеет размеры 25 см × 25 см. Можно найти площадь одной плитки: 25 см × 25 см=625 см 2 .
Теперь находим количество плиток для двух дорожек: 60000_625=96 плиток.
Так как сказано, что плитки продаются в упаковках по 10 штук, то разделим 96 на 10, получим 9,6. Необходимо округлить результат до целого числа, так как отдельно несколько плиток нам не продадут, поэтому 9,6 ≈ 10.
Задание №3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение
Ширина теплицы – это диаметр полуокружности. По условию задачи Виктор Николаевич покупал дуги длиной 5 метров, значит, длина полуокружности и есть 5 метров.
Вспомним формулу, которая связывает длину окружности и радиус: С=2 π R, также можно воспользоваться и формулой С= π d, так как нам надо найти ширину теплицы, т.е. диаметр.
Подставим значения в формулу, помня о том, что полная длина окружности будет равна 10 м: 10=3,14d. Отсюда d=10:3,14=3,184… ≈ 3,2 (так как по условию требуется округлить до десятых).
1 УРОК: КАК ПОСАДИТЬ ДОМ на участок и учесть все ОГРАНИЧЕНИЯ // Линии // Охранные зоны // Рельеф
Задание №4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.
Решение
Покажем на рисунке, как выглядят грядки и дорожки внутри теплицы, расставим известные данные: 50 см – по условию, а 320 см – из решения задания №3.
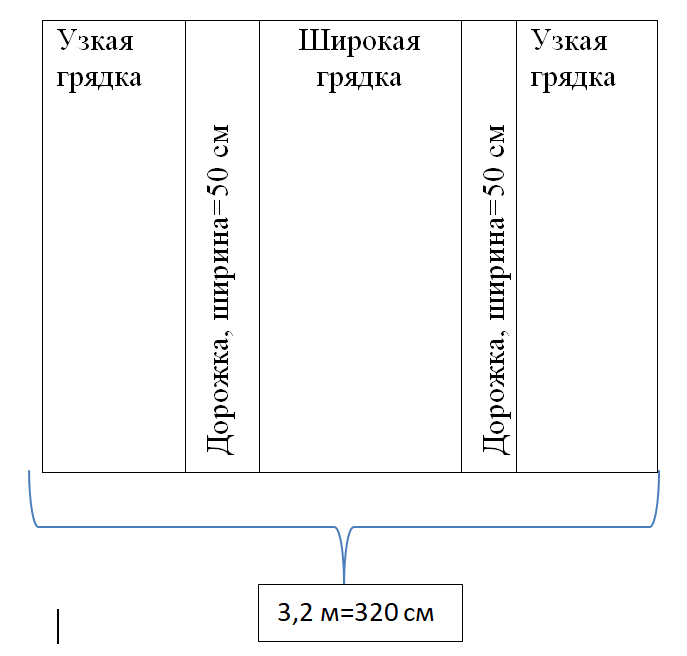
Для удобства решения определим ширину всех грядок вместе, то есть уберем ширину дорожек: 320-50-50=220 см.
По условию задачи ширина центральной грядки относится к ширине узкой грядки как 5:3, т.е. можно сказать, что на центральную грядку (широкую) приходится 5 частей, а на крайние грядки (узкие) по 3 части. Значит, всего на три грядки приходится 3+5+3=11 равных частей. Так как вся ширина грядок 220 см, то 220_11=20 см ширина одной части. Значит, ширина узкой грядки будет равна 20 см × 3=60 см.
Задание №5. Сколько квадратных метров пленки необходимо купить для передней и задней стенок теплицы, если с учетом крепежа ее нужно брать с запасом 15%? Ответ округлить до десятых.
Решение
Передняя и задняя стенки теплицы являются полукругами одинакового диаметра, следовательно, два полукруга вместе – это круг, диаметр которого (ширина теплицы) мы нашли в задаче №3, т.е.3,2 метра. Площадь круга находится по формуле S= π R 2 . Зная, что диаметр равен 3,2 м, найдем радиус: 3,2:2=1,6 м. Подставим в формулу данные и найдем площадь круга: S=3,14 × 1,6 2 =8,0384 м 2
По условию задачи сказано, что с учетом крепежа пленку надо покупать с запасом 15%. Найдем 15% от данного числа, переведя 15% в десятичную дробь: 0,15 × 8,0384=1,20576.
Источник: spadilo.ru
Разработка урока по теме: «Применение производной в решении практических задач на наибольшее и наименьшее значение». 11-й класс
Цель урока: Усвоение умений самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.
- Закрепление, систематизация и обобщение знаний и умений в понятии наибольшее и наименьшее значение функции, практическое применение формируемых умений и навыков.
- Развитие умений самостоятельно работать, ясности выражений мысли, проведение самооценки учебной деятельности на уроке.
- Умение участвовать в дискуссии, умение слушать и слышать.
I. Слово учителя: (2 мин.)
Каждый человек время от времени оказывается в ситуации, когда надо отыскать наилучший способ решения какой-либо задачи, и математика становится средством решения проблем организации производства, поисков оптимальных решений. Важным условием повышения эффективности производства и улучшения качества продукции является широкое внедрение математических методов в технику.
Среди задач математики большую роль отводят задачам на экстремумы, т.е. задачам на отыскание наибольшего и наименьшего значения, наилучшего, наиболее выгодного, наиболее экономного. С такими задачами приходиться иметь дело представителям самых разных специальностей: инженеры-технологи стараются так организовать производство, чтобы получилось как можно больше продукции, конструкторы хотят так спланировать прибор на космическом корабле, чтобы масса прибора была наименьшей, экономисты стараются спланировать прикрепление заводов к источникам сырья так, чтобы транспортные расходы оказывались минимальными. Можно сказать, что задачи на отыскание наименьшего и наибольшего значения, имеют большое практическое применение. Сегодня на уроке мы и займемся решением таких задач.
II. К доске вызываются два “ сильных” ученика решать задания: (10мин)
Дан бак без крышки в виде прямоугольного параллелепипеда, в основании которого лежит квадрат и объем равен 108 см 3 . При каких размерах бака на его изготовление пойдет наименьшее количество материала?
Обозначим сторону основания через х см, тогда высота параллелепипеда будет .
Пусть S(х) площадь поверхности, тогда S(х) =х 2 +4**х=х 2 +;
2х 3 =432; х 3 =216; х=6;
По условию задачи х (0;)
Найдем знак производной на промежутке (0;6) и на промежутке (6; ?). Производная меняет знак с “-” на “+”. Отсюда х=6 точка минимума, следовательно, S(6)=108 см 2 наименьшее значение. Значит, сторона основания равна 6 см, высота 12см.
В окружность радиуса 30 см вписан прямоугольник наибольшей площади. Найти его размеры.
Обозначим одну сторону прямоугольника через х см, тогда вторая будет, S(х) площадь прямоугольника, тогда S(х)=х;
S / (х)= — S / (х)=0; Приведем дробь к общему знаменателю, получим
3600-2х 2 =0; х=30; Берем только положительное значение по условию задачи. По смыслу задачи х (0;60);
Найдем знак производной на промежутке (0;30) и на промежутке (30;60). Производная меняет знак с “+” на “-”. Отсюда х=30 точка максимума. Следовательно, одна сторона прямоугольника30, вторая 30.
III. В это время выполняется взаимопроверка по теме “Применение производной” (за каждый правильный ответ выставляется 1 балл) Каждый ученик отвечает и для проверки передает свой ответ соседу по парте.
- Функция называется возрастающей на данном промежутке, если…
- Функция называется убывающей на данном промежутке, если…
- Точка х0 называется точкой минимума, если…
- Точка х0 называется точкой максимума, если…
- Стационарными точками функции называют точки…
- Написать общий вид уравнения касательной.
- Физический смысл производной.
IV. Класс садится по группам. Группы выполняют задания на отыскание минимума и максимума функции.
Для функции f(х)=х 2 + найти минимум на промежутке (0; ?);
Для функции f(х)=х найти максимум на промежутке (0;60);
V. Предоставляется слово “сильным” ученикам. Учащиеся класса проверяют свои решения.(10мин).
VI. Выдаются задачи по выбору для каждой группы. (10 мин)
Для функции f(х)=х 2 *(6-х) найти наименьшее значение на отрезке[0;6]
f(х)=х 2 *(6-х)=6х 2 +х 3 ;
Из проволоки длиной 20см надо сделать прямоугольник наибольшей площади. Найти его размеры.
Обозначим одну сторону прямоугольника через х см, тогда вторая будет (10-х)см, площадь S(х)=(10-х)*х=10х-х 2 ;
S / (х)=10-2х; S / (х)=0; х=5;
По условию задачи х (0;10)
Найдем знак производной на промежутке (0;5) и на промежутке (5;10 ). Производная меняет знак с “+” на “-”. Отсюда: х=5 точка максимума, S(5)=25см 2 –наибольшее значение. Следовательно, одна сторона прямоугольника 5см, вторая 10-х=10-5=5см;
Участок, площадью 2400м 2 , надо разбить на два участка прямоугольной формы так, чтобы длина изгороди была наименьшей. Найти размеры участков.
Обозначим одну сторону участка через х м, тогда вторая будет м, длина изгороди Р(х)=3х+;
Р / (х)= 3-; Р / (х)=0;3х 2 =4800;х 2 =1600; х=40. Берем только положительное значение по условию задачи.
По условию задачи х (0; )
Найдем знак производной на промежутке (0;40) и на промежутке (40; ?). Производная меняет знак с “-” на “+”. Отсюда х=40 точка минимума, следовательно, Р(40)=240м наименьшее значение, значит, одна сторона 40м, вторая =60м.
Для функции f(х)=х 2 +(16-х) 2 найти наименьшее значение на отрезке[8;16]
f / (х)=2х-2(16-х)х=4х-32; f / (х)=0; 4х-32=0; х=8;
f(0)=256; f(16)=256; f(8)=128-min;
Участок прямоугольной формы одной стороной прилегает к зданию. При заданных размерах периметра в м, надо огородить участок так, чтобы площадь была наибольшая.
Обозначим одну сторону прямоугольного участка через х м, тогда вторая будет (-2х)м, площадь S(х)= ( -2х)х =х -2х 2 ;
S / (х)= -4х; S / (х)=0; -4х; х =;
По условию задачи х (0;)
Найдем знак производной на промежутке (0; )и на промежутке (;). Производная меняет знак с “+” на “-”. Отсюда х = точка максимума. Следовательно, одна сторона участка = м, вторая -2х= м ;
Из прямоугольного листа картона со сторонами 80см и 50см нужно сделать коробку прямоугольной формы, вырезав по краям квадраты и загнув образовавшиеся края. Какой высоты должна быть коробка, чтобы ее объем был наибольшим?
Обозначим высоту коробки (это сторона вырезанного квадрата) через х м, тогда одна сторона основания будет (80-2х)см, вторая (50-2х)см, объем V(х)= х(80-2х)(50-2х)=4х 3 -260х 2 +4000х;
V / (х)=12х 2 -520х+4000; V / (х)=0; 12х 2 -520х+4000=0; х1=10; х2=
По условию задачи х (0; 25); х1 (0; 25), х2(0;25)
Найдем знак производной на промежутке (0; 10) и на промежутке (10; 25). Производная меняет знак с “+” на “-”. Отсюда х = 10 точка максимума. Следовательно, высота коробки = 10см.
Для функции f(х)=х*(60-х) найти наибольшее значение на отрезке [0;60]
f / (х)=60-2х ; f / (х)=0; 60-2х=0; х=30;
f(0)=0; f(60)=0; f(30)=900-max
Участок прямоугольной формы одной стороной прилегает к зданию. При заданных размерах периметра 20 м, надо огородить участок так, чтобы площадь была наибольшая.
Обозначим одну сторону прямоугольника через х м, тогда вторая будет (20 -2х) м, площадь S(х)= (20-2х)х=20х -2х 2 ;
S / (х)= 20 -4х; S / (х)=0; 20 -4х =0; х = =5;
По условию задачи х (0; 10)
Найдем знак производной на промежутке (0; 5) и на промежутке (5; 10). Производная меняет знак с “+” на “-”. Отсюда х = 5точка максимума. Следовательно, одна сторона участка = 5м, вторая 20 -2х= 10м;
Чтобы уменьшить трение жидкости о стены и дно канала, нужно смачиваемую ею площадь сделать возможно малой. Требуется найти размеры открытого прямоугольного канала с площадью сечения 4,5м 2 , при которых смачиваемая площадь будет наименьшей.
Обозначим глубину канавы через х м, тогда ширина будет м, Р(х)=2х+;
Р / (х)=2-; Р / (х)=0;2х 2 =4,5; х=1,5. Берем только положительное значение по условию задачи.
По условию задачи х (0; )
Найдем знак производной на промежутке (0;1,5) и на промежутке (1,5; ?). Производная меняет знак с “-” на “+”. Отсюда х=1,5 точка минимума, следовательно, Р(1,5)=6м наименьшее значение, значит, одна сторона канавы 1,5м, вторая =3м.
Для функции f(х)=х 2 (18-х) найти наибольшее значение на отрезке[0;18]
f(х)=х 2 (18-х)=18х 2 -х 3 ;
f / (х)= (18х 2 -х 3 ) / ; f / (х)=0; 36х-3х 2 =0; х1=0; х2=12
f(0)=0; f(18)=0; f(12)=864-max
Участок прямоугольной формы одной стороной прилегает к зданию. При заданных размерах периметра 200м, надо огородить участок так, чтобы площадь была наибольшая.
Обозначим одну сторону прямоугольного участка через х м, тогда вторая будет (200 -2х) м, площадь S(х)= (200-2х)х=200х -2х 2 ;
S / (х)= 200 -4х; S / (х)=0; 200 — 4х =0; х = 200/4=50;
По условию задачи х (0; 100)
Найдем знак производной на промежутке (0; 50) и на промежутке (50; 100). Производная меняет знак с “+”на “-”.Отсюда х = 50 точка максимума. Следовательно, одна сторона участка = 50м, вторая 200 -2х= 100м;
Требуется изготовить открытую коробку в форме прямоугольного параллелепипеда с квадратным основанием, с наименьшим объемом, если на ее изготовление можно потратить 300см 2 .
Обозначим одну сторону основания через х см, тогда высота будет см, объем V(х)=х 2 =;
V / (х)= = V / (х)=0 300-3х 2 =0; х 2 =100; х=10. Берем только положительное значение по условию задачи.
По условию задачи х (0; )
Найдем знак производной на промежутке (0;10) и на промежутке (10; ). Производная меняет знак с “-” на “+”. Отсюда х=10 точка минимума, следовательно, V(10)=500см 3 — наименьшее значение, значит, сторона основания 10см, высота = 50см
VII. Делегаты от групп рассказывают решение выбранных задач.(10мин)
VIII. С учетом баллов в разминке и работе в группах выставляются отметки за урок.
IX. Подводится итог урока.
X. Домашнее задание: Решение задачи на балл выше, кто выполнял задачу на “5”, они освобождаются от домашней работы.
Источник: urok.1sept.ru