
.jpg)
Решебник — страница 28Готовое домашнее задание
Сравни числа в каждом столбике. Что обозначает цифра 3 в записи чисел 3, 30, 300, 3000? Во сколько раз 30 больше, чем 3? 300 больше, чем 3? 3000 больше, чем 3? 300 больше, чем 30?
3 5 9 17
30 50 90 170
300 500 900 1700
3000 5000 9000 17000
Во сколько раз 900 меньше, чем 9000? 90 меньше, чем 9000? 9 меньше, чем 9000? Продолжи сравнение.
Закончи выводы: Если в записи числа справа приписать 1 нуль, 2, 3 нуля, то получим число, которое больше данного в . раз. Если в записи числа отбросить 1 нуль, 2, 3 нуля, то . .
Цифра 3 в записи числа 3 обозначает 3 единицы, в 30 – 3 десятка, в 300 – 3 сотни, в 3000 – 3 единицы тысяч. 30 больше, чем 3 в 10 раз. 300 больше, чем 3 в 100 раз. 3000 больше, чем 3 в 1000 раз. 300 больше, чем 30 в 10 раз.
ЕГЭ 2017 по математике, базовый уровень. Задания 8
900 меньше, чем 9000 в 10 раз. 90 меньше, чем 9000 в 100 раз. 9 меньше, чем 9000 в 1000 раз.
Если в записи числа справа приписать 1 нуль, 2, 3 нуля, то получим число, которое больше данного в 10, в 100, в 1000 раз. Если в записи числа отбросить 1 нуль, 2, 3 нуля, то получим число, которое меньше данного в 10, в 100, в 1000 раз.
1) Числа 57, 90, 200 увеличить в 10 раз, в 100 раз.
2) Числа 4000, 60000, 152000 уменьши в 1000 раз.
1) 570, 900, 2000 5700, 9000, 20000 2) 4, 60, 152
67000 : 1000 = 67 9600 : 100 = 96
39000 ∙ 10 = 390000 9600 ∙ 100 = 960000
102000 : 10 = 10200 102000 : 100 = 1020
В альбоме 100 листов. Сколько таких альбомов получится из 15000 листов? Сколько листов в 1000 таких альбомов?

1) 15000 : 100 = 150 (альб.) 2) 100 ∙ 1000 = 100000 (л.) Ответ: 150 альбомов; 100000 листов.
Сравни пары уравнений. Сравни их решения.

Уравнения, то есть числа в них записаны одинаково в каждой паре, но действия над ними производятся различные.
Длина участка прямоугольной формы 70 м, а ширина − 30 м. Сколько шагов надо сделать, чтобы пройти по его периметру? (Два шага составляют 1 м)
1) (70 + 30) ∙ 2 = 200 (м) – периметр участка. 2) 200 ∙ 2 = 400 (ш.) – надо сделать. Ответ: 400 шагов.
Начерти:
1) отрезок AB, длина которого равна половине длины отрезка в 1 дм;
2) отрезок CD, длина половины которого равна 2 см.
1) Так как 1 дм = 10 см, а отрезок AB равен половине 1 дм, то: AB = 10 : 2 = 5 (см)
Разбор Демоварианта ЕГЭ по математике Базовый уровень Задания №7 8

2) Если длина половины отрезка CD равна 2 см, то: СD = 2 ∙ 2 = 4 (см)

Проверь, верны ли равенства.
800 − 296 = 168 ∙ 3 – верно 800 − 296 = 504 168 ∙ 3 = 504 504 = 504
888 : 3 = 703 − 407 – верно 888 : 3 = 296 703 − 407 = 296 296 = 296
Записали подряд все трехзначные числа. Сколько всего цифр записано в этом ряду?
10 цифр В числах есть цифра: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задание внизу страницы
34800 : 10 = 3480 4900 : 100 = 49 540 ∙ 10 = 5400
Задание на полях страницы
1 : 1 = 1 7 ∙ 1 = 7 7 : 1 = 7 Ответ: квадрат – 1, треугольник – 7 (может быть любое число, кроме 0).
Источник: gdz-raketa.ru
Школьный этап ВсОШ 2022/23, Математике 5 класс, 1 группа 18.10.2022

1. У Пети есть четыре карточки с цифрами 1, 2, 3, 4. Каждая цифра встречается ровно один раз. Сколько натуральных чисел, больших 2234, может составить из этих карточек Петя?
2. На доске написаны девять целых чисел от 1 до 5. Известно, что семь из них не меньше 2, шесть — больше 2, три — не меньше 4, одно — не меньше 5.
Найдите сумму всех чисел.
3. Кафе «Буратино» работает 6 дней в неделю с выходным по понедельникам. Коля сказал, что с 1 по 20 апреля кафе работало 17 дней, а с 10 по 30 — 18 дней. Известно, что один раз он ошибся.
Какого числа был последний вторник апреля?

4. Прямоугольник разрезали на три других прямоугольника, два из которых имеют размеры 9 м × 12 м и 10 м × 15 м.
Какую максимальную площадь мог иметь исходный прямоугольник? Ответ выразите в квадратных метрах.
5. В примере на сложение, в котором цифры были написаны на карточках, перепутали местами две карточки и получили неправильное выражение: 27641+43739=70280.
Найдите ошибку и запишите правильное значение суммы.
6. Незнайка назвал четыре числа, а Пончик на шести карточках написал все их попарные суммы. Затем одну карточку он потерял, а на оставшихся были написаны числа 270, 360, 390, 530, 620.
Какое число Пончик написал на потерянной карточке?

7. По кругу выписано 101 натуральное число. Известно, что среди любых трёх подряд идущих чисел есть чётное число.
Какое наименьшее количество чётных чисел может быть среди выписанных?
8. Одинаковые монеты выложены на столе в форме шестиугольника. Если выложить их так, чтобы сторона шестиугольника состояла из 2 монет, то хватит 7 монет, а если сторона будет состоять из 3 монет, то всего потребуется 19 монет.
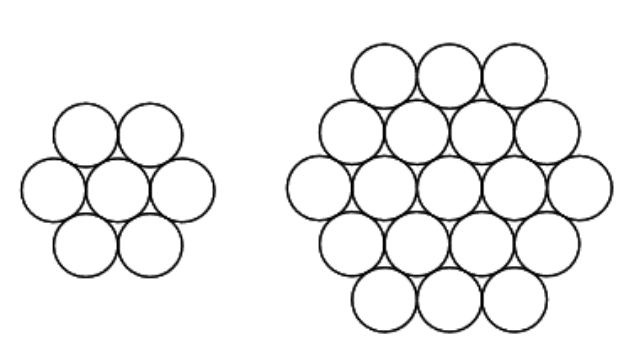
Сколько нужно монет для построения шестиугольника со стороной из 10 монет?
Источник: pndexam.ru
функциональная грамотность. Задания на формирование функциональной грамотности обучающихся 56 классов. Учитель Чайко Н. А. Задание 1

Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма

Скачать 0.66 Mb.
Задания на формирование функциональной грамотности обучающихся 5-6 классов.
Учитель: Чайко Н.А.
Количество вариантов при одном дополнительном ингредиенте в течение недели равно 7
Количество вариантов при двух дополнительных различных ингредиентах в течение недели равно 7∙6 =42
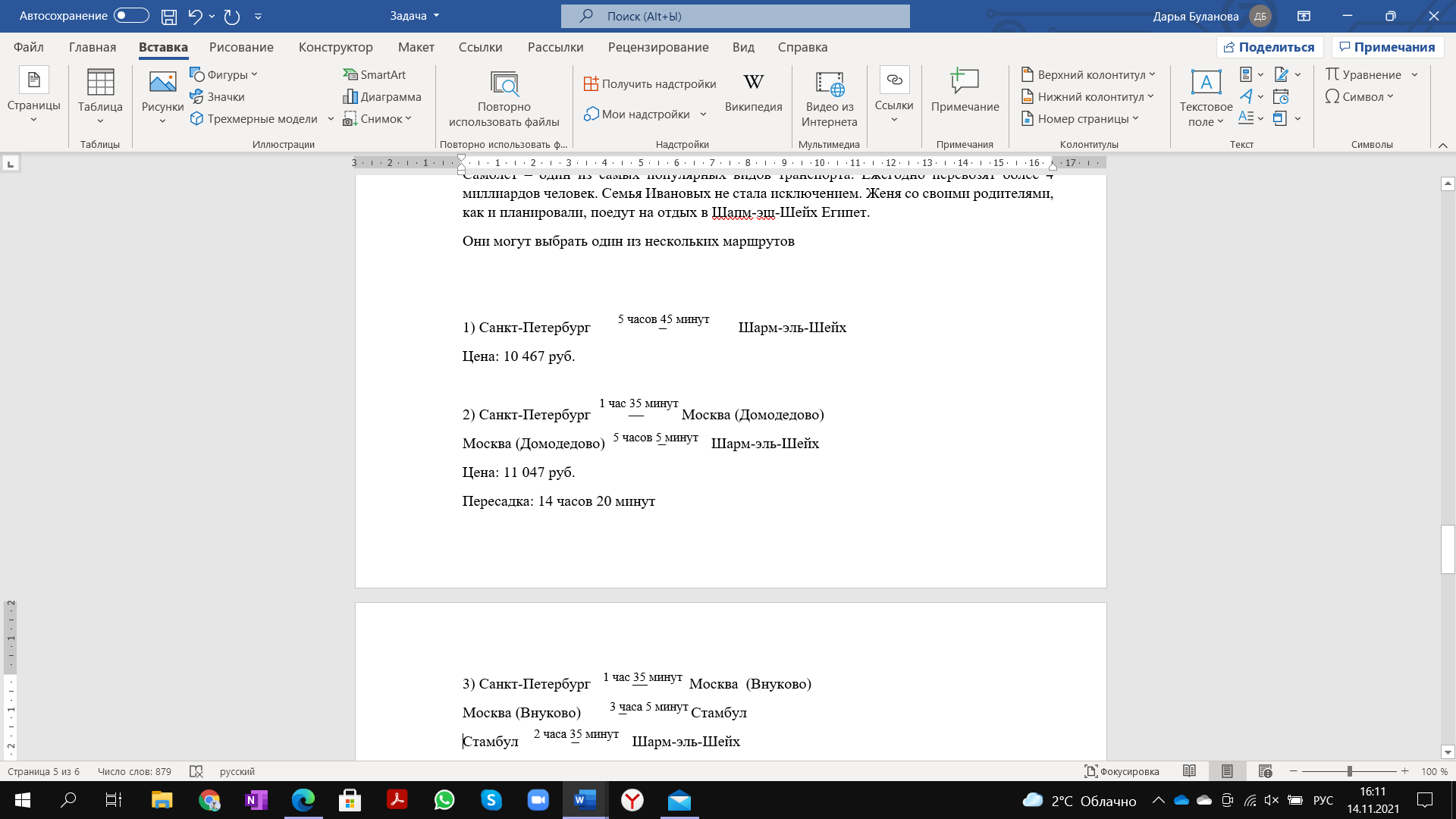
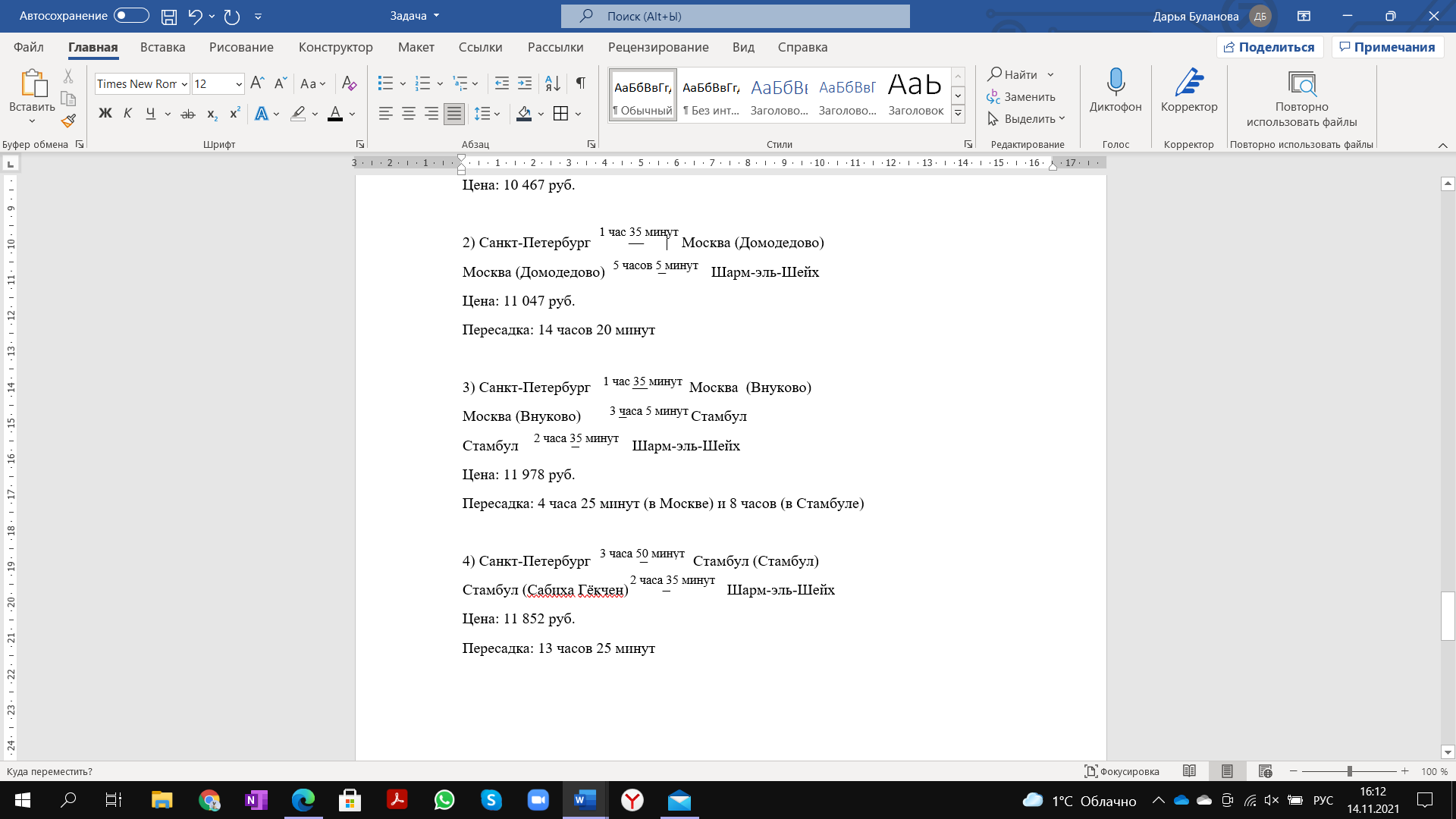
Они могут выбрать один из нескольких маршрутов:
 |
 |
 |
 |
A – Из предложенных вариантов самый быстрый – самый дешевый.
Б – Перелет с 3 пересадками займет суммарно равно 21 час.
В – Любой перелет с двумя пересадками дешевле, чем перелет с тремя пересадками.
Б, т.к. перелет из Санкт-Петербурга в Шарм-эль-Шейх займет 20 часов 20 минут
Г, т.к. при первом варианте время в небе будет составлять 5 часов 45 минут, а при четвертом варианте время в небе – 6 часов 25 минут
1. Более 2/3 смотрели исторические фильмы.
2. Тех, кто никогда не смотрел исторические фильмы, меньше, чем ребят, которые смотрели.
1) 47*24 = 1128 – сумма, которую ребята потратили на магнитики
2) 55*9 = 495 – сумма, которая была у всех девочек
3) 65*15 = 975 – сумма, которая была у всех мальчиков
4) (495+975) – 1128 = 342 – вся сдача, которую получили все ребята после покупки магнитиков
5) 342/25 = 13, 68 – количество открыток, которые могут купить ребята на сдачу
После подсчета и распределения обязательных трат за месяц у семьи Ивановых осталось 50 000 рублей. Так как летом мама, папа и Саша планируют полететь в Египет, было принято решение отложить 73% от полученной суммы.
2 декабря, на следующий день после ежемесячного распределения средств, у семьи появилась неожиданная трата, т.к. кот уронил телевизор с тумбы и тот разбился. Мастер по ремонту сказал, что телевизор можно починить, но нужно устранять неисправность инвертора, проблемы задней подсветки матрицы и выход из строя платы питания.
| Услуга | Цена |
| Устранение неисправности инвертора | 6 900 рублей |
| Устранение проблему задней подсветки матрицы | 4 800 рублей |
| Ремонт платы питание | 8 300 рублей |
1) 6 900+4 800+8 300 = 20 000 рублей – сумма ремонта телевизора
Ответ: выгоднее покупать новый телевизор
50 000 – 36 500 = 13 500 – сумма свободных денег
19 900- 13 500 = 6 400 – сумма денег, которых не хватает на покупку телевизора (эту сумму нужно взять из денег, отложенных на поездку)
(6 400/ 36 500) * 100% = 17,5 %
Они выявили следующую закономерность:
| Уровень посещаемости | Доплата к начальной цене |
| 0 – 29% | 0 рублей |
| 30 – 49% | 50 рублей |
| От 50 % и более | 100 рублей |
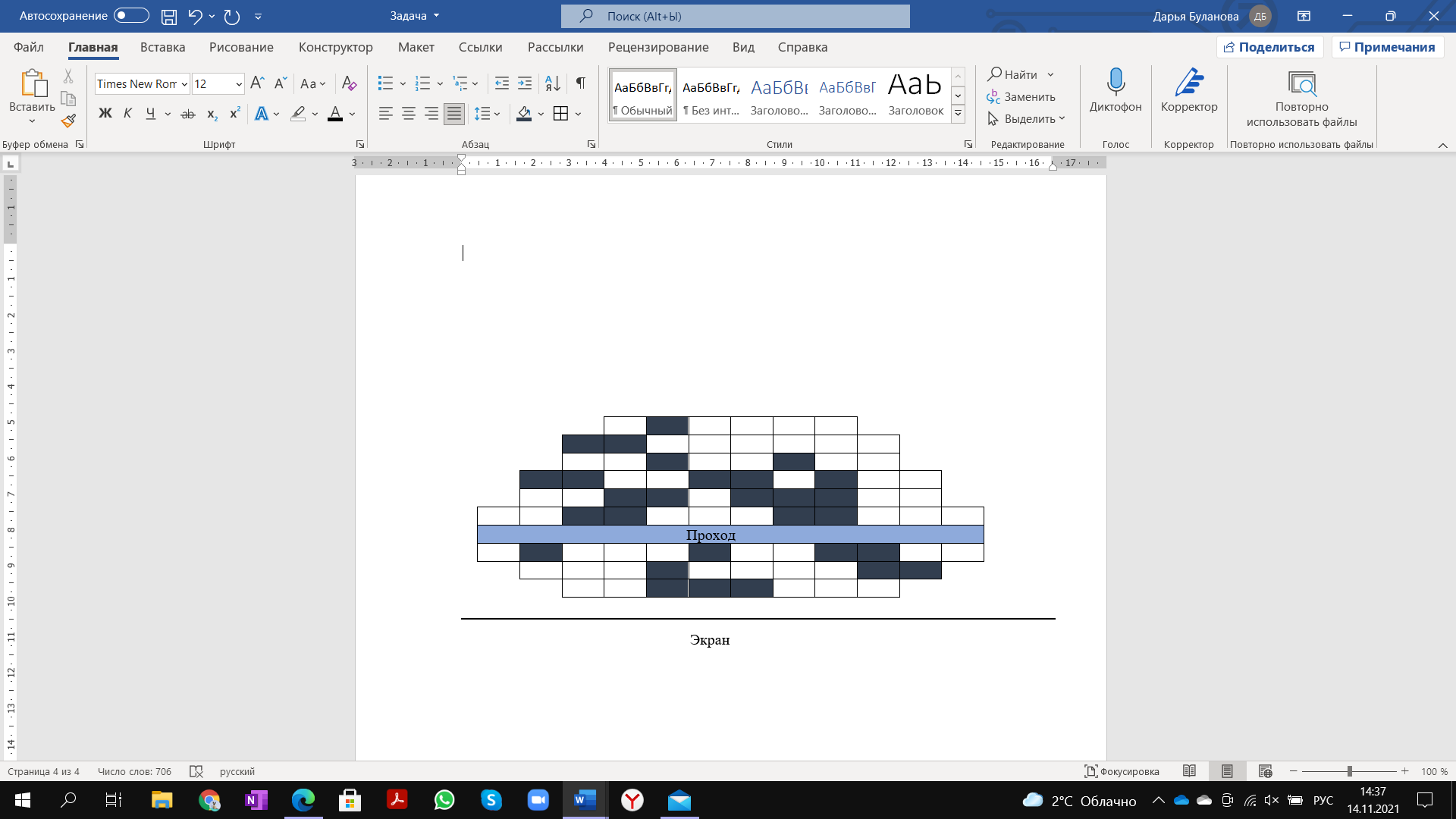
Схема зрительного зала
Учитывайте, что папа Жени работает с 9.00 по 18.00 с понедельника по пятницу, а Женя ходит на занятия в школу также с понедельника по пятницу с 9.00 до 15.00
Женя, его папа и дедушка выбрали фильм, который начинается в субботу в 11.10. Им необходимо купить билеты. Но при выборе мест у них появилось несколько условий:
Источник: topuch.ru