ВЕКТОР
В физике и математике вектор — это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей.
Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами». Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, мы хотим описать положение предмета относительно некоторой точки.
Мы можем сказать, сколько километров от точки до предмета, но не можем полностью определить его местоположение, пока не узнаем направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как на рис. 1. Например, для того чтобы представить графически силу в пять килограммов, надо нарисовать отрезок прямой длиной в пять единиц в направлении действия силы. Стрелка указывает, что сила действует от A к B; если бы сила действовала от B к A, то мы бы записали или Для удобства векторы обычно обозначаются полужирными прописными буквами (A, B, C и так далее); векторы A и -A имеют равные численные значения, но противоположны по направлению. Численное значение вектора А называется модулем или длиной и обозначается A или |A|. Это величина, конечно, скаляр. Вектор, начало и конец которого совпадают, называется нулевым и обозначается O.
Вектор: Зачем Он Нужен. Что Такое Вектор? Palsan Показал свое лицо.

Рис. 1. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВЕКТОРА. Направленный отрезок AB представляет вектор — физическую величину, описываемую численным значением и направлением. Стрелка показывает, что вектор направлен от А в B, а не от B к A.
Два вектора называются равными (или свободными), если их модули и направления совпадают. В механике и физике этим определением, однако, надо пользоваться с осторожностью, так как две равных силы, приложенные к различным точкам тела в общем случае будут приводить к различным результатам.
В связи с этим векторы подразделяются на «связанные» или «скользящие», следующим образом: Связанные векторы имеют фиксированные точки приложения. Например, радиус-вектор указывает положение точки относительно некоторого фиксированного начала координат. Связанные векторы считаются равными, если у них совпадают не только модули и направления, но они имеют и общую точку приложения. Скользящими векторами называются равные между собой векторы, расположенные на одной прямой.
Зачем нужен ВЕКТОР. Объяснение математического смысла.
Сложение векторов. Идея сложения векторов возникла из того, что мы можем найти единственный вектор, который оказывает то же воздействие, что и два других вектора вместе. Если для того, чтобы попасть в некоторую точку, нам надо пройти сначала A километров в одном направлении и затем B километров в другом направлении, то мы могли бы достичь нашей конечной точки пройдя C километров в третьем направлении (рис. 2). В этом смысле можно сказать, что
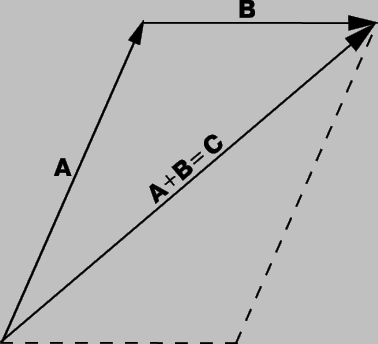
Рис. 2. СЛОЖЕНИЕ ВЕКТОРОВ. Векторы подчиняются определенному закону сложения. Если вектор А и вектор B складываются, то результирующий вектор C, являющийся суммой векторов А и B, получается с помощью построения параллелограмма, сторонами которого служат А и B, а вектор С — диагональ, соединяющая начало А и конец B.
A + B = C.
Вектор C называется «результирующим вектором» A и B, он задается построением, показанным на рисунке; на векторах A и B как на сторонах построен параллелограмм, а C — диагональ, соединяющая начало А и конец В. Из рис. 2 видно, что сложение векторов «коммутативно», т.е. A + B = B + A. Аналогичным образом можно сложить несколько векторов, последовательно соединяя их «непрерывной цепочкой», как показано на рис. 3 для трех векторов D, E и F. Из рис. 3 также видно, что

Рис. 3. СЛОЖЕНИЕ ТРЕХ ВЕКТОРОВ подчиняется тому же закону, что и сложение двух векторов. Результирующий вектор D + E + F — сумма трех векторов, получен с помощью соединения векторов непрерывной цепью, и суммарный вектор соединяет начало первого вектора с концом последнего.
(D + E) + F = D + (E + F), т.е. сложение векторов ассоциативно. Суммировать можно любое число векторов, причем векторы необязательно должны лежать в одной плоскости. Вычитание векторов представляется как сложение с отрицательным вектором. Например, A — B = A + (-B), где, как определялось ранее, -B — вектор, равный В по модулю, но противоположный по направлению.
Это правило сложения может теперь использоваться как реальный критерий проверки, является ли некоторая величина вектором или нет. Перемещения обычно подчиняются условиям этого правила; то же можно сказать и о скоростях; силы складываются таким же образом, как можно было видеть из «треугольника сил». Однако, некоторые величины, обладающие как численными значениями так и направлениями, не подчиняются этому правилу, поэтому не могут рассматриваться как векторы. Примером являются конечные вращения.
Умножение вектора на скаляр. Произведение mA или Am, где m (m № 0) — скаляр, а A — ненулевой вектор, определяется как другой вектор, который в m раз длиннее A и имеет тоже направление что и A, если число m положительно, и противоположное, если m отрицательно, как показано на рис. 4, где m равно 2 и -1/2 соответственно. Кроме того, 1A = A, т.е. при умножении на 1 вектор не изменяется.
Величина -1A — вектор, равный A по длине, но противоположный по направлению, обычно записывается как -A. Если А — нулевой вектор и(или) m = 0, то mA — нулевой вектор. Умножение дистрибутивно, т.е.
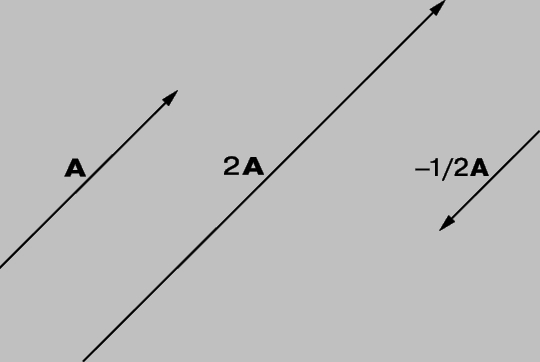
Рис. 4. ПРОИЗВЕДЕНИЕ ВЕКТОРА И СКАЛЯРА. Вектор 2A имеет удвоенный модуль и то же направление, что и A; вектор -(1/2)A имеет половинный модуль и противоположное направление.
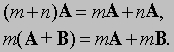
Мы можем складывать любое число векторов, причем порядок слагаемых не влияет на результат. Верно и обратное: любой вектор раскладывается на две или более «компоненты», т.е. на два вектора или более, которые, будучи сложенными, в качестве результирующего дадут исходный вектор. Например, на рис.
2, A и B — компоненты C. Многие математические действия с векторами упрощаются, если разложить вектор на три компоненты по трем взаимно перпендикулярным направлениям. Выберем правую систему декартовых координат с осями Ox, Oy и Oz как показано на рис. 5. Под правой системой координат мы подразумеваем, что оси x, y и z располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки. Из одной правой системы координат всегда можно получить другую правую систему координат соответствующим вращением. На рис. 5, показано разложение вектор A на три компоненты и Они в сумме составляют вектор A , так как
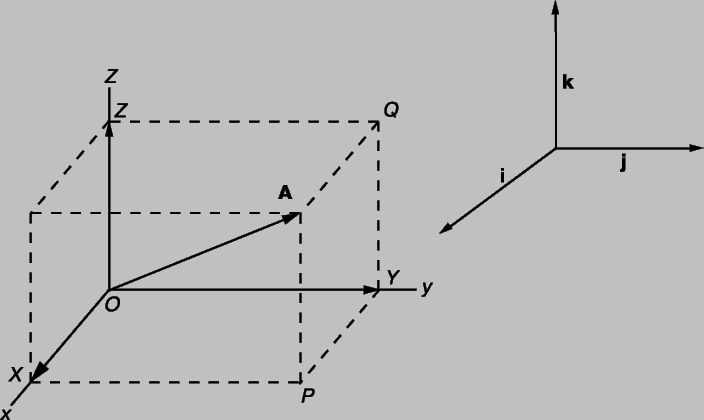
Рис. 5. ВЕКТОРЫ (при использовании декартовых координат) сложенные вместе, дают результирующий вектор А и поэтому называются компонентами A. Координаты в этом случае ориентированы по правилу правой руки (правая декартова система координат).

Следовательно,
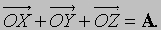
Можно было бы также сначала сложить и получитьа затем к прибавить Проекции вектора А на три координатные оси, обозначенные Ax, Ay и Az называются «скалярными компонентами» вектора A:
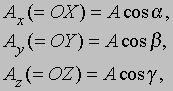
где a, b и g — углы между A и тремя координатными осями. Теперь введем три вектора единичной длины i, j и k (орты), имеющие то же самое направление, что и соответствующие оси x, y и z. Тогда, если Ax умножить на i, то полученное произведение — это вектор, равный и
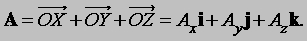
Два вектора равны тогда и только тогда, когда равны их соответствующие скалярные компоненты. Таким образом, A = B тогда и только тогда, когда Ax = Bx, Ay = By, Az = Bz. Два вектора можно сложить, складывая их компоненты:
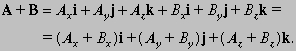
Кроме того, по теореме Пифагора:
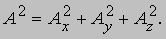
Линейные функции. Выражение aA + bB, где a и b — скаляры, называется линейной функцией векторов A и B. Это вектор, находящийся в той же плоскости, что A и B; если A и B не параллельны, то при изменении a и b вектор aA + bB будет перемещаться по всей плоскости (рис. 6). Если A, B и C не все лежат в одной плоскости, то вектор aA + bB + cC (a, b и c изменяются) перемещается по всему пространству. Предположим, что A, B и C — единичные векторы i, j и k. Вектор ai лежит на оси x; вектор ai + bj может перемещаться по всей плоскости xy; вектор ai + bj + ck может перемещаться по всему пространству.

Рис. 6. ЛИНЕЙНЫЕ ФУНКЦИИ ВЕКТОРОВ. Если A и B — два произвольных непараллельных вектора на плоскости, то существуют скалярные величины a и b такие, что вектор aA + bB, называемый линейной функцией векторов A и B, может представить любой третий вектор в этой плоскости.
Можно было бы выбрать четыре взаимно перпендикулярных вектора i, j, k и l и определить четырехмерный вектор как величину A = Axi + Ayj + Azk + Awl
с длиной
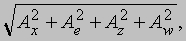
а можно было бы продолжать до пяти, шести или любого числа измерений. Хотя визуально такой вектор представить невозможно, никаких математических трудностей здесь не возникает. Такая запись часто бывает полезна; например, состояние движущейся частицы описывается шестимерным вектором P (x, y, z, px, py, pz), компоненты которого — ее положение в пространстве (x, y, z) и импульс (px, py, pz). Такое пространство называется «фазовым пространством»; если мы рассматриваем две частицы, то фазовое пространство 12-мерное, если три, то 18-ти и так далее. Число размерностей можно неограниченно увеличивать; при этом величины, с которыми мы будем иметь дело, ведут себя во многом также, как те, которые мы рассмотрим в оставшейся части этой статьи, а именно, трехмерные векторы.
Умножение двух векторов. Правило сложения векторов было получено путем изучения поведения величин, представленных векторами.
Нет никаких видимых причин, по которым два вектора нельзя было бы каким-либо образом перемножить, однако это умножение будет иметь смысл только в том случае, если можно показать его математическую состоятельность; кроме того, желательно, чтобы произведение имело определенный физический смысл. Существуют два способа умножения векторов, которые соответствуют этим условиям. Результатом одного из них является скаляр, такое произведение называется «скалярным произведением» или «внутренним произведением» двух векторов и записывается AЧB или (A, B). Результатом другого умножения является вектор, называемый «векторным произведением» или «внешним произведением» и записывается A*B или [[A, B]]. Скалярные произведения имеют физический смысл для одного-, двух- или трех измерений, тогда как векторные произведения определены только для трех измерений.
Скалярные произведения. Если под действием некоторой силы F точка, к которой она приложена, перемещается на расстояние r, то выполненная работа равна произведению r и компоненты F в направлении r. Эта компонента равна F cos бF, rс, где бF, rс — угол между F и r, т.е. Произведенная работа = Fr cos бF, rс. Это — пример физического обоснования скалярного произведения, определенного для любых двух векторов A, B посредством формулы
A*B = AB cos бA, Bс.
Так как все величины правой части уравнения — скаляры, то A*B = B*A; следовательно, скалярное умножение коммутативно. Скалярное умножение также обладает свойством дистрибутивности: A*(B + С) = A*B + A*С. Если векторы A и B перпендикулярны, то cos бA, Bс равен нулю, и, поэтому, A*B = 0, даже если ни A, ни B не равны нулю. Именно поэтому мы не можем делить на вектор.
Допустим, что мы разделили обе части уравнения A*B = A*C на A. Это дало бы B = C, и, если бы можно было бы выполнить деление, то это равенство стало бы единственным возможным результатом. Однако, если мы перепишем уравнение A*B = A*C в виде A*(B — C) = 0 и вспомним, что (B — C) — вектор, то ясно, что (B — C) необязательно равен нулю и, следовательно, B не должен быть равным C. Эти противоречивые результаты показывают, что векторное деление невозможно. Скалярное произведение дает еще один способ записи численного значения (модуля) вектора: A*A = AA*cos 0° = A2;
поэтому
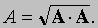
Скалярное произведение можно записать и другим способом. Для этого вспомним, что: A = Ax i + Ayj + Azk. Заметим, что

Тогда,

Поскольку последнее уравнение содержит x, y и z в качестве нижних индексов, уравнение, казалось бы, зависит от выбранной конкретной системы координат. Однако это не так, что видно из определения, которое не зависит от выбранных координатных осей.
Векторные произведения. Векторным или внешним произведением векторов называется вектор, модуль которого равен произведению их модулей на синус угла, перпендикулярный исходным векторам и составляющий вместе с ними правую тройку. Это произведение легче всего ввести, рассматривая соотношение между скоростью и угловой скоростью.
Первая — вектор; мы теперь покажем, что последнюю также можно интерпретировать как вектор. Угловая скорость вращающегося тела определяется следующим образом: выберем любую точку на теле и проведем перпендикуляр из этой точки до оси вращения. Тогда угловая скорость тела — это число радиан, на которые эта линия повернулась за единицу времени.
Если угловая скорость — вектор, она должна иметь численное значение и направление. Численное значение выражается в радианах в секунду, направление можно выбрать вдоль оси вращения, можно его определить, направив вектор в том направлении, в котором двигался бы правосторонний винт при вращении вместе с телом. Рассмотрим вращение тела вокруг фиксированной оси. Если установить эту ось внутри кольца, которое в свою очередь закреплено на оси, вставленной внутрь другого кольца, мы можем придать вращение телу внутри первого кольца с угловой скоростью w1 и затем заставить внутреннее кольцо (и тело) вращаться с угловой скоростью w2. Рисунок 7 поясняет суть дела; круговые стрелки показывают направления вращения. Данное тело — это твердая сфера с центром О и радиусом r.

Рис. 7. СФЕРА С ЦЕНТРОМ O, вращается с угловой скоростью w1 внутри кольца BC, которое, в свою очередь, вращается внутри кольца DE с угловой скоростью w2. Сфера вращается с угловой скоростью, равной сумме угловых скоростей и все точки на прямой POP’ находятся в состоянии мгновенного покоя.
Придадим этому телу движение, которое является суммой двух различных угловых скоростей. Это движение довольно трудно представить наглядно, но достаточно очевидно, что тело больше не вращается относительно фиксированной оси. Однако все-таки можно сказать, что оно вращается.
Чтобы показать это, выберем некоторую точку P на поверхности тела, которая в рассматриваемый нами момент времени находится на большом круге, соединяющем точки, в которых две оси пересекают поверхность сферы. Опустим перпендикуляры из P на оси. Эти перпендикуляры станут радиусами PJ и PK окружностей PQRS и PTUW соответственно. Проведем прямую POPў, проходящую через центр сферы. Теперь точка P, в рассматриваемый момент времени одновременно перемещается по окружностям, которые соприкасаются в точке P. За малый интервал времени Dt, P перемещается на расстояние

Это расстояние равно нулю, если

В этом случае точка P находится в состоянии мгновенного покоя, и точно также все точки на прямой POP’. Остальная часть сферы будет в движении (окружности, по которым перемещаются другие точки, не касаются, а пересекаются). POPў является, таким образом, мгновенной осью вращения сферы, подобно тому, как колесо, катящееся по дороге в каждый момент времени, вращается относительно своей нижней точки. Чему равна угловая скорость сферы? Выберем для простоты точку A, в которой ось w1 пересекает поверхность. В момент времени, который мы рассматриваем, она перемещается за время Dt на расстояние

по кругу радиуса r sin w1. По определению, угловая скорость
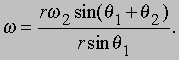
Из этой формулы и соотношения (1) мы получим
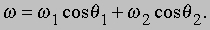
Другими словами, если записать численное значение и выбрать направление угловой скорости так, как это описано выше, то эти величины складываются как векторы и могут быть рассмотрены как таковые. Теперь можно ввести векторное произведение; рассмотрим тело, вращающееся с угловой скоростью w. Выберем любую точку P на теле и любое начало координат О, которое находится на оси вращения. Пусть r — вектор, направленный от О к P. Точка P движется по окружности со скоростью V = w r sin (w, r). Вектор скорости V является касательным к окружности и указывает в направлении, показанном на рис. 8.
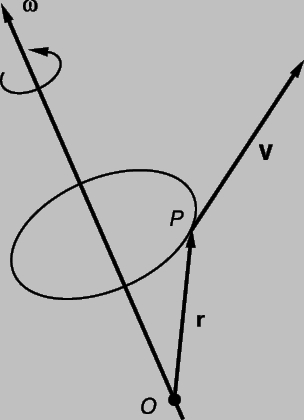
Рис. 8. ОТНОШЕНИЯ МЕЖДУ СКОРОСТЬЮ И УГЛОВОЙ СКОРОСТЬЮ. Вектор w представляет угловую скорость вращающегося твердого тела. Вектор r — это вектор, проведенный из точки О, любой точки на оси вращения, в точку P — любую точку на теле. V — вектор скорости точки.
Это уравнение дает зависимость скорости V точки от комбинации двух векторов w и r. Используем это соотношение, чтобы определить новый вид произведения, и запишем: V = w * r. Так как результатом такого умножения является вектор, это произведение названо векторным. Для любых двух векторов A и B, если A * B = C, то C = AB sin бA, Bс, и направление вектора C таково, что он перпендикулярен плоскости, проходящей через А и B и указывает в направлении, совпадающем с направлением движения правовращающегося винта, если он параллелен C и вращается от A к B. Другими словами, мы можем сказать, что A, B и C, расположенные в таком порядке, образуют правый набор координатных осей. Векторное произведение антикоммутативно; вектор B * A имеет тот же модуль, что и A * B, но направлен в противоположную сторону: A * B = -B * A. Это произведение дистрибутивно, но не ассоциативно; можно доказать, что
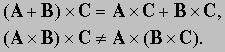
Посмотрим, как записывается векторное произведение в терминах компонент и единичных векторов. Прежде всего, для любого вектора A, A * A = AA sin 0 = 0.
Следовательно, в случае единичных векторов, i * i = j * j = k * k = 0 и i * j = k, j * k = i, k * i = j. Тогда,
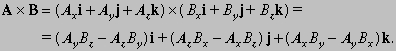
Это равенство также можно записать в виде определителя:
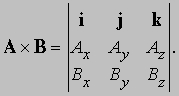
Если A * B = 0, то либо A или B равно 0, либо A и B коллинеарны. Таким образом, как и в случае скалярного произведения, деление на вектор невозможно. Величина A * B равна площади параллелограмма со сторонами A и B. Это легко видеть, так как B sin бA, Bс — его высота и A — основание. Существует много других физических величин, которые являются векторными произведениями.
Одно из наиболее важных векторных произведений появляется в теории электромагнетизма и называется вектором Пойтинга P. Этот вектор задается следующим образом: P = E * H, где E и H — векторы электрического и магнитного полей соответственно. Вектор P можно рассматривать как заданный поток энергии в ваттах на квадратный метр в любой точке. Приведем еще несколько примеров: момент силы F (крутящий момент) относительно начала координат, действующей на точку, радиус-вектор которой r, определяется как r * F; частица, находящаяся в точке r, массой m и скоростью V, имеет угловой момент mr * V относительно начала координат; сила, действующая на частицу, несущую электрический заряд q через магнитное поле B со скоростью V, есть qV * B.
Тройные произведения. Из трех векторов мы можем сформировать следующие тройные произведения: вектор (A*B) * C; вектор (A * B) * C; скаляр (A * B)*C. Первый тип — произведение вектора C и скаляра A*B; о таких произведениях мы уже говорили.
Второй тип называется двойным векторным произведением; вектор A * B перпендикулярен к плоскости, где лежат A и B, и поэтому (A * B) * C — вектор, лежащий в плоскости A и B и перпендикулярный C. Следовательно, в общем случае, (A * B) * C не равно A * (B * C). Записав A, B и C через их координаты (компоненты) по осям x, y и z и умножив, можно показать, что A * (B * C) = B * (A*C) — C * (A*B). Третий тип произведения, который возникает при расчетах решетки в физике твердого тела, численно равен объему параллелепипеда с ребрами A, B, C. Так как (A * B)*C = A*(B * C), знаки скалярного и векторного умножений можно менять местами, и произведение часто записывается как (A B C). Это произведение равно определителю

Заметим, что (A B C) = 0, если все три вектора лежат в одной и той же плоскости или, если А = 0 или (и) В = 0 или (и) С = 0.
ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА
Предположим, что вектор U является функцией одной скалярной переменной t. Например, U может быть радиус-вектором, проведенным из начала координат до перемещающейся точки, а t — временем. Пусть t изменится на небольшую величину Dt, что приведет к изменению U на величину DU. Это показано на рис. 9. Отношение DU/Dt — вектор, направленный в том же направлении, что и DU. Мы можем определить производную U по t, как
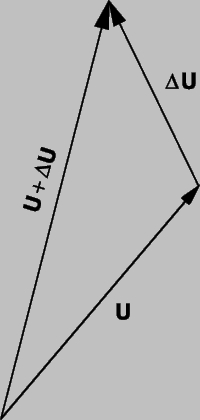
Рис. 9. ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА. Если U — функция переменной t, то изменение t на величину Dt повлечет изменение U на величину DU. В этом случае можно определить производную U по t.
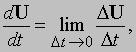
при условии, что такой предел существует. С другой стороны, можно представить U как сумму компонент по трем осям и записать

Если U — радиус-вектор r, то dr/dt — скорость точки, выраженная как функция времени. Продифференцировав по времени еще раз, мы получим ускорение. Предположим, что точка перемещается вдоль кривой, показанной на рис. 10. Пусть s — расстояние, пройденное точкой вдоль кривой. В течение малого интервала времени Dt точка пройдет расстояние Ds вдоль кривой; положение радиус-вектора изменится на Dr.
Следовательно Dr/Ds — вектор направленный как Dr. Далее
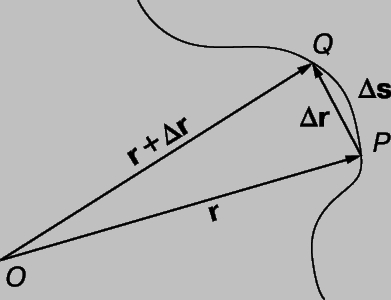
Рис. 10. СЛЕД ЧАСТИЦЫ. Если частица перемещается вдоль кривой на расстояние s, то она пройдет расстояние Ds (от P до Q) в течение малого интервала времени.
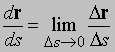
есть единичный вектор, касательный к кривой. Это видно из того, что при приближении точки Q к точке P, PQ приближается к касательной и Dr приближается к Ds. Формулы для дифференцирования произведения подобны формулам для дифференцирования произведения скалярных функций; однако, так как векторное произведение антикоммутативно, порядок умножения должен быть сохранен. Поэтому,

Таким образом, мы видим, что, если вектор является функцией одной скалярной переменной, то мы можем представить производную почти также, как в случае скалярной функции.
Вектор и скалярные поля. Градиент. В физике часто приходится иметь дело с векторными или скалярными величинами, которые меняются от точки к точке в заданной области. Такие области называются «полями». Например, скаляр может быть температурой или давлением; вектор может быть скоростью движущейся жидкости или электростатическим полем системы зарядов.
Если мы выбрали некоторую систему координат, то любой точке P (x, y, z) в заданной области соответствует некоторый радиус-вектор r (= xi + yj + zk) и также значение векторной величины U (r) или скаляра f (r), связанных с ним. Предположим, что U и f определены в области однозначно; т.е. каждой точке соответствует одна и только одна величина U или f, хотя различные точки могут, конечно, иметь различные значения.
Допустим, что мы хотим описать скорость, с которой U и f изменяются при передвижении по этой области. Простые частные производные, такие, как dU/dx и df/dy, нас не устраивают, потому что они зависят от конкретно выбранных координатных осей. Однако можно ввести векторный дифференциальный оператор, независимый от выбора осей координат; этот оператор называется «градиентом».
Пусть мы имеем дело со скалярным полем f. Сначала в качестве примера рассмотрим контурную карту области страны. В этом случае f — высота над уровнем моря; контурные линии соединяют точки с одним и тем же значением f. При движении вдоль любой из этих линий f не меняется; если двигаться перпендикулярно этим линиям, то скорость изменения f будет максимальной. Мы можем каждой точке сопоставить вектор, указывающий величину и направление максимального изменения скорости f; такая карта и некоторые из этих векторов показаны на рис. 11. Если мы проделаем это для каждой точки поля, то получим векторное поле, связанное со скалярным полем f. Это поле вектора, называемого «градиентом» f, который записывается как grad f или Сf (символ С также называется «набла»).
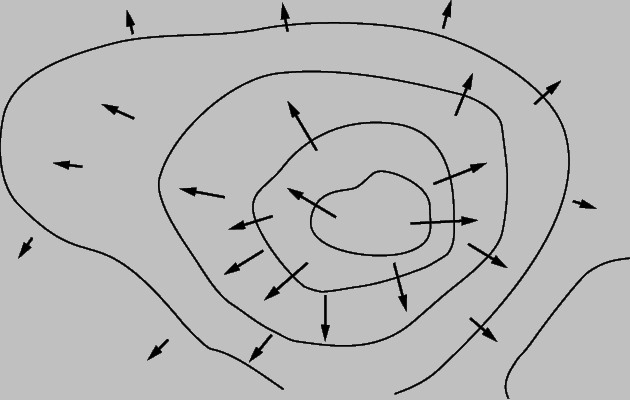
Рис. 11. СКАЛЯРНОЕ ПОЛЕ И ГРАДИЕНТЫ.
В случае трех измерений, контурные линии становятся поверхностями. Малое смещение Dr (= iDx + jDy + kDz) приводит к изменению f, которое записывается как
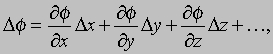
где точками обозначены члены более высоких порядков. Это выражение можно записать в виде скалярного произведения

Разделим правую и левую части этого равенства на Ds, и пусть Ds стремится к нулю; тогда

где dr/ds — единичный вектор в выбранном направлении. Выражение в круглых скобках — вектор, зависящий от выбранной точки. Таким образом, df/ds имеет максимальное значение, когда dr/ds указывает в том же направлении, выражение, стоящее в скобках, является градиентом. Таким образом,
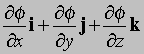
— вектор, равный по величине и совпадающий по направлению с максимальной скоростью изменения f относительно координат. Градиент f часто записывается в виде
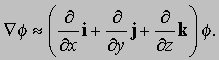
Это означает, что оператор С существует сам по себе. Во многих случаях он ведет себя как вектор и фактически является «векторным дифференциальным оператором» — одним из наиболее важных дифференциальных операторов в физике. Несмотря на то, что С содержит единичные векторы i, j и k, его физический смысл не зависит от выбранной системы координат. Какова связь между Сf и f? Прежде всего предположим, что f определяет потенциал в любой точке. При любом малом смещении Dr величина f изменится на
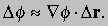
Если q — величина (например масса, заряд), перемещенная на Dr, то работа, выполненная при перемещении q на Dr равна
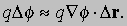
Так как Dr — перемещение, то qСf — сила; -Сf — напряженность (сила на единицу количества), связанная с f. Например, пусть U — электростатический потенциал; тогда E — напряженность электрического поля, задается формулой E = -СU. Допустим, что U создается точечным электрическим зарядом в q кулонов, помещенным в начало координат. Значение U в точке P (x, y, z) с радиус-вектором r задается формулой

где e0 — диэлектрическая постоянная свободного пространства. Поэтому
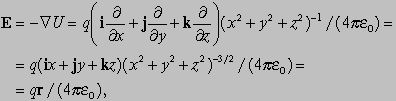
откуда следует, что E действует в направлении r и его величина равна q/(4pe0r3). Зная скалярное поле, можно определить связанное с ним векторное поле. Также возможно и обратное. С точки зрения математической обработки скалярными полями оперировать легче, чем векторными, так как они задаются одной функцией координат, в то время как векторное поле требует три функции, соответствующие компонентам вектора в трех направлениях. Таким образом, возникает вопрос: дано векторное поле, может ли мы записать связанное с ним скалярное поле?
Дивергенция и ротор. Мы видели результат действия С на скалярную функцию. Что произойдет, если С применить к вектору? Имеются две возможности: пусть U (x, y, z) — вектор; тогда мы можем образовать векторное и скалярное произведения следующим образом:
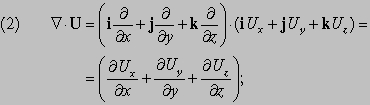
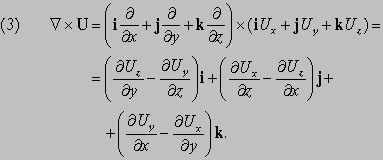
Первое из этих выражений — скаляр, называемый дивергенцией U (обозначается divU); второе — вектор, названный ротор U (обозначается rotU). Эти дифференциальные функции, дивергенция и ротор, широко используются в математической физике. Представьте, что U — некоторый вектор и что он и его первые производные непрерывны в некоторой области. Пусть P — точка в этой области, окруженная малой замкнутой поверхностью S, ограничивающей объем DV. Пусть n — единичный вектор, перпендикулярный к этой поверхности в каждой точке (n меняет направление при движении вокруг поверхности, но всегда имеет единичную длину); пусть n направлен наружу. Покажем, что
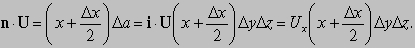
и

Здесь S указывает, что эти интегралы берутся по всей поверхности, da — элемент поверхности S. Для простоты мы выберем удобную для нас форму S в виде небольшого параллелепипеда (как показано на рис. 12) со сторонами Dx, Dy и Dz; точка P — центр параллелепипеда. Вычислим интеграл из уравнения (4) сначала по одной грани параллелепипеда. Для передней грани n = i (единичный вектор параллелен оси x); Da = DyDz. Вклад в интеграл от передней грани равен
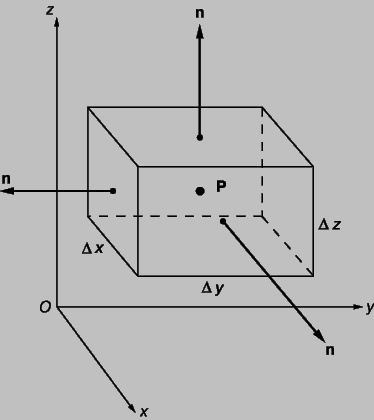
Рис. 12. ОБЪЕМ ДЛЯ ВЫЧИСЛЕНИЯ ДИВЕРГЕНЦИИ. Стороны параллелепипеда Dx, Dy и Dz; P — центр; n — единичные векторы, перпендикулярные к поверхностям.
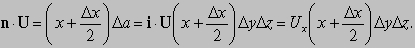
На противоположной грани n = -i; эта грань дает вклад в интеграл
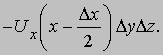
Используя теорему Тейлора, получим общий вклад от двух граней
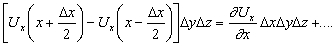
Заметим, что DxDyDz = DV. Аналогичным образом можно вычислить вклад от двух других пар граней. Полный интеграл равен
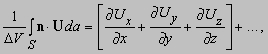
и если мы положим DV (r) 0, то члены более высокого порядка исчезнут. По формуле (2) выражение в скобках — это divU, что доказывает равенство (4). Равенство (5) можно доказать таким же образом. Воспользуемся снова рис. 12; тогда вклад от передней грани в интеграл будет равен
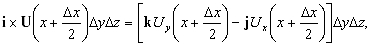
и, используя теорему Тейлора, получим, что суммарный вклад в интеграл от двух граней имеет вид
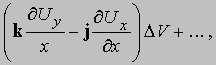
т.е. это два члена из выражения для rotU в уравнении (3). Другие четыре члена получатся после учета вкладов от других четырех граней. Что, в сущности, означают эти соотношения? Рассмотрим равенство (4). Предположим, что U — скорость (жидкости, например).
Тогда nЧU da = Un da, где Un является нормальной компонентой вектора U к поверхности. Поэтому, Un da — это объем жидкости, протекающей через da в единицу времени, а- это объем жидкости, вытекающей через S в единицу времени. Следовательно,

— скорость расширения единицы объема вокруг точки P. Отсюда дивергенция получила свое название; она показывает скорость, с которой жидкость расширяется из (т.е. расходится от) P. Чтобы объяснить физическое значение ротора U, рассмотрим другой поверхностный интеграл по маленькому цилиндрическому объему высотой h, окружающему точку P; плоско-параллельные поверхности могут быть ориентированы в любом направлении, которое мы выбираем. Пусть k -единичный вектор перпендикулярный к каждой поверхности, и пусть площадь каждой поверхности DA; тогда полный объем DV = hDA (рис. 13). Рассмотрим теперь интеграл
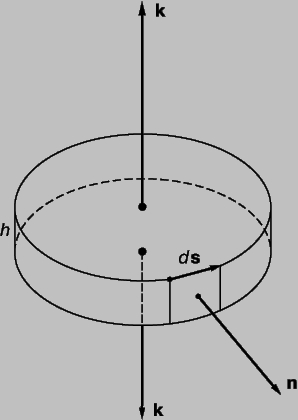
Рис. 13. ОБЪЕМ ДЛЯ ВЫЧИСЛЕНИЯ РОТОРА. Цилиндрическая область имеет высоту (h), единичные векторы (k) перпендикулярны к каждой плоскости, n — единичный вектор, перпендикулярный к малой области, представленной как элемент поверхности ds.
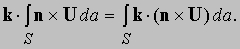
Подынтегральное выражение — уже упоминавшееся ранее тройное скалярное произведение. Это произведение будет равно нулю на плоских поверхностях, где k и n параллельны. На кривой поверхности
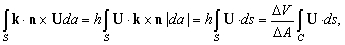
где ds — элемент кривой как показано на рис. 13. Сравнивая эти равенства с соотношением (5), получаем, что
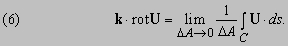
Мы по-прежнему предполагаем, что U — скорость. Чему в таком случае будет равна средняя угловая скорость жидкости вокруг k? Очевидно, что
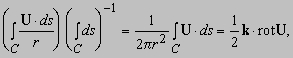
если DA не равно 0. Это выражение максимально, когда k и rotU указывают в одном и том же направлении; это означает, что rotU — вектор, равный удвоенной угловой скорости жидкости в точке P. Если жидкость вращается относительно P, то rotU № 0, и векторы U будут вращаться вокруг P. Отсюда и возникло название ротора. Теорема дивергенции (теорема Остроградского — Гаусса) является обобщением формулы (4) для конечных объемов. Она утверждает, что для некоторого объема V, ограниченного замкнутой поверхностью S,
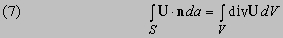
и справедлива для всех непрерывных векторных функций U, имеющих непрерывные первые производные всюду в V и на S. Мы не будем приводить здесь доказательство этой теоремы, но ее справедливость можно понять интуитивно, представляя объем V разделенным на ячейки. Поток U через поверхность, общую для двух ячеек обращается в нуль, и только ячейки, находящиеся на границе S внесут вклад в поверхностный интеграл. Теорема Стокса является обобщением уравнения (6) для конечных поверхностей. Она утверждает, что
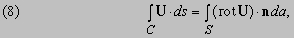
где C — замкнутая кривая и S — любая поверхность, ограниченная этой кривой. U и ее первые производные должны быть непрерывны всюду на S и C.
ЛИТЕРАТУРА
Александров П.С. Лекции по аналитической геометрии. М., 1968 Погорелов А.В. Аналитическая геометрия, 3 изд. М., 1968
Источник: dic.academic.ru
Вектор
Прямолинейный отрезок с определенным направлением, выходящий из начальной точки и приходящий в конечную точку. Характеризуется числовым значением и направлением.
Смотрите так же
Высота точки (отметка) — Расстояние, отсчитанное по направлению отвесной линии от данной точки до поверхности отсчета.
Визир — Приспособление, устройство для визуального наведения угломерного, дальномерного или наблюдательного прибора на определенную точку в пространстве.
Вершина — Верхняя точка горы или наиболее высокая часть горного массива или отрога.
Восток (точка востока) — Точка пересечения математического горизонта с небесным экватором, лежащая справа (посередине между точками севера и юга) от наблюдателя, стоящего лицом к северу; обозначается В., О (нем. Ost) или Е (англ. East).
Верньер — Приспособление, с помощью которого отсчитывают доли делений основной шкалы лимба в геодезических приборах. Действие верньера основано на способности глаза уверенно устанавливать совпадение 2 штрихов, когда один из них является продолжением другого и концы их совпадают.
Высшая геодезия — Раздел геодезии занимающийся определением фигуры, размеров и гравитационного поля Земли. В задачи высшей геодезии входит также изучение теорий и методов основных геодезических работ, служащих для построения опорной геодезической сети и доставляющих данные для решения научных и практических задач геодезии.
Водораздел — Линия на земной поверхности, проходящая вдоль хребта по гребню и соединяющая его наиболее возвышенные точки.
Вертикал — Большой круг небесной сферы, проходящий через зенит и надир. Вертикал, плоскость которого перпендикулярна меридиану называют первым вертикалом. Пересечение первого вертикала с небесным горизонтом дает точку запада и востока.
Высотная сеть — Сеть пунктов земной поверхности, высоты которых над уровнем моря определены из нивелирования. Пункты нивелирной сети закрепляют на местности марками нивелирными и реперами, которые закладывают в стены долговечных сооружений или непосредственно в грунт на некоторую глубину. Нивелирная сеть служит высотной основой топографических съёмок, а при повторных определениях нивелирных высот её пунктов используется также для изучения вертикальных движений земной коры.
Векторное изображение — Цифровое представление точечных, линейных и полигональных пространственных объектов в виде набора координатных пар.
Водосбор — Линия на земной поверхности, с которой поверхностные и подземные воды стекают в определенный водоем.
Величина геодезическая — Физическая величина, подлежащая измерению в процессе геодезических работ. Например, горизонтальный угол, длина, приращение координат и т. д.
Военная топография — Отрасль топографии, изучающая способы и средства получения информации о местности в интересах боевой деятельности войск.
Вертикальный угол — Угол в вертикальной плоскости (угол наклона, зенитное расстояние и прочее).
Высотная разбивочная основа — Геодезическое построение на строительной площадке, обеспечивающее определение высотных отметок проектных элементов комплекса. Отметки пунктов высотной разбивочной основы определяются нивелированием IV класса. Пункты государственной нивелирной сети (ГНС) дополняются строительными реперами из расчетов не менее 2-х для каждого объекта строительства, а для многосекционных зданий по одному строительному реперу на каждую станцию.
Высокоточная геодезическая сеть — Сеть, обеспечивающая следующую по точности после фундаментальной сети реализацию координатной системы, опирающаяся на пункты ФАГС. Основную часть методики создания ВГС составляют спутниковые определения.
Вращение земли — вращение Земли вокруг своей оси с запада на восток, или против часовой стрелки, если смотреть с Северного полюса мира. Вращение Земли вызывает смену дня и ночи, определяет длительность суток. Происходит неравномерно: под влиянием главным образом лунных и солнечных приливов (приливного трения) длительность суток непрерывно возрастает на 1-2 мс в столетие, а из-за сезонных изменений (выпадения осадков и т.п.), тектонических процессов и других в течение года колеблется в пределах 1-2 мс. Положение оси вращения Земли, а следовательно и земных географических полюсов, меняется из-за прецессии и нутации.
Источник: tochno-rostov.ru
ВЕКТОР
ВЕКТОР. В физике и математике вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами».
Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, мы хотим описать положение предмета относительно некоторой точки. Мы можем сказать, сколько километров от точки до предмета, но не можем полностью определить его местоположение, пока не узнаем направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как на рис. 1. Например, для того чтобы представить графически силу в пять килограммов, надо нарисовать отрезок прямой длиной в пять единиц в направлении действия силы.
Стрелка указывает, что сила действует от A к B; если бы сила действовала от B к A, то мы бы записали или . Для удобства векторы обычно обозначаются полужирными прописными буквами (A, B, C и так далее); векторы A и –A имеют равные численные значения, но противоположны по направлению. Численное значение вектора А называется модулем или длиной и обозначается A или |A|. Это величина, конечно, скаляр. Вектор, начало и конец которого совпадают, называется нулевым и обозначается O.
Два вектора называются равными (или свободными), если их модули и направления совпадают. В механике и физике этим определением, однако, надо пользоваться с осторожностью, так как две равных силы, приложенные к различным точкам тела в общем случае будут приводить к различным результатам. В связи с этим векторы подразделяются на «связанные» или «скользящие», следующим образом:
Связанные векторы имеют фиксированные точки приложения. Например, радиус-вектор указывает положение точки относительно некоторого фиксированного начала координат. Связанные векторы считаются равными, если у них совпадают не только модули и направления, но они имеют и общую точку приложения.
Скользящими векторами называются равные между собой векторы, расположенные на одной прямой.
Сложение векторов.
Идея сложения векторов возникла из того, что мы можем найти единственный вектор, который оказывает то же воздействие, что и два других вектора вместе. Если для того, чтобы попасть в некоторую точку, нам надо пройти сначала A километров в одном направлении и затем B километров в другом направлении, то мы могли бы достичь нашей конечной точки пройдя C километров в третьем направлении (рис. 2). В этом смысле можно сказать, что
A + B = C.
Вектор C называется «результирующим вектором» A и B, он задается построением, показанным на рисунке; на векторах A и B как на сторонах построен параллелограмм, а C – диагональ, соединяющая начало А и конец В. Из рис. 2 видно, что сложение векторов «коммутативно», т.е.
A + B = B + A.
Аналогичным образом можно сложить несколько векторов, последовательно соединяя их «непрерывной цепочкой», как показано на рис. 3 для трех векторов D, E и F. Из рис. 3 также видно, что
(D + E) + F = D + (E + F),
т.е. сложение векторов ассоциативно. Суммировать можно любое число векторов, причем векторы необязательно должны лежать в одной плоскости. Вычитание векторов представляется как сложение с отрицательным вектором. Например,
A – B = A + (–B),
где, как определялось ранее, –B – вектор, равный В по модулю, но противоположный по направлению.
Это правило сложения может теперь использоваться как реальный критерий проверки, является ли некоторая величина вектором или нет. Перемещения обычно подчиняются условиям этого правила; то же можно сказать и о скоростях; силы складываются таким же образом, как можно было видеть из «треугольника сил». Однако, некоторые величины, обладающие как численными значениями так и направлениями, не подчиняются этому правилу, поэтому не могут рассматриваться как векторы. Примером являются конечные вращения.
Умножение вектора на скаляр.
Произведение mA или Am, где m (m № 0) – скаляр, а A – ненулевой вектор, определяется как другой вектор, который в m раз длиннее A и имеет тоже направление что и A, если число m положительно, и противоположное, если m отрицательно, как показано на рис. 4, где m равно 2 и –1/2 соответственно.
Кроме того, 1A = A, т.е. при умножении на 1 вектор не изменяется. Величина –1A – вектор, равный A по длине, но противоположный по направлению, обычно записывается как –A. Если А – нулевой вектор и(или) m = 0, то mA – нулевой вектор. Умножение дистрибутивно, т.е.
Мы можем складывать любое число векторов, причем порядок слагаемых не влияет на результат. Верно и обратное: любой вектор раскладывается на две или более «компоненты», т.е. на два вектора или более, которые, будучи сложенными, в качестве результирующего дадут исходный вектор. Например, на рис. 2, A и B – компоненты C.
Многие математические действия с векторами упрощаются, если разложить вектор на три компоненты по трем взаимно перпендикулярным направлениям. Выберем правую систему декартовых координат с осями Ox, Oy и Oz как показано на рис. 5. Под правой системой координат мы подразумеваем, что оси x, y и z располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки. Из одной правой системы координат всегда можно получить другую правую систему координат соответствующим вращением. На рис. 5, показано разложение вектор A на три компоненты и . Они в сумме составляют вектор A, так как
Можно было бы также сначала сложить и получить , а затем к прибавить .
Проекции вектора А на три координатные оси, обозначенные Ax, Ay и Az называются «скалярными компонентами» вектора A:
где a , b и g – углы между A и тремя координатными осями. Теперь введем три вектора единичной длины i, j и k (орты), имеющие то же самое направление, что и соответствующие оси x, y и z. Тогда, если Ax умножить на i, то полученное произведение – это вектор, равный , и
Два вектора равны тогда и только тогда, когда равны их соответствующие скалярные компоненты. Таким образом, A = B тогда и только тогда, когда Ax = Bx, Ay = By, Az = Bz.
Два вектора можно сложить, складывая их компоненты:
Кроме того, по теореме Пифагора:
Линейные функции.
Выражение aA + bB, где a и b – скаляры, называется линейной функцией векторов A и B. Это вектор, находящийся в той же плоскости, что A и B; если A и B не параллельны, то при изменении a и b вектор aA + bB будет перемещаться по всей плоскости (рис. 6).
Если A, B и C не все лежат в одной плоскости, то вектор aA + bB + cC (a, b и c изменяются) перемещается по всему пространству. Предположим, что A, B и C – единичные векторы i, j и k. Вектор ai лежит на оси x; вектор ai + bj может перемещаться по всей плоскости xy; вектор ai + bj + ck может перемещаться по всему пространству.
Можно было бы выбрать четыре взаимно перпендикулярных вектора i, j, k и l и определить четырехмерный вектор как величину
A = Axi + Ayj + Azk + Awl
а можно было бы продолжать до пяти, шести или любого числа измерений. Хотя визуально такой вектор представить невозможно, никаких математических трудностей здесь не возникает. Такая запись часто бывает полезна; например, состояние движущейся частицы описывается шестимерным вектором P (x, y, z, px, py, pz), компоненты которого – ее положение в пространстве (x, y, z) и импульс (px, py, pz). Такое пространство называется «фазовым пространством»; если мы рассматриваем две частицы, то фазовое пространство 12-мерное, если три, то 18-ти и так далее. Число размерностей можно неограниченно увеличивать; при этом величины, с которыми мы будем иметь дело, ведут себя во многом также, как те, которые мы рассмотрим в оставшейся части этой статьи, а именно, трехмерные векторы.
Умножение двух векторов.
Правило сложения векторов было получено путем изучения поведения величин, представленных векторами. Нет никаких видимых причин, по которым два вектора нельзя было бы каким-либо образом перемножить, однако это умножение будет иметь смысл только в том случае, если можно показать его математическую состоятельность; кроме того, желательно, чтобы произведение имело определенный физический смысл.
Существуют два способа умножения векторов, которые соответствуют этим условиям. Результатом одного из них является скаляр, такое произведение называется «скалярным произведением» или «внутренним произведением» двух векторов и записывается A Ч B или (A, B). Результатом другого умножения является вектор, называемый «векторным произведением» или «внешним произведением» и записывается A ґ B или [A, B]. Скалярные произведения имеют физический смысл для одного-, двух- или трех измерений, тогда как векторные произведения определены только для трех измерений.
Скалярные произведения.
Если под действием некоторой силы F точка, к которой она приложена, перемещается на расстояние r, то выполненная работа равна произведению r и компоненты F в направлении r. Эта компонента равна F cos б F, r с , где б F, r с – угол между F и r, т.е.
Произведенная работа = Fr cos б F, r с .
Это – пример физического обоснования скалярного произведения, определенного для любых двух векторов A, B посредством формулы
A Ч B = AB cos б A, B с .
Так как все величины правой части уравнения – скаляры, то
A Ч B = B Ч A;
следовательно, скалярное умножение коммутативно.
Скалярное умножение также обладает свойством дистрибутивности:
A Ч (B + С) = A Ч B + A Ч С.
Если векторы A и B перпендикулярны, то cos б A, B с равен нулю, и, поэтому, A Ч B = 0, даже если ни A, ни B не равны нулю. Именно поэтому мы не можем делить на вектор. Допустим, что мы разделили обе части уравнения A Ч B = A Ч C на A.
Это дало бы B = C, и, если бы можно было бы выполнить деление, то это равенство стало бы единственным возможным результатом. Однако, если мы перепишем уравнение A Ч B = A Ч C в виде A Ч (B – C) = 0 и вспомним, что (B – C) – вектор, то ясно, что (B – C) необязательно равен нулю и, следовательно, B не должен быть равным C. Эти противоречивые результаты показывают, что векторное деление невозможно.
Скалярное произведение дает еще один способ записи численного значения (модуля) вектора:
A Ч A = AA Ч cos 0 ° = A 2 ;
Скалярное произведение можно записать и другим способом. Для этого вспомним, что:
A = Ax i + Ayj + Azk.
Поскольку последнее уравнение содержит x, y и z в качестве нижних индексов, уравнение, казалось бы, зависит от выбранной конкретной системы координат. Однако это не так, что видно из определения, которое не зависит от выбранных координатных осей.
Векторные произведения.
Векторным или внешним произведением векторов называется вектор, модуль которого равен произведению их модулей на синус угла, перпендикулярный исходным векторам и составляющий вместе с ними правую тройку. Это произведение легче всего ввести, рассматривая соотношение между скоростью и угловой скоростью. Первая – вектор; мы теперь покажем, что последнюю также можно интерпретировать как вектор.
Угловая скорость вращающегося тела определяется следующим образом: выберем любую точку на теле и проведем перпендикуляр из этой точки до оси вращения. Тогда угловая скорость тела – это число радиан, на которые эта линия повернулась за единицу времени.
Если угловая скорость – вектор, она должна иметь численное значение и направление. Численное значение выражается в радианах в секунду, направление можно выбрать вдоль оси вращения, можно его определить, направив вектор в том направлении, в котором двигался бы правосторонний винт при вращении вместе с телом.
Рассмотрим вращение тела вокруг фиксированной оси. Если установить эту ось внутри кольца, которое в свою очередь закреплено на оси, вставленной внутрь другого кольца, мы можем придать вращение телу внутри первого кольца с угловой скоростью w 1 и затем заставить внутреннее кольцо (и тело) вращаться с угловой скоростью w 2. Рисунок 7 поясняет суть дела; круговые стрелки показывают направления вращения. Данное тело – это твердая сфера с центром О и радиусом r.
Придадим этому телу движение, которое является суммой двух различных угловых скоростей. Это движение довольно трудно представить наглядно, но достаточно очевидно, что тело больше не вращается относительно фиксированной оси. Однако все-таки можно сказать, что оно вращается.
Чтобы показать это, выберем некоторую точку P на поверхности тела, которая в рассматриваемый нами момент времени находится на большом круге, соединяющем точки, в которых две оси пересекают поверхность сферы. Опустим перпендикуляры из P на оси. Эти перпендикуляры станут радиусами PJ и PK окружностей PQRS и PTUW соответственно. Проведем прямую POP ў , проходящую через центр сферы. Теперь точка P, в рассматриваемый момент времени одновременно перемещается по окружностям, которые соприкасаются в точке P. За малый интервал времени D t, P перемещается на расстояние
Это расстояние равно нулю, если
В этом случае точка P находится в состоянии мгновенного покоя, и точно также все точки на прямой POP ў . Остальная часть сферы будет в движении (окружности, по которым перемещаются другие точки, не касаются, а пересекаются). POP ў является, таким образом, мгновенной осью вращения сферы, подобно тому, как колесо, катящееся по дороге в каждый момент времени, вращается относительно своей нижней точки.
Чему равна угловая скорость сферы? Выберем для простоты точку A, в которой ось w 1 пересекает поверхность. В момент времени, который мы рассматриваем, она перемещается за время D t на расстояние
по кругу радиуса r sin w 1. По определению, угловая скорость
Из этой формулы и соотношения (1) мы получим
Другими словами, если записать численное значение и выбрать направление угловой скорости так, как это описано выше, то эти величины складываются как векторы и могут быть рассмотрены как таковые.
Теперь можно ввести векторное произведение; рассмотрим тело, вращающееся с угловой скоростью w . Выберем любую точку P на теле и любое начало координат О, которое находится на оси вращения. Пусть r – вектор, направленный от О к P. Точка P движется по окружности со скоростью
V = w r sin ( w , r).
Вектор скорости V является касательным к окружности и указывает в направлении, показанном на рис. 8.
Это уравнение дает зависимость скорости V точки от комбинации двух векторов w и r. Используем это соотношение, чтобы определить новый вид произведения, и запишем:
V = w ґ r.
Так как результатом такого умножения является вектор, это произведение названо векторным. Для любых двух векторов A и B, если
A ґ B = C,
C = AB sin б A, B с ,
и направление вектора C таково, что он перпендикулярен плоскости, проходящей через А и B и указывает в направлении, совпадающем с направлением движения правовращающегося винта, если он параллелен C и вращается от A к B. Другими словами, мы можем сказать, что A, B и C, расположенные в таком порядке, образуют правый набор координатных осей. Векторное произведение антикоммутативно; вектор B ґ A имеет тот же модуль, что и A ґ B, но направлен в противоположную сторону:
A ґ B = –B ґ A.
Это произведение дистрибутивно, но не ассоциативно; можно доказать, что
Посмотрим, как записывается векторное произведение в терминах компонент и единичных векторов. Прежде всего, для любого вектора A,
A ґ A = AA sin 0 = 0.
Следовательно, в случае единичных векторов,
i ґ i = j ґ j = k ґ k = 0
i ґ j = k, j ґ k = i, k ґ i = j.
Это равенство также можно записать в виде определителя:
Если A ґ B = 0, то либо A или B равно 0, либо A и B коллинеарны. Таким образом, как и в случае скалярного произведения, деление на вектор невозможно. Величина A ґ B равна площади параллелограмма со сторонами A и B. Это легко видеть, так как B sin б A, B с – его высота и A – основание.
Существует много других физических величин, которые являются векторными произведениями. Одно из наиболее важных векторных произведений появляется в теории электромагнетизма и называется вектором Пойтинга P. Этот вектор задается следующим образом:
P = E ґ H,
где E и H – векторы электрического и магнитного полей соответственно. Вектор P можно рассматривать как заданный поток энергии в ваттах на квадратный метр в любой точке. Приведем еще несколько примеров: момент силы F (крутящий момент) относительно начала координат, действующей на точку, радиус-вектор которой r, определяется как r ґ F; частица, находящаяся в точке r, массой m и скоростью V, имеет угловой момент mr ґ V относительно начала координат; сила, действующая на частицу, несущую электрический заряд q через магнитное поле B со скоростью V, есть qV ґ B.
Тройные произведения.
Из трех векторов мы можем сформировать следующие тройные произведения: вектор (A Ч B) ґ C; вектор (A ґ B) ґ C; скаляр (A ґ B) Ч C.
Первый тип – произведение вектора C и скаляра A Ч B; о таких произведениях мы уже говорили. Второй тип называется двойным векторным произведением; вектор A ґ B перпендикулярен к плоскости, где лежат A и B, и поэтому (A ґ B) ґ C – вектор, лежащий в плоскости A и B и перпендикулярный C.
Следовательно, в общем случае, (A ґ B) ґ C № A ґ (B ґ C). Записав A, B и C через их координаты (компоненты) по осям x, y и z и умножив, можно показать, что A ґ (B ґ C) = B ґ (A Ч C) – C ґ (A Ч B). Третий тип произведения, который возникает при расчетах решетки в физике твердого тела, численно равен объему параллелепипеда с ребрами A, B, C. Так как (A ґ B) Ч C = A Ч (B ґ C), знаки скалярного и векторного умножений можно менять местами, и произведение часто записывается как (A B C). Это произведение равно определителю
Заметим, что (A B C) = 0, если все три вектора лежат в одной и той же плоскости или, если А = 0 или (и) В = 0 или (и) С = 0.
ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА
Предположим, что вектор U является функцией одной скалярной переменной t. Например, U может быть радиус-вектором, проведенным из начала координат до перемещающейся точки, а t – временем. Пусть t изменится на небольшую величину D t, что приведет к изменению U на величину D U. Это показано на рис. 9. Отношение D U/ D t – вектор, направленный в том же направлении, что и D U. Мы можем определить производную U по t, как
при условии, что такой предел существует. С другой стороны, можно представить U как сумму компонент по трем осям и записать
Если U – радиус-вектор r, то dr/dt – скорость точки, выраженная как функция времени. Продифференцировав по времени еще раз, мы получим ускорение. Предположим, что точка перемещается вдоль кривой, показанной на рис. 10. Пусть s – расстояние, пройденное точкой вдоль кривой.
В течение малого интервала времени D t точка пройдет расстояние D s вдоль кривой; положение радиус-вектора изменится на D r. Следовательно D r/ D s – вектор направленный как D r. Далее
есть единичный вектор, касательный к кривой. Это видно из того, что при приближении точки Q к точке P, PQ приближается к касательной и D r приближается к D s.
Формулы для дифференцирования произведения подобны формулам для дифференцирования произведения скалярных функций; однако, так как векторное произведение антикоммутативно, порядок умножения должен быть сохранен. Поэтому,
Таким образом, мы видим, что, если вектор является функцией одной скалярной переменной, то мы можем представить производную почти также, как в случае скалярной функции.
Вектор и скалярные поля.
Градиент.
В физике часто приходится иметь дело с векторными или скалярными величинами, которые меняются от точки к точке в заданной области. Такие области называются «полями». Например, скаляр может быть температурой или давлением; вектор может быть скоростью движущейся жидкости или электростатическим полем системы зарядов.
Если мы выбрали некоторую систему координат, то любой точке P (x, y, z) в заданной области соответствует некоторый радиус-вектор r (= xi + yj + zk) и также значение векторной величины U (r) или скаляра f (r), связанных с ним. Предположим, что U и f определены в области однозначно; т.е. каждой точке соответствует одна и только одна величина U или f , хотя различные точки могут, конечно, иметь различные значения. Допустим, что мы хотим описать скорость, с которой U и f изменяются при передвижении по этой области.
Простые частные производные, такие, как ¶ U/ ¶ x и ¶f / ¶ y, нас не устраивают, потому что они зависят от конкретно выбранных координатных осей. Однако можно ввести векторный дифференциальный оператор, независимый от выбора осей координат; этот оператор называется «градиентом».
Пусть мы имеем дело со скалярным полем f . Сначала в качестве примера рассмотрим контурную карту области страны. В этом случае f – высота над уровнем моря; контурные линии соединяют точки с одним и тем же значением f . При движении вдоль любой из этих линий f не меняется; если двигаться перпендикулярно этим линиям, то скорость изменения f будет максимальной. Мы можем каждой точке сопоставить вектор, указывающий величину и направление максимального изменения скорости f ; такая карта и некоторые из этих векторов показаны на рис. 11. Если мы проделаем это для каждой точки поля, то получим векторное поле, связанное со скалярным полем f . Это поле вектора, называемого «градиентом» f , который записывается как grad f или Сf (символ С также называется «набла»).
В случае трех измерений, контурные линии становятся поверхностями. Малое смещение D r (= i D x + j D y + k D z) приводит к изменению f , которое записывается как
где точками обозначены члены более высоких порядков. Это выражение можно записать в виде скалярного произведения
Разделим правую и левую части этого равенства на D s, и пусть D s стремится к нулю; тогда
где dr/ds – единичный вектор в выбранном направлении. Выражение в круглых скобках – вектор, зависящий от выбранной точки. Таким образом, d f /ds имеет максимальное значение, когда dr/ds указывает в том же направлении, выражение, стоящее в скобках, является градиентом. Таким образом,
– вектор, равный по величине и совпадающий по направлению с максимальной скоростью изменения f относительно координат. Градиент f часто записывается в виде
Это означает, что оператор С существует сам по себе. Во многих случаях он ведет себя, как вектор, и фактически является «векторным дифференциальным оператором» – одним из наиболее важных дифференциальных операторов в физике. Несмотря на то, что С содержит единичные векторы i, j и k, его физический смысл не зависит от выбранной системы координат.
Какова связь между Сf и f ? Прежде всего предположим, что f определяет потенциал в любой точке. При любом малом смещении D r величина f изменится на
Если q – величина (например масса, заряд), перемещенная на D r, то работа, выполненная при перемещении q на D r равна
Так как D r – перемещение, то q Сf – сила; – Сf – напряженность (сила на единицу количества), связанная с f . Например, пусть U – электростатический потенциал; тогда E – напряженность электрического поля, задается формулой
E = – С U.
Допустим, что U создается точечным электрическим зарядом в q кулонов, помещенным в начало координат. Значение U в точке P (x, y, z) с радиус-вектором r задается формулой
где e 0 – диэлектрическая постоянная свободного пространства. Поэтому
откуда следует, что E действует в направлении r и его величина равна q/(4 pe 0r 3 ).
Зная скалярное поле, можно определить связанное с ним векторное поле. Также возможно и обратное. С точки зрения математической обработки скалярными полями оперировать легче, чем векторными, так как они задаются одной функцией координат, в то время как векторное поле требует три функции, соответствующие компонентам вектора в трех направлениях. Таким образом, возникает вопрос: дано векторное поле, может ли мы записать связанное с ним скалярное поле?
Дивергенция и ротор.
Мы видели результат действия С на скалярную функцию. Что произойдет, если С применить к вектору? Имеются две возможности: пусть U (x, y, z) – вектор; тогда мы можем образовать векторное и скалярное произведения следующим образом:
Первое из этих выражений – скаляр, называемый дивергенцией U (обозначается divU); второе – вектор, названный ротор U (обозначается rotU).
Эти дифференциальные функции, дивергенция и ротор, широко используются в математической физике.
Представьте, что U – некоторый вектор и что он и его первые производные непрерывны в некоторой области. Пусть P – точка в этой области, окруженная малой замкнутой поверхностью S, ограничивающей объем D V. Пусть n – единичный вектор, перпендикулярный к этой поверхности в каждой точке (n меняет направление при движении вокруг поверхности, но всегда имеет единичную длину); пусть n направлен наружу. Покажем, что
Здесь S указывает, что эти интегралы берутся по всей поверхности, da – элемент поверхности S.
Для простоты мы выберем удобную для нас форму S в виде небольшого параллелепипеда (как показано на рис. 12) со сторонами D x, D y и D z; точка P – центр параллелепипеда. Вычислим интеграл из уравнения (4) сначала по одной грани параллелепипеда. Для передней грани n = i (единичный вектор параллелен оси x); D a = D y D z. Вклад в интеграл от передней грани равен
На противоположной грани n = –i; эта грань дает вклад в интеграл
Используя теорему Тейлора, получим общий вклад от двух граней
Заметим, что D x D y D z = D V. Аналогичным образом можно вычислить вклад от двух других пар граней. Полный интеграл равен
и если мы положим D V ® 0, то члены более высокого порядка исчезнут. По формуле (2) выражение в скобках – это divU, что доказывает равенство (4).
Равенство (5) можно доказать таким же образом. Воспользуемся снова рис. 12; тогда вклад от передней грани в интеграл будет равен
и, используя теорему Тейлора, получим, что суммарный вклад в интеграл от двух граней имеет вид
т.е. это два члена из выражения для rotU в уравнении (3). Другие четыре члена получатся после учета вкладов от других четырех граней.
Что, в сущности, означают эти соотношения? Рассмотрим равенство (4). Предположим, что U – скорость (жидкости, например). Тогда n Ч U da = Un da, где Unявляется нормальной компонентой вектора U к поверхности. Поэтому, Un da – это объем жидкости, протекающей через da в единицу времени, а – это объем жидкости, вытекающей через S в единицу времени. Следовательно,
– скорость расширения единицы объема вокруг точки P. Отсюда дивергенция получила свое название; она показывает скорость, с которой жидкость расширяется из (т.е. расходится от) P.
Чтобы объяснить физическое значение ротора U, рассмотрим другой поверхностный интеграл по маленькому цилиндрическому объему высотой h, окружающему точку P; плоско-параллельные поверхности могут быть ориентированы в любом направлении, которое мы выбираем. Пусть k –единичный вектор перпендикулярный к каждой поверхности, и пусть площадь каждой поверхности D A; тогда полный объем D V = h D A (рис. 13). Рассмотрим теперь интеграл
Подынтегральное выражение – уже упоминавшееся ранее тройное скалярное произведение. Это произведение будет равно нулю на плоских поверхностях, где k и n параллельны. На кривой поверхности
где ds – элемент кривой как показано на рис. 13. Сравнивая эти равенства с соотношением (5), получаем, что
Мы по-прежнему предполагаем, что U – скорость. Чему в таком случае будет равна средняя угловая скорость жидкости вокруг k? Очевидно, что
если D A ® 0. Это выражение максимально, когда k и rotU указывают в одном и том же направлении; это означает, что rotU – вектор, равный удвоенной угловой скорости жидкости в точке P. Если жидкость вращается относительно P, то rotU № 0, и векторы U будут вращаться вокруг P. Отсюда и возникло название ротора.
Теорема дивергенции (теорема Остроградского – Гаусса)
Теорема дивергенции (теорема Остроградского – Гаусса) является обобщением формулы (4) для конечных объемов. Она утверждает, что для некоторого объема V, ограниченного замкнутой поверхностью S,
и справедлива для всех непрерывных векторных функций U, имеющих непрерывные первые производные всюду в V и на S. Мы не будем приводить здесь доказательство этой теоремы, но ее справедливость можно понять интуитивно, представляя объем V разделенным на ячейки. Поток U через поверхность, общую для двух ячеек обращается в нуль, и только ячейки, находящиеся на границе S внесут вклад в поверхностный интеграл.
Теорема Стокса
является обобщением уравнения (6) для конечных поверхностей. Она утверждает, что
где C – замкнутая кривая и S – любая поверхность, ограниченная этой кривой. U и ее первые производные должны быть непрерывны всюду на S и C.
Александров П.С. Лекции по аналитической геометрии. М., 1968
Погорелов А.В. Аналитическая геометрия, 3 изд. М., 1968
Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?
Источник: www.krugosvet.ru
Вектор

Сегодня нас ждёт увлекательное путешествие, которое можно озаглавить словосочетанием «векторы в геометрии». Да, достаточно самонадеянно думать, что меньше чем за час можно стать экспертом в этой теме. Но познакомиться, выяснить нюансы, а главное, увидеть всю картину целиком — можно! Мы постараемся стать вашими проводниками в этот удивительный мир и охватить все темы о векторах, которые могут встретиться в школе.
20 сентября 2022
· Обновлено 23 сентября 2022
Определение и обозначение вектора
Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.
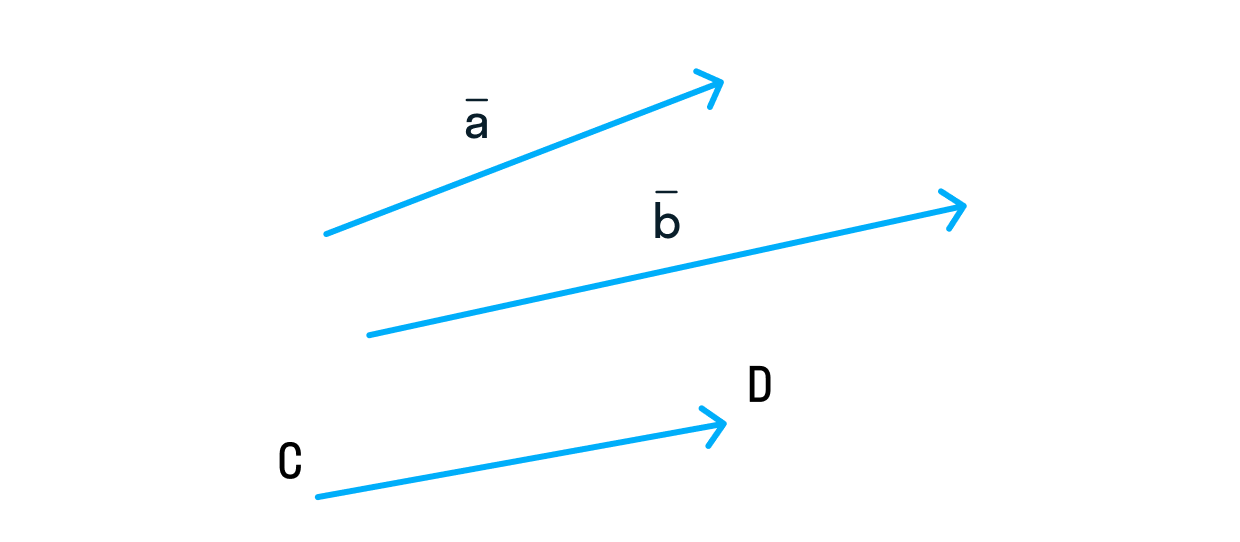
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому и — абсолютно разные векторы.

Виды векторов
Во-первых, векторы бывают коллинеарными и неколлинеарными.
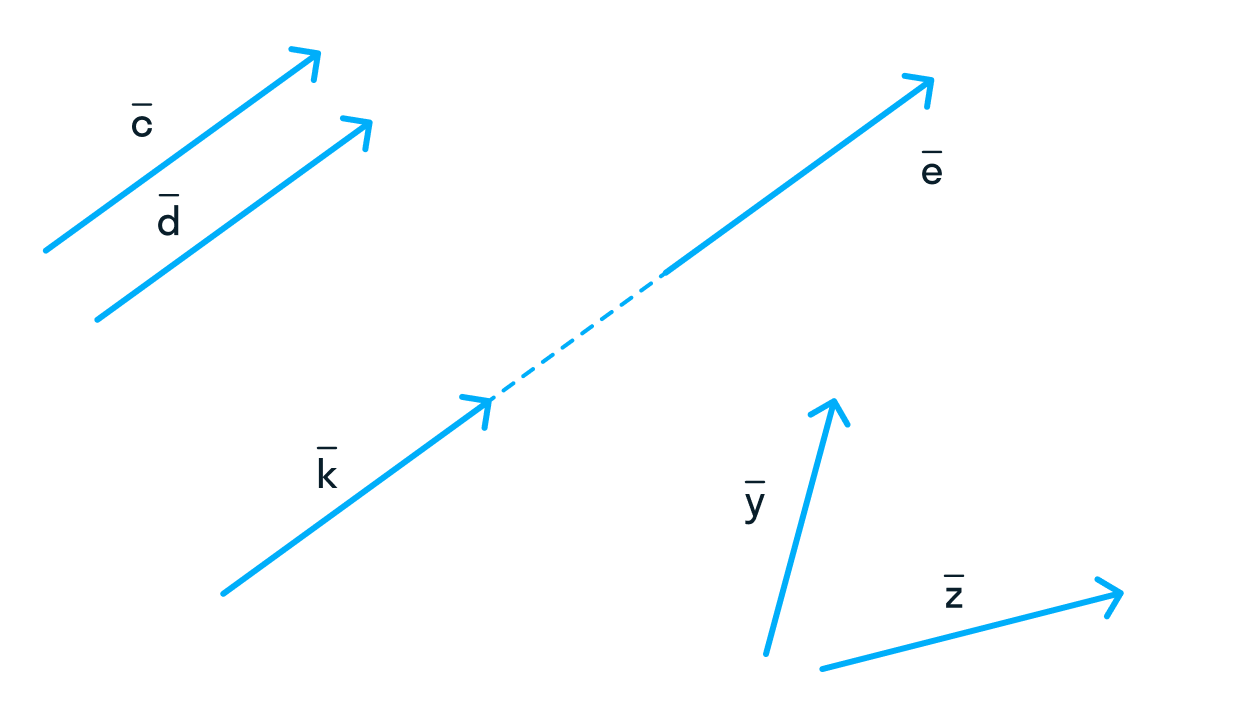
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке и и являются коллинеарными, а и относительно друг друга — нет.
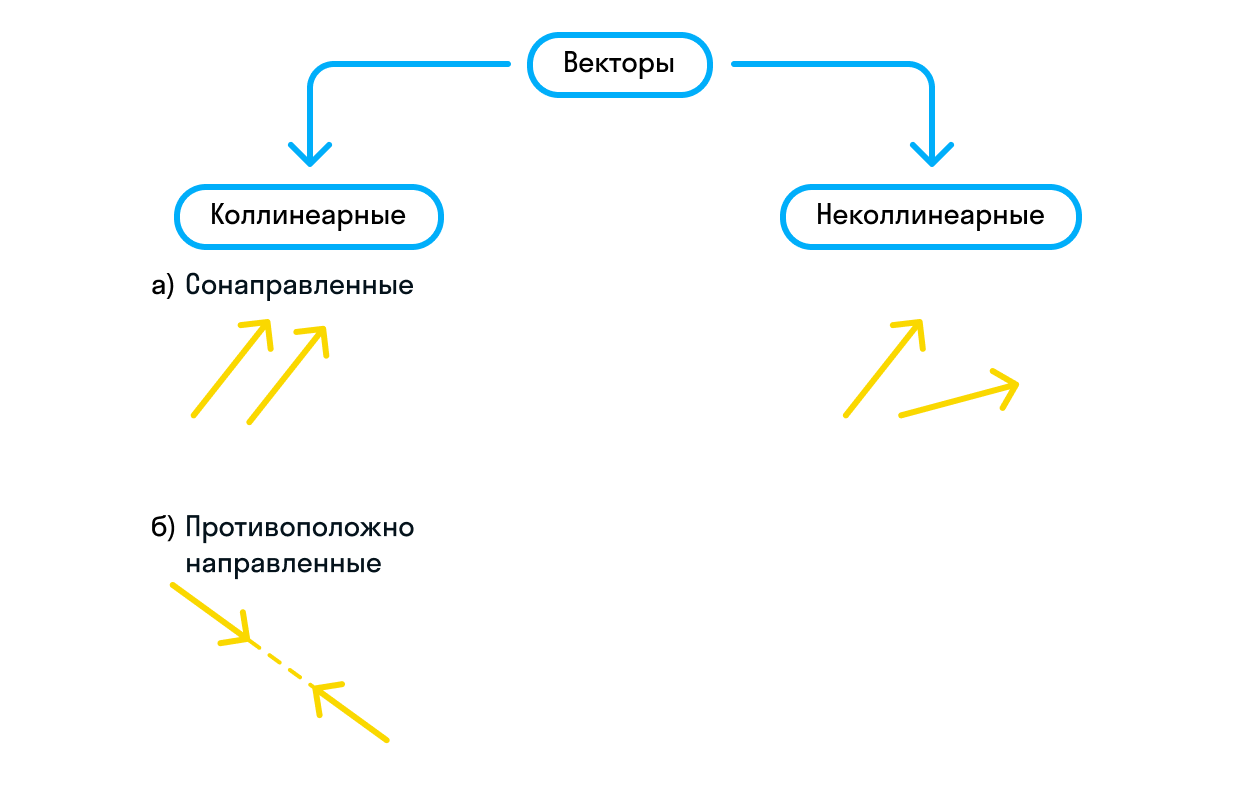
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так: Если же они противоположно направлены, мы можем записать это следующим образом:
Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.
Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так: Он считается коллинеарным любому вектору.
Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:
Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда (это то, что мы понимаем под обычным вектором в школьной геометрии).
Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Сложение и вычитание векторов
Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.
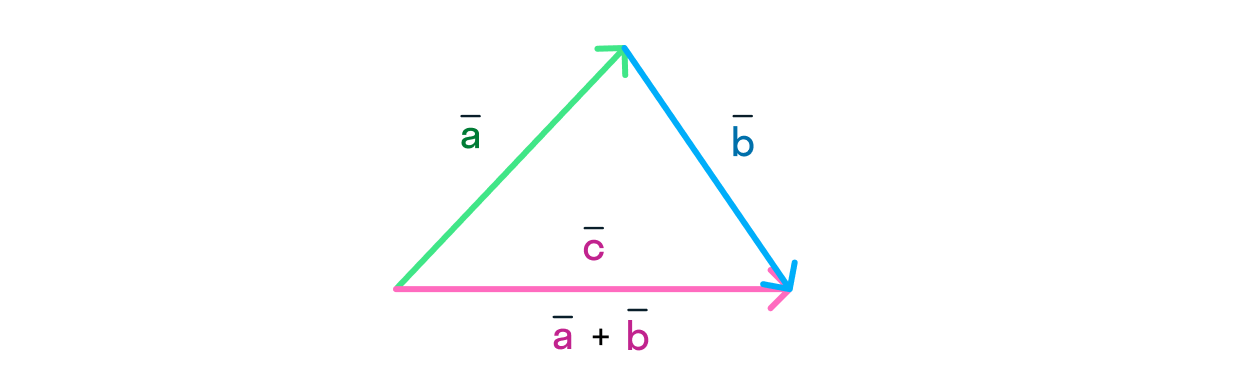
Сложение: метод треугольника
Представим, что в пространстве заданы векторы и которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:
Отложить начало одного вектора от конца другого.
Вектор их суммы будет совпадать с вектором , который соединяет начало вектора с концом вектора
Сложение: метод параллелограмма
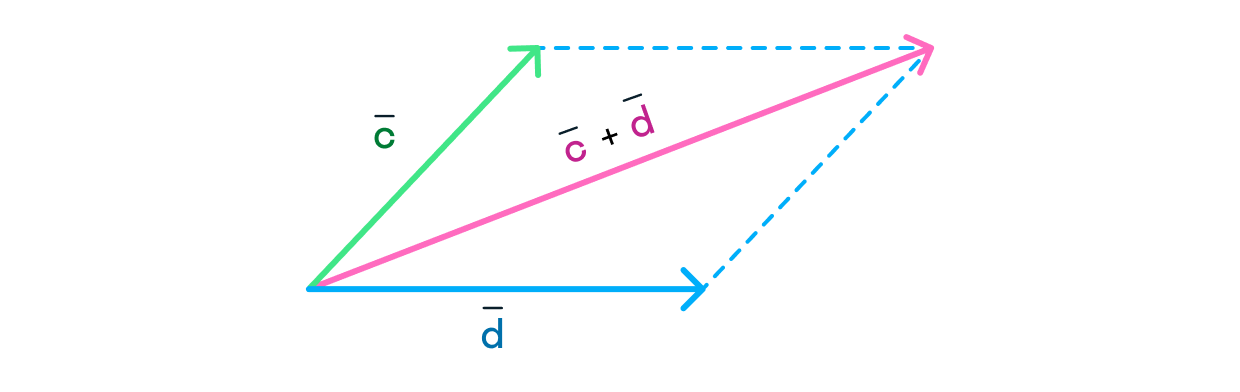
Сложить векторы можно и по-другому, используя метод параллелограмма:
Совместим между собой концы и
Отложим от конца вектор, равный
Отложим от конца вектор, равный
Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).
Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и
Задача решена, вы великолепны!
Как метод параллелограмма, так и метод треугольника подразумевает перемещение векторов в пространстве: мы или совмещаем их концы, или откладываем от конца одного вектора начало другого. Получить сумму векторов, не имеющих общей точки, с этими методами не представляется возможным.
Сложение: метод многоугольника
А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».
Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:

Вычитание векторов
Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание. Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:
Изобразим разность векторов с помощью уже знакомого нам правила треугольника:
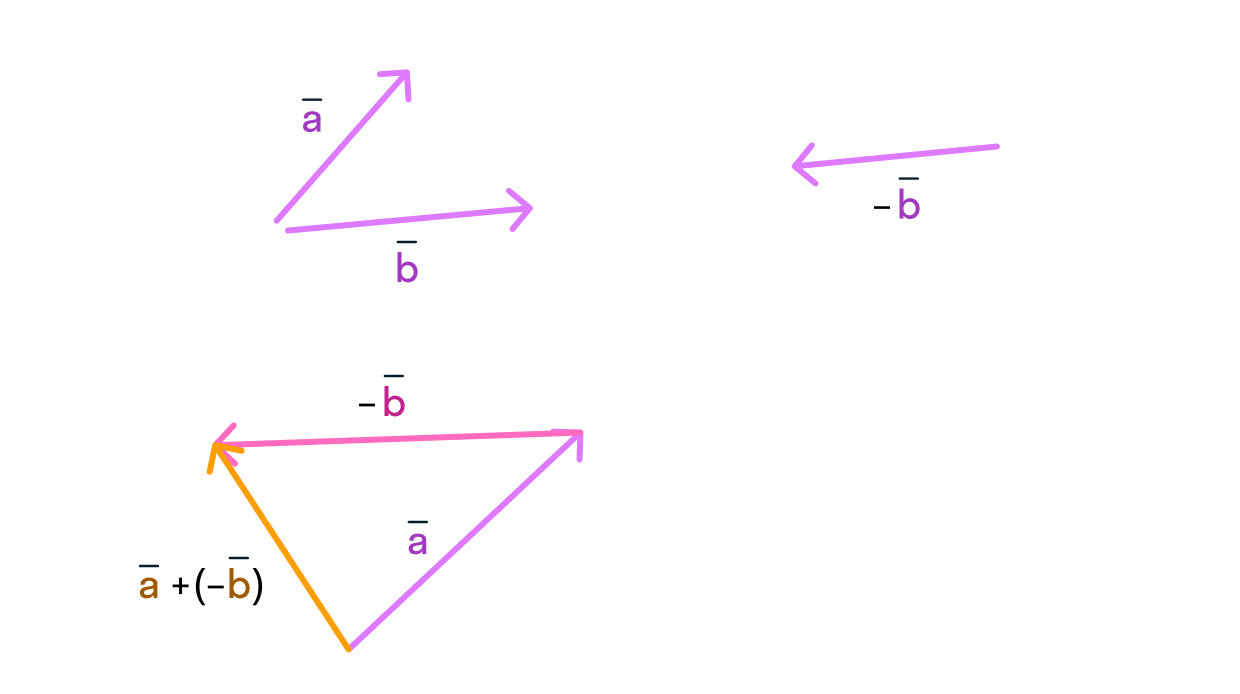
Боитесь запутаться в векторах сонаправленных и противоположно направленных? Существует отдельное правило для их вычитания:
Отложим один вектор от начала другого.
Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а начало — с концом уменьшаемого.

Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Координаты вектора на плоскости и в пространстве
Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно пользоваться как на плоскости с осями X и Y, так и в пространстве с осями X, Y, Z.
Тогда, если находится на плоскости, его координаты можно выразить как если в пространстве —
Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают
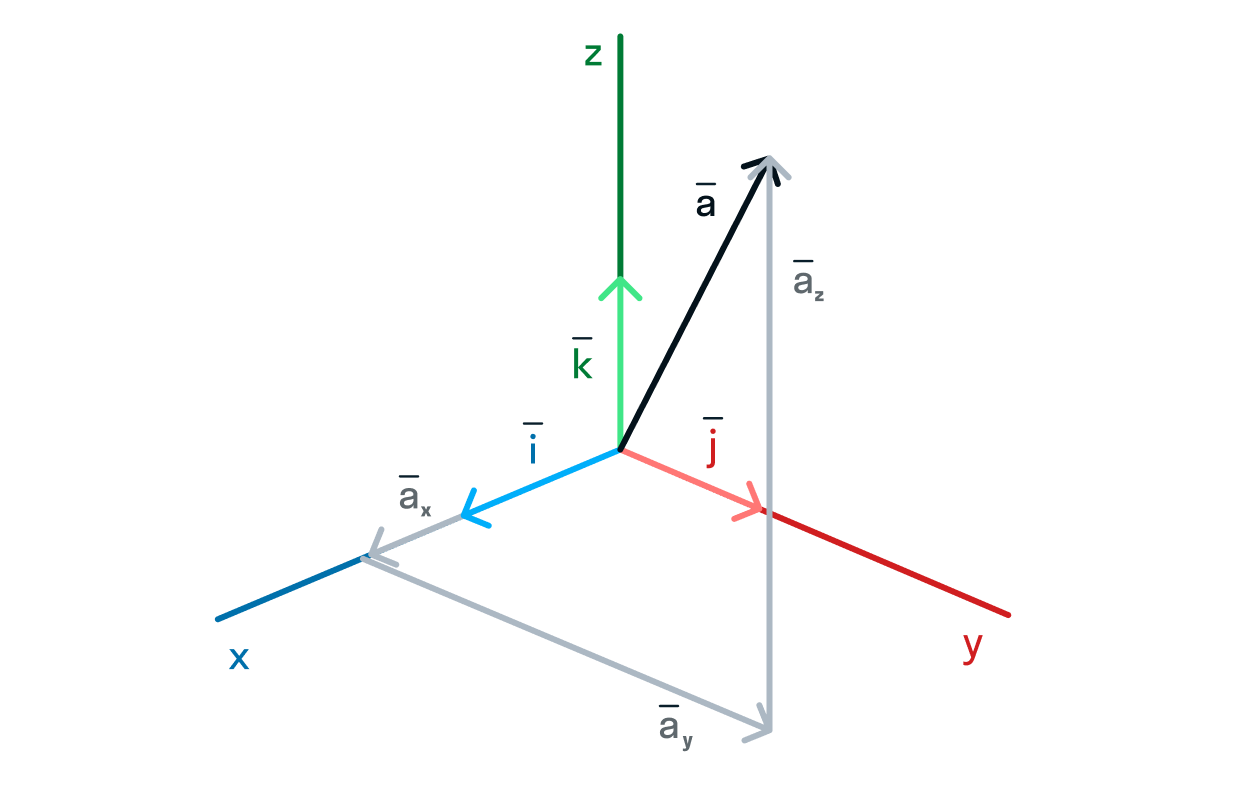
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.
с координатами можно записать так:
Умножение вектора на число
Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает одна простая задача: умножение вектора на число.
Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора на это число.
Таким образом, если задан координатами то — Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:
Длина вектора
Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в пространстве и выражается числом.
Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что отражается и в обозначении. Если нам необходимо найти длину мы так и запишем:
Длину вектора можно найти разными способами, вот основные:
через координаты вектора;
через координаты точек начала и конца вектора;
через теорему косинусов.
Давайте вместе разберём все методы!
Длина вектора через его координаты
Если задан через координаты то его длину можно найти как
Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор в декартовой системе координат.
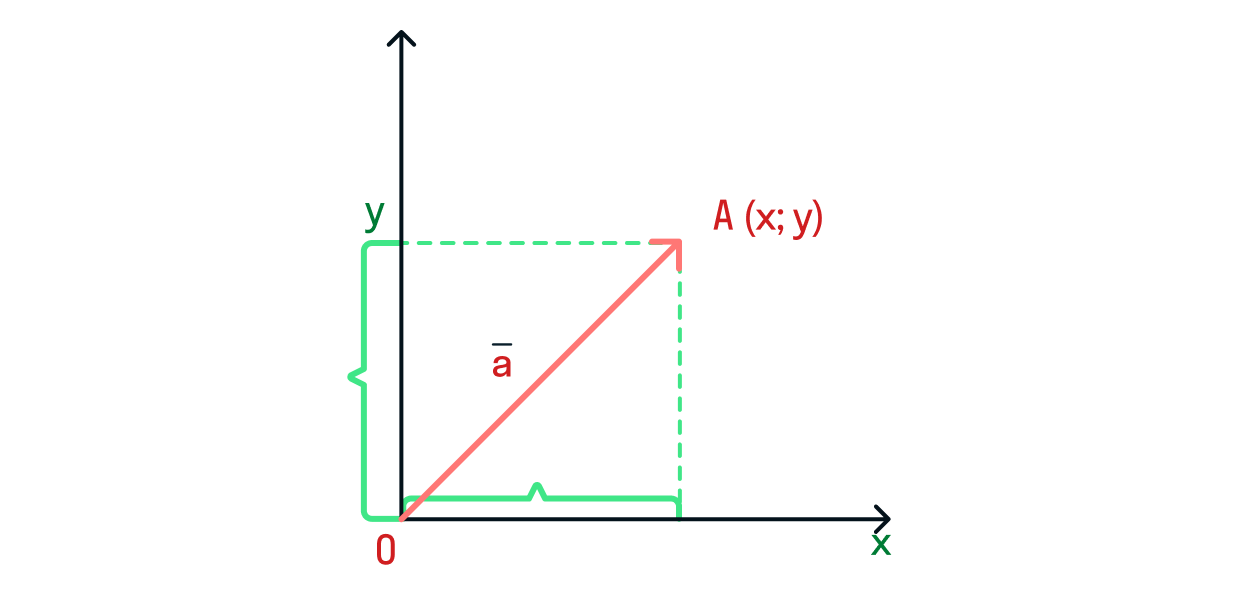
Отложим вектор от точки с координатами Тогда этот вектор можно назвать , и так как мы строили его из начала координат, координаты вектора могут быть найдены как
Рассчитаем длину через теорему Пифагора:
Задача 1
Посчитайте, чему равен модуль , если его координаты
Модуль вектора — это его длина, а значит,
Задача 2
Длина Чему равна координата по оси , если координата по оси
Длина вектора через координаты точек начала и конца
Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.

Рассмотрим где и Тогда координаты вектора можно выразить так:
Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:
Задача 3
Найдите длину если и
Задача 4

Рассчитайте координату по точки вектора , если его длина равна а
Остановимся здесь и подставим известные числа в формулу:
Длина вектора через теорему косинуса
К сожалению, в задачах не всегда даны координаты точек вектора или его самого. В таком случае мы воспользуемся теоремой косинуса. Давайте вспомним её формулировку.
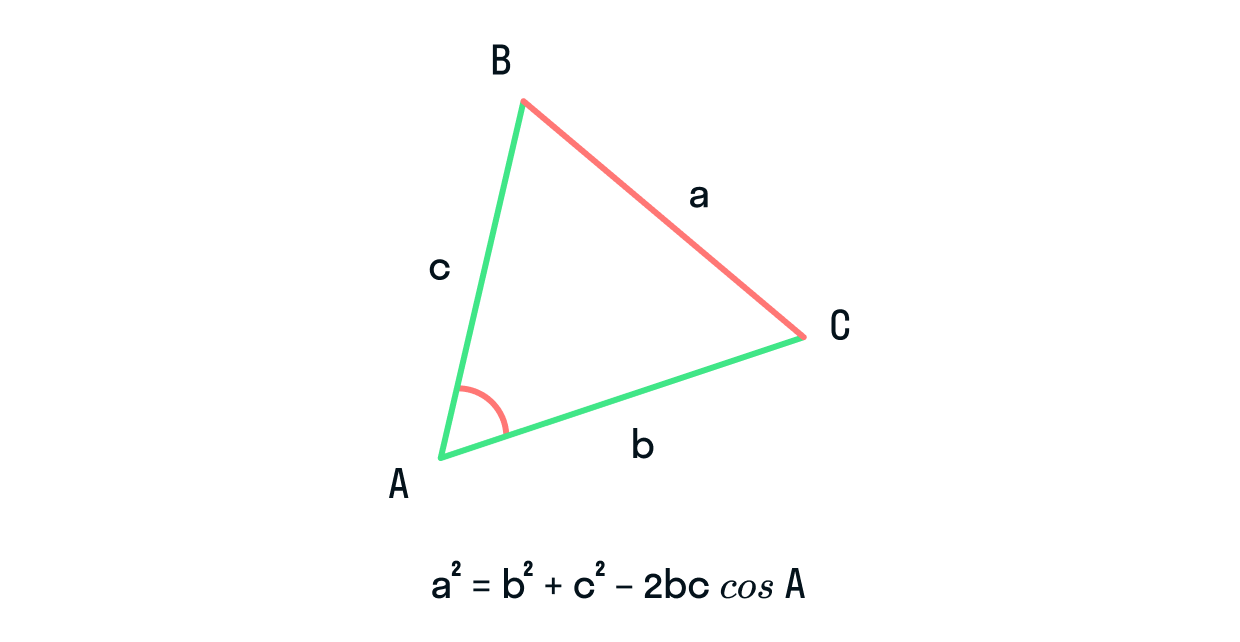
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
Эту теорему можно применить и в векторной форме. Немного изменим рисунок:
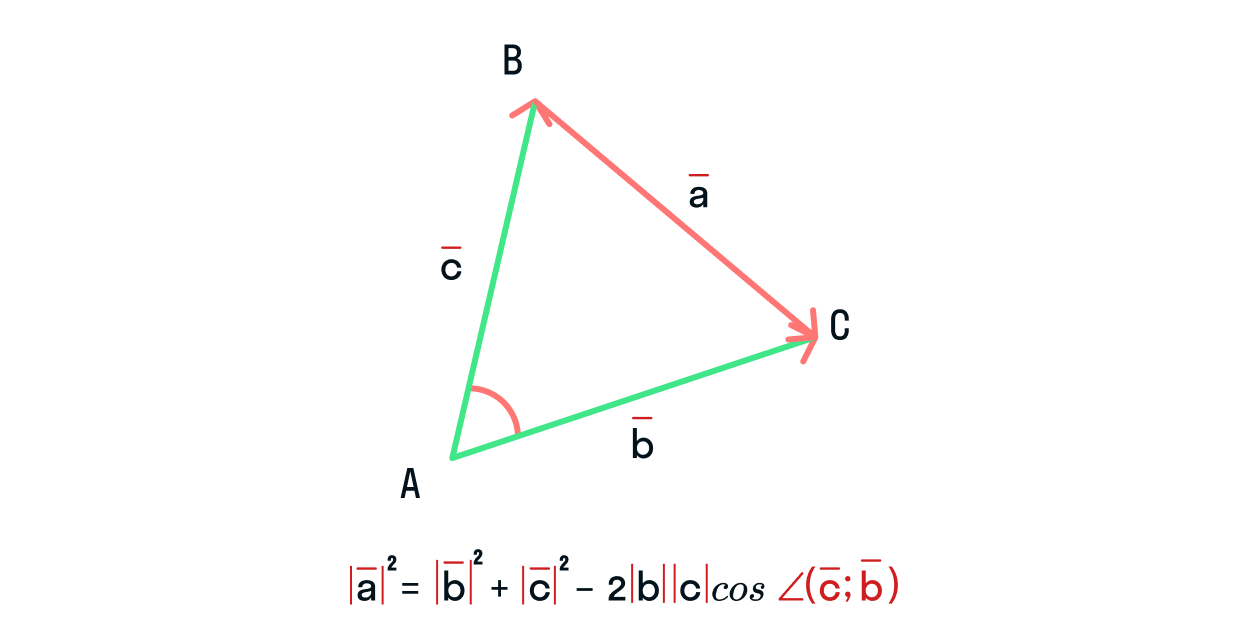
Тогда, чтобы найти длину , необходимо знать (или иметь возможность вычислить) длины и , знать угол между ними, а также уметь рассчитать произведение длин этих векторов.
Задача 5
Длины и равны 4 и 6 соответственно, а угол между ними равен Вычислите длину
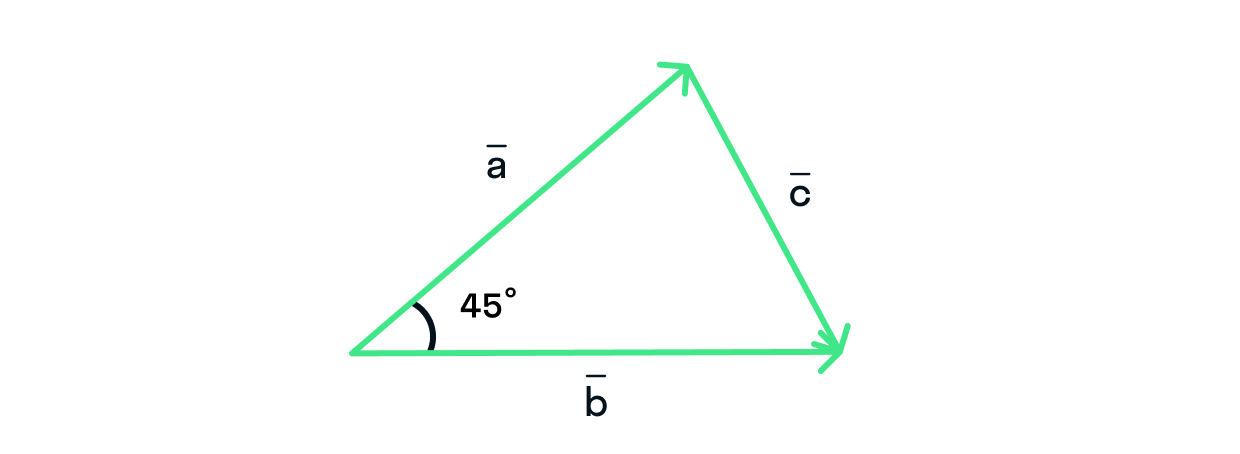
Задача 6
Рассчитайте модуль вектора в треугольнике, если длина = 8, длина = 10, а угол между ними равен
Скалярное произведение векторов
Мы практически дошли до финала нашего путешествия по царству векторов. Нам осталось изучить только скалярное произведение векторов. Что это?
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Скалярным произведением и будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные (имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.
Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:
Скалярное произведение вектора на само себя равно квадрату его модуля: В данном случае значение скалярного произведения является наибольшим из возможных.
Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как
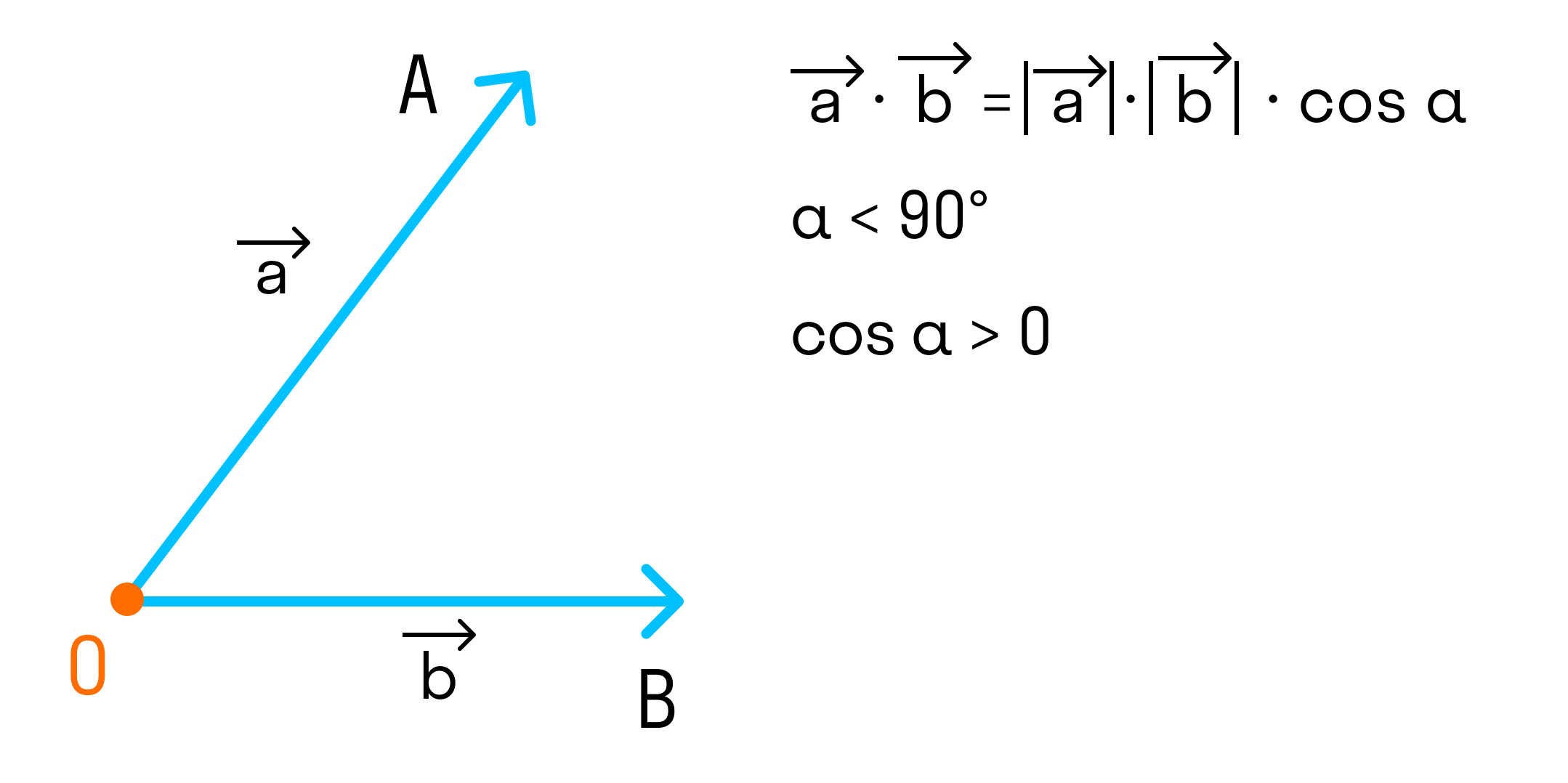
Если угол между векторами прямой, то скалярное произведение равно 0, так как

Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как

Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их длин . В данном случае значение скалярного произведения является наименьшим из возможных.
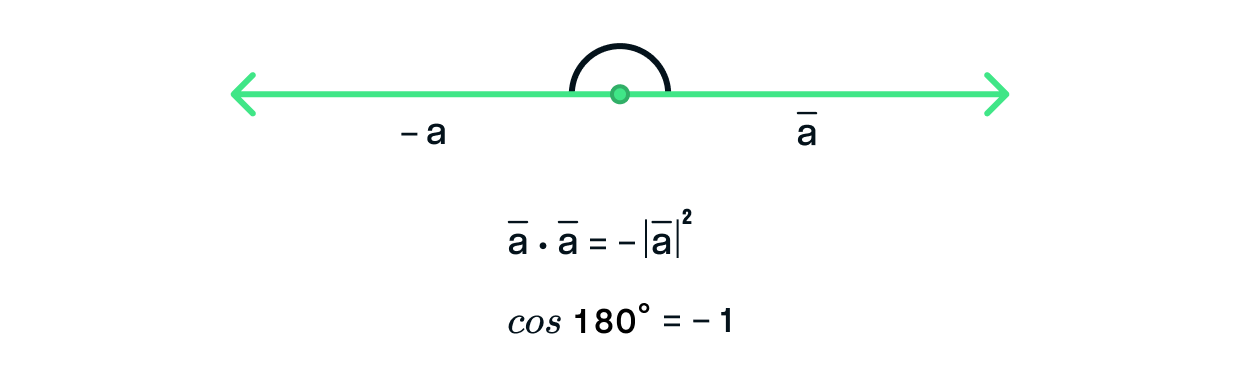
Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное произведение — просто, особенно если рассмотреть его через координаты.
Если выражен координатами а то скалярное произведение этих векторов описывается формулой: В пространстве скалярное произведение через координаты векторов будет задаваться так:
Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой раз.
Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.
Источник: skysmart.ru