Геодезия — наука, изучающая форму и размеры Земли, геодезические приборы, способы измерений и изображений земной поверхности на планах, картах, профилях и цифровых моделях местности. В современной геодезии находят применение новейшие измерительные средства, используют последние достижения в физике, механике, электронике, оптике, вычислительной технике. По разнообразию решаемых народнохозяйственных задач геодезия подразделяется на ряд самостоятельных дисциплин, каждая из которых имеет свой предмет изучения:
— высшая геодезия (гравимметрия, космическая геодезия, астрономическая геодезия) изучает форму и размеры Земли, занимается высокоточными измерениями с целью определения координат отдельных точек земной поверхности в единой государственной системе координат;
— топография и гидрография развивают методы съемки участков земной поверхности и изображения их на плоскости в виде карт, планов и профилей;
— фотограмметрия занимается обработкой фото-, аэрофото- и космических снимков для составления карт и планов;
Решение обратной геодезической задачи
— картография рассматривает методы составления и издания карт;
— маркшейдерия — область геодезии, обслуживающая горнодобывающую промышленность и строительство тоннелей;
— инженерная (прикладная) геодезия изучает методы геодезических работ, выполняемых при изысканиях, проектировании, строительстве и эксплуатации различных зданий и сооружений, а также рациональном использовании и охране природных ресурсов.
Задачами инженерной геодезии являются:
1) топографо-геодезические изыскания различных участков, площадок и трасс с целью составления планов и профилей;
2) инженерно-геодезическое проектирование — преобразование рельефа местности для инженерных целей, подготовка геодезических данных для строительных работ;
3) вынос проекта в натуру, детальная разбивка осей зданий и сооружений;
4) выверка конструкций и технологического оборудования в плане и по высоте, исполнительные съемки;
5) наблюдения за деформациями зданий и сооружений.
При топографо-геодезических изысканиях выполняют:
а) измерение углов и расстояний на местности с помощью геодезических приборов (теодолитов, нивелиров, лент, рулеток и др.);
б) вычислительную (камеральную) обработку результатов полевых измерений на ЭВМ;
в) графические построения планов, профилей, цифровых моделей местности (ЦММ).
Понятие о фигуре Земли.
За форму Земли принимают геометрическое тело, ограниченное поверхностью морей и океанов, мысленно продолженной под континентами. Такая фигура называется геоид, а поверхность, ограничивающая ее называется нормальной или уровенной. По форме геоид наиболее близок к эллипсоиду вращения, полученному вращением эллипса вокруг малой оси.
Размеры земного эллипсоида, в м:
, где — коэффициент сжатия
Так, как — невелико, форму Земли можно принимать за шар:
Картографическая прямоугольная система координат Гаусса- Крюгера.
В основу этой системы положено поперечно-цилиндрическая равноугольная проекция Гаусса-Крюгера (названа по имени немецких ученых ее предложивших). В этой проекции поверхность земного эллипсоида меридианами делят на шестиградусные зоны и номеруют с 1-й по 60-ю от Гринвичского меридиана на восток (рис.7). Средний меридиан шестиугольной зоны принято называть осевым.
Лекция 1 Понятие и задачи геодезии
Рис.7.Зональная система прямоугольных координат
Его совмещают с внутренней поверхностью цилиндра и принимают за ось абсцисс. Чтобы избежать отрицательного значения ординат (у), ординату осевого меридиана принимают не за нуль,
а за 500 км, т.е. перемещают на запад на 500 км. Перед ординатой указывают номер зоны.
Например, запись координат XМн=6350 км, YМн=5500 км указывает, что точка расположена в 5-й зоне на осевом меридиане (lМн=27° СШ, jМн=54° ВД). Для приближенных расчетов при переходе от географических к прямоугольным зональным координатам считают, что 1° соответствует 111 км (40000км/360° ).
Системы высот
Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей.
Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.
Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 2.5 отрезки отвесных линий Аа и Вв — абсолютные высоты точек А и В.
Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 2.5 отрезки отвесных линий Аа¢ и Вв¢ — условные высоты точек А и В.

В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока.

Численное значение высоты принято называть отметкой. Например, если высота точки А равна HА = 15,378 м, то говорят, что отметка точки равна 15,378 м.
Рис. 2.5. Абсолютные и условные высоты: a¢b¢ – уровенная поверхность; ab –поверхность геоида; Ab² – уровенная поверхность точки A;
Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно
Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле
Измерение превышений и последующее вычисление высот точек называется нивелированием.
Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.
В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому в России принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.
План и карта.
Их сходство и различие.
Топографический план — это уменьшенная ортогональная проекция местности на горизонтальную плоскость.
Картой называется построенное в картографической проекции с учетом кривизны Земли, уменьшенное, обобщенное изображение Земли или отдельных ее частей.
Профиль представляет уменьшенное изображение вертикального разреза земной поверхности по заданному направлению. Профили используют для проектирования и строительства линейных инженерных сооружений.
Отличительные признаки плана и карты:
1) На планах изображается меньшая площадь, нет искажений длин линий и углов.
2) На планах не учитывается кривизна Земли.
3) На планах используют более крупные масштабы: 1:500, 1:1000, 1:2000, 1:5000;
на картах — 1:10000, 1:25000, 1:50000, 1:100000.
4) На планах нет параллелей и меридианов, а имеется только координатная сетка.
5) Различается номенклатура, т.е. система разграфки и обозначений отдельных листов карт и планов.
2.2. Масштабы планов и карт. Точность масштабов.
Масштаб — отношение длины отрезков на планах или картах к горизонтальному проложению этого отрезка на местности. Масштабы бывают: а) численный (в виде дроби), б) линейный (в виде линии), в) поперечный, позволяющий строить на чертежной бумаге с помощью измерителя и масштабной линейки отрезки с погрешностью равной 0,1 мм.
Под точностью масштаба понимают отрезок на местности соответствующий минимальному расстоянию на плане в 0,1 мм. Например, точность масштаба 1:500 соответствует 0.05м.
Масштаб – отношение длины линии на плане к соответствующему отрезку на местности.
ü Числовой – это правильная дробь, в числителе которой единица, а знаменатель показывает во сколько раз уменьшена местность при изображении ее на плане.
ü Именованный – показывает, сколько метров местности соответствует одному сантиметру данного чертежа.
ü Линейный – графическое изображение числового масштаба представляющий собой шкалу с делениями соответствующую числовому масштабу.

ü Поперечный – Он представляет собой график в виде металлической линейки длиной 10 или 12 см, Отрезок линейки АВ, равный 2 см и разбитый на 10 равных частей, называется основанием поперечного масштаба. Графическая точность определения длин отрезков, на плане с помощью поперечного масштаба составляет 1/100 его основания. Измерение длин линий на плане по поперечному масштабу выполняется с помощью измерителя (циркуля).

Точность масштаба – это расстояние на местности соответствующая 0,1 мм данного чертежа.
2.3. Условные знаки планов и карт.
На топографических планах и картах объекты местности отображаются едиными условными знаками, которые подразделяются на масштабные, внемасштабные, линейные, пояснительные, специальные.
1. Масштабные знаки – показывают местоположение объекта и его фактические размеры. Границы таких объектов могут отображаться тонки сплошными линиями или точечным пунктиром.
2 – этажность; К – кирпич; Н – нежилое
2. Внемасштабные знаки – показывают местоположение объекта, но не отображают его размеры.
— столбы — колодцы — отдельно стоящие деревья
3. Линейные – отображают местоположение и протяженность линейных объектов.
4. Пояснительные – показывают название Ии характеристики объектов в буквенных и цифровых обозначениях.
5. Специальные – используются для отображения объектов на специальных картах различных ведомств.
2.4. Рельеф местности и его изображение на планах и картах.
Рельеф – совокупность неровностей земной поверхности.
Рельеф отображается на картах мелкого масштаба интенсивностью цвета, на крупномасштабных планах горизонталями, бергштрихами, абсолютными отметками.
Горизонтали – это замкнутая кривая линия на плане, все точки которой на местности имеют одинаковые отметки.
Кратчайшее расстояние между соседними горизонталями на плане называется – заложением.
Вертикальное расстояние между соседними горизонталями на местности называется – высота сечение рельефа.
Бергштрихи – это короткие черточки на горизонталях, указывающие направление склона.
Изображение рельефа на планах и картах
Для решения инженерных задач изображение рельефа должно обеспечивать: во-первых, быстрое определение с требуемой точностью высот точек местности, направления крутизны скатов и уклонов линий; во-вторых, наглядное отображение действительного ландшафта местности.
Рельеф местности на планах и картах изображают различными способами (штриховкой, пунктиром, цветной пластикой), но чаще всего с помощью горизонталей (изогипсов), числовых отметок и условных знаков.
Горизонталь на местности можно представить как след, образованный пересечением уровенной поверхности с физической поверхностью Земли. Например, если представить холм, окружённый неподвижной водой, то береговая линия воды и есть горизонталь (рис. 30). Лежащие на ней точки имеют одинаковую высоту.
Допустим, что высота уровня воды относительно уровенной поверхности 110 м (рис. 30). Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Кривая линия пересечения поверхностей воды и холма будет соответствовать горизонтали с высотой 105 м. Если последовательно снижать уровень воды по 5 м и проектировать кривые линии, образованные пересечением поверхности воды с земной поверхностью, на горизонтальную плоскость в уменьшенном виде, то получим изображение рельефа местности горизонталями на плоскости.
Таким образом кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.
При решении ряда инженерных задач необходимо знать свойства горизонталей:
1. Все точки местности, лежащие на горизонтали, имеют равные отметки.
2. Горизонтали не могут пересекаться на плане, поскольку они лежат на разных высотах. Исключения возможны в горных районах, когда горизонталями изображают нависший утес.

3. Горизонтали являются непрерывными линиями. Горизонтали, прерванные у рамки плана, замыкаются за пределами плана.
4. Разность высот смежных горизонталей называется высотой сечения рельефа и обозначается буквой h.
Высота сечения рельефа в пределах плана или карты строго постоянна. Её выбор зависит от характера рельефа, масштаба и назначения карты или плана. Для определения высоты сечения рельефа иногда пользуются формулой
где М – знаменатель масштаба.
Такая высота сечения рельефа называется нормальной.
5. Расстояние между соседними горизонталями на плане или карте называется заложением ската или склона. Заложение есть любое расстояние между соседними горизонталями (см. рис. 30), оно характеризует крутизну ската местности и обозначается d.
2.5. Основные формы рельефа и его числовые характеристики. (+2.4)
Основные формы рельефа:
Гора – куполообразная (коническая) возвышенность.
Котловина – чашеобразное понижение.
Хребет – возвышенность вытянутая в одном направлении.
Лощина (лог) – вытянутое понижение.
Седловина – понижение между двумя возвышенностями на хребте.
Уступ (терраса) – горизонтальная площадка на склоне горы или хребта.
2.6. Измерение площадей на планах и картах
Определение площади аналитическим, графическим (геометрическим) и механическим способами. При аналитическом способе площадь любого многоугольника, заданного координатами вершин вычисляется по следующим формулам: Р = 1/2 SХi (Уi+1 — Уi-1),
где i — порядковый номер вершин многоугольника, изменяющийся от 1 до N (числа вершин).
Относительная погрешность вычисления площади зависит в основном от погрешностей координат точек и составляет около 1/2000.
Графический способ определения площади предусматривает разбивку контура на элементарные геометрические фигуры (треугольники, четырехугольники и трапеции), площади которых вычисляют по измеренным на карте с учетом масштаба длинам сторон и высот. Относительная погрешность суммарной площади, полученной графически, обычно составляет более 0.5-1.0% (1/100).
Механический способ основан на применении специального прибора -полярного планиметра, который состоит из полюсного и обводного рычагов и счетного механизма. Перед измерением площади контура вычисляют цену деления планиметра с — площадь, соответствующую одному делению планиметра. Для этого на карте обводят планиметром один квадрат километровой сетки с известной площадью Ризв.= 100 га. Отсчеты по счетному механизму берут до обводки n1 и после обводки n2, вычисляют их разность DU, которую уточняют несколько раз.
Например, n1 = 3546, n2 = 4547. Тогда цена деления планиметра с = Ризв./DU = 100/1001=0.09990 га.
Площадь заданного контура сначала получают в результате обводки в делениях планиметра МU, а затем, используя цену деления с, — в гектарах Р = с . DU. Контроль полученных результатов выполнятся повторными измерениями и вычислениями цены деления планиметра и определяемой площади. Относительная погрешность измерений площади планиметром составляет порядка 1/300.
Графический – при графическом способе площадь разбивают на треугольники: S=∑(a1h1/2+a2h2/2+a3h3/2) .
Аналитический (по координатам вершин тр-ка) – вычисление площади аналитическим способом, по координатным вершин угло многоугольника, обеспечивает более высокую точность (до 1/1000 измеряемой величины). Расчётная формула: S1-2-3=Sa-1-2-b+Sb-2-3-c-Sa-1-3-c=(x1+x2)*(y2-y1)/2+(x2+x2)*(y3-y2)/2-(x1+x3)*(y3-y1)/2; S=1/2∑xi(yi+1-yi-1); S=1/2∑yi(xi-1-xi+1); где i = 1, 2, 3… — номер вершин полигона (рис.).
При помощи палеток – для измерения площадей небольших участков с криволинейными контурами (квадратные и прямоугольные). Квадратная палетка применяется для малых участков, имеющих площадь на плане до 2см2, подсчитывают число полных клеток, доли неполных клеток учитывают на глаз (точность измерения примерно 1/50). Параллельную палетку применяют для участков, площадь которых на плане до 10см2, палетку на измеряемый контур накладывают так, чтобы точки 1 и 2 расположились между параллельными линиями, тогда отрезки 3-4, 5-6 и т. д. можно считать полусуммой оснований соответствующих трапеций, найдя суммарную длину этих отрезков и умножив её на высоту трапеции, получим площадь контура.
Механический — при механическом способе применяют планиметры различных конструкций, чаще всего — полярный планиметр. Он состоит из трех основных частей: двух рычагов – полюсного и обводного и каретки со счетным механизмом.
При механическом способе применяют планиметры различных конструкций, чаще всего — полярный планиметр. Он состоит из трех основных частей: двух рычагов – полюсного и обводного и каретки со счетным механизмом. Полюсный рычаг на одном конце имеет грузик с иглой. Иглу перед обводкой контура вкалывают в бумагу. Она является осью вращения планиметра и поэтому называется полюсом.
На другом конце полюсного рычага жестко прикреплен стержень с шариком на конце.
При помощи этого стержня и гнезда в каретке счетного механизма полюсный и обводной рычаги шарнирно соединяются перед работой. На конце обводного рычага расположен обводной шпиль или обводное стекло с точкой. При измерении площади шпиль (точку) перемещают по контуру участка.
Перед измерением обводный шпиль устанавливают над какой-либо точкой контура площади и по счётному механизму делают начальный отсчёт u1, после обвода контура площади делают конечный отсчёт u2. Искомая площадь при полюсе вне контура вычисляется по формуле: П=c(u2-u1), при полюсе внутри контура – по формуле: П=c(u2-u1+q). Здесь c – цена одного деления планиметра, q – постоянная планиметра. Перед измерением определяют c и q по формулам: c=П/(u2-u1), q=П/c-(u2-u1). Величина c определяется несколькими обводами контура геометрической фигуры известной площади.
Если на плане имеются координатная или километровая сетка, обводят несколько раз контур одного квадрата и по среднему значению из разности отсчётов каждого обвода вычисляют c, а затем определяют q. Счетный механизм состоит из счетчика оборотов (циферблата), счетного колеса и верньера. Отсчет по счетному механизму составляется из четырех цифр: с циферблата берется число полных оборотов счетного колеса; по нулевому индексу верньера берутся вторая и третья цифры на счетном колесе (фиксирующие десятые и сотые доли его оборота); четвертая цифра (показывающая тысячные доли оборота счетного колеса) определяется по номеру совпадающего штриха верньера с каким-либо штрихом счетного колеса.
Планиметр должен удовлетворять следующим требованиям, выполнение которых перед работой следует проверять: счётное колесо должно вращаться легко и свободно; плоскость счетного колеса должна быть перпендикулярна к оси обводного рычага.
2.7. Номенклатура карт и планов.

Под картой понимается построенное в картографической проекции, уменьшенное, обобщенное изображение на плоскости поверхности Земли или отдельного ее участка, показывающее расположенные на них объекты в определенной системе условных знаков.
Под топографическим планом понимают изображение на плоскости в ортогональной проекции в крупном масштабе ограниченного участка местности, в пределах которого кривизна уровенной поверхности не учитывается.
Разграфкой называется деление листов одного масштаба на листы более крупного масштаба, номенклатурой – система обозначений отдельных листов карт (трапеций). Границами (рамками) топографических карт являются географические меридианы и параллели.
Номенклатурой называют систему обозначения (нумерации) отдельных листов топографических карт. В основу номенклатуры топографических карт различных масштабов положены листы карты масштаба 1:1000000, являющейся международной картой.
Для получения листов этой карты вся земная поверхность делится параллелями на пояса (ряды) через четыре градуса и меридианами – на колонны через шесть градусов. В пересечении поясов и колонн образуется трапеции в 4° по широте и 6° по долготе, каждая из которых изображается на отдельном листе бумаги. Пояса обозначаются заглавными буквами латинского алфавита, начиная от экватора к северу и югу, а колонны нумеруются арабскими цифрами от 1 до 60, начиная от меридиана с долготой 180° в направлении с запада на восток. Номенклатура листа карты масштаба 1:1000000 слагается из букв пояса и числа – номера колонны.
Колонны совпадают с шестиградусными зонами. Но так как колонны начинают считать от меридиана с долготой 180°, их номера отличаются от номера зон на 30.
Переход к листам карты более крупных масштабов осуществляется делением листа карты масштаба 1:1000000.
Лист карты масштаба 1:500000 получается делением каждого масштаба 1:1000000 на 4 части с обозначением каждой части заглавными буквами русского алфавита А, Б, В, Г, которые добавляются к номенклатуре листа карты масштаба 1:1000000.
Лист карты масштаба 1:200000 получается путем деления миллионного листа на 36 частей, которые обозначаются римскими цифрами I, II,…, XXXVI, добавляемыми к соответствующей номенклатуре исходного листа карты 1:1000000.
Лист карты масштаба 1:100000 получается путем деления миллионного листа на 144 части, которые обозначаются арабскими цифрами, добавляемыми к номенклатуре масштаба 1:1000000.
Лист карты масштаба 1:50000 получается путем деления листа карты масштаба 1:100000 на четыре части, обозначаемых одной из заглавных букв русского алфавита А, Б, В, Г, например N-37-49-А.
Лист карты масштаба 1:25000 получается путем деления листа карты масштаба 1:50000 на четыре части, каждая из которых обозначается одной из строчных букв а, б, в, г, которые ставятся после номенклатуры масштаба 1:50000, например, N-37-49-А-б.
Лист карты масштаба 1:10000 получается путем деления листа карты масштаба 1:25000 на четыре части, обозначаемые арабскими цифрами 1, 2, 3, 4, которые приписываются к номенклатуре карты 1:25000, например, N-37-49-А-б-2.
Лист карты масштаба 1:5000 получают путем деления листов карты масштаба 1:100000 на 256 частей. Номенклатура этих листов образуется прибавлением к номенклатуре листа 1:100000 номера в скобках соответствующего листа карты масштаба 1:5000, например N-37-49-(253).
Для разграфки листа карты масштаба 1:2000 лист карты масштаба 1:5000 делят на девять частей, обозначаемых строчными буквами русского алфавита от а до и, записываемыми в круглых скобках после цифры, обозначающей номер листа карты масштаба 1:5000, например, N-37-49-(253-д).
Элементы теории ошибок.
Линейные измерения
Расстояния измеряются и откладываются на местности специальными мерными приборами, к которым относятся стальные рулетки, а так же свето-радио-нитяные дальномеры.
Рулетки выпускаются длиной 10, 20, 30, 50, 100 м, шириной 10-12 мм и толщиной 0,15-0,30 мм. На полотно рулетки наносят штрихи через 1 мм и подписывают каждое дециметровое деление.
Длинномерные рулетки применяют в комплекте с приборами для натяжения.
До начала работ стальные мерные приборы компарируют, т. е. сравнивают с эталоном. При измерении линий вводится поправка в измеряемое расстояние, которая называется поправка закомпорирования:
Также вводится поправка за разность t при измерении и компорировании:
α – коэффициент линейного расширения
t – Температура при измерении
t0 – температура при компорировании
L – Длина измеряемой линии.
Наклонные расстояния на местности пересчитываются в их горизонтальные проложения введением поправки за превышение:
L – Расстояние на местности
d – Горизонтальное проложение.
Угловые измерения
Для измерения горизонтальных и вертикальных углов в геодезии используют специальный прибор, называемый – теодолитом.
Углы в теодолите проецируются на плоскости горизонтального и вертикального круга.
Вертикальным кругом или углом наклона называется угол составленный воображаемой плоскостью горизонта и направлением на объект.
Мерой горизонтального угла между направлениями в пространстве называется проекция этого угла в горизонтальную плоскость.
В строительстве в основном используют теодолиты средней точности Т-30.
Геодезические сети.
Топографические съемки.
Вынос пикета на кривую.
Чтобы уточнить положение кривой на местности, обычно выполняют разбивку кривой способом прямоугольных координат и обозначают пикетные и плюсовые точки. Для каждой точки определяют расстояние к от начала или конца кривой. Прямоугольные координаты вычисляют в соответствии с рис.46 по следующим формулам:
Рис.46.Вынос пикетов на кривую
где к — расстояние от начала или конца кривой до переносимого пикета.
Из рис.46 кпк10= 70.00 м, кпк11 =170.00 м, кпк12 = 44.16 м, тогда
Епк10 =(кпк10 . 180° ) /pR = (70.00м . 180° ) /3.1416 . 200м =20.053 .
Епк11 =(кпк11 . 180° ) /pR =(170.00м . 180° ) /3.1416 . 200м =48.701 .
Епк12 =(кпк12 . 180° ) /pR =(44.16м . 180° ) /3.1416 . 200м =12.651 .
Xпк10=R . sinЕпк10=200.00 . sin20.054 =68.58 м,
Yпк10 =2R . sin2(Епк10/2)=400.00 . sin 2(20.054/2)=12.13 м,
Xпк11=R . sinЕпк11=200.00 . sin 48.702 =150.26 м,
Yпк11=2R . sin2(Епк11/2)=400.00 . sin 2(48.702/2)=68.00 м,
Xпк12=R . sinЕпк12=200.00 . sin12.651 =43.80 м,
Yпк12=2R . sin2(Епк12/2)=400.00 . sin 2(12.651/2)=4.86 м.
На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.
Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.
Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.
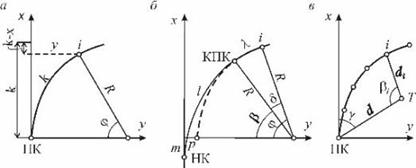
а) б) в)
Рис. 15.7 Детальная разбивка кривых:
а – способом ординат от касательной для круговой кривой;
б – то же, для переходной и следующей за ней круговой кривой;
Электронный тахеометр устанавливают в точке Т. Зная координаты точек Т, НК и i, вычисляют разбивочные элементы — углы bi и расстояния di. Построив тахеометром вычисленные углы и расстояния, находят и закрепляют положение точек кривой на местности.
Элементы разбивочных работ.
Элементами геодезических разбивочных работ принято считать проектные углы, отрезки, точки с проектными отметками, линии проектного уклона, которые необходимо построить для перенесения проекта планировки и застройки с плана на местность.
Для построения проектного угла bпр от линии АВ (рис.59а) на местности приводят теодолит над точкой А в рабочее положение, закрепляют лимб, наводят зрительную трубу на точку В и берут отсчет bкл при КЛ. Затем к этому отсчету прибавляют значение проектного угла, если угол откладывают по ходу часовой стрелки (если против хода часовой стрелки — значение проектного угла вычитают).
Вычисленный отсчет устанавливают на горизонтальном круге и на местности закрепляют точку Скл. Действия повторяют при КП и находят точку Скп. Полученный отрезок между точками делят пополам и получают точку С, которая соответствует значению проектного угла. Для контроля построенный угол измеряют способом приемов.
Рис.59.Схема построения проектного угла
с помощью теодолита (а) и рулетки (б)
Часто на строительных площадках выполняют построение прямых углов (рис.59б) с помощью рулетки, используя известные свойства «египетского» треугольника с отношением сторон 3:4:5. Для этого от вершины А прямого угла по линии АВ откладывают отрезок кратный 3, например 6 м, и получают точку В. От точек А и В линейными засечками со сторонами соответственно 8 и 10 м получают точку С.
Выверка колонн
Плановое, высотное и вертикальное положение монтируемых сборных конструкций контролируют геодезическим инструментом.
Выверка колонн. Точность установки в нижнем сечении контролируют совмещением установйчных рисок. Вертикальность колонны проверяет двумя теодолитами, установленными под прямым углом. Вначале зрительную трубу прибора наводят на риску в нижней части Колонны, затем ее переводят вверх, при этом риска верхнего сечения Колонны, совмещенная с крестом сетки зрительной трубы, показывает, что конструкция установлена вертикально.
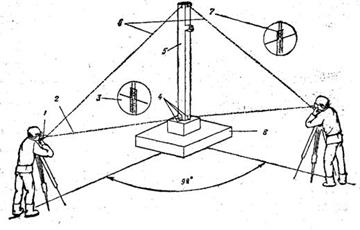
Вертикальность смонтированного ряда колонн проверяют теодолитом и, рейкой. Инструмент устанавливают у первой колонны ряда, отступая на м йнутрь пролета. Пятку нивелирной рейки совмещают с риской оси последней колонны ряда.
Выверка вертикальности колонны двумя теодолитами
1 — теодолит; 2 — визирный луч на нижнюю риску; 3 — нижняя риска в поле зрительной трубьд теодолита: 4 — установочные риски 5 —колояна; 6 визирный луч на верхнюю риску; 7 верхняя риска в поле зрительной трубы теодолита; 8 — фундамент
По вертикальной нити в поле зрительной трубы берут отсчет по нивелирной рейке, равной величине смещения инструмента.
Рейку поочередно переносят к каждой колонне ряда, выполняя замеры вверху и внизу. Отсчеты по рейке меньше проектных показывают на смещение колонн внутрь пролета, а отсчет больше проектных — на смещение в противоположную сторону.
Контроль высотного положения опорных поверхностей колонн ведут по маркировочным рискам. Еще до установки колонн от верха консолей или оголовка отмеряют целое число метров и наносят краской маркировочную риску (на расстоянии около 5 м от пяты). Нивелируя маркировочные риски, прибавляют к отсчетам измеренные ранее размеры, подсчитывают высотные отметки торцов колонн и верха консолей.

Контроль высотного положения консолей и оголовка колонны
1 — нивелир; 2 — визирные лучи нивелира; 3 — маркировочная риска; 4— нивелирная рейка; 5 — консоли; 6 — оголовок колонны
Нивелирование
1. Сущность и виды нивелирования.
2. Геометрическое нивелирование. Способы нивелирования.
3. Последовательное нивелирование.
4. Стандарт на нивелиры и их классификация.
5. Инструментальные погрешности нивелиров.
6. Поверка нивелиров.
7. Назначение, комплектность и общее устройство нивелиров.
8. Порядок работы на станции технического нивелирования.
9. Сущность тригонометрического нивелирования.
Угловые измерения
1. Принцип измерения углов.
2. Назначение, комплектность и общее устройство теодолита.
3. Зрительная труба теодолита и ее параметры.
4. Уровень и его основные параметры.
5. Стандарт на теодолиты, их классификация.
6. Инструментальные погрешности теодолитов.
7. Поверка теодолита.
8. Измерение горизонтального угла способом приемов.
9. Измерение вертикального утла.
1.Меры и единицы длины принятые в геодезии.
2. Рабочие меры длины и их компарирование.
3. Порядок измерения длины линии стольной лентой или рулеткой.
4. Вычисление горизонтального проложения длииы линии.
5. Сущность оптического дальномера. Нитяный дальномер. Дальномер двойного изображения.
6. Понятие об измерении длин линий при помощи светодальномеров.
7. Измерение недоступных расстояний.
Общая часть.
Инженерная геодезия и ее задачи.
Геодезия — наука, изучающая форму и размеры Земли, геодезические приборы, способы измерений и изображений земной поверхности на планах, картах, профилях и цифровых моделях местности. В современной геодезии находят применение новейшие измерительные средства, используют последние достижения в физике, механике, электронике, оптике, вычислительной технике. По разнообразию решаемых народнохозяйственных задач геодезия подразделяется на ряд самостоятельных дисциплин, каждая из которых имеет свой предмет изучения:
— высшая геодезия (гравимметрия, космическая геодезия, астрономическая геодезия) изучает форму и размеры Земли, занимается высокоточными измерениями с целью определения координат отдельных точек земной поверхности в единой государственной системе координат;
Источник: lektsia.com