Существует общее математическое соотношение, найденное в природе, которое может быть использовано в дизайне для создания приятных, натурально-выглядящих композиций. Его называют Золотым Сечением или греческой буквой “фи”. Если вы иллюстратор, арт директор или графический дизайнер, вам определенно стоит использовать Золотое Сечение в каждом проекте.
В этой статье мы объясним, как его использовать, а также поделимся несколькими отличными инструментами для дальнейшего вдохновения и изучения.
Тесно связанная с Последовательностью Фибоначи (Fibonacci Sequence), которую вы, возможно, помните из уроков математики или романа Дэна Брауна “Код Да Винчи”, Золотое Сечение описывает идеально симметричное взаимоотношение между двумя пропорциями.
Приблизительно равное соотношению 1 : 1.61, Золотое Сечение может быть иллюститровано как Золотой Прямоугольник: большой прямоугольник, включающий квадрат (в котором стороны равны длине самой короткой стороны прямоугольника) и прямоугольник поменьше.
Золотое Сечение наглядно простой метод

Если убрать квадрат из прямоугольника, останется другой, маленький Золотой Прямоугольник. Этот процесс может продолжаться до бесконечности, как и цифры Фибоначи, которые работают в обратном порядке. (Добавление квадрата со сторонами, равными длине самой длинной стороны прямоугольника, приближает вас к Золотому Прямоугольнику и Золотому Сечению.)


Золотое Сечение в действии
Считается, что Золотое Сечение используется уже около 4000 лет в искусстве и дизайне. Однако, многие люди соглашаются, что при строительстве Египетских Пирамид также использовался этот принцип.
В более современные времена это правило может быть замечено в музыке, искусстве и дизайне вокруг нас. Применяя аналогичную рабочую методологию, вы можете привнести в свою работу те же особенности дизайна. Давайте взглянем на несколько вдохновляющих примеров.
Греческая архитектура

В древнегреческой архитектуре Золотое Сечение использовалось для определения приятных пространственных отношений между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих структуру.
В результате получается идеально пропорциональное строение. Движение неоклассической архитектуры также использовало эти принципы.
Тайная вечеря

Леонардо Да Винчи, как и многие другие художники прошлых лет, часто использовал Золотое Сечение для создания приятных композиций.
В Тайной вечере фигуры расположены в нижних двух третях (самая большая из двух частей Золотого Сечения), а Иисус идеально зарисован между золотых прямоугольников.
Золотое сечение в природе
Существует множество примеров Золотого Сечения в природе – их вы можете обнаружить вокруг себя. Цветы, морские раковины, ананасы и даже пчелиные соты демонстрируют одинаковое соотношение.
Как рассчитать Золотое Сечение
Рассчет Золотого Сечения достаточно прост, и начинается с простого квадрата:
01. Нарисуйте квадрат

Он образует длину короткой стороны прямоугольника.
02. Разделите квадрат

Разделите квадрат пополам с помощью вертикальной линии, образуя два прямоугольника.
03. Проведите диагональ

В одном из прямоугольников проведиде линию из одного угла в противоположный.
04. Поверните

Поверните эту линию так, чтобы она легла горизонтально по отношению к первому прямоугольнику.
05. Создайте новый прямоугольник

Создайте прямоугольник, используя новую горизонтальную линию и первый прямоугольник.
Как использовать Золотое Сечение
Использовать этот принцип проще, чем вы думаете. Существует пара быстрых трюков, которые вы можете использовать в своих макетах, или потратить немного больше времени и полностью раскрыть концепт.
Быстрый способ
Если вы когда-нибудь сталкивались с “Правилом третей”, то вам будет знакома идея разделения пространства на равные трети по вертикали и горизонтали, при этом места пересечения линий создают естественные точки для объектов.
Фотограф размещает ключевой объект на одной из этих пересекающихся линий, чтобы создать приятную композицию. Этот прицип может также использоваться в вашей разметке страниц и дизайне постеров.
Правило третей можно применять к любой форме, но если вы примените его к прямоугольнику с пропорциями примерно 1 : 1.6, вы окажетесь очень близко к золотому прямоугольнику, что сделает композицию более приятной для глаз.
Полная реализация
Если вы хотите реализовать Золотое Сечение в вашем дизайне в полной мере, то просто расположите основной контент и сайдбар (в веб дизайне) в соотношении равном 1 : 1.61.
Можно округлить значения в меньшую или большую стороны: если контент-зона равна 640px, а сайдбар 400px, то эта разметка вполне подойдет под Золотое Сечение.

Разумеется, вы также можете разделить области контента и боковой панели на одно и то же отношение, а связь между заголовком веб-страницы, областью содержимого, футером и навигацией также может быть спроектирована с использованием того же приципа.
Полезные инструменты
Вот несколько инструментов, которые помогут вам в использовании Золотого Сечения в дизайне и создании пропорциональных проектов.

GoldenRATIO – это приложение для создания дизайна веб сайтов, интерфейсов и шаблонов, подходящих под Золотое Сечение. Доступно в Mac App Store за 2,99$. Включает визуальный калькулятор Золотого Сечения.
Так же в приложении есть функция “Избранное”, которое сохраняет настройки для повторяющихся задач и “Click-thru” мод, позволяющий сворачивать приложение в Photoshop.
Этот калькулятор Золотого Сечения от Pearsonified помогает в создании идеальной типографики для вашего сайта. Введите размер шрифта, ширину контейнера в поле, и нажмите кнопку Set my type! Если вам нужно оптимизировать количество букв в строчке, вы можете дополнительно ввести значение CPL.

Это простое, полезное и бесплатное приложение доступно для Mac и PC. Введите любое число, и приложение вычислит вторую цифру в соответствии с приципом Золотого Сечения.

Это приложение позволяет проектировать с золотыми пропорциями, экономя кучу времени на вычислениях.
Вы можете менять формы и размеры, фокусируясь на работе над своим проектом. Постоянная лицензия стоит 49$, но вы можете скачать бесплатную версию на месяц.
Обучение Золтому Сечению
Вот несколько полезных туториалов по Золотому Сечению (английский язык):
В этом туториале для Digital Arts Роберто Маррас (Roberto Marras) показывает, как использовать Золотое Сечение в художественной работе.
Туториал от Tuts+, рассказывающий, как использовать золотые принципы в веб дизайн проектах.
Туториал от Smashing Magazine, рассказывающий о пропорциях и правиле третей.
Источник: wordyblend.com
Калькулятор золотого сечения
Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.
История
Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618.
В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.
Число Фи в математике
Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.
В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]
Число Фи в реальности
Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.
После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.
Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.
Калькулятор золотого сечения
Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.
Пример из реальной жизни
Живопись
Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.
Заключение
Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.
Источник: bbf.ru
Просто о саженях и золотой пропорции
Приветствую, Человек!
Великий Google привёл вас на эту страницу, а значит вас интересуют серьёзные темы. В этой статье я покажу, как рождается число Φ, где прячется золотая пропорция и как она применима. А также научу умножать и делить на два. Весь материал является размышлениями на заданную тему — на абсолютную истину не претендует.
Призываю вместе проверить всё написанное, математика и геометрия дадут нам ключ. Все желающие приглашаются к обсуждению по электронной почте.
Наверняка вы уже имеете какое-то представление о Золотом сечении, здесь я не буду подробно останавливаться на историческом и культурном аспектах — в Интернете полно информации об этом. Здесь я хочу изучить этот феномен с помощью точной науки — математики.
§1. Начало. Ряд Фибоначчи
Запишем ряд чисел, начиная с единицы, в котором каждое следующее число является суммой двух предыдущих. Найдём соотношение (пропорцию) каждой пары соседних чисел друг другу, поделив следующее на предыдущее.
- 1 + 1 = 2;
- 1 + 2 = 3;
- 2 + 3 = 5;
- 3 + 5 = 8;
- 5 + 8 = 13;
- 8 + 13 = 21;
- 13 + 21 = 34;
- 21 + 34 = 55;
- 34 + 55 = 89;
- 55 + 89 = 144.
- 1 : 1 = 1;
- 2 : 1 = 2;
- 3 : 2 = 1,5;
- 5 : 3 = 1,667;
- 8 : 5 = 1,619;
- 13 : 8 = 1,618;
- 21 : 12 = 1,618;
- 34 : 21 = 1,618;
- 55 : 34 = 1,618;
- 89 : 55 = 1,618.
1 1 2 3 5 8 13 21 34 55 89
На шестой паре чисел появляется постоянное соотношение 1,618, которое остаётся неизменным до бесконечности, что само по себе уже интересно. Ряд может начинаться с любой пары чисел и соотношение всегда выравнивается до 1,618.
§2. Число Фи
Φ — бесконечное иррациональное число. Но для наших примеров нам такая точность не нужна, достаточно 1,618.
Число Φ вычисляется по формуле (1 + √5) : 2
§3. Золотое сечение
Золотое сечение определяют как отношение меньшего отрезка к большему отрезку как отношение большего к их сумме:
Термин «Золотое сечение» я считаю не совсем корректным, не отражающим процесс. По-английски golden ratio дословно: золотое соотношение. Более уместен термин «Золотая пропорция».
§4. Метрическая система
Так гласит официальное определение метра, принятое XVII Генеральной конференцией по мерам и весам в 1983 году. Метр был введён в СССР 14 сентября 1918 указом СНК РСФСР «О введении международной метрической десятичной системы мер и весов».
Расстояние, пройденное светом за одну трехсотмиллионную долю секунды. Вам это ясно? Как это применять в обычной жизни? Как проектировали и строили сооружения в более ранние века? Неужели мужик, строя дом, будет руководствоваться иррациональными числами и вычислять квадратные корни?
Конечно же нет. Очевидно, что существовала другая система мер, и её отголоски сохранились в Королевской системе мер, а также в русских саженях. Нужен простой и понятный инструмент пропорционирования и соизмерения.
§5. Пропорции квадрата
Мы знаем, что у квадрата все стороны равны. А это значит, что квадрат можно нарисовать или построить, имея в руках лишь одну меру любой длины: карандаш, палку и т.д. Примем его сторону за единицу.
Диагональ квадрата — редко используемая величина, но и она весьма полезна и интересна (рис. 1).
По теореме Пифагора длина диагонали квадрата (она же гипотенуза треугольника) равна корню из суммы квадратов катетов:
Пропорцию 1 : √2 также называют серебряным сечением. Самый известный пример этой пропорции — лист формата А4. Эта пропорция обладает интересным свойством, что сохраняется неизменной при удвоении какой-либо из сторон.
Что собой представляет корень из пяти √5 в формуле Φ = (1 + √5) ÷ 2? Это всего навсего диагональ двух квадратов (рис. 2)! Проверим по теореме Пифагора:
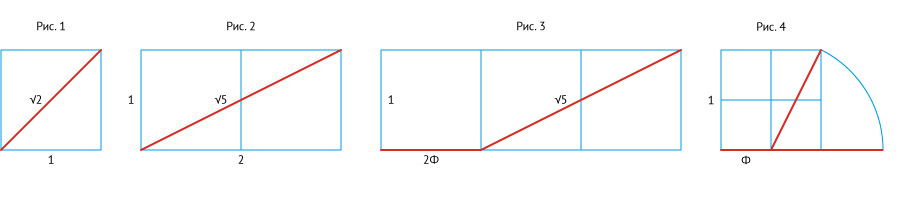
Суммируем величину стороны квадрата (1) и диагональ двух квадратов (2,236). Поделим пополам и получим число Φ. Получается, что длина стороны квадрата и длина диагонали двух квадратов в сумме равны удвоенному числу Φ (рис. 3)!
Φ = 3,236 : 2 = 1,618
Удвоенный квадрат по своей сути также является половиной квадрата большего размера. А значит √5 — это также диагональ половины квадрата, а число Φ можно получить, опустив диагональ половины квадрата на продолжение его стороны (рис. 4).
Квадрат хранит число Φ
Нам не нужно знать иррациональные числа, математика лишь подтверждает расчёты, но не является их основой! Квадрат хранит в себе все нужные нам пропорции. Он инструмент пропорционирования! Умножая эти пропорции квадрата на целый коэффициент, мы можем получить пропорциональные величины любой нужной длины.
Построение прямоугольника в пропорции Золотого сечения
§6. Интересные превращения числа Φ
Теперь стало понятно, где прячется число Φ, я покажу, как оно меняется с точки зрения математики — здесь очень много волшебных превращений! Все они пригодятся нам в дальнейшней работе с саженями.
1). Если от Φ отнять единицу, получится тоже самое, если единицу поделить на Φ:
Φ − 1 = 1 ÷ Φ = 0,618
2). Если из двух Φ вычесть диагональ двух квадратов, получим единицу (рис. 2, 4):
3). Помним, число Φ равно половине суммы стороны квадрата и диагонали двух квадратов:
Φ = (1 + √5) ÷ 2 = 1,618
4). Если Φ умножить на диагональ двух квадратов минус единица, будет 2:
5). Если к Φ прибавить единицу, получится тоже самое, если Φ умножить само на себя:
Φ + 1 = Φ 2 = 2,618
6). Если к Φ прибавить двойку, получится тоже самое, если Φ умножить на диагональ двух квадратов:
Φ+2 = Φ 2 +1 = Φ·√5 = 3,618
7). Если двойку поделить на Φ получится тоже самое, если из 2Φ вычесть два:
2 ÷ Φ = 2Φ − 2 = 1,236
8). Если из 2Φ вычесть единицу, получим диагональ половины квадрата (рис. 2, 4):
9). Если удвоить любым способом Φ, получим 1 + √5 или 2Φ (рис. 3):
10). Если возвести Φ в куб, получим 2 + √5, а это две стороны квадрата + диагональ двух квадратов:
Φ 3 = 2 + √5 = 4,236
Трудно не заметить, две группы чисел с одинаковыми знаками после запятой, и это не спроста!
§7. Система пропорций
Возвращаясь к Золотой пропорции. Суть вовсе не в том, что какой-то отрезок делит какой-то другой. Недостаточно нарисовать спираль улитки поверх фото, чтобы понять, что это означает и как этим пользоваться. Для работы на плоскости нужно два отрезка, а для построения объёма нужны три!
Появляется система пропорций 1 : 2÷Φ : Φ, которую уже можно использовать как коэффициенты при соизмерении. Рабочая система состоит из трех отрезков и выглядит так:
§8. Образ, подобие, мера и каравай
С математекой, должно быть ясно. Вспомним, что мы, человеки, созданы по образу и подобию Бога, или нашего Создателя, или Вселенной, или Природы, или чего-либо ещё. Оставим религиозные смыслы и обратимся к геометрии. Подобными в ней назвают фигуры одинаковых геометрических пропорций и свойств. Квадраты, круги и равносторонние треугольники всегда подобны таким же фигурам.
А раз мы уже нашли золотую пропорцию в числах Фибоначии и в квадрате, давайте искать её в самих себе!
Тело человека уже хранит в себе образ и подобие — Золотую пропорцию!
Вспоминим русскую народную песенку про каравай:

Как на наши именины испекли мы каравай,
Вот такой вышины (поднимаем руки вверх)
Вот такой нижины (опускаем руки вниз)
Вот такой ширины (раскидываем руки вширь)
Вот такой ужины (сводим руки вместе)
Каравай, каравай, кого любишь выбирай!
Я люблю, конечно, всех, но вот (этих) — больше всех.
Какие движения при этом делают дети? Водят хоровод и показывают руками вышину, нижину, ширину и ужину! Проделайте сами те же движения и вы сразу поймёте, какими мерами показывают высоту, ширину и длину. Эта песенка и есть ключ!
Ключ к системе измерений саженями хранится в русской народной культуре! В простой детской песенке, которую знают все с малых лет. Мерить всё по себе — это правильно, логично и само собой разумеется! Однако, теперь это признак эгоизма — выбросим этот нонсенс из своей головы.
§9. Золотая пропорция тела человека
Рука вверх — это мера высоты (великая сажень),
Размах рук в стороны — это мера ширины (маховая сажень),
Рука вперёд — это мера длины (полсажени длины).
Эти меры являются вашими личными мерами!
Все три меры образуют единую систему соизмерений на основе пропорции 2÷Φ к 1. Разные измерения (длина, ширина, высота) должны мериться своей соответствующей мерой, то есть саженью. И тогда мы можем забыть об иррациональных числах, корнях и прочем, используя вместо них целые количества своих саженей.
§10. Казённая сажень отдельно
Важно отметить, что вопреки официально утверждённой казённой сажени, существовали и другие. И лишь она одна была приравнена к 7 английским футам и позже к 213 см в Российской империи и по другим источникам 218 см в СССР. На то она и являлась казённой. В корне неверно считать, что сажень была одна, как метр. Чтобы понять гармонию, не думайте о метре — это изобретение XIX века, а Вселенная со своими пропорциями вечна. 🙂
§11. Погрешность измерений
Я намеренно буду округлять сотые и тысячные доли чисел и подтягивать расчёты под единый вид, так как они заведомо не абсолютно точны. Иррациональные числа не делятся до конца, поэтому не везде удастся получить красивые целые числа. А мы должны увидеть картину в целом, понять всю единую систему, где тысячные доли лишь детали.
Сантиметр — это сотая доля метра, достаточно точно, поэтому предлагаю не использовать миллиметры в своих расчётах, чтобы они не создавали лишний шум. К тому же, тело гибкое и руки можно растянуть ещё шире или поднять ещё выше. Этого делать не нужно, положение должно быть комфортным.
§12. Измерим себя и проверим
Пора проверить всё на себе и удивиться, что всё так и есть. Я мужчина среднего роста, мой размах рук примерно 188 см. Высота поднятой руки примерно 232,5 см. Вытянутая рука вперёд (плюс столько же назад) примерно 152 см. Сначала я измерил всё рулеткой, а потом посчитал на калькуляторе.
Меня поразило с какой точностью совпали все цифры.
- 188 / 152 = 1,236
- 152 / 188 = 0,809
- 232,5 / 188 = 1,236
- 188 / 232,5 = 0,809
- 232,5 / 152 = 1,529
- 152 / 232,5 = 0,655
Здесь мы видим четыре любопытных числа. Где же здесь число 1,618? Да вот же оно:
Опишем это словами, чтобы появилось понимание, что всё это значит. Поделив сажень высоты на сажень ширины мы получим пропорцию 1 к 2 ÷ Φ, точно также как поделив сажень ширины на сажень длины. Если поменять местами величины, получится пропорция 1 к Φ ÷ 2. Пропорции остаются одинаковы. А значит мы можем подставлять сюда любые величины и любые значения в сантиметрах!
Источник: www.artdesigner.ru