1. Рассматриваются интервалы времени и , определяется величина .
2. Если эта величина находится в столбце , то -ю деталь помещаем на первый станок в первую очередь. Если эта величина находится в столбце , то -я деталь занимает последнее место на первом станке.
3. Вычеркиваем выбранную деталь, и продолжаем процедуру поиска, повторяя шаги 1 и 2. В случае одинаковых значений выбираем любую деталь. Полученная последовательность обработки деталей будет оптимальной.
Пример. Пусть время обработки пяти деталей на двух машинах задана в таблице:
| i | ai | bi |
Построим диаграмму Ганта обработки деталей в начальный момент времени (рис. 6.2).
Рисунок 6.2 – Начальное расписание
По графику видно, что начальный порядок обработки деталей допускает простои второго станка (суммарное время простоев 8 единиц), длина производственного цикла равна 30 единицам времени.
По алгоритму Джонсона определим величину . В нашем примере эта величина равна . Таким образом, деталь 2 на первом станке обрабатывается последней.
Алгоритм Джонсона. Календарное планирование.
| i | ai | bi | i¢ |
| 2 |
Продолжаем процедуру поиска. Среди не вычеркнутых элементов ищем . После выбора второй детали минимальное время равно 3, и оно соответствует и . Мы можем выбрать любую деталь, поэтому произвольно выбираем , т. е. помещаем на первое место деталь 1. Теперь минимальное время соответствует . Следовательно, деталь 4 ставится на предпоследнее место.
| i | ai | bi | i¢ |
| 1 | |||
| 2 | |||
| 4 |
Следующая минимальная величина равна 4 ( и ). Можем назначить 2-е место на первом станке для детали 3 и 3-е место для детали 5.
| i | ai | bi | i¢ |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Полученная последовательность обработки деталей на двух станка =(1, 3, 5, 4, 2) будет оптимальной.
Эта последовательность представлена диаграммой Ганта на рис.6.3.
Рисунок 6.3 – Оптимальное расписание
Из рис. 6. 3 видно, что время обработки всех деталей равно 28 единиц и суммарное время простоев — 6 единиц.
Замечание. Алгоритм Джонсона применим для последовательности деталей, проходящих последовательную обработку на 3-х станках, в двух нижеследующих случаях:
Тогда осуществляется поиск оптимальных строк по суммам
Пример. Пусть операции над деталями задаются сроками выполнения :
| i | ai | bi | ci |
Условие , например, выполняется. Таким образом, мы имеем:
| i | ai | bi | ci | ai+ bi | bi+ ci |
Алгоритм Джонсона || Johnson’s algorithm
и алгоритм Джонсона позволяет выбрать =(4, 2, 3, 1, 5).
Задания для самостоятельной работы
Найти решение задачи Джонсона для двух последовательных приборов. Длительности обслуживания приборами А и В приведены в таблице.
| вариант | Требование время |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB | |
| tA | |
| tB |
ЗАДАЧА О НАЗНАЧЕНИЯХ
Почему человек чувствует себя несчастным?: Для начала определим, что такое несчастье. Несчастьем мы будем считать психологическое состояние.
Как распознать напряжение: Говоря о мышечном напряжении, мы в первую очередь имеем в виду мускулы, прикрепленные к костям .
Генезис конфликтологии как науки в древней Греции: Для уяснения предыстории конфликтологии существенное значение имеет обращение к античной.

Источник: megaobuchalka.ru
Методика формирования и расчета на основе изменения очередности строительства комплекса объектов.Оптимизация по Джонсону
За счет изменения очередности освоения частных фронтов работ можно добиться сокращения общей продолжительности.
Критерием оптимальности является минимальная продолжительность.
Для получения оптимального расписания работ используется известный в математике метод ветвей границ, при этом формируется дерево целей — порфириан.
Данный метод характеризуется развитием перспективных ветвей, т.е. в отличие от полного перебора (m!) получение оптимального варианта достигается быстрее.
Оптимизация по критерию минимальной продолжительности может осуществляться за счет изменения состава бригад, технологии строительного производства, очередности ввода объектов в эксплуатацию, за счет ввода дополнительных однотипных бригад (переход от индивидуально-поточной к параллельно-поточной организации работ).
В основе алгоритма оптимизации заложен модифицированный алгоритм Джонсона, который позволяет определить ту очередность строительства, которая дает нам минимальную продолжительность (т.е. достигается минимум продолжительности за счет изменения очередности освоения частных фронтов работ).
Для формирования матриц по Джонсону рассматриваем два смежных потока и располагаем предшествующие работы по возрастанию, а последующие работы — по убыванию.
Выбирается минимальное значение продолжительности предшествующей работы и заносится на первое место парной матрицы, а минимальное значение последующего вида работ ставится на последнее место.
Такое упорядочение должно привести к уменьшению периода развертывания, а само переформирование производится за счет парных матриц.
Цель формирования матриц по Джонсону — добиться уменьшения значений периодов развертывания. В худшем случае это значение равно периоду развертывания (Тр) исходной матрицы.
Первый шаг раcчета: закрепляем поочередно все строки исходной матрицы и определяем значение предельно-возможного минимума продолжительности (ПВМП), который используется для оценки перспективности развития ветвей порфириана. Значение ПВМП определяется как сумма периодов развертывания (Тр) (условных) и продолжительности последнего вида работ. Выбираем минимальное значение ПВМП по результатам первого шага и считаем, что данное направление перспективно (все остальные ветви отбрасываем).
Второй шаг расчета: закрепляются две строки исходной матрицы, причем на первом месте строка, выявленная на первом шаге работы как перспективная, а на втором поочередно все строки исходной матрицы (незафиксированные).
Третий шаг расчета: позволяет определить продолжительность и очередность, которая обеспечивает ее минимальное значение.
5. Календарные планы при реконструкции объектов.
НОФР – непрерывное освоение частных фронтов работ (для неритмичных потоков).
Транспонируем матрицу, т.е. переводим из системы ОФР в систему ОВР (ординаты — виды работ).
Источник: cyberpedia.su
Лекция 4. Задача Джонсона в теории расписаний
Сформулируем классическую задачу теории расписаний — задачу Джон-сона:
пусть — множество работ, которые выполняются на m машинах, каждая из которых имеет свой номер; пусть — время выполнения i-ой работы на j-ой машине; требуется так организовать выполнение работ, чтобы суммарное время простоя машин оказалось минимальным.
В этой постановке задачи предполагается, что
1) в любой момент времени на одной машине выполняется не более одной работы;
2) в любой момент времени одна работа выполняется не более, чем на
Рассмотрим простейший случай задачи Джонсона – случай двух машин в последовательном варианте; это означает, что все работы выполняются толь-ко на одних и тех же двух машинах, причем все выполняются сначала на пер-вой, а потом на второй машине.
Джонсону принадлежит алгоритм решения такой задачи, который мы сейчас сформулируем по шагам. Доказательство сходимости этого алгоритма (т.е. того, что действия по алгоритму приводят именно к нужной цели) не при-водится.
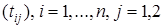
Шаг 0. Записывается матрица времен выполнения данных работ.
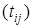
Шаг 1. В матрице фиксируется минимальный элемент (любой); если он оказался в первом столбце (машина №1), то соответствующую работу назначают первой к исполнению; если он оказался во втором столбце (машина №2), то соответствующую работу назначают последней к исполнению.
Шаг 2. Исключают из дальнейшего рассмотрения время выполнения упорядоченной работы (т.е. вычеркивают из матрицы строку). Если после этого от матрицы ничего не остается, то задача решена; в противном случае переходим к Шагу 1.
Напомним, что описанный алгоритм минимизирует суммарное время простоя обеих машин.
Имеется обобщение алгоритма Джонсона для последовательного случая на случай произвольный, но для двух машин. А именно:
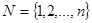
пусть по-прежнему — множество работ, которые выполня-
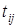
ются на двух машинах (№1 и №2), пусть по-прежнему — — время выполнения i-ой работы на j-ой машине, но:
N1 — подмножество работ, которые выполняются только на первой маши-не;
N2 — подмножество работ, которые выполняются только на второй маши-не;
N1,2 — подмножество работ, которые выполняются сначала на первой, а потом на второй машине;
N2,1 — подмножество работ, которые выполняются сначала на второй, а потом — на первой машине.
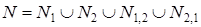
Таким образом, .
Можно доказать, что суммарный простой двух имеющихся машин будет минимальным, если организовать выполнение работ так:
1) в соответствии с алгоритмом Джонсона для последовательного
варианта задачи для двух машин упорядочим работы из множеств N1,2 и N2,1;
2) на первую машину запускаются сначала работы из N1,2, затем — из
3) на вторую машину запускаются сначала работы из N2,1, затем — из
Рассмотренный общий случай задачи Джонсона для двух машин часто называют смешанным вариантом задачи Джонсона.
Рассмотрим иллюстративный пример смешанного варианта задачи Джонсона для двух машин. Условие задается следующей таблицей:
| N | N1,2 | N2,1 | N1 | N2 | |||||||
| МР | р1 | р2 | р3 | р4 | р5 | р6 | р7 | р8 | р9 | р10 | р11 |
| М1 | |||||||||||
| М2 |
здесь рj — имя работы, Мi — имя машины.
По алгоритму Джонсона:
оптимальные режимы работ.
Записи (р8,р9) и (р10,р11) означают, что порядок выполнения
этих работ — произвольный.
Перейдем к случаю трех машин.
Ограничимся здесь далеко не общей ситуацией; итак,
m=3 — число машин;
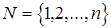
— множество работ;
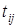
— время выполнения i-ой работы на j-ой машине;
предполагается, что у все работ одна и та же последователь-
ность прохождения по машинам.
В этой ситуации справедливы нижеследующие два утверждения, которые приводятся без доказательства.
Утверждение №1. Пусть работы можно пронумеровать так, что окажутся выполненными одновременно следующие неравенства:
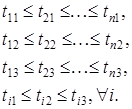
Тогда суммарный простой машин будет минимальным при следующем порядке запуска работ на исполнение: 1¾2¾. ¾n.
Утверждение №2. Пусть для матрицы выполнено хотя бы одно из двух следующих условий:
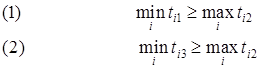
Построим новую матрицу , в которой i=1,2. n, j=1,2 и , и будем считать ее матрицей времен задачи Джонсона для двух машин в последовательном варианте и множества тех же работ . Тогда суммарное время простоя исходных трех ма-шин при выполнении исходных работ будет минимальным, если эти работы направлять на исполнение в том порядке, который является оптимальным в задаче с матрицей .
Источник: studopedia.ru