Что такое интерполирование в строительстве

Содержание

Задача 1. Определить продолжительность строительства завода строительных стальных конструкций мощностью 40 тыс.т конструкций в год.

Расчет. Согласно п.7 Общих положений принимается метод линейной интерполяции исходя из имеющихся в нормах мощностей 20 тыс.т и 60 тыс.т конструкций в год с нормами продолжительности строительства соответственно 18 и 23 мес.

Продолжительность строительства на единицу прироста мощности равна (23-18)/(60-20)=0,125 мес. Прирост мощности равен 40-20=20 тыс.т.

Задача 2. Определить продолжительность строительства завода строительных стальных конструкций мощностью 150 тыс.т конструкций в год.

Расчет. Согласно п.7 Общих положений принимается метод экстраполяции исходя из имеющейся в нормах максимальной мощности 90 тыс.т конструкций в год с продолжительностью строительства 30 мес.

Задача 3. Определить продолжительность строительства завода строительных стальных конструкций мощностью 15 тыс.т в год.

Расчет. Согласно п.7 Общих положений принимается метод экстраполяции исходя из имеющейся в нормах минимальной мощности 20 тыс.т конструкций в год с продолжительностью строительства 18 мес.

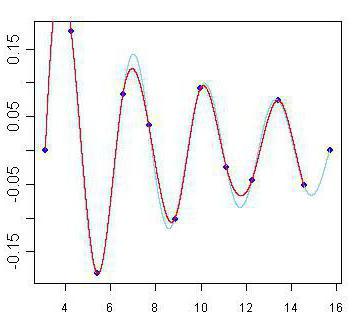
Определение отметок методом интерполяции

Приложение 2

РАСЧЕТ ЗАДЕЛА В СТРОИТЕЛЬСТВЕ

Показатель готовности объекта определяется отношением сметной стоимости строительства (стоимости строительно-монтажных работ), которая должна быть освоена по объекту от начала строительства до конца -го квартала (месяца), к полной сметной стоимости строительства объекта (сметной стоимости строительно-монтажных работ).

Показатель промежуточного ввода в действие основных фондов объекта (или очереди строительства) определяется отношением стоимости основных фондов по вводимым пусковым комплексам к полной сметной стоимости строительства объекта или его очереди (сметной стоимости строительно-монтажных работ).

Показатель задела по капитальным вложениям (строительно-монтажным работам) определяется разностью между показателями готовности строительства объекта и промежуточного ввода в действие основных фондов.

Щебеночный завод с карьером для месторождений карбонатных пород проектной мощностью 1500 тыс.куб.м щебня и 200 тыс.куб.м песка в год строится в средней полосе европейской части РСФСР, нормативная продолжительность строительства завода — 36 мес, сметная стоимость строительства — 21 млн.руб., в том числе строительно-монтажных работ — 14 млн.руб.

Распределение объемов капитальных вложений и строительно-монтажных работ по годам строительства завода в соответствии с показателями задела и в зависимости от сроков начала строительства приведено в табл.2.

Таблица 1

Продолжительность строи-тельства,

Интерполяция. Тема

Показатели задела
в строительстве по кварталам, % сметной стоимости

Источник: www.dokipedia.ru

Интерполяция — это. Определение, особенности расчета и примеры интерполяции

Многие из нас сталкивались с непонятными терминами в разных науках. Но находится очень мало людей, которых не пугают непонятные слова, а наоборот, приободряют и заставляют всё больше углубиться в изучаемый предмет. Сегодня речь пойдёт о такой вещи, как интерполяция. Это способ построения графиков по известным точкам, позволяющий с минимальным количеством информации о функции предсказать её поведение на конкретных участках кривой.

Перед тем как перейти к сути самого определения и рассказать о нём подробнее, немного углубимся в историю.

интерполяция это

История

Интерполяция была известна ещё с древнейших времён. Однако своим развитием это явление обязано нескольким самым выдающимся математикам прошлого: Ньютону, Лейбницу и Грегори. Именно они развили это понятие с помощью более продвинутых математических способов, доступных в то время. До этого интерполяцию, конечно, применяли и использовали в вычислениях, но делали это совершенно неточными способами, требующими большого количества данных для построения модели, более-менее близкой к реальности.

Сегодня мы можем даже выбирать, какой из способов интерполяции подходит больше. Всё переведено на компьютерный язык, который с огромной точностью может предсказывать поведение функции на определённом участке, ограниченном известными точками.

Интерполяция представляет собой достаточно узкое понятие, поэтому её история не так богата фактами. В следующем разделе разберёмся, что такое интерполяция на самом деле и чем она отличается от своей противоположности — экстраполяции.

Что такое интерполяция?

Как мы уже говорили, это общее название способов, позволяющих построить график по точкам. В школе в основном это делают с помощью составления таблицы, выявления точек на графике и примерного построения линий, их соединяющих. Последнее действие делается исходя из соображений похожести исследуемой функции на другие, вид графиков которых нам известен.

Однако есть другие, более сложные и точные способы выполнить поставленную задачу построения графика по точкам. Итак, интерполяция — это фактически «предсказание» поведения функции на конкретном участке, ограниченном известными точками.

Существует схожее понятие, связанное с этой же областью, — экстраполяция. Она представляет собой также предсказание графика функции, но за пределами известных точек графика. При таком способе предсказание делается на основе поведения функции на известном промежутке, и потом эта функция применяется и для неизвестного промежутка. Такой способ очень удобен для практического применения и активно используется, например, в экономике для прогнозирования взлётов и падения на рынке и для предсказания демографической ситуации в стране.

Но мы отошли от основной темы. В следующем разделе разберёмся, какая бывает интерполяция и с помощью каких формул можно произвести эту операцию.

линейная интерполяция

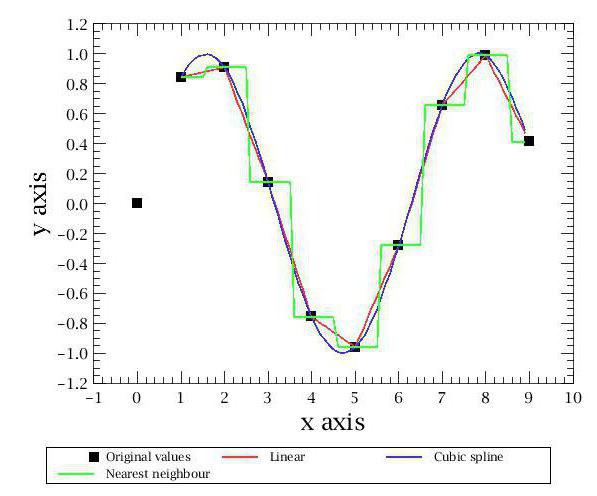
Виды интерполяции

Самым простым видом является интерполяция методом ближайшего соседа. С помощью этого способа мы получаем очень приблизительный график, состоящий из прямоугольников. Если вы видели хоть раз объяснение геометрического смысла интеграла на графике, то поймёте, о каком графическом виде идёт речь.

Кроме этого, существуют и другие методы интерполяции. Самые известные и популярные связаны с многочленами. Они более точны и позволяют предсказывать поведение функции при достаточно скудном наборе значений. Первым методом интерполяции, который мы рассмотрим, будет линейная интерполяция многочленами.

Это самый простой способ из данной категории, и им наверняка каждый из вас пользовался в школе. Суть его заключается в построении прямых между известными точками. Как известно, через две точки плоскости проходит единственная прямая, уравнение которой можно найти исходя из координат данных точек. Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.

двойная интерполяция

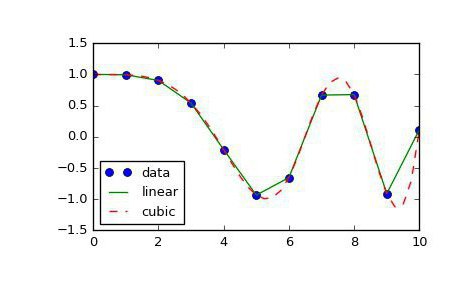
Усложнённые виды интерполяции

Есть более интересный, но при этом более сложный способ интерполяции. Его придумал французский математик Жозеф Луи Лагранж. Именно поэтому расчет интерполяции по этому методу назван его именем: интерполяция по методу Лагранжа.

Фокус тут вот в чём: если способ, изложенный в предыдущем абзаце, использует для расчета только линейную функцию, то разложение методом Лагранжа предполагает также использование многочленов более высоких степеней. Но не так просто найти сами формулы интерполяции для разных функций. И чем больше точек известно, тем точнее получается формула интерполяции. Но есть и масса других методов.

Существует и более совершенный и приближенный к реальности метод расчета. Формула интерполяции, используемая в нём, представляет собой совокупность многочленов, применение каждого из которых зависит от участка функции. Такой метод называется сплайн-функцией. Кроме того, есть ещё и способы, позволяющие провести такую вещь, как интерполяция функций двух переменных.

Тут всего два метода. Среди них билинейная или двойная интерполяция. Этот способ позволяет без труда построить график по точкам в трёхмерном пространстве. Другие методы затрагивать не будем.

Вообще, интерполяция — это универсальное называние для всех этих способов построения графиков, но многообразие способов, которыми можно осуществить это действие, заставляет делить их на группы в зависимости от вида функции, которая подлежит этому действию. То есть интерполяция, пример которой мы рассмотрели выше, относится к прямым способам. Есть также обратная интерполяция, которая отличается тем, что позволяет вычислить не прямую, а обратную функцию (то есть x от y). Рассматривать последние варианты мы не будем, так как это достаточно сложно и требует хорошей математической базы знаний.

Перейдём к, пожалуй, одному из важнейших разделов. Из него мы узнаем, как и где обсуждаемая нами совокупность методов применяется в жизни.

интерполяция функций

Применение

Математика, как известно, царица наук. Поэтому даже если вы сначала не видите смысла в тех или иных операциях, это не значит, что они бесполезны. Вот, например, кажется, что интерполяция — это бесполезная вещь, с помощью которой только графики строить можно, которые сейчас мало кому нужны.

Однако при любых расчётах в технике, физике и многих других науках (например, биологии), крайне важно представлять достаточно полную картину о явлении, имея при этом определённый набор значений. Сами значения, разбросанные по графику, не всегда дают чёткие представления о поведении функции на конкретном участке, значениях её производных и точек пересечения с осями. А это очень важно для многих областей нашей с вами жизни.

интерполяция пример

А как это пригодится в жизни?

На подобный вопрос бывает очень сложно ответить. Но ответ прост: никак. Именно эти знания вам никак не пригодятся. А вот если вы поймёте этот материал и методы, с помощью которых осуществляются эти действия, вы потренируете свою логику, которая в жизни очень пригодится. Главное — не сами знания, а те навыки, которые человек приобретает в процессе изучения.

Ведь недаром существует поговорка: «Век живи — век учись».

расчет интерполяции

Смежные понятия

Вы можете сами понять, насколько важна была (и до сих пор не теряет свою важность) эта область математики, взглянув на многообразие других концепций, связанных с данной. Мы уже говорили об экстраполяции, но есть ещё и аппроксимация. Может быть, вы уже слышали это слово. В любом случае то, что оно обозначает, мы тоже разбирали в этой статье.

Аппроксимация, как и интерполяция, — это понятия, связанные с построением графиков функций. Но отличие первой от второй в том, что она представляет собой приблизительное построение графика на основе сходных известных графиков. Эти два понятия очень похожи между собой, и тем интереснее изучать каждое из них.

формула интерполяции

Заключение

Математика — не такая сложная наука, как кажется на первый взгляд. Она, скорее, интересная. И в этой статье мы попытались вам это доказать. Мы рассмотрели понятия, связанные с построением графиков, узнали, что такое двойная интерполяция, и разобрали на примерах, где она применяется.

Источник: www.syl.ru

Применение метода интерполяции по коэффициенту формы для решения задач строительной механики

Фетисова, М. А. Применение метода интерполяции по коэффициенту формы для решения задач строительной механики / М. А. Фетисова, С. С. Володин. — Текст : непосредственный // Молодой ученый. — 2013. — № 3 (50). — С. 114-116. — URL: https://moluch.ru/archive/50/6296/ (дата обращения: 08.10.2022).

В статье предлагается способ применения метода интерполяции по коэффициенту формы для определения максимального прогиба пластинок с комбинированными граничными условиями. Для отыскания опорных решений применяются простейшие аффинные преобразования .

In article the way of application of a method of interpolation on factor of the form for definition of the maximum deflection of plates with the combined boundary conditions is offered. The elementary affine transformations are applied to search of basic figures.

Одним из основных научных направлений строительной механики по-прежнему остается разработка и развитие простых аналитических приближенных методов, которые позволяют путем сравнительно несложных инженерных расчётов получать оценки интегральных физических параметров конструкций. С помощью таких методов удаётся установить аналитическую связь параметров прочности, жесткости и устойчивости от отдельных геометрических характеристик конструкций и физико-механических свойств материала. Это способствует более правильному представлению о силовых схемах в исследуемых конструкциях. Одним из таких методов расчета плитных конструкций является метод интерполяции по коэффициенту формы (МИКФ) [2].

В основе МИКФ лежит изопериметрический метод, основоположниками которого являются Д. Пойа и и Г. Сеге [1], так как основным аргументом в получаемых аналитических зависимостях является отношение коэффициента формы [2;3] к площади области ( К f /А ). Отличие его заключается в том, что, если при использовании изопериметрического метода поведение интегральных параметров внутри множества решений между опорными не известно, то при использовании МИКФ получается аналитическая зависимость, позволяющая найти решение для любой фигуры из рассматриваемого множества.

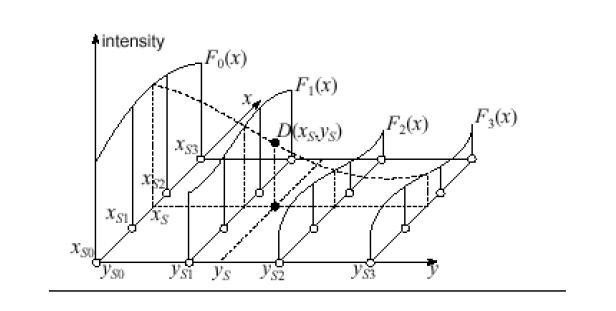
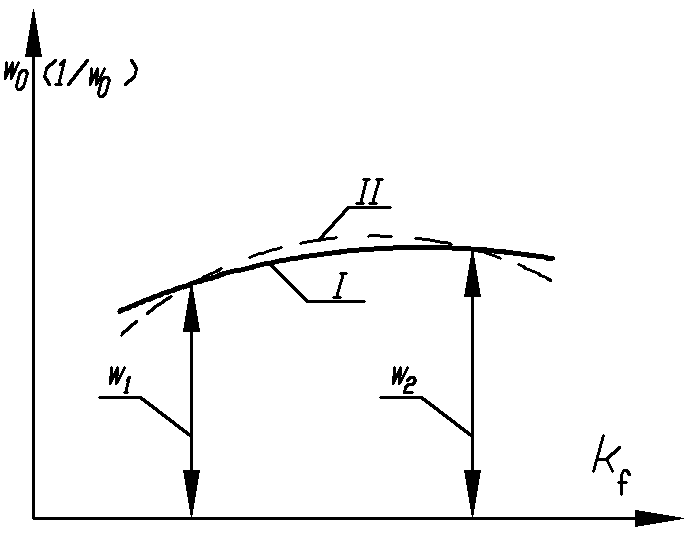
С учетом изопериметрических свойств и закономерностей коэффициента формы [3] для областей с выпуклым контуром график изменения w 0 (1/ w 0 ) — 1/ K f изображен на рисунке 1.

Пластинкам в виде правильных фигур соответствует кривая I, пластинкам в виде равнобедренных треугольников — кривая II, прямоугольным пластинкам — кривая III, эллиптическим пластинкам — кривая IV, пластинкам в виде ромба — кривая V.

Если рассмотрим некоторое конкретное геометрическое преобразование, например, прямоугольника в равносторонний треугольник, то изменение максимального прогиба опишется кривой 3–5, причем изменение этой кривой будет носить монотонной характер. При этом кривая 3–5 пересечет вертикальную прямую в некоторой точке а, которая будет являться графическим образом решения для трапеции с коэффициентом формы К f =9. Если эту кривую описать аналитической зависимостью, то она будет давать решения для всего рассматриваемого подмножества трапеций в зависимости от коэффициента формы.

Сущность метода интерполяции по коэффициенту формы заключается в следующем. Пусть необходимо записать решение для некоторого множества фигур, полученных путем какого-либо непрерывного (или дискретного) геометрического преобразования. При анализе фигур (форм пластинок) этого множества следует выделить среди них хотя бы две пластинки, решения для которых известны («опорные» решения). Желательно чтобы эти две пластинки при выбранном геометрическом преобразовании отстояли друг от друга на «небольшом расстоянии».

Известные решения (w o ) 1 и (w o ) 2 для этих пластинок могут быть представлены в виде зависимостей:

Предположим, что при выбранном преобразовании А 1 = А 2 (с изменением фигуры меняется и ее масштаб). Разделив второе выражение на первое, найдем значение параметра n для заданного геометрического преобразования.

Структура этих формул соответствует зависимости (1).

К такому виду можно привести все получаемые решения при любом геометрическом преобразовании, предварительно представив в безразмерном виде (приведя к единичной площади). Если вместо (w o ) 2 подставить значение w o для любой пластинки, относящейся к выбранному геометрическому преобразованию, то получим:

Легко заметить, что опорные решения в (3) удовлетворяются автоматически.

Графически рассмотренная аппроксимация изображена на рисунке 2, где кривая I соответствует действительным значениям wo, а кривая II — приближенным решениям, полученным по формуле (3).

Приведенные выше рассуждения основывались на непрерывных геометрических преобразованиях, когда изменение формы фигур рассматриваемого множества происходит непрерывно и монотонно, а также можно вполне успешно применять дискретные геометрические преобразования, когда переход от одной фигуры к другой осуществляется скачкообразно.

Пусть требуется найти максимальный прогиб для пластинки в виде равнобедренной трапеции, применив преобразование аффинного растяжения (сжатия) прямоугольника (рис. 3). Параметры пластинки: угол при основании  = 80 о , отношение основания к высоте а/ h = 1 ; a = 1м; b = 0,65м ; площадь A = 0,825м 2 ; коэффициент формы К f = 8,2925. Для этой пластинки найдено значение изгиба с помощью МКЭ .

Заданная трапеция может быть получена путем преобразования квадрата с коэффициентом формы К f = 8 ; площадью A = 1м 2 , . Путем геометрических построений (см. рис. 2) и проведения необходимых вычислений найдем, что другой опорной фигурой будет являться равнобедренный треугольник с углом при вершине  = 90 о ; a = 1м; h = 0,5м; A = 0,25м 2 ; К f = 11,669 ; .

Рис. 3. Аффинное преобразование сжатием прямоугольника

По опорным решениям, применив методику МИКФ, получим:

что отличается от решения, полученного МКЭ, на 3,07 %.

Таким образом, применение МИКФ позволяет получать простые аналитические зависимости для определения максимального прогиба в задачах поперечного изгиба пластинок. Этот метод позволяет также производить контрольные проверки решений для конкретных видов пластинок, полученных другими приближенными способами, путем построения этих фигур с помощью различных геометрических преобразований.

Полиа Г., Сеге Г. Изопериметрические неравенства в математической физике. — [Текст] / Полиа Г., Сеге Г — М.: Госматиздат, 1962. — 336с.

Коробко А. В. Геометрическое моделирование формы области в двумерных задачах теории упругости. — [Текст] / В. И. Коробко — М.: Изд-во АВС, 1999. — 320с.

Основные термины (генерируются автоматически): коэффициент формы, пластинка, решение, геометрическое преобразование, кривая, максимальный прогиб, метод интерполяции, аналитическая зависимость, выбранное геометрическое преобразование, изопериметрический метод.

Методическое пособие по ПК «ГРАНД-Смета» версия 7

Расчёт с использованием интерполяции и экстраполяции

До сих пор мы рассматривали примеры групповых расценок, где для каждой единичной расценки в группе определены постоянные величины A и B, позволяющие учитывать при расчёте стоимости проектируемого объекта его точные характеристики (производительность, протяжённость и т. п.). Наряду с этим в нормативной базе также имеются группы расценок, для которых в таблице приведено только значение постоянной величины А, и вместо диапазонов указаны конкретные значения основного показателя проектируемого объекта.

В качестве наглядного примера рассмотрим в том же сборнике СБЦ11. Объекты водоснабжения и канализации (2008) группу расценок СБЦ11-4-1-65÷СБЦ11-4-1-73 для объектов Сооружения очистки промывной воды производительностью по промывной воде.

При работе с такими группами расценок прямой расчёт возможен только в случаях, когда основной показатель объекта в точности совпадает с каким-либо значением в таблице. А если требуется расчёт стоимости проектирования объекта, основной показатель которого не совпадает с приведёнными в таблице, производится расчёт путём интерполяции или экстраполяции – причём в отличие от предыдущего пункта здесь рассматривается экстраполяция с участием двух граничных значений.

Интерполяция выполняется в ситуации, когда заданный основной показатель проектируемого объекта находится между двумя показателями, приведёнными в таблице. Тогда как экстраполяция выполняется в ситуации, когда заданный основной показатель проектируемого объекта выше или ниже всех показателей, приведённых в таблице – в этом случае производится расчёт с участием нормативных показателей двух граничных единичных расценок из группы: последней и предпоследней или, соответственно, первой и второй.

Таким образом, в каждом из приведённых ниже примеров расчёта стоимости позиции сметы участвуют две единичных расценки из группы; при этом соответствующие строки в таблице стоимостей в окне с дополнительной информацией о позиции выделены синим цветом.

Замечание: Как и в предыдущем пункте, подчеркнём, что выбор нужной формулы для расчёта стоимости позиции сметы осуществляется в программе автоматически, немедленно при вводе (корректировке) значения в колонке Количество. Также отметим, что в расчёте участвует обязательный для применения коэффициент из технической части Ки1 (на стадию проектирования).

Описанная в данном пункте методика интерполяции и экстраполяции с участием двух табличных значений реализована исключительно для групповых расценок, где приведено только значение постоянной величины А. При этом существует возможность и в таких случаях производить расчёт по базовым формулам, описанным в предыдущем пункте. Переключение между двумя способами расчёта осуществляется при помощи кнопки Интерполировать в окне с дополнительной информацией о позиции на закладке Стоимости.

Источник: www.grandsmeta.ru