Момент силы (момент силы относительно точки; также: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — эо векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Момент силы
Система сходящихся сил, которая будет рассмотрена в главе 2, является особой среди
систем сил. Только в этой системе линии действия сил имеют одну точку пересечения. Поэтому для ее изучения достаточно основных понятий статики, рассмотренных в разделе 1. Для изучения других систем сил необходимо ознакомиться с понятиями момента силы и пары сил.
Понятие о моменте силы — одно из основных понятий механики, которое широко используется и в теоретических исследованиях и при практических расчетах. К понятию момента силы человечество пришло, рассматривая равновесие и движение тел, имеющих точку или ось вращения (в частности блоков и рычагов, которые использовались в практике еще до нашей эры).
РЫЧАГ МОМЕНТ СИЛЫ физика 7 класс Перышкин
Например, на неподвижный блок (рис. 3.1) действует сила , вращающей его вокруг горизонтальной оси О. Стержень АВ (рис. 3.2), который имеет неподвижную шарнирную опору A, будет вращаться вокруг оси шарнира под действием собственной силы тяжести В обоих примерах сила обуславливает вращательное движение тела. По мере вращательного действия силы на тело является момент силы.


Момент силы относительно точки (центра)
Заданная сила , изображена вектором , приложенная к некоторому телу в точке А. Определим момент силы относительно точки О (рис. 3.3). Векторным моментом силы относительно точки О называется вектор, приложенный в точке О, равный векторному произведению радиуса вектора точки приложения силы на вектор силы:


где — радиус-вектор точки приложения силы относительно точки О.
Определим величину (модуль) и направление вектора . Согласно понятиям и свойствам векторного произведения двух векторов, величина (Модуль) момента силы относительно точки О равна:

Обозначим . Поскольку Тогда:

где (рис. 3.3) — высота опущенная из вершины В (с точки О) на сторону АВ этого треугольника, совпадает с линией действия силы. Короткое расстояние от точки О до линии действия силы называется плечом силы относительно этой точки. Из этого следует, что модуль (величина) момента силы относительно точки равна произведению величины силы на ее плечо относительно этой точки.
Момент силы

Вектор направляется по правилу векторного произведения: векторный момент силы относительно точки (Центра) является перпендикулярным к плоскости, в которой размещены сила и точка (центр) так, чтобы с его конца было видно попытки силы возвращать тело вокруг точки (Центра) против хода часовой стрелки.
Заметим, что . Поэтому:


Модуль момента силы относительно точки равен удвоенной площади треугольника, вершинами которого является точка и начало и конец вектора
Если линия действия силы проходит через точку (центр), то h = 0, и из формулы (3.2) видно, что момент силы относительно этой точки будет равняться нулю.
Момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, поскольку неизменным остается плечо силы относительно точки (рис. 3.4).

Если на тело действует плоская система сил, то векторы моментов всех сил системы относительно некоторого центра, что лежит в плоскости действия сил, будут перпендикулярны этой плоскости, а следовательно, параллельные и их можно считать скалярными величинами, которые отличаются только величиной и знаками.
В этом случае целесообразно ввести понятие алгебраического момента силы относительно точки (центра), равный взятом со знаком «+» или «-» произведения модуля силы на плечо относительно этой точки (центра)


Будем считать момент положительным, если сила пытается вращать тело вокруг точки (центра) против хода часовой стрелки (рис. 3.5, а), и отрицательным — если по ходу часовой стрелки (рис. 3.5, б). Единицы момента силы:

Момент силы относительно оси
Изучая пространственные системы сил, будем использовать понятие момента силы относительно оси.
Моментом силы относительно оси называется величина, равная алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Пусть к телу в некоторой точке А приложена сила (Рис. 3.6). определим момент силы относительно произвольной оси . Проведем плоскость П, перпендикулярную оси .
Точку пересечения плоскости П с осью обозначим А. Спроектируем силу на плоскость П и получим силу


Согласно определению
Таким образом, чтобы определить момент силы относительно оси, необходимо:
— спроектировать эту силу на плоскость, перпендикулярную оси;
— найти точку пересечения оси с этой перпендикулярной плоскостью;
— определить алгебраический момент полученной проекции относительно точки пересечения оси с плоскостью.
Из формулы (3.5) следует, что момент силы относительно оси равен нулю, если:
1) сила параллельна оси, тогда
2) линия действия силы пересекает ось, тогда

Эти два условия эквивалентны одному условию: момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости. поскольку момент силы относительно оси , то согласно принятому правилу знаков моментов следует, что момент силы относительно оси положительный, если, смотря с конца оси, видим, что проекция этой силы на плоскость, перпендикулярную оси, пытается вращать тело вокруг оси против часовой стрелки (рис. 3.7, а). если вращение происходит в направлении хода часовой стрелки, то момент силы относительно оси будет отрицательным (рис. 3.7, б). Можно доказать, что момент силы относительно оси не зависит от выбора точки О на этой оси.

Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
Теорема 3.1. Проекция векторного момента силы относительно точки на ось, проходящей через эту точку, равен моменту силы относительно этой оси.
Доказательство. Сила приложена в точке А пространства. Выберем произвольную точку О и проведем оси (рис. 3.8). Определим момент силы относительно оси и относительно точки О на ней.
Известно, что


где

Из курса элементарной геометрии известно, что

где — угол между плоскостями этих треугольников, а следовательно, и угол между перпендикулярами к этим плоскостей.
Поскольку вектор перпендикулярный плоскости, а ось перпендикулярна к


Учитывая равенства (3.6), (3.7), получим
Знак полностью определяется знаком .

что и требовалось доказать.
Моменты силы относительно координатных осей
Пусть на тело действует сила приложенная в точке А (рис. 3.9). выберем произвольную точку О и из нее проведем оси декартовой системы координат.
Определим момент силы относительно этих осей. Для этого запишем выражение для момента силы относительно точки О.

Согласно (3.1),где — радиус-вектор точки А относительно точки О.
Вектор силы и радиусвектор через проекции на оси координат выражаются:

где — координаты точки А; — орты выбранной системы координат.

Тогда векторное произведение можно записать в виде определителя:

Раскрывая этот определитель, получим


Представим векторный момент через его проекции на оси координат:

Сравнивая правые части равенств (3.9) и (3.10), получим:


Поскольку точка О принадлежит осями , то из формул (3.11), учитывая зависимость (3.8), получим выражения:

Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Теорема 3.2. Момент равнодействующей пространственной системы сходящихся сил
относительно некоторого центра (точки) равна векторной сумме моментов составляющих сил относительно того же центра (точки).
Доказательство. На тело действует пространственная система сходящихся сил линии действия которых пересекаются в точке В (Рис. 3.10, а). заменим
данную систему сил эквивалентной системой, все силы которой приложенные в точке В
(Рис. 3.10, б). Равнодействующую системы, прилагаемую в той же точке В, обозначим . Найдем момент равнодействующей относительно точки (центра) О. Согласно формуле (3.1), где — радиус-вектор точки приложения всех сил системы и равнодействующей относительно центра О.

Известно, что . Тогда

Итак, получили равенство
Уравнение (3.13) является математическим записи теоремы Вариньона для пространственной системы сходящихся сил.
В случае плоской системы сходящихся сил теорема Вариньона запишется так:

Итак, момент равнодействующей плоской системы сходящихся сил относительно некоторого центра (точки), лежащий в плоскости действия сил, равна алгебраической сумме моментов составляющих сил относительно этого самого центра (точки).
Рассмотрим пример на применение теоремы Вариньона.
Задача. На согнутый под прямым углом стержень АВС действуют силы и как показано на рис. 3.11. Найти моменты этих сил относительно точки А, если

Решение.

Для определения момента силы относительно точки используем теорему Вариньона.
Разложим силу на две составляющие: горизонтальную и вертикальную . Величины этих составляющих Тогда, согласно теоремой 3.2, получим:

Услуги по теоретической механике:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, является мерой действия тела на другое тело.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии, вдоль которой действует сила — это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Правило равновесия рычага
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
F1, F2 — силы, действующие на рычаг
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Для примера представьте, что вы забыли, как открывать двери. Стоите перед дверью и раздумываете, как легче это сделать.
Для начала приложим силу к краю двери — туда, где самый длинный рычаг. Открылась!
А что если толкнуть дверь ближе к креплению — там, где плечо намного короче? Для этого придется приложить силу большего значения.
Вывод: чтобы повернуть дверь, нужен крутящий момент определенного значения. Чем больше плечо силы, тем меньше значение силы, которую нужно приложить — и наоборот. Поэтому нам легче толкать дверь там, где плечо силы больше.

Похожая история с гаечным ключом. Чтобы закрутить гайку, нужно взяться за ручку подальше от гайки. За счет увеличения плеча мы уменьшаем значение силы, которую нужно приложить.

Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
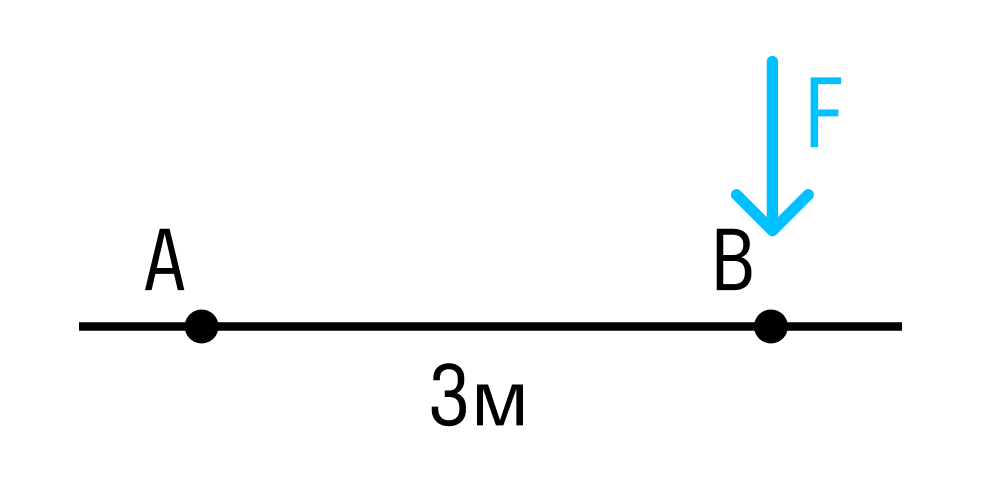
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
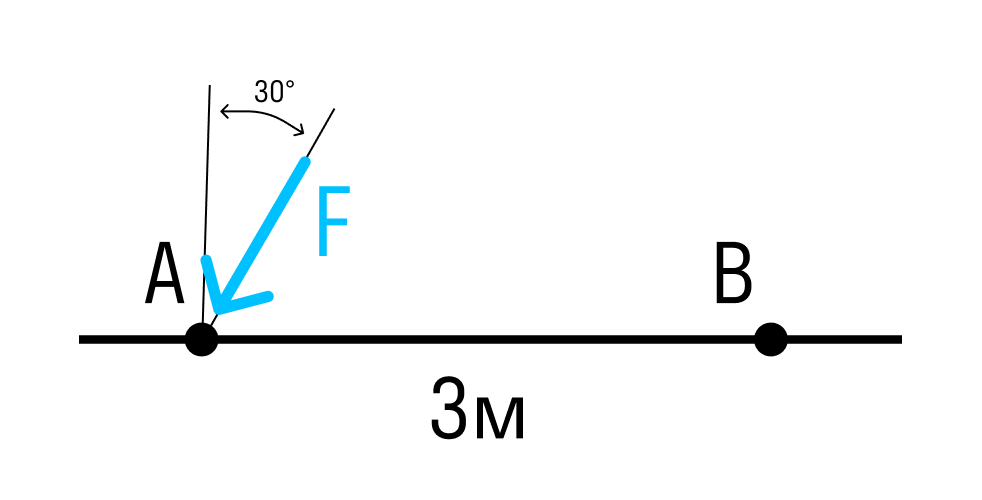
Момент силы относительно точки B:
Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
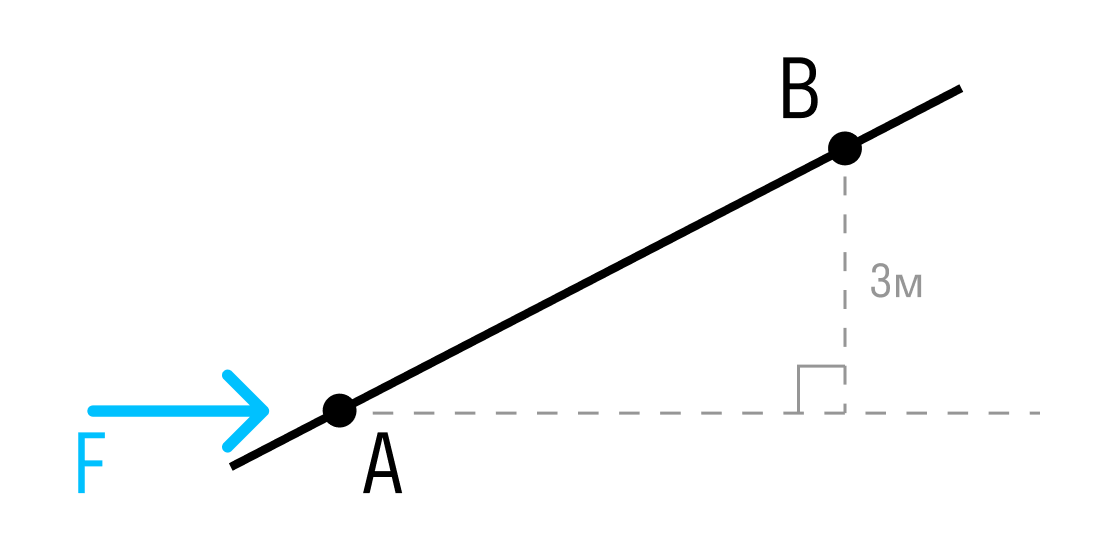
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
M’1 + M’2 +. + M’n — сумма моментов сил, поворачивающих рычаг против часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
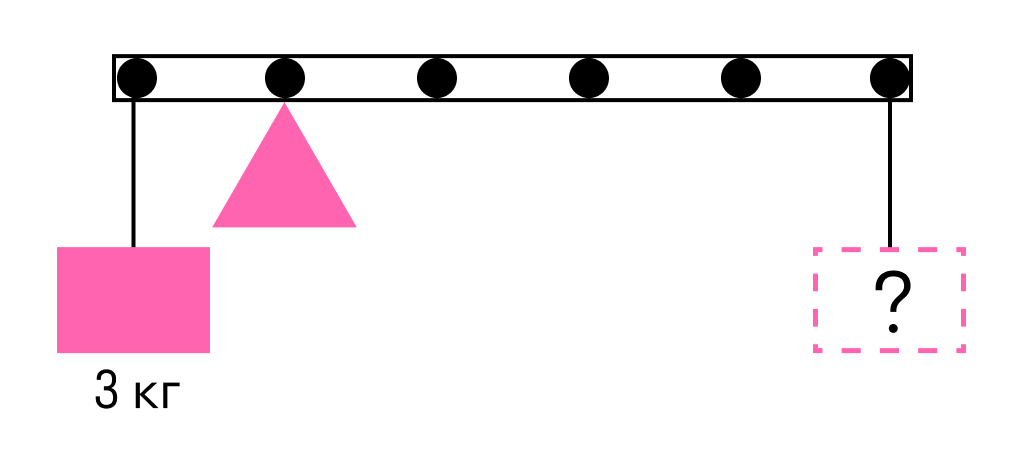
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом: — он вращает по часовой.
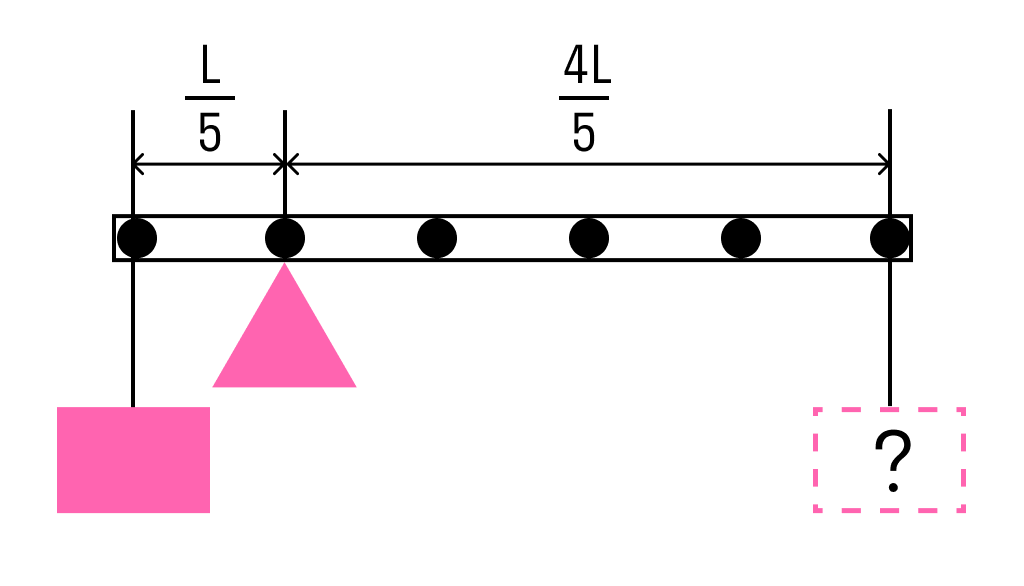
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
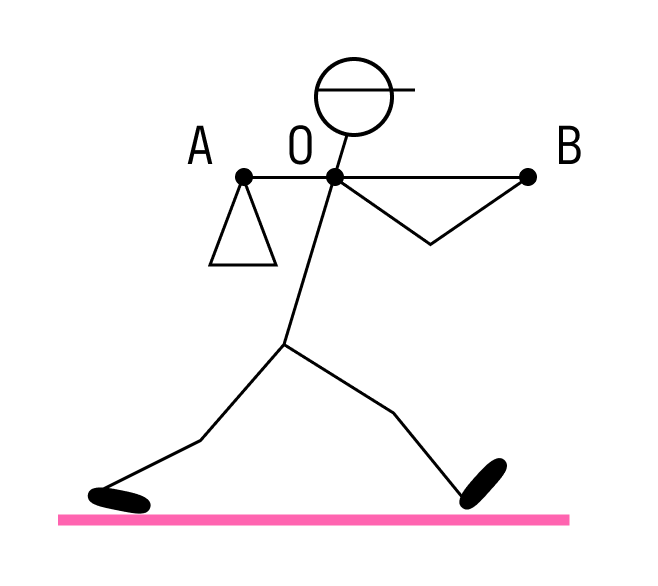
Решение:
По правилу рычага:
где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
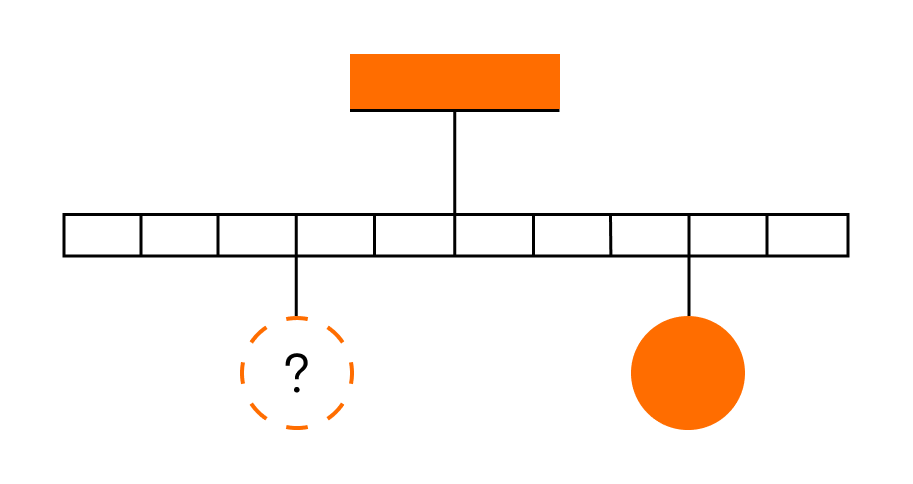
Решение:
По правилу рычага
Ответ: Масса груза равна 0,3 кг
Задача 4 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Уточним, что 0,8 м — это расстояние от центра тяжести груза до опоры, т. е. перпендикуляр до оси вращения. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
Источник: skysmart.ru
Момент силы
Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки — полюса) и относительно оси.
Если имеется материальная точка О, к которой приложена сила , то момент силы относительно этой точки равен векторному произведению радиус-вектора , соединяющего точку О и точку приложения силы, на вектор силы :
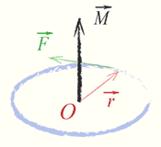
Момент силы — аксиальный вектор[3]. Он направлен вдоль оси вращения.
Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.4).
Модуль момента силы:
M =F• l =F •r •sin α,
где: M – момент силы (Ньютон •метр),
F – приложенная сила,
r – расстояние от центра вращения до места приложения силы,
l = r.sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,
α — угол, между вектором силы F и вектором положения r.
Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора Ммомента силы относительно любой точки О оси.
Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:
если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:
Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.5, силам F1 и F2 следует приписать положительный момент, а силе F3— отрицательный.
Источник: studopedia.ru
Определение и свойства момента силы
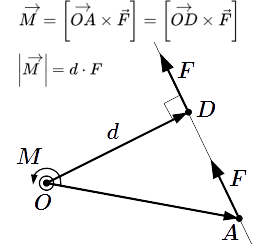
Определения момента силы относительно точки и оси. Определение плеча силы относительно точки. Формулировки и доказательства свойств момента силы. Выражение абсолютного значения момента в виде произведения плеча силы на модуль силы.
Момент силы относительно точки
Определение момента
Момент силы относительно точки O – это векторное произведение вектора , проведенного из точки O в точку приложения силы A , на вектор силы :
(1) .
Если выбрать прямоугольную систему координат Oxyz с центром в точке O , то момент силы будет иметь следующие компоненты:
(1.1) ;
(1.2) ;
(1.3) .
Здесь – координаты точки A в выбранной системе координат:
.
Компоненты представляют собой значения момента силы относительно осей , соответственно.
Определение плеча силы
Плечо силы относительно точки – это расстояние между линией действия силы и точкой, относительно которой определяется плечо. То есть плечо силы – это длина перпендикуляра, опущенного из точки на линию действия силы.
Свойства
Если точку приложения силы переместить вдоль линии ее действия, то момент, при таком перемещении, не изменится.
Доказательство ⇓
Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство ⇓
Момент относительно точки O , от силы, линия действия которой проходит через эту точку, равен нулю.
Доказательство ⇓
Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство ⇓
Тоже самое относится и к силам, чьи линии продолжения пересекаются в одной точке. При этом в качестве точки приложения суммы сил берется точка пересечения линий их действия.
Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство ⇓
Момент силы является псевдовектором или, что то же самое, аксиальным вектором.
Это свойство следует из свойства векторного произведения. Поскольку векторы и являются истинными (или полярными) векторами, то их векторное произведение является псевдовектором. Это означает то, что мы можем определить только абсолютное значение и ось, вдоль которой направлено векторное произведение.
Само же направление по этой оси мы задаем произвольным образом, используя правило правого винта. То есть мы мысленно откладываем векторы и из одного центра. Затем поворачиваем ручку из положения в положение . В результате правый винт смещается в направлении, перпендикулярном плоскости, в которой расположены векторы. Это направление мы и берем за направление векторного произведения.
Но если бы мы определили направление по правилу левого винта, то векторное произведение было бы направлено в противоположную сторону. При этом никакого противоречия не возникает. То есть фактически, аксиальные векторы могут иметь два взаимно противоположных направления. Чтобы не усложнять математические формулы, мы выбираем одно из них, применяя правило правого винта.
По этой причине, псевдовекторы нельзя геометрически складывать с истинными векторами. Но их можно перемножать, используя скалярное или векторное произведение.
Момент силы относительно оси
Определение
Часто встречаются случаи, когда нам не нужно знать все компоненты момента силы относительно выбранной точки, а нужно знать только момент силы относительно выбранной оси.
Момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси.
Пусть – единичный вектор, направленный вдоль оси. И пусть O – произвольная точка, принадлежащая ей. Тогда момент силы относительно оси является скалярным произведением:
.
Такое определение возможно, поскольку для любых двух точек O и O′ , принадлежащих оси, проекции моментов относительно этих точек на ось равны. Покажем это.
Воспользуемся векторным уравнением :
;
.
Умножим это уравнение скалярно на единичный вектор , направленный вдоль оси:
.
Поскольку вектор параллелен оси, то . Отсюда
.
То есть проекции моментов на ось, относительно точек O и O′ , принадлежащих этой оси, равны.
Свойства
Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство ⇓
Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство ⇓
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
Все свойства ⇑ Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.
Пусть сила приложена в точке A . Через точку A проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку A приложения силы в точку A′ , принадлежащую линии действия. Тогда
.
Вектор проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где λ – параметр; . , если точка A′ смещена относительно A в направлении вектора . В противном случае .
Таким образом, вектор, проведенный из O в A′ , имеет вид:
.
Найдем момент силы, приложенной в точке A′ , применяя свойства векторного произведения:
.
Мы видим, что момент не изменился:
.
Абсолютная величина момента силы
Все свойства ⇑ Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
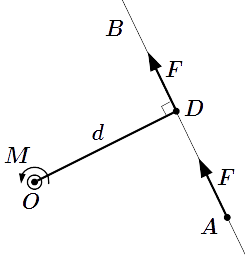
Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD| .
Пусть мы имеем силу , приложенную в точке A . Рассмотрим момент этой силы относительно некоторой точки O . Заметим, что точки O , A и вектор лежат в одной плоскости. Изобразим ее на рисунке. Через точку A , в направлении вектора проводим прямую AB . Эта прямая называется линией действия силы . Через точку O опустим перпендикуляр OD к линии действия. И пусть D является точкой пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра O . Обозначим его буквой . Воспользуемся предыдущим свойством ⇑, согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку D . Момент силы:
.
Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:
,
где – абсолютное значение силы.
Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку O перпендикулярно плоскости рисунка, в направлении силы F , то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.
Момент относительно точки от силы, проходящей через эту точку
Все свойства ⇑ Момент относительно точки O , от силы, линия действия которой проходит через эту точку, равен нулю.
Пусть линия действия силы проходит через точку O . Тогда плечо этой силы относительно O равно нулю: . Согласно предыдущему свойству ⇑, абсолютное значение момента силы относительно выбранной точки равно нулю:
.
Момент суммы сил, приложенных в одной точке
Все свойства ⇑ Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Пусть силы приложены в одной точке A . Пусть – векторная сумма этих сил. Находим момент относительно некоторой точки O от векторной суммы , приложенной в точке A . Для этого применяем свойства векторного произведения:
.
Момент системы сил, векторная сумма которых равна нулю
Все свойства ⇑ Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Пусть силы приложены в точках , соответственно. И пусть точки O и C обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения:
.
Используем их при вычислении суммы моментов относительно точки O :
.
Здесь мы воспользовались тем, что по условию,
.
Момент относительно оси от силы, проходящей через эту ось
Все свойства ⇑ Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
В определении ⇑ указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно доказанному выше ⇑, момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.
Момент относительно оси от силы, параллельной этой оси
Все свойства ⇑ Момент относительно оси от силы, параллельной этой оси равен нулю.
Пусть O – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению:
.
Согласно свойству векторного произведения, вектор момента перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки O на ось равна нулю.
Источник: 1cov-edu.ru