Лекция 1. Реальный объект и расчётная схема Одна из основных целей расчёта строительных конструкций – определение их напряжённо-деформированного состояния (НДС) при заданных граничных условиях (наложенных связях и нагрузках) для обеспечения прочности, жесткости и устойчивости. Конструкции, анализ НДС которых необходимо выполнить, являются реальными физическими объектами.
Их поведение под нагрузкой достаточно сложно и не изучено в полной мере. Тем не менее, специалисты обладают инструментом, позволяющим спрогнозировать поведение таких объектов при заданных условиях на достаточном количественном и качественном уровне. Для решения поставленной задачи прибегают к моделированию поведения конструкции.
Первым шагом в данном направлении является упрощение (схематизация) исследуемой реальной модели конструкции, т.е. освобождение от несущественных в данной задаче особенностей, которые не могут заметным образом повлиять на работу системы в целом. Степень упрощений зависит от требуемой точности, математических возможностей, а также от того, какая сторона явления рассматривается в задаче.
Что такое расчетная схема
Полученная в итоге модель есть расчётная схема объекта – идеализированная схема, отражающая наиболее существенные особенности реального объекта, определяющие его поведение под нагрузкой (рис. 1.1). Реальный объект – рама промышленного здания с движущимся по ней мостовым краном Расчётные схемы отдельных элементов рамы: а – трос, б – колонна, в – подкрановая балка а) б) в) Рис. 1.1.
Реальный объект и расчётная схема Так, например, при расчете на прочность троса, поднимающего груз, можно не учитывать форму груза, сопротивление воздуха, изменение давления и температуры воздуха с высотой, силу тяжести троса и многие другие 1 факторы, учет которых усложняет расчет троса, но практически не влияет на конечный результат. Трос, свитый из большого числа тонких проволочек, в данном примере можно рассматривать как однородный стержень круглого поперечного сечения, нагруженный растягивающей силой, сосредоточенной в месте крепления груза и т.д.
В качестве ещё одного примера на рис. 1.2 приведена консольная балка, как при испытаниях изобразил её Галилео Галилей (а), и её расчётная схема (б). Рис. 1.2. Консольная балка: а – рисунок Галилео Галилея, иллюстрирующий испытание балки (XVII в.); б – расчётная схема балки К числу существенных факторов расчетной схемы относят следующие (рис.
1.3): 1) геометрию элементов схемы, их форму и размеры; 2) физические характеристики материала; 3) нагрузки, прикладываемые к схеме; 4) связи (опоры). Рис. 1.3. Существенные факторы расчетной схемы сооружения 2 По геометрическому признаку элементы схемы в зависимости от соотношения основных габаритных размеров (длина l, ширина b и высота h) относят к одной из категорий (рис.
1.4): стержень (рис. 1.4, а) − тело, два размера которого (b и h) одного порядка и значительно меньше третьего (l); представителями стержня являются его ось и поперечное сечение; оболочка (рис.
Расчетные схемы и нагрузки
1.4, б) − тело, два размера которого одного порядка и значительно больше третьего; в расчетной схеме оболочку представляют срединной поверхностью (поверхностью, расположенной посередине толщины) и толщиной; пластинка (рис. 1.4, в) − оболочка, срединная поверхность которой является плоскостью; массив (рис. 1.4, г) − тело, все три размера которого одного порядка. а) б) в) г) Рис. 1.4.
Классификация элементов расчётной схемы по геометрическому признаку: а – стержень; б – оболочка; в – пластинка; г – массив Важным шагом при выборе расчетной схемы является отражение механических свойств материала. Известно, что работа материала, как и работа всей конструкции, под нагрузкой является достаточно сложной (рис.
1.5), и пока ещё не разработана такая физическая модель, которая бы достаточно хорошо отражала поведение всех материалов. Для одних пригодны одни предпосылки, для других − другие.
Тем не менее, на практике достаточно часто рассматривается модель идеального материала, для которого принят ряд гипотез, позволяющих схематизировать его свойства и поведение: гипотеза континуальности – согласно ей считают, что материал занимает объем тела без разрывов и пустот; гипотеза о ненапряженном начальном состоянии – в соответствии с этой гипотезой в ненагруженном теле внутренних сил нет; гипотеза однородности – свойства тела во всех точках одинаковы; 3 2 1 3 4 5 6 Рис. 1.5.
Диаграммы деформирования различных материалов при растяжении (1, 2) / сжатии (3–6): 1, 3 – малоуглеродистая сталь Ст.3; 2 – легированная сталь 40Х; 4 – серый чугун; 5, 6 – дерево (сосна) вдоль и поперёк волокон гипотеза изотропии – изотропным называется такой материал, свойства которого во всех направлениях одинаковы; гипотеза упругости – тело, которое после устранения внешнего воздействия восстанавливает свои размеры и форму, называется упругим; в таком теле внутренние силы и деформации зависят только от тех нагрузок, которые действуют в рассматриваемый момент. Внешняя нагрузка, фигурирующая в расчетной схеме, − это силы, с которыми исключенные из анализа конструкции действуют на рассматриваемую конструкцию.
Любые силы взаимодействия распределены в пределах контактных поверхностей. Установить характер распределения этих сил практически невозможно, поэтому внешнюю нагрузку также идеализируют.
В зависимости от размеров площади загружения (размеров контактной поверхности) усилие относят к одной из следующих категорий: сосредоточенные силы – ими представляют давления, передаваемые через площадку, размеры которой малы по сравнению с размерами исследуемой области; количественные меры сосредоточенных сил − Н, кН, МН и т.п.; 4 нагрузки, распределенные по линии – с их помощью схематизируют давления, передаваемые по поверхности, длина которой, с одной стороны, значительно превышает ширину, с другой, соизмерима с бόльшим размером тела; величину такой нагрузки измеряют интенсивностью в Н/м, кН/м, МН/м и т.п.; нагрузка, распределённая по поверхности, рассматривается, если размеры поверхности, по которой передается нагрузка, соизмеримы с размерами тела; интенсивность распределенной такой нагрузки измеряют давлением в Н/м2 (Па), кН/м2 (кПа), МН/м2 (МПа) и т.п.; сосредоточенный момент –нагрузка, представленная парой сил с малым плечом; такая нагрузка имеет размерность Нм, кНм, МНм и т.п. Связи, фигурирующие в расчетной схеме, − это элементы соседних конструкций, накладывающие ограничения на перемещения соединяемых точек.
Кинематическое и силовое действие связей сложно и многообразно. Поэтому их также идеализируют: шарнирно-подвижная опора (рис. б) в) а) 1.6, а) – её выбирают при слабом сопротивлении реальной связи повороту вокруг опорной точки и смещению в каком-либо направлении, но практически исключению перемещения в другом направлении, перпендикулярном первому; Рис. 1.6.
Идеализированные типы связей (опор): шарнирно-неподвижная опора а – шарнирно-подвижная; (рис. 1.6, б) – так имитируют реб – шарнирно-неподвижная; альную опору при сильном сопров – жёсткое защемление тивлении линейному перемещению в любом направлении, но при слабом препятствии повороту; жёсткое защемление (рис.
1.6, в) – ту связь вводят, когда заменяемый ею элемент практически исключает перемещения места соединения. Идеализация связей влечет за собой и идеализацию реакций, однозначно определяемых способом закрепления элемента. Трудно назвать все приемы, которые используют при выборе расчетной схемы.
В конкретных условиях появляются конкретные возможности, определяющие необходимую и допустимую степень идеализации объекта. Нередко 5 оказывается, что предпосылки, пригодные для расчета одних конструкций, неприменимы для других. В зависимости от поставленной задачи для одной и той же конструкции возможен выбор различных расчетных схем.
Например, при определении усилий в ферме стержни считают соединенными шарнирно. Основанное на этом решение вполне доверительно для усилий на средних участках стержней. Если же интерес представляют усилия в местах соединения стержней, необходимо точнее отразить силовое взаимодействие сочлененных элементов.
С другой стороны, одной и той же расчетной схеме может быть поставлено в соответствие несколько разных объектов. Скажем, растянутый стержень может моделировать и канаты подъемных машин, и стойки, раскосы, пояса ферм, и т.п. Переход от реального объекта к расчетной схеме является важным шагом, так как от введенных предпосылок зависит результат расчета.
При этом, расчет состоит не только в выборе расчетных формул и вычислениях по ним. Нельзя забывать о первом шаге − идеализации реальных свойств, который неизбежно в определенной степени отразится на конечном результате. С какой бы точностью ни производились вычисления, результат оказывается приближенным. Поэтому получаемые решения всегда необходимо оценивать критически на фоне использованных предпосылок. 6
Источник: spravochnick.ru
ПОСОБИЕ по проектированию жилых зданий Конструкции жилых зданий (к СНиП 2.08.01-85) — Расчетные схемы
3.9. Расчетные схемы бескаркасных зданий классифицируются:
по характеру учета пространственной работы — на одно-, двух- и трехмерные;
по виду неизвестных — на дискретные, дискретно-континуальные и континуальные;
по виду конструкции, положенной в основу расчетной схемы, — на стержневые, пластинчатые, комбинированные.
3.10. При одномерной расчетной схеме здание рассматривается как тонкостенный стержень или система стержней, упруго или жестко защемленных в основании. Предполагается, что поперечный контур стержня (системы стержней) неизменяем.
При двухмерной расчетной схеме (рис. 22) здание рассматривается как плоская конструкция, способная воспринимать только такую внешнюю нагрузку, которая действует в ее плоскости. Для определения усилий в стенах от горизонтальной нагрузки условно принимается, что все стены, параллельные действию нагрузки, расположены в одной плоскости и имеют одинаковые горизонтальные перемещения в уровне перекрытий.
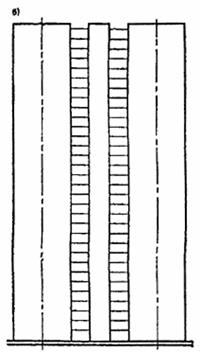
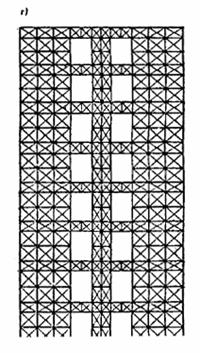
Рис. 22. Двухмерные (плоские) расчетные схемы бескаркасных зданий
а — вертикальная диафрагма с проемами; б — плоский составной стержень; в ¾ заменяющая рама; г — ферменная модель
При трехмерной расчетной схеме (рис. 23) здание рассматривается как пространственная система, способная воспринимать приложенную к ней пространственную систему сил. Трехмерная расчетная схема наиболее точно учитывает особенности взаимодействия несущих конструкций, но расчет на ее основе наиболее сложен.
Рис. 23. Пространственные (трехмерные) расчетные схемы бескаркасных зданий.
а — фрагмент здания; б — расчетная схема в виде системы консольных стержней; в ¾ то же, пространственного составного стержня; г — пластинчатой системы, рассчитываемой методом конечных элементов
3.11. В дискретных расчетных схемах неизвестные усилия или перемещения определяют для конечного количества узлов системы решения систем алгебраических уравнений. Дискретные расчетные системы наиболее приспособлены к условиям расчета на цифровых вычислительных машинах.
В дискретно-континуальных расчетных схемах неизвестные силовые факторы или перемещения задают в виде непрерывных функций вдоль одной из координатных осей (функциональные неизвестные). Неизвестные функции определяются решением краевой задачи для системы обыкновенных дифференциальных уравнений.
В континуальных расчетных схемах неизвестные силовые факторы или перемещения задают в виде непрерывных функций вдоль двух или трех координатных осей. Неизвестные функции определяются решением краевой задачи для системы дифференциальных уравнений в частных производных.
3.12. При стержневых расчетных схемах несущая система здания рассматривается в виде: набора параллельно расположенных балок с податливыми связями (составная балка), перекрестной системы балок, многоэтажной многопролетной рамы, решетчатой системы и др. Для определения динамических характеристик здания вся несущая система здания может рассматриваться как один консольный стержень.
В расчетных схемах в виде перекрестных стержневых систем несущие балочные элементы расположены в двух плоскостях (вертикальной и горизонтальной). Вертикальные несущие элементы эквивалентны по жесткости стенам, горизонтальные — перекрытиям здания. Принимается, что в местах пересечения несущих элементов их поперечные перемещения одинаковы.
Перекрестная расчетная схема позволяет учесть изгиб перекрытий в собственной плоскости. Недостатком расчетной схемы является то, что при ее использовании не учитывается совместность продольных деформаций параллельно расположенных стен, обеспечиваемая в здании стенами перпендикулярного направления. Поэтому расчетную схему рекомендуется применять для расчета на горизонтальные нагрузки только зданий с поперечными несущими стенами при ненесущих продольных стенах.
В рамных расчетных схемах стены с проемами рассматриваются как многоэтажные плоские или пространственные многопролетные рамы. Стойками рам являются глухие (без проемов) участки стен, а ригелями — перемычки и перекрытия. При расчете рекомендуется принимать, что ригели имеют переменную жесткость (бесконечно большую в пределах длины простенков и конечную в местах проемов). Для определения усилий в конструкциях зданий на основе рамной расчетной схемы используют универсальные программы расчета рамных систем.
При решетчатых расчетных схемах здание в целом или его отдельные элементы (например, стены) заменяют системой вертикальных, горизонтальных и наклонных стержней, шарнирно соединенных между собой.
3.13. При пластинчатых расчетных схемах стены и перекрытия здания рассматриваются как система тонкостенных плоскостных элементов (пластинок), соединенных, как правило, в отдельных узлах. Для расчета отдельных пластинок используют численные методы теории упругости (метод сеток, прямые вариационные и др.), а также методы, в которых рассчитываемая непрерывная система заменяется дискретной (метод конечных элементов, ферменной аналогии).
3.14. При комбинированных расчетных схемах здание рассматривается как пластинчато-стержневая система. Такие расчетные схемы рекомендуется применять для расчета зданий, в которых сочетаются каркасные элементы и стены.
3.15. При выборе расчетной схемы рекомендуется учитывать, что все они имеют ограниченные области применения, определяемые положенными в их основу допущениями. Чем меньше допущений использует тот или иной метод, тем шире область его применения, но вместе с тем более трудоемок расчет.
Наиболее совершенными и универсальными являются расчетные схемы в виде пространственной (трехмерной) системы пластин или (и) стержней с дискретными связями между ними. При таких расчетных схемах рекомендуется использовать для расчета метод конечных элементов. Расчет выполняется по специальным программам на ЭВМ
Для расчета зданий, конструктивно-планировочные решения которых не изменяются по высоте (регулярная система) или изменяются небольшое число раз (ступенчато-регулярная система), рекомендуется использовать расчетную схему в виде вертикальной составной системы. В составной системе различают несущие и связевые элементы.
Несущими элементами многоэтажного здания являются участки стен, ограниченные в плане проемами или вертикальными стыковыми соединениями, а также стволы (ядра) жесткости, колонны, пилоны и другие вертикальные несущие конструкции. Связевыми элементами являются диски перекрытий, надпроемные перемычки, ригели, соединения сборных элементов в вертикальных стыках. При расчете составных систем дискретные связевые элементы заменяют эквивалентными по жесткости (или податливости) непрерывными и используется дискретно-континуальная расчетная схема. Для бескаркасных зданий несущие элементы составной системы рекомендуется рассматривать как консольные тонкостенные стержни, деформирующиеся за счет продольных усилий сжатия — растяжения, изгиба и сдвига.
3.16. На начальных этапах проектирования здания рекомендуется использовать упрощенные расчетные схемы, позволяющие выполнять расчет без специальных программ.
Для зданий стеновой конструктивной системы расчетную схему рекомендуется принимать в виде системы вертикальных и горизонтальных диафрагм жесткости.
В одну вертикальную диафрагму жесткости рекомендуется включать поперечную или продольную стену здания и примыкающие к ней участки стен перпендикулярного направления. Стены, имеющие по длине в плане разрывы или проемы, перемычки над которыми не обеспечивают перераспределение усилий между простенками, расчленяют на несколько вертикальных диафрагм жесткости.
Размеры в плане простенков, примыкающих к основной стене диафрагмы жесткости, рекомендуется принимать не более 0,1 высоты здания и не более половины расстояния до соседней стены, параллельно стенке рассматриваемого несущего элемента.
3.17. Вертикальную диафрагму жесткости, имеющую регулярно расположенные по высоте проемы, вертикальные стыки или швы бетонирования, рекомендуется рассматривать как составную систему из т столбов, соединенных (т ‑ 1) рядами связей сдвига (рис. 24).
Рис. 24. Расчет вертикальной диафрагмы жесткости с проемами (а) как составного стержня (б)
Для каждого столба рекомендуется определять приведенный модуль деформации Еred учитывающий влияние горизонтальных стыков сборных элементов или горизонтальных швов бетонирования стен из монолитного бетона, а также продолжительность действия нагрузки и вычисляемый по формуле
где Еb — начальный модуль упругости бетона стены, принимаемый по нормам проектирования бетонных и железобетонных конструкций; для сборных элементов, изготавливаемых в кассетных установках, а также стен из монолитного бетона, возводимых в переставных опалубках, приведенные в нормах значения начальных модулей упругости следует умножать на коэффициент 0,85; jtb — коэффициент, учитывающий влияние ползучести бетона и зависящий от длительности действия нагрузки; при расчете на кратковременные нагрузки коэффициент jtb принимается равным: 1,2 — для тяжелого бетона и легких бетонов при плотном мелком заполнителе; 1,4 — для легких бетонов на пористом мелком заполнителе; 1,1 — для плотных силикатных бетонов;
при расчете на длительно действующие нагрузки коэффициент jtb вычисляется по формуле
Сb — предельная мера ползучести бетона, принимаемая для сборных элементов стен по табл. 5; lс — коэффициент податливости горизонтального стыка при сжатии определяемый в зависимости от длительности действия нагрузки по рекомендациям прил. 4.
Бетон и технология
Предельная мера ползучести Сb × 10 5 , МПа для бетонов класса по прочности на сжатие
Источник: normativa.ru
РАСЧЕТНАЯ СХЕМА сооружения
РАСЧЕТНАЯ СХЕМА сооружения — упрощенное (условное) изображение сооружения, применяемое в расчете. Методы расчета сооружений основаны на рассмотрении расчетной схемы, при выборе которых, пренебрегая некоторыми (главным образом второстепенными) факторами, стремятся получить простые и в то же время достаточно точные инженерные решения. Все расчетные схемы подразделяются на несколько видов, отличающихся друг от друга основными гипотезами, принимаемыми в расчетных схемах, а также используемым для расчета математическим аппаратом. Как правило, чем более точно расчетная схема соответствует действительному сооружению, тем более трудоемким оказывается его расчет; поэтому часто для одного и того же сооружения в первом приближении выбирается сравнительно простая расчетная схема и производится ориентировочный расчет и подбор сечений элементов, а затем принимается более точная расчетная схема, в которой фигурируют и установленные на основе предварительного расчета размеры.
Выбор расчетной схемы в известной степени отражает уровень развития строительной механики, а также квалификацию исполнителя; он зависит от наличия вычислительной техники и других условий.Одним из основных требований, предъявляемых к выбору расчетной схемы, является учет конструктивных особенностей сооружения, существенно влияющих на его работу. Развитие вычислительной техники и использование электронно-счетных машин для механизации инженерных расчетов позволяют применять все более точные расчетные схемы, совершенствовать существующие и разрабатывать новые методы расчета.
Энциклопедия современной техники строительство, главный редактор В. А. Кучеренко, издательство «Советская энциклопедия», Москва 1964

от: MarinaF, https://www.zdanija.ru/TermsR1/p2_articleid/4150″ target=»_blank»]www.zdanija.ru[/mask_link]