Экстраполяция в строительстве это

Оконтуривание площади тела полезного ископаемого можно проводить методами интерполяции и экстраполяции.

Метод интерполяции заключается в определении мощности или содержания ценных компонентов для участка тела полезного ископаемого, расположенного между двумя смежными выработками, при допущении, что они между выработками изменяются постепенно.

Метод экстраполяции заключается в определении мощности или содержания ценных компонентов для участка тела полезного ископаемого, находящегося за пределами выработок, вскрывших полезное ископаемое, исходя из предположения об их постепенном изменении. Различают ограниченную экстраполяцию, при которой внешняя контурная линия проводится между выработками, вскрывшими полезное ископаемое и не обнаружившими ее, и неограниченную экстраполяцию, когда внешняя контурная линия проводится за пределами внутреннего контура, где нет разведочных выработок.

где х – расстояние от пробы а, взятой по выработке, вскрывшей кондиционные руды, до точки с минимальными кондиционными рудами;

Экстраполяция

mn – минимальное кондиционное значение мощности или содержания или их произведение в точке n;

L – расстояние между пробами a и k.

Используя эту формулу, вычисляют расстояние х по данным каждой ближайшей пары выработок, между которыми должна пройти линия контура, и, отмерив их от выработок, вскрывших кондиционные руды, получают опорные точки. Соединив эти точки, получают контур месторождения.

Положение опорной точки может быть определено графическими способами: с помощью транспаранта или соответствующим построением. Транспарант представляет собой кальку или восковку с прочерченными на ней параллельными линиями, отстоящими одна от другой на равном расстоянии.

Определение контурной линии экстраполированием. Если одна из смежных выработок характеризуется положительными показателями, а другая отрицательными, то нулевой контур мощности, содержания полезного компонента и метропроцента между ними определяют методом ограниченной экстраполяции.

Обычно предполагают, что залежи выклиниваются на половине расстояния между выработками, пресекшими рудное тело и показавшими отсутствие его. Их соединяют прямыми линиями. Линия, соединяющая эти точки, будет нулевым контуром. В некоторых случаях при редкой разведочной сети или по геологическим данным экстраполирование иногда проводят лишь на ¼ расстояния между ближайшими положительными выработками. В случае, когда линзообразное тело выклинивается с глубиной, точку выклинивания находят графически и соответственно переносят ее с разреза на план.

Источник: mydocx.ru

ЭКСТРАПОЛЯЦИЯ ХАРАКТЕРИСТИК СЛОЖНОЙ СИСТЕМЫ

Технические характеристики оборудования сложных систем, как правило, изменяются не случайным образом, а в соответствии с некоторой детерминированной основой, которая всегда известна исходя из физической природы рассматриваемого явления, опыта эксплуатации оборудования, экспериментальных данных, полученных при проведении специальных испытаний. Примерами таких характеристик являются буксировочная кривая для судов, уравнения теплообмена, гидравлические потери и т.п.

Метод экстраполяции и скользящей средней. Константин Терёхин. Часть 2 (серия 44)

Отмеченное свойство полезно использовать для анализа информации в процессе эксплуатации, в том числе для анализа диагностических моделей. В этом случае обрабатывать информацию можно методами экстраполяции. Они особенно полезны для предотвращения аварийных ситуаций, неблагоприятных событий и повышения безопасности.

Эффективность и необходимость экстраполяции подтверждают следующие типичные ситуации. Для выбора безопасного режима работы оборудования необходимо оценить степень его удаленности от опасного состояния при увеличении нагрузки или параметров окружающей среды. Например, при изменении температуры окружающей среды вероятен нежелательный рост отдельных характеристик оборудования. Предотвращение необратимых процессов возможно, если известен запас до предельного значения параметра. Другой пример, путем проведения измерений на режимах малой нагрузки (интервал наблюдения) можно с заданной степенью достоверности оценить значения параметров при развитии полной мощности и сравнить их с заданными.

В ИИС для этих целей могут служить алгоритмы экстраполяции технических характеристик. Главная задача алгоритмов состоит в том, чтобы определить коэффициенты уравнения, отражающего детерминированную основу анализируемого явления, и найти значение интересующего параметра в заданной точке. Подобная постановка задачи совпадает с задачами, решаемыми при прогнозировании. Отличие заключается в том, что при прогнозировании аргументом является время, а в задачах экстраполяции аргументом может быть любая физическая величина, от значения которой зависит анализируемая характеристика.

Для получения достоверной информации при экстраполяции технических характеристик для объекта измерения необходимо провести исследования:

• • вида экстраполируемой технической характеристики;
• • интервала наблюдения и допустимых границ экстраполяции;
• • выбора числа точек наблюдения и частоты измерений в них;
• • точности оценки значений экстраполируемой характеристики в заданной области.

Все перечисленные вопросы решают теми же способами, как и при прогнозировании, с некоторыми видоизменениями в формулах путем замены переменной t на х. Процедуру метрологического обоснования алгоритмов экстраполяции рассмотрим на конкретных примерах.

Пример 1. Найти значение давления масла р за импеллером турбоагрегата при достижении им предельной частоты вращения п. Это значение необходимо для проверки правильности срабатывания защиты механизма в опасной ситуации. Найдем предполагаемое значение давления методом экстраполяции.

Увеличение давления масла с ростом частоты вращения определяется математической моделью вида

Пределы изменения давления масла за импеллером в точке экстраполяции в соответствии с техническими условиями равны 8. 10 %.

Для определения неизвестных коэффициентов модели, являющейся многочленом второй степени, достаточно провести измерения в трех точках. В качестве независимых переменных приняты нормированные отклонения частоты вращения импеллера от среднего значения

где пип — текущее и среднее значения независимой переменной соответственно.

Измерение значений давления масла р в новых координатах проведено в трех точках vk (к — 1,2, 3) по восемь значений в каждой. Результаты измерений сведены в табл. П.5.

Давление масла, МПа

Среднее значение рк, МПа

Среднеквадратичное отклонение на участке наблюдения равно Sy — = 0,0076 МПа, что составляет в среднем 3,8 %. Коэффициенты математической модели вычислены по формулам

Математическая модель зависимости давления масла за импеллером от числа его оборотов с числовыми коэффициентами имеет вид

В предполагаемой точке экстраполяции при vM = 2 давление масла равно р — 0,772 МПа. Коэффициент дисперсии предсказания для параболы, рассчитанный по формуле (3.31), равен 4,36. Коэффициент Стьюдента для проведенного числа измерений равен двум при доверительной вероятности Р = 0,95. Расчетное значение давления масла с учетом доверительного интервала в соответствии с выражением (3.17) равно

Расчеты показывают, что доверительный интервал составляет 8,5 % от экстраполируемого значения. Он учитывает погрешность измерения, доверительную вероятность и соотношение интервалов наблюдения и экстраполяции. Таким образом, путем экстраполяции можно убедиться в надежности срабатывания защиты механизма при разгоне турбины путем сравнения полученного значения с заданным и тем самым обеспечить безопасность технической системы.

Пример 2. Рассмотрим процедуру экстраполяции для определения максимальной скорости судна при изменении буксировочной кривой из-за увеличения сопротивления его движению.

Одним из факторов, ограничивающих максимальную скорость судна, является упор на главном упорном подшипнике. При буксировке, плавании во льдах, затоплении части отсеков и в других случаях повышается сопротивление воды движению судна, и значение упора растет. Увеличение упора допускается до тех пор, пока его значение не станет выше предела, указанного в документации. Максимально возможную частоту вращения гребного винта можно определить, используя буксировочную кривую. Для обеспечения достоверности экстраполяции алгоритм необходимо дополнить оценкой доверительного интервала.

Из теоретических соображений и опыта эксплуатации известно, что детерминированная основа зависимости скорости судна от частоты вращения гребного винта представляет собой квадратичную функцию:

При экстраполяции действует гипотеза о том, что детерминированная основа не изменяется при любых условиях плавания судна. Конкретные условия, увеличивающие сопротивление движению, изменяют лишь коэффициенты уравнения (3.36). Естественно, что при п = 0 скорость судна также равна нулю, поэтому минимальное число точек замера скорости и частоты вращения в интервале наблюдения для этой функции равно двум. Коэффициенты уравнения, отражающие конкретные условия плавания, рассчитываются по формулам

где v, v2 — средние значения скорости при измерениях в точках / и 2 интервала наблюдения; янаб — частота вращения, соответствующая середине интервала наблюдения.

При известных значениях коэффициентов уравнение можно использовать для экстраполяции значений скорости судна при различных значениях частоты вращения. Ограничением для развития скорости, как уже отмечалось, является упор на главный упорный подшипник. Из паспортных данных для каждого судна это ограничение отражается линейной зависимостью вида

где Ь, Ь2 — постоянные коэффициенты, известные для конкретного корабля. Совместное решение уравнений (3.36) и (3.38) позволяет получить максимально возможные частоту вращения линии вала и скорость судна в условиях измерений.

Замеры проводились в двух точках при л, = 100 об/мин, п2 — 200 об/мин по пять замеров в каждой. Коэффициенты математической модели найдены с помощью выражений (3.37). В результате совместного решения уравнений (3.36) и (3.38) найдены искомые значения экстраполируемых величин (рис. 3.7). При нормальных условиях в экстраполируемой точке частота вращения равна п — 313 об/мин, а скорость — v — 32,8 уз. В аварийных условиях соот-

Р и с. 3.7. Экстраполяция буксировочной кривой ветственно п = 262 об/мин и v = 21,8 уз. В относительных единицах (см. (3.26)) частота вращения равна соответственно vn = 2,13 и vn= 1,62.

Для используемого числа измерений при доверительной вероятности 0,95 коэффициент Стьюдента равен 2,41. При расчетах доверительного интервала для оценки коэффициента дисперсии предсказания использовали выражение (3.28).

В табл. П.6 приведены окончательные результаты замеров и расчетов скорости движения судна в нормальных и аварийных условиях плавания. Метрологическое обеспечение алгоритма гарантирует с вероятностью 0,95, что экстраполируемое значение частоты вращения линии вала, соответствующее нижней границе доверительного интервала максимальной скорости, не приведет к превышению допустимого упора на гребном валу.

Источник: studref.com

Научная электронная библиотека

При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта. Экстраполируются оценочные функциональные системные и структурные характеристики. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогно­зирования.

С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результа­тивности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др.

Однако степень реальности такого рода прогнозов и соответ­ственно мера доверия к ним в значительной мере обусловливаются аргументированностью выбора пределов экстраполяции и стабиль­ностью соответствия «измерителей» по отношению к сущности рас­сматриваемого явления. Следует обратить внимание на то, что слож­ные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при статистическом анализе тенден­ций и экстраполировании, которое состоит в следующем:

— во-первых, должно быть четкое определение задачи, выдвиже­ние гипотез о возможном развитии прогнозируемого объекта, обсуж­дение факторов, стимулирующих и препятствующих развитию данного объекта, определение необходимой экстраполяции и её допустимой дальности;

— во-вторых, выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;

— в-третьих, сбор и систематизация данных. Перед сведением их в соответствующие таблицы еще раз проверяется однородность дан­ных и их сопоставимость: одни данные относятся к серийным изде­лиям, а другие могут характеризовать лишь конструируемые объекты;

— в-четвертых, когда вышеперечисленные требования выполнены, задача состоит в том, чтобы в ходе статистического анализа и не­посредственной экстраполяции данных выявить тенденции или симп­томы изменения изучаемых величин. В экстраполяционных прогнозах особо важным является не столько предсказание конкретных значе­ний изучаемого объекта или параметра в таком-то году, сколько своевременное фиксирование объективно намечающихся сдвигов, ле­жащих в зародыше назревающих тенденций.

Для повышения точности экстраполяции используются различные приемы. Один из них состоит, например, в том, чтобы экстраполи­руемую часть общей кривой развития (тренда) корректировать с уче­том реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируемый объект.

Под трендом понимается характеристика основной закономер­ности движения во времени, в некоторой мере свободной от случай­ных воздействий. Тренд — это длительная тенденция изменения эко­номических показателей. При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого времен­ного ряда, на которую уже накладываются другие составляющие. Ре­зультат при этом связывается исключительно с ходом времени. Пред­полагается, что через время можно выразить влияние всех основ­ных факторов.

Под тенденцией развития понима­ют некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.

Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20-25 лет. Применяе­мый в прогнозировании метод экстраполяции не дает точных резуль­татов на длительный срок прогноза, потому что данный метод исхо­дит из прошлого и настоящего, и тем самым погрешность накапли­вается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.

Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпиричес­ким значениям применяется метод наименьших квадратов. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи.

Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неуч­тенных.

Рассмотрим простейшие приемы экстраполяции. Операцию экстра­поляции в общем виде можно представить в виде определения значе­ния функции:

где — экстраполируемое значение уровня; L – период упреждения; Уt – уровень, принятый за базу экстраполяции.

Под периодом упреждения при прогнозировании понимается от­резок времени от момента, для которого имеются последние статис­тические данные об изучаемом объекте, до момента, к которому относится прогноз.

Экстраполяция на основе среднего значения временного ряда. В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции к изменению или если это изменение незначительно, можно принятьт.е. прогнозируемый уровень равен среднему значению уровней в прошлом.

Доверительные границы для средней при небольшом числе на­блюдений определяются следующим образом:

где ta – табличное значение t – статистики Стьюдента с n-1 степенями и уровнем вероятности p;- средняя квадратическая ошибка средней величины. Значение ее определяется по формуле . В свою очередь, среднее квадратическое отклонение для выборки равно:

где yt – фактические значения показателя.

Доверительный интервал, полученный как ta, учитывает неопределенность, которая связана с оценкой средней величины.

Общая дисперсия, связанная как с колеблемостью выборочной средней, так и с варьированием ндивидуальных значений вокруг средней, составит величину S 2 +S 2 /n. Таким образом, доверительные интервалы для прогностической оценки равны:

Экстраполяция по скользящей и экспоненциальной средней. Для краткосрочного прогнозирования наряду с другими приемами могут быть применены адаптивная или экспоненциальная скользящие сред­ние. Если прогнозирование ведется на один шаг вперед, то или , где Мt — адаптивная скользящая средняя; Nt — экспоненциальная средняя. Здесь доверительный интервал для скользящей средней можно определить по формуле (2.10), в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой фор­муле n на m, равным нечетным числам.

При экспоненциальном сглаживании дисперсия экспоненциальной средней равна , где S -среднее квадратическое отклонение, вместо величины в фор­муле (2.10) при исчислении доверительного интервала прогноза следует взять величину или . Здесь a- коэффициент экспоненциального сглаживания, изменяется от 0 до 1. Если 0a<0,5, то при расчете прогноза учитываются прошлые значения временного ряда, а при 0,5a

где m – число уровней временного ряда, входящих в интервал сглаживания.

Экстраполяция на основе сред­него темпа. Если в основу прогностического расчета положен средний темп роста, то экстраполируемое значение уровня можно получить с помощью формулы: , где — средний темп роста, Уt — уровень, принятый за базу для экстра­поляции. Здесь принят только один путь развития — развитие по геометрической прогрессии, или по экспонентной кривой. Во мно­гих же случаях фактическое развитие явления следует иному зако­ну, и экстраполяция по среднему темпу нарушает основное допуще­ние, принимаемое при экстраполяции, — допущение о том, что раз­витие будет следовать основной тенденции — тренду, наблюдавшему­ся в прошлом. Чем больше фактический тренд отличается от экспоненты, тем больше данные, получаемые при экстраполяции тренда, будут отличаться от экстраполяции на основе среднего темпа.

Средний темп или определяется на основе изучения прошлого, или оценивается каким-либо другим путем (например, подбор вари­антов для различных ситуаций). В качестве исходного (базового) уровня для экстраполяции представляется естественным взять по­следний уровень ряда, поскольку будущее развитие начинается имен­но с этого уровня.

Статистическая надежность вышеприведенных методов оценивается с помощью коэффициента вариации:

где- среднее квадратическое отклонение;

— среднее значение временного ряда.

Метод считается статистически надежным и может быть использован для прогнозирования, если значение коэффициента вариации не превышает 10%.

Однофакторные прогнозирующие функции

Это такие функции, в которых прогнозируемый показатель зависит только от одного факториального признака.

В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а действие многочисленных влияющих на него факторов. Однако каждому моменту времени соответствуют определенные характеристики всех этих факториальных признаков, которые со временем в той или иной мере изменяются. Таким образом, время можно рассматривать как интегральный показатель суммарного воздействия всех факториальных признаков.

В качестве фактора-аргумента в однофакторной прогнозирующей функции можно использовать не только время, но и другие факторы, если известна их количественная оценка на перспективу.

Наиболее простым из методов прогнозирования является экстраполяция тренда явления (процесса) за истекший период. Тренд (или вековая тенденция) характеризует процесс изменения показателя за длительное время, исключая случайные колебания. Тренд явления находят путем аппроксимации фактических уровней временного ряда на основе выбранной функции. Наиболее часто применяемые при прогнозировании функции показаны в табл. 2.3. В них фактор-аргумент обозначен символом t.

Источник: monographies.ru

Сущность и методы экстраполяции

Сложное слово «экстраполяция» составлено из двух простых. Первое на латыни звучит extra и означает «вне», «за», «снаружи». Второе на той же латыни звучит polire и означает «изменять», «выправлять», «приглаживать». В целом экстраполяция может быть определена как значение вне двух заданных точек.

Она считается оценкой того, что извлечено из известных фактов, которые расширяют данные в неизвестной области, чтобы прийти к предполагаемому результату. Эта концепция также может быть отнесена к предсказанию образа будущего, предполагающего истинность настоящих и прошлых тенденций.

Метод экстраполяции предполагает, что данные или наблюдения в будущем будут по-прежнему похожи. Таким образом, будущие результаты могут быть предсказаны. Ее можно рассматривать как математическую гипотезу. При экстраполяции используются данные и факты определенной ситуации и приводятся прогнозы о том, что может произойти в конечном итоге.

История процесса экстраполяции

Этот метод часто называют экстраполяцией Ричардсона или методом Ромберга. Но это не совсем правильно, поскольку на протяжении веков уже существовали похожие численные методы решения подобных задач. Поэтому знаменитая h2 Ричардсона (экстраполяция для численного решения) не является первой. Подобный метод был применим в вычислениях Гюйгенса еще в 1654 году. Сам термин «экстраполяция» был впервые введен Томасом Д. Кларесоном в 1959 году в книге о науке и художественной литературе.

Методы экстраполяции могут пониматься как расширение данных или процессов, предполагающих, что аналогичный процесс будет применяться и за их пределами. Экстраполяция — важная концепция, используемая не только в математике, но и в других областях, таких как социология, психология, прогнозирование. Например, водитель обычно экстраполирует дорожные условия за пределами своего видения. Экстраполяция может быть отнесена к способу, в котором значения данных рассматриваются как точки x1, x2 . xn, а затем значение приближается к пределу заданного диапазона точек.

1. Простой метод прогнозирования.
2. Не так много данных требуется.
3. Быстрая и дешевая аналитика.

Метод существует в статистических данных. Если какие-то значения периодически убираются, ответ приближается к следующей точке данных. Примером методом экстраполяции является прогноз погоды, в котором рассматривается предыстория данных и экстраполируется прогнозируемая модель будущего. Еще более простой пример, если есть информация о воскресеньях, понедельниках и вторниках, можно экстраполировать среду или четверг.

Недостатки использования экстраполяции:

1. Ненадежность, если имеются значительные колебания в исторических данных.
2. Предположение, что прошлая тенденция будет продолжаться и в будущем, вряд ли возможно во многих конкурентных бизнес-средах.
3. Игнорирует качественные факторы, например изменения вкусов и моды.

Ускорение последовательности

Методы экстраполяции заключается в создании касательной линии в конце известных данных и расширении ее за пределы этой области. Подобно интерполяции, экстраполяция использует множество методов, требующих предварительного знания процесса, который создает существующие точки данных. Метод включает в себя экстраполяцию линейную и полиномиальную, экстраполяцию коники и французской кривой.

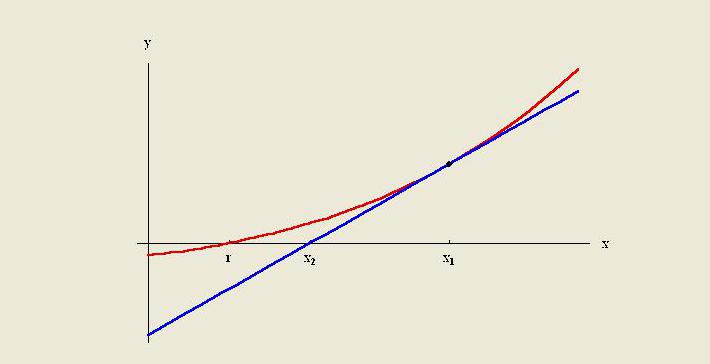
Как правило, качество конкретного метода ограничено предположениями о функции. В численном анализе экстраполяция Ричардсона представляет собой метод ускорения последовательности, используемый для улучшения скорости ее сходимости. Он назван в честь Льюиса Фрая Ричардсона. Он представил технику расчета в начале XX века, полезность которой для практических вычислений вряд ли можно переоценить.

Практические применения экстраполяции Ричардсона включают интеграцию Ромберга, которая применяет ее к правилу трапеции и алгоритму Булирша — Стоера для решения обыкновенных дифференциальных уравнений.

Линейный метод

Метод линейной экстраполяции полезен, когда задана линейная функция. Это делается путем рисования касательной линии в конечной точке заданного графика и расширения ее за пределы. Этот метод экстраполяции в прогнозировании дает хорошие результаты, когда точка, которая должна быть предсказана, не слишком далека от данных. Линейная интерполяция полезна при поиске значения между заданными точками. Его можно рассматривать как «заполнение пробелов» таблицы данных.

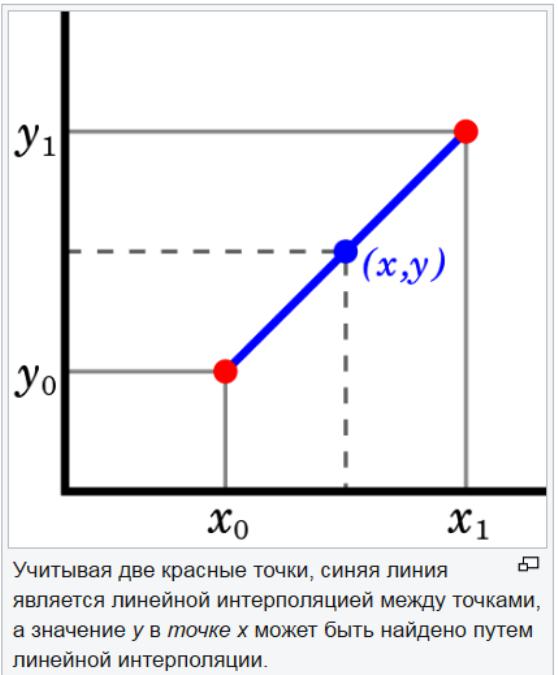
Стратегия линейной интерполяции заключается в использовании прямой линии для соединения известных точек значений по обе стороны от неизвестной. Линейная интерполяция неточна для нелинейных параметров. Если точки в наборе данных меняются на большую величину, линейная интерполяция может дать неправильную оценку.

Линейная экстраполяция может помочь оценить значения, которые выше или ниже значений в наборе данных. Стратегия ее заключается в использовании подмножества данных вместо всего набора. Для этого типа значений полезно применять в прогнозировании метод экстраполяции, используя последние две или три точки, чтобы оценить значение, превышающее диапазон данных.

Полиномиальная и коническая экстраполяции

Известно, что три точки дают уникальный многочлен. Полиномиальная кривая может быть продолжена после окончания таких данных. Она обычно выполняется методом Ньютона с конечной разностью или с использованием интерполяционной формулы Лагранжа. Полином высшего порядка должен быть экстраполирован с должным вниманием, потому что при полиномиальной экстраполяции есть справедливые шансы на ошибку. Если это произойдет, оценка ошибки будет экспоненциально возрастать вместе со степенью полинома.

В математике минимальная полиномиальная экстраполяция представляет собой преобразование последовательности, используемое для ускорения сходимости. Хотя метод Айткена является самым известным, он часто терпит неудачу, особенно для векторных последовательностей. При этом выполняется итерация, которая строит матрицу. Ее столбцы являются отличиями.

К примеру, методом экстраполяции для конического разреза может быть произведен с помощью 5 точек, указанных ближе к концу данных. В случае, если коническая секция представляет собой круг или эллипс, то она будет образовывать петли назад и воссоединиться с собой. Парабола или гипербола никогда не пересекутся. Но они могут быть изогнуты назад относительно оси X. Экстраполяция конуса может быть выполнена на бумаге с конической секцией или с помощью компьютера.

Математический метод оценки

В этом методе экстраполяции прогнозируется значение за базовый период. Действия, описанные ниже, автоматически выполняются системой и не видны пользователю. Описание предназначено для уточнения алгоритма, который выводит ожидаемые значения из количества, хранящегося в системе, и прогнозирует результат измерения счетчика.

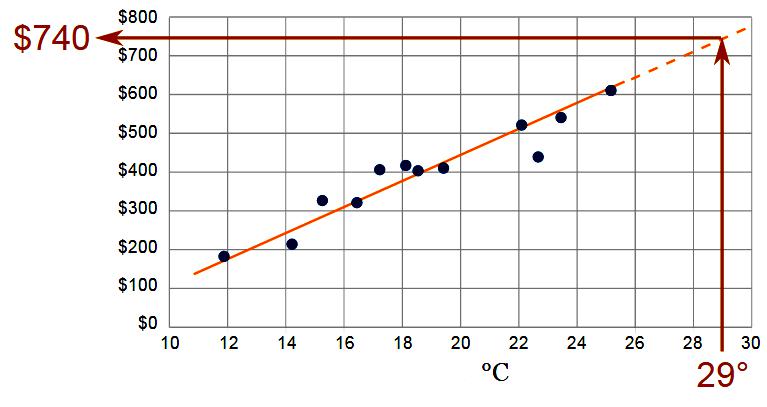
Экстраполяция при использовании определения количества процедуры выполняется с помощью функции: Yt = f (yi, t, aj).

В качестве основы для экстраполяции добавляются округленные данные типичного базового периода, хранящегося в результатах считывания. Система определяет вес Yt данных временного ряда в t (время прогнозируемого периода) для получения правильного решения методом экстраполяции. Где в точке отсчета взяты yi – уровень ряда и aj – параметр уравнения тренда.

Прогнозирование функциональных возможностей

Метод фиксации статистической кривой применим к прогнозированию функциональных возможностей. Статистические процедуры соответствуют прошлым данным одной или нескольких математических функций, таких как линейные, логарифмические, Фурье или экспоненциальные. Наилучшие выбираются статистическим тестом. Тогда этот прогноз экстраполируется из этой математической связи методом математической экстраполяции. Одним из самых простых способов получения приблизительных оценок будущих (или прошлых) условий является экстраполяция данных, которые изменяются со временем.

Например, если нужно провести грубую оценку будущих уровней загрязняющих веществ в питьевых водах на 20 лет вперед, можно экстраполировать эту тенденцию с последних 20 лет. То же наблюдается, если нужно оценить распространенность курения или рак легких в фоновом режиме в будущем. Прогноз можно составить путем расчета тенденции за последние годы. Экстраполяции этого типа можно сделать с использованием менее сложных методов. Во многих случаях (особенно в областях маркетинга и управления бизнесом) традиционно используется метод экстраполяции, например путем просмотра последних данных и интуитивной оценки того, что подразумевается в будущем.

Методы, основанные на правилах, также могут быть использованы путем применения набора предопределенных принципов или ожиданий на основе предварительного понимания системы и учета последних данных для интерпретации будущих событий.

При любом методе в экстраполяции важна осторожность из-за наличия многочисленных неопределенностей. Любая процедура экстраполяции основана на предположении, что в прошлых данных и знаниях имеется достоверная информация. Следовательно, будущее обусловлено теми же факторами, которые действовали ранее.

Ошибки прогнозирования

Ошибочность экстраполяции (точнее, ошибочность неоправданной экстраполяции) возникает, когда явление, ответственное за ряд тривиальных локальных эффектов, считывается в качестве великих глобальных явлений. Еще одна причина ошибки заключается в том, что иногда обобщенные правила выводятся на основе слишком немногочисленных фактов. Так, теория Дарвина об эволюции является фантастическим примером применения метода экстраполяции, в которой механизмы случайных изменений и естественного отбора объявляются для учета развития таких сложных структур, как зрение млекопитающих или иммунная система живых организмов.

При попытке интерпретации результатов исследований ученый должен избегать экстраполяции вне диапазона данных и осознавать лежащие в основе предположения, чтобы избежать принятия недействительных выводов. В общем, экстраполяция является законным научным инструментом. Есть два аспекта, которые помогают различать действительную и ошибочную экстраполяцию. Вероятность ошибочной экстраполяции выше, когда для ее построения были получены точки на недостаточных данных.

Статистические инструменты Excel

Чтобы найти корреляцию между годами и результатами (например, в бизнесе), можно воспользоваться Excel.

Для этих задач используют статистические инструменты для моделирования методом экстраполяции, встроенные во все версии Excel, начиная с 97. Порядок действия:

1. Ввести известные значения, например общие продажи за 2016-2017 годы, если нужно определить их за 2018 и 2020 годы.
2. Установить утилиту Analysis, функцию, требующую использования надстройки.
3. Чтобы установить ее, извлечь из меню «Инструменты», «Дополнения».
4. Проверить окно утилиты анализа и подтвердить с помощью «ОК».
5. Измерить корреляции между двумя сериями.
6. Экстраполяция, которую нужно сделать, имеет смысл только в том случае, если между двумя наборами чисел (годы и продажи) складывается четкая тенденция (корреляция) по методу экстраполяции тенденций.
7. Чтобы измерить эту корреляцию, используют меню «Инструменты», «Утилиты анализа».
8. В списке «Инструменты анализа» выбирают «Анализ корреляции» и нажимают «ОК».
9. В поле Input Range вводят анализируемый диапазон, например A6: B18, Excel добавит символ «$».
10. В области «Параметры вывода» проверяют выходной диапазон и вводят в соседнее поле.
11. Подтверждают с помощью OK.
12. Excel создает массив из двух строк по двум столбцам. Находят расчетное значение (например, 0.981). Поскольку это значение близко к 1, это означает, что существует сильная корреляция между годами и цифрами продаж. Если пользователь получит значение, близкое к нулю, это будет означать, что тенденция не возникает. В этом случае экстраполяция не имеет смысла.
13. Запускается оценка будущих значений.
14. Выбирают необходимый диапазон и нажимают кнопку «Мастер диаграмм».
15. Выбирают диаграмму (например, облака точек) и нажимают «Готово».

Применение скользящих средних

Эти два метода экстраполяции предполагают широкое использование данных по продажам для прогнозирования будущего. Скользящее среднее значение принимает серию данных и «сглаживает» флуктуации в них. Цель состоит в том, чтобы извлекать экстремумы данных из периода в период. Скользящие средние часто вычисляются ежеквартально или еженедельно.

Для прогнозирования будущих значений экстраполяция предполагает использование трендов, установленных историческими данными. Основное предположение экстраполяции заключается в том, что образец будет продолжаться и в будущем, если фактические данные не указывают на иное. Чтобы подробнее разобраться в этих методах, можно рассмотреть диаграмму, показывающую продажи гаджетов для крупного бизнеса с 2012 по 2015 годы.

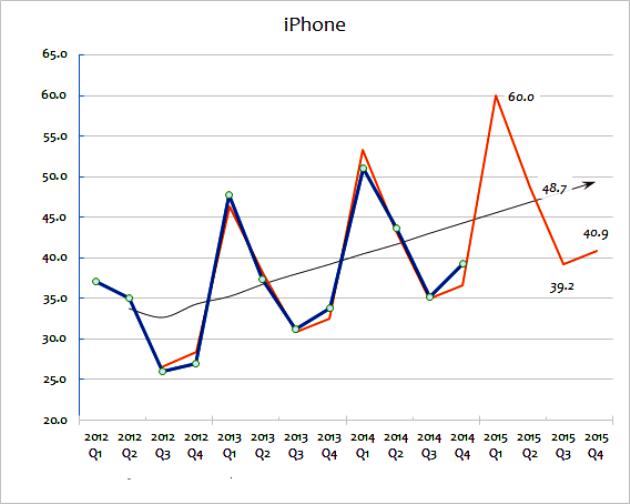
Этот метод экстраполяции расчета показывает фактическую цифру продаж. Как можно увидеть, общая сумма продаж колеблется от года к году, хотя можно догадаться (глядя на данные), что общая тенденция для роста продаж имеется. Черная линия показывает скользящую среднюю. Это рассчитывается путем добавления последних лет продаж (например, Q1 + Q2 + Q3 + Q4), а затем деления на четыре.

Этот метод сглаживает годовые изменения и дает хорошее представление об общей тенденции в годовых продажах. Скользящее среднее помогает указать тенденцию роста, выраженную в процентных значениях. Именно это экстраполяция будет использовать сначала, чтобы предсказать путь будущих продаж. Это можно сделать математически, используя электронную таблицу. В качестве альтернативы экстраполированный тренд можно просто нарисовать на диаграмме в качестве приблизительной оценки.

Корреляция трендов

Всегда одна технология является предшественником другой. Это случается, когда достижения, достигнутые в технологии прекурсоров, могут быть приняты технологией последователей. Когда такие отношения существуют, знание изменений в технологии предшественников может быть использовано для прогнозирования хода технологии последователей в будущем. Кроме того, экстраполяция предшественника позволяет прогнозировать продолжение следования за пределами времени запаздывания.

В этом случае используют метод экстраполяции трендов, в котором сравниваются, например, тенденции скорости боевых и транспортных самолетов. Другим примером прогноза корреляции трендов является прогнозирование размера и мощности будущих компьютеров, основанное на достижениях в области микроэлектронной технологии. Иногда технология последователей зависит от нескольких технологий прекурсоров, а не от одного предшественника.

Фиксированные комбинации предшественников могут влиять на изменение в последовательности, но чаще комбинации не фиксируются, а входы предшественников различаются как по комбинации, так и по силе. Например, увеличение скорости воздушных судов может происходить за счет улучшения двигателей, материалов, элементов управления, топлива, аэродинамики и различных комбинаций этих факторов.

Пример прогноза корреляции, полученной методом экстраполяции трендов: общие пассажирские мили, общие географические мили и средняя посадочная мощность. Экстраполяция статистически определенных тенденций позволяет объективно подходить к прогнозированию. Однако этот подход имеет серьезные ограничения и ловушки. Любые ошибки или неправильный выбор, сделанный при определении исторических данных, будут отражены в прогнозе, что снижает его ценность.

Приложения, атрибуты и лимиты

Метод экстраполяции относится к сфере прогнозирования. Он предполагает, что шаблоны, которые существовали в прошлом, будут продолжаться и в будущем, а также то, что эти шаблоны являются регулярными и могут быть измерены. Другими словами, прошлое является хорошим индикатором будущего. Приложения полезны для разработки базовых данных.

Атрибуты и лимиты — это простые и дешевые инструменты вычислений, как и сложные теоретические модели.

1. Данные процесса — графика и наблюдения.
2. Ключ — наличие хорошей базы данных и понимание структуры внутри нее.
3. Техника — наилучшая подгонка, соотношение и так далее.

Временные стандартные статистические процедуры не приводят к аккуратным подборам тенденций, которые прогнозист может экстраполировать с комфортом, выполняя прогноз методом экстраполяции. В таких случаях прогнозист может «скорректировать» статистические результаты, применяя суждение. Также он может полностью игнорировать статистику и экстраполировать тренд целиком на основе суждения.

Прогнозы, генерируемые таким образом, менее точны, чем статистические, но не обязательно неудовлетворительные. Одним из примеров такой экстраполяции качественного тренда является прогнозирование сложности воздушного судна. Попытки количественной оценки этой тенденции не были успешными. Но процент подвижных или регулируемых частей самолета был экстраполирован с частотой, с которой такие элементы были введены в прошлом. Эти прогнозы были достаточно точными.

Специфические технические изменения не могут быть предсказаны таким образом, но степень изменения может. Это дает полезные материалы для планирования, указывая тенденцию прошлого поведения.

Источник: businessman.ru