Этапы моделирования в строительстве

Все здания, как правило, отличаются друг от друга, как объемно-планировочными, так и конструктивными решениями. Одни объекты относительно просты, другие достаточно сложные, но очевидно, что построить их быстро, с отличным качеством без предварительной оценки особенностей объекта, сложных условий, которые могут возникнуть в процессе строительства теоретически можно, но практически невозможно.

В связи с этим возникает вопрос, а как же можно оценить и проанализировать будущий характер строительства объекта, выявить те особенности, которые могут возникнуть и повлиять на процесс строительства объекта? Выходом является такой прием как — разработка модели строительного производства, позволяющей задолго до начала строительства выявить «узкие» места и предусмотреть организационные мероприятия, обеспечивающие нормальный ход строительства.

Модель – это условный образ объекта, сконструированный для упрощения его исследования. Свойства модели, как правило, отражают свойства оригинала и рассматриваются как элементы для исследования.

Современное проектирование домов: BIM технологии. Библиотеки информационных моделей // FORUMHOUSE

Таким образом, моделируя организацию строительства, появляется возможность получения информации о поведении предполагаемой организационной системы строительства в реальных условиях.

Известны следующие группы моделей: физические, символические, графические.

Физические модели представляют собой некоторую материальную систему, отличающуюся от оригинала в основном размерами, материалами изготовления, расцветкой и т.д. Простейшим представителем физической модели является макет здания. Как правило, физический макет дает общее представление об объекте, на нем можно оценить цветовую гамму, оценить насколько вписывается рассматриваемый объект в существующую застройку. Однако сам макет и его изготовление не могут и не помогут строителям предвидеть сложности, которые могут возникнуть в процессе строительства объекта. Например, изготовление макета корпуса №15 БНТУ вряд ли могло помочь строителям грамотно подобрать и разместить монтажные механизмы, увязать работу всех субподрядчиков, предвидеть сложности, которые могли возникнуть при устройстве монолитных конструкций перекрытия над вестибюлем и другие сложности организации строительства.

Символическиемодели – это модели, отражающие непосредственно сам процесс создания того или иного объекта (системы) и описываемые с использованием языковых или математических способов в виде уравнений;

Графическое моделирование (графические модели) наиболее применимо для отображения процессов организации строительства объекта.

Графическая модель — это способ графического изображения установленной (принятой) последовательности выполнения определенных действий при выполнении комплекса работ или строительства отдельного объекта. Разработка графической модели, например, строительства объекта, является первым шагом (этапом) в разработке основного документа организации строительства — календарного плана строительства объекта.

Модель, как правило, отражает только последовательность выполнения работ, совмещенность и взаимосвязь их между собой. Разработанная в той или иной форме модель строительства должна быть согласована со всеми заинтересованными физическими и юридическими лицами.

Что такое BIM. BIM моделирование. BIM проектирование.

В теории известны и на практике используются следующие виды графических моделей организации строительного производства:

Источник: studopedia.ru

Основы моделирования строительных конструкций и сооружений

Исследование работы конструкций, зданий и сооружений на моделях с применением методов теории подобия называется моделированием. Теория подобия, применяемая при постановке эксперимента и обработке его результатов, позволяет по определенным признакам выявить суть физических явлений, происходящих в испытываемых конструкциях. Различают подобие геометрическое, кинематическое, материальное, динамическое, тепловое, упругое, пластическое и т.д.

Все виды подобия подчиняются трем теоремам.

Первая теорема определяет необходимые условия подобия и формулирует свойства подобных систем: явления или системы называются подобными, если равны их соответствующие критерии подобия, составленные из параметров системы.

Вторая теорема подобия (л-теорема) доказывает возможность приведения уравнения процесса к критериальному виду: функциональная связь между характеризующими процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия.

Третья теорема подобия показывает пределы закономерного распространения единичного опыта: необходимыми и достаточными условиями подобия являются пропорциональность сходственных параметров, входящих в условия однозначности, а также равенство критериев подобия изучаемого в натуре и на модели явления.

К условиям однозначности относятся факторы, независящие от механизма физического явления: геометрические свойства; начальные условия; начальное состояние; граничные или краевые условия; взаимодействие с внешней средой. Если рассматриваются сложные, нелинейные или анизотропные системы, то необходимо соблюдать и ряд дополнительных положений.

При соответствующем техническом обеспечении на моделях возможно решение практически любых задач, связанных с обеспечением надежности конструкций и объектов в целом. Применение моделирования в строительной науке позволяет проводить исследования в более короткие сроки, чем при анализе натурных образцов, а в ряде случаев является единственно возможным.

Моделирование позволяет эффективно решать большое число сложных задач:

• • выявить при минимальных затратах материала, трудоемкости и стоимости действительную картину распределения усилий во всех характерных сечениях и узловых сопряжениях элементов конструкций;
• • произвести анализ напряженного состояния сложного сооружения взамен аналитического расчета, когда затруднительно использовать методы строительной механики и теории упругости;
• • проверить правильность гипотез, положенных в основу аналитического расчета;
• • уточнить расчетную схему сооружения;
• • определить характер разрушения и разрушающую нагрузку;
• • определить реальный запас прочности сооружения;
• • установить влияние различных факторов на работу конструкции — свойств материалов, условий сопряжении, податливости основания и др.

Для новых сложных и малоизученных сооружений исследование может проводиться по следующей схеме:

• • математическое моделирование или исследование маломасштабной модели ( в масштабе 1/10—1/20) с использованием компьютерных программ;
• • исследование крупномасштабной модели (в масштабе 1/2— 1/5);
• • натурные испытания сооружения или его отдельных узлов и элементов с практическим использованием либо физического, либо аналогового, либо математического моделирования с применением поляризационно-оптических методов или голографических моделей.

Существует несколько методов моделирования — создание физических моделей объектов, предметно-математическое и логико-математические моделирование.

На физических моделях можно определять: а) схему разрушения и несущую способность конструкции; б) силовые воздействия на сооружения от ветра, морских волн, давления сыпучих сред, взрывов и др.; в) напряженно-деформированное состояние конструкций и сооружений (надземных, подземных); г) частоты, амплитуды и форму колебаний сооружений при динамических, сейсмических и взрывных воздействиях и др.

Физическое подобие требует полного или частичного воспроизведения физических процессов, протекающих в натурном объекте. Такие модели строительных конструкций имеют меньшие, чем натурный образец, размеры при сохранении их геометрического подобия. При этом натура и модель являются одинаковыми по физической природе: соответственные величины модели и натуры отличаются лишь количественно, но не качественно.

Физическое подобие является основой механического моделирования. С использованием принципов механического моделирования решаются две основные задачи: замена расчета внутренних усилий в элементах конструкций определением напряженно-деформированного состояния идеализированных моделей и моделирование действительной работы конструкций в неупругой и предельной стадии нагружения.

Предметно-математические модели базируются на тождественности математических уравнений, описывающих явления различной физической природы (например, электрическое моделирование задач строительной механики и др.).

Логико-математическими моделями могут быть системы дифференциальных уравнений теории упругости, выражающие взаимосвязь напряжений, деформаций и перемещений тела с силовыми, температурными и другими воздействиями.

Математическое подобие может существовать между явлениями разной физической природы, но описываемыми тождественными уравнениями. Например, уравнение Лапласа описывает распределение суммы главных напряжений в плоской задаче теории упругости; этим же уравнением определяется электрический потенциал в каждой точке плоского проводника, к которому подведен ток. Таким образом, измерение физической величины — электрического потенциала — позволяет исследовать распределение механических напряжений. На этом принципе основаны модели-аналоги, представляющие собой электрические цепи замещения, сеточные интеграторы, а также аналоговые машины непрерывного действия.

В зависимости от целей и требуемой точности результатов различают полное, неполное и приближенное моделирование.

При полном моделировании воспроизводят все свойства моделируемого процесса во всех точках модели, изменяющейся во времени.

Неполное моделирование позволяет воспроизводить свойства оригинала, которые зависят от положения сооружения в пространстве и во время эксплуатации.

При приближенном моделировании ряд свойств объекта учитывается весьма грубо или вообще не воспроизводится на модели.

Для построения физической модели и перехода от результатов испытания модели к оригиналу необходимо знать индикаторы (константы) подобия.

При моделировании физических задач различают физические явления, имеющие математическое описание (класс А); явления, для которых нет уравнений, описывающих процесс, но известны величины, их характеризующие (класс Б); явления, для которых неизвестны даже характеризующие их величины (класс В).

Для явлений класса А можно использовать методы теории подобия, основанные на анализе уравнений, класса Б — методы, базирующиеся на методе анализа размерностей, для явлений класса В применение теории подобия невозможно.

На рис. 3.5 приведена классификация методов моделирования.

При моделировании можно выделить лишь основные факторы, изучение которых является целью данного эксперимента, а при построении модели предусмотреть варьирование этих факторов на заданных уровнях. Достоинством моделирования по сравнению с натурными испытаниями является то, что в лабораторных условиях намного проще обеспечить требуемую точность измерений всех изучаемых параметров.

Следует отметить, что испытание в лаборатории конструкций, например, фермы пролетом 24 м или плиты перекрытия 3 х 12 м, также относится к моделированию в масштабе 1:1, поскольку в этом случае и нагружение, и опирание конструкций моделируются. Вместе с тем, испытания моделей во многом дополняют натурные испытания. Так, изучение воздействий на сооружения кранов, технологического оборудования, ветра и т.д. может быть выполнено только в реальных условиях. Тщательное изучение распределения воздействия между элементами сооружения успешно изучается на моделях, например, при продувке высотных конструкций в аэродинамической трубе или при генерировании морского волнения в лотках.

Моделирование включает следующие операции: построение модели, изучение свойств этой модели при заданных условиях или воздействиях и перенос полученных сведений на моделируемый объект. Моделирование рассматривает только подобные явления. Параметры, характеризующие подобные явления, связаны между собой определенными преобразованиями, позволяющими от эффектов, изучаемых на модели, перейти к исследуемым явлениям в натуре.

Механическое моделирование использует геометрическое и физическое подобие. Пусть координаты натурного объекта описываются функцией — /(Хн, Ун, Z//), а координаты соответственных точек модели — /т(хм, ум, 1Л)? Тогда при полном геометрическом подобии масштаб м = хХ1/Хн = ум/Ун = 1>М/Хн.

При механическом моделировании помимо геометрического подобия необходимо также воспроизвести физическое подобие

Рис. 3.5. Классификация современных методов моделирования

явлений, протекающих и в модели, и в натуре, например, напряженного состояния, форм колебаний и т. п. Если в натурном объекте изучаемая величина, например, перемещение является функцией ряда определяющих ее параметров ин = Г( и„ р 11нп), где ин р ин2. IIн п — механические характеристики материала, физические величины, характеризующие нагрузки и т.д., а соответственные величины, определяющие перемещение точек модели, связаны зависимостью ии = Ф(им р им 2. им п), то для установления условия подобия необходимо найти взаимосвязь между масштабами перечисленных физических величин: т] = им х/11н т 2 = и м 2 и т — д — Значения всех указанных масштабов не могут быть приняты произвольно. Например, можно произвольно назначить линейный масштаб двух геометрических фигур, однако для геометрического подобия фигур необходимо, чтобы масштаб углов всегда был равен единице.

Физическое подобие явлений, протекающих в натуре и модели, обеспечивается только при определенной взаимосвязи между значениями масштабов физических величин. Чтобы назначить эти масштабы и установить взаимосвязь между ними, необходимо определить критерии подобия.

Существует два способа получения критериев подобия: анализ размерностей и критериальный анализ уравнений, которые описывают изучаемое явление. Первый способ применяется для малоизученных явлений, для которых можно составить лишь перечень определяющих эти явления физических величин. Для большинства задач строительной механики успешно реализуется второй способ, так как для них составлены системы уравнений, описывающих поведение изучаемого объекта при заданных воздействиях и граничных условиях. В этом случае условия моделирования могут быть получены методом анализа уравнений, дающим наиболее точные результаты.

При составлении условий моделирования иногда удобнее пользоваться не критериями подобия, а уравнениями масштабов или индикаторами подобия. Для их получения входящие в критерии подобия физические величины заменяют индикаторами подобия.

Очевидно, что для подобных явлений все индикаторы подобия равны единице

Метод анализа размерности применяется для установления критериев полного подобия, когда все величины одинаковой размерности моделируются в одном и том же масштабе. Однако в отдельных случаях по этому методу могут быть получены безразмерные величины, характеризующие условия приближенного подобия.

Для обеспечения подобия изучаемых явлений необходимо, кроме равенства единице индикаторов подобия, обеспечить также подобие начальных и граничных условий. Начальные и граничные условия определяют однозначность результатов моделирования. Условия однозначности включают соответствие способа закрепления модели и натуры, заданных на контуре или поверхности сил и перемещений, соответствие предельных соотношений, в рамках которых рассматривается исследуемая расчетная модель.

Источник: studref.com

4D-моделирование в строительстве

BIM — информационное 3D­моделирование зданий — по­прежнему остается наиболее передовой технологией для реализации комплексных проектов, поэтому строительные организации ищут различные способы внедрения BIM­моделей в строительные рабочие процессы. Но уже сегодня инженеры начинают применять в своей работе технологию 4D­моделирования. Эта концепция добавляет к 3D­модели САПР временной аспект, с помощью которого проектные команды могут анализировать последовательность событий на временной шкале и визуализировать выполнение строительных задач. Эта концепция может быть расширена до «n­мерной», где дополнительные измерения представляют собой другие типы информации, добавленные в контекст 3D­модели.

Ричард Хамфри (Richard Humphrey) — вице­президент по управлению продуктами для строительства в Bentley. Его отдел специализируется на разработке строительных решений. Ричард имеет более 20 лет опыта работы в сфере маркетинга и управления продуктами в высокотехнологичных компаниях.

В недавнем времени он занимал должность вице­президента по маркетингу в компании B2W Software, где под его руководством шла разработка маркетинговой стратегии для продуктов, специализирующихся на проектировании крупных объектов гражданского строительства. В течение 10 лет г­н Хамфри работал старшим директором в Autodesk, где он руководил бизнесом по разработке программного обеспечения для гражданского проектирования и строительства. Получив степень магистра в области гражданского строительства в Университете Карнеги­Меллонан, он начал свою карьеру в области машиностроения, архитектуры и строительства в качестве менеджера проектов в инженерных войсках США и компании Clark Construction. Ричард Хамфри является лидером в области энергетического и экологического проектирования, аккредитованным профессионалом. Он сотрудничает с лидерами в строительной и инфраструктурной отраслях, чтобы обеспечить дальнейшее развитие устойчивого проектирования, технологических инноваций и BIM/VDC.

В строительстве 4D­моделирование используется инженерами, руководителями строительных работ и подрядчиками, и их выбор вполне обоснован: данный тип моделирования вносит положительные изменения в рабочие процессы, которые ранее считались слишком рискованными и неэффективными на этапе строительства. Вот несколько примеров:

• визуализация и планирование на основе модели. 4D­модель позволяет планировщикам и строителям визуализировать как последовательность строительных работ, так и саму строительную площадку (например, краны, зону складирования материалов и доступ к объекту). 4D­модель помогает выявить ошибки на этапе планирования и оптимизирует строительный процесс. Кроме того, это очень удобный способ донести идею проекта до всей строительной команды. Гораздо лучше заранее выполнить строительные работы в виртуальной среде и тем самым оградить себя от ошибок, чем выявлять несостыковки уже на строительной площадке;
• оценка расхода материалов на основе модели. Подход с использованием модели базируется на средствах, методах, количественных расчетах и кодах категорий затрат, позволяющих получать более точную оценку. Данный подход также обеспечивает быструю итерацию при внесении изменений в проект. Кроме того, он позволяет включать затраты уже на этапе планирования, что существенным образом оптимизирует процесс создания проекта. Наличие всей этой информации помогает организациям составлять более точные заявки для участия в тендере;
• альтернативная/виртуальная реальность, контроль процесса строительства и отслеживание хода выполнения работ на основе модели. Мобильные и веб­приложения позволяют использовать строительную модель с географической привязкой на строительной площадке: они обеспечивают доступ к данным и оптимизируют их поиск с применением 3D­модели в качестве контекста. Этот процесс гарантирует, например, то, что сотрудники на площадке собирают данные о правильно сконструированном объекте, потому что используют его модель (виртуальную копию) в качестве ориентира для задачи, которую они выполняют.

Смысл использования 4D­моделирования в том, что разработка строительной модели из проектной BIM­модели с выстроенными рабочими 4D­процессами приводит к созданию проектов, которые с большей вероятностью будут выполнены в установленные сроки и принесут ожидаемую прибыль.

Нынешняя ситуация с крупными проектами в сфере гражданского строительства

Итак, если применение 4D­моделирования в строительстве является практичным, почему оно не используется в каждом проекте? И почему оно так редко применяется при проектировании объектов гражданского строительства? Зачастую в строительстве гораздо проще использовать рабочие процессы на основе моделей, если соответствующие проектные модели созданы. Но это не всегда так.

В частности, в случае с проектами строительства объектов гражданской инфраструктуры это происходит реже (по сравнению с проектами строительства зданий или промышленных предприятий), поскольку владельцы инфраструктуры (например, министерства транспорта) не указывают 3D­модели в качестве проектной документации, поставляемой подрядчикам. Однако время вносит свои коррективы: такие крупные страны, как Великобритания, продвигают применение BIM­технологий, поэтому проектные/строительные модели постепенно получают признание.

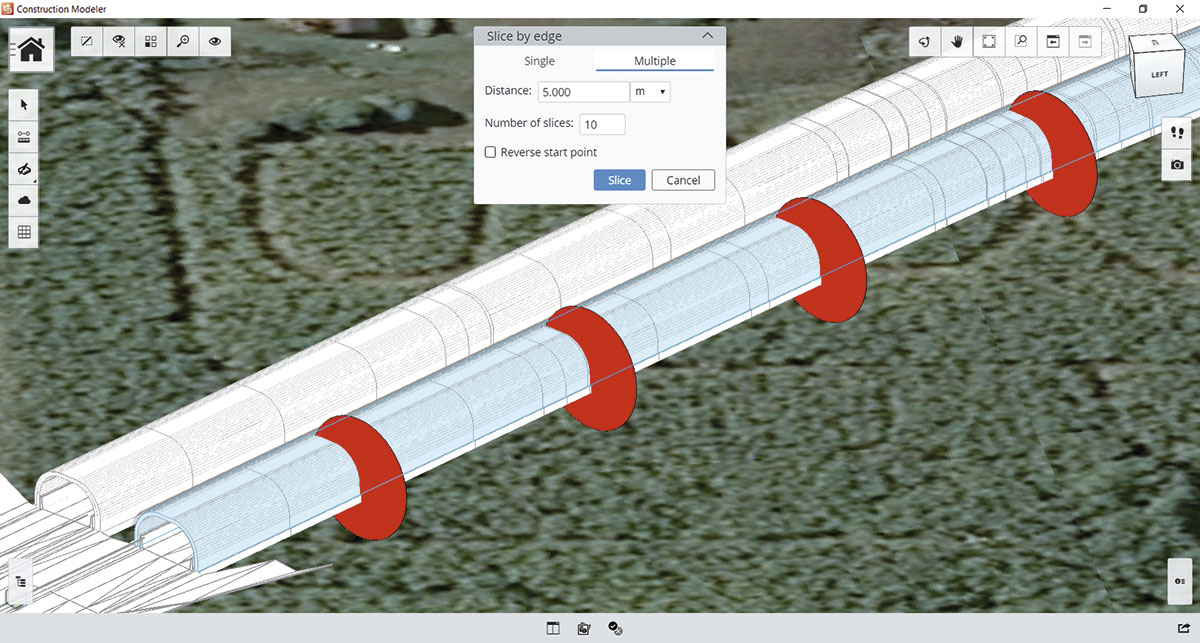
Разбейте крупные проекты на небольшие части и компоненты конструкций для более качественных расчетов и эффективного планирования

Кроме того, в отличие от BIM­моделей зданий или заводов, модели объектов гражданской инфраструктуры не очень удобны для использования в формате 4D. Такая ситуация сложилась еще в прошлом десятилетии, когда появились первые программные инструменты для 4D­моделирования. Модели зданий и заводов проектируются с высокой степенью детализации и соответствующей технической информацией.

Например, модель здания включает двери, окна, стены, освещение, трубы и т.д. — это очень точные элементы, поэтому они могут быть напрямую включены в график строительства. Модели проектов гражданского строительства таким образом не компонуются и поэтому требуют дополнительных этапов обработки, которые превращают объекты модели в компоненты конструкции.

Например, модель 40­километровой дороги/трассы часто представляет собой один длинный объект, если он не разделен мостом или развязкой. Этот тип модели не является компонентом конструкции, поскольку он не создает представление о том, как именно спроектированы 40 километров дорожного покрытия с наполнителями, ограждениями, бордюрами, в результате чего данная модель не может быть напрямую привязана к временным и финансовым затратам. Именно эта дилемма на протяжении всего последнего десятилетия вынуждала строительные организации делать из одной модели множество моделей объекта в рамках всего набора инструментов для проектирования. Это послужило серьезным препятствием для внедрения BIM: моделирование комплексных проектов требует большого багажа знаний в этой области.

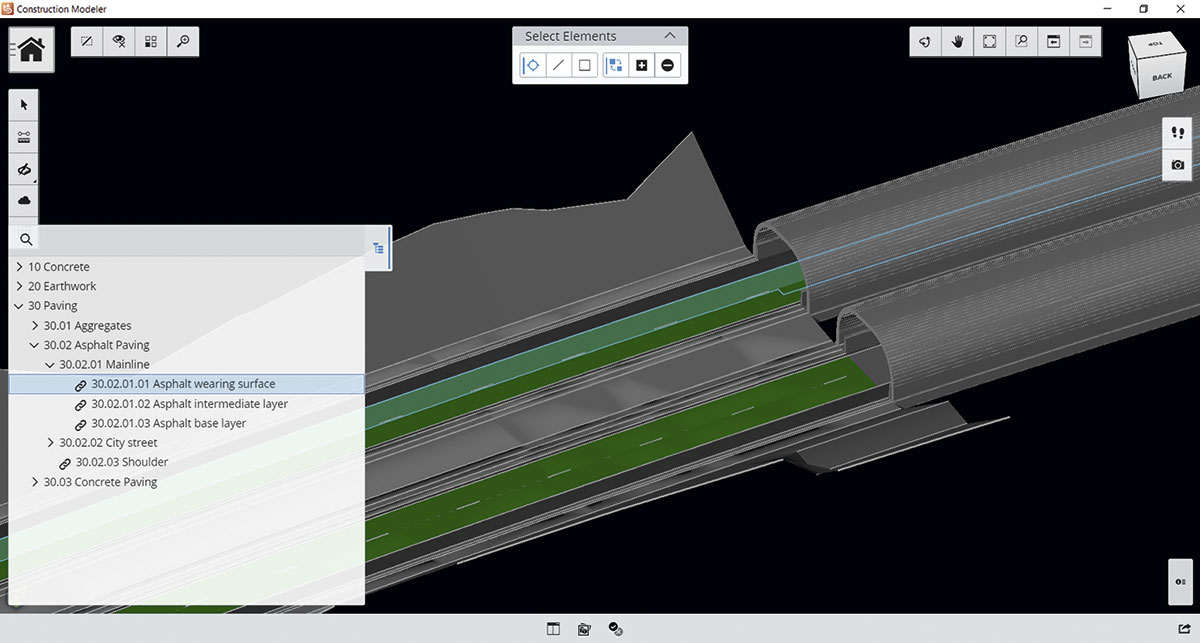
Укажите коды затрат и перечень работ, а также количество материалов, ресурсы и другие структурированные данные

Решение, которое позволит проектировать объекты гражданской инфраструктуры в режиме 4D

Многим строительным организациям пришлось взять решение проблемы в свои руки. Они стали нанимать инженеров по виртуальному проектированию и строительству (VDC), у которых уже был опыт работы с программным обеспечением для проектирования объектов гражданской инфраструктуры или ими предпринимались попытки самостоятельно разработать решения в рамках данного направления. Всё это может измениться в ближайшее время, поскольку компания Bentley Systems, лидер в разработке программных приложений для инженерно­технического проектирования гражданской инфраструктуры, усовершенствовала свое лидирующее в отрасли решение для 4D­моделирования, а это значит, что теперь вы можете с легкостью создавать комплексные модели горизонтальных объектов гражданской инфраструктуры. В частности, Bentley SYNCHRO 4D расширило новый портфель SYNCHRO Construction для решения всех вышеуказанных проблем. SYNCHRO 4D включает среду моделирования, созданную специально для строительных организаций, которая позволяет:

• осуществлять простую навигацию по любой модели (гражданской, промышленной или строительной) и объединять модели;
• разбивать объекты моделей, включая модели объектов гражданской инфраструктуры, на компоненты конструкции. Это включает разбивку сеток и объектов монолитной модели вдоль осей, граней объектов и внутри многоугольников. Данный процесс позволяет инженерам легко создавать модели, которые могут быть построены на основе поэтапной реализации проекта (строительные площадки) или средств и методов (рабочие пакеты);
• применять строительные данные к новым объектам модели, которые сохраняют свою связь с исходным объектом родительской модели. Эти данные включают пооперационный перечень работ, графики, ресурсы, коды категорий затрат и количественные расчеты. В результате получается единая строительная модель, которая обеспечивает последующие рабочие процессы: оценку расхода материалов на основе моделей, составление графика работ и визуализацию в 4D, планирование производственных работ и отслеживание хода выполнения работ на площадке.

Теперь все типы проектов и все классы объектов моделей могут быть частью рабочих процессов 4D­моделирования, а значит создание крупных проектов гражданского строительства становится проще.

Источник: sapr.ru

Презентация на тему: Моделирование в строительстве

Первый слайд презентации: Моделирование в строительстве

В этом разделе будут рассмотрены основные понятия моделирования и виды экономико-математических моделей в области организации, планирования и управления строительством

Слайд 2: Основные положения

Практически для любой задачи организации, планирования и управления строительством характерна множественность ее возможных решений, зачастую большая неопределенность и динамичность осуществляемых процессов. В процессе разработки плана работы строительной организации, плана возведения объекта строительства приходится сравнивать между собой огромное количество вариантов и выбирать из них оптимальный в соответствии с выбранным критерием.

Критерий — это тот показатель, который является мерилом эффективности плана (пути) достижения цели. Для предварительного анализа и поиска эффективных форм организации, а также планирования и управления строительством используется моделирование. Моделирование — это создание модели, сохраняющей существенные свойства оригинала, процесс построения, изучения и применения модели.

Моделирование является основным инструментом анализа, оптимизации и синтеза строительных систем. Модель — это упрощенное представление некоторого объекта (системы), процесса, более доступное для изучения, чем сам объект. Моделирование дает возможность проводить эксперименты, анализировать конечные результаты не на реальной системе, а на ее абстрактной модели и упрощенном представлении-образе, привлекая, как правило, для этой цели ЭВМ. При этом необходимо иметь в виду, что модель является лишь орудием исследования, а не средством получения обязательных решений. Вместе с тем она дает возможность выделить наиболее существенные, характерные черты реальной системы.

Слайд 3

Современное строительство как системный объект характеризуется высокой степенью сложности, динамичностью, вероятностным характером поведения, большим числом составляющих элементов со сложными функциональными связями и другими особенностями. Для эффективного анализа и управления такими сложными системными объектами необходимо иметь достаточно мощный аппарат моделирования.

В настоящее время интенсивно ведутся исследования в области совершенствования моделирования строительства, однако практика пока еще располагает моделями с довольно ограниченными возможностями полного адекватного отображения реальных процессов строительного производства. Разработать универсальную модель и единый метод ее реализации в настоящее время практически невозможно.

Одним из путей решения данной проблемы является построение локальных экономико-математических моделей и методов их машинной реализации. В общем случае модели подразделяются на физические и знаковые. Физические модели, как правило, сохраняют физическую природу оригинала.

Для построения знаковых моделей может использоваться, в принципе, любой язык — естественный, алгоритмический, графический, математический. Наибольшее значение и распространение имеют математические модели в силу универсальности, строгости, точности математического языка. Математическая модель представляет собой совокупность уравнений, неравенств, функционалов, логических условий и других соотношений, отражающих взаимосвязи и взаимозависимости основных характеристик моделируемой системы. Проблема выбора оптимальных решений имеет, применительно к каждой конкретной задаче, свои специфические особенности, а круг таких задач весьма широк. Тем не менее возможно и полезно выделить некоторые характерные черты и вытекающие из них общие подходы к постановке задач оптимизации и поиску наивыгоднейших решений.

Слайд 4

Оптимальные решения в технико-экономических задачах должны отбираться не путем использования интуитивных представлений, а, как правило, на основе строгого расчета. Для этого исходную технико-экономическую задачу необходимо соответствующим образом формализовать, т.е. описать с помощью математических выражений характерные для нее связи, зависимости между параметрами.

Совокупность всех этих математических выражений и составляет, вместе с экономической характеристикой входящих в них величин, экономико-математическую модель задачи (объекта исследования, системы). Таким образом, экономико-математическая модель — это математическое описание экономического процесса (объекта, системы).

Корректно составленная и предназначенная для практического использования модель должна удовлетворять двум условиям: — адекватно отражать наиболее существенные черты анализируемого явления, процесса, системы; — должна быть разрешима, т.е. в описывающей ее системе условий должны отсутствовать математические, экономические, технологические противоречия и иметься эффективные вычислительные алгоритмы для поиска решений. Так как экономико-математическая модель — это всего лишь постановка экономической задачи на математическом языке, то для ее решения необходимо разработать или подобрать из существующих метод решения (алгоритм). Экономико-математические модели подразделяются на описательные (не содержащие управляемых переменных) и конструктивные, (бывают статистическими и динамическими, открытыми, учитывающими внешние воздействия на моделируемый объект, и закрытыми, содержащими управляемые переменные), а по форме представления аналитическими, графоаналитическими, графическими и т.д. Экономико-математические модели являются основой применения математических методов и электронно-вычислительной техники в экономике.

Слайд 5

Экономико-математические методы (термин введен В.С.Немчиновым) представляют собой комплекс экономических и математических дисциплин, таких как: — экономико-статистические методы (экономическая статистика, математическая статистика); — эконометрия — наука, изучающая конкретные количественные взаимосвязи экономических объектов и процессов (с помощью математических и статистических методов и моделей); — исследование операций (методы принятия оптимальных решений); — экономическая кибернетика — отрасль науки, занимающаяся приложением идей и методов кибернетики к экономическим системам. Использование экономико-математических методов и ЭВМ в целях оптимального планирования и управления строительным производством требует последовательного выполнения ряда ниже перечисленных работ математического, технического, информационного и экономического поряд­ка, таких как: — разработка экономико-математических моделей; — подготовка соответствующих алгоритмов и вычислительных схем; — программирование для электронных вычислительных машин; — формирование необходимой информации или исходных данных, требующихся для соответствующих расчетов; — классификация и кодирование объектов для расчетов на ЭВМ; — анализ полученных результатов и их использование в практической деятельности.

Слайд 6: Модели линейного программирования

Слайд 7

Пример. Пусть фирма специализируется на строительстве двух типов складских помещений. Известны производственные и ресурсные возможности фирмы, стоимость 1кв.м каждого из складских помещений. Требуется определить, сколько нужно строить складских помещений каждого типа, чтобы выручка от их продажи была максимальной.

Введем следующие обозначения: — количество изготавливаемых складских помещений J -ого типа; — рыночная стоимость складского помещения; — затраты i -ого вида ресурсов на одно складское помещение J -ого типа; — общий объем имеющихся ресурсов i -ого вида. Составим математическую модель. Показатель эффективности, который необходимо максимизировать, — выручка от реализации складских помещений (обозначим ее С), линейно зависит от элементов решения и x 2 :

Слайд 8

Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х 1 и х 2. Постановка задачи сводится к следующему: найти такие неотрицательные значения переменных х 1 и х 2, чтобы они удовлетворяли ограничениям — неравенствам (1) и одновременно обращали в максимум целевую функцию этих переменных: Поскольку в задаче фигурируют только две неизвестных величины, то решение задачи может быть получено графически.

Слайд 9: Нелинейные модели

Слово нелинейные показывает, что соответствующие задачи описываются нелинейными уравнениями. Свойство нелинейности состоит в том, что о результат взаимодействия нескольких факторов не равен простой алгебраической сумме их действий.

Например, если планировать одновременную работу двух рабочих, то их производительность будет одна, если четырех — она может быть и меньше из-за недостаточности фронта работ, несогласованности действий рабочих и т.д. Нелинейная зависимость между переменными характерна и для задач размещения, в которых неизвестными являются не только пункты производства, но и объемы производства в каждом из них.

Затраты на выпуск единицы строительной продукции обычно уменьшаются с ростом объема производства нелинейно. Поэтому в критерии оптимальности задачи размещения производства, представляющем собой приведенные затраты на производство и транспортировку продукции, будут содержаться нелинейные члены. Алгоритмом для поиска решений в случае нелинейных моделей является математический аппарат нелинейного программирования. Если целевая функция отыскивается в условиях неопределенности, то такая задачи относится к стохастическому программированию. Применительно к экономико-технологическим явлениям и процессам нелинейное программирование относится к наиболее неизученному математическому направлению.

Слайд 10: Модели динамического программирования

Динамическое программирование — это метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы (шаги). Он включает многошаговые детерминированные модели задач оптимального распределения ресурсов; расчет развития на перспективу производственной базы стройиндустрии, производства и хранения продукции во времени, при меняющемся спросе на нее, рациональная загрузка транспортных средств и др. В основе метода динамического программирования лежит принцип оптимальности, который может быть сформулирован следующим образом: чтобы получить оптимальное решение, надо руководствоваться правилом -каков бы ни был путь достижения исследуемой системой некоторого состояния, последующие решения должны принадлежать оптимальной стратегии для остающейся части пути, начинающейся с данного состояния. Сущность метода динамического программирования описывается так называемым динамическим рекурентным соотношением Fn(S) – стоимость, отвечающая стратегии минимальных затрат для пути из состояния S до конечного состояния системы, если остаток пути состоит из n шагов; Jn (S) – решение, позволяющее достичь ; Csj – стоимость перевода исследуемой системы из состояния s в состояние j

Слайд 11: Оптимизационные модели

Оптимизационные модели представляют собой обширный класс экономико-математических моделей, позволяющих выбрать из всех возможных решений самый лучший, оптимальный вариант. В математическом смысле оптимальность понимается как достижение экстремума критерия оптимальности. Оптимизационные модели решаются с помощью методов математического программирования с использованием электронно — вычислительной техники и формируются в общем виде следующим образом: «Надо отыскать значения показателей Х 2. Х n, характеризующие экономический объект или процесс, придающие максимальное или минимальное значение нулевой (целевой) функции F (Х 1, Х 2. Х n ), при соблюдении ограничений, накладываемых на область изменения показателей, Х 2. Х n, и связей между ними в виде Если решение Х 1, Х 2. Х n не противоречит ограничениям, принятым в задаче, то его называют допустимым. Допустимое решение, при котором нулевая функция принимает экстремальное считается оптимальным. Иначе говоря, полученные таким обратом значения неизвестных Х 1, Х 2. Х n будут искомыми величинами в рассматриваемой задаче Оптимизационные модели в строительстве чаще всего встречаются в задачах отыскания лучшего способа использования экономических и материальных ресурсов, размещения производственных мощностей предприятий по производству строительных изделий, парка строительных машин и т.д.

Слайд 12: Модели управления запасами

Модели управления запасами используются при необходимости определения в строительстве объема запаса строительных материалов, конструкций и изделий, характера изменения его в процессе возведения объекта, обновления запаса в связи с поступлением и расходованием ресурсов, с целью обеспечения бесперебойности и надежности строительного процесса при минимальных затратах, связанных с хранением, пополнением, расходованием запаса. Так как уровень спроса неожиданно возникающих потребностей в ресурсах носит чаще всего случайный характер, то модели управления запасами должны быть стохастическими, вероятностными, в упрощенной постановке возможно использование детерминированных моделей. В строительстве чаще всего применяются модели управления складскими запасами. В общем виде экономико-математическая модель управления запасами может быть представлена: где З (t) — текущий уровень запаса стройматериалов на складе в момент t ; Знач — начальный запас материалов на складе в момент t = 0; P(t) — поступление материалов на склад за время t ; R(t) — расходование материалов со склада за время t ;

Слайд 13

Слайд 14: Целочисленные модели

Найти целочисленный оптимальный план — задача непростая. Для решения ее требуется применение довольно тонких специальных математических методов (например, метод «Гомори», основанный на идеях симплекс-метода) Одним из примеров целочисленного программирования является задача о назначениях.

Покажем на примере сущность этой задачи и алгоритм ее решения, в основе которого лежит так называемый венгерский метод. Пример. Пусть имеется необходимость перебросить пять строительных бригад к месту строительства пяти различных объектов. Под назначением понимается факт приписки бригады к одному из объектов Задача состоит в том, чтобы найти такое назначение, при котором общее время доставки бригад к месту работы было минимальным. Представим время доставки i -ой бригады в j — ый пункт назначения и виде табл.5.

Слайд 15

3 5 7 2 4 6 7 3 1 3 4 5 6 3 7 8 5 4 3 9 1 4 5 1 2 5 5 2 0 1 3 4 4 2 6 7 3 3 1 8 Таблица 5 Таблица 6 Основной принцип задачи о назначениях состоит в следующем: оптимальность решения не нарушается при уменьшении (увеличении) элементов t ij строки (или столбца) таблицы (матрицы) на одну и ту же величину t.. Алгоритм решения может быть представлен в виде этапов.

Слайд 16

Этап 1. Образование нулей. Среди элементов каждого столбца табл. 1 выбирается наименьший элемент (в таблице эти элементы обведены кружочками) и вычитается из всех элементов этого столбца. В результате этих действий получаем таблицу 6, в которой элементами являются разности Таблица 7 Таблица 8

Слайд 17

Этап 2. Поиск возможного оптимального решения Оптимальное решение в данной постановке означает, что все затраты имеют нулевое значение. Если такое решение найти не удалось, то следует перейти к третьему этапу. Последовательность действий при поиске оптимального решения состоит в следующем.

Анализ табл.6 начинается с выявления строк, содержащих минимальное число нулей, при этом один из нулей такой строки обводится квадратиком. Затем вычеркиваются все остальные нули, находящиеся в этой строке. Процесс продолжается до тех пор, пока в таблице все нули будут либо обведены квадратиками, либо вычеркнутыми. На данном этапе оптимального решения получить не удалось, так как во второй строке таблицы нет нулевого элемента. Возьмем, например, элемент = 5, тогда решение будет иметь вид: = 5 + 0+0 + 0 + 0 = 5, а это решение не оптимально (см. табл.6).

Слайд 18

Этап 3. Образование набора строк и столбцов, содержащих все нули, имеющиеся в таблице (см. табл.7) Последовательность действий: 1. Пометим крестиком (х) строки, не содержащие ни одного обведенного квадратиком нуля. В нашем случае строка 2. 2. Отметим каждый столбец, содержащий зачеркнутый нуль хотя бы одной из помеченных строк. В нашем случае 5-ый столбец. 3. Пометим каждую строку, в которой содержится обведенный квадратиком нуль хотя бы в одном из помеченных столбцов. В нашем случае строка 1 4. Далее повторяем перечисленные действия 2 и 3 пока не останется строк и столбцов, которые еще можно пометить. Переходим к этапу 4.

Слайд 19

Этап 4. Завершение этапа 3 Прочеркнем каждую непомеченную строку и каждый помеченный столбец (см. табл.7). Прочеркнем строки 3, 4, 5 и 5-ый столбец. Переходим к этапу 5. Этап 5. Добавление нулей В части таблицы, состоящей из неперечеркнутых элементов, выберем наименьший элемент (см.табл.7). Это будет элемент 1-ой строки, равный 1. Вычтем этот элемент из всех элементов столбцов 1, 2, 3, 4, 5 и прибавимего ко всем элементам перечеркнутых строк, т.е. строк 3, 4, 5. В результате получаем табл.8. Этап 6. Получение оптимального решения или переход к этапу 3 Оптимальное решение определяется в последовательности, описанной в этапе 2. Повторив этап 2, получим таблицу 8. В табл. 8 нули, обведенные квадратиками, образуют оптимальное решение: t 11 +t 25 +t 32 +t 43 +t 54 =3+1+1+2+1=8

Слайд 20: Цифровое моделирование (метод перебора)

Одним из простейших и, пожалуй, наиболее распространенных методов оптимизации является метод перебора (сканирования). Сущность этого метода состоит в следующем. Пусть в процессе моделирования производственной ситуации, по которой необходимо принять решение, получена символьная модель вида: где w — общий критерий функционирования; c i — множество управляемых переменных; v i — множество неуправляемых переменных; f — соотношение, связывающее управляемые и неуправляемы переменные. Чтобы получить желаемое решение, нужно определить значения управляемых переменных, максимизирующие или минимизирующие критерии функционирования системы W. Основной недостаток — большие затраты времени, особенно в связи с возрастанием размерности задачи.

Слайд 21: Имитационные модели

Для количественного анализа и решения задач, не имеющих строгого аналитического описания, используется имитационное моделирование. Имитационная модель не ставит целью получение точного решения задачи, но она и не связывает себя слишком жесткими математическими предписаниями. Она не решается в аналитическом смысле, а осуществляется именно «проигрывание», «прогон» модели. Имитационное моделирование имеет ряд преимуществ по сравнению с аналитическим: это возможность применять модели, адекватные реальным системам, неограниченно экспериментировать с моделью, внося различные допущения, фактор неопределенности и т.д. (напомним, что аналитическая оптимизация динамических вероятностных процессов наталкивается на очень большие трудности). Имитационные модели могут применяться в самых различных областях управленческой деятельности: для исследования, принятия и проверки решений, полученных другими методами; построения и оценки альтернатив, расчета широкого диапазона прогнозов и оценок будущего состояния производсвенной системы; оценки долгосрочных последствий от принято решения ; формирования календарного расписания производственной деятельности с вероятностными сроками начала и окончания работ или этапов и.т.д.

Слайд 22: Вероятностно — статистические модели

Это модели, учитывающие влияние случайных факторов в процессе функционирования строительных систем, основаны на статистической, т.е. количественной оценке массовых явлений, позволяющей учитывать их нелинейность, динамику, случайные возмущения, описанные разными законами распределения. Вероятностно-статистические модели изучаются как с привлечением традиционного арсенала средств и методов теории вероятности и математической статистики (теория массового обслуживания, факторный анализ, стохастическое программирование и т.д.), так и путем статистического моделирования, представляющего собой числовую имитацию с помощью ЭВМ функционирования модели.

Слайд 23: Модели теории игр

Теория игр — это математическая теория разрешения таких ситуаций, в которых сталкиваются интересы сторон, преследующих различные цели. Игра представляет собой математическую модель конфликтной ситуации, с помощью которой участвующие в ней стороны, действуя по определенным правилам, пытаются найти стратегию поведения, гарантирующую, в результате разрешения конфликта, достижение желаемой цели. Результат действий одной из сторон зависит не только от ее действий, но и от действий, выбранных противниками. Таким образом, задачей теории игр является установление таких способов действий, которые обеспечивают наибольшую выгоду каждого из участников игры. C тратегия — это совокупность правил и рекомендаций по ведению игры от начала до конца.

Слайд 24: Модели итеративного агрегирования

Итерация (от лат. iteratio — повторение) — повторное применение каких-либо математических операций. При использовании математических моделей на различных уровнях иерархии управления приходится иметь дело с агрегированием (укреплением ) информации. Очевидно, что для моделей более высоких уровней управления характерна большая степень агрегирования показателей, чем для моделей низких уровней, система показателей которых может быть весьма детализированной. Поэтому при согласовании решений «по вертикали» приходится иметь дело с проблемой, связанной с неодинаковой степенью детализации показателей моделей разных уровней. Для решения этой проблемы разрабатываются модели и методы итеративного агрегирования.

Слайд 25: Организационно-технологические модели

Организационные, организационно-технологические и технологические модели представляют графическое или формализованное описание процессов возведения зданий, сооружений, структуру управления этими процессами, строительной организацией и т.д. В любой организационно-технологической модели должны быть описаны перечень строительно-монтажных работ, порядок их выполнения, характер взаимосвязей между работами, отражающих специфику технологии строительства, строительные нормы и правила, необходимость рационального использования ресурсов и т.д. Организационная модель наглядно и просто отображает структуру управления строительно-монтажной организацией, в то время как экономико-математическая модель строительной организации чрезвычайно сложна ввиду ее многозвенности и динамичности. Различают дискриптивный и нормативный (прескриптивный) методы разработки организационных моделей. Организационные, организационно-технологические и технологические модели являются одним из инструментов организации, планирования и управления производственно-хозяйственной деятельностью строительно-монтажных организаций и строительным производством

Слайд 26: Графические модели

Для анализа структуры, связей, процессов и отношений в производных системах используются графические модели, обладающие определенной наглядностью и универсальностью, позволяющей рассматривать их в любых направлениях, по частям или в целом. На практике графические методы моделирования классифицируются по содержанию и форме на три основные группы: оргограммы, т.е. графики, отражающие организационные отношеия в производственных системах. К ним относятся классификационные схемы, оргасхемы, оперограммы, органиграммы и т.д. Оргограммы используются для моделирования организационных структур и процессов; хронограммы (пооперационные, контрольные, сборочные и другие графики); томограммы (схемы обслуживания рабочих мест, маршрутные схемы, циклограммы и т.д.). диаграммы и номограммы — это графики количественных отношений (соотношений) различных величин. Номограммы дают также возможность определить некоторые величины без специальных вычислений.

Последний слайд презентации: Моделирование в строительстве: Сетевые модели

Сетевая модель, помимо графической интерпретации, может быть представлена, например, и виде таблицы или массива исходных данных для ЭВМ. Термин сетевая модель (сетевой график, логическая сеть) основывается на понятии ориентированного графа. Ориентированным графом называется совокупность множества точек и множества ориентированных дуг, соединяющих эти точки.

Область графа, ограниченная несколькими т очками (вершинами), некоторые из них не имеют входящих или выходящих дуг, носит название сети. Сеть, моделирующая определенный с троительный процесс (программу), называется сетевой моделью данного процесса (программы). При этом ориентация дуг графа осуществляется в соответствии с логикой (технологией) этого процесса. Сетевые модели могут описать взаимосвязи между работами и определенный класс организационно-технологических схем строительных процессов. Значительным достижением, в настоящее время, является разработка способов построения стохастических сетевых моделей, в которых анализируемые параметры имеют вероятностный характер.

Источник: slide-share.ru