Применение тройных интегралов
Когда просто относительно осей понимаю, а вот такие не совсем. Не могли бы объяснить как составить.
Вычисление кратных интегралов повторное применение квадратурных формул
Здравствуйте уважаемые 🙂 тут такое дело. мне курсач задали по численке на тему «Вычисление.
Применение определенных интегралов
Правила форума CyberForum.ru 4.7. Как можно более полно описывайте суть проблемы или вопроса, что.
Информационные технологии в строительстве
В этой работе мы рассмотрим основные направления применения IT-технологий в строительстве.
Информационные технологии в строительстве
Какие Информационные технологии в строительстве?
програмка для сдельной оплаты труда в строительстве
нужна программа для расчета сдельной оплаты труда на 200 человек, и никак не могу решить этот.
Техника безопасности в строительстве , сначала теория базы данных подключения к тесту
Техника безопасности в строительстве , сначала теория базы данных подключения к тесту. Я не могу.
Зачем нужен ИНТЕГРАЛ. Объяснение математического смысла.

Определить минимально возможное количество мостов, которые необходимо задействовать при строительстве метрополитена
Помогите, пожалуйста #include <iostream> using namespace std; int main() < int.
Источник: www.cyberforum.ru
II. Применение определенного интеграла при решении физических и технических задач.
Определенный интеграл широко используется при вычислениях различных геометрических и физических величин: вычисление площади плоских фигур, вычисление объемов тел вращения, вычисление длины дуги, вычисление пути, пройденного телом, вычисление работы силы.
I. Вычисление площадей плоских фигур.
Фигура, ограниченная кривой y = f(x), осью 0х, прямыми х = а, х = в называется криволинейной трапецией.
Расположение графиков функций
на координатной плоскости
№1. Используя данные из таблицы, для каждого рисунка напишите формулу, по которой вычисляется площадь заштрихованной фигуры.
1) 2) 3) 4)
Алгоритм нахождения площади фигуры:
1. Построить на одной координатной плоскости графики данных функций.
2. Заштриховать фигуру, ограниченную построенными линиями.
3. Найти точки, ограничивающие фигуру справа и слева.
4. Найти площадь фигуры по соответствующей формуле.
Пример 1. Найти площадь фигуры, ограниченную линиями: и
Решение: Построим графики данных функций
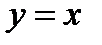
— прямая
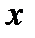 |
1 | 0 | -1 |
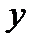 |
1 | 0 | -1 |
Применение производной и интеграла в технике
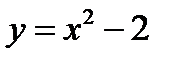
— парабола, ветви вверх
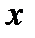 |
0 | 1 | -1 | 2 | -2 |
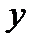 |
-2 | -1 | -1 | 2 | 2 |
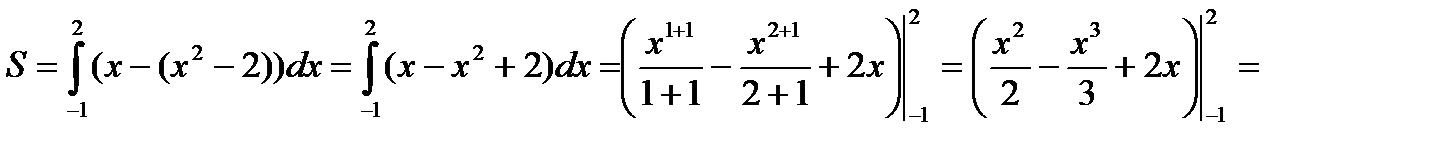
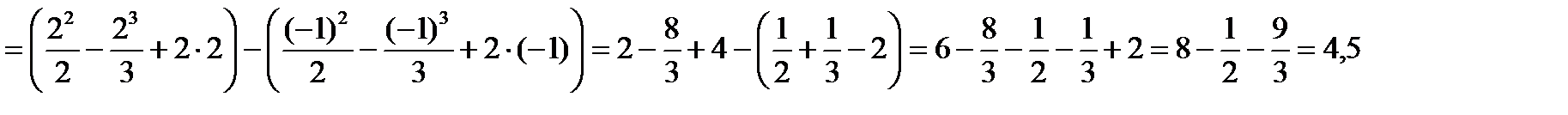
№2.Найти площадь фигуры, ограниченную линиями: и
II. Применение определенного интеграла при решении физических и технических задач.
1. Задача о вычислении пути.
Пусть материальная точка движется прямолинейно с некоторой мгновенной скорость v = v(t). Требуется найти путь, который пройдет тело за промежуток времени от t = T1 до t = T2.
В простейшем случае, если мгновенная скорость постоянна, то путь, пройденный телом равен (по определению, известном из курса физики) произведению скорости на время движения: . В общем случае, когда мгновенная скорость не постоянна, её вычисляют по формуле:
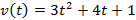
Пример 2: Тело движется прямолинейно со скоростью м/с. Найти путь, пройденный телом за первые 3 сек.
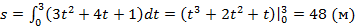
Решение: по формуле получим
Пример 3: Точка движется прямолинейно со скоростью v(t) = at + v0 . Какой путь пройдет точка за промежуток времени от t = T1 до t = T2 ?
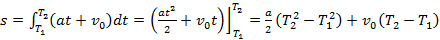
Решение: По формуле получим
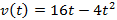
Пример 4: Тело движется прямолинейно со скоростью . Найти длину пути от начала движения до его остановки.
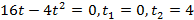
Решение: Скорость тела в момент начала его движения и остановки равна 0. Найдем момент остановки тела. Приравняв для этого его скорость к нулю и решив уравнение, получим: .
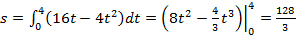
Далее, по формуле имеем:
Источник: studopedia.ru
Интегралы в курсе «Механика грунтов»
Ключевые слова: интеграл, механика, грунты.
При подготовке специалистов в области промышленного, гражданского, транспортного, сельскохозяйственного и других видов строительства осваиваются геотехнические дисциплины, изучение которых требует знание основ по методам расчета грунтов. Среди геотехнических дисциплин особое место занимает курс «Механика грунтов», который выделен в самостоятельную дисциплину и является теоретической подготовкой по другим дисциплинам, включающих грунтоведение, инженерную геологию, основания и фундаменты.
В работе Карташова В.Ф. [1] проведен анализ межпредметных связей курсов математики в ЧИПСе и «Механики грунтов». Почти треть от числа всех связей приходится на интеграл и его применение. Это свидетельствует о том, что данный раздел математики является профессионально значимым при подготовке будущих строителей железных дорог.
Покажем, каким образом понятие интеграла используется в курсе «Механика грунтов». Вычисление интегралов используется в теме «Растяжение и сжатие». Чтобы более детально разобраться, рассмотрим пример, в котором с помощью интегрирования мы найдем деформацию и перемещение.
На примере вывода формулы осадки в задаче Фламана, который взят из пособия [2], покажем, как определяются деформации и перемещения, если известны напряжения. Согласно закону Гука и уравнениям Коши ,



Отсюда после подстановки выражения для напряжений и интегрирования получаем:

где f(x) — произвольная функция х.
Входящие в это выражение интегралы можно найти в любой справочной таблице интегралов:


После их подстановки получим:

Осадки точек поверхности основания получим, положив здесь

Предположим, что при х = ± x0 имеем s = s0. Тогда

Подставив значение f(x) в предыдущее выражение, окончательно получим:

где С — произвольная постоянная в силу произвольности величины sq.
Таким образом, в задаче Фламана осадку можно определить только с точностью до произвольного слагаемого. [1 с.134-135]
Далее рассмотрим пример с использованием определенных интегралов в «Механике грунтов» из темы «Задача о равномерной полосовой нагрузке (задача Мичелла, 1902 г).
Задача является важной в практическом отношении, поскольку считается, что ленточный фундамент создает равномерное полосовое давление на основание. В этом же случае наиболее просто выполняется интегрирование в формулах. Однако предпочтительнее получить решение в переменных r,θ, используя в качестве исходных формулы задачи Фламана. Полученные при этом выражения имеют более компактный вид.

Приложенное к полоске давление p0 заменим элементарной сосредоточенной силой:

Используя формулы, определим бесконечно малые значения напряжений:



В результате интегрирования имеем:


(1)

Эти формулы можно преобразовать к более компактному виду, если ввести углы β, δ с помощью равенств:




Подставляя пределы интегрирования и заменяя углы θ1 и θ2 на β и δ, имеем:


теперь формулы (1) могут быть переписаны так:

В соответствии с этими формулами показано распределение компонент напряжений в двух вертикальных и горизонтальных сечениях в основании.[1]
Чтобы правильно (расчитать) оценить инженерно-геологические условия площадок строительства , свойства грунтов в основаниях и совместную работу этих грунтов с деформирующими фундаментами и коснтрукциями сооружений , рациональность выбранных типов оснований , качество выполнения работ , нужно правильно произвести математические расчеты с использованием интеграла для надежности основания и фундаментов и удешевления работ.
Таким образом, мы определили главные напряжения и убедились, что с применением интегрирования решать подобные задачи можно намного легче.
1. Карташов В.Ф. Начала анализа с профессиональной направленностью. – Екатеринбург: Изд-во УрГУПС, 2016.
2. Механика грунтов: Учебник для вузов ж.-д. транспорта / Ю.И.Соловьев и др.; Под ред. А.М. Караулова, — М.:ГОУ «Учебно-методический центр по образованию на железнодорожном транспорте»,2007, — 286 с. ISBN 978-5-89035-477-8

Источник: megalektsii.ru