29 января 1949 г. было принято решение о строительстве 501-й стройки. Сейчас, с лёгкой руки журналистов 90-хх прошлого столетия она вошла как «мёртвая», «сталинская» и т.д. Но не всё так просто в этой истории, дело в том, что многие историки считают, и кстати, правильно делают, что дорогу начали строить за два года до этого решения.
Ещё 4 февраля 1947 года Совет министров СССР принял постановление «О производстве проектно-изыскательских работ по выбору места для строительства порта, судоремонтного завода в районе Обской губы и железной дороги от Северо-Печорской магистрали до порта». И через две недели группа специалистов специальным авиарейсом вылетела в район Мыса Каменного. 22 апреля Совет Министров, не дожидаясь результатов исследований, обязало МВД немедленно приступить к строительству крупного морского порта на Мысе Каменном.
Так что эту дату, — 22 апреля 1947 года видимо и следует считать днём рождения железной дороги «Чум – Салехард – Игарка» вошедшей в историю под номерами «501» и «503». Но, увы, строителей ждало жестокое разочарование, оказалось, что в районе Мыса Каменного никакого камня нет, дно реки песчаное и мелкое, фарватер постоянно меняется. Зедсь сказались «чудеса перевода»с ненецкого языка.
«НЕ ДАВАЙТЕ СВЯТЫНИ ПСАМ» (Мф. 7:6) Иеромонах Нектарий (Соколов)
Поэтому стройку № 502 быстро свернули. Но от мысли протянуть железнодорожную колею вдоль Северного морского пути не отказались. Было решено морской порт строить в районе Игарки. Для чего требовалось продолжить линию Чум – Лабытнанги на восток, через Салехард до посёлка Ермаково. Это было более экономично.
Строительные работы начались весной 1949 г. сразу по всей протяжённости трассы от Салехарда до Игарки. Прокладывали только одну колею железнодорожного полотна, планировалось построить 28 станций и 106 разъездов. За границей были заказаны два парома – для переправы через Енисей и Обь. К концу 1949 г. проложили телефонную линию Салехард – Игарка.
Кстати она исправно работала вплоть до конца 70-х гг. соединяя Салехард, Игарку и Москву, между собой. Но в 1953 г., после смерти Сталина, все работы были в спешном порядке свёрнуты, дорога была законсервирована, из полутора тысяч километров было построено 800 километров, и ещё больше отсыпки под полотно. Позже железнодорожники приняли в эксплуатацию участок «чугунки» от станции Чум до Лабытнанги.
До сих пор вокруг 501-й стройки кружат бессчётные легенды, жуткие мифы. Как обычно, истина где-то рядом, но найти её ох как нелегко.
Давайте чуть приоткроем туманную завесу этой стройки, разберёмся, где здесь истина, а где ложь, и неважно, преднамеренная или врёт «как свидетель».

Железная дорога
Напомню, постановлением Совета Министров Союза ССР за № 1255-331-сс от 22 апреля 1947 г. и приказом Министра от 28 апреля 1947 г. за №00457 для осуществления строительства ж/д линии от ст. Чум до места нового порта в Обской губе было организовано Северное Управление ж/д строительства МВД СССР с присвоением ему наименования «Строительство № 501 МВД СССР».
Девелопмент в строительстве. Что это и «с чем едят»?
Начальником строительства был утверждён заместитель начальника ГУЛЖДС МВД полковник Барабанов В.А., главным инженером – тов. Цвелодуб Б.И. К месту работ в мае 1947 г. прибыл основной командный состав Управления строительства с дислокацией штаба управления в пос. Абезь (там ранее находилось Печорское управление ГУЛЖДС, строившее трассу Котлас-Воркута). Там же находилась штабная колонна заключённых, работавших в культурных учреждениях и в управлении стройки (геодезисты, топографы), а также производственные лагерные колонны – авторемонтная, мотостроительная и т.д.
Стройку поделили на два отделения: № 501 – проведение железной дороги от ст. Чум до ст. Лабытнанги и № 502 – от ст. Лабытнанги до Мыса Каменного.
К будущим станциям Новый Порт и Мыс Каменный поплыли лихтёры и пароходы, забрасывая людей, уголь, продовольствие, лесоматериалы, горюче-смазочные материалы и оборудование. Строился порт и железная дорога. Все шло своим чередом, пока в 1948 г. проектно-изыскательная экспедиция не обнаружила роковую ошибку. Оказалось, что район Мыса Каменного непригоден для расположения крупного морского порта, так как глубина этой части не превышает 5, а возле берега полутора метров. К тому же мелкий песок и ил быстро меняли рельеф дна.
Здесь сказалась неточность перевода с ненецкого языка – все поверили что здесь много камней, а на самом деле, в переводе «песок».

Зима, 501-я стройка
Строителям оставалось либо углубить до 10 метров дно Обской губы, либо прекратить строительство дороги к Мысу Каменному. Для решения первой задачи требовалось доставить 90 тысяч тонн металлического шпунта и 26 млн. кубических метров камня, песка и щебня, для страны, только начавшей восстанавливаться после страшной войны, это было не под силу. Сохранились документы, как обсуждалось снабжение на самом верху.
Именно по этой причине решили идти по второму пути – ликвидации строительства железной дороги к Мысу Каменному и отказ от морского порта в данном районе. Поэтому уже 29 января 1949 г. решением ЦК ВКП (б) и Совета Министров СССР строительство железнодорожной линии на Мыс Каменный было прекращено, объекты Главсевморпути перенесены в Игарку на Енисей.
Этим же решением устанавливалось новое направление железнодорожной магистрали Чум–Салехард–Надым–Игарка, длиной 1459 км, летом – с паромными, а зимой – с ледовыми переправами через Обь и Енисей. Изменение маршрута привело к изменениям в управлении.
Северное Управление было реорганизовано, в его составе осталось Обское строительное управление (строительство № 501): начальник В.В. Самодуров, главный инженер Г.Д. Чхеидзе, а с 1951 года – А.Д. Жигин. Вместо прежних подразделений создано Енисейское строительное управление (строительство № 503): руководители А.И. Боровицкий и Б.И.
Степанов.
В 1953 г., после смерти Сталина, все работы были в спешном порядке свёрнуты, дорога была законсервирована, из полутора тысяч километров было построено 800 километров, и ещё больше отсыпки под полотно. Позже железнодорожники приняли в эксплуатацию участок от станции Чум до Лабытнанги.
В XXI веке практически по местам 500-х строек спроектирована железнодорожная магистраль в Ямало-Ненецком автономном округе протяженностью 707 километров по маршруту Обская — Салехард — Надым — Новый Уренгой — Коротчаево, которая должна связать западную и восточную части автономного округа, Северную железную дорогу со Свердловской. Новый проект получил название «Северный широтный ход».
В миниатюре – Открытие моста через р. Воркуту.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник: ural-meridian.ru
Степень с натуральным показателем
Степенью называют произведение из нескольких одинаковых множителей. Например:
Значение данного выражения равно 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
Это выражение читается так: « два в третьей степени равно восемь» или « третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 5 3 , то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5 .
Число, которое повторяется называют основанием степени. В выражении 5 3 основанием степени является число 5 .
А число, которое надписано над числом 5 называют показателем степени. В выражении 5 3 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
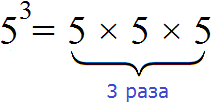
Саму операцию перемножения одинаковых множителей называют возведением в степень.
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
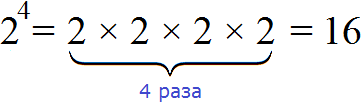
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида a n , которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
![]()
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
![]()
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 0 0 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 0 0 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
2 4 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
10 2 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
Пример 3. Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 10 1
Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10 2
Пример 3. Представим число 1 000 в виде степени с основанием 10.
Пример 4. Представим число 10 000 в виде степени с основанием 10.
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
Если бы мы не заключили в скобки число −2 , то получилось бы что мы вычисляем выражение −2 2 , которое не равно 4 . Выражение −2² будет равно −4 . Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −2 2 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −2 2 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2) 2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2) 3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2) 4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
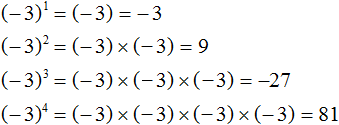
В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5) 3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4) 4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений
При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.
Пример 1. Найти значение выражения 2 + 5 2
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 5 2 = 2 + 25 = 27
Пример 10. Найти значение выражения −6 2 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−6 2 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−6 2 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 2 2
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 2 2 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12. Найти значение выражения (3 2 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3 , затем складываем результаты возведения в степень числа 3 и умножения 1 × 3 . Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
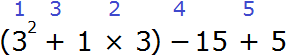
(3 2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 5 3 + 5 × 2 3
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 5 3 + 5 × 2 3 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (2 3 ) 2 . В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(2 3 ) 2 это произведение двух степеней, каждая из которых равна 2 3
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
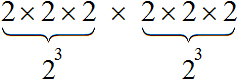
Получили произведение 2 × 2 × 2 × 2 × 2 × 2 , которое равно 64. Значит значение выражения (2 3 ) 2 или равно 64
![]()
Этот пример можно значительно упростить. Для этого показатели выражения (2 3 ) 2 можно перемножить и записать это произведение над основанием 2
Получили 2 6 . Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
![]()
Данное свойство работает по причине того, что 2 3 это произведение 2 × 2 × 2 , которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 2 6
Вообще, для любого основания a с показателями m и n , выполняется следующее равенство:
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают» .
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (3 2 ) 2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:

Получили 3 4 . А число 3 в четвёртой степени есть 81
![]()
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 2 2 на 3 3 .
2 2 это число 4 , а 3 3 это число 27 . Перемножаем числа 4 и 27 , получаем 108
2 2 × 3 3 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 2 2 на 2 3
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 2 2 и 2 3 . Иными словами, о снование оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 2 5 . Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 2 2 это произведение 2 × 2 , а 2 3 это произведение 2 × 2 × 2 . Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2 . Это произведение представимо в виде 2 5
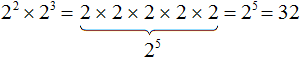
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: « При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают» .
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 2 1 × 2 2 × 2 3 . Основание 2 оставим без изменений, а показатели сложим:
![]()
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 5 8 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 5 8 × 25 получилась одна степень.
Число 25 можно представить в виде 5 2 . Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 5 8 × 25 в виде одной степени, а именно в виде степени 5 10 .
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 2 9 × 32
Число 32 можно представить в виде 2 5 . Тогда получим выражение 2 9 × 2 5 . Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3 , используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 3 1 и 3 1
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
3 1 × 3 1 = 3 2 = 9
Пример 4. Вычислите произведение 2 × 2 × 3 2 × 3 3 , используя основное свойство степени.
Произведение 2 × 2 заменим на 2 1 × 2 1 , затем на 2 1 + 1 , а затем на 2 2 . Произведение 3 2 × 3 3 заменим на 3 2 + 3 , а затем на 3 5
![]()
Далее вычисляем значение каждой степени и находим произведение:
![]()
Пример 5. Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
![]()
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x 2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
![]()
Пример 7. Выполнить умножение y 3 y 2 y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
![]()
Пример 8. Выполнить умножение aa 3 a 2 a 5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
![]()
Пример 9. Представить степень 3 8 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3 , и сумма показателей которых будет равна 8 . Можно использовать любые показатели. Представим степень 3 8 в виде произведения степеней 3 5 и 3 3
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 3 5 × 3 3 можно записать как 3 5 + 3 , откуда 3 8 .
Конечно можно было представить степень 3 8 в виде произведения других степеней. Например, в виде 3 7 × 3 1 , поскольку это произведение тоже равно 3 8
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x 12 в виде различных произведений степеней с основаниями x .
Воспользуемся основным свойство степени. Представим x 12 в виде произведений с основаниями x , и сумма показателей которых равна 12
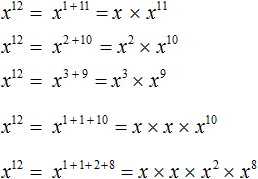
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3 . Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
![]()
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 2 2 , а произведение 3 × 3 можно заменить на 3 2 . Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 2 2 × 3 2 .
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n , нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4) 2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4 . Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
![]()
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
![]()
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
Возведём в третью степень каждый множитель данного произведения:
Число 3 в третьей степени равно числу 27 . Остальное оставим без изменений:
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 5 2 × 3 2 . Возведем каждое число во вторую степень и перемножим полученные результаты:
5 2 × 3 2 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3) 2 . Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
5 2 × 3 2 = (5 × 3) 2 = (15) 2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b) n = a n × b n , то a n × b n = (a × b) n . То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
К примеру, выражение (2 3 ) 2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(2 3 ) 2 = 2 3 × 2 = 2 6
Далее вычислить степень 2 6 , которая равна 64
(2 3 ) 2 = 2 3 × 2 = 2 6 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (2 3 ) 2 . Выражение в скобках 2 3 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (2 3 ) 2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2 .
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6
Как и раньше получили 2 6 . Значение этой степени равно 64
(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (2 2 × 3 2 ) 3 . Здесь показатели каждого множителя нужно умножить на общий показатель 3 . Далее найти значение каждой степени и вычислить произведение:
(2 2 × 3 2 ) 3 = 2 2×3 × 3 2×3 = 2 6 × 3 6 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2 1 × 4 1 . А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
![]()
Пример 2. Найти значение выражения (3 3 ) 2
Основание оставляем без изменений, а показатели перемножаем:
Получили 3 6 . Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax) 3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2) 3 — получится −8 . Буквенная часть останется без изменений:
![]()
Пример 6. Выполнить возведение в степень в выражении (10xy) 2
![]()
Пример 7. Выполнить возведение в степень в выражении (−5x) 3
![]()
Пример 8. Выполнить возведение в степень в выражении (−3y) 4
![]()
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
![]()
Пример 10. Упростите выражение x 5 × (x 2 ) 3
Степень x 5 пока оставим без изменений, а в выражении (x 2 ) 3 выполним возведение степени в степени:
Теперь выполним умножение x 5 × x 6 . Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
Пример 9. Найти значение выражения 4 3 × 2 2 , используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 4 3 . Основание у этой степени есть число 4, которое можно представить в виде 2 2 . Тогда исходное выражение примет вид (2 2 ) 3 × 2 2 . Выполнив возведение степени в степень в выражении (2 2 ) 3 , мы получим 2 6 . Тогда исходное выражение примет вид 2 6 × 2 2 , вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
![]()
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 4 3 на 2 2 .
Вычислим 4 3 , получим 64 . Вычислим 2 2 , получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 2 3 : 2 2
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 2 3 : 2 2 равно 2 .
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 2 3 : 2 2 . Здесь делимое это 2 3 , а делитель 2 2 .
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 2 3 на 2 2 означает найти такую степень, которая при умножении на делитель 2 2 даст в результате 2 3 . А какую степень можно умножить на 2 2 , чтобы получить 2 3 ? Очевидно, что только степень 2 1 . Из основного свойства степени имеем:
Убедиться, что значение выражения 2 3 : 2 2 равно 2 1 можно непосредственно вычислив само выражение 2 3 : 2 2 . Для этого сначала найдём значение степени 2 3 , получим 8 . Затем найдём значение степени 2 2 , получим 4 . Разделим 8 на 4, получим 2 или 2 1 , поскольку 2 = 2 1 .
2 3 : 2 2 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
Например, найдём значение выражения 2 2 : 2 2 . Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 2 2 : 2 2 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 2 2 и 2 2 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 2 2 : 2 2 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 4 12 : 4 10
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
4 12 : 4 10 = 4 12 − 10 = 4 2 = 16
Пример 3. Представить частное x 3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
![]()
Пример 4. Представить частное x 3 : x 2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x 3 можно записать как x × x × x , а степень x 2 как x × x . Тогда конструкцию x 3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x . В результате останется один множитель x

Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x 2 . Чтобы сократить дробь на x 2 нужно числитель и знаменатель дроби разделить на x 2

Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Пример 5. Выполнить деление x 12 : x 3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x 12 : x 3 запишем в виде . Далее сократим данную дробь на x 3 .
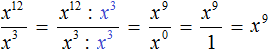
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
![]()
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
![]()
Завершаем пример, вычислив степень 7 2
![]()
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (2 3 ) 4
![]()
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
![]()
Теперь применяем правило деления степеней с одинаковыми основаниями:
![]()
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 4 3 запишем в виде возведения степени в степень (2 2 ) 3 . Тогда получим следующее выражение:
![]()
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (2 2 ) 3
![]()
В числителе и в знаменателе получившегося выражения содержится степень 2 6 , которую можно сократить на 2 6
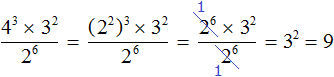
Видим, что в результате осталась единственная степень 3 2 , значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 7 5 × 4 5 можно представить в виде степени с одним показателем (7 × 4) 5 . Далее перемножим выражение в скобках, получим 28 5 . В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
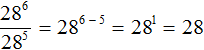
Значит, значение выражения равно 28 . Запишем решение полностью:

Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности

Значит обыкновенная дробь во второй степени равна дроби .
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
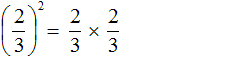
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
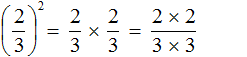
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 2 2 и 3 2 соответственно:
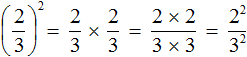

Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
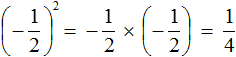
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби
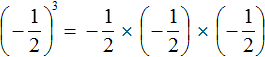
Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ
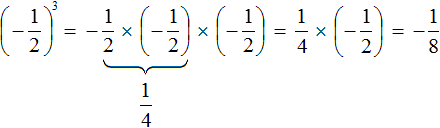
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
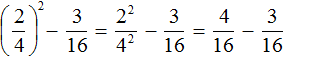
Далее вычислим значение получившегося выражения:

Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
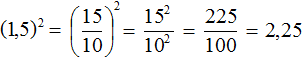
Пример 2. Найти значение степени (−1,5) 3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
![]()
Пример 3. Найти значение степени (−2,4) 2
Показатель степени является чётным числом. Значит ответ будет положительным:
Источник: spacemath.xyz
Строители автомобильной трассы М-12 раскрыли детали проекта прохождения автобана в наиболее проблемных местах Владимирской области
2 развязки, 15 искусственных сооружений, 1 многофункциональный дорожный сервис, 1 000 строителей, 300 единиц техники, 3 года работ — подрядчик ответил на вопросы Зебра ТВ о том, как будут строить федеральную трассу М-12 на отрезке от Ворши до Барак

интервью
Под Владимиром начались подготовительные работы под строительство скоростной платной автомобильной дороги М-12 «Москва — Казань». В районе деревень Столбищи и Колокша Собинского района, а также у городского кладбища «Высоково» и около микрорайона Мостострой уже идет вырубка леса.
О деталях строительства платной трассы М-12 на самом проблемном участке Владимирской области — под Воршей, Энергетиком, Мостостроем и Улыбышево — Зебра ТВ рассказал подрядчик II этапа М-12 — ООО «Региональная строительная компания». Ответы на вопросы в редакцию прислали в письменном виде.
Кто является основным подрядчиком на втором этапе? Какие объекты до этого были уже возведены этим подрядчиком в России?
На втором этапе основным подрядчиком является ООО «РСК» (Региональная строительная компания) на основании Договора ДРиС-2020-1153 от 21.09.2020 года с Государственной компанией «Российские автомобильные дороги».
Объекты которые были уже возведены подрядчиком в России представлены в сведениях ниже:
| 1 | ОАО «Внуково-Инвест» | Ангар для самолётов типа А-340-300 и А-319 на территории ОАО «ВАРЗ-400″ Ангар № 25» | 2014 год |
| 2 | Департамент развития новых территорий города Москвы | «Реконструкция автомобильной дороги от Боровского шоссе до Киевского шоссе, от деревни Рассказовка до города Московский» | 2014 год |
| 3 | АО «Международный аэропорт Внуково» | «Аэровокзальный комплекс Внуково-1» (в осях 8-18/Т1-Ю) | 2015 год |
| 4 | ООО «Трансстроймеханизация» | г.Москва, аэропорт Внуково-1, строительство этап 4.1.3, 5 (удлинение ИВПП) | 2015 год |
| 5 | ООО «ТАД-индастриес» | Ангар для самолётов типа А-340-300 и А-319 на территории ОАО «ВАРЗ-400″ Ангар № 26» | 2015 год |
| 6 | ООО «Трансстроймеханизация» | Строительство скоростной автомобильной дороги Москва – Санкт-Петербург на участке км 58 – км 684 (с последующей эксплуатацией на платной основе) — 5 этап, 6 этап | 2015 год |
| 7 | Департамент развития новых территорий города Москвы | «Реконструкция центральной автодороги в поселок Коммунарка с выходом на район Бутово» | 2015 год |
| 8 | Департамент развития новых территорий города Москвы | «Проектирование и строительство объектов инженерной инфраструктуры для жилых домов в пос. Марушкинское « | 2016 год |
| 9 | ООО «Трансстройинвест» | «Аэродромно-технический комплекс объединенного авиационного отряда специального назначения ФСБ России на аэродроме Москва (Внуково).» | 2016 год |
| 10 | Департамент развития новых территорий города Москвы | Административно-деловой центр Троицкого и Новомосковского административных округов в г.Москва | 2017 год |
| 11 | Департамент развития новых территорий города Москвы | «Реконструкция автодороги Боровское ш. — Киевское шоссе — деревня Ботаково, через д. Рогозинино, Верховье» | 2017 год |
| 12 | Департамент развития новых территорий города Москвы | Строительство эстакады автодороги Боровское шоссе — Киевское шоссе — деревня Ботаково через деревни Рогозино, Верховье | 2017 год |
| 13 | Департамент развития новых территорий города Москвы | «Строительство трех пешеходных переходов через автодорогу Боровское шоссе — Киевское шоссе — деревня Ботаково, через деревни Рогозинино, Верховье (Этап I) — этап 1.1, этап 1.2 | 2017 год |
| 14 | Департамент развития новых территорий города Москвы | Проектирование и строительство объектов инженерной инфраструктуры для жилых домов, поселок Марушкинское» (завершение работ) | 12.06.18 |
| 15 | Департамент развития новых территорий города Москвы | Реконструкция автодороги от Минского шоссе до Боровского шоссе (Внуковское шоссе) | 29.05.20 |
| 16 | Департамент развития новых территорий города Москвы | Выполнение подрядных работ по объекту: «Реконструкция и строительство автомобильной дороги от М-3 «Украина» — деревня Середнево — деревня Марьино — деревня Десна» | 28.08.20 |
Поясните характеристики второго этапа: начальная точка, конечная точка, километраж, окончательный маршрут?
М-12 «Строящаяся скоростная автомобильная дорога Москва — Нижний Новгород — Казань», 2 этап: км 80 – км 116, Владимирская область (от пересечения с автомобильной дорогой федерального значения М-7 «Волга» до пересечения с автомобильной дорогой регионального значения 17Р-2 «Владимир – Гусь – Хрустальный – Тума»).
Какие сейчас существуют утвержденные документы по второму этапу трассы М-12?
В настоящий момент утверждены Проект планировки территории (Распоряжение Росавтодор №3946-р от 21.12.2020) и Проект межевания территории (Распоряжение Росавтодор №4142-р от 28.12.2020)
Какие проектные работы продолжаются? Каковы сроки их окончания и сроки защиты проекта? Возможно ли на этом этапе внесение изменений в проект? Куда можно обращаться с предложениями?
В настоящее время Главгосэкспертизой рассматривается под этап проектной документации «Подготовка территории строительства», разработка под этап «Основные объекты строительства» будет выдан в Главгосэкспертизу в апреле 2021 года. Окончание рассмотрения проекта и получение положительного заключения Главгосэкспертизы России — август 2021 года.
Предложения о внесении изменений можно направлять в Государственную компанию «Российские автомобильные дороги» (Заказчику).
Защищен ли проект подготовительного этапа строительства? Какие подготовительные работы ведутся сейчас? В каких точках?
Проект на подготовку территории строительства находится на рассмотрении в Главгосэкспертиза России, окончание рассмотрения – апрель 2021 года. Ведутся подготовительные работы касающиеся размещения производственных баз, временных дорог к строительным площадкам мостов через реки Ворша и Колокша в начале трассы.
Сколько будет вырублено леса под трассу на втором этапе и будут ли компенсационные посадки? Какова ширина вырубаемого коридора? Переведены ли защитные леса под Владимиром в категорию «земли промышленности»?
Площадь лестных участков в полосе постоянного отвода составляет — 231,046 га, временный отвод — 119,014 га. В соответствии с постановлением правительства №566 от 07.05.2019 г. ГК «Автодор» будет осуществляться компенсационные лесовосстановления на площади 350 га. Ширина вырубаемого коридора — 60-100 метров. Все защитные леса переведены из защитных в обычные и далее переведены в земли промышленности и строительства (S=203 га.)
Какие коммуникации будут перенесены в целях строительства второго этапа?
Планируется перенос коммуникации сети связи, сети газоснабжения, воздушные и кабельные линии электропередач.
Где конкретно будет располагаться городок строителей второго этапа М-12? Есть ли хотя бы приблизительные данные: сколько людей и техники будут строить второй этап?
Площадка под строительный городок ООО «РСК» будет располагаться в районе д. Одерихино на км 168 по М-7. В строительстве второго этапа будут привлечены более 1 000 человек и 300 единиц техники.
Какие месторождения песка и щебня будут использовать строители? Где конкретно будут располагаться площадки под складирования этих строительных материалов?
Площадка для складирования строительных материалов будет располагаться в границах постоянной полосы отвода. Месторождения песка: ОАО «Нерудные ресурсы» Ленинский районн, г. Владимир; Месторождение Высоковский Луг, Судогорского р-на, д. Высоково; ООО «Карьероуправление М-7» Петушинский р-н, Липна. Месторождения щебня будут использоваться как местных, так и приводных месторождений.
Где конкретно на втором этапе будет располагаться многофункциональный дорожный сервис?
В соответствии с документацией по планировке территории в районе км 81 предусмотрено устройство перспективной многофункциональной зоны дорожного сервиса (МФЗ).
Сколько транспортных развязок будет на втором этапе, где они будут располагаться?
В составе проектной документации на 2 этапе трассы ЕЗК предусмотрено устройство двух транспортных развязок:
транспортная развязка №2 – на 91 км ЕЗК (пересечение с автодорогой М-7 «Волга»);
транспортная развязка №3 – на 117 км ЕЗК (пересечение с автодорогой Р-132 «Золотое кольцо»).
Транспортные развязки предусмотрены в соответствии с утвержденной документацией по планировке территории.
Параметры съездов транспортных развязок отвечают требованиям СП 34.13330.2012 и ОДМ 218.2.071-2016. Кольцевые пересечения устраиваются в соответствии с ОДМ 218.2.071-2016. Правоповоротные съезды с шириной проезжей части 5,0 метров и левоповоротные съезды с шириной проезжей части 5,5 метров имеют внешнюю обочину 3,0 метров, внутреннюю – из условия установки барьерного ограждения 2,0 метров, согласно п.6.23 СП 34.13330.2012. Ширина полос двухполосных съездов составляет 3,75 метра, обочинами — 2,0 метра (внешняя и внутренняя). На участках кривых в плане предусмотрено уширение проезжей части.
С какими основными линейными объектами будет пересекаться М-12 на втором этапе?
Участок работ начинается на подходе к мосту через р. Ворша (км 80+000), далее в северо-восточном направлении объект пересекает р. Колокша, на км 88 трасса поворачивает на юго-восток пересекает автомобильную дорогу М-7 «Волга» в месте примыкания к ней южного обхода г. Владимира, далее ветку железной дороги между станциями «Юрьевец» и «Колокша» и до пересечения с рекой Клязьма трасса проходит параллельно южному обходу г. Владимира в 300-100 метрах с южной стороны , на км 102 проходит в границах поселка Мостострой пересекая а/д «г. Владимир- пос. Мостострой» и железную дорогу недалеко от платформы «10 км» далее в восточном направлении пересекает реку Клязьма, которая одновременно является границей между городским округом Владимир и Судогодским районом и автомобильную дорогу 17Н-60 «Владимир — Улыбышево — Коняево» проходит по лесистой местности, пересекает автодорогу «ур. Переведеново – д. Неврюево», огибает военную часть, пересекает р. Сухорика и впадающие в нее ручьи, затем в восточном направлении объект пересекает лесной участок и заканчивается пересечением с автомобильной дорогой федерального значения Р-132 «Золотое кольцо» Ярославль — Кострома — Иваново — Владимир — Гусь-Хрустальный — Рязань — Михайлов — Тула — Калуга — Вязьма — Ржев – Тверь — Углич – Ярославль км 304+312 – км 411+353 (ранее автомобильная дорога регионального значения 17Р-2 «Владимир – Гусь – Хрустальный – Тума»).
Сколько водных объектов будет пересекать М-12?
Всего трасса будет пересекать 4 водных объекта. Мост через р. Ворша км 80+125, мост через р. Колокша на км 85+505, мост через р. Клязьма на км 104+200, мост через р. Юрик на км 105+147.
Сколько на втором этапе будет искусственных сооружений? Какие и где конкретно?
Всего постоянных искусственных сооружений, планируемых к возведению — 15 штук (Плюс 2 временных моста).
Какое расстояние от дорожного полотна М-12 до крайних домов микрорайона Мостострой, поселка Улыбышево, деревень Захарово Судогодсткого района и Колокша, Одерихино, Столбищи Собинского района? Какие предусмотрены мероприятия для минимизации негативного воздействия на жителей данных населенных пунктов?
Расстояние от дорожного полотна М-12 до д. Захарово – 182 метра, д. Колокша – 125 метра, д. Одерихино -352 метра, п. Улыбышево – 565 метра, микрорайон Мостострой – 242 метра, д. Столбищи – 267 метра.
Проектной документацией предусмотрено для минимизации негативного воздействия на жителей данных населенных пунктов возведение шумозащитных валов и акустических экранов.
Как изменится конфигурация дорожной развязки в районе Мостостроя в связи со строительством М-12?
Принципиальных изменений не будет, въезды и выезды будут сохранятся на М-7.
На каком расстоянии от полотна Южной объездной дороги города Владимира (М-7) будет проходить М-12? Не помешает ли строительство М-12 планируемой реконструкции (расширению) Южной объездной дороги?
Строительство М-12 не помешает планируемой реконструкции Южной объездной. Все расстояния учтены проектом.
Как планируется преодоление трассой озера Банное в микрорайоне Мостострой?
Проектным решением предусмотрено частичное пересечение озеро Банное строящейся трассой М-12.
Какие инженерные сооружения планируется возвести для прохождения трассой поймы реки Клязьма? Какова их высота?
Через реку Клязьма на км 104+200 проектной документации предусматривается возведение мостового перехода длиной 220 метров под мостовой габарит порядка 12 метров от уровня меженных вод.
Расскажите о технических характеристиках моста М-12 через реку Клязьма?
Предварительное проектное решение: Схема моста 72+84+51. Представляет собой сталежелезобетонные пролетное строение с опиранием на монолитные железобетонные опоры. Мостовой переход запроектирован с учетом расчетного расхода воды (с учетом разлива р. Клязьма) 2190 м 3 /с. Габарит проезда 2Г-11.
Какая нагрузка ляжет на трассу «Владимир — Радужный» на время строительства второго этапа М-12?
Увеличение нагрузки на трассу «Владимир-поселок Улыбышево-Радужный» на время строительства второго этапа М-12 не предвидится так как увеличение интенсивности движения не будет.
Какое инженерное сооружение будет построено на месте пересечения М-12 и дороги «Владимир — Радужный»? Как будет осуществляться движение транспорта на время строительства данного пересечения?
Проектным решением запланировано строительство путепровода, который будет проходить над строящейся трассой М-12.
Предусмотрено ли на втором этапе строительство скотопрогонов для животных? Сколько их будет?
На втором этапе не предусмотрено строительство скотопрогонов для животных так как нет путей миграции диких животных.
Какие результаты должны быть в 2021, 2022 и 2023 годах? Назовите примерное время сдачи второго этапа?
2021 год — планируется выполнить: 70% насыпи земляного полотна, уложить 100 тысяч тонн асфальтобетона, построить 60% искусственных сооружений.
2022 год — завершить устройство мостов, 100% насыпи земляного полотна, 100% укрепительных работ.
2023 год — получения заключение о соответствии (ЗОС) и получение разрешения на ввод в эксплуатацию (РВЭ).
Источник: zebra-tv.ru
Размеры обрезной доски по ГОСТу
При строительстве до сих пор один из самых востребованных материалов — обрезная доска. При покупке вам могут продать пиломатериалы в заданный вами размер. Но чаще всего размеры досок соответствуют стандарту ГОСТ. Для обрезных досок хвойных пород этот стандарт называется ГОСТ 24454-80.
Он представляет собой таблицу, в которой указаны все возможные сочетания толщины, ширины доски. Стандартная длина доски — 6000мм (6 метров).
Размеры досок по ГОСТ 24454-80
| 16 | 75 | 100 | 125 | 150 | — | — | — | — | — |
| 19 | 75 | 100 | 125 | 150 | 175 | — | — | — | — |
| 22 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | — | — |
| 25 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 32 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 40 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 44 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 60 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 75 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 100 | — | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 125 | — | — | 125 | 150 | 175 | 200 | 225 | 250 | — |
| 150 | — | — | — | 150 | 175 | 200 | 225 | 250 | — |
| 175 | — | — | — | — | 175 | 200 | 225 | 250 | — |
| 200 | — | — | — | — | — | 200 | 225 | 250 | — |
| 250 | — | — | — | — | — | — | — | 250 | — |
Пользоваться таблицей просто. Пусть вам нужна доска толщиной 75мм. Это значит, что ширина такой доски может составлять 75, 100, 125, 150, 175, 200, 225, 250 и 275 миллиметров. Или другой пример — вы хотите купить доску шириной 125мм. Значит толщина такой доски может быть 16, 19, 22, 25, 32, 40, 44, 50, 60, 75, 100 или 125 миллиметров.
При строительных работах может потребоваться определить количество досок в кубометре и вес доски.
Размер доски дюймовки
Сначала нужно понять какую доску называют дюймовкой. Мы знаем, что в одном дюйме примерно 25 миллиметров. Поэтому доску толщиной 25 мм и стали называть дюймовкой. А значить, воспользовавшись таблицей размеров доски мы можем увидеть, что доска дюймовка имеет размер (ширину) 75, 100, 125, 150, 175, 200, 225, 250 или 275мм.
Размер половой доски

Тут необходимо уточнение. Чаще всего для пола используют шпунтованную доску (см. фото). В случае, если применяется нешпунтованная доска, то ее размеры можно определить из таблицы выше.
Размеры обрезной доски по ГОСТу
При покупке материалов, лучше быть в курсе того, какого размера они должны быть, как определить сорт и в чем различия между разными видами. Все это обговорим, а еще приведем стандартные размеры обрезной доски и допустимые отклонения.
Что такое обрезная доска, брус и брусок
Несведущему человеку не так легко разобраться в строительной терминологии. Если вы затеяли стройку, это делать придется. Для начала разберемся, что такое доска, чем она отличается от бруса и бруска. Все определения пиломатериалов даны в ГОСТ 18288-87. Опираются они на размеры. Согласно этому документу:

Чем отличаются брус и брусок? Брус в сечении имеет форму квадрата со стороной больше 100 мм. Брусок может быть квадратным, но сторона должна быть меньше 100 мм, но чаще всего брусок имеет вид прямоугольника
- Доска — это пиломатериал, имеющий толщину не более 100 мм и ширину больше двукратной толщины.
- Брус — шириной и толщиной более 100 мм. Максимальный размер бруса не нормируется. Только минимальный.
- Брусок — толщиной до 100 мм и шириной не более удвоенной толщины.
Итак, если посмотреть на брус с торца, все его стороны должны быть равны. Поперечное сечение бруса даст нам квадрат. Доска и брусок — прямоугольники. Просто у доски ширина более чем в два раза больше толщины, а у бруска меньше. Например, 25*75 мм — это доска, а 25*45 мм — это брусок.
И, кстати, 50*50 мм и 75*75 мм — это тоже брусок, а не брус, потому что по стандарту брусом считается изделие со стороной от 100 мм. С этими названиями, вроде, разобрались.

Что такое горбыль и дощатый горбыль, понятно по фото
Для черновых работ еще иногда применяют горбыль. Что это такое? По тому же стандарту, это боковая часть бревна, одна сторона которой пропилена, вторая нет. Есть еще дощатый горбыль — это когда наружная часть горбыля пропилена частично.
Обрезная и необрезная доска
Еще стоит определиться с тем, что такое пласть и кромка. Это любая из двух более широких поверхностей в доске или бруске, и любая из поверхностей в брусе. Кромка, соответственно — более узкая часть пиломатериала.

Пласть доски или бруска — это широкая поверхность
Вот теперь можно выяснять, что такое обрезная доска и чем она отличается от необрезной. Обрезная доска имеет кромки, опиленные перпендикулярно пластям. На кромке может быть обзол (остатки коры), но не более чем допустимо по сортности. Необрезная доска, соответственно, имеет не обрезанные или частично обрезанные кромки. В ту же категорию попадает обрезной пиломатериал, в котором обзол превышает допустимые пределы.
Есть еще полуобрезная доска. Это когда только одна кромка ровная, а на второй может быть обзол. Брус, кстати, тоже может быть с обзолом. У двухкантного обработаны две противоположные стороны, у трехкантного три, у четырехкантного — все четыре.

Обрезная и необрезная доска. Разница в виде кромок. У обрезной они гладкие; у низких сортов допускается наличие небольшого количества обзола. У необрезной доски кромки не обрезаны совсем или только частично
Может понадобиться еще такое понятие, как калиброванный пиломатериал. Бывает калиброванная доска, брусок и брус. Это пиломатериал высушенный и обработанный (на рейсмусе или строгальном станке) до требуемого размера. Надо понимать так, что некалиброванный может иметь отклонения по размерам (пределы отклонений нормированы), калиброванный отличаться по габаритам не должен. Вернее, допустимые отклонения очень маленькие.
Есть еще строганная доска. Отличается от обрезной более гладкими сторонами, так как подвергается дополнительной обработке. Обрезная доска высушивается, а после этого отправляется на дополнительную обработку на строгальном станке. Там снимается ее шероховатость, которую оставила пила. Одновременно может происходить калибровка, но это необязательно.
Строганная доска может быть некалиброванной.
Деловая и строительная доска: в чем разница
Еще в прайсах есть доска с одинаковыми размерами, одного сорта, но одна строительная, а другая деловая. Разница в том, что деловая изготавливается из не сухостойных стволов. Она высушена, не имеет грибковых или бактериологических поражений, червоточин, даже если они разрешены стандартами. Поэтому стоит существенно дороже.
Деловая доска применяется при устройстве кровли. Идет на лаги, стропила. Ее же применяют в каркасном домостроении. Деловую доску могут прямо на предприятии обработать нужными составами, но это обговаривается конкретно перед поставкой.

Чтобы понять строительный перед вами пиломатериал или деловой, смотрите на сучки. В деловой доске или брусе могут быть только здоровые (светлые) сросшиеся сучки
Требования к древесине и сортность
Сорт доски или ее сортность — это классификация, в которой указаны допустимые изъяны древесины и их количество. Доска и бруски могут быть пяти сортов — отборный, 1-й, 2-й, 3-й и 4-й. Брус отборным не бывает, так что имеет только четыре сорта, обозначаемых цифрами.
Пиломатериалы отборного, первого, второго и третьего сортов изготавливают:
- из сухой древесины влажностью не более 22%;
- из сырой;
- сырой, обработанной антисептиками.
Древесина для четвертого сорта не регламентирована. Сортность определяется по худшей пласти или кромке. То есть, находите худшую часть, и по наличию и количеству дефектов и изъянов определяете сортность. Все они приведены в таблицах, а сами возможные дефекты в виде картинок.
Обратите внимание, данные по сортности взяты из ГОСТа 2140. Он применяется для пиломатериалов для внутреннего рынка и идущих на экспорт. Недавно был принят другой стандарт: ГОСТ 26002 для пиломатериалов, которые продаются только на внутреннем рынке. Там сорта определяются по-другому (и допустимые отклонения по размерам тоже). Так что будьте внимательны, уточняйте по какому ГОСТу определялась сортность.
Как определить сортность доски
Знаете, как определяют сорт доски на производстве? На глаз. Никто не считает сучки, трещины и другие дефекты. Да и разница между, скажем, первым и вторым сортом очень невелика. И не все производители стараются действительно правильно ее рассортировать.
Так что лучше контролировать все самому. Но таблицы такие большие, а дефектов очень много — запомнить все нереально. Но есть определенные критерии, которые могут вам помочь определить насколько качество соответствует заявленному.
Отборная и первосортная обрезная доска не может иметь такие повреждения
- Если есть хоть один выпавший сучок, перед вами точно не отборный и не первый сорт. Как минимум второй, а то и ниже.
- На досках и брусе первого сорта не должно быть гнили, грибков и сердцевины. Это все места, которые в первую очередь разрушаются. Так что их быть не должно.
- При выборе бруса обращайте внимание на количество годовых колец. Чем их больше, тем выше качество древесины.
А еще стоит посмотреть на условия хранения. Вообще, доска высоких сортов должна храниться хотя бы под навесом. Она должна быть сложена в проветриваемые штабеля, а не лежать навалом. Проветриваемые штабеля — это с прокладками, которые отделяют один ряд от другого и позволяют лесу равномерно сохнуть.
Стандартные размеры обрезной доски
По ГОСТу 24454-80 есть пиломатериалы хвойных пород стандартных габаритов. Толщина и ширина доски приведена в таблице. По толщине обрезной доски, бруска и бруса отклонения допустимы, но они не могут быть больше:
- ±1 мм для досок и бруска толщиной до 32 мм;
- ±2 мм для пиломатериала от 40 мм до 100 мм;
- ±3 мм при толщине 110 мм и больше.
Также есть ограничения по отклонениям ширины: разбег может быть до 2 мм при ширине до 100 мм, и до 3 мм при ширине 125 мм и более.
Стандартные размеры обрезной доски указаны для древесины влажностью 20%. Для материалов более высокой и низкой влажности изменяются. Величина усушки прописана в ГОСТ 6782.1.
Кроме того, нормируется длина пиломатериалов. Она может быть от 1 метра до 6,5 метров. Шаг градации — 25 см. По длине допустимые отклонения — 25 мм или +50 мм .

В новом стандарте для внутреннего рынка приемлемы другие отклонения от стандартных размеров обрезной и необрезной доски
Обратите внимание, введен ГОСТ 26002, в котором для внутреннего рынка допускаются другие отклонения. Но стоит приписка: по согласованию с потребителем. То есть, при покупке доски «стандартных размеров», смотрите ГОСТ. В 24454-80 требования более жесткие. В нем же, кстати, установлены другие критерии сортности.
Так что, действительно, стоит спрашивать, по какому ГОСТу маркирована продукция.
Стандартные размеры обрезной доски, бруса и бруска. ГОСТ

Оглавление:
Стандартные размеры древесины полезно знать как при выполнении различных самоделок своими руками так и при основательном строительстве. Размеры пиломатериалов регламентируются ГОСТ и продукция каждой пилорамы ориентирована на стандартизованные размеры. Пиломатериалы бывают обрезные, необрезные, доски, бруски и брусья и др.
Качество древесины
Лиственные породы древесины разделяют на три сорта, хвойные — на пять. Пиломатериалы наилучшего сорта называются отборными (маркируется горизонтальной полосой или буквой «О») , остальные сорта обозначают цифрами 1-4 (маркируются соотв. количеством точек, вертикальных полос или просто цифрой).
Оценка качества пиломатериалов производится по наихудшей стороне или кромке. Сорт определяют по наличию/отсутствию сучков, гнили, трещин, коробления и деформаций, червоточин, степени точности механической обработки (непараллельность плоскостей и кромок регламентирует ГОСТ 24454-80 ).
Древесина 1-го сорта используется для изготовления элементов строительных конструкций, окон, дверей,лестниц (стандартные размеры элементов лестниц см. в этой статье) , чистовой отделки пола и стен.
2-й сорт идет на настилы, несущие строительные конструкции ( II категории) опалубки, обрешетки и строганые детали (ГОСТ 8442-75 и ГОСТ 475 -78).
3-й сорт используют для изготовления несущих конструкций (III категории).
4-й сорт годен на изготовление тары, мелких заготовок.
Условные обозначения
В обозначении прямым текстом пишется материал (доска, брусок, брус), далее цифра указывающая на сорт , порода древесины (хв. — хвойные или отдельные породы — сосна, ель, лиственница, кедр, пихта), размер поперечного сечения в мм. и обозначения регламентирующего стандарта.
Ответственные производители указывают в прайсах также длину и кубатуру, т.е: Доска — 2 — сосна — 40 х 150 х 6000 — ГОСТ 8486-86 Количество в кубе: 27 шт
Как правильно измерять пиломатериалы
Длину пиломатериалов и заготовок фиксируют по наименьшему расстоянию между торцами, а ширину в любом месте, но отступая 150 мм от торцов.
Толщина измеряется аналогично в произвольной точке с отступом 150 мм. Ширина необрезных пиломатериалов определяется посредине длины (без учета коры). Объем может быть определен в кубических метрах исходя из размеров определенных ГОСТ 5306 — 83.
Обрезные доски. Размеры. Вес. Таблицы
Размеры поперечного сечения ( a x b ) и длины (L) обрезных досок определены ГОСТ 8486-86
Межгосударственный стандарт. ГОСТ на пиломатериалы хвойных пород смотрите здесь >>>
Длина 1 — 6.5 м. с градацией через 0.25 м. Сегодня все чаще потребителю предлагаются пиломатериалы длиной ровно 6 м., что уже стало стандартом.
Размер а (ширина) обрезной доски: 75, 100, 125, 150, 175, 200, 225, 250, 275 мм.
b (толщина) 16, 19, 22, 25, 32, 40, 44, 50 ,60, 75 мм.
Размеры обрезной доски

Обрезной доской называют строительный материал, который применяют в строительстве зданий, сооружений и возведении разных строительных конструкций. Важнейшей характеристикой пиломатериала является экологическая безопасность. Он удобен при погрузке, транспортировке, производстве, монтаже и эксплуатации. Кроме того, за изделиями из натурального дерева легко ухаживать и поддерживать в надлежащем состоянии.
Доску обрезную получают посредством выпиливания цельного бревна. При этом грани обрезной доски должны находиться под углом 90 градусов. Это свойство позволяет использовать обрезную доску в строительстве зданий, т. к. обеспечивает точность «подгона» досок друг к другу. Основным отличием высококачественной доски обрезной является полное отсутствие обзола.
Если вести речь о стандартных размерах доски обрезной, то следует обозначить следующие размерные параметры:
Бережное хранение
в упаковке
Лучшие
породы дерева
Сырье заготавливается
строго в зимнее время!
Наши пиломатериалы
— Не подвержены гниению!
Таблица сколько досок 1 кубе (штук/метров)
| Размеры доски | Объем 1-й доски | Досок в одном кубе (штук) |
| 25х100х6000 | 0,015 м3 | 66,6 шт |
| 25х130х6000 | 0,019 м3 | 51,2 шт |
| 25х150х6000 | 0,022 м3 | 44,4 шт |
| 25х200х6000 | 0,030 м3 | 33,3 шт |
| 30х200х6000 | 0,036 м3 | 27,7 шт |
| 40х100х6000 | 0,024 м3 | 41,6 шт |
| 40х200х6000 | 0,048 м3 | 20,8 шт |
| 40х150х6000 | 0,036 м3 | 27,7 шт |
| 50х100х6000 | 0,030 м3 | 33,3 шт |
| 50х150х6000 | 0,045 м3 | 22,2 шт |
| 50х200х6000 | 0,060 м3 | 16,6 шт |
По ГОСТу, длина доски обрезной составляет 6 м. С учетом индивидуальных особенностей строительного объекта потребитель может заказать и другой размер, но это должно быть согласовано с нормами транспортировки, хранения, монтажа и эксплуатацией готового объекта.

Толщина стандартной обрезной доски составляет, обычно 25, 40 или 50 мм. при толщине 100 — 150 мм. Длина, как было указано выше, составляет 6 метров.
Бруски малых размеров бывают 40 х 40 мм и 50 х 50 мм. при длине 3 или 6 метров. Стоимость обрезной доски зависит от того, к какой категории пиломатериалов относится брус: стандартный или не стандартный. Окончательная стоимость обрезной доски формируется с учетом качества полученного материала и его эксплуатационных качеств.
Для обеспечения надлежащего качества готовых изделий необходимо соблюдать правила хранения и транспортировки. В частности, при складировании доски обрезной надо учитывать ее способность впитывать влагу из земли. Поэтому материал необходимо складывать на поддоны и использовать перекладные промежуточные бруски. В таком виде доски лучше проветрятся, сохранят предельный уровень влажности и слегка подсохнут.
Основными материалами, используемые для производства доски обрезной, являются: осина, пихта, лиственница, сосна и кедр. Для внутренней отделки зданий применяют красное дерево, ясень, дуб, липу и другие породы дерева. Необходимо отметить, что по стоимости эти материалы превышают аналогичные продукты, изготовленные из других пород деревьев, но по эстетическим и эксплуатационным характеристикам они превосходят другие породы дерева.
На практике нередки случаи, когда в результате неправильного хранения качество доски пострадало, и товар перевели в категорию более низшего сорта. В таком случае товароведы торгующих организаций должны провести переоценку товара и с учетом имеющихся дефектов присвоить соответствующий сорт и цену. На маркировочном ярлыке должна быть проставлена отметка о проведенной уценке.
Источник: remstroy.pro