Библиотеки конечных элементов содержат их модели — матрицы жесткости. Модели конечных элементов различны для разных задач, разных форм конечных элементов, разных наборов координатных функций.
Исходными данными для препроцессора являются геометрическая модель объекта, чаще всего получаемая из подсистемы конструирования. Основная функция препроцессора — представление исследуемого объекта (детали) в сеточном виде, т.е. в виде множества конечных элементов.
Решатель — это программа, которая собирает модели отдельных конечных элементов в общую систему алгебраических уравнений и решает эту систему одним из методов разреженных матриц.
Постпроцессор служит для визуализации результатов решения в удобной для пользователя форме.
Основным методом для проведения различных видов анализа является метод конечных элементов. Первое применение этого метода относится к интервалу 1950-1960 года; в этот период он был использован для проведения анализа в строительной механике и самолетостроении. Этот метод получил популярность и в таких сферах, как решение инженерных задач из области статики, динамики, электроники, радиационного анализа.
Метод конечных элементов. Основы 1.1.1 — Введение
С его помощью можно решать задачи следующего характера:
- Анализ устойчивости навигационной системы к вибрациям;
- Способность монтажной платы выдерживать высокие температуры;
- Моделировать взрывы;
- Оптимизировать конструкцию.
Метод конечных элементов позволяет конструктору успешно решать задачи расчета сложных конструкций или деталей, путем разбиения их на более мелкие части — конечные элементы. Эти элементы часто называют дискретными, а процесс их выделения — дискретизацией формы.
После разбивки дальнейшее расчет на нагрузку проводятся уже для отдельных конечных элементов, каждый из которых вносит свой вклад в характеристику прочности детали. Точки, ограничивающие элемент называются узлами и вместе с проходящими через них линиями образуют конечно-элементную сетку.
Для двумерных областей наиболее часто используются элементы в форме треугольников или четырехугольников; как с прямо-, так и с криволинейными границами, чтобы в дальнейшем с достаточной степенью точности аппроксимировать границу любой формы. Для трехмерных областей наиболее употребимы элементы в форме тетраэдра и параллелипипеда, которые также могут иметь прямо- или криволинейные границы.
В общем случае метод конечных элементов состоит из 4 этапов:
1. Выделение конечных элементов (разбиение области на конечные элементы);
Разбиение области на элементы обычно начинают от её границы, с целью наиболее точной аппроксимации формы границы. Затем производится разбиение внутренних областей. Часто разбиение области на элементы производят в несколько этапов.
Сначала разбивают на крупные части, границы между которыми проходят там, где изменяются свойства материалов, геометрия, приложенная нагрузка (другие физические величины). Затем каждая подобласть разбивается на элементы. Стараются избегать резкого изменения размеров конечных элементов на границах подобластей.
Основы метода конечных элементов. Часть 1. Идея МКЭ в задачах конструкционного анализа
После разбиения области на конечные элементы осуществляют нумерацию узлов, причем порядок нумерации имеет существенное значение, так как влияет на эффективность последующих вычислений. Это связано со следующим: матрица коэффициентов системы линейных алгебраических уравнений, к которым приводит метод конечных элементов, является сильно разреженной матрицей ленточной структуры.
Ненулевые элементы такой матрицы располагаются параллельно главной диагонали. Обозначим через число, представляющее наибольшую разность между номерами ненулевых элементов в строке. Число называется шириной полосы. Чем меньше ширина полосы, тем меньший объем памяти требуется для хранения матрицы при реализации метода конечных элементов в САПР, и тем меньше затраты машинного времени на решение результирующей системы уравнений. Ширина полосы зависит от числа степеней свободы узлов и способа нумерации последних.
Информация о способе разбиения на конечные элементы и нумерация узлов является исходной для всех последующих этапов алгоритма метода конечных элементов. При этом требуется указывать не только номер, но и координаты каждого узла, его принадлежность к определенным конечным элементам, информацию о соединении элементов между собой, значения физических параметров объекта в пределах каждого элемента.
2. Определение аппроксимирующей функции для каждого элемента.

На этом этапе искомая непрерывная функция аппроксимируется кусочно-непрерывной, определенной на множестве конечных элементов. Эту процедуру можно выполнить один раз для типичного элемента области и затем полученную функцию использовать для остальных элементов области того же вида. В качестве аппроксимирующей функции элементов чаще всего используют полиномы, которые подбираются так, чтобы обеспечить непрерывность искомой функции в узлах и на границах элементов.
3. Объединение конечных элементов в ансамбль.
На этом этапе уравнения, относящиеся к отдельным элементам, объединяются в ансамбль, то есть в систему алгебраических уравнений. Полученная система является моделью искомой непрерывной функции. Мы получаем матрицу жесткости.
4. Решение полученной системы алгебраических уравнений.
Реальная конструкция аппроксимируется многими сотнями конечных элементов, возникают системы уравнений со многими сотнями и тысячами неизвестных. Решение таких систем уравнений — основная проблема реализации метода конечных элементов. Методы решения зависят от размера разрешающей системы уравнений. В связи с большой размерностью и сильной разреженностью матрицы коэффициентов системы для реализации метода конечных элементов в САПР разработаны специальные способы хранения матрицы жесткости, позволяющее уменьшить необходимый для этого объем оперативной памяти.
Матрицы жесткости используются в каждом методе прочностного расчета, используя конечную элементную сетку. Название матрицы жесткости пришло из строительной механики, где МКЭ начал использоваться раньше, чем в других областях техники.
Для решения систем уравнений применяются методы двух групп: прямые методы (метод Гаусса), косвенные методы, когда решение определяется на основе последовательной аппроксимации (метод Гаусса-Зейделя).
Методы разбиения области на конечные элементы
http://www.keldysh.ru/papers/2006/prep09/prep2006_09.html
Среди двух классов методов триангуляции — прямых и итерационных — последние обладают достаточной универсальностью и поэтому, в отличие от прямых, могут быть использованы для триангуляции областей довольно произвольного вида. За эту универсальность приходится расплачиваться существенно большим потреблением ресурсов и более трудоемкой реализацией метода в конкретном алгоритме.
В настоящее время разработано большое количество программных пакетов на основе того или иного итерационного метода, реализующих построение сеток (частично или полностью) в автоматическом режиме.
Сетки, построенные итерационными методами, как правило, неструктурированы и неоднородны. Неструктурированность обусловлена тем, что топология сетки формируется в процессе построения, и поэтому естественно может варьироваться даже в пределах одной подобласти. По этой же причине однородность если и может возникнуть, то только случайно.
Существует алгоритм, который позволяет учитывать информацию о геометрии заданной области и таким образом строить своего рода адаптивные сетки (правда, адаптированные к геометрии, а не к конкретной задаче). Этот алгоритм был разработан группой Марка Шепарда (Mark Shephard) из университета Ренсселаера (США) в 80 годах ХХ столетия и получил название «octree» (его двумерный вариант называется «quadtree»).
Идея алгоритма заключается в следующем: исходная область помещается в квадратную сетку, элементы которой последовательно дробятся на более мелкие квадраты до тех пор, пока размеры получаемых в итоге квадрвтных ячеек не достигнут желаемой величины; при этом каждый куб дробится только в том случае, если его грани пересекаются границей области (либо внутри куба целиком оказывается особенности вроде отверстия или полости). Таким образом удается добиться «естественного» увеличения плотности узлов вблизи границ области и ее «особенных» участков. Чтобы избежать значительных перепадов размеров элементов, дополнительно вводят ограничение на степень «раздробленности» соседних элементов — она не должна отличаться более чем на единицу. Рис. 1 иллюстрирует идею метода для двумерного случая.
Рис. 1. Раздробление области на квадратные ячейки по алгоритму «quadtree»
Следующим этапом метода является построение треугольной (тетраэдрической) сетки на основе полученного разбиения на квадраты (кубы). Поскольку возможных вариантов размещения узлов на ребрах и гранях кубов/квадратов в такой сетке немного (для квадрата с учетом отражения и поворота — всего 6), для каждого варианта используется свой заранее заданный шаблон. На рис. 2 и рис. 3 показаны 2 набора таких шаблонов: «классический», предложенный Шепардом, и разработанный авторами вариант, основанный на вставке дополнительного узла, позволяющий получить сетки из подобных элементов (и лучшего качества).
Рис. 2. «Классический» набор шаблонов для разбиения квадратов в методе «quadtree»
Рис. 3. Набор шаблонов с использованием дополнительного внутреннего узла, дающий лучшее качество сетки
На рис. 4 приведена сетка, получающаяся в результате применения указанных наборов шаблонов. Заметим, что описанный алгоритм без каких-либо особенностей переносится на случай 3 измерений, поэтому дополнительно рассматривать его нет смысла. Следует также обратить внимание, что полученная сетка не является структурированной, хотя в дальнейшем это не играет никакой роли (так как при граничной коррекции свойство структурированности в любом случае утрачивается).
Рис. 4. Сетка, полученная на основе алгоритма «quadtree»: вверху — по классическим шаблонам, внизу — по улучшенным.
Триангуляция Делоне
Треугольная сетка на плоскости удовлетворяет критерию Делоне (или является триангуляцией Делоне), если внутрь окружности, описанной вокруг любого треугольника, не попадают никакие другие узлы этой сетки.
Рис. 5. Сетка, удовлетворяющая критерию Делоне (слева), и не удовлетворяющая ему (справа).
В двумерном случае существует простой метод приведения произвольной триангуляции к триангуляции Делоне. Идея основана на том факте, что пару треугольников, не удовлетворяющих критерию Делоне, можно заменить на пару дуальных к ним треугольников, которые уже обязательно удовлетворяют критерию. Это достигается перестановкой внутреннего ребра четырехугольника, образованного треугольниками (см. рис. 5). Операцию (так называемый «флип», от англ. flip) продолжают итерационно для каждой пары треугольников, не удовлетворяющих критерию, до тех пор, пока такие треугольники остаются.
Проверка условия Делоне
Проверка условия Делоне. Одна из важнейших операций, выполняемых при построении триангуляции, является проверка условия Делоне для заданных пар треугольников. На практике обычно используют несколько способов проверки.
1. Проверка через уравнение описанной окружности.
2. Проверка с заранее вычисленной описанной окружностью.
3. Проверка суммы противолежащих углов.
Проверка через уравнение описанной окружности. Уравнение окружности, проходящей через точки (х1, у1), (х2, y2) ,(x3, у3) можно записать в таком виде:
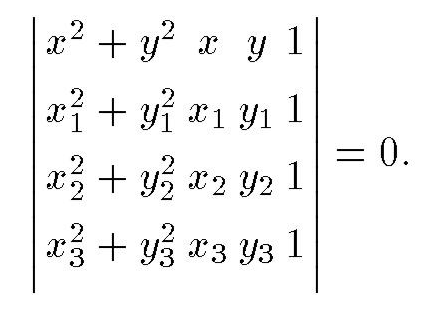
Другая запись уравнения этой окружности имеет вид


Тогда условие Делоне для Δ((х1, у1), (х2, y2), (x3, у3)) выполняется только тогда, когда для любой другой точки (x0, y0) триангуляции справедливо неравенство
Непосредственная реализация такой процедуры проверки требует 29 операций умножения и возведения в квадрат, а также 24 операции сложения и вычитания.
Проверка с заранее вычисленной описанной окружностью. Предыдущий вариант проверки требует значительного количества арифметических операций. Тем не менее, в большинстве алгоритмов триангуляции количество проверок условия многократно (в разных алгоритмах эта цифра колеблется от 2 до 25 и больше) превышает общее число различных треугольников, присутствовавших в триангуляции на разных шагах ее построения. Поэтому основная идея алгоритма проверки через заранее вычисленные окружности заключается в предварительном вычислении для каждого построенного треугольника центра и радиуса описанной вокруг него окружности, после чего проверка условия Делоне будет сводиться к вычислению расстояния до центра этой окружности и сравнению результата с радиусом. Центр (хс,ус) и радиус r окружности, описанной вокруг Δ((х1, у1), (х2, y2), (x3, у3)) можно найти как хс = b/2a, ус = –с/2а, r 2 = (b 2 + с 2 — 4аd)/4а 2 , где значения a, b, с, d определены выше.
Тогда условие Делоне для Δ((х1, у1), (х2, y2), (x3, у3)) будет выполняться только тогда, когда для любой другой точки (x0, y0) триангуляции будет
Реализация такой процедуры проверки требует для каждого треугольника 36 операций умножения, возведения в квадрат и деления, а также 22 операции сложения и вычитания. На этапе непосредственного выполнения проверок требуется всего только два возведения в квадрат, два вычитания, одно сложение и одно сравнение.
Если принять, что алгоритм триангуляции тратит в среднем по пять проверок на каждый треугольник, то в среднем данный способ проверки требует около девяти операций типа умножения и семь операций типа сложения. Если алгоритм тратит в среднем по 12 проверок на каждый треугольник, то количество операций уменьшается соответственно до шести и шести. Точная же оценка среднего числа операций должна выполняться для конкретного алгоритма триангуляции и типичных видов исходных данных.
Проверка суммы противолежащих углов. Показано, что условие Делоне для треугольника Δ((х1, у1), (х2, y2), (x3, у3)) будет выполняться только тогда, когда для любой другой точки (x0, y0) триангуляции будет α +β ≤ π (рис. 11). Это условие эквивалентно sin(α +β) ≥0, т.е.
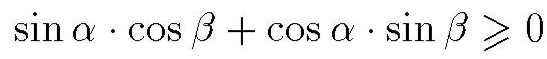
(1)
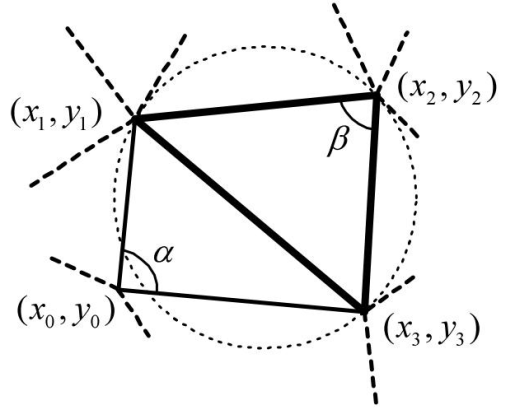
Рис. 6. Проверка суммы противолежащих углов
Значения синусов и косинусов углов можно вычислить через скалярные и векторные произведения векторов:


Подставив эти значения в формулу (1) и сократив знаменатели дробей, получим следующую формулу проверки:

Итеративные алгоритмы
Все итеративные алгоритмы имеют в своей основе идею последовательного добавления точек в частично построенную триангуляцию Делоне. Формально этот процесс может быть описан так.
Пусть имеется триангуляция Делоне на множестве из (n – 1) точек. Очередная п-я точка добавляется в уже построенную структуру триангуляции следующим образом.
Шаг 1. Вначале производится локализация точки, т.е. находится треугольник (построенный ранее), в который попадает очередная точка. Если точка не попадает внутрь триангуляции, то находится треугольник на границе триангуляции, ближайший к очередной точке.
Шаг 2. Если точка попала на ранее вставленный узел триангуляции, то у нас три варианта:
· Если точка попала на некоторое ребро, то оно разбивается на два новых, а оба смежных с ребром треугольника также делятся на два меньших.
· Если точка попала строго внутрь какого-нибудь треугольника, он разбивается на три новых.
· Если точка попала вне триангуляции, то строится один или более треугольников. Затем проводятся локальные проверки вновь полученных треугольников на соответствие условию Делоне и выполняются необходимые перестроения.
Рис. 7. Две ситуации, возникающие при триангуляции после добавления новой внутренней точки
Чтобы несколько упростить алгоритм, можно вообще избавиться от третьего случая, предварительно внеся в триангуляцию несколько таких дополнительных узлов, что построенная на них триангуляция заведомо накроет все исходные точки триангуляции. Такая структура обычно называется суперструктурой.
Суперструктура — произвольный выпуклый многогранник с треугольными гранями такой, что все заданные узлы лежат внутри него. Вершинами многогранника могут быть как элементы заданного множества, так и дополнительные узлы.
Описанный алгоритм позволяет гарантированно строить триангуляцию Делоне для произвольного набора точек, причем граница сетки будет представлять собой (в общем случае невыпуклый) многогранник с треугольными гранями, опирающимися на наиболее удаленные от центра триангуляции узлы. К сожалению, на практике приходится иметь дело с областями, представляют собой более сложные геометрические формы.
Пример итеративного алгоритма построения треангуляции Делоне
| а) Заданный набор точек | б) Постройка суперструктуры (квадрат), один из заданных узлов используется как вершина квадрата |
| в) Постройка исходной триангуляции Делоне. Т.к. квадрат является правильным многоугольником, для этого можно использовать любой из заданных узлов | г) Выбор нового (произвольного) узла и удаление всех треугольников, для которых выбранный узел лежит внутри описанной окружности |
| д) Соединение ребрами новой вершины с углами образовавшегося многоугольника | е) Выбор следующего узла и дальнейшее повторение процедуры, пока не останется неиспользованных заданных узлов |
| ж) Обработка еще одной точки | з) Еще одной |
| и) Сетка построена | к) Удаление из сетки всех треугольников, среди вершин которых были вспомогательные узлы суперструктуры |
Лекция 18. CAE системы
Комплекс критериев сравнения систем КЭ-анализа
Основные факторы выбора CAE-систем — состав решаемых задач; достоверность результатов расчета; интеграция с CAD; легкость освоения. Этот общий перечень должен быть детализирован для каждой из областей применения систем.
Для систем CAE, как и для CAD-систем, можно выделить общие для всех (стандартные) возможности и дополнительные функции, реализованные лишь в отдельных системах. К общим показателям функциональности можно отнести число типов конечных элементов, число видов граничных условий, производительность как при подготовке модели, так и при решении типовых задач, а к дополнительным возможностям — задание граничных условий для задач КЭ-анализа непосредственно в модуле CAD с передачей в модуль CAE; возможности программирования (например, в ANSYS — язык APDL, в CFX — язык CEL) и т.п.
Пример комплекса критериев сравнения систем КЭ-анализа
Сравнительный анализ систем расчета конструкций, выполненный Советом Международных стратегий и менеджмента (Франция, 1992-1993 гг.), включал тестирование по 352 параметрам, в том числе:
· удобство подготовки исходной информации;
· скорость автоматического формирования конечно-элементных моделей (плоских и пространственных);
· результаты решения тестовых задач, рекомендованных нормами AFNOR 1990 для оценки точности дискретных моделей (100 задач с известными аналитическими решениями — линейные и нелинейные задачи статики, линейные задачи динамики и термостатики);
· скорость решения системы линейных уравнений методом КЭ;
· состав библиотеки КЭ;
· возможность вычисления геометрических характеристик (моменты инерции при изгибе, кручении и сдвиге) для сечений произвольной формы;
· контроль расчетной модели для объектов, теряющих устойчивость в процессе нагружения;
В условиях выбора системы КЭ анализа для задач конкретного конструкторского бюро вряд ли возможно подробное исседование по столь большому числу показателей. Пример сокращенного набора тестов для относительно быстрой сравнительной оценки возможностей систем среднего уровня приведен в цикле статей А.Аведьяна и А.Данилина «Прочность не для прочнистов» [САПР и графика, 2000, №№ 1, 2, 3, 5].
Сравнительному анализу были подвергнуты системы «Золотых партнеров» SolidWorks, полностью интегрированные в среду CAD-системы. Сравнение выполнено по 10 критериям:
· Круг решаемых задач.
· Сложность решаемых задач (10 задач различных уровней сложности как в смысле геометрии модели, так и по содержанию анализа).
· Достоверность результатов (сравнение с известными аналитическими решениями нескольких задач — изгиб и колебания балки, прогиб круглой пластинки, растяжение вала с выточкой, нагрев толстостенного цилиндра и др.).
· Возможности задания граничных условий и нагрузок.
· Возможности работы с БД материалов.
· Степень влияния пользователя на точность расчетов.
· Доступность для инжнеров-конструкторов, не обладающих углубленной подготовкой в области прочности.
· Качество оформления результатов и удобство работы с отчетом.
· Качество и возможности визуализации.
· Устойчивость работы на ПК малой и средней мощности.
ПО реализующее метод конечных элементов (FEM):
1-2-3D, проект рассчитаный на решение задач из разных областей физики: теплопроводности, гидродинамики, механики твёрдого тела, акустики, электромагнетизма, квантовой механики; задачи описываются в виде легко читаемых текстовых файлов, есть неплохой графический интерфейс, поддерживает распараллеливание по MPI, лицензия GPL
2D, свой язык программирования транслируемый в C++, типизированный C-подобный, со встроенными типами триангуляций и пространств конечных элементов, код получается понятен, краток и приближен к математической записи задачи в слабой форме — но поддерживаются только треугольные элементы (включая DG- и мини-элементы), хорошая документация, много примеров использования на разных задачах, кроссплатформенный инструмент, лицензия LGPL
3D вариант FreeFEM++, с другими разработчиками, но со схожей идеологией, на сегодняшний день с несколько меньшей фукнциональностью, поддерживает конструктивное описание геометрии задачи
1-2-3D, формальное описание проблемы с помощью специального языка, приближенное к математической формулировке, в некотором смысле идеологически близок FreeFEM++, может решать интегро-дифференциальные задачи, в данный момент заточен под задачи из области электромагнетизма, акустики, теплопроводности и механики, ищут добровольцев готовых применить GetDP в области гидродинамики, лицензия GPL
3D, пакет для расчётов методом конечных элементов упругих и упругопластичных деформаций при ударах, написан на Java, имеет графический интерфейс, лицензия GPL, для визуализации полагается на несвободный, но бесплатный для академичекого использования, GiD
1-2-3D, очень большой (миллион строк кода, более 360 разных конечных элементов) пакет для расчётов задач механики сплошных сред, термо- и гидродинамики, акустики и магнетизма и других, заметна ориентация проекта на инженерные приложения, поддерживается язык программирования Python, лицензия GPL, документация преимущественно на французском языке
1-2-3D, библиотека для C++, получила в 2007 году премию Вилкинсона, хорошая документация, локальная адаптация сеток, p- и hp- методы, встроенные средства создания сеток, автоматическое распараллеливание сборки линейной системы и других операций на многоядерных/многопроцессорных машинах (SMP), поддержка кластерного параллелизма (MPI), но выбор элементов беднее, чем в GetFEM++, лицензия QPL
2D-3D, набор объектно-ориентированных библиотек Си, ориентирован на решение эллиптических уравнений, поддерживает адаптивные сетки и предлагает необычный способ распараллеливания решения (помимо MPI), можно использовать все возможности из bash-подобной оболочки (интерпретатора), есть упрощённая 2D версия для matlab, лицензия GPL
С++ и Python интерфейсы к системе решения задач FEniCS, хорошая поддержка в Debian и Ubuntu, код приближен к математической постановке задачи в слабой форме, но получается длиннее, чем в FreeFEM++, в силу того, что Python язык универсальный; вообще под зонтиком FEniCS объединено сразу несколько интересных проектов
1-2-3-…-ND, библиотека для C++, есть интерфейсы высокого уровня для Matlab и для Python (!), поддерживает большое количество типов конечных элементов, включая экзотичные, вроде X-FEM, практически любой размерности, есть возможность программирования типовых задач с помощью готовых «кирпичиков», избегая явной сборки линейной системы, отсутствуют встроенные средства создания сеток, можно пользоваться внешними, библиотека кроссплатформенна
1-2-3D, библиотека для C++ с возможностью локальной адаптации сеток, параллельное решение линейных систем с помощью PETSc (MPI), поддерживает безматричные методы, выбор элементов шире, чем в Deal.II
2D-3D, C++, основные области применения: гидродинамика, теплопроводность, перенос массы и взаимодействие жидкость–структура в пористых средах
2D-3D, библиотека C++, среди примеров есть задачи теплопроводости, решения уравнения Навье–Стокса для несжимаемой жидкости, теории упругости (2D и 3D), электромагнетизма, лицензия GPL
1-2-3D, библиотека для C++, код получается краток и приближен к математической записи задачи в слабой форме, автоматическая адаптация сеток для 2D задач
довольно продвинутая библиотека для Fortran77
2D-3D, библиотеки для Fortran, пакет ориентирован на решение уравнений Навье–Стокса для течения несжимаемых жидкостей, лицензия типа BSD
довольно продвинутая библиотека для Matlab и Scilab, но версия для свободного Scilab развивается менее активно
2D-3D, библиотека для Fortran, документирована исключительно на французском языке
библиотека для Fortran, для задач теории упругости и теплопроводности, распространяется бесплатно и в качестве приложения к книге, но лицензия неясна, является урезанной версией несвободной библиотеки FEAP
1D-2D-3D, библиотека для C, адаптивные сетки, контроль невязок, лицензия GPL, но на данный момент несвободная документация (для старой версии — книжка на Amazon). Release candidate новой версии 3.0 можно найти здесь, там же и черновик книжки к ней (без права копирования).
ПО реализующее метод конечных объёмов (FVM):
библиотека для Python, удобная запись задачи, приближенная к математической записи в сильной форме, получается простой и краткий код, решает задачи типа реакция–диффузия–конвекция в 1-2-3D, но не работает с областями со сложной геометрией, библиотека кроссплатформенна
2D-3D, пакет ориентированный на решение задач вычислительной гидродинамики (несжимаемаемые течения, уравнения Эйлера, Стокса или Навье–Стокса), поддерживает адаптивные сетки, расчёт переноса веществ в жидкости, распараллеливание по MPI, использует метод Volume-of-Fluid для отслеживания границы между жидкостями, постановка задачи описывается в виде графа, геометрия твердых объектов может быть импортирована из приложений CAD и 3D-моделирования, лицензия GPL
визуальная среда + библиотека C++, огромный проект, заточен прежде всего под задачи гидродинамики, кроссплатформенный, у меня пока с ним не сложилось
пакет C++ библиотек для расчётов на сложных и перекрывающихся сетках методами конечных разностей и конечных объёмов, поддерживает MPI, основной упор на гидродинамику и теорию горения. Лицензия несвободная, запрещает коммерческое использование.
Метод конечных разностей (FD):Здесь можно резко упростить себе жизнь: для этого годится любая библиотека, предоставляющая удобный интерфейс для работы с разреженными матрицами и решателями линейных систем. Заполнение матрицы обычно очевидно из используемой численной схемы. Можно порекомендовать следующие комбинации:
Источник: lektsia.com
Метод конечных элементов и его связь с основными методами строительной механики. Влияние ЭВМ на развитие методов расчета строительных конструкций. Оптимальное проектирование и его критерии.
Метод конечных элементов в строительстве впервые на практике был использован в начале 50-х годов двадцатого века. Изначально его развитие происходило в двух независимых друг от друга направлениях: инженерном и математическом. На раннем этапе становления формулировки метода отталкивались только от принципов строительной механики, и это существенно ограничивало область его применения. И лишь после формулировки основ МКЭ с возможностью небольших отклонений, стало возможным его использование и в решении других задач. Активному развитию метода конечных элементов способствовал и прогресс в области компьютерной техники, а также появляющаяся возможность его использования в большинстве областей науки и практики
Перед началом выполнения расчета конструкции следует представить ее в виде, понятном электронному мозгу, то есть компьютеру. И так как компьютер может оперировать только с цифрами, то и конструкция должна быть представлена именно в цифровом варианте. Таким образом, нужно создать математическую модель, которая будет не только полностью соответствовать рассчитываемой конструкции, но и состоять только из цифр. Целью работы будет решение этой математической модели и определение неизвестных.
Суть метода конечных элементов заключается в разбиении всей области, занимаемой конструкцией, на некоторое количество малых подобластей с конечным размером. Эти подобласти носят название конечных элементов, а само разбиение называется дискретизацией.
Форма конечных элементов будет зависеть от типа самой конструкции и характера деформации. Например, конечными элементами в расчете стержневых конструкций (ферм, балок или рам) будут участки стержней, при расчетах двумерных континуальных систем (пластин, плит или оболочек) — прямоугольные или треугольные подобласти, а при расчете трехмерных конструкций (массивов или толстых плит) — подобласти в виде тетраэдров или параллелепипедов. Но в отличие от настоящей конструкции в такой дискретной модели связывание конечных элементов происходит только в отдельных узлах (точках) некоторым известным количеством узловых параметров.
Функционалом энергии всей конструкции при дискретизации будет алгебраическая сумма отдельных функционалов конечных элементов, и для каждой подобласти должен быть задан независимый от других закон распределения требуемых для решения функций. С помощью этих законов возможно выражение перемещений (искомых непрерывных величин) в пределах заданного конечного элемента через значения величин в конечных точках.
Число узлов и число их возможных перемещений (степень свободы) для конечного элемента могут варьироваться, но меньше минимального количества, необходимого для рассмотрения состояний конечных элементов под действием напряжения или деформации в данной принятой модели, их быть не должно. Степени свободы конечных элементов определяются числом независимых перемещений во всех их узлах. Степень свободы всей рассчитываемой конструкции и, как следствие, алгебраический порядок уравнений системы будет определяться суммированием числа перемещений всех известных ее узлов. Исходя из того, что основные неизвестные в расчете методом перемещений — искомые узловые перемещения, то понятия степени свободы конечных элементов и конструкции целиком становятся особо важными в методе конечных элементов.
Способ дискретизации рассматриваемой области, количество конечных элементов, число их степеней свободы, а также форма используемых приближенных функций оказывают непосредственное влияние на точность расчета всей конструкции. Таким образом, метод конечных элементов, как наиболее алгебраический, помогает не только при расчете отдельных строительных конструкций, но и в целом при решении строительных задач.
Метод конечных элементов (МКЭ) — основной метод современной строительной механики, лежащий в основе подавляющего большинства современных программных комплексов, предназначенных для выполнения расчетов строительных конструкций на ЭВМ.
Но диапазон его применения чрезвычайно широк: строительство и машиностроение, гидро- и аэродинамика, горное дело и новейшая техника, а также различные задачи математической физики – теплопроводности, фильтрации, распространения волн и т. д.
Метод конечных элементов впервые был применен в инженерной практике в начале 50-х гг. XX в. Первоначально он развивался по двум независимым один от другого направлениям – инженерному и математическому. На раннем этапе формулировки МКЭ основывались на принципах строительной механики, что ограничивало сферу его применения. И только когда были сформулированы основы метода в вариационной форме, стало возможным распространение его на многие другие задачи. Быстрое развитие МКЭ шло параллельно с прогрессом современной компьютерной техники и ее применением в различных областях науки и инженерной практики.
Значительный вклад в разработку МКЭ был сделан Дж. Аргирисом. Им впервые дана общая матричная формулировка расчета стержневых систем на базе фундаментальных энергетических принципов, определена матрица податливости, а также введено понятие матрицы жесткости (как обратной матрице податливости). Работы Дж. Аргириса и его сотрудников, опубликованные в период 1954–1960 гг., дали отправную точку для матричной формулировки известных численных методов и применения ЭВМ в расчетах конструкций.
Для развития МКЭ особое значение имели вариационные принципы механики и математические методы, основанные на этих принципах. Дискретизацию задачи на основе вариационного метода Ритца впервые в 1943 г. применил Р. Курант. Лишь в 50-е гг. появились аналогичные работы Ж. Поли, Ж. Герша и др.
Первая работа, в которой была изложена современная концепция МКЭ, относится к 1956 г. Американские ученые М. Тэрнер, Р. Клафф, Г. Мартин и Л. Топп, решая плоскую задачу теории упругости, ввели элемент треугольного вида, для которого сформировали матрицу жесткости и вектор узловых сил. Название – метод конечных элементов ввел в 1960 г. Р. Клафф.
В период 1960–1965 гг. опубликованы работы, в которых на основе вариационных принципов получены конечные элементы для решения задач изгиба плит, тонких оболочек, массивов. Среди них можно отметить работы Р. Мак-Лейа, Р. Мелоша, Дж. Бесселина, Ф. де Веубеке, М. Джонса, Т. Пиана. В 1967 г. издана первая монография о МКЭ О. Зенкевича и И. Чанга, в которой изложены основы метода и области его применения.
К семидесятым годам относится появление математической теории конечных элементов. Здесь можно выделить труды И. Бабушки, Р. Галлагера, Ж. Дек-лу, Дж. Одена, Г. Стренга, Дж. Фикса. Значительный вклад в разработку теоретических основ МКЭ внесли и российские ученые. В. Г. Корнеев указал на совпадение математической сущности МКЭ и ВРМ.
Сопоставление МКЭ с рядом вариационных методов приведено в трудах Л. А. Розина. Под руководством А. С. Сахарова разработана моментная схема конечных элементов.
Период последних десятилетий особенно характерен для развития и применения МКЭ в таких областях механики сплошных сред, как оптимальное проектирование, учет нелинейного поведения, динамика конструкций и т. п.
Метод конечных элементов, как и многие другие численные методы, основан на представлении реальной континуальной конструкции ее дискретной моделью и замене дифференциальных уравнений, описывающих НДС сплошных тел, системой алгебраических уравнений. Вместе с тем МКЭ допускает ясную геометрическую, конструктивную и физическую интерпретацию.
Суть метода заключается в том, что область (одно- , двух- или трехмерная), занимаемая конструкцией, разбивается на некоторое число малых, но конечных по размерам подобластей (рис. 9.3). Последние носят название конечных элементов (КЭ), а сам процесс разбивки – дискретизацией.
В зависимости от типа конструкции и характера ее деформации КЭ могут иметь различную форму. Так, при расчете стержневых систем (фермы, балки, рамы) КЭ представляют собой участки стержней; для двумерных континуальных конструкций (пластины, плиты, оболочки) чаще всего применяют треугольные и прямоугольные (плоские или изогнутые) КЭ; а для трехмерных областей (толстые плиты, массивы) – КЭ в форме тетраэдра или параллелепипеда. В отличие от реального сооружения в дискретной модели конечные элементы связываются между собой только в отдельных точках (узлах) определенным конечным числом узловых параметров.
МКЭ – это вариационный метод. Функционал энергии для всей рассматриваемой области здесь представляется в виде суммы функционалов отдельных ее частей – конечных элементов. По области каждого элемента, независимо от других, задается свой закон распределения искомых функций. Такая кусочно-непрерывная аппроксимация выполняется с помощью специально подобранных аппроксимирующих функций, называемых также координатными или интерполирующими. С их помощью искомые непрерывные величины (перемещения, напряжения и т.д.) в пределах каждого КЭ выражаются через значения этих величин в узловых точках, а произвольная заданная нагрузка заменяется системой эквивалентных узловых сил.
При такой кусочно-непрерывной аппроксимации обеспечивается условие совместности лишь в узлах, а в остальных точках по границам КЭ это условие удовлетворяется в общем случае приближенно (в связи с этим различают КЭ разной степени совместности).
Наибольшее распространение получил метод конечных элементов в перемещениях, имеющий много общего с методом Ритца и вариационно-разностным методом (в дальнейшем мы будем в основном рассматривать именно этот вариант МКЭ). Различие между традиционной схемой метода Ритца и МКЭ в форме метода перемещений заключается в выборе системы аппроксимирующих функций. Если в методе Ритца аппроксимация перемещений производится по всей области их определения, то в МКЭ – по каждому конечному элементу в отдельности, что позволяет использовать аппроксимирующие функции более простого вида. В первом случае функционал полной потенциальной энергии варьируется по неопределенным коэффициентам , во втором – по перемещениям в узлах сетки, что приводит к системе алгебраических уравнений метода перемещений (основными неизвестными являются непосредственно узловые перемещения). При этом использование кусочно-непрерывной аппроксимации позволяет получить редко заполненную или ленточную структуру матрицы коэффициентов системы уравнений и таким образом дает возможность применения более эффективных методов ее решения.
Число узлов и число перемещений в узле (степень свободы узла), принятые для конечного элемента, могут быть различными, однако не должны быть меньше минимально необходимых для описания напряженно-деформированного состояния КЭ в рамках принятой физической модели. Число независимых перемещений во всех узлах элемента определяет степень свободы КЭ. Степень свободы всей конструкции и соответственно порядок системы разрешающих уравнений определяется суммарным числом перемещений всех ее узлов. Поскольку основными неизвестными МКЭ в форме метода перемещений считаются узловые перемещения, степень свободы КЭ и всей конструкции в целом является чрезвычайно важным понятием в МКЭ. Понятия о степени свободы узла, КЭ и конструкции и степени их же кинематической неопределимости идентичны.
Способ разбивки рассматриваемой области на конечные элементы, их число и число степеней свободы, а также вид аппроксимирующих функций в конечном итоге предопределяют точность расчета конструкции. Следует отметить, что простым увеличением числа конечных элементов не всегда удается достичь повышения точности расчетов. Вопросы устойчивости и сходимости решения, а также оценки точности полученных результатов являются основными при использовании МКЭ.
По сравнению с другими численными методами МКЭ в лучшей степени алгоритмизирован и более гибок при описании геометрии и граничных условий рассчитываемой области. Кроме того, к достоинствам метода следует отнести его физическую наглядность и универсальность.
Применительно к стержневым системам МКЭ в форме метода перемещений может рассматриваться как матричная форма классического метода перемещений, отличающаяся только более глубокой формализацией алгоритма и ориентацией его на использование ЭВМ.
Метод конечных элементов позволяет практически полностью автоматизировать расчет стержневых систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами строительной механики. Однако, в современных условиях большой объем вычислений не является серьезной проблемой, и, в связи с этим, при внедрении ЭВМ в инженерную практику МКЭ получил широчайшее распространение. Поэтому, знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.
Творческий процесс проектирования условно можно разбить на три стадии: анализ, синтез, оценка полученного решения.
С развитием электронной вычислительной техники использование итерациональных процедур позволяет автоматизировать поиск рациональных решений и создает новые возможности в совершенствовании вариантного проектирования сравнением практически неограниченного числа вариантов.
расходы с учетом их отдаленных во времени эксплуатаций.
Оптимальное проектирование заключается в разработке проекта конструкций, удовлетворяющей требованиям нормальной эксплуатации и имеющей наилучшие показатели из возможных.
Основу метода оптимального проектирования представляют аналитические закономерности, связывающие расчетно-конструктивные параметры изделия и организационно-технологические процессы его изготовления и монтажа с соответствующими им экономическими показателями. Преимуществом данного метода является то, что создаются условия для управления параметрами проектируемой конструкции.
Оптимальной называется система, удовлетворяющая заданным противоречивым требованиям к конфигурации конструкции, её прочности, деформативности, устойчивости, технологичности и оптимизирующая при этом решение по заданным критериям (масса конструкции, трудоемкость, стоимость с учетом расходов в течение срока эксплуатации).
Предварительно напряженные железобетонные конструкции. Преимущества и недостатки. Способы создания предварительного обжатия железобетонных конструкций. Методы натяжения арматуры. Потери предварительных напряжений.
Первые, вторые и полные потери. Особенности конструирования предварительно напряженных железобетонных конструкций
Идея предварительного напряжения заключается в создании в конструкции до ее загружения внешними нагрузками усилий, позволяющих регулировать напряжения, вызываемые внешними нагрузками.
1. Снижение расхода материалов(бетона 40%, стали — 80% при использовании высоких классов бетона и высокопрочной арматуры).2. Снижение собственного веса конструкций за счет применения высокопрочных бетонов и арматуры
2. Повышение жесткости конструкции за счет повышения трещиностойкости, уменьшения прогибов.
3. Увеличение долговечности конструкции( в агрессивной среде и большой влажности.
4. Повышение жесткости( уменьшение прогиба за счет обратного выгиба).
5. Повышение выносливости конструкции при динамических нагрузках.
1. Усложненное проектирование и изготовление
2. При передаче усилий с арматуры на бетон возможно появление трещин в бетоне вдоль напрягаемой арматуры в виду радиального давления арматуры на бетон.
3. При чрезмерных усилиях обжатия возможно появление трещин в верхних растянутых при обжатии зонах, что приводит к более раннему образованию трещин от внешних нагрузок, увеличению прогибов, ширины раскрытия трещин.
В качестве напрягаемой арматуры — А600, А800, А1000, Вр1200-Вр1600, канаты арматурные К7 и К19. Бетон назначается в зависимости от класса и диаметра арматуры. Rb больше 15Мпа и больше 0,5В, где В — класс бетона.
Способы предварительного напряжения ЖБ:
Сначала производится бетонирование, при котором предусматриваются каналы или пазы для дальнейшего размещения арматуры. После набора бетона передаточной прочности арматура заводится в каналы и производится ее натяжение. Затем каналы заполняются мелкозернистым бетоном. В некоторых конструкциях не заполняется — резервуары, атомные реакторы, тв башни.
Арматура закрепляется в упорах и натягивается механическим, электромеханическим или электротермическим способом (300 С). Натяжение может производится с одной или нескольких сторон, затем производится бетонирование и после достижения бетоном передаточной прочности Rbp арматура плавно освобождается от упоров и усилия, ранее передаваемые на упоры, начинают обжимать бетон.
-использование бетона на напрягающем цементе
Такие бетоны при твердении вместо усадки в объеме увеличиваются. Технология аналогична ненапрягаемым жб конструкциям.
Потери предварительных напряжений в арматуре
Начальные предварительные напряжения в арматуре не остаются постоянными, с течением времени они уменьшаются. Различают первые потери предварительного напряжения в арматуре, происходящие при изготовлении элемента и обжатии бетона, и вторые потери, происходящие после обжатия бетона.
1. Потери от релаксации напряжений в арматуре при натяжении на упоры зависят от способа натяжения и вида арматуры: при механическом способе натяжения, МПа: высокопрочной арматурной проволоки и канатов, стержневой арматуры;
при электротермическом и электротермомеханическом способах натяжения: высокопрочной арматурной проволоки и канатов, стержневой арматуры.
2. Потери от температурного перепада, т. е. от разности температуры натянутой арматуры и устройств, воспринимающих усилие натяжения при пропаривании или прогреве бетона.
3. Потери от деформации анкеров, расположенных у натяжных устройств вследствие обжатия шайб, смятия высаженных головок, смещения стержней в зажимах или в захватах при механическом натяжении на упоры.
4. Потери от трения арматуры: а) о стенки каналов или поверхность конструкции при натяжении на бетон б) об огибающие приспособления при натяжении на упоры
6. Потери от быстронатекающей ползучести бетона зависят от условий твердения, уровня напряжений и класса бетона; развиваются они при обжатии (и в первые 2—3 ч после обжатия).
7. Потери от релаксации напряжений в арматуре при натяжении на бетон высокопрочной арматурной проволоки и стержневой арматуры принимаются такими же, как и при натяжении на упоры.
8. Потери от усадки бетона и укорочения элемента зависят от вида бетона, способа натяжения арматуры, условий твердения.
9. Потери от ползучести бетона (следствие соответствующего укорочения элемента) зависят от вида бетона, условий твердения, уровня напряжений
10. Потери от смятия бетона под витками спиральной или кольцевой арматуры (при диаметре труб, резервуаров до 3 м)
11. Потери от деформаций обжатия стыков между блоками сборных конструкций. Для конструкций, эксплуатируемых при влажности воздуха окружающей среды ниже 40 %, потери от усадки и ползучести бетона увеличиваются на 25 %. Для конструкций, эксплуатируемых в районах с сухим жарким климатом, эти потери увеличиваются на 50 %.
При натяжении арматуры на упоры учитывают: первые потери — от релаксации напряжений в арматуре, температурного перепада, деформации анкеров, трения арматуры об огибающие приспособления, деформации стальных форм, деформации бетона от быстронатекающей ползучести; вторые потери — от усадки и ползучести.
При натяжении арматуры на бетон учитывают: первые потери — от деформации анкеров, трения арматуры о стенки каналов (или поверхности бетона конструкций); вторые потери — от релаксации напряжений в арматуре, усадки и ползучести бетона, смятия бетона под витками арматуры, деформации стыков между блоками. Суммарные потери при любом способе натяжения могут составлять около 30 % начального предварительного напряжения. В расчетах конструкций суммарные потери должны приниматься не менее 100 МПа.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Источник: cyberpedia.su
Метод конечных элементов и его применение
Метод конечных элементов возник как один из приемов исследования различных конструкций. В настоящее время он повсеместно признан как общий способ решения широкого круга задач в различных областях техники.
Определение
Инженерный анализ методом конечных элементов заключается в аппроксимации сплошной среды с бесконечно большими числами степеней свободы совокупностью элементов (подобластей), имеющих конечные числа степеней свободы. Между этими элементами устанавливается взаимосвязь. Признание метода объясняется простотой его математической формы и физического толкования.
Применение в механике
Метод конечных элементов в механике разрушения и в задачах строительной механики выражается как соотношение МКЭ в форме перемещений. Вначале задаются в рамках каждого элемента так называемые функции формы. Они определяют перемещение во внутренней области элемента по перемещению в узлах. Последние – это точки, где сочетаются конечные элементы.
Неизвестными МКЭ являются возможные и независимые перемещения узлов конечно элементной модели (КЭМ). Таким образом, КЭМ конструкции представляет собой систему закрепленных узлов. Дополнительные связи соотносятся с направлением возможных перемещений узлов.
Суть метода
По своей сути элементная модель конструкции аналогична основной системе классического метода перемещений, которая применяется при расчете стержневых систем. Для достижения восприимчивой точности результатов расчетов по методу конечных элементов приходится уменьшать размеры элементов, увеличивая тем самым точность аппроксимации геометрических характеристик и функций перемещений в пределах конечного элемента.
КЭМ сложных конструкций достигают сотен и даже миллионов степеней свободы, а потому метод конечных элементов в технике является машинно-ориентированным, реализация которого возможна только посредством компьютеров.
Практическая реализация
Для применения МКЭ на практике необходимо разбираться не только в теории механики, но и обладать знаниями в области программирования. Применение метода конечных элементов зачастую строится на базе вариационных принципов механики, в основе которых заложены два фундаментальных скаляра: потенциальная и кинетическая энергия упругой конструкции. Определение этих скаляров, независимых от выбранной системы координат, позволяет записывать соотношение МКЭ в инвариантной форме.
Для обеспечения удобства программирования соотношения МКЭ записываются в компактной матричной, или тензорной форме. На сегодня моделирование методом конечных элементов достаточно полно математически обосновано, созданы высокоэффективные программные продукты, которые все время совершенствуются вместе со средствами программирования.
Учебно-вычислительные программы
Технический прогресс, особенно в области ЭВМ, существенно изменил взгляды на постановку и решение инженерных задач. Построение расчетной модели тесно связано с процессом вычислений, и разделить эти два этапа на пути получения практических результатов почти невозможно.
Метод конечных элементов широко применяется в инженерной практике, что также способствовало включению его в учебные программы вузов. МКЭ предоставляет способы построения математической модели исследуемого явления исходя из его физической сущности.
Первые учебники по МКЭ были написаны сложным языком, но вскоре методика преподавания была упрощена благодаря внедрению специализированных программ. Например, хорошо себя зарекомендовал программный комплекс «Ассистент». Он позволяет проверить знания студентов в интерактивном режиме и способствует развитию навыков работы с программными продуктами при решении практических задач.
Расчет линейных деформаций
Сегодня основы метода конечных элементов базируются на том, что величины и понятия, ему присущие, не вводятся заранее, а вытекают из существа задачи строительной механики. Круг проблем, которые можно решать с помощью МКЭ, практически неограничен. Рассмотрим для примера задачу по расчету линейной деформации упругих конструкций от действия статических нагрузок.
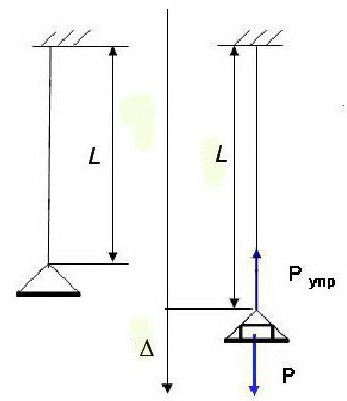
Английский физик Р. Гук провел исследования деформаций центрально-нагруженных стержней, выполненных из разных упругих материалов, под действием статической силы: ∆=Pl/EA.
Он также установил зависимость между величинами, определяющими этот процесс: σ=Eε, где деформация выражена соотношением ε=∆/l, напряжение обозначено как σ=P/A (здесь A – площадь сечения стержня).
Коэффициент пропорциональности E определяет упругие характеристики материала и имеет физическую суть – напряжение, соответствующее единичной деформации.
Влияние статической силы
Статически действующая сила растет во времени постепенно (G≥P≥0). Перемещения, которые она порождает, тоже растут постепенно, без ускорений.
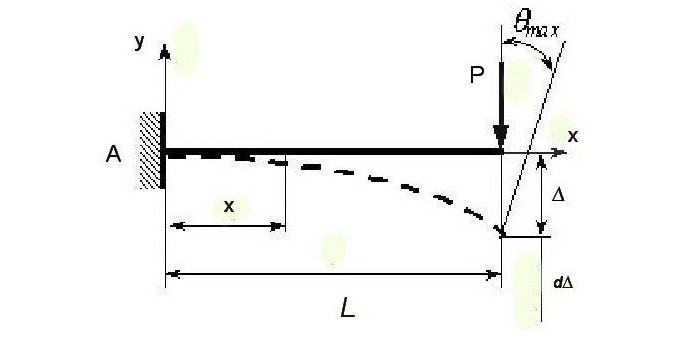
Анализ методом конечных элементов позволяет определить воздействие статической силы на перемещение, учитывая, что эти показатели меняются. Возрастанию (приросту) силы на бесконечно маленькую величину dP соответствует возрастание (прирост) перемещения d∆. Работа силы (P+∆P) на перемещение d∆ имеет значение dA=(P+∆P)×d∆.
Окончательное значение работы силы определяется по формуле A=∫Pd∆.
Введем зависимость между разномерными величинами под знаком интеграла ∆=Pα, где α – коэффициент податливости, который выражает физическую сущность перемещения точки, к которой добавлена единичная сила, в направлении этой силы. Соотношение ∆=Pα устанавливает единицу измерения α (м/Н). Отсюда следует, что d∆=dPα.
Коэффициенту податливости соответствует другая важная характеристика конструкции – коэффициент жесткости k=l/α (н/м), который определяет силу, вызывающую единичное перемещение конструкции в направлении этой силы.
С учетом всех характеристик и коэффициентов итоговое уравнение принимает вид: A=∫PdPα = α×(P 2 /2)=(G∆)/2.
Получена формула Клапейрона, которая определяет действительную работу статически действующей силы на перемещение, ею же порожденное в упругом теле. По этой методике рассчитываются и другие численные методы.
Метод конечных элементов для стержневых систем
Стержень является пространственным телом, два размера которого, ширина и высота, гораздо меньше длины. Это дает возможность рассматривать его физическую модель в виде линии, проходящей через центры сечений. Если внешние силы, приложенные к стержню, расположены в одной плоскости с его моделью, то можно считать, что деформации его происходят в этой же плоскости.
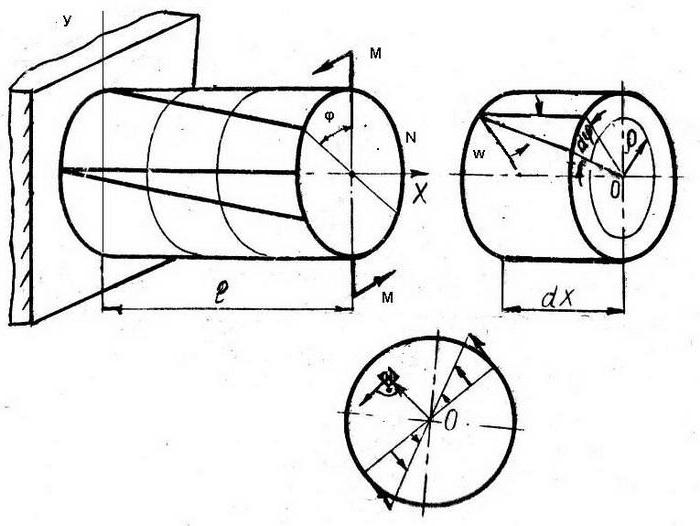
С математической точки зрения геометрические характеристики перемещения и напряжения в пределах стержня являются функциями одного аргумента. Соотношения теории упругости базируются на гипотезе плоских сечений стержня. Связь между деформациями и напряжениями соответствует линейному закону Гука. В каждом сечении стержня проявляются три плоскости перемещения:
- координата u – продольная сила;
- координата w – прогиб;
- координата φ – угол поворота.
При этом продольная u и прогиб w независимы, а угол поворота выражается формулой φ=dw/dx, где dw – величина прогиба после воздействия на стержень внешней силы, dx – участок прогиба (определяемый значением w+dw).
Для бесконечно малой величины стержня dx действует соотношение dx=dφ×P.
Потенциальную энергию деформации стержня естественно вычислять в локальной системе координат, ось x которой совпадает с осью стержня, а ось y перпендикулярна оси стержня: U=½∫N×du+½∫M×dφ=½∫N×(du/dx)dx+½∫M×(d²w/dx²)dx.
Изопараметрический подход в МКЭ
Рассмотрим применение метода конечных элементов в изопараметрической системе конечных элементов плоско-напряженной конструкции. Процесс создания конечно элементной модели конструкций состоит из нескольких этапов, первым из которых является построение сетки конечных элементов (КЭ), выбор глобальной системы координат относительно целой конструкции и локальной системы, связанной с конечным элементом.
Ответственным этапом является определение функций формы, которые обеспечивают определение перемещений в пределах конечного элемента из-за перемещения его узлов. Есть разные способы построения функций формы, но они должны обеспечить выполнение нескольких условий по аппроксимации функций перемещений.
- Выполнение условий неразрывности перемещений не только в узлах конечных элементов, но и на их границах.
- Обеспечение сохранения производных от функций перемещений, которые относятся к упругому потенциалу.
- Движение перемещения конечного элемента как жесткого целого. Это означает, что при смещении элемента как твердого тела компоненты вектора деформаций равны нулю.
Проблемы и решения
Теория методов конечных элементов гласит, что соотношения МКЭ формируются в локальной системе координат. Поэтому перечисленные требования относительно функций формы выполняются автоматически, если оси локальной системы ориентированы по сторонам конечного элемента. Такие случаи имеют место для конечных элементов стержневых конструкций, прямоугольных стеновых панелей, прямоугольных плит.
Но на практике встречаются конструкции с контуром произвольного определения. В этом случае приходится выполнять преобразование для аппроксимации перемещений в глобальной системе координат, что приводит к разрывам перемещений на границах конечных элементов и, как следствие, – к потере точности приближенных расчетов.
Возникла идея отобразить плоский четырехугольный конечный элемент общего вида на квадрат с локальной системой координат, начало которой находится в центре этой фигуры, и осями, ориентированными по его сторонам. Для дальнейшего использования конечных элементов в форме квадрата необходимо установить взаимно однозначную связь между локальными координатами произвольного четырехугольного КЭ и локальной системой координат КЭ в форме квадрата. Ведь для квадратного конечного элемента функции формы строятся достаточно просто.
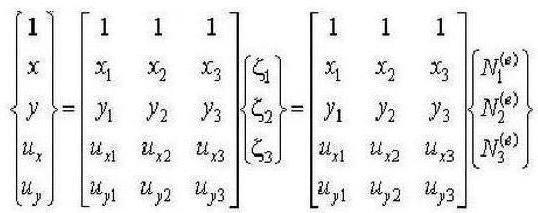
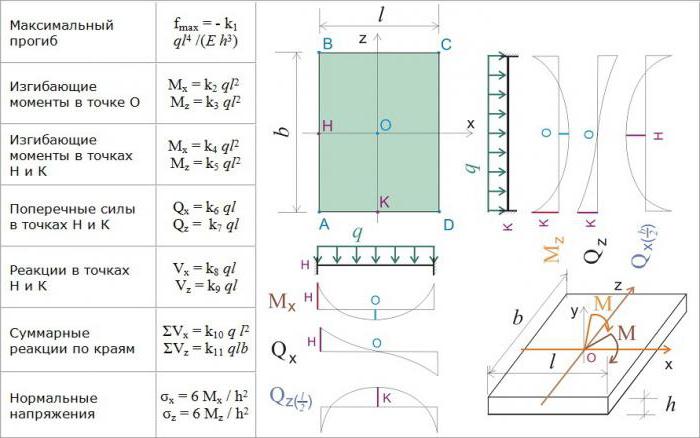
Метод конечных элементов для расчета пластин
Пластина – это вставка или цилиндрическое тело, высота которого значительно меньше размеров в плане. Размер по высоте называется толщиной пластины. Плоскость, которая делит высоту пластины пополам, называется срединной или базовой плоскостью. Линия пересечения боковой поверхности со срединной плоскостью называется контуром пластины.
Тонкой считается пластина, для которой отношение толщины к меньшему размеру в плане находится в пределах h≤L/5, где h – толщина пластины, L – ее ширина.
Пластина считается жесткой, если под действием поперечной нагрузки наибольший ее прогиб при деформации не превышает 1/5 толщины.
При расчете методом КЭ сначала вводят систему координат: X1, X2 и X3. Начала осей X1 и X2 расположены в срединной плоскости. Ось X3 ориентируют по нормали к срединной плоскости.
Расчеты обычно сводятся к вычислению перемещения (сдвига) пластины в некоей точке под воздействием нагрузок (сил). В произвольной точке пластины, которая рассматривается как трехмерное тело, проявляются три направления перемещения: U1, U2, U3. Определяющим является перемещение по нормали к срединной плоскости, которое называется прогибом и обозначается буквой W.
Расчеты считаются выполненными, если от заданной нагрузки (а это обычно равномерно распределенная, направленная к поверхности) установлен способ вычисления перемещений U и сдвига W в произвольной точке пластины. Соотношения МКЭ строятся на основе положений технической теории упругости, предложенных физиком Кирхгофом.
Гипотезы Кирхгофа
Метод конечных элементов во многом основывается на гипотезах, сформулированных в 1845 немецким физиком Г. Киргофом. Гипотеза прямых нормалей утверждает, что любая прямая линия, нормальная к срединной плоскости недеформированной пластины, остается прямой и нормальной к срединной поверхности деформированной пластины, а длина прямой линии не меняется. Суть ее заключается в отсутствии сдвига между слоями пластины по толщине.
Если оси декартовых координат размещены так, что плоскости X1, X2 совпадают со срединной плоскостью, то из первой части гипотезы вытекают следующие равенства: y13=0, y23=0. Гипотеза о неизменности длины прямой линии предполагает, что линейная деформация в направлении оси X3 равна нулю: ε33=0.
Гипотеза об отсутствии давления между слоями пластины, параллельными срединной поверхности, предполагает, что напряжениями σ33 по сравнению с напряжениями σ11 и σ22 можно пренебречь, то есть σ33=0.
Гипотеза о недеформируемости срединной плоскости предполагает, что в срединной плоскости пластины отсутствуют деформации растяжения, сжатия и сдвига. То есть срединная плоскость является нейтральной. Так что в ней перемещения U1=U2=0.
Вывод
Метод конечных элементов, широко применяемый в строительстве и механике, позволяет рассчитывать смещения различных элементов, подвергающихся определенным нагрузкам. Система, сформулированная еще в 1936 году советскими учеными, начала широко применяться лишь спустя десятилетия, так как требовала большого объема расчетов. С внедрением ЭВМ эта задача упростилась.
Источник: www.syl.ru