Организация сетевого планирования в строительстве

Современное строительное производство в условиях резко возросших масштабов, усложнившихся условий и характера возводимых объектов, постоянно развиваю­щейся специализации и кооперации деятельности много­численных его участников представляет собой крупно­масштабную динамическую систему со сложными взаи-имосвязями элементов и постоянно изменяющимся состоянием возводимых объектов.

Традиционные графические модели строительного производства, такие, как линейные календарные графики и циклограммы строительных потоков, по своей структу­ре и характеру построения не способны отображать все взаимосвязи элементов строительного производства и тем более не могут оперативно учитывать происходя­щие в ходе строительства объектов изменения (отклоне­ния) от первоначально принятых параметров развития процессов. Кроме того, в этих моделях не выделяются ра­боты, от сроков выполнения которых непосредственно за­висит продолжительность строительства объекта, что за­трудняет разработку обоснованных плановых решений.

Календарно-сетевое планирование

При оперативном управлении строительным произ­водством линейные календарные графики и циклограм­мы подвергаются многократной переработке, но и при этом они отражают статичное состояние развития строи­тельных процессов на какой-то определенный момент.

Для достижения хороших результатов планирование и управление строительным производством необходимо осуществлять на строго научной основе с использовани­ем организационно-технологических моделей, отражаю­щих динамику процессов строительного производства и охватывающих деятельность всех участников и весь период времени, начиная от подготовительных работ и кончая вводом объектов в эксплуатацию. Этим требова­ниям в полной мере отвечают сетевые модели или сетевые графики.Сетевые графики представляют собой схему, на кото­рой наглядно показаны все работы, выполняемые всеми участниками строительного производства в их рацио­нальной последовательности и очередности. Сетевые гра­фики позволяют расчетным путем определять сроки вы­полнения каждой работы и состав работ, от которых за­висит общая продолжительность строительства (крити­ческие работы). В ходе строительства сетевые графики корректируются без общей их переработки.

Основные преимущества сетевых графиков: возмож­ность комплексного рассмотрения всех работ по созданию объекта с требуемой степенью их детализации и с ука­занием взаимосвязей между работами и технологичес­кой последовательности их выполнения; возможность увязки работ всех исполнителей, принимающих участие в строительстве и определении технологически обосно­ванных сроков выполнения каждой работы, а также пе­речня работ, от завершения которых в первую очередь зависит выполнение заданий в установленные сроки; ва­риантность в выборе последовательности и продолжи­тельности работ с целью нахождения оптимального ре­шения для более эффективного использования потребля­емых материально-технических и трудовых ресурсов; возможность оперативного контроля за ходом строитель­ства с обработкой больших массивов информации совре­менными средствами вычислительной техники, а также непрерывного планирования работ на основе обоснован­ного прогнозирования событий и уточнения планов с уче­том возникших изменений.

График графику рознь? Календарно–сетевое планирование на промышленной стройке: Елена Колосова, «К4»

Сетевые модели позволяют смоделировать основные этапы работ по созданию объектов: проектно-изыскательские работы, включая мероприятия по разработке и ут­верждению проектно-сметной документации, разработку ПОС и ППР; отвод территории под застройку; поставку необходимых ресурсов; строительство объекта; поставку и монтаж оборудования; испытания, наладку и сдачу объ­екта в эксплуатацию.

С использованием сетевых графиков решается ряд принципиальных и сложных задач планирования и управ­ления строительным производством, главными из которых являются: возможность вариантного анализа путей дости­жения производственных целей, прогнозирования хода строительства в пространстве и во времени, организации деятельности всех участников строительства в требуемом направлении; разработка и реализация управленческих решений, позволяющих осуществлять оптимальные или улучшенные планы выполнения комплексов строительно-монтажных работ, выявлять и более рационально исполь­зовать резервы строительного производства, существенно повышая эффективность управления в целом; выявление в системе управления строительством объективных при­чин допускаемых отклонений, что способствует конкре­тизации ответственности исполнителей и позволяет объ­ективно оценивать вклад каждого участника в реализа­цию общего плана.

Использование сетевых графиков для планирования и управления особенно эффективно при возведении слож­ных объектов. Они получили распространение с возрас­танием крупности объектов и увеличением числа участ­ников строительства. Наиболее полно реализовать пре­имущества сетевых моделей можно в условиях их приме­нения при планировании и управлении всей программы строительства определенного структурного подразделе­ния. Однако сетевые модели не могут заменить всего мно­гообразия методов планирования и управления строитель­ным производством. Обеспечивая системный подход в ре­шении проблем организации, планирования и управления строительным производством, используя средства мате­матического моделирования, вычислительную технику и сетевые графики, можно добиться улучшения использо­вания и повышения эффективности внедрения современ­ных научных методов строительного производства.

ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕВЫХ ГРАФИКОВ

Основные элементы сетевых графиков. Построение сетевых графиков основывается на двух основных элемен­тах: работах и событиях.

Работа — производственный процесс, требующий за­трат времени и ресурсов (отрывка котлована, монтаж фундаментов, кровельные работы и т. д.). Работа обоз­начается на графике сплошной стрелкой, ограниченной двумя событиями. Различают работы действительные, требующие затрат времени и ресурсов, и работы фиктив­ные (ожидания), требующие только затрат времени.

При изображении действительной работы (рис. XVII.1) под стрелкой обычно указывают наименование работы, строительное подразделение — исполнителя, фи­зические объемы работ, сметную стоимость (тыс. руб.), трудоемкость (чел.-дн.). Над стрелкой указывают про­должительность работы (дн.), число рабочих в первую смену, число рабочих во вторую смену, наименование мес­та выполнения работы (в осях здания, участок, захватка).

XVII .1. Обозначения действитель­ ной работы в сетевом графике

/ — продолжительность работы, дн.; 2 — число рабочих в первую смену;

3 — число рабочих во вто­рую смену; 4— место работы, оси здания;

5— трудоемкость, чел.-дн.; 6 — сметная стоимость, тыс. руб.;

7— физический объем (шт., м’); 8 — организация-исполнитель

При обозначении действительной работы объем ин­формации может быть сокращен до двух обозначений— продолжительности и наименования работ.

В сетевых графиках отображают также фиктивные работы, не требующие затрат ресурсов. Фиктивные ра­боты (ожидание) обусловлены технологическими пере­рывами в строительном процессе либо необходимостью ожидания завершения выполнения одной работы для на­чала выполнения другой (набор проектной прочности монолитных бетонных конструкций). Ожидание изобра­жается так же, как и работа, — сплошной стрелкой с ука­занием продолжительности и наименования работы (рис. XVII.2).

Зависимость — пунктирная линия, соединяющая два взаимозависящих события, показывает последователь­ность выполнения работ, не требует затрат времени и ре­сурсов.

Событие — это окончательный результат одной или нескольких предшествующих работ, определяющих дос­таточность и возможность начала выполнения последую­щих работ. События определяются технологической и ор­ганизационной последовательностью работ и изобража­ются кружками или другими геометрическими фигурами, внутри которых (или рядом) указывается определенный номер — код события. Событие, которое непосредствен­но предшествует началу работы, называется начальным, а событие, показывающее завершение данной работы — конечным. Кроме того, различают исходное событие— событие, которое не имеет предшествующих работ в рам­ках рассматриваемого сетевого графика, и завершающее событие — событие, которое не имеет последующих ра­бот.

Наряду с целевыми событиями в сетевом графике це­лесообразно отмечать контрольные события, которые оп­ределяют сроки выполнения определенных технологичес­ких процессов или комплексов работ различных исполнителей.

Для характеристики основных параметров сетевые графиков вводится понятие пути.

Путь — непрерывная технологическая последовательность работ в сетевом графике. Между исходным и завершающим событиями сетевого графика обычно имеется несколько путей.

На рис. XVII.3 показан сетевой график, в котором от исходного до завершающего события имеется несколько путей. Длина каждого из этих путей (сумма продолжительностей составляющих их работ) различна, что под­тверждается расчетом в (табл. XVII. 1).

Как видно из табл. XVII.1, от исходного события к за­вершающему ведут пять различных путей продолжитель­ностью 20. 35 дн.

Путь № 2, имеющий наибольшую продолжительность по выполнению всех составляющих его работ, называет­ся критическим. Длина критического пути определяет продолжительность выполнения работ по сетевому графи­ку. Критический путь, проходящий по событиям 01, 02, 03, 09, 10, 11 (рис. XVII.3), показан жирными стрелками. Он равен 35 дн.

Работы и события, лежащие на этом пути, называются критическими.

На практике обычно ставится задача сокращения критического пути, так как это обеспечивает уменьшение общей продолжительности строительства.

Пути, продолжительность которых несколько меньше продолжительности критического пути, но более мини­мальной продолжительности, называют подкритически ми путями. Совокупность всех критических и подкрити-ческих работ называют критической зоной.

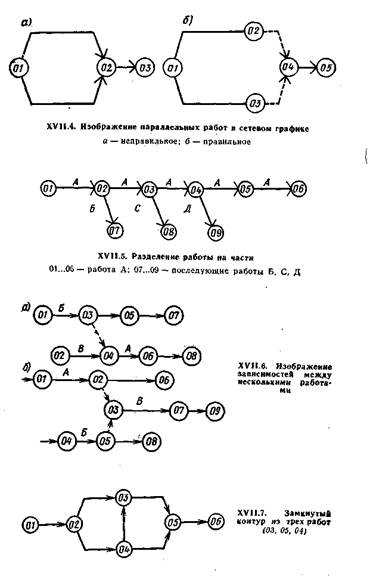
Основы построения сетевых графиков. При проекта ровании сетевых графиков рекомендуется соблюдать сле­дующие общие правила и условия: сетью должны охва­тываться все виды работ, включенные в проектно-техно-логическую документацию на возведение объекта; каждая работа должна иметь свой код, поэтому при изобра­жении параллельных работ вводят зависимости или фиктивные работы (рис. XVII.4); стрелки в сетевом графике должны быть направлены слева направо; форма сетево­го графика должна быть предельно простой, без лишних пересечений; большинство основных работ следует изоб­ражать горизонтальными линиями; монтажные работы по установке конструкций и оборудования увязываются с их поставками и укрупнительной сборкой, а при значи­тельных объемах поставок данные работы могут быть представлены в виде отдельной сетевой модели; при оп­ределенной последовательности исполнителей для вы­полнения работ в график вводят организационные (ре­сурсные зависимости — ограничения), показывающие возможность начала следующей работы лишь после ос­вобождения рабочих и механизмов, выполняющих пред­шествующую работу. Ресурсные связи позволяют зара­нее увязать работу исполнителей в специализированный поток как внутри одного объекта, так и между объек­тами.

Если необходимо начинать последующие работы пос­ле частичного выполнения предшествующей работы, то эта работа делится на части, каждая из которых счита­ется самостоятельной работой (рис. XVII.5).

При наличии зависимости начала выполнения опреде­ленной работы А от завершения работ Б и В, на сетевом графике вводится дополнительное событие (рис. XVII.6, а) 04 и дополнительная зависимость 03—04.

Если при выполнении работ двух видов А и Б появ­ляется возможность начать третий вид работ В, то на сетевом графике это изображается с помощью двух спе­циальных зависимостей: 02—03 и 05—03 (рис. XVII.6, б). При разработке сетевого графика не должно быть цепочек работ, возвращающихся к тому событию, из ко­торого они вышли, т. е. не должно быть замкнутых кон­туров (циклов). На рис. XVII.7 представлен неправиль­ный замкнутый контур, образованный работами.

При разработке сетевого графика не должно быть «тупиков» и «хвостов». «Тупик» — событие (кроме завер­шающего), из которого не выходит ни одна работа, на­пример событие 04 (рис. XVII.8). «Хвост» — событие (кроме исходного), в которое не входит ни одна рабо­та, например событие 02 (рис. XVII.8).

Если при разработке сетевых графиков обнаружены «тупики» и «хвосты», значит в исходных данных ошибка и график необходимо пересмотреть.

При укрупнении сетей необходимо соблюдать следу­ющие положения: группа однородных работ может изо­бражаться как одна работа, если в этой группе имеется одно начальное или одно конечное событие; укрупнять в одну работу следует только работы, которые выполня­ет один исполнитель (звено, бригада, участок); в укруп­ненную сеть нельзя вводить новые события, которых не было на более детальном графике до укрупнения; наи­менование работ при укрупнении сетей должно быть увя­зано с наименованием укрупняемых работ.

Поставки и другие внешние работы изображают специальной символикой. К внешним работам относят по­ступление технической документации, поставку материа­лов или оборудования, завоз строительных машин, по­ставку сантехнического оборудования. Обычно такие работы графически выделяют утолщенной стрелкой с двойным кружком (рис. XVII.9) и в график вводят до­полнительное событие, например 04.

При поставках определенного оборудования обычно приняты варианты символов обозначения внешних ра­бот, показанные на рис. XVII. 10.

События кодируют в соответствии с последовательно­стью работ во времени после окончательного построения сетевого графика. Работы кодируют таким образом, что­бы номер начального события был меньше номера конеч­ного события (рис. XVII.11).

Кодирование сети выполняется горизонтальным или вертикальным методом (рис. XVII.12). При горизонталь­ном методе события кодируют слева направо по прямым до первого пересечения работ. При вертикальном спосо­бе нумерацию начинают сверху вниз и снизу вверх с уче­том следующего условия: последующее событие получает номер после предыдущего.

Дата добавления: 2019-01-14 ; просмотров: 1323 ; Мы поможем в написании вашей работы!

Источник: studopedia.net

Календарно сетевое планирование. Сетевой метод планирования

Календарное планирование — одно из ключевых понятий организации строительства, обеспечивает развитие проекта во времени, подобно тому, как стройгенплан обеспечивает развитие проекта в пространстве. Календарное планирование создает основу для управления ресурсами всех видов, для планирования работ и эффективности строительного производства.

Календарный график является наглядным средством представления развития строительства во времени, удобен для определения расхода ресурсов. Однако рассчитывать по нему общую продолжительность строительства сложно, а иногда невозможно. Трудно также выделить важные и неважные для достижения конечного результата процессы. Для устранения этих недостатков в середине XX в. была разработана математическая модель развития проекта, получившая в строительстве название «сетевой график».

Задачи календарного планирования

Управление сроками строительства является прямой задачей руководителя любого ранга, служб заказчика и подрядчика, независимо от масштаба и вида строительства. При этом в сферу управления попадает целый ряд вопросов, включая финансовое и ресурсное планирование, контроль сроков и стоимости выполнения работ, корректировку технологии и последовательности работ. При управлении сроками может меняться продолжительность строительных работ и отдельных производственных операций, могут изменяться потребление ресурсов и затраты на строительство.

При корректировке сроков строительства теоретически может быть выгодно как уменьшение, так и увеличение продолжительности, поскольку есть факторы, улучшающие технико-экономические показатели как в том, так и в другом случае. Например, при сокращении продолжительности строительства сокращаются накладные расходы, уменьшается риск невыполнения договорных обязательств, а при увеличении продолжительности строительства сокращаются необходимый объем временных сооружений и количество одновременно привлекаемых работников на площадке (см. параграф 25.4). Таким образом, имеется некоторая оптимальная продолжительность работ. Однако в подавляющем большинстве случаев строительство запаздывает по отношению к оптимальному графику, поэтому сокращение продолжительности строительства является наиболее насущной задачей. Эта задача одинаково важна для инвестора, заказчика и подрядчика.

Второй задачей календарного планирования является улучшение равномерности расходования ресурсов. Наиболее важна эта задача для нерасхо- дуемых ресурсов (трудовых и технических), так как неравномерность их потребления сразу приводит к простоям и, как следствие, финансовым потерям. Впрочем, равномерность использования расходуемых ресурсов (материалов) также полезна, поскольку приводит к уменьшению размера складов и количества транспортных средств. При заданном максимальном размере расходования ресурсов (например, максимальном количестве квалифицированных рабочих) зачастую приходится уменьшать интенсивность их потребления за счет искусственного растягивания продолжительности работ. Наибольшее значение решение этой задачи имеет для подрядчиков.

Третьей задачей календарного планирования, которая решается в основном генеральным подрядчиком, является оптимальное распределение работ между субподрядчиками и подразделениями со своевременной подготовкой фронта работ, взаимной увязкой производственной деятельности, установлением понятных ориентиров и сдаточных этапов. При этом приходится интегрировать планово-распорядительные функции субподрядчиков в единую систему, устанавливать контроль сроков выполнения разнородных работ, создавать резервы как по производительности, так и по времени производства работ.

При постановке задачи выявления оптимального календарного плана возникает вопрос о критериях оценки качества разрабатываемых планов. Могут быть использованы различные критерии, наиболее важным из которых является минимум дисконтированных затрат, учитывающих различные эффекты от изменения продолжительности, интенсивности, последовательности работ. Одновременно могут быть использованы частные критерии сокращения продолжительности строительства, снижения трудозатрат, улучшение равномерности работ. В частности, для оценки равномерности может использоваться показатель неравномерности использования ресурсов (например, трудовых):

где R max и R c р — максимальная и средняя интенсивность использования ресурсов.

Таким образом, составление оптимального календарного плана является сложной многокритериальной задачей, в идеале решаемой с учетом интересов всех участников строительства. При этом календарный план, независимо от его вида, должен являться основой для разработки договорных сроков и выполняемых исполнителями объемов, для установления взаимных санкций и договорных условий.

Изучив материал главы, студент должен:

знать

• какую роль играет сетевое и календарное планирование в управлении проектом;
• основные принципы сетевого планирования;
• основные инструменты сетевого и календарного планирования;

уметь

• строить сетевые графы проекта;
• определять на основании сетевых графов длительность проекта, его критические операции;
• определять резервы времени для каждой операции;
• определять длительность выполнения операций на основе метода PERT;
• распределять ресурсы проекта с учетом их дефицитности;

владеть

• общепринятыми методами сетевого анализа;
• навыками составления сетевых графов, диаграмм Ганта;
• навыками определения длительности проекта;
• навыками формирования расписания проекта.

Ключевые термины: сетевой анализ, календарное планирование,

сетевой граф, критический путь, резерв времени, диаграмма Ганта.

Функции сетевого анализа в планировании проекта

Для успешной реализации проекта необходимо составить его реалистичное расписание , позволяющее распределить ресурсы и контролировать ход выполнения проекта. С этой целью составляются и анализируются сетевые модели проекта, определяющие конкретные взаимосвязи между задачами (пакетами работ). На основе сетевого анализа можно определить вероятную продолжительность выполнения работ, их стоимость, возможные размеры экономии времени или денежных средств, а также то, выполнение каких операций можно отложить без ущерба для расписания проекта в целом, а какие являются критическими, т.е. их задержка означает срыв сроков реализации всего проекта. Сетевое планирование является также базой для распределения ресурсов проекта, в том числе дефицитных.

Сетевой анализ осуществляется в последовательности, приведенной на рис. 8.1.

Рис. 8.1.

Первые три этапа составляют сущность сетевого анализа, а последний – календарного планирования. Как правило, процесс проходит несколько итераций.

Первый этап был описан нами в гл. 7. На втором этапе устанавливаются взаимосвязи между работами проекта, которые в рамках сетевого анализа называются операциями.

Можно выделить следующие типы зависимостей.

• 1. Обязательные зависимости – зависимости, которые внутренне (физически) присущи выполняемым работам (например, при строительстве дома нельзя настелить крышу раньше, чем будут возведены стены).
• 2. Зависимости по усмотрению – определяются командой проекта на основе их предпочтений или общепринятой практики. Такие зависимости следует строго документировать во избежание нарушения сроков реализации проекта.
• 3. Внешние зависимости – определяют взаимосвязи проектных и непроектных работ.

Для установления логических взаимосвязей между операциями составляется таблица предшествования, в которой каждой операции сопоставляется непосредственно предшествующая (предшествующие, если их несколько) операция.

Компания АВС заключила контракт на производство партии станков, которые должны быть использованы для производства определенного типа деталей. Ниже приведена таблица предшествования, где перечислены операции, которые необходимо выполнить в процессе разработки и производства этих станков.

Непосредственно предшествующая операция

Составление сметы затрат проекта

Согласование сметы затрат

Покупка собственного оборудования

Подготовка конструкторской документации

Определение типа модели

Проектирование внешнего корпуса

Создание внешнего корпуса

Инструментом сетевого анализа выступают сетевые графы . Существуют различные типы сетевых графов, но наиболее часто используются стрелочные графы .

В стрелочных графах каждая операция обозначается буквой и представлена стрелкой, каждая операция начинается и заканчивается событием, имеющим определенный номер (рис. 8.2).

Рис. 8.2.

В процессе планирования следует учитывать, что многие операции будут выполняться одновременно, следовательно, одному событию могут соответствовать (начинаться или заканчиваться им) несколько операций. Событие не считается свершившимся, пока не закончатся все входящие в него операции. Операция, выходящая из некоторого события, не может начаться, пока не будут закончены все входящие в него операции. Так, на рис. 8.3 операция С не может быть начата до момента, пока не будут окончены работы А и В.

Рис. 8.3.

Иногда для изображения логической последовательности операций в графы вводятся так называемые фиктивные операции, изображаемые пунктирными стрелками и имеющие нулевую продолжительность. Они используются тогда, когда необходимо отразить, что некоторое событие не может появиться раньше другого события, а с помощью обычных стрелок, соответствующих действительным операциям, этого сделать нельзя.

Такая ситуация показана на рис. 8.4. Операция С не может начаться раньше, чем завершится операция А, а работу D нельзя начинать раньше, чем завершатся операции А и В. События принято нумеровать так, чтобы номер конечного события был больше номеров предшествующих событий.

Рис. 8.4.

После того как на основе таблицы предшествования строится стрелочный граф, он, как правило, пересматривается с целью исключения ненужных фиктивных операций. Это можно сделать на основе следующего принципа – если единственная операция, выходящая из некоторого события, фиктивная, скорее всего, без нее можно обойтись.

Сетевой граф должен начинаться с единственного начального события (с него начинаются все операции, не имеющие предшествующих) и заканчиваться единственным конечным событием.

Построим сетевой граф для таблицы предшествования из примера 8.1.

После установления последовательности и логической взаимосвязи операций оценивается их продолжительность, а следовательно, и продолжительность всего проекта.

Помимо стрелочных графов, используют также вершинные графы (диаграммы предшествования), где узлы содержат операции проекта, а стрелки между ними характеризуют продолжительность операций (рис. 8.5).

Нестеров А.К. Сетевое планирование // Энциклопедия Нестеровых

Основное назначение методологии сетевого планирования в управлении сократить до минимума продолжительность проекта. С помощью сетевых моделей руководитель может системно оценивать текущий и перспективный ход запланированных операций, за счет чего возможно управление процессом реализации проекта в целом. Календарно-сетевое планирование позволяет также рационально оперировать имеющимися в распоряжении ресурсами.

Цель и задачи сетевого планирования

Основная цель сетевого планирования следует из его назначения: построить модель реализации проекта на основе формирования комплекса работ, задания их очередности, определить необходимые ресурсы и задачи, которые должны быть решены для завершения проекта. В итоге необходимо добиться сокращения до минимума продолжительности проекта.

Метод сетевого планирования позволяет координировать деятельность участников проекта, определить порядок, согласно которому должны выполняться запланированные работы, операции, действия. При этом основу составляет продолжительность каждой операции, действия, которые должны быть определены с учетом потребностей в материальных, трудовых и финансовых ресурсах.

– это метод управления, основанный на математическом аппарате теории графов и системного подхода, преследует задачи объективного построения плана операций на заданный период времени за счет алгоритмизации взаимосвязанных работ. Благодаря такому подходу достигается поставленная цель.

Применение методологии сетевого планирования в управлении предполагает формализацию структуры операций в информационно-табличном виде, на основе чего осуществляется структуризация операций по отрезкам времени и группировка параллельных операций для оптимального выполнения всего проекта в целом. На основе этого осуществляется построение таблицы операций, в которую сводятся все значимые данные по каждой операции в соответствии с формализованной структурой операций и группами параллельных операций. Результатом является построение сетевой диаграммы, которая подлежит корректировке в случае несоответствия запланированных действий общему сроку их выполнения, либо отдельным промежуткам времени внутри общей временной структуры проекта.

Задачи сетевого планирования:

1. Определить перечень критических работ или операций (т.е. таких операций, которые имеют наибольшее влияние на общую продолжительность проекта);
2. Построить сетевой план проекта таким образом, чтобы все запланированные работы и операции были произведены с соблюдением заданных сроков и минимальных затратах.

Единица такой сетевой модели – операция (работа или задача), которая означает какую-либо деятельность, в результате выполнения которой будут достигнуты определенные результаты.

Результатом сетевого планирования является графическое отображение последовательности операций, выполнение которых приведет к достижению конечной цели проекта. Основным способом отображения являются сетевые экономико-математические модели. Для управленческой деятельности наиболее подходят . С помощью сетевой модели формируется возможность системного представления всех операций и условия для управления процессом осуществления проекта. При необходимости метод сетевого планирования позволяет маневрировать ресурсами в рамках модели для достижения конечной цели.

Часто руководители склонны опираться лишь на личный опыт, который ограничен и субъективен. Такой ограниченный уровень компетентности редко помогает в динамичном окружении, а иногда может принести прямой вред.

Сетевое планирование позволяет исключить влияние субъективных факторов на управление проектом, способствуя сокращению сроков реализации проекта минимум на 15-20%, рационализации использования имеющихся ресурсов и оптимизации затрат. При этом отдельные операции рассматриваются как отдельные элементы целостной системы, а исполнители выступают звеньями данной системы.

Методы сетевого планирования

Применяя (граф сети, PERT-диаграммы), следует учитывать следующие аспекты:

• сетевая диаграмма отражает полный комплекс работ и этапов проекта;
• на сетевом графике должны быть установлены зависимости между операциями;
• сетевые графики не являются блок-схемами;
• сетевые диаграммы содержат только операции и логические зависимости между ними (отсутствуют входы, процессы, выходы и т.д.);
• сетевые модели не допускают повторяющихся циклов, этапов, «петель» операций.

Сетевое планирование ориентировано на сокращение до минимума продолжительности проекта, для жтого могут применяться два метода:

1. Метод критического пути,
2. Метод оценки и пересмотра планов.

«Максимальный по продолжительности полный путь в сети называется критическим; работы, лежащие на этом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом» . Увеличение или сокращение времени выполнения операций критического пути ведет к росту и снижению продолжительности проекта соответственно. Метод критического пути предполагает расчет графиков работ, продолжительности каждой работы, чтобы определить критический путь проекта, а затем принять меры по его сокращению.

Метод оценки и пересмотра планов заключается в соблюдении графиков проектирования, производства, организации работ и других установленных сроков. Согласно этой методике, весь проект «разбивается» на ряд подзадач, и для каждой задачи оценивается время, необходимое для ее выполнения, каждой задаче также назначается приоритет выполнения. В зависимости от приоритета задачи и ее влияния на проект предпринимаются меры по оптимизации ее выполнения для снижения продолжительности проекта.

Таким образом, процесс сетевого планирования заключается в описании конкретного проекта или плана действий на заданный период в виде определенного комплекса мероприятий, задач, мер, процедур или работ.

При этом соблюдается объектная взаимосвязь между всеми процедурами и операциями, которые включены в структуру проекта или плана действий на заданный период. Развитие методик управления проектами в начале XXI века привело к тому, что в случае несоответствия реальной технологии выполнения работ сетевое планирование превращается в «формальную галочку», как следствие, дискредитируется сама идея использования технологий календарно-сетевого планирования.

Методика построения сетевых моделей

Сетевые диаграммы отображают сетевую модель конкретного проекта или плана действий на заданный период в виде множества вершин, которые соответствуют запланированным в рамках данного плана операциям и процедурам. Каждая вершина соединена с предшествующей и следующей вершинами логическими линиями, представляющими взаимосвязь между операциями. Исключение составляют начальная и финальная вершина, соответствующие первой и последней операции в рамках конкретного проекта или плана действий в заданном периоде.

Перед непосредственным построением сетевой диаграммы проводится работа по формированию операций в рамках конкретного проекта или плана действий на заданный период. Предварительно составляется формализованная структура операций в табличной форме.

На основании формализованной структуры операций проводится расчет календарного времени реализации плана действий, который осуществляется по календарю соответствующего года и периода, в котором планируется реализация данных операций. Если планируемые операции должны быть выполнены в определенный календарный период, например, месяц, то расчет осуществляется исходя из рабочих дней.

Например, с 01.09.2018 по 30.09.2018 каждая рабочая неделя включает в себя 5 рабочих дней, следовательно, расчет должен быть осуществлен исходя из наличия 20 дней на выполнение всех запланированных операций.

Распределение исполнителей в рамках формализованной структуры операций в сетевом планировании осуществляется на основе их функциональных обязанностей с соблюдением трех принципов:

1. Каждый отдел или конкретный сотрудник выполняет только те операции, которые предусмотрены его функциональными обязанностями. Привлекать специалистов на несоответствующую его полномочиям и обязанностям работу нельзя.
2. Регулярные и обязательные виды работ включаются в проект или план действий на заданный период в соответствии с их заданной периодичностью, например, еженедельной. Игнорирование их в рамках плана операций чревато несоблюдением запланированного срока.
3. Параллельные работы группируются в рамках всего проекта или плана действий на заданный период, либо по отдельным временным промежуткам. Например, если проект рассчитан на один календарный месяц, то целесообразно группировать параллельные работы в рамках рабочих недель при наличии такой возможности.

На основе проделанной работы по расчету календарного времени реализации проекта или плана действий на заданный период составляется структуризация операций по неделям и группировка параллельных работ.

Построение сетевой диаграммы

После структуризации операций осуществляется первичное планирование и построение сетевой модели в соответствии с запланированными операциями. Для этого составляется формуляр операций в виде таблицы, в которой содержатся следующие данные:

• последовательный перечень всех операций, которые должны быть выполнены в рамках проекта или плана действий на заданный период;
• по каждой операции должна быть указана ее продолжительность и количество исполнителей, которые задействованы в ее реализации;
• каждой операции, кроме начальной, должны соответствовать предшествующие операции.

Пример таблицы операций по проекту проведения конкурса на выбор лучшей школы города приведен в таблице.

Кол-во исполнителей, чел.

Подписание распоряжения о проведении конкурса

Поиск помещения для проведения конкурса

Отбор персонала для проведения конкурса

Разработка плана проведения конкурса

Обустройство помещения перед проведением конкурса

Подведение итогов конкурса

В соответствии с формализованной структурой операций и таблицы операций необходимо осуществить построение сетевой модели.

Воспользуемся данными по операциям из таблицы и представим сетевую диаграмму данных работ.

Пример построения сетевой диаграммы

В данной сетевой модели вершина представляет собой конкретную операцию, а линии – взаимосвязь между ними. В данной диаграмме в каждой вершине верхняя цифра обозначает номер операции, нижняя указывает на продолжительность данной операции в днях, неделях или иных единицах. Данный подход также называется построением диаграммы предшествования и следования и является наиболее распространенным представлением сетевых моделей в планировании.

Построение сетевых моделей по типу «вершина-работа» наиболее распространено в практике управления и активно применяется в сфере государственного и муниципального управления, в планировании на промышленных, производственных и коммерческих предприятиях различных отраслей экономики.

Критический путь, как видно из рисунка, составляют следующие операции: 1, 2, 6, 9 и 10.

Следовательно, длина критического пути составляет:

По результатам планирования и построения сетевой модели можно сделать один из двух выводов:

1. В случае, если сетевая модель и длина критического пути свидетельствуют о том, что вся совокупность операций по продолжительности укладывается в заданный срок, то считается, что реализация проекта или заданного плана действий будет произведена корректно.
2. В случае, если деятельность по реализации проекта или заданного плана действий не укладывается в отведенный для этого срок, производится корректировка сетевой модели.

Корректировка сетевой модели

Корректировка сетевой модели может проводиться и в первом случае, если имеется возможность для повышения эффективности реализации запланированных операций.

В сетевом планировании выделяют три способа корректировки модели:

1. изменение сроков выполнения критических операций за счет привлечения дополнительных ресурсов, в качестве которых могут выступать денежные средства, материалы или человеческие ресурсы;
2. изменение сроков выполнения критических операций за счет привлечения исполнителей, занятых на других операциях, при сохранении изначальных параметров ресурсов;
3. изменение сроков выполнения операций за счет совмещения их выполнения.

В первом случае корректировка сетевой модели осуществляется без изменения сетевой диаграммы. Данный подход чаще всего практикуется в тех случаях, когда для выполнения операций остаются свободные ресурсы, не задействованные в других операциях.

Во втором случае сетевая диаграмма также остается неизменной. Данный подход используется в тех случаях, когда возможно увеличить срок выполнения операций, не принадлежащих к критическому пути.

Третий случай применяется при невозможности использования дополнительных ресурсов и подразумевает повторное построение сетевой диаграммы.

После проведения корректировки осуществляется построение альтернативной сетевой модели.

Следует отметить, что в корректировке сетевой модели заключается фундаментальное назначение сетевого планирования. Благодаря построению сетевых моделей уже на ранней стадии планирования могут быть выявлены условия, свидетельствующие о том, что в заданные директивные сроки проект невозможно будет выполнить. Поэтому для получения приемлемых с точки зрения целей проекта сроков возможно осуществление коррекции расписания операций по принципу изменения продолжительности критических операций. Таким образом, если проект или заданный план действий не укладывается в директивные сроки, то предпринимается попытка сократить сроки выполнения критических операций за счет изменения их зависимости от первоначально заданных параметров их выполнения.

1. Черняк В.З., Довдиенко И.В. Методы принятия управленческих решений. – М.: Академия, 2013.
2. Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г., Полковников А.В. Управление проектами. – М.: Омега-Л, 2012.
3. Новыш Б.В., Шешолко В.К., Шаститко Д.В. Экономико-математические методы принятия решений. – М.: Инфра-М, 2013.
4. Урубков А.Р., Федотов И.В. Методы и модели оптимизации управленческих решений. – М.: изд-во АНХ, 2011.
5. Сухачев К.А., Колосова Е.С. Практика применения технологий календарно-сетевого планирования. // Нефтегазовая вертикаль. – 2010. – №11 (240), июнь 2010. – С. 28-30.

Аннотация: Структурное планирование. Календарное планирование. Оперативное управление. Практические занятия по структурному и календарному планированию. Задания для контрольной работы.

2.1. Теоретический курс

2.1.1. Структурное планирование

Структурное планирование включает в себя несколько этапов:

1. разбиение проекта на совокупность отдельных работ, выполнение которых необходимо для реализации проекта;
2. построение сетевого графика, описывающего последовательность выполнения работ;
3. оценка временных характеристик работ и анализ сетевого графика.

Основную роль на этапе структурного планирования играет сетевой график.

Сетевой график – это ориентированный граф, в котором вершинами обозначены работы проекта, а дугами – временные взаимосвязи работ.

Сетевой график должен удовлетворять следующим свойствам .

1. Каждой работе соответствует одна и только одна вершина. Ни одна работа не может быть представлена на сетевом графике дважды. Однако любую работу можно разбить на несколько отдельных работ, каждой из которых будет соответствовать отдельная вершина графика.
2. Ни одна работа не может быть начата до того, как закончатся все непосредственно предшествующие ей работы. То есть если в некоторую вершину входят дуги, то работа может начаться только после окончания всех работ, из которых выходят эти дуги.
3. Ни одна работа, которая непосредственно следует за некоторой работой, не может начаться до момента ее окончания. Другими словами, если из работы выходит несколько дуг, то ни одна из работ, в которые входят эти дуги, не может начаться до окончания этой работы.
4. Начало и конец проекта обозначены работами с нулевой продолжи­тельностью. Такие работы называются вехами и обозначают начало или конец наиболее важных этапов проекта.

Пример . В качестве примера рассмотрим проект «Разработка программного комплекса». Предположим, что проект состоит из работ, характеристики которых приведены в табл.2.1 .

Таблица 2.1.

Номер работы Название работы Длительность

1	Начало реализации проекта	0
2	Постановка задачи	10
3	Разработка интерфейса	5
4	Разработка модулей обработки данных	7
5	Разработка структуры базы данных	6
6	Заполнение базы данных	8
7	Отладка программного комплекса	5
8	Тестирование и исправление ошибок	10
9	Составление программной документации	5
10	Завершение проекта	0

Сетевой график для данного проекта изображен на рис.2.1 . На нем вершины, соответствующие обычным работам, обведены тонкой линией, а толстой линией обведены вехи проекта .

Сетевой график позволяет по заданным значениям длительностей работ найти критические работы проекта и его критический путь.

Критической называется такая работа, для которой задержка ее начала приведет к задержке срока окончания проекта в целом. Такие работы не имеют запаса времени. Некритические работы имеют некоторый запас времени, и в пределах этого запаса их начало может быть задержано.

Критический путь – это путь от начальной к конечной вершине сетевого графика, проходящий только через критические работы. Суммарная длительность работ критического пути определяет минимальное время реализации проекта.

Нахождение критического пути сводится к нахождению критических работ и выполняется в два этапа.

1. Вычисление раннего времени начала каждой работы проекта. Эта величина показывает время, раньше которого работа не может быть начата.
2. Вычисление позднего времени начала каждой работы проекта. Эта величина показывает время, позже которого работа не может быть начата без увеличения продолжительности всего проекта.

Критические работы имеют одинаковое значение раннего и позднего времени начала.

Обозначим – время выполнения работы , – раннее время начала работы , – позднее время начала работы . Тогда

где – множество работ, непосредственно предшествующих работе . Раннее время начальной работы проекта принимается равным нулю.

Поскольку последняя работа проекта – это веха нулевой длительности, раннее время ее начала совпадает с длительностью всего проекта. Обозначим эту величину . Теперь принимается за позднее время начала последней работы, а для остальных работ позднее время начала вычисляется по формуле:

Здесь – множество работ, непосредственно следующих за работой .

Схематично вычисления раннего и позднего времени начала изображены, соответственно, на рис. 2.2 и рис.2.3 .

Пример . Найдем критические работы и критический путь для проекта «Разработка программного комплекса», сетевой график которого изображен на рис.2.1 , а длительности работ исчисляются днями и заданы в табл.2.1 .

Сначала вычисляем раннее время начала каждой работы. Вычисления начинаются от начальной и заканчиваются конечной работой проекта. Процесс и результаты вычислений изображены на рис.2.4 .

Результатом первого этапа помимо раннего времени начала работ является общая длительность проекта .

На следующем этапе вычисляем позднее время начала работ. Вычисления начинаются в последней и заканчиваются в первой работе проекта. Процесс и результаты вычислений изображены на рисунке 2.5 .

Сводные результаты расчетов приведены в табл.2.2 . В ней выделены заливкой критические работы. Критический путь получается соединением критических работ на сетевом графике. Он показан пунктирными стрелками на рис.2.6 .

Таблица 2.2.

Работа	1	2	3	4	5	6	7	8	9	10
Раннее время начала	0	0	10	16	10	16	24	29	29	39
Позднее время начала	0	0	12	17	10	16	24	29	34	39
Резерв времени	0	0	2	1	0	0	0	0	5	0

Сетевое планирование – метод, при котором используется графическое моделирование планируемого комплекса выполняемых работ, отражающее их логическую последовательность, существующую взаимосвязь и планируемую продолжительность, а затем оптимизация модели по двум критериям:

• – минимизация времени выполнения комплекса планируемых работ при заданной стоимости проекта;
• – минимизация стоимости всего комплекса работ при заданном времени выполнения проекта.

Для оптимизации сетевого графика используются два метода.

• Метод критического пути позволяет рассчитать возможные календарные графики выполнения комплекса работ на основе описанной логической структуры сети и оценок продолжительности выполнения каждой работы, определить критический путь проекта. Метод разработан в 1956 г. для составления планов-графиков крупных комплексов работ по модернизации заводов фирмы «Дюпон».
• PERT (Program Evaluation and Review Technique) – способ анализа задач, необходимых для выполнения проекта, в особенности анализа времени, которое требуется для выполнения каждой отдельной задачи, а также определения минимально необходимого времени для выполнения всего проекта. Метод разработан корпорацией «Локхид» и консалтинговой фирмой «Буз, Аллен энд Гамильтон» для реализации крупного проекта разработки ракетной системы «Поларис».

Рис. 2.2. :

И – исходные данные; С1. С6 – планируемые события (мероприятия); Р – результат

В современных системах управления сетевые методы планирования могут быть реализованы на высоком профессионально-техническом уровне в процессе применения программного обеспечения пакета Microsoft Office Project, обеспечивающего широкий спектр функциональных возможностей решения и анализа задач организации, планирования и управления самыми разнообразными процессами, проектами и производственными системами.

Сетевой метод планирования основан на построении сетевой модели, простейшую форму которой иллюстрирует рис. 2.2, как форме представления информации об управляемом комплексе работ.

Сетевая модель – это форма графического отражения содержания, продолжительности и последовательности выполнения мероприятий по реализации планов любого характера и назначения, а также потребностей в экономических ресурсах. В отличие от простых линейных графиков и табличных расчетов сетевые методы планирования позволяют разрабатывать и оптимизировать развитие сложных производственных систем в аспекте их долгосрочного использования.

Впервые планы-графики выполнения производственных процессов были применены на американских фирмах Г. Гантом. Тогда использовались линейные или ленточные графики (рис. 2.3), где по горизонтальной оси в выбранном масштабе времени откладывалась продолжительность работ по всем стадиям и этапам производства. Содержание циклов работ изображалось по вертикальной оси с необходимой степенью их расчленения на отдельные части или элементы. Цикловые или линейные графики обычно применялись в целях оперативно-календарного планирования производственной деятельности.

Рис. 2.3.

В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде ориентированного графа.

Граф – условная схема, состоящая из заданных точек (вершин), соединенных между собой определенной системой линий. Отрезки, соединяющие вершины, называются ребрами (дугами) графа. Ориентированным считается такой граф, на котором стрелками указаны направления всех его ребер (или дуг). Графы носят название карт, лабиринтов, сетей и диаграмм.

Исследование этих схем проводится методами теории, получившей название «теория графов». Она оперирует такими понятиями, как пути, контуры и др.

Путь – последовательность дуг (или работ), когда конец каждого предыдущего отрезка совпадает с началом последующего. Контур означает такой конечный путь, у которого начальная вершина или событие совпадает с завершающим, конечным. В теории графов сетевой график – это ориентированный граф без контуров, дуги (или ребра) которого имеют одну либо несколько числовых характеристик. На графике ребрами считаются работы, а вершинами – события.

Работа в плане представляет некоторую деятельность, которая необходима для достижения конкретных результатов (конечных продуктов нижнего уровня). Работа является основным элементом деятельности на самом нижнем уровне детализации плана, на се выполнение требуется время, которое может задержать начало выполнения других работ. Момент окончания работы означает факт получения конечного продукта (результата работы).

Иногда в качестве синонима понятия работы используется термин задача. Однако этот термин может принимать и другое формальное значение в специфических контекстах планирования. Например, в аэрокосмической и оборонной областях задача часто относится к верхнему суммарному уровню работ, который может содержать множественные группы пакетов работ.

Работа-ожидание – это событие, которое обычно не требует использования ресурсов. Кроме действительных работ и работ-ожиданий, существуют фиктивные работы или зависимости. Фиктивной работой считается логическая связь или зависимость между какими-то конечными процессами или событиями, не требующая затрат времени. На сетевом графике фиктивная работа изображается пунктирной линией.

Событиями считаются конечные результаты предшествующих работ. Событие фиксирует факт выполнения работы, конкретизирует процесс планирования, исключает возможность различного толкования итогов выполнения различных процессов и работ. В отличие от работы, требующей времени на ее совершение, событие представляется только моментом свершения планируемого действия, например цель выбрана, план составлен, товар произведен, продукция оплачена, деньги поступили и т.д. События бывают начальными или исходными, конечными или завершающими, простыми или сложными, а также промежуточными, предшествующими или последующими и т.д. Существуют три основных способа изображения событий и работ на сетевых графиках: вершины-работы, вершины-события и смешанные сети.

Веха – событие или дата в ходе осуществления проекта. Веха используется для отображения состояния завершенности тех или иных работ. В контексте сетевого планирования вехи используют для того, чтобы обозначить важные промежуточные результаты, которые должны быть достигнуты в процессе реализации плана. Последовательность вех называется планом по вехам.

Даты достижения соответствующих вех образуют календарный план по вехам. Важным отличием вех от работ является то, что они не имеют длительности. Из-за этого свойства их часто называют событиями.

Сетевая диаграмма – графическое отображение работ проекта и их взаимосвязей. В планировании и управлении проектами под термином «сеть» понимается полный комплекс работ, событий и вех проекта с установленными между ними зависимостями – путями.

Сетевые диаграммы отображают сетевую модель в графическом виде как множество вершин, соответствующих работам, связанных линиями, представляющими взаимосвязи между работами. Этот граф, называемый сетью типа вершина-работа или диаграммой предшествования, является наиболее распространенным представлением сети на сегодняшний день (рис. 2.4).

Существует другой тип сетевой диаграммы, называемый «вершина-событие», который на практике используется реже. В этом случае работа представляется в виде линии между двумя событиями (узлами графа), которые, в свою очередь, отображают начало и конец данной работы (PERT- диаграммы являются примерами этого типа диаграмм).

Хотя в целом различия между этими двумя подходами представления сети незначительны, представление более сложных связей между работами сетью типа «вершина-событие» может быть достаточно затруднительно, что и является причиной более редкого использования данного типа (подобный сетевой график был представлен на рис. 2.2).

Сетевая диаграмма не является блок-схемой в том смысле, в котором это средство используется для моделирования деловых процессов. Принципиальным отличием от блок-схемы является то, что сетевая диаграмма моделирует только логические зависимости между элементарными работами. Она не отображает входы, процессы и выходы и не допускает повторяющихся циклов или петель.

Во всех сетевых графиках важным показателем служит путь.

Путь в сетевом графике – всякая последовательность работ (стрелок), связывающая между собой несколько событий.

Путь, соединяющий исходное и завершающее событие сети, считается полным, все другие – неполными. Каждый путь характеризуется своей продолжительностью, которая равняется сумме длительностей составляющих его работ. Полный путь, имеющий наибольшую продолжительность, называется критическим путем.

Критический путь – наиболее протяженная по времени последовательная цепочка работ, ведущих от исходного к завершающему событию.

Рис. 2.4. Сетевой график тина «вершина-работа»

Работы, лежащие на критическом пути, также называются критическими. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом. Длительность выполнения всего проекта может быть сокращена за счет сокращения длительности задач, лежащих на критическом пути. Соответственно, любая задержка выполнения задач критического пути повлечет увеличение длительности проекта. Основным достоинством метода критического пути является возможность манипулирования сроками выполнения задач, не лежащих на критическом пути, через выявление и использование резервов времени совершения событий.

Резерв времени выполнения события – промежуток времени, на который может быть отсрочено свершение события без нарушения планируемых сетевым графиком сроков окончания проектных работ.

Вычисляется временной резерв (или запас времени) как разность между самым ранним возможным сроком завершения работы и самым поздним допустимым временем ее выполнения. Управленческий смысл временного резерва заключается в том, что при необходимости урегулировать технологические, ресурсные или финансовые ограничения плана наличие резерва позволяет задержать работу на эго время без влияния на общую продолжительность реализации плана и продолжительность непосредственно связанных с ним задач. Работы, лежащие на критическом пути, имеют временной резерв, равный нулю. Это означает, что если расчетное время свершения какого-либо события, находящегося на критическом пути, будет задержано, то тем самым будут отодвинуты на этот же период планируемые сроки наступления завершающего события.

Важнейшими этапами сетевого планирования самых разнообразных производственных систем или иных экономических объектов являются:

• – расчленение комплекса работ (плана) на отдельные части: единичные работы-события осуществляются путем декомпозиции задач плана на подзадачи и т.д. Структура разбиения работ является изначальным инструментом для организации работ, обеспечивающим разделение общего объема работ по проекту в соответствии со структурой их выполнения в организации. На нижнем уровне детализации выделяются работы, соответствующие детализированным элементам деятельности, отображаемым в сетевой модели;
• – определение ответственных исполнителей каждой единичной работы;
• – построение сетевых графиков и уточнение содержания планируемых работ;
• – обоснование или уточнение времени выполнения каждой работы в сетевом графике;
• – оптимизация плана (сетевого графика).

Управляемыми факторами в сетевой модели являются:

• – продолжительность выполнения работ, которая зависит от большого числа как внутренних, так и внешних факторов и поэтому считается случайной величиной. Для установления длительности любых работ в сетевой модели можно пользоваться нормативными, расчетно-аналитическими, экспертными методами;
• – потребность в ресурсах, необходимых для выполнения всего комплекса работ или процессов. Планирование потребности различных ресурсов в сетевых моделях сводится в основном к разработке календарного плана поставки ресурсов, необходимых для выполнения предусмотренных комплексов работ.

Ресурсы – компоненты, обеспечивающие реализацию планов: исполнители, энергия, материалы, оборудование и т.д. Для выполнения каждой работы требуются определенные ресурсы.

Процесс назначения и выравнивания ресурсов в сетевой модели позволяет проанализировать план, построенный с помощью метода критического пути, с тем чтобы обеспечить доступность и использование определенных ресурсов на протяжении всего времени выполнения проекта. Назначение ресурсов состоит в определении потребности каждой работы в различных типах ресурсов. Методики выравнивания ресурсов представляют собой, как правило, программно-реализованные эвристические алгоритмы планирования при ограниченных ресурсах. Эти средства помогают менеджеру создать реальное расписание плана с учетом его потребности в ресурсах и фактически доступных в данный момент времени ресурсов.

Ресурсная гистограмма – гистограмма, отображающая потребности проекта в конкретных ресурсах в определенный момент времени.

В зависимости от выбранного критерия оптимальности и имеющихся ограничений ресурсов задачи их рационального распределения в сетевой модели можно свести к минимизации отклонения от заданных моделью сроков выполнения проектных работ при соблюдении существующих ограничений по использованию производственных ресурсов. В итоге в процессе оптимизации сетевых графиков достигается улучшение процессов планирования, организации и управления комплексом работ в целях сокращения расходования экономических ресурсов и повышения финансовых результатов при заданных плановых ограничениях.

Завершается сетевое моделирование анализом реализуемости проекта:

• – логическая реализуемость: учет логических ограничений на возможный порядок выполнения работ во времени;
• – временно́й анализ: расчет и анализ временных характеристик работ (ранняя/поздняя, дата начала/окончания работы, полный, свободный временной резерв и др.);
• – физическая (ресурсная) реализуемость: учет ограниченности наличных или доступных ресурсов в каждый момент времени выполнения проекта;
• – финансовая реализуемость: обеспечение положительного баланса денежных средств как особого вида ресурса.

Сетевое планирование может успешно применяться в различных сферах производственной и предпринимательской деятельности, например:

Источник: floritus.ru

Сетевое планирование в строительстве пример. Сетевое планирование строительного производства

Жаропонижающие средства для детей назначаются педиатром. Но бывают ситуации неотложной помощи при лихорадке, когда ребенку нужно дать лекарство немедленно. Тогда родители берут на себя ответственность и применяют жаропонижающие препараты. Что разрешено давать детям грудного возраста? Чем можно сбить температуру у детей постарше?

Какие лекарства самые безопасные?

Введение

Планирование и управление комплексом работ по проекту представляет сложную и, как правило, противоречивую задачу. Оценка временных и стоимостных параметров функционирования системы, осуществляемая, а рамках этой задачи, производится различными методами. Среди существующих большое значение имеет метод сетевого планирования. Методы сетевого планирования могут широко и успешно применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, которые требуют участия большого числа исполнителей и затрат ограниченных ресурсов.

Следует отметить, что главной целью сетевого планирования является сокращение до минимума продолжительности проекта, таким образом, использование сетевых моделей обусловлено необходимостью грамотного управления крупными народнохозяйственными комплексами и проектами, научными исследованиями, конструкторской и технологической подготовкой производства, новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов и т.п.

С помощью сетевой модели руководитель работ или операции может системно и масштабно представлять весь ход работ или оперативных мероприятий управлять процессом их осуществления, также маневрировать ресурсами.

Можно выделить следующие задачи моей курсовой работы:

1) Рассмотреть и выделить основные понятия сетевого планирования.

2) Изучить правила построения и построить сетевой график.

Сетевое планирование в строительстве

Сетевое планирование — набор методов, который предназначен для управления расписанием проекта. Сетевое планирование позволяет определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.

Сетевой график- это графическое изображение технологической последовательности выполнения работ на объекте или нескольких объектах с указанием их продолжительности и всех временных параметров, а также общего срока строительства.

В основе управления строительством должна лежать заранее разработанная модель процесса производства строительных и монтажных работ, начиная с подготовительных работ и кончая вводом объекта в эксплуатацию.

Сетевой график — это информационная модель, отображающая процесс выполнения комплекса работ, направленных на достижение единой цели.

Отличительными особенностями сетевого графика являются:

Наличие взаимосвязи между работами и технологической последовательностью их выполнения;

Возможность выявления работ, от завершения которых в первую очередь зависит продолжительность строительства объекта;

Возможность выбора вариантов последовательности и продолжительности работ с целью улучшения сетевого графика;

Облегчение осуществления контроля работ за ходом строительства;

Возможность использования ЭВМ для расчетов параметров графика при планировании и управлении строительством.

Сетевая модель изображается в виде графика, состоящего из стрелок икружков.

Сетевой график состоит из четырёх элементов: работы, ожидания, зависимости и события.

приводимых параметров работы может меняться, но продолжительность и наименование работ указывают всегда.

2. Ожидание — процесс, требующий только затрат времени и не потребляющий никаких материальных ресурсов. Ожидание, в сущности, является технологическим или организационным перерывом между работами, непосредственно выполняемыми друг за другом (пример технологического ожидания — набор бетона прочности; пример организационного ожидания — если бригада плотников занята на других работах, и по этой причине не выполняются работы по распалубке бетонных конструкций).

Ожидание изображается, так же, как, и работа, сплошной стрелкой с указанием продолжительности и наименованием ожидания.

3. Зависимость (фиктивная работа) вводится для отражения технологической и организационной взаимосвязи работ и не требует ни времени, ни ресурсов. Зависимость изображается пунктирной стрелкой. Она определяет последовательность свершения событий.

4. Событие — это факт окончания одной или нескольких работ, необходимый и л остаточный lля начала следующих работ. В любой естественной модели события устанавливают технологическую и организационную последовательность работ. События изображаются кружками или другими геометрическими фигурами, внутри которых указывается определенный номер — код события. События ограничивают рассматриваемую работу и по отношению к ней могут быть начальными и конечными.

Начальное событие — определяет начало данной работы и является конечным для предшествующих работ.

Конечное событие — определяет окончание данной работы и является начальным для последующих работ.

Исходное событие — событие, которое не имеет предшествующих работ в рамках рассматриваемого сетевого графика.

Завершающее событие — событие, которое не имеет последующих работ в рамках рассматриваемого сетевого графика.

Сложное событие — событие, в которое входят или из которого выходят две и более работы.

Строительное производство представляет собой сложную организационно-технологическую систему, которую для облегчения изучения можно представить в виде модели.

Модель в широком понятии — это любой упрощенный образ образец или аналог какого-либо сложного объекта, процесса или явления («оригинала» данной модели), используемый в качестве его «представителя».

Процесс исследования на моделях, должным образом представляющих изучаемую систему, называется моделированием.

Моделирование строительного производства — исследование строительных процессов путем построения и изучения их моделей, являющихся упрощенным представлением о некотором объекте, более удобном для восприятия, чем сам объект.

В организационно-технологических моделях строительства объектов производят взаимную увязку выполнения отдельных видов строительных работ, сроков и интенсивность ведения работ, а так же рационального порядка использования ресурсов.

Строительный процесс и вид работы могут быть представлены в виде мысленной описательной или графической модели.

В качестве графических моделей строительного производства служат (как частично отмечалось в главе 5): линейные (ленточные) графики Г.Л. Ганта, циклограммы М.С. Будникова, таблицы (матрицы), а также сетевые графики.

Сетевые модели позволяют лучше всего отобразить порядок возведения сложного объекта, осуществлять научно-обоснованные методы строительства, определять и разрешать многие проблемные ситуации, возникающие в процессе производства строительных работ.

Сетевой график является документом, позволяющим оперативно руководить строительством и перераспределять ресурсы в зависимости от фактического состояния строительства. Он имеет и ряд других преимуществ по сравнению с другими моделями.

Однако применение сетевых графиков не означает, что тем самым исключается применение линейных графиков, циклограмм и матриц.

Эти модели взаимно дополняют друг друга и применяются в тех случаях, где они наиболее целесообразны.

Сетевые графики наиболее целесообразны для сооружения сложных промышленных и других комплексов, где участвуют многие организации, причем сетевые графики учитывают все работы, от которых зависит успешный ход строительства, в т.ч. проектирование, внешние поставки материалов, технологического оборудования и др. Сетевые модели используются в строительстве для решения задач перспективного планирования, определения продолжительности и сроков выполнения основных этапов создания объектов (проектирования, строительно-монтажных работ, поставки технологического оборудования, освоения производственной мощности), а также планирование капитальных вложений по периодам строительства объекта.

Сетевые модели используются также для решения задач оперативного планирования строительным производством по отдельному объекту, зданий, сооружений.

В сетевом моделировании строительного производства используется два основных понятия: сетевые модели и сетевые графики.

Сетевые модели бывают разные в зависимости от характера объекта строительства, целей и ряда других показателей.

Классифицируются сетевые модели по следующим основным признакам:

• 1. по виду целей — одноцелевые модели и многоцелевые (например, при строительстве разных объектов, возводимых одной строительной организацией;
• 2. по числу охвата объектов: частная модель и комплексная (например, на один объект и на весь промышленный комплекс завода);
• 3. по характеру оценок параметров модели: детерминированные (с заранее и полностью обусловленными данными) и вероятностные (учитывающие влияние случайных факторов);
• 4. модели с учетом целевой направленности (временные, ресурсные, стоимостные).

В последующих параграфах, в основном, будем рассматривать простые модели: детерминированные, одноцелевые, частные и комплексные с учетом времени.

Элементами сетевого графика являются (при типе «вершины — события»):

• 1. работа — процесс, требующий затраты времени и ресурсов (например, рытье котлованов, бетонирование фундаментов, монтаж колонн и т.д.;
• 2. событие — факт окончания одной или нескольких работ, необходимых и достаточных для начала одной или нескольких последующих работ, не требующий затрат ни времени, ни ресурсов (например, окончание рытья котлованов, бетонирование фундаментов, устройство кровли и т.д.);
• 3. ожидание — технологический и организационный перерыв между работами, требующий только затраты времени (например, твердение бетона, сушка штукатурки и т.д.);
• 4. зависимость (или фиктивная работа) — элемент сетевого графика, который вводится для отражения правильной технологической взаимосвязи между работами, не требующая затраты ни времени, ни труда исполнителей (как, например, завершение копки траншеи на 1-й захватке и возможность начала укладки фундаментных блоков на этой же захватке);

Для элементов сетевого графика приняты следующие обозначения:

Работы и ожидания изображают сплошными линиями со стрелками, направленными по ходу технологического процесса (слева направо); события — кружками, а зависимости- пунктирными линиями со стрелками.

События нумеруются одним числом, а работы — двумя. Наименование работы указывают над стрелкой, а продолжительность работы (n) — под стрелкой.

Основным методом решения плановых и управленческих задач в строительстве является метод сетевого планирования и управления (СПУ). Метод СПУ включает построение, расчет, анализ и оптимизацию сетевых моделей и применяется для решения задач, связанных с планированием и управлением строительства.

Метод СПУ объединяет автоматизированный учет и контроль, выбор и принятие управленческих решений. Результаты расчета сетевой модели содержат оценку выполнения исполнителями работ для достижения поставленной цели. Это позволяет руководителям концентрировать внимание на вопросах, от которых в данный момент времени зависит срок достижения цели. На основе информации о временных, объемных и ресурсных параметрах моделируются варианты регулирующих воздействии, наиболее рациональный из которых применяется. В качестве модели процесса производства используется сетевая модель.

Сетевая модель с требуемой степенью детализации отображает взаимосвязь отдельных работ по возведению объекта (комплекса) и дает возможность осуществить математический анализ календарного плана, прогнозировать его будущее состояние, а также оценивать эффективность принимаемых решений.

Сетевой моделью называется ориентированный граф, отражающий последовательность и организационно- технологические взаимосвязи между работами, выполнение которых необходимо для достижения поставленной цели.

Сетевая модель, представленная графически на плоскости с рассчитанными временными и ресурсными параметрами, называется сетевым графиком. Сетевые графики используются для расчета временных параметров и оптимизации календарных планов.

Правила построения сетевых графиков. Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.

Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объемов работ и продолжительности строительства.

Имеется два типа сетевых графиков: вершины — работы

Временные параметры сетевого графика.

Каждая работа сетевого графика имеет временную оценку — продолжительность. Продолжительность (t) выполнения работы измеряется в единицах времени: часах, днях, неделях и т.д.

Любая непрерывная последовательность работ в сетевом графике называется путем. Путь от исходной до завершающей работы (события) является полным путем сетевого графика. Если известна продолжительность выполнения каждой работы, то может быть определена продолжительность пути. Продолжительность любого пути равна сумме продолжительностей составляющих его работ.

Полный путь, имеющий наибольшую продолжительность, называется критическим.

Продолжительность критического пути (Т„р) определяет общую продолжительность строительства. Следовательно, чтобы сократить продолжительность строительства, необходимо уменьшить продолжительность критических работ, т.е. работ, находящихся на критическом пути. Одной из главных задач руководителей строительства является тщательный контроль за соблюдением установленных продолжительностей выполнения именно этих работ, изыскание путей их сокращения и принятие оперативных мер по предотвращению их срыва.

Для определения продолжительности критического пути и сроков выполнения каждой работы определяют следующие временные параметры сетевой модели:

Раннее начало работы — самый ранний момент начала работы. Раннее начало исходных работ сетевого графика равно нулю. Раннее начало любой работы равно максимальному раннему окончанию предшествующих работ:

Раннее окончание работы — самый ранний момент окончания данной работы. Он равен сумме раннего начала и продолжительности работы.

Позднее окончание работы — самый поздний момент окончания работы, при котором продолжительность критического пути не изменится. Позднее окончание завершающих работ равно продолжительности критического пути. Позднее окончание любой работы равно минимальному позднему началу последующих работ.

Позднее начало работы — самый поздний момент начала работы, при котором продолжительность критического пути не изменится. Он равен разности между поздним окончанием данной работы и ее продолжительностью.

У работ критического пути ранние и поздние сроки совпадают, поэтому они не имеют резервов времени. Работы, не лежащие на критическом пути, имеют резервы времени.

Полный резерв времени – максимальное время, на которое можно увеличить продолжительность работы или перенести ее начало без увеличения продолжительности критического пути. Он равен разности между поздним и ранним сроком начала или окончания.

Свободный резерв времени – время, на которое можно увеличить продолжительность работы или перенести ее начало, не изменив при этом раннего начала последующих работ. Он равен разности между ранним началом последующей работы и ранним окончанием данной работы.

Календарный план — это такой проектно — технологический документ, который определяет последовательность, интенсивность и продолжительность производства работ, их взаимоувязку, а также потребность (с распределением во времени) в материальных, технических, трудовых, финансовых и других ресурсах, используемых в строительстве.

В основу составления рациональных календарных планов строительства закладывается нормализованная технология возведения зданий и сооружений. Она находит, как правило, отражение в технологических моделях строительства объектов.

Основная задача календарного планирования состоит в составлении таких расписании выполнения работ, которые удовлетворяют всем ограничениям, отражающим в технологических моделях строительства объектов взаимоувязку, сроки интенсивности ведения работ, а также рациональный порядок использования ресурсов.

Если заранее сформулирован критерий качества календарного плана (скажем, минимальная продолжительность возведения объекта или максимальная равномерность использования бригад рабочих и строительных машин), то наилучшим считается календарный план, оптимальный по этому критерию.

Организация и планирование строительства предполагают согласование работ во времени и пространстве, т.е. разработку модели выполнения согласованного во времени и пространстве комплекса работ с целью достижения высоких технико-экономических показателей строительного производства.

Критерий оптимальности должен отражать наиболее существенную характеристику плана (например, продолжительность строительства, себестоимость, прибыль строительной организации, производительность труда и др.). В разных условиях может приниматься за критерий любой из существенных показателей, при этом остальные показатели тоже учитываются в задаче планирования, но уже в качестве тех или иных ограничений.

Существует множество допустимых вариантов планов, И методика календарного планирования должна позволять выбрать из всего этого множества оптимальный вариант по принятому критерию. По своему содержательному характеру задачи такого рода относятся к классу комбинаторных задач полного упорядочения во времени множества работ. Эффективное решение таких задач достигается при использовании экономико-математических методов и ЭВМ.

При организации, планировании и управлении строительством используются все виды моделей, но наиболее широко изобразительные (графические): линейный календарный график, циклограмма, сетевой график в форме графа, а также табличные, например, матрицы.

Важным этапом разработки планов является определение ресурсов, необходимых для выполнения проекта и их распределения. В зависимости от стадии проектирования календарные планы (КП) подразделяются на следующие виды:

• календарный план или комплексный укрупненный сетевой график (КУСГ) поточной застройки комплекса зданий или сооружений в составе ПОС;
• календарный план строительства отдельных объектов в составе ППР; на стадии рабочих чертежей;
• календарный план осуществления отдельных строительных процессов — технологические карты на стадии разработки ППР;
• разрабатывают также почасовые сменные графики, которые находят применения в работе домостроительных комбинатов (ДСК) при монтаже конструкций с транспортных средств («с колес»).

В комплексный поток включаются работы по возведению всех постоянных зданий и сооружении, входящих в состав строящегося комплекса, в том числе по тем сооружениям, зданиям, инженерным сетям, дорогам и т.п., которые строятся в подготовительный период.

В составе проекта организации строительства для сложных строительных комплексов разрабатывается комплексный укрупненный сетевой график (КУСГ).

Исходными данными для разработки КУСТ являются:

• заданный срок строительства проектируемого предприятия (комплекса), а также имеющиеся решения по вопросам его материально-технического обеспечения;
• технологические и компоновочные решения проекта (рабочего проекта): состав пусковых комплексов по очередям строительства, полный перечень объектов, технологическая последовательность ввода в действие производства и пр.;
• состав и мощности организаций, намечаемых для осуществления строительства.

При разработке КУСТ целесообразно выявить главную цель работ, отражающую технологическую последовательность строительства, монтажа и ввода в действие основного производства, основных жилых или других объектов соответствующего комплекса и принять ее за основу компоновки сетевой модели. При определении продолжительности работ КУСТ следует руководствоваться как действующими нормативами, так и данными о продолжительности проектирования и строительства аналогичных объектов.

В основу календарных планов закладывается научно- обоснованная организация взаимодействия всех участников строительства и нормализационная технология производства работ, разработка которых осуществляется путем построения тех или иных организационно-технологических моделей строи- тельного производства. При этом независимо от способа моделирования, в календарных планах должны предусматриваться поточные методы организации производства, обеспечивающие наиболее рациональное и равномерное потребление ресурсов и непрерывный выпуск строительной продукции в нормативные или заданные сроки.

После составления и расчета КУСТ проводится его оптимизация. На этой стадии путем последовательного, иногда многократного, улучшения первоначального варианта графика решаются следующие основные задачи:

• выявление оптимальной продолжительности строительства, не превышающей директивной или нормативной;
• выявление возможностей наиболее целесообразного использования капиталовложений, материально-технических и людских ресурсов путем распределения работ в пределах имеющихся резервов времени для более равномерного использования ресурсов и финансовых средств.

Планирование работы всегда начинается с определения количества задач, ответственных за их исполнение лиц и времени, необходимого для полного завершения. При такие схемы просто необходимы. Во-первых, для того чтобы понимать, какое общее время будет затрачено, во-вторых, чтобы знать, как планировать ресурсы. Именно этим занимаются проектные менеджеры, они в первую очередь осуществляют построение сетевого графика. Пример возможной ситуации рассмотрим далее.

Исходные данные

Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.

Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.

Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:

Построение матрицы

Перед тем как сформировать необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки — j (завершающее событие).

Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.

Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.

Основные элементы, используемые для сетевого графика

Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:

1. Любое событие обозначается кружком, в середине которого находится цифра, соответствующая порядку действий.
2. Сама работа — это стрелка, ведущая от одного события к другому. Над стрелкой пишут время, необходимое для ее совершения, а под стрелкой обозначают ответственное лицо.

Работа может выполниться в трех состояниях:

— Действующая — это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.

— Ожидание — процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.

— Фиктивная работа — это логическая связь между событиями. Она не требует ни времени, ни ресурсов, но чтобы не прервать сетевой график, ее обозначают Например, подготовка зерна и приготовление мешков для него — это два отдельных процесса, они не связаны последовательно, но их связь нужна для следующего события — фасовки. Поэтому выделяют еще один кружочек, который соединяют пунктиром.

Основные принципы построения

Правила построения сетевых графиков заключаются в следующем:

Построение сетевого графика. Пример

Вернемся к исходному примеру и попробуем начертить сетевой график, используя все данные, указанные ранее.

Начинаем с первого события. Из него выходят два — второе и третье, которые соединяются в четвертом. Далее все идет последовательно до седьмого события. Из него выходят три работы: восьмая, девятая и десятая. Постараемся все отобразить:

Критические значения

Это еще не все построение сетевого графика. Пример продолжается. Далее нужно рассчитать критические моменты.

Критический путь — это наибольшее время, затраченное на выполнение задания. Для того чтобы его рассчитать, нужно сложить все наибольшие значения последовательных действий. В нашем случае это работы 1-2, 2-4, 4-5, 5-6, 6-7, 7-8, 8-11. Суммируем:

30+2+2+5+7+20+1 = 67 дней

Таким образом, критический путь равен 67 дням.

Если такое время на проект не устраивает руководство, его нужно оптимизировать согласно требованиям.

Автоматизация процесса

На сегодняшний день мало кто из проектных менеджеров вручную построения сетевых графиков — это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.

Кратко рассмотрим самые распространенные программы:

1. Microsoft Project 2002 — офисный продукт, в котором очень удобно рисовать схемы. Но проводить расчеты немного неудобно. Для того чтобы совершить даже самое простое действие, нужен немалый багаж знаний. Скачивая программу, позаботьтесь о приобретении инструкции по пользованию к ней.
2. SPU v2.2. Очень распространенный бесплатный софт. Вернее, даже не программа, а файл в архиве, для использования которого не нужна установка. Изначально она была разработана для выпускной работы одного студента, но оказалась настолько полезной, что автор выложил ее в сеть.
3. NetGraf — еще одна разработка отечественного специалиста из Краснодара. Очень легка, проста в использовании, не требует установки и огромного багажа знаний, как с ней управляться. Плюсом является то, что поддерживает импорт информации из других текстовых редакторов.
4. Часто можно встретить вот такой экземпляр — Borghiz . О разработчике мало что известно, как и о том, как пользоваться программой. Но по примитивному методу «тыка» ее можно освоить. Главное, что она работает.

1.Сущность и значение метода сетевого планирования и управления. Основные элементы сетевого графика.

2.Общие принципы построения сетевого графика. Параметры сетевого графика.

3.Аналитический и графический расчет сетевого графика. Оптимизация сетевого графика. 4.Планирование и управление строительным производством на основе сетевых графиков.

1.Сущность и значение метода сетевого планирования и управления. Основные элементы сетевого графика.

Сетевой график – схематическое изображение процесса строительства одного объекта или комплекса объектов, в котором в наглядной форме показывается последовательность выполнения работ и приводятся как технологические, так и организационные их взаимосвязи.

Метод сетевого планирования помогает устанавливать зависимость продолжительности строительства от сроков выполнения отдельных видов работ.

Сетевая модель позволяет:

Четко отобразить структуру проекта и установить взаимосвязь отдельных разделов;

Прогнозировать критические работы;

Более эффективно использовать ресурсы;

По-новому подойти к учету и отчетности в строительстве и др.

Основные элементы сетевого гра­фика:

1.работа – производственный процесс, требующий затрат трудовых, материальных ресурсов, а также времени (сплошная линия со стрелкой наимен.работы)

Продолжит., число раб. в смену

2.событие – начало или окончание одной либо нескольких работ. Каждому событию присваивается номер (код). Все работы ограничиваются двумя событиями. Изображается кружками. Событие бывает начальное и конечное.

3.ожидание – это организационный или технологический перерыв между работами, не требующий затрат ресурсов, но занимающий время (например, естественная сушка штукатурки).

4.зависимость (фиктивная работа) – не связана с расходом ресурсов времени и вводится для отражения взаимосвязей между реальными работами. Показывается пунктирной линией со стрелкой

5.путь – непрерывная линия, характеризующая продолжительность работ от начального до конечного события в сетевом графике. Длина пути – это сумма продолжительностей работ, находящихся на данном пути.

В сетевом графике между начальным и конечным событиями может быть несколько путей. Путь, имеющий наибольшую продолжительность, называется критическим (обозначается двумя сплошными линиями), а работы, входящие в состав критического пути – критическими.

2.Общие принципы построе­ния сетевого графика. Параметры сетевого графика.

Построение сетевого графика ведется по определенным правилам:

1. Направление стрелок – слева направо. Код начального события меньше кода конечного события.

2. Графики должны иметь простую форму, по возможности без пересечения векторов. Большинство работ следует изображать горизонтальными линиями.

3. На графике не должно быть «тупиков» (замкнутых контуров).

4. Между двумя событиями может быть только одна работа.

5. Если после окончания двух работ можно начинать третью, а по окончании каждой из них – другие работы, то показываются зависимости между событиями.

6. Не допускаются события, из которых не выходит ни одна работа (кроме конечного).

Сетевое планиров ание — это метод планирования работ, операции в которых, как правило, не повторяются (например, разработка но-вых продуктов, строительство зданий, ремонт оборудования, проек-тирование новых работ).

Для проведения сетевого планирования вначале необходимо рас-членить проект на ряд отдельных работ и составить логическую схе-му (сетевой граф).

Работа — это любые действия, трудовые процессы, сопровожда-ющиеся затратами ресурсов или времени и приводящие к определен-ным результатам. На сетевых графах работы обозначаются стрелка-ми. Для указания того, что одна работа не может выполняться раньше другой, вводят фиктивные работы, которые изображаются пунктирными стрелками. Продолжительность фиктивной работы принимается равной нулю.

Событие — это факт окончания всех входящих в него работ. Счи-тается, что оно происходит мгновенно. На сетевом графе события изображаются в виде вершин графа. Ни одна выходящая из данного события работа не может начаться до окончания всех работ, входя-щих в это событие.

С исходного события (которое не имеет предшествующих работ) начинается выполнение проекта. Завершающим событием (которое не имеет последующих работ) заканчивается выполнение проекта.

После построения сетевого графа необходимо оценить продолжи-тельность выполнения каждой работы и выделить работы, которые определяют завершение проекта в целом. Нужно оценить потреб-ность каждой работы в ресурсах и пересмотреть план с учетом обес-печения ресурсами.

Часто сетевой граф называют сетевым графиком .

Правила построения сетевых графиков.

1. Завершающее событие лишь одно.

2. Исходное событие лишь одно.

3. Любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Если два события связаны более чем одной работой, рекомендуется ввести дополнительное событие и фиктивную работу:

4. В сети не должно быть замкнутых циклов.

5. Если для выполнения одной из работ необходимо получить ре-зультаты всех работ, входящих в предшествующее для нее событие, а для другой работы достаточно получить результат нескольких из этих работ, то нужно ввести дополнительное событие, отражающее результаты только этих последних работ, и фиктивную работу, свя-зывающую новое событие с прежним.

Например, для начала работы D достаточно окончания рабо-ты А. Для начала же работы С нужно окончание работ А и В.

Метод критического пути

Метод критического пути исполь-зуется для управления проектами с фиксированным временем вы-полнения работ.

Он позволяет ответить на следующие вопросы:

1. Сколько времени потребуется на выполнение всего проекта?

2. В какое время должны начинаться и заканчиваться отдельные
работы?

3. Какие работы являются критическими и должны быть выпол-нены в точно определенное графиком время, чтобы не сорвать уста-новленные сроки выполнения проекта в целом?

4. На какое время можно отложить выполнение некритических работ, чтобы они не повлияли на сроки выполнения проекта?

Самый продолжительный путь сетевого графика от исходного со-бытия к завершающему называется критическим. Все события и рабо-ты критического пути также называются критическими. Продолжи-тельность критического пути и определяет срок выполнения проекта. Критических путей на сетевом графике может быть несколько.

Рассмотрим основные временные параметры сетевых графиков.

Обозначим t (i, j) — продолжительность работы с начальным со-бытием i и конечным событием j .

Ранний срок t р (j) свершения события j — это самый ранний момент, к которому завершаются все работы, предшествующие этому собы-тию. Правило вычисления:

где максимум берется по всем событиям i , непосредственно предше-ствующим событию j (соединены стрелками).

Поздний срок t n (i) свершения события i — это такой предельный мо-мент, после которого остается ровно столько времени, сколько необ-ходимо для выполнения всех работ, следующих за этим событием.

Правило вычисления:

где минимум берется по всем событиям j , непосредственно следую-щим за событием i .

Резерв R(i) события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:

R(i)= t n (i) — t р (i)

Критические события резервов не имеют.

При расчетах сетевого графика каждый круг, изображающий событие, делим диаметрами на 4 сектора:

Управление проектами с неопределенным временем выполнения работ

В методе критического пути предполагалось, что время выполне-ния работ нам известно. На практике же эти сроки обычно не опре-делены. Можно строить некоторые предположения о времени вы-полнения каждой работы, но нельзя предусмотреть все возможные трудности или задержки выполнения. Для управления проектами с неопределенным временем выполнения работ наиболее широкое применение получил метод оценки и пересмотра проектов , рассчитанный на исполь-зование вероятностных оценок времени выполнения работ, предус-матриваемых проектом.

Для каждой работы вводят три оценки:

— оптимистическое время а — наименьшее возможное время вы-полнения работы;

— пессимистическое время b — наибольшее возможное время вы-полнения работы;

— наиболее вероятное время т — ожидаемое время выполнения работы в нормальных условиях.

По а, b и т находят ожидаемое время выполнения работы :

и дисперсию ожидаемой продолжительности t :

Используя значения t , находят критический путь сетевого графика.

Оптимизация сетевого графика

Стоимость выполнения каждой работы плюс дополнительные расходы определяют стоимость проекта. С помощью дополнитель-ных ресурсов можно добиться сокращения времени выполнения критических работ. Тогда стоимость этих работ возрастет, но общее время выполнения проекта уменьшится, что может привести к сни-жению общей стоимости проекта. Предполагается, что работы можно выполнить либо в стандартные, либо в минимальные сроки, но не в промежутке между ними.

График Ганта

Иногда бывает полезным изобразить наглядно имеющийся в на-личии резерв времени. Для этого используется график Ганта . На нем каждая работа (i, j ) изображается горизонтальным отрезком, длина которого в соответствующем масштабе равна времени ее выполне-ния. Начало каждой работы совпадает с ранним сроком свершения ее начального события.

График Ганта очень полезен при составлении расписания работ. Он показывает рабочее время, время простоев и относительную загрузку системы. Ожидающие выполнения работы могут быть распределены по другим рабочим центрам.

График Ганта используется для управления работами в процессе. Он указывает, какая работа выполняется по расписанию, а какая опережает его или отстает. Существует много возможностей исполь-зования графика Ганта на практике.

Стоит заметить, что график Ганта не учитывает разнообразия производственных ситуаций (например, поломки или человеческие ошибки, которые требуют повторения работы). График Ганта должен регулярно пересчитываться при появлении новых работ и при пере-смотре продолжительности работ.

График Ганта особенно полезен при работе над проектом с не свя-занными между собой работами. А вот при анализе проекта с тесно взаимосвязанными работами лучше воспользоваться методом кри-тического пути.

Распределение ресурсов, графики ресурсов

До сих пор мы не обращали внимания на ограничения в ресурсах и считали, что все необходимые ресурсы (сырье, оборудование, рабочая сила, денежные средства, производственные площади и т. д.) имеются в достаточном количестве. Рассмотрим один из простейших методов решения проблемы распределения ресурсов — «метод проб и ошибок».

Пример . Произведем оптимизацию сетевого графика по ре-сурсам. Наличный ресурс равен 10 единицам.

Первое число, приписанное дуге графика, означает время выпол-нения работы, а второе — требуемое количество ресурса для выпол-нения работы. Работы не допускают перерыва в их выполнении.

Находим критический путь. Строим график Ганта. В скобках для каждой работы укажем требуемое количество ресурса. По графику Ганта строим график ресурса. На оси абсцисс мы откладываем время, а на оси ординат — потребности в ресурсах.

Считаем, что все работы начинаются в наиболее ранний срок их выполнения. Ресурсы складываются по всем работам, выполняемым одновременно. Также проведем ограничительную линию по ресурсу (в нашем примере это у = 10).

Из графика мы видим, что на отрезке от 0 до 4, когда одновремен-но выполняются работы В, А, С, суммарная потребность в ресурсах составляет 3 + 4 + 5 = 12, что превышает ограничение 10. Так как ра-бота С критическая, то мы должны сдвинуть сроки выполнения или А, или В.

Запланируем выполнение работы В с 6-го по 10-й день. На сроках выполнения всего проекта это не скажется и даст возможность ос-таться в рамках ресурсных ограничений.

Параметры работ

Напомним обозначения: t (i, j) — продолжительность работы (i, j ); t р (i) — ранний срок свершения события i ; t n (i) — поздний срок свер-шения события /.

Если в сетевом графике лишь один критический путь, то его лег-ко отыскать по критическим событиям (событиям с нулевыми резер-вами времени). Ситуация усложняется, если критических путей не-сколько. Ведь через критические события могут проходить как критические, так и некритические пути. В этом случае нужно ис-пользовать критические работы.

Ранний срок начала работы (i, j) совпадает с ранним сроком свер-шения события i: t p н (i, j) = t р (i).

Ранний срок окончания работы (i, j ) равен сумме t р (i) и t(i, j) : t p о (i, j) = t р (i)+ t (i, j).

Поздний срок начала работы (i, j) равен разности t n (j) (позднего срока свершения события j ) и t (i, j) : t пн (i, j) = t п (j) — t (i, j).

Поздний срок окончания работы (i, j ) совпадает с t n (j): t по (i, j) = t п (j).

Полный резерв времени R n (i, j) работы (i, j ) — это максимальный за-пас времени, на которое можно задержать начало работы или увели-чить ее продолжительность, при условии, что весь комплекс работ будет завершен в критический срок:

R n (i, j)= t n (j) — t р (i) — t (i, j)= t по (i, j) — t p о (i, j).

Свободный резерв времени R с (i, j) работы (i, j) — это максимальный запас времени, на которое можно отсрочить или (если она началась в свой ранний срок) увеличить ее продолжительность при условии, что не нарушатся ранние сроки всех последующих работ: R с (i, j)= t р (j) — t р (i) — t (i, j)= t р (j) — t p о (i, j).

Критические работы, как и критические события, резервов не имеют.

Пример. Посмотрим, каковы резервы работ для сетевого гра-фика.

Находим t р (i), t n (i) и составляем таблицу. Значения первых пяти колонок берем из сетевого графика, а остальные колонки просчитаем по этим данным.

Работа (i, j)	Продолжительность t (i, j)	t р (i)	t р (j)	t n (j)	Срок начала работы
t p н (i, j) = t р (i)	t пн (i, j) = t п (j) — t (i, j)
(1,2)	6-6 = 0
(1,3)	7-4 = 3
(1,4)	8-2 = 6
(2,4)	8-2 = 6
(2,5)	12-6 = 6
(3,5)	12-5 = 7
(4,5)	12-4 = 8

Работа (i, j)	Срок окончания работы	Резервы времени работы
t p о (i, j) = t р (i)+ t (i, j)	t по (i, j) = t п (j)	Полный R n (i, j)= = t по (i, j) — t p о (i, j)	Свободный R с (i, j)= = t р (j) — t p о (i, j)
(1,2)	0 + 6 = 6	6-6 = 0	6-6 = 0
(1,3)	0 + 4 = 4	7-4 = 3	4-4 = 0
(1,4)	0 + 2 = 2	8-2 = 6	8-2 = 6
(2,4)	6 + 2 = 8	8-8 = 0	8-8 = 0
(2,5)	6 + 6= 12	12-12 = 0	12-12 = 0
(3,5)	4 + 5 = 9	12-9 = 3	12-9 = 3
(4,5)	8 + 4=12	12-12 = 0	12-12 = 0

Критические работы (работы с нулевыми резервами): (1, 2), (2,4), (2, 5), (4, 5). У нас два критических пути: 1 — 2 — 5 и 1 — 2 — 4 — 5.

Методы сетевого планирования и управления позволяют сосре-доточиться на важнейших для выполнения проекта моментах. При этом требуется, чтобы работы были взаимно независимы, то есть в пределах определенной последовательности работ можно начи-нать, приостанавливать, исключать работы, а также выполнять одну работу независимо от другой работы. Все работы должны выполнять-ся в определенной последовательности. Поэтому методы сетевого планирования и управления широко применяются в строительстве, самолетостроении и судостроении, а также в промышленных отрас-лях с быстро меняющимися тенденциями.

Скептическое отношение к методам сетевого планирования и уп-равления часто основывается на их стоимости, которая может со-ставлять около 5% общей стоимости проекта. Но эти расходы обыч-но полностью компенсируются экономией, достигаемой с помощью более точного и гибкого графика, а также сокращения сроков выпол-нения проекта.

Источник: chaspeek.ru