Понятно, что плиток не больше 99. От полного ряда восьмёрок отнимаем единицу, подбираем от 95, 87, 79, 71 . до 55.55= 8*6(48)+755= 9*6(54)+17 -1= 6После строительства дома осталась 55 плиток.
Также наши пользователи интересуются:
⭐⭐⭐⭐⭐ Лучший ответ на вопрос «Пожалуйста помогите решить задачу: после стротроительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на участке рядом с домом. Если укладывать в ряд по 10 плиток,то для квадратной площадки плиток не хватит. При укладывании по 8 плиток в ряд остаётся один неполный ряд,а при укладывании по 9 плиток тоже остаётся неполный ряд,в котором 6 плиток меньше,чем в неполном ряду при укладывании по 8. Сколько всего плиток осталось после строительства дома?» от пользователя ASIYA VIDYAEVA в разделе Математика. Задавайте вопросы и делитесь своими знаниями.
Источник: shpora.org
DIY. Газоблок курит в сторонке? ДЕШЁВЫЙ МАТЕРИАЛ ДЛЯ СТРОИТЕЛЬСТВА ДОМА!
ВПР по математике 5 класс
ВПР по математике для 5 класса состоит из 14 заданий. В 12 номере нужно изобразить требуемые в условии части рисунка, а в заданиях 6, 9, 10 и 14 – записать не только ответ, но и решение. Во всех остальных заданиях необходимо только записать ответ. На выполнение всей работы дается 60 минут.
Верное выполнение учеником заданий 13 и 14 при условии высокого результата в целом говорит о его способностях к данному предмету.
Система оценок
За ВПР по математике всего можно набрать 20 баллов. Они переводятся в отметки следующим образом:
| От 0 до 6 баллов | 2 |
| От 7 до 10 баллов | 3 |
| От 11 до 14 баллов | 4 |
| От 15 до 20 баллов | 5 |
Примеры заданий с разбалловкой и пояснениями
Задание 1
В этом задании проверяются знания учеников о натуральных числах. В нем нужно привести пример любого числа, соответствующего условию, например – двузначное число больше 30, которое делится на 12 и не делится на 9, или: двузначное число больше 70, которое делится на 10 и на 6.
Подобрать число по условию не так сложно – верный ответ оценивается в 1 балл.
Задание 2
Данное задание направлено на умение учеников оперировать понятием «обыкновенная дробь». Условия могут быть различных типов, например:
- представить целое число в виде дроби с конкретным знаменателем (например, число 7 со знаменателем дроби 4);
- представить в виде обыкновенной дроби сумму обыкновенных дробей (как правило, с общим знаменателем);
- представить в виде обыкновенной дроби смешанное число.
За это также можно получить 1 балл.
Задание 3
В третьем задании ВПР по математике в 5 классе представлено четыре десятичные дроби – например, 29,29; 30,67; 29,9; 30,7. Нужно найти наибольшее или наименьшее число и выписать его в ответ. Если это сделано правильно, ученик получает 1 балл.
математика 5класс ВПР Задание14
Задание 4
Четвертое задание ВПР по математике – задача на нахождение части числа или числа по его части: например, дано, сколько всего учеников участвовали в олимпиаде, и нужно найти одну девятую от этого числа, или же указано число мест в автобусе и сказано, что треть занята – требуется определить, сколько свободных мест осталось. За верное решение задачи также можно набрать 1 балл.
Задание 5
В этом задании нужно найти один из компонентов примера – одно из слагаемых, делимое или делитель. Условие может выглядеть так: 17 • x = 272. Если число найдено правильно, ученик получает 1 балл.
Задание 6
Шестое задание ВПР по математике содержит в себе задачу, связывающую три величины. Задача может быть на работу, на скорость или на движение, в том числе – на скорость объекта, движущегося по течению реки и против него. Пример задачи:
Искусственный спутник Земли делает три оборота вокруг Земли за 600 минут. За сколько минут этот же искусственный спутник делает пять оборотов вокруг Земли?
В данном задании проверяющий оценивает как ответ, так и решение. Если все правильно – ставят 2 балла. Если в ходе решения допущена одна ошибка и ответ неправильный, но все нужные преобразования и рассуждения логичны и верны – 1 балл. Если рассуждения неверны, либо в них допущено более одной ошибки – 0 баллов.
Задание 7
В седьмом номере учащемуся нужно решить несложную сюжетную задачу, в которой в зависимости от варианта могут быть отражены все арифметические действия. Задача может выглядеть так:
На одной тарелке на 10 орехов больше, чем на другой. Сколько орехов нужно переложить с одной тарелки на другую, чтобы орехов стало поровну?
Правильный ответ на это задание приносит пятикласснику 1 балл.
Задание 8
Задача из восьмого задания ВПР по математике – на проценты. Она проверяет, как ученики 5 класса умеют находить процент от числа либо число по проценту, процентное соотношение чисел, процентное уменьшение или увеличение величины. Часто в таких заданиях приводится цена на товар без скидки и величина скидки – соответственно, нужно найти стоимость товара со скидкой. Но могут быть и другие, более сложные задания, например:
В парке отдыха в течение недели брали напрокат роликовые коньки 900 человек, а велосипеды за эту же неделю — на 20% меньше. На сколько меньше человек брало в аренду велосипеды, чем роликовые коньки?
За верный ответ ученик получает 1 балл.
Задание 9
В девятом задании необходимо решить большой пример в несколько (чаще всего 5) действий, например –
Здесь ученик записывает не только ответ, но и решение – ведь в таких примерах очень важно не только правильно сосчитать, но и соблюсти порядок действий.
Если проведены все вычисления, и ответ правильный – ученик получает 2 балла. Если ход решения верный, но в нем есть одна арифметическая ошибка, из-за чего ответ неправильный – 1 балл, а в иных случаях – 0.
Задание 10
Десятое задание ВПР по математике предполагает решение задач на покупки, а также – логических задач, часто с опором на данные таблицы. К примеру, есть несколько принтеров, для каждого из которых дано время печати и число страниц, напечатанных за это время. Нужно определить, сколько страниц в минуту может напечатать принтер с самой большой скоростью печати.
За верное решение и ответ можно суммарно набрать 2 балла: их ставят, если в решении и ответе нет ошибок. Если ход решения и рассуждения верный, но допущена одна ошибка, которая стала причиной ошибочного ответа – 1 балл. Во всех остальных случаях ученик не получает баллы за это задание.
Задание 11
Данное задание состоит из двух частей. Всего за него можно набрать 2 балла. В условии представлена диаграмма (иногда – таблица) с определенными данными – к примеру, вот такая:
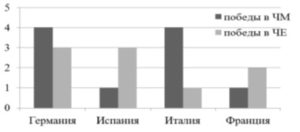
В первой части задается вопрос, проверяющий умение читать диаграммы и внимательность – для данной диаграммы, к примеру, такой:
Перечислите страны, команды которых побеждали в чемпионатах мира больше, чем в чемпионатах Европы.
Верный ответ оценивается в 1 балл.
Во второй части также задается вопрос на умение извлечения информации из диаграмм и ее интерпретации, например: Укажите страну, у команды которой число побед в чемпионатах Европы больше числа побед в чемпионатах мира в три раза. Правильный ответ также приносит ученику 1 балл.
Задание 12
В двенадцатом задании ВПР по математике проверяется умение пятиклассников рассчитывать расстояния на местности, а также выполнять несложные построения на местности. Всего за это задание можно получить 2 балла. Пример задания:
Винни-Пух пошёл от дуба на восток, а потом повернул на юг и дошёл до фонаря. На рисунке показан путь Винни-Пуха от дуба до фонаря. Сторона квадратной клетки равна 1 км.
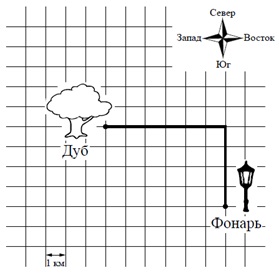
В первом вопросе нужно найти длину пути – в данном случае пути от дуба до фонаря, но на рисунке могут быть и другие вещи – к примеру, схематический план района города и путь от одного дома до другого при одинаковой ширине улиц и квадратной форме всех домов с указанной величиной стороны. За верный ответ ставят 1 балл.
Во втором вопросе пятиклассник должен сам отобразить маршрут – для данного рисунка задание звучит так:
Винни-Пух от дуба прошёл 2 км на юг, затем 3 км на восток, 6 км на север и 1 км на запад. Изобразите на рисунке путь Винни-Пуха.
Могут указать начальную и конечную точки маршрута и диапазон его длины. За правильно начерченный маршрут ученик также получает 1 балл.
Задание 13
Тринадцатое задание ВПР по математике проверяет развитие представлений о пространстве – знаний о таких понятиях, как куб, шар, параллелепипед. Задания могут быть различными: или определить параметры (объем либо периметр) нарисованной фигуры с указанными величинами сторон, или определить, из скольких кубиков состоит фигура на рисунке, или решить небольшую задачу – к примеру, сколько кубиков с определенной стороной поместится в коробке с данными габаритами. Верный ответ на задание оценивается 1 баллом.
Задание 14
В этом задании ученик раскрывает умение проводить логические обоснования и решать задачи различных типов, включая задачи повышенной сложности. Примеры задач:
В семи аквариумах было поровну рыбок; всего рыбок было менее 100. Затем установили восьмой аквариум, и рыбок расселили так, что во всех аквариумах, кроме одного, их стало поровну, а в одном – на одну больше, чем в каждом из остальных. Сколько всего было рыбок?
После строительства дома осталось некоторое количество плиток.
Их можно использовать для выкладывания прямоугольной площадки на участке рядом с домом. Если укладывать в ряд по 10 плиток, то для квадратной площадки плиток не хватит. При укладывании по 8 плиток в ряд остаётся один неполный ряд, а при укладывании по 9 плиток тоже остаётся неполный ряд, в котором на 6 плиток меньше, чем в неполном ряду при укладывании по 8. Сколько всего плиток осталось после строительства дома?
У Серёжи и Маши семизначные номера телефонов, причём оба номера не начинаются с нуля. Серёжин номер отличается от Машиного только первой цифрой — у Маши она на 2 меньше. Известно, что номер телефона Маши даёт остаток 3 при делении на 8. Какой остаток даёт номер телефона Серёжи при делении на 8?
Если ученик привел все нужные рассуждения и получил правильный ответ, он получает 2 балла. В случае, если рассуждения неполные, но ответ верный – например, ученик нашел ответ методом подбора, но не доказал отсутствие возможных других верных ответов – 1 балл, а если приведен только верный ответ совсем без рассуждений или же ответ неверен – 0 баллов.
Источник: spadilo.ru