1) Согласно п. 9 Общих указаний (часть I) СНиП [2] принимается метод интерполяции, исходя из имеющихся в нормах общих площадей для 9-этажного кирпичного жилого дома 8000 м 2 и 10000 м 2 с продолжительностью строительства 12 и 13 мес. соответственно.
Продолжительность строительства на единицу прироста общей площади равна
(13 – 12) / ( 10000– 8000) = 0,0005 мес. Прирост общей площади равен
8609 – 8000 = 609 м 2 .
Продолжительность строительства Т с учётом интерполяции будет равна:
2) Согласно п. 8 Общих указаний (часть II) СНиП [2], продолжительность строительства зданий на свайных фундаментах увеличивается из расчёта 10 рабочих дней на каждые сто свай. Рассчитаем увеличение срока строительства с учётом свайных фундаментов в количестве 402 шт
Источник: psihdocs.ru
Что такое интерполяция в строительстве
Расчет продолжительности строительства объектов методами интерполяции и экстраполяции
Пример 1. Определить продолжительность строительства завода строительных стальных конструкций мощностью 50 тыс.т. конструкций в год.
Переходные процессы | Классический метод расчета переходных процессов. Теория и задача
Поскольку заданная характеристика завода находится в интервале указанных в [1] мощностей 20 тыс.т и 60 тыс. т строительных стальных конструкций в год с нормами продолжительности строительства соответственно 18 мес. и 23 мес., применяем метод линейной интерполяции.
Определяем продолжительность строительства на единицу прироста мощности:
Прирост мощности 50 тыс.т – 20 тыс.т = 30 тыс.т
Продолжительность строительства завода мощностью 50 тыс. т конструкций в год с учетом интерполяции:
Пример 2. Определить продолжительность строительства завода строительных стальных конструкций мощностью 120 тыс.т. конструкций в год.
Так как максимальная мощность завода, указанная в [1] составляет 90 тыс.т. конструкций в год, применяем метод экстраполяции.
Продолжительность строительства завода мощностью 90 тыс.т. конструкций в год, согласно [1] составляет 30 мес.
Увеличение мощности составит:
Учитывая, что на каждый процент изменения мощности, указанной в [1], продолжительность строительства изменяется на 0,3%, прирост к норме продолжительности строительства составит:
Продолжительность строительства с учетом экстраполяции:
Пример 3. Определить продолжительность строительства завода строительных стальных конструкций мощностью 12 тыс.т. конструкций в год.
Так как минимальная мощность завода, указанная в [1] составляет 20 тыс.т., конструкций в год, применяем метод экстраполяции.
Продолжительность строительства завода мощностью 20 тыс.т конструкций в год составляет 18 мес.
Уменьшение мощности составит:
Уменьшение нормы продолжительности строительства:
Продолжительность строительства с учетом экстраполяции:
Согласно оглавлению [1] данный объект относится к разделу З – «Непроизводственное строительство» пункту «Жилые здания».
Лекция № 9 (ч. 2) Табличные методы расчета неритмичных потоков
Поскольку заданная характеристика здания находится в интервале указанных в [1] площадей 3000м 2 и 6000м 2 с нормами продолжительности соответственно 6 мес. и 8 мес., применяем метод линейной интерполяции.
Определяем продолжительность строительства на единицу прироста мощности:
Прирост мощности 4,5 тыс.м 2 – 3,0 тыс.м 2 = 1,5 тыс.м 2
Продолжительность строительства жилого дома общей площадью 4500м 2 с учетом интерполяции:
Продолжительность строительства крупнопанельного жилого дома общей площадью 12000м 2 составит 10 мес.
Увеличение площади составит:
Учитывая, что на каждый процент изменения мощности (площади), указанной в [1], продолжительность строительства изменяется на 0,3%, прирост к норме продолжительности строительства составит:
Продолжительность строительства с учетом экстраполяции:
Продолжительность строительства крупнопанельного жилого дома общей площадью 3000м 2 составляет 6 мес.
Уменьшение мощности (площади)составит:
Уменьшение нормы продолжительности строительства:
Продолжительность строительства с учетом экстраполяции:
Для выполнения данной работы студент получает вариант индивидуального задания согласно перечню объектов, приведенному в приложении 1.
Дата добавления: 2014-12-21 ; просмотров: 8566 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Многие из нас сталкивались с непонятными терминами в разных науках. Но находится очень мало людей, которых не пугают непонятные слова, а наоборот, приободряют и заставляют всё больше углубиться в изучаемый предмет. Сегодня речь пойдёт о такой вещи, как интерполяция. Это способ построения графиков по известным точкам, позволяющий с минимальным количеством информации о функции предсказать её поведение на конкретных участках кривой.
Перед тем как перейти к сути самого определения и рассказать о нём подробнее, немного углубимся в историю.
История
Интерполяция была известна ещё с древнейших времён. Однако своим развитием это явление обязано нескольким самым выдающимся математикам прошлого: Ньютону, Лейбницу и Грегори. Именно они развили это понятие с помощью более продвинутых математических способов, доступных в то время. До этого интерполяцию, конечно, применяли и использовали в вычислениях, но делали это совершенно неточными способами, требующими большого количества данных для построения модели, более-менее близкой к реальности.
Сегодня мы можем даже выбирать, какой из способов интерполяции подходит больше. Всё переведено на компьютерный язык, который с огромной точностью может предсказывать поведение функции на определённом участке, ограниченном известными точками.
Что такое интерполяция?
Как мы уже говорили, это общее название способов, позволяющих построить график по точкам. В школе в основном это делают с помощью составления таблицы, выявления точек на графике и примерного построения линий, их соединяющих. Последнее действие делается исходя из соображений похожести исследуемой функции на другие, вид графиков которых нам известен.
Но мы отошли от основной темы. В следующем разделе разберёмся, какая бывает интерполяция и с помощью каких формул можно произвести эту операцию.
Виды интерполяции
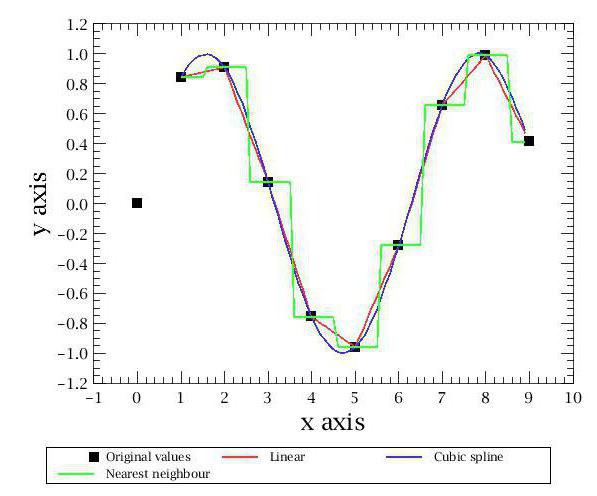
Самым простым видом является интерполяция методом ближайшего соседа. С помощью этого способа мы получаем очень приблизительный график, состоящий из прямоугольников. Если вы видели хоть раз объяснение геометрического смысла интеграла на графике, то поймёте, о каком графическом виде идёт речь.
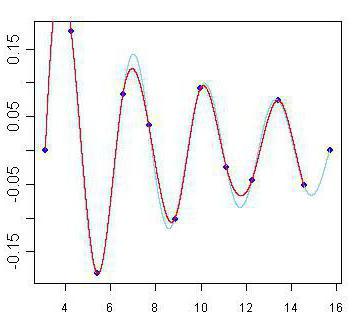
Кроме этого, существуют и другие методы интерполяции. Самые известные и популярные связаны с многочленами. Они более точны и позволяют предсказывать поведение функции при достаточно скудном наборе значений. Первым методом интерполяции, который мы рассмотрим, будет линейная интерполяция многочленами.
Это самый простой способ из данной категории, и им наверняка каждый из вас пользовался в школе. Суть его заключается в построении прямых между известными точками. Как известно, через две точки плоскости проходит единственная прямая, уравнение которой можно найти исходя из координат данных точек. Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.
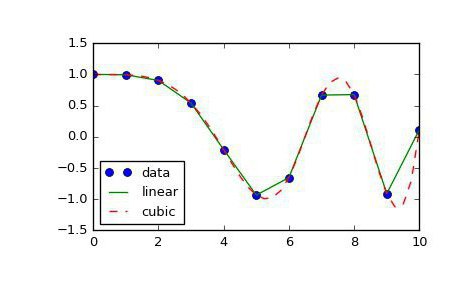
Усложнённые виды интерполяции
Есть более интересный, но при этом более сложный способ интерполяции. Его придумал французский математик Жозеф Луи Лагранж. Именно поэтому расчет интерполяции по этому методу назван его именем: интерполяция по методу Лагранжа.
Фокус тут вот в чём: если способ, изложенный в предыдущем абзаце, использует для расчета только линейную функцию, то разложение методом Лагранжа предполагает также использование многочленов более высоких степеней. Но не так просто найти сами формулы интерполяции для разных функций. И чем больше точек известно, тем точнее получается формула интерполяции. Но есть и масса других методов.
Перейдём к, пожалуй, одному из важнейших разделов. Из него мы узнаем, как и где обсуждаемая нами совокупность методов применяется в жизни.

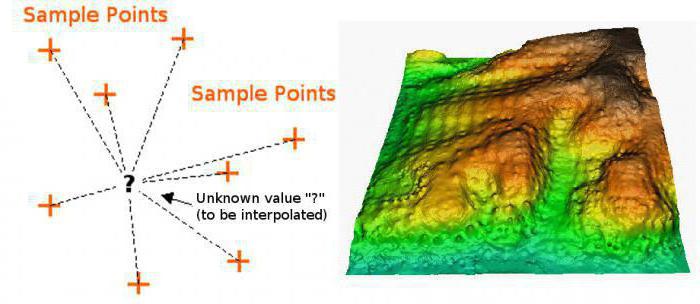
Применение
А как это пригодится в жизни?
Смежные понятия
Заключение
Интерполяция и экстраполяция
1) определение длины базисного периода, закономерность которого распространяют на будущее;
2) определение длины будущего периода, на который распространяют обнаруженную закономерность.
Существуют следующие способы экстраполяции данных:
1) если для измерения основной тенденции производилось аналитическое выравнивание ряда динамики, то для экстраполяции используется уравнение тренда, в которое подставляются значения t в будущие периоды. Так как в базисном периоде уровень колеблется около тренда, то колебания вероятны и в будущем. Следовательно, фактический уровень в будущем не обязательно точно совпадает с экстраполированным по тренду;
2) экстраполяция на будущее средней абсолютной или относительной скорости изменения уровня. Этот метод основан на предположении о равномерном изменении уровня:
а) если в базисном периоде цепные показатели динамики не имели резких колебаний, экстраполяцию осуществляют с помощью следующих формул:



или

; t- срок прогноза; б) если цепные показатели динамики в базисном периоде сильно колебались и ежегодный прирост (или темпы роста и прироста) вычислялись на базе средних уровней, рассчитанных за равные периоды, то для экстраполяции используют следующие формулы:
При интерполяции предполагают, что выявленная тенденция и ее характер, существенно не изменялись в том промежутке времени, уровень которого неизвестен. Существуют следующие способы интерполяции данных:
1) на основе среднего абсолютного прироста, среднего темпа роста. Формулы для интерполяции имеют следующий вид:



;

— длина промежутка времени между годом, для которого делается интерполяция, и базисным годом;
2) если, кроме конечного и базисного уровней, известны также некоторые промежуточные уровни, интерполяцию можно осуществить на основе уравнения тренда.
Интерполяция– способ определения неизвестных промежуточных значений динамического ряда.
Интерполяция заключается по существу в приближенном отражении сложившейся закономерности внутри определенного отрезка времени – в отличие от экстраполяции, которая требует выхода за пределы этого отрезка времени.
Экстраполяция– метод определения количественных характеристик для совокупностей и явлений, не подвергшихся наблюдению, путем распространения на них результатов, полученных из наблюдения над аналогичными совокупностями за прошедшее время, на будущее и т. д.
Средний уровень ряда динамики характеризует типичную величину абсолютных уровней.
Источник: dom-srub-banya.ru
Интерполяция данных: соединяем точки так, чтобы было красиво
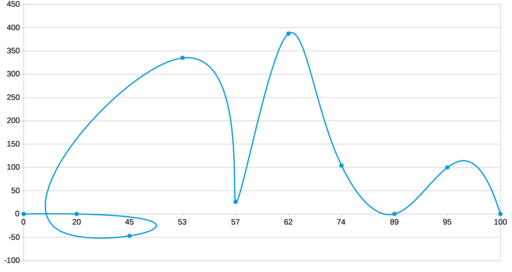
Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво.
Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:
Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1nbspPn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти nnbsp1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:
Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):
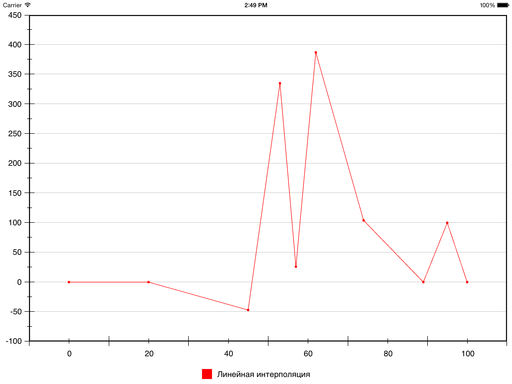
Результат линейной интерполяции этих точек выглядит так:
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a;nbsp–nbsp+nbsp–nbsp=nbsp–nbsp=nbsp–nbsp–nbsp–nbsp+nbsp=nbsp=nbspyi) и Pinbsp1(xinbsp1,nbsp+nbsp+nbsp–https://habr.com/ru/post/264191/» target=»_blank»]habr.com[/mask_link]