Конструкции из керамических камней должны соответствовать требованиям СНиП II-22-81(1995) «Каменные и армокаменные конструкции», СНиП 2.03.01-84, СНиП III-17-78 «Каменные конструкции», а также СНиП 23-02-2003 «Тепловая защита зданий».
При выполнении кладочных работ руководствуются СНиП III-B.4 «Техника безопасности в строительстве».
Кладка углов здания из кирпича.
Кладка углов здания — наиболее ответственная работа, и её выполняют квалифицированные каменщики.
Какие углы будут выложены, такими будут и стены дома. Поэтому все размеры разбивки углов дома необходимо тщательно выверять и перепроверять как в начальной стадии, так и в процессе выполнения кладочных работ. Кладка углов должна выполняться из отборного кирпича.
После выполнения разбивочных работ, установки порядовок и натягивания причалок приступают к каменной кладке углов. Установку порядовок и натягивание причалок смотрите в разделе сайта «тут.
Углы намечают с помощью маяков. Как устанавливать маяки для кирпичной кладки стен смотрите в разделе сайта «здесь«. После установки маяков кирпичной кладки приступают к выполнению кладки углов стен.
Как узнать прямой угол с помощью рулетки. Египетский треугольник в строительстве
Сильно нагруженные углы кладки армируют стальной сеткой, а также продольной растянутой или сжатой арматурой.
Чаще всего в кирпичной кладке применяют сетчатое армирование прямоугольными сварными или вязаными сетками. При этом диаметр проволок сеток должен быть не менее 3 мм и не более 8 мм, чтобы толщина шва кладки превышала толщину проволоки сетки.
Варианты армирования кладки смотрите в разделе сайта «Армирование кирпичной кладки».
ПРИМЕЧАНИЕ: Тычковые кирпичи кладки являются опорными рядами кладки. Поэтому для тычковых рядов следует подбирать кирпичи без поперечных трещин.
Для соблюдения правильной кладки рядов углов стен применяют деревянные или металлические порядовки, устанавливаемые на границах захваток в местах пересечения стен и на углах.
Применение в работе порядовок смотрите в разделе сайта «Установка порядовок кирпичной кладки».
Прямолинейность углов и стен в процессе кирпичной кладки обеспечивают с помощью причалки — прочного крученого шнура. Вертикальность кладки углов проверяют отвесом, горизонтальных рядов кладки — правилОм и уровнем.
Установку причалка смотрите в разделе сайта «Установка шнура-причалки в ряду кладки».
В настоящее время широко применяют однорядную (цепную) и многорядную системы перевязки кладки. Прочность кладки, выполненной с этими перевязками на растворах марки М-25 и выше практически одинакова.
Схемы кирпичной кладки фасада с однорядной цепной, многорядной и трёхрядной перевязкой швов показаны на рис.1
Перевязка углов кирпичной кладки

Кладка с многорядной перевязкой менее трудоёмка по сравнению с однорядной и её следует выполнять в летних условиях на прочных растворах, а также зимой на растворах с химическими добавками.
90°60°30° Как определить прямой угол?
Однорядная перевязка РЕКОМЕНДУЕТСЯ для кладки, выполненной методом замораживания на растворе без химических добавок.
В строительстве используют различные схемы кладки. Схемы порядовой раскладки кирпича при сплошной цепной кирпичной кладке наружных стен толщиной 250 мм, 380 мм, 510 мм и 640 мм с образованием прямого угла и четвертей оконных и дверных проёмов при цепной перевязке швов кладки показаны на рис.2-25… рис.2-64.
Эта кладка требует большого числа трёхчетвертных кирпичей и относительно высокой квалификации каменщика. Значительно проще многорядная кирпичная кладка со сплошной перевязкой всех швов через 4; 5 или 6 рядов (см. ниже).
В тех случаях, когда требуется повышенная прочность стены, наибольший эффект обеспечивает горизонтальное армирование кирпичной кладки проволочной сеткой.
Для замоноличивания кладки в вертикальные швы через каждые 2 м по высоте закладывают связи в виде трёх стальных стержней d=8 мм.
Толщина горизонтальных швов при кладке из кирпича в среднем не должна превышать 12 мм, толщина вертикальных швов должна быть 10 мм.
Швы между кирпичами снаружи могут быть полностью заполнены раствором и иметь выпуклую, вогнутую или прямоугольную внешнюю форму, а также оставаться незаполненными раствором на глубину 5-10 мм.
Ниши, борозды и отверстия, а также монтажные проёмы, предусмотренные проектом, выполняют в процессе кладки стен. Как их выполняют смотрите в следующих разделах сайта.
ВНИМАНИЕ! Ослабление кладки в местах, не предусмотренных в проекте, без согласования с проектной организацией ЗАПРЕЩАЕТСЯ.
Для успешной кладки кирпичных стен необходим специальный инструмент.
Кладка углов по однорядной цепной системе перевязки швов.
Прямые углы выкладывают по схеме, показанной на рис.3 и рис.4. Кладку углов начинают с двух четверток, уложенных в наружную версту ложками (рис.3). Промежутки между трёхчетвертками и тычковыми кирпичами заполняют четвертками.
Варианты кладки прямого угла и ограничения стен при цепной перевязке кладки толщиной в 1 кирпич и толщиной в 1,5 кирпича показаны на рис.3.

Варианты кладки прямого угла и ограничения стен при цепной перевязке кладки толщиной в 2 кирпича и толщиной в 2,5 кирпича показаны на рис.4.

Кладка углов может выполняться и по другой схеме, когда первый ряд одной из стен, составляющих прямой угол, доводят до наружной поверхности второй стены и заканчивают трёхчетвертками, первый ряд второй стены присоединяют к первому ряду первой стены.
Во втором ряду кладка идёт в обратной последовательности, т.е. второй ряд другой стены доводят до наружной поверхности первой стены и заканчивают трёхчетвертками.
В результате ложковые ряды одной стены выходят тычками на лицевую поверхность другой стены. Стена, пропускаемая до лицевой поверхности другой стены, должна заканчиваться трёхчетвертками, расположенными продольно. Пропускают наружные ложковые ряды, примыкают наружные тычковые.
При такой схеме раскладки кирпича углы выкладывают без четвёрток, но со значительно большим количеством трёхчетверток.
Кладка углов из кирпича по многорядной системе перевязки швов.
При многорядной перевязке первый ряд кирпичной кладки выкладывают так же, как и при однорядной — тычками.
Кирпичную кладку углов стен целесообразно выполнять по многорядной системе перевязки швов. Для прочности кирпичную кладку ведут с перевязкой швов, используя при этом не только целый кирпич, но и его части.
Два первых ряда угла выкладывают таким же способом, как и при однорядной системе перевязки кладки. Третий-шестой ряды наружных верст выполняют ложками, перевязывая вертикальные швы.
Схема кладки прямого угла и ограничения стен при многорядной перевязке кладки толщиной в 1,5 кирпича показана на рис.5-38.

Кладка с многорядной перевязкой менее трудоёмка по сравнению с однорядной и её следует выполнять в летних условиях на прочных растворах, а также зимой на растворах с химическими добавками.
Схема кладки прямого угла и ограничения стен при многорядной перевязке кладки толщиной в 2 кирпича показана на рис.5-51

Прямые углы при многорядной системе перевязки швов выкладывают с применением трёхчетверток и четвертинок. Кладку угла начинают с двух трёхчетверток, из которых каждую устанавливают ложком в наружную версту соответствующей сопрягаемой стены.
Схема кладки прямого угла и ограничения стен при многорядной перевязке кладки толщиной в 2,5 кирпича показана на рис.5-64 .

Промежуток, образующийся между трёхчетвертками и тычковыми кирпичами, заполняют четвертинками (см. 1-й ряд кладки).
Во втором ряду кладку версты выполняют ложкАми, а забутовку — тычками. Кладку следующих ложковых рядов ведут с перевязкой вертикальных швов.
Кирпичная кладка углов с вертикальным ограничением стен.
Прямые углы с вертикальным ограничением стен при многорядной системе перевязки швов выкладывают с применением трёхчетвёрток и четвертинок кирпича. Примеры перевязок показаны на рис.6.
При толщине стены, кратной целому кирпичу (рис.6-25 и рис.6-51) во 2-ом ряду:
- наружную и внутреннюю вёрстывыкладывают — ложковыми рядами,
- а забутовку — тычковыми рядами.
Схема кладки углов для стен толщиной в 1 кирпич при многорядной системе перевязки швов показана на рис.6-25.

- 1-ый ряд выкладывают тычковыми рядами — на фасад, а ложковыми рядами — в внутрь помещения;
- 2-ой ряд наоборот — ложковыми рядами — на фасад, а тычковыми рядами — в внутрь помещения.
Схема кладки углов для стен толщиной в 1,5 кирпича при многорядной системе перевязки швов показана на рис.6-38.

Кладку угла начинают с двух трёхчетверток. Каждую трёхчетвёртку устанавливают ложком кирпича в наружную версту соответствующей сопрягаемой угловой стены.
Также, почитайте про забора для частного дома вот здесь
Промежуток, образующийся между трёхчетвертками и тычковыми кирпичами, заполняют четвертками (см. 1-ый ряд кладки).
Во 2-ом ряду версты выполняют ложками, а забутку — тычками. Кладку следующих ложковых рядов ведут с перевязкой вертикальных швов.
Источник: camremont.ru
Как померить угол стены
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов – длинна сторон не ограничена. Основной инструмент для измерений – рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b – катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c – гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием “египетский треугольник”. Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 – ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 – все сходится!
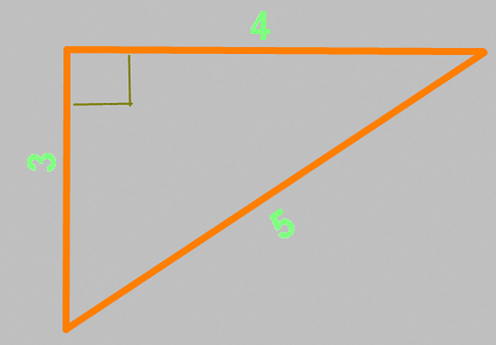
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого – проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены – это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой.
Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 – это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 – 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали – проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало – простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см.
Таким образом, у прямого угла со сторонами 2 м. – диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике – это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем – в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе “египетского треугольника”. Однако это только в теории линии просто чертятся на бумаге, “ловить” же все выбранные размеры растянутыми шнурами или линиями на полу – задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!




Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами – дело это непростое. Поэтому я предлагаю использовать упрощенный метод.
Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера – непрофессионально.
Как измерить комнату за 16 минут.
Главная → Ремонт → Ремонт комнаты → Как измерить комнату за 16 минут.
Добрый день, уважаемые читатели сайта Алгоритмсинтез , сегодня продолжаем тему ремонта. Речь пойдет о том, как измерить комнату за 16 минут, для чего нужны обмеры, какую информацию мы получаем и как это сделать. Берем во внимание алгоритм плана ремонта комнаты, где определили вид — простой косметический ремонт, приступаем к обмерному плану.
1. Как измерить комнату, для чего это необходимо.
- проверка геометрии. Зачастую оказывается, что углы в помещении не 90 градусов, стены не вертикальны, полы не горизонтальны. Если заказывается встроенная мебель, то есть вероятность что она не встанет на запланированное место или будет расстояние между стеной и мебелью указывающее на неровность.
- для составления сметы.
- посчитать и соответственно купить необходимое количество материалов
- сколько платить денег за работу, проверка объёмов
- предварительный подсчет объемов работ
2. Какую информацию мы получим, если сделать обмеры помещения.
- площадь пола (м2), устройство, замена напольного покрытия.
- количество плинтуса (мп), количество внутренних и внешних углов пластикового плинтуса.
- площадь потолка (м2) – следующие работы: штукатурка, шпатлевка, окраска, натяжной потолок для предварительного расчета стоимости.
- количество потолочного багета, мп.
- площадь стен (м2) – виды работ: штукатурка, шпатлевка, окраска, оклейка обоями
- габариты дверей и количество наличника – позволит сделать предварительный просчет двери, если собираетесь заказывать или просто подобрать в магазине.
- размеры окна или дверного блока, ширина, высота и толщина существующего подоконника. Этих данных вполне достаточно, чтобы узнать предварительную стоимость новых изделий.
- количество (мп) и диаметр труб отопления – сколько покупать краски, сколько платить за выполненную работу.
- размеры радиатора.
3. Что понадобиться, чтобы выполнить обмеры.
Для выполнения обмеров помещения понадобятся следующие измерительные инструменты:
- водяной уровень, лазерный уровень, двухметровое правило с уровнем, отвес, угломер. Для определения горизонтальности, вертикальности и проверка.
- измерительный инструмент: рулетка шириной ленты 20-25 мм и длиной 7,5 — 10 метров или электронный измерительный прибор.
- 3 листа чистой бумаги формата А4 или просто обычные листы в клеточку.
- карандаш, ручка.
- помощник, вдвоём удобнее и веселее.
Совсем не обязательно иметь весь перечень измерительных инструментов, в данный момент рулетки достаточно. Если планируете капитальный ремонт полов, тогда обязательно понадобиться уровень обычный водяной или лазерный.
4. Как измерить комнату за 15 минут с точностью 95%.
Это способ подходит в следующих случаях.
- Если небольшой процент расхождения для Вас непринципиален.
- Для приблизительной проверки объёмов работ у исполнителей.
- Для подсчета, покупки, проверки расхода материалов.
- Для простого косметического ремонта.
- Если у Вас совершенно нет времени и доверяете полностью бригаде выполняющей ремонтные работы, но контроль потраченных денег обязательно нужен, то потратьте всего 16 минут на замеры помещения и всё будет нормально.
Итак, пошаговый алгоритм, как измерить комнату за 16 минут с точностью 95% следующий.
1 шаг. Как измерить комнату, творческий процесс.
На первом листе рисуем план помещения. Для этого проходим вдоль плинтуса и чертим от руки такую же конфигурацию, включая выступы, уступы, приблизительно соблюдая пропорции. Как правило, необходимо обратить внимание на сторону с окном или балконным блоком. Дальше каждую сторону на плане нумеруем цифрами 1,2,3,4, по часовой стрелке от входа в помещение.
На 2-ом листе отображаем стены № 1,3,4, где всё просто и выглядят в виде прямоугольника. Их можно уместить несколько, потому что там будет на каждой по два размера.
На третьем листе чертим стену №2 сложной конфигурации, в моём случае с оконным блоком, где будет множество размеров.
Таки образом времени было затрачено всего 5 минут. Красота здесь не требуется, но всё должно быть понятно и хорошо видно.
2-ой шаг. Как измерить комнату, обмеры.
Замеры старайтесь делать на уровне 1-1,5 от пола, рулетку необходимо держать горизонтально полу или перпендикулярно полу, в зависимости от того, что измеряем, длина, высота.
- Замеряем стену № 1 с дверным проёмом. Нам нужны следующие размеры длина, высота, расстояние от угла стены до дверной коробки (привязка). Размеры дверной коробки. Ширина наличника, длина планок, если будет устанавливаться однотипный.
- Обмеры стены № 2
- ширина
- высота
- размеры дверного блока, отдельно окна и отдельно двери.
- ширина откосов
- высота балки над балконным блоком
- длина, ширина, толщина подоконника
- все выступы и уступы по плинтусу и их длина.
- диаметр трубы отопления и длина в мп.
- габариты радиатора отопления
- расстояние между радиатором и подоконником и между радиатором и полом.
- высота порога.

3. Замеряем стены № 3 и № 4 . Принцип остаётся прежним. Если сложная конфигурация, тогда понадобиться чертить на отдельном листе.
Ещё 11 минут и обмерный план готов, он подойдет для простого косметического ремонта. Для капитального ремонта требуется более тщательное обследование.
Теперь Вы знаете, как измерить комнату за 16 минут до начала ремонта и сделать все необходимые обмеры, которые принесут в дальнейшем только пользу.
P.S После проделанной работы предлагаю посмотреть видео, о том как красиво и быстро рисуются картинки на стекле.
Его величество – Замер!

Здравствуйте уважаемые друзья!
В этом посте, я хотел бы поговорить о такой важной вещи, как замер помещения для дальнейших расчетов планируемой в него мебели.
О его важности, я думаю, говорить не нужно. Если, например, вы замеряя нишу под шкаф купе (или под кухню) ошибетесь в размерах (да еще и в большую сторону) – можно смело сказать, что вы «попали».
И в случае, если вы делаете мебель для себя, то вы «попали» на деньги, а если вы делаете мебель «на заказ», то вы «попали» на деньги и на
Скорее всего, вы смогли бы отыскать три варианта:
Прямые параллельны друг другу;
Прямые совпадают, накладываются друг на друга;
И были бы абсолютно правы! Интересно, что в пункте № 3 скрывается один интересный случай, который мы рассмотрим подробнее сегодня, а именно: прямые могут быть перпендикулярны друг другу .
Что это означает? Рассмотрим определение перпендикулярных прямых.
Основные определения
Перпендикулярные прямые — это прямые, которые пересекаются друг с другом под углом 90 градусов. Обозначение перпендикулярных прямых: а ┴ b.
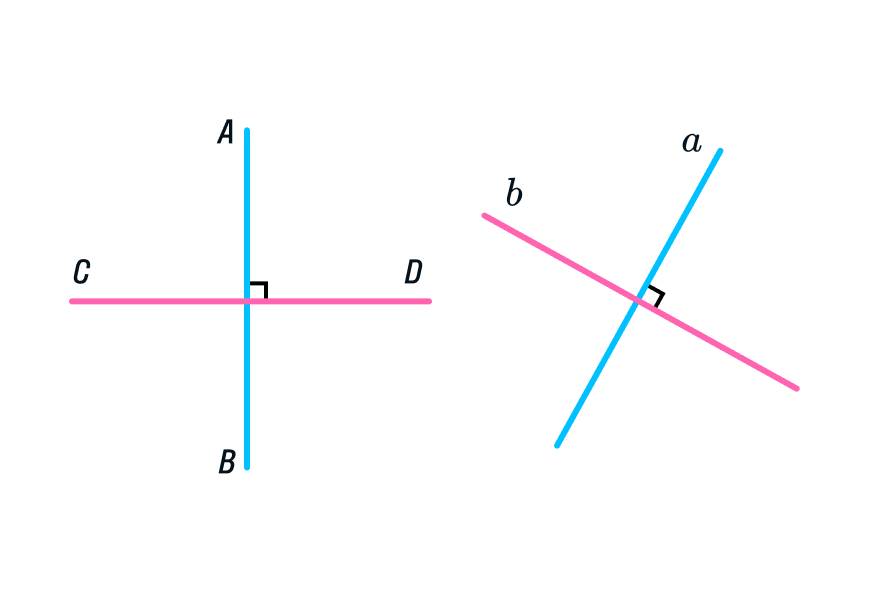
Угол, равный 90 градусам, в математике называют прямым и помечают на чертеже квадратиком.
Еще один интересный факт из мира геометрии: если при пересечении двух прямых один из образовавшихся углов равен 90°, то и все остальные углы — прямые, а их сумма будет равна 360°.
Перпендикулярные отрезки — это отрезки, лежащие на перпендикулярных прямых.
Чтобы называться перпендикулярными, отрезкам не обязательно пересекаться самим. Достаточно, чтобы угол между прямыми, на которых они лежат, был равен 90°.
В качестве задачки со звездочкой давайте вспомним, в каких фигурах могут встречаться перпендикулярные отрезки (стороны)? Наверняка вы сразу назовете квадрат и прямоугольник, но также подходит прямоугольный треугольник и даже прямоугольная трапеция — с ней вы познакомитесь на уроках геометрии в 8-м классе.
Также перпендикулярно к стороне могут располагаться различные элементы внутри фигуры. Попробуйте расположить перпендикулярно друг другу диаметр и радиус окружности, две хорды, биссектрису угла треугольника (кстати, последнее задание получится выполнить только в случае, если проводить биссектрису угла к основанию равнобедренного треугольника).
Как мы видим, прямые очень часто пересекаются под углом 90 градусов. Можно сказать, это своего рода обычное, будничное поведение прямых. Прямые углы окружают нас повсюду: в комнате, на оживленных улицах города, в бассейне и даже в любимой книге.

Способы построения перпендикулярных прямых
Но как можно построить перпендикулярные прямые? Что для этого может понадобиться? Давайте разберем все доступные нам способы.
Самый легкий — воспользоваться транспортиром. Построим прямую а и точку А, не лежащую на этой прямой. Совместим значение 90 градусов с точкой таким образом, чтобы нижняя часть транспортира в виде линейки полностью совпала с прямой, и сделаем засечку в отверстии транспортира. Соединим точку А с поставленной засечкой до пересечения с прямой.
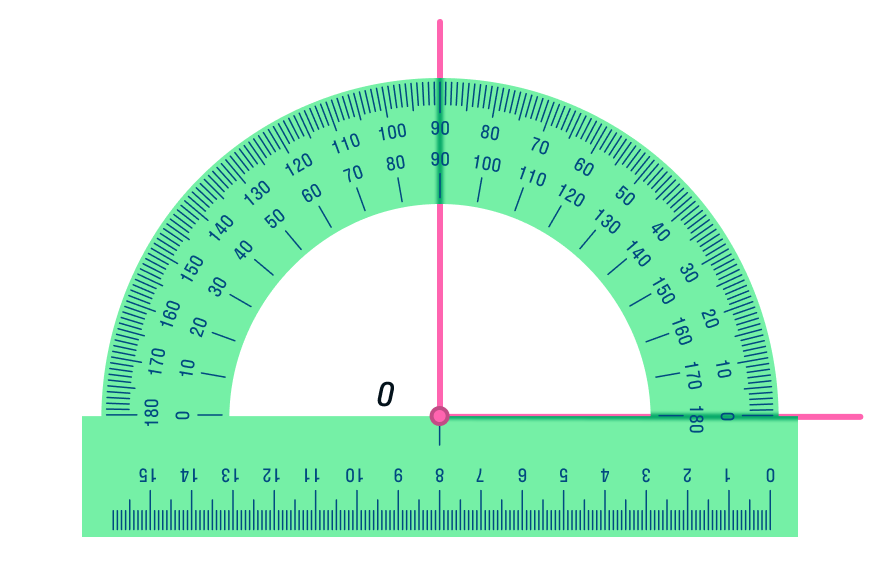
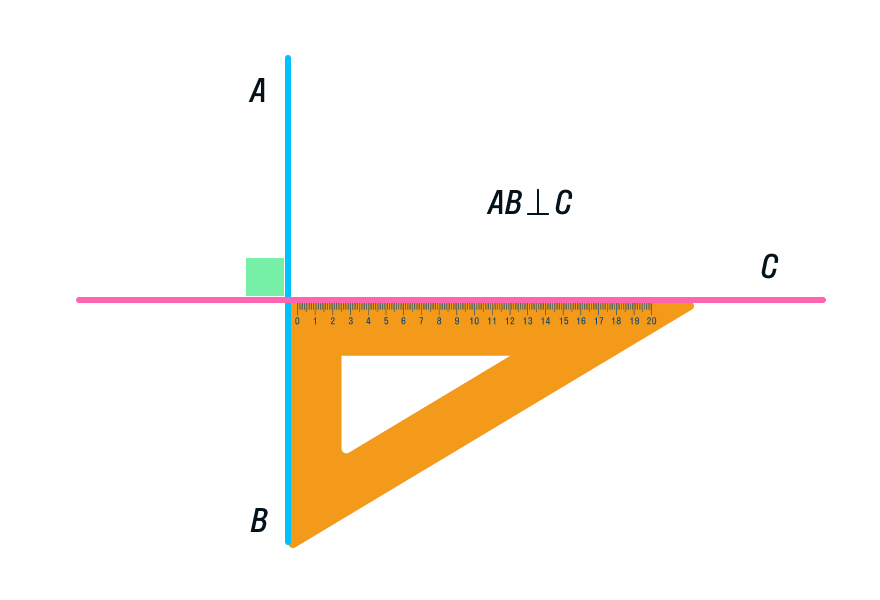
Но что делать, если транспортир благополучно забыт дома и у нас есть только линейка и угольник? Внимательно рассмотрите рисунок и попрактикуйтесь в построении дома.
Теорема о перпендикулярных прямых и ее доказательство
«Кто это вообще придумал?», — можете возразить вы. «Почему мы должны этому верить? Вдруг все иначе, а нас обманывают». Если это так, то ваши опасения — показатель пытливости ума!
Что такое теорема? Это утверждение, нуждающееся в доказательстве. Это означает, что его не принимает на веру никто: ни вы, ни учитель, ни самый великий ученый. Есть много способов доказательства теорем, один из которых — метод от противного. Используя его, мы будто соглашаемся с противоположным заявлением и рассуждаем, что из этого последует.
Например, попробуем доказать утверждение «осенью грачи улетают на юг» методом от противного. Предположим, что грачи остаются зимовать в наших городах. Тогда мы должны видеть их осенью и зимой повсеместно, а в небе не должно быть видно признаков масштабного перелета. Так ли это на самом деле? Конечно же, нет.
Теперь с помощью этого метода попробуем доказать теорему о перпендикулярных прямых.
Предположим, что теорема ложна, а значит, через точку, лежащую на прямой, можно провести несколько перпендикулярных прямых.
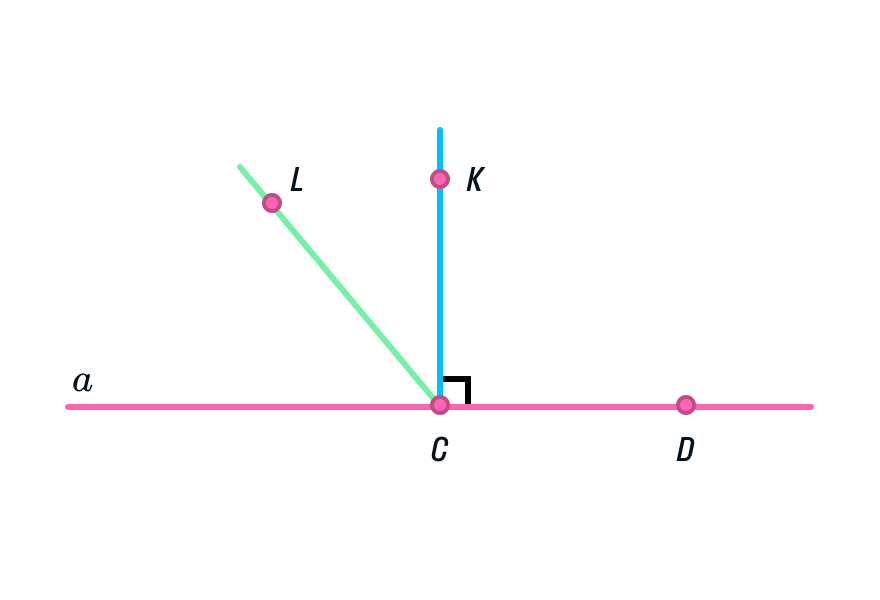
Возьмем линейку и проведем прямую а, отметив на ней точки С и D.
Далее построим перпендикулярную прямую из точки С. Угол КСD равен 90°.
Отрезок КС находится на прямой, перпендикулярной а.
Предположим, что есть еще одна прямая, перпендикулярная а. Проведем ее через точку С и отметим на ней точку L.
Тогда угол LCD равен 90° и угол КСD равен 90°.
Пункт номер 5 невозможен: от отрезка CD можно отложить только один прямой угол в данной плоскости.
А значит, через точку С можно провести только одну прямую, перпендикулярную прямой а.
Что и требовалось доказать: вы — молодцы!
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Свойства перпендикулярных прямых
Перпендикулярные прямые обладают свойствами, которые можно использовать при решении геометрических задач. Давайте изучим их и приведем доказательство каждого.
Две прямые, перпендикулярные к третьей, не пересекаются
Конечно же, это свойство хорошо просматривается при построении. Но как мы уже выяснили, математики — народ сомневающийся, поэтому попробуем обосновать, почему это так.
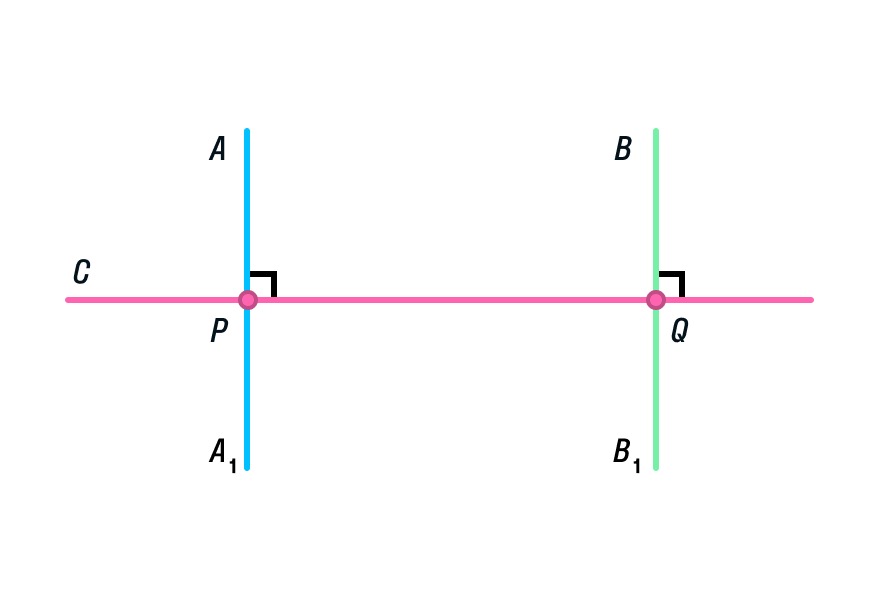
Предположим, что прямые АА1 и ВВ1 все же пересекутся в точке К. Что бы это значило? Что мы совершили невероятное и опровергли теорему о перпендикулярных прямых! Ведь тогда получается, что через точку К проходит несколько перпендикулярных прямых, которые в свою очередь пересекают прямую а под углом 90 градусов! Как было сказано выше, это невозможно, а значит и прямые АА1 и ВВ1 не пересекаются.
Перпендикуляр, проведенный из точки к прямой, называется расстоянием от прямой до этой точки
Интересно, что такое расстояние является кратчайшим.
Представьте, что вам необходимо проложить путь от вас до огромного торгового центра, состоящего из множества магазинчиков. Вам не важно, в какой из них заглянуть, вы просто хотите потратить на дорогу как можно меньше времени. Какой путь вы выберете?
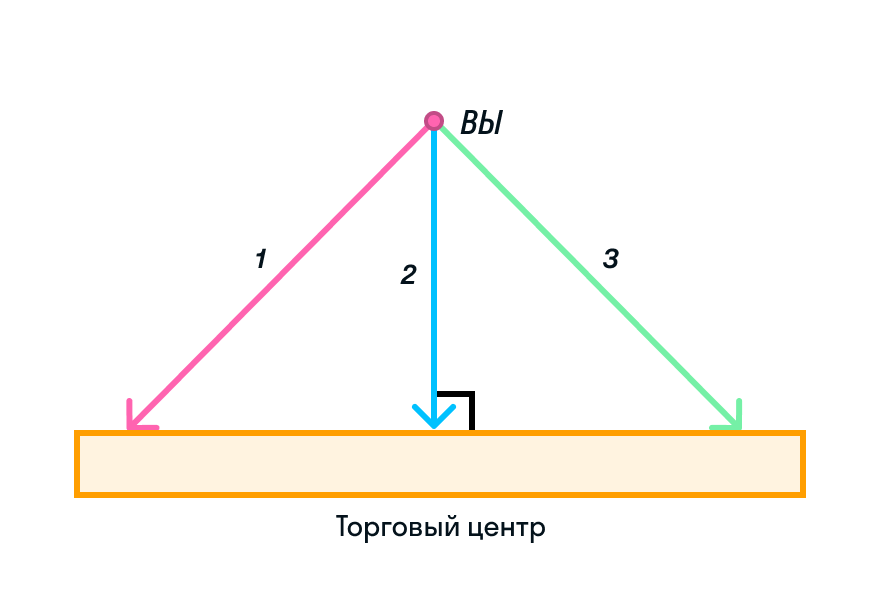
Конечно же, путь номер 2! Но есть ли этому научное объяснение?
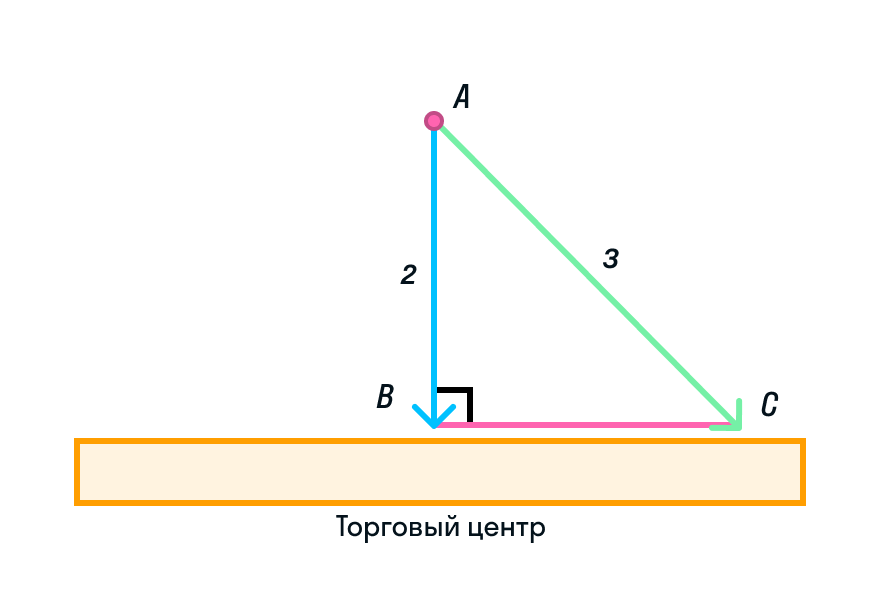
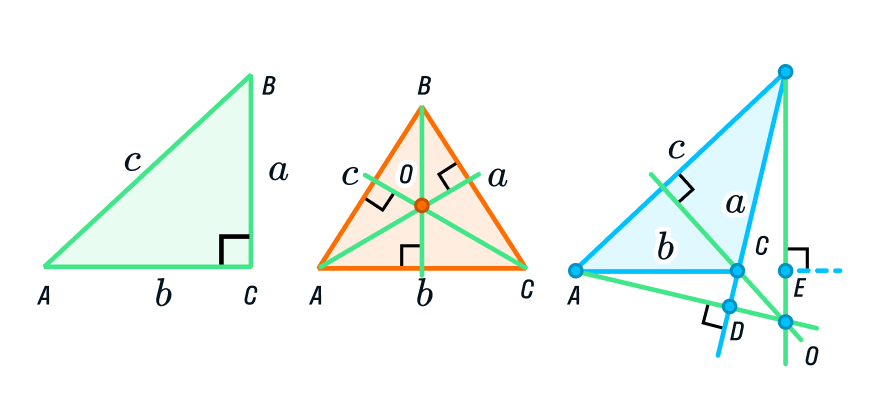
Треугольник АВС прямоугольный, АВ и ВС— катеты, АС — гипотенуза. Согласно соответствию углов и сторон, в треугольнике наибольшая сторона лежит напротив наибольшего угла. Таким углом является прямой угол В, а наибольшая сторона — гипотенуза АС. Под каким бы углом мы ни расположили гипотенузу, она всегда будет больше остальных сторон.
В задачах по геометрии часто просят найти расстояние между различными элементами: между двумя точками, между точкой и прямой, между двумя прямыми. Теперь вы знаете, что под расстоянием подразумевают перпендикуляр ! Благодаря этому знанию вы избежите множества ошибок, ведь между двумя элементами можно провести бесконечное множество прямых (и кривых), но только один вариант будет верным.
Кстати, перпендикуляр, проведенный из вершины угла фигуры на прямую, содержащую противоположную сторону, известен под именем высота. С высотами связано множество теорем и свойств, которые вы будете изучать немного позже. В качестве интриги оставим вам пример того, где находится точка пересечения высот в треугольниках разного типа. Заметили что-то необычное?
Применение знания о перпендикулярных прямых
Напоследок ответим на вопрос, который мог возникнуть у некоторых из вас: «А как в древности люди решали вопрос с построением перпендикулярных прямых, прямых углов в частности? Были ли у них приспособления для этого?»
Построение прямых углов было важным умением даже в древности, так как от этого зависела крепость и устойчивость возведенных стен зданий, мостов, механизмов для строительства. Один лишний градус — и целый город мог оказаться в опасности из-за обрушившегося дворца или башни.
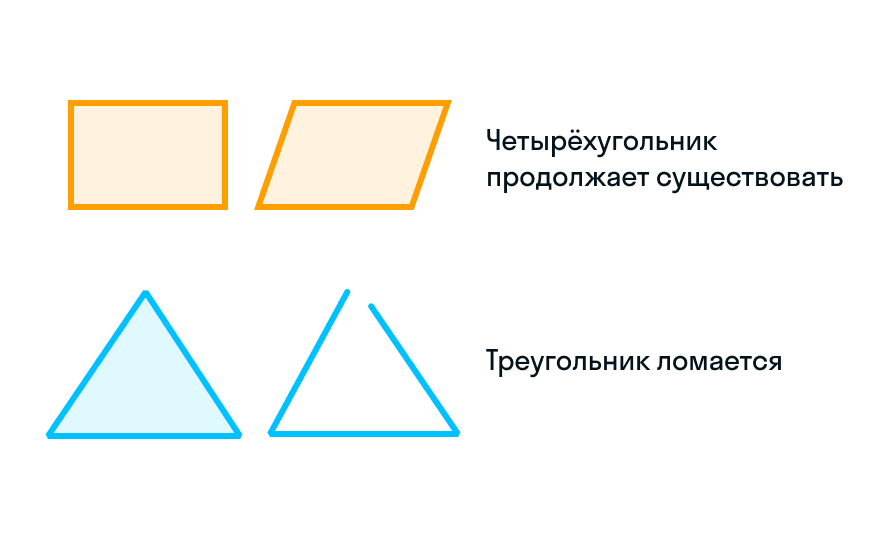
Древние зодчие поняли, что возлагать все надежды на четырехугольники не стоит, потому что квадраты и прямоугольники легко превращаются в параллелограммы, меняя величину углов и оставляя неизменными длины сторон. Стоит только немного потянуть за «ушки» квадрата, как он начинает беспощадно ломать прямые углы, а ведь в условиях строительства многое может пойти не так и искривить конструкцию: ветер, изменение температуры, неточность мастера.
Хорошо, что есть более стабильная фигура — треугольник. Все дело в соотношении его сторон и углов, а еще в невозможности создать несколько треугольников из сторон заданной длины. Если у вас есть отрезки длиной 6, 8 и 10 сантиметров, из них можно составить только один треугольник. В случае, если одна сторона растянется под действием нагрузки или сожмется из-за понижения температуры — треугольник просто перестанет существовать.
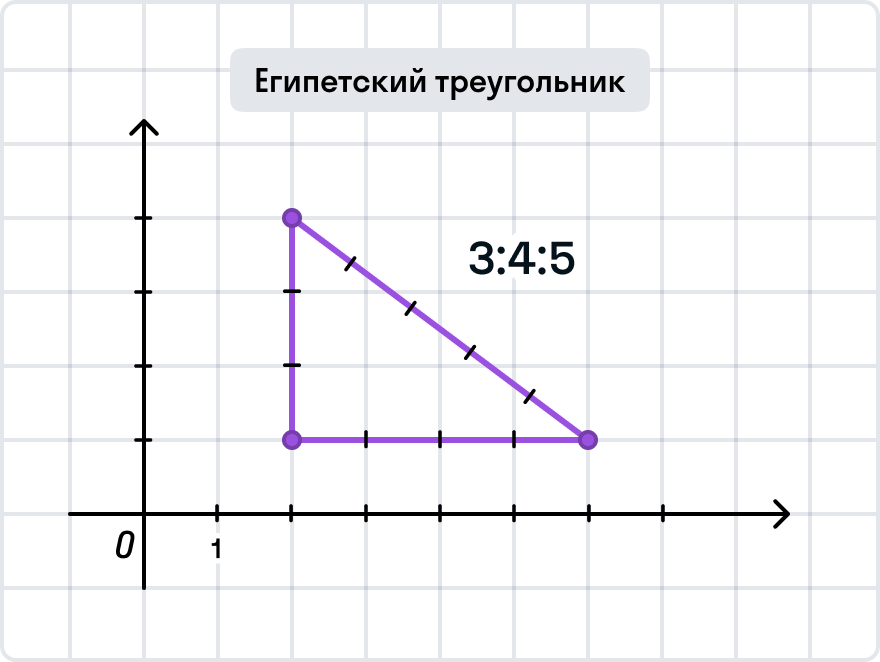
С этой точки зрения прямоугольные треугольники — лучшие друзья архитекторов, которые хотят строить ровные и красивые здания. Зодчие Древнего Египта использовали шнур или веревку, на которых через равные расстояния были завязаны 12 узлов. Строители натягивали такой шнур, создавая прямоугольный треугольник со сторонами 3, 4 и 5 единиц. Такой метод получения угла, равного 90 градусам, был сверхточным, а по сторонам-катетам-шнурам можно было выкладывать кирпичи или камни.
Удивлены? Еще больше поразительных фактов и, самое главное, помощь в понимании алгебры и геометрии вы получите на курсах профильной математики в онлайн-школе Skysmart. Секреты древних архитекторов, бытовые задачки и подготовка к экзаменам — все на удобной платформе с опытными учителями. Ждем вас!
Источник: skysmart.ru