Наиболее опасные предельные состояния связаны с потерей устойчивости элементов и системы в целом. В расчётном комплексе SCAD Office имеется режим проверки устойчивости, который позволяет вычислить:
- Коэффициент запаса устойчивости (показывает во сколько раз нужно увеличить заданную нагрузку, чтобы система потеряла устойчивость);
- Форму потери устойчивости;
- Расчётные длины стержневых элементов.
Требования норм
Требования к проверке общей устойчивости стальных конструкций содержится в пункте 4.3.2 СП 16.13330.2011
Отношение критической нагрузки к расчетной для стержневых конструкций, рассчитываемых как идеализированные пространственные системы с использованием сертифицированных вычислительных комплексов (согласно 4.2.5, 4.2.6), должно быть не меньше коэффициента надежности по устойчивости системы ys = 1,3.
А к проверке железобетонных конструкций в приложении В СП 63.13330.2012 пункт В.8
При расчете на устойчивость конструктивной системы следует производить проверку устойчивости формы конструктивной системы, а также устойчивости положения конструктивной системы на опрокидывание и на сдвиг.
и в пункте 6.2.8 СП 52-103-2007:
Расчет стального каркаса на устойчивость в ЛИРА-САПР
…При расчете устойчивости формы конструктивной системы рекомендуется принимать пониженные жесткости элементов конструктивной системы (учитывая нелинейную работу материала), поскольку устойчивость конструктивной системы связана с деформативностью системы и отдельных элементов. При этом значение понижающих коэффициентов в первом приближении рекомендуется принимать, как указано в пп. 6.2.6, 6.2.7 с учетом того, что устойчивость конструктивной системы зависит от сопротивления в основном внецентренно сжатых вертикальных элементов при длительном действии нагрузки и в стадии, приближающейся к предельной. Запас по устойчивости должен быть не менее чем двукратным.
Задание исходных данных
Исходные данные для расчёта общей устойчивости системы находятся в специальных исходных данных:

В появившемся окне задаётся вид расчёта, верхняя граница поиска (граница выше которой поиск коэффициента запаса устойчивости не будет производиться, и от каких нагрузок или комбинаций будет производиться расчёт:
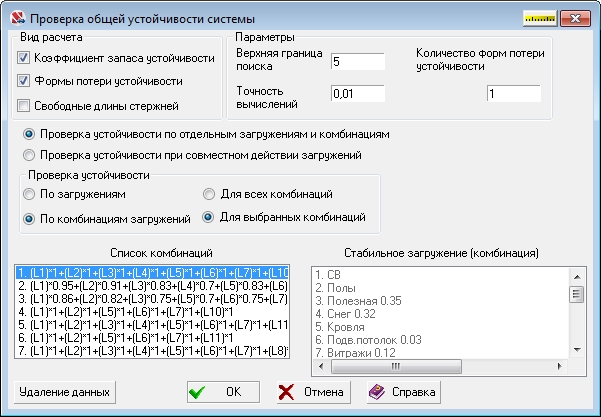
Более подробно об теоретическом обосновании можно прочитать в справке SCAD Office, особенно стоит обратить внимание на различия в результатах расчёта устойчивости стержней между строительными нормами и SCAD.
Анализ результатов
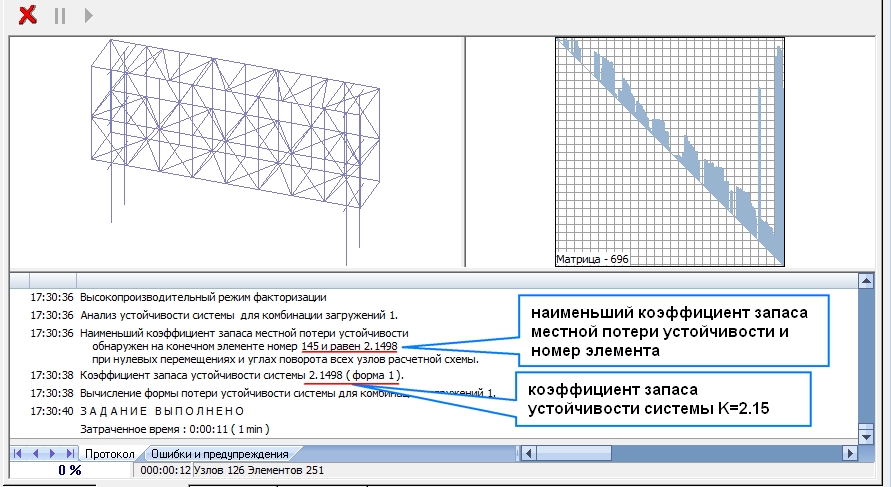
Коэффициент запаса устойчивости системы будет указан в протоколе, также там будет указан элемент с наименьшим коэффициентом запаса при неподвижных узлах системы.
«ПК ЛИРА 10 в задачах». Тема 14 «Расчёт строительных сооружений на устойчивость»
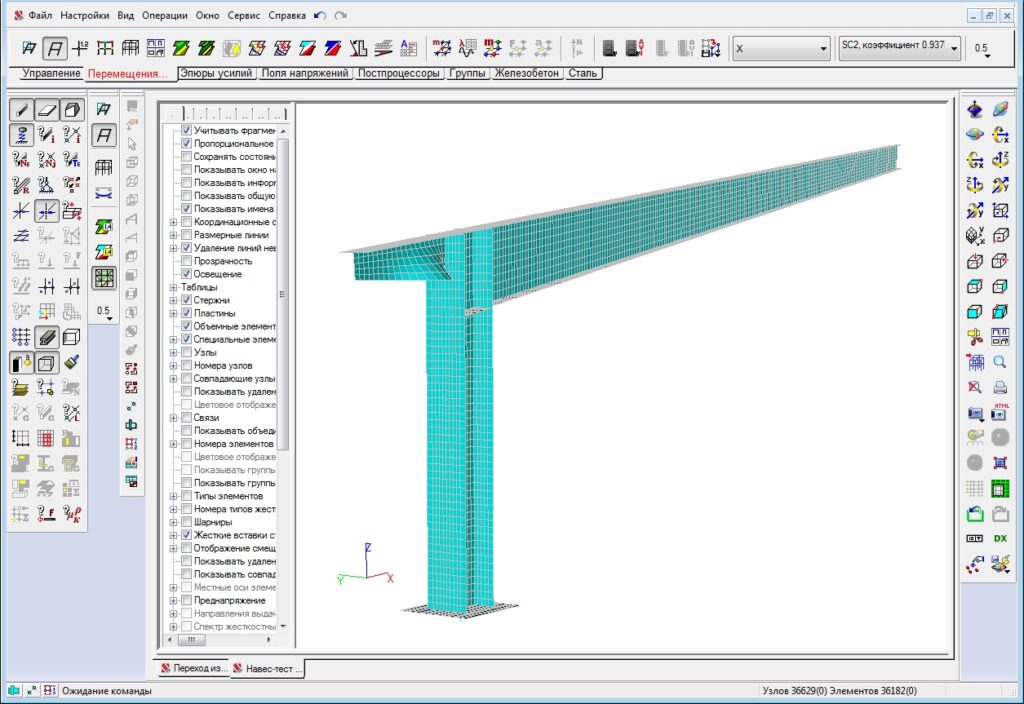
Во вкладке перемещения — можно посмотреть формы потери устойчивости.
Во вкладке «Постпроцессоры»/»энергетический процессор» — элементы с отрицательной энергией будут ответственны за потерю устойчивости. Чем больше отрицательное значение у элемента, тем больше он отвечает за потерю устойчивости..
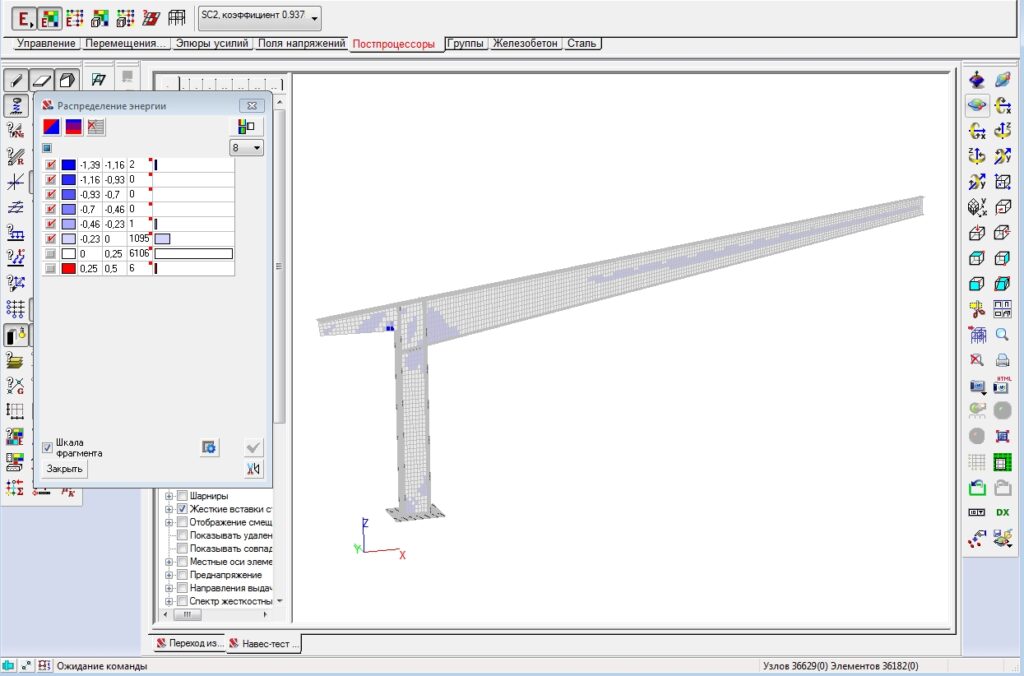
Дополнительная информация
А.В. Перельмутер В.И. Сливкер Расчетные модели сооружений и возможность их анализа. 2011. Раздел 9. Задачи устойчивости и смежные вопросы.
Источник: konstruktor.spb.ru
Расчет элементов на устойчивость
Потеря устойчивости заключается в выпучивании сжатых гибких элементов под действием нагрузок. Чаще всего при сжатии потеря устойчивости происходит раньше, чем исчерпание прочности, и наступает внезапно. Большинство аварий и катастроф металлических конструкций происходили из-за потери устойчивости. Различают потерю общей и местной устойчивости.
Потерей общей устойчивости называется изменение первоначальной формы деформирования всей конструкции под действием сжимающей нагрузки.

Структура расчетных формул для проверки общей устойчивости металлических конструкций аналогична структуре формул для проверки прочности, но расчётное сопротивление умножается на понижающий коэффициент устойчивости , учитывающий, что потеря
устойчивости происходит при меньших напряжениях, чем исчерпание прочности:

Потерей местной устойчивости называется изменение первоначальной формы отдельного сжатого элемента конструкции при сохранении первоначальной формы всей конструкции.
Условия проверки местной устойчивости элементов составляются таким образом, чтобы потеря устойчивости сжатых элементов конструкции не наступала раньше, чем потеря устойчивости всей конструкции.
Расчет на общую устойчивость центрально-сжатых элементов. При осевом (центральном) сжатии продольная сила приложена в центре тяжести сечения элемента. Центральное сжатие возникает, например, в сжатых элементах ферм при узловом приложении нагрузки, в ветвях сквозных колонн, в сплошных колоннах при отсутствии изгибающих моментов.
Критическая сила Ncr при которой происходит потеря устойчивости центрально-сжатого стержня, была установлена Леонардом Эйлером в 1744 году:

где EJ — изгибная жёсткость, /еу — расчетная длина стержня.
Напряжение, которое возникает в стержне от критической силы, называется критическим напряжением

где i — радиус инерции сечения, характеризующий соотношение изгибной и осевой жёсткости стержня EJ/EA


X — гибкость стержня, равная отношению расчетной длины стержня /еу к радиусу инерции его сечения i
Расчётная (эффективная) длина стержня позволяет применять обобщенные расчетные зависимости при различных условиях закрепления стержня и является эквивалентной из условия устойчивости длиной шарнирно опёртого стержня той же жесткости. Геометрически расчётная длина определяется как расстояние между точками перегиба изогнутой оси стержня (полуволна синусоиды). Численно связь расчетной и геометрической длиной стержня выражается с помощью коэффициента расчетной длины р:

Гибкость стержня X обобщенно учитывает жесткостные характеристики стержня и условия его закрепления. Потеря устойчивости происходит относительно оси с наименьшей гибкостью (при этом стержень выпучивается в направлении, перпендикулярном этой оси).
Центрально-сжатый стержень устойчив, если действующее напряжение не превышает критического:

Для сохранения единой записи формул для расчёта на прочность и устойчивость обозначают

и условие устойчивости (3.21) приобретает вид

где ф — коэффициент устойчивости при центральном сжатии (ранее его называли коэффициентом продольного изгиба).
Формула Эйлера справедлива только при постоянном модуле упругости Е, то есть при напряжениях, не превышающих предел пропорциональности ( и момента Мх могут быть определены по формуле


где — эксцентриситет;

— радиус ядра сечения;

— относительный эксцентриситет


Потеря устойчивости внецентренно сжатых стержней обычно происходит в упругопластической стадии, а развитие пластических деформаций зависит от формы сечения. Поэтому при определении критических напряжений для сечений, отличающихся от прямоугольного, вместо относительного эксцентриситета тх используют приведенный относительный эксцентриситет


где — коэффициент, учитывающий развитие пластических деформаций в стержне при потере устойчивости.

При расчёт следует выполнять как для изгибаемых элементов.
По аналогии с коэффициентом устойчивости ср при центральном сжатии записывается коэффициент устойчивости сре при внецентрен- ном сжатии, равный отношению критических напряжений внецентрен- но сжатого стержня к расчётному сопротивлению стали Ry, и условие проверки устойчивости внецентренно сжатого стержня в плоскости действия момента приобретает почти такой же вид, как при центральном сжатии:

Аналогично выглядит условие проверки устойчивости внецентренно сжатого стержня из плоскости действия момента:


где — коэффициент устойчивости при центральном сжатии, найденный по гибкости Ху
с — коэффициент, учитывающий влияние изгибающего момента Мх на устойчивость аналогичного центрально-сжатого стержня, определяемый в зависимости от тх и формы сечения.
Местная устойчивость полок и стенок двутавра. Любую металлическую конструкцию можно рассматривать как набор тонких пластинок — плоских элементов, толщина которых во много раз меньше длины и ширины. Например, двутавр состоит из двух типов пластинок — полок и стенок (рис. 3.4).
Каждый их свесов полки является длинной пластинкой с одним свободным краем; при сжатии полка образует конусообразную складку. Стенка при отсутствии ребер жесткости представляет собой пластинку, края которой защемлены в полках; при сжатии стенка выпучивается по волнообразной поверхности.
Потеря местной устойчивости полки чрезвычайно опасна, так как оставшаяся часть поперечного сечения становится несимметричной, после чего стержень очень быстро закручивается и теряет общую устойчивость.

Рис. 3.4. Форма потери местной устойчивости полок и стенок двутавра:
а) изгибаемого элемента; б) центрально-сжатого элемента
Потеря местной устойчивости стенки в большинстве случаев не представляет особой опасности, если стенка деформируется в упругой стадии. Выпучивание стенки приводит к перераспределению внутренних усилий и конструкция продолжает воспринимать эксплуатационные нагрузки, значительно превышающие критические (по устойчивости стенки). Однако если выпучивание стенки будет появляться при действии часто меняющейся временной нагрузки, а затем исчезать, то это ухудшит работу конструкции. Поэтому нормы допускают проектирование балок и колонн с гибкой (неустойчивой) стенкой лишь при соблюдении определенных условий.
Устойчивость стенки и полки следует считать обеспеченной, если их условная гибкость не превышает соответствующих предельных значений :

Условная гибкость стенки определяется по формуле где tw — толщина стенки;
hej — расчётная высота стенки, в качестве которой следует принимать: полную высоту стенки
hw — в сварных элементах; расстояние между началами внутренних закруглений — в прокатных профилях.

Условная гибкость полки определяется по формуле где tj — толщина полки;
bej — расчётная ширина свеса полки, в качестве которой следует принимать: от грани стенки до края поясного листа (полки) — в сварных элементах; от начала внутреннего закругления до края полки — в прокатных профилях.
Как видно из (3.34), обеспечить местную устойчивости полки можно уменьшением свеса bej и увеличением толщины tj. Аналогично из (3.35) видно, что местная устойчивость стенки повышается при увеличении её толщины tw и уменьшении высоты hef, однако экономически эффективны тонкие стенки, а высота задается из соображений жесткости и не может быть уменьшена. Поэтому для повышения местной устойчивости стенки применяют иной способ — устанавливают поперечные, а иногда и продольные ребра жесткости.

Предельные значения гибкости стенки и полки регламентируются СП 16.13330.2011 в зависимости от различных факторов, прежде всего, от типа сечения, характера напряжённого состояния и гибкости элемента. Чем больше гибкость всего элемента (конструкции), тем меньше критические напряжения, при которых происходит потеря его устойчивости, а значит, меньшие напряжения будут действовать в полках и стенке. Это позволяет устраивать их более гибкими без опасности потери ими устойчивости раньше, чем у всего стержня.
Устойчивость стенки существенно зависит от характера распределения напряжений в ней. В наихудших условиях находится стенка центрально-сжатого стержня, где максимальные сжимающие напряжения действуют по всей ширине стенки. Во внецентренно сжатом стержне двутаврового сечения максимальные сжимающие напряжения действуют лишь на одном крае стенки, следовательно, предельная гибкость будет больше. В запас такой стержень можно проверить и как центрально-сжатый. В наилучших условиях находится стенка изгибаемого двутавра, которая на половине своей высоты работает на растяжение (растянутая часть стенки поддерживает сжатую); в этом случае предельная гибкость стенки максимальная.
Источник: bstudy.net