Решение задач в области строительства

Известны две типические группы людей с разным годовым доходом (тыс. руб. в месяц):

• Группа А: 2; 2; 2; 3.
• Группа Б: 5; 6; 7.

В какую из этих групп следует отнести лицо с годовым доходом: 4 тыс. руб./мес.

Рассмотрим два варианта: в соответствии с первым вариантом лицо с годовым доходом отнесем в группу «А», а в соответствии со вторым вариантом это лицо отнесем в группу «Б». Для каждого из этих вариантов рассчитаем межгрупповую дисперсию. Чем больше величина межгрупповой дисперсии, тем в большей степени отличаются указанные группы. В связи с этим лицо будем относить к конкретной группе на основе максимума межгрупповой дисперсии.

Таким образом, если лицо с доходом 4 тыс. руб./мес. попадет в группу «А», то различия между группами «А» и «Б» будут существеннее, чем если бы это лицо попало в группу «Б». Следовательно, лицо с доходом 4 тыс. руб./мес. следует отнести в группу «А».

Подробное решение задачи представлено в ролике

Решение геотехнических задач в транспортном строительстве. Введение и Нормативная база

Обновить

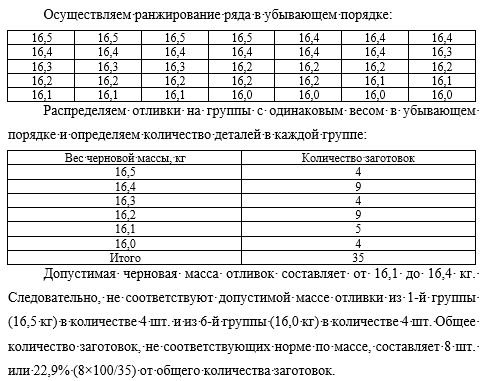
В литейном цехе черновой вес отливок детали №3 в килограммах равен:

Допустимая черновая масса отливок составляет от 16,1 до 16,4 кг.
Распределите отливки на группы с одинаковым весом в убывающем порядке. Определите количество деталей в каждой группе. Установите, сколько отливок и по каким группам пойдет в брак.

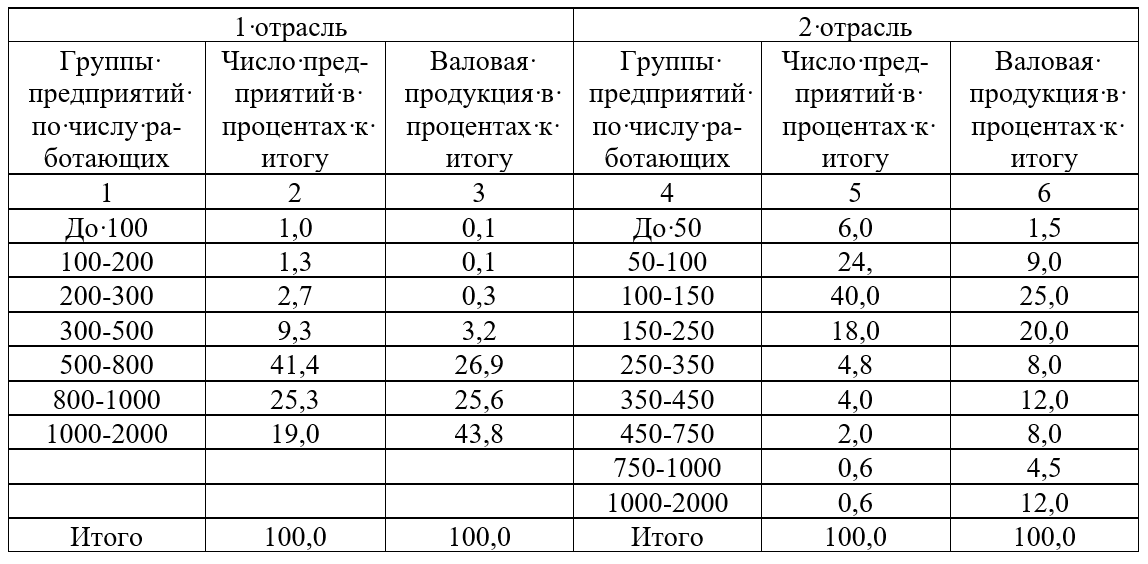
Имеются следующие данные о распределении предприятий в двух отраслях промышленности по числу работающих:

С целью сравнения показателей произведите перегруппировку предприятий 2 отрасли по числу работающих, взяв за основу группировку предприятий 1 отрасли.
Перейти к демонстрационной версии решения задачи

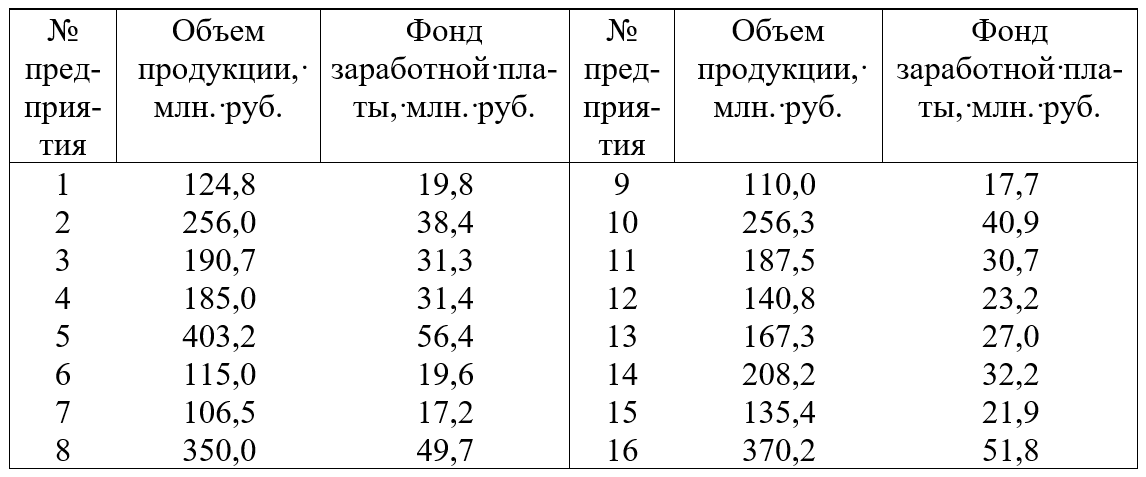
По промышленным предприятиям города имеются следующие данные за отчетный год:

Сгруппируйте предприятия по объему выработанной продукции, выделив три группы (интервалы группировки разработать самостоятельно). По каждой группе определить число предприятий, объем продукции, фонд заработной платы, размер заработной платы (тыс. руб.) на 1 млн. руб. объема продукции. Решение оформить в виде статистической таблицы. Сформулировать вывод.
Перейти к демонстрационной версии решения задачи

Продажа телевизоров в России характеризуется следующими данными (тыс. шт.): 2002 г. – 5527; 2003 г. – 5563; 2004 г. – 5628; в том числе было продано телевизоров цветного изображения (тыс. шт.): 2002 г. – 3427; 2003 г. – 3616; 2004 г. – 3915.
Приведенные данные представить в виде статистической таблицы. Сформулировать выводы, охарактеризовав происшедшие изменения в объеме и составе продаж телевизоров.
Перейти к демонстрационной версии решения задачи

Имеются данные по зарплате за месяц рабочих бригады:

Для выявления зависимости зарплаты рабочих от % выполнения норм выработки произвести аналитическую группировку рабочих бригады по % выполнения норм выработки, выделив 3 группы:
1. рабочие, выполнившие норму до 105%;
2. рабочие, выполнившие норму от 105% до 110%;
3. рабочие, выполнившие норму свыше 110%.
На основе выполненной группировки построить групповую таблицу, сформулировать вывод.
Перейти к демонстрационной версии решения задачи

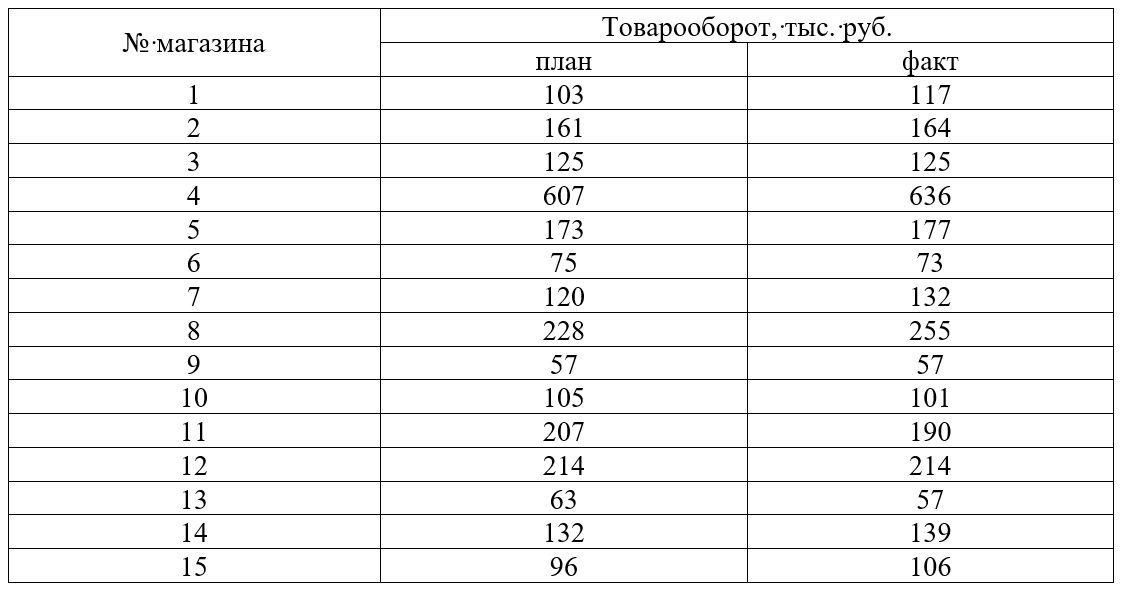
Сгруппировать 15 магазинов по степени выполнения плана товарооборота на основе данных, приведённых в таблице.

Выделите 3 группы магазинов:
1. не выполнившие план;
2. выполнившие на 100%;
3. перевыполнившие план (100,1% и более).
Перейти к демонстрационной версии решения задачи

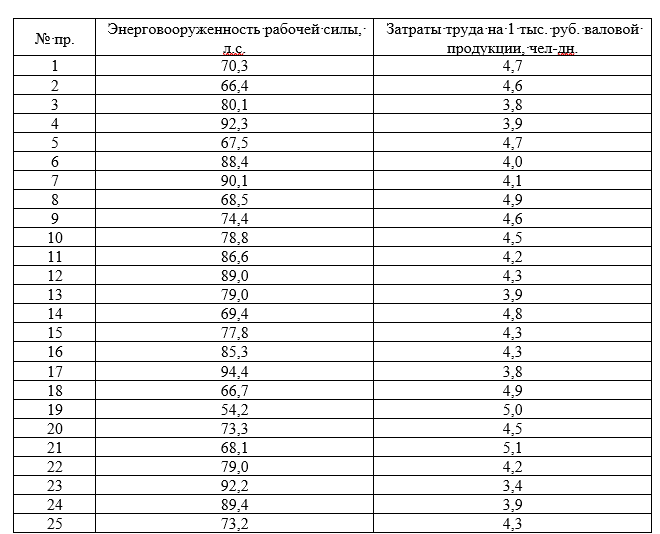
Провести группировку 25 сельхозпредприятий, характеризующую зависимость между энерговооруженностью рабочей силы и затратами труда на производство 1 тыс. руб. валовой продукции, разбив совокупность на 3-4 группы. Сделать выводы.
Таблица 1 – Исходные данные

Перейти к демонстрационной версии решения задачи

Имеются следующие данные о сумме вкладов населения, тыс. руб.

На основании этих данных:
а) ранжируйте ряд в порядке возрастания;
б) составьте равновеликий интервальный ряд, выделив оптимальное число групп вкладов по формуле Стерджесса;
в) подсчитайте по каждому интервалу чистоты и частости, сумму накопленных частот;
г) постройте кумуляту по накопленным частотам.
Перейти к демонстрационной версии решения задачи

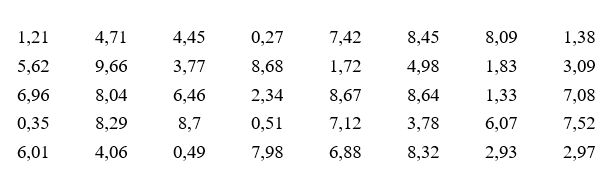
Проверяющий в течение контрольного периода записывал время ожидания нужного автобуса (в минутах) и получил следующие данные:

Построить интервальную группировку данных по шести интервалам равной длины и соответствующую гистограмму. Найти среднее время ожидания и исправленную дисперсию для выборки. Построить доверительный интервал надежности 95% для среднего времени ожидания автобуса.
Перейти к демонстрационной версии решения задачи

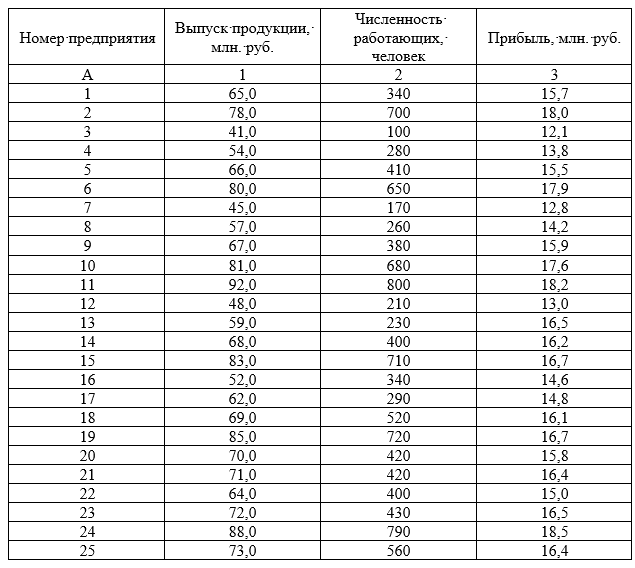
Имеются данные о работе 25 предприятий одной из отраслей промышленности за год:

По предложенным данным постройте структурную и аналитическую группировки, образовав 6 групп предприятий с равными интервалами. В качестве группировочного признака следует выбрать численность работающих. Результаты представьте в табличной форме.
Сформулируйте выводы.
Перейти к демонстрационной версии решения задачи

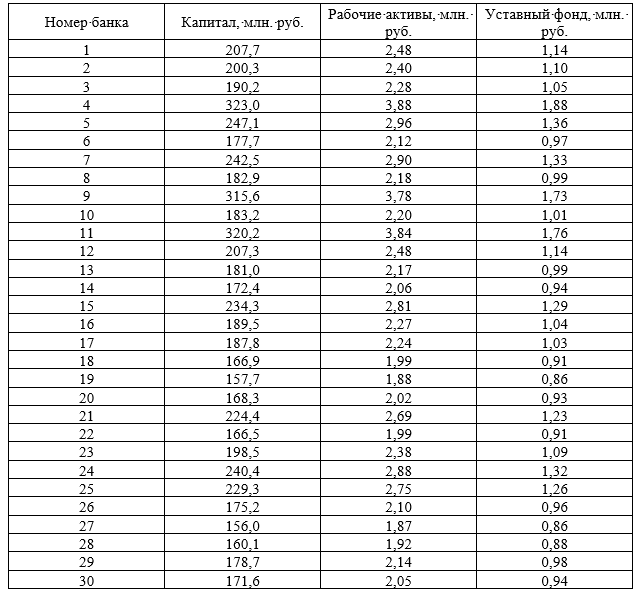
Требуется произвести группировку совокупности 30 банков РФ по следующим данным:

Перейти к демонстрационной версии решения задачи

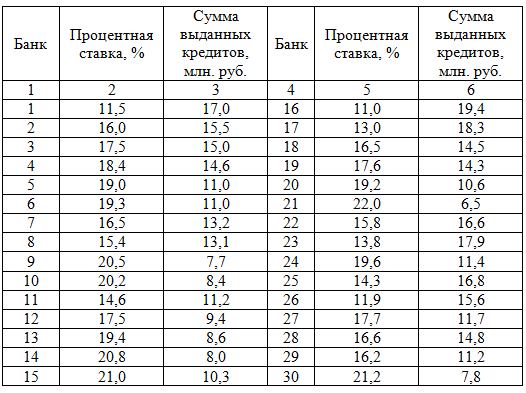
На основании данных таблицы о величине процентной ставки и сумме выданных кредитов коммерческими банками, составить: комбинированную группировку банков по этим признакам; аналитическую группировку, которая отражает зависимость суммы выданных кредитов от процентной ставки банка. Результаты расчетов оформить в табл. 2 и табл. 3. Сделать выводы.
Таблица 1. Исходные данные

Перейти к демонстрационной версии решения задачи

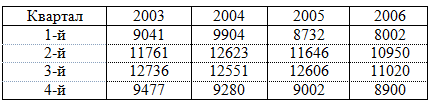
Имеются данные объема производства молока в области по кварталам за 2003-2006 гг. (тонн)

1. Постройте график исходных данных и определите наличие сезонных колебаний.
2. Постройте прогноз объема производства молока в области на 2007-2008 гг. с разбивкой по кварталам.
3. Рассчитайте ошибки прогноза.
Перейти к демонстрационной версии решения задачи

Имеются данные, характеризующие уровень безработицы в регионе, %:

1. Постройте прогноз уровня безработицы в регионе на октябрь, ноябрь, декабрь месяцы, используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните результаты.
Перейти к демонстрационной версии решения задачи

Практическое задание. По данным таблицы составить гистограммы, характеризующие время исполнения заказа на поставку товаров двумя отделами фирмы:
Время исполнения заказа, час.

Сравнив гистограммы отдела 1 и отдела 2, сформулировать рекомендации по совершенствованию процессов.
Перейти к демонстрационной версии решения задачи

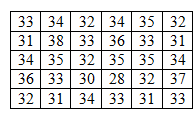
Прогнозирование надёжности и определение вероятности безотказной работы нефтепромыслового оборудования по статистическим данным.
Цель работы: Научиться определять показатели надёжности статистическими методами и прогнозировать работу оборудования.
Имеются данные наблюдений за временем безотказной работы (в днях) тридцати насосных установок (см. табл. 1).
Таблица 1 – Исходные данные

Необходимо построить:
1. Ряд распределения (таблицу частот), образовав при этом пять групп с равными интервалами.
2. Гистограмму, полигон и кумулянту распределения.
3. Определить вероятность безотказной работы между вторым и четвёртым интервалами и сделать соответствующие выводы.
Перейти к демонстрационной версии решения задачи

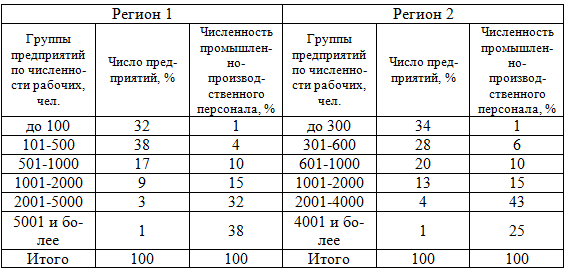
Имеются следующие данные о распределении промышленных предприятий двух регионов по численности занятого на них промышленно-производствен ного персонала (ППП):

Постройте вторичную группировку данных о распределении промышленных предприятий, пересчитав данные: а) региона 2 в соответствии с группировкой региона 1; б) региона 1, образовав следующие группы промышленных предприятий по численности ППП: до 500, 500-1000, 1000-2000, 2000-3000, 3000-4000, 4000-5000, 5000 и более.
Перейти к демонстрационной версии решения задачи

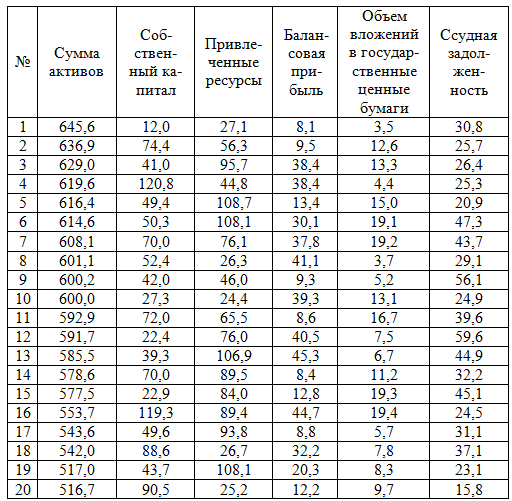
Известны следующие данные по основным показателям деятельности крупнейших банков одной из областей Российской Федерации в млн. руб.

Постройте группировку коммерческих банков по двум признакам: величине балансовой прибыли и сумме активов. По каждой группе и подгруппе определите число банков, величину балансовой прибыли и сумму активов и другие два-три показателя, взаимосвязанных с группировочными. Результаты группировки оформите в виде таблицы и сформулируйте выводы.
Перейти к демонстрационной версии решения задачи

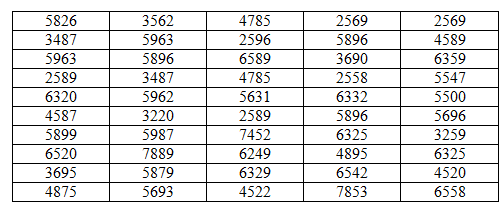
Из 550 сельскохозяйственных предприятий условного региона было обследовано 50 предприятий и установлена площадь их земелепользований:

На основании полученных данных произвести следующие вычисления:
1. Выполнить группировку по площади землепользования (вычислить частоту и частость, в том числе накопленные).
2. На основании произведенной группировки вычислить среднюю арифметическую взвешенную площади землепользования, моду и медиану (по формулам и по графикам). Объяснить предназначение вычисленных показателей.
3. На основании произведенной группировки вычислить показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию, коэффициент осцилляции, линейный коэффициент вариации, коэффициент вариации. Сделать выводы по полученным данным, объяснить предназначение вычисленных показателей.
4. Вычислить ошибку выборочной средней, предельную ошибку и доверительный интервал для средней при уровне достоверности 0,950. Сделать выводы по полученным данным. Вычислить предельную ошибку и определить необходимый объем выборки при уровне предельной ошибки, равном 5%.
5. Определить выборочную долю предприятий с площадью землепользования менее 4000 га, вычислить ошибки выборочной доли и доверительный интервал для нее. Сделать выводы по полученным данным.
Перейти к демонстрационной версии решения задачи

Источник: vipreshebnik.ru

Лучшие сайты для заказа решения задач онлайн

Решение задач (уравнений, неравенств, радикалов, построение графиков) — выполнение действий или мыслительных операций для достижения цели в рамках определенного вопроса. Процедура помогает закрепить практические навыки, умения студентов по заданной теме. Подобные задания дают преподаватели гуманитарных, точных наук.

Способы решения задач определяются классификацией задания (логической, сетевой, продукционной модели, сценария). Основной список методов включает поиск состояний в пространстве, редукцию, дедуктивный выбор, логика. Качественное решение задач любой сложности предлагают лучшие сервисы Москвы.

ТОП 5 лучших сайтов, где заказать решение задач онлайн срочно, недорого и без обмана в 2022 — рейтинг

1. HomeWork

HomeWork за 20 лет работы на российском рынке добился стабильного потока заказов, снизив стоимость решения задач. Компания «ХоумВорк» располагает онлайн платформой, филиалами в крупных городах России: Москве, Санкт-Петербурге, Новосибирске, Екатеринбурге, Казани и Нижнем Новгороде. Штат организации насчитывает 2 000 исполнителей. Заказчик не выбирает авторов, поиском компетентных специалистов занимается персональный менеджер.

Располагая собственной базой авторского состава, «Хоумфорк», решает множество задач:

• гарантирует профессиональную поддержку в решении задач — отзывчивый колл-центр работает 24/7 по телефону, в чате;
• учитывает требования клиентов, соблюдает сроки выполнения работ;
• использует актуальные, проверенные источники информации;
• обеспечивает доступ к онлайн площадке, мобильному приложению, офисам компании;
• сопровождает выполненные работы до проверки, бесплатно корректирует решение;
• сохраняет персональные данные клиентов от 3-х лиц;
• предлагает услуги менеджера, оповещающего о результатах по почте, телефону.

Эксперты HomeWork помогут решить задачи по ряду предметов:

• высшей математике;
• эконометрике;
• статистике;
• математическому моделированию;
• психологии труда;
• расчету фонда заработной платы;
• механике;
• физике;
• сопромату.

Предоставят подробные пояснения, законченные, обоснованные выводы. Визуально выделят условие задачи, решение, ответ. Результат предоставляется в электронном виде, от руки. Перед сдачей работы подвергаются перекрестной проверке качества кураторами, согласно стандартам компании. Уникальность задач 85% — 95% по Адвего.

Решение объемных работ проводится частями, проверяется клиентом поэтапно.

Лучшие сроки, недорогие цены

HomeWork предлагает недорогие цены на решение задач — 150 рублей, популярные направления (теоретическая механика, материаловедение, химия, право, экономика) обходятся на 5-10% дешевле конкурентов, так же проходят регулярные акции, скидки 20%. Срок исполнения задания — 1…4 дня. Средний объем — 30 страниц.

Предоплата 50 %, внесение платежей доступно удобным способом: банковскими картами, е-кошельками, со счета мобильного телефона, салоны связи. Гарантийный срок выполненных работ — 30 дней. Предупредив о длительном сроке проверки задания, клиент получает увеличенный срок бесплатных правок.

2. Zaochnik

Компания Zaochnik с 2000 года консультирует студентов по решению задач. Десятки тысяч клиентов выполнили задания «на отлично», рекомендуют сервис друзьям. Сайт «Заочник» официально зарегистрирован, несет ответственность, предусмотренную законодательством России, за предоставляемый сервис. К услугам клиентов «Заочник» 3005 сотрудников, эксперты 600+ предметов (термех, БЖД, микро-, макроэкономика, строительная механика) круглосуточная помощь 24/7.

Оформление заявки на сервисе Zaochnik требует минимум действий:

1. Клиент описывает задачу по сопротивление материалов, математической физике, дискретной математике, финансовому менеджменту, ТОЭ.
2. Менеджер находит компетентного специалиста, обсуждает детали сотрудничества.
3. Заказчик вносит предоплату 25 %, эксперт выполняет задание недорого, оперативно.
4. Погасив 100% стоимости услуги, клиент получает готовую работу.

Упростить оформление заявки помогает мобильное приложение Zaochnik. Программа позволяет быстро размещать недорогие заказы, управлять аккаунтом, поддерживать связь с менеджером.

Лучшее решение задач сервисом «Заочник»

Решение задач – распространенный способ проверить знания студента, часто требующий нестандартного, творческого подхода. Задачи «со звездочкой», срочные контрольные работы стоит доверить опытным экспертам. «Заочник» принимает заявки по различным дисциплинам: физике, математике, схемотехнике, биологии, астрономии, гидравлике.

Сотрудники Zaochnik быстро готовят стандартные задания в 1-2 действия или комплексные прикладные задачи в Ворде, Эксель, PDF. Поясняют ход решения. Личный менеджер контролирует своевременную сдачу работы. Отдел контроля качества осуществляет перекрестную проверку на грамотность оформления работы, соответствие ТЗ, ГОСТу. При необходимости внести уточнения, специалисты выполнят правки бесплатно на протяжении 2 месяцев.

Недорогая стоимость решения

Стоимость услуг Zaochnik обусловлена сложностью, сроком исполнения, количеством задач, подробное решение заданий по физической химии, социологи, налогам, бухучету стоит минимум 150 рублей.

Пользователям мобильного приложения «Заочник» доступна скидка 15%. Дополнительный бонус 500 рублей поступит на личный счет при указании в профиле даты следующей сессии. Также пользователям для получения 500 бонусов рекомендуется указать личную информацию, место обучения, специальность, курс.

Пополнить баланс Zaochnik предлагает банковской картой, Яндекс.Деньгами, Qiwi, WebMoney, салонами связи. Размер комиссии 4,5% от общей суммы заказа.

3. Author24

Сервис «Автор24» более 7 лет обеспечивает прямое взаимодействие авторов, студентов. Размещая заявку на сайте, пользователи получают десятки предложений высококлассных экспертов, педагогов, доцентов учебных заведений. Общение с профи проводится без посредников, цены формируются по принципу аукциона. Клиенты «Автор24» надежно защищены гарантиями, плата взимается за результат. Спорные вопросы разбирает служба поддержки.

Биржа предлагает оценить новые возможности сервиса:

1. Срочные консультации экспертов с использованием видео-чата, интерактивной доски Author24.
2. Выбор помощника по тарифам, рейтингу, отзывам.
3. Справочник. Более 15000 статей, охватывающие школьные, ВУЗовские программы позволяют найти интересующий учебный материал.
4. Полезные, увлекательные ролики про учебу на «Ютуб» от лучших блогеров, интересный инстаграм, VK.
5. Честные цены, исключающие переплату агентствам.
6. Перечисление денег автору после проверки решения задачи (гарантийный период 20 дней).
7. Бесплатное оформление заявки, поиск исполнителей.
8. Выбор автора среди 6000 кандидатов.
9. Широкий выбор тем: решение финансовых задач, по логике, инвестициям, банковскому делу, электродинамике, семейному праву. Построение матриц, использование инвариантов, динамического, линейного программирования, расчетно-графических инструментов.

Сервис располагает официальным мобильным приложением для Android. Программа обеспечивает функции сайта: удобное размещение заявок, переписку с исполнителем, управление заявками, простую оплату. Персональная информация пользователей хранится в закрытом доступе.

Минимальный срок исполнения заказа – 4 часа. Средняя цена — 200 рублей. Дешевле обойдется материал, предложенный в банке готовых работ (по теории вероятности, экономической и бухгалтерской экспертизе, электротехнике, генетике, начертательной геометрии) — минимум 40 рублей/задача. Готовые работы проверены экспертами на правильность оформления, корректность решения задачи, обнаружение плагиата по ETXT.

Сервис «Автор24» начисляет бонусные баллы в рамках акций, регистрации на сайте. Письма с промокодами поступают на электронную почту. Бонусы дают 30% скидки на стоимость работы. Спецпредложения не действуют при покупке готовых работ, оформлении «премиум-заказа», попадающего в ТОП аукциона, рассрочки.

4. Napishem

Napishem – безопасная онлайн-платформа помощи студентам. Клиенты напрямую получают помощь специалистов, сайт гарантирует безопасность, недорогие цены услуг. Онлайн платформа защищена SSL-протоколом. Выбор автора соответствует рейтингу, отзывам, стоимости работ. Эксперты устанавливают цены, учитывая сложность темы (технология сварки, парикмахерское искусство, строительная техника, макроэкономика), сроки исполнения.

Особенности сервиса Napishem

Napishem дает студентам:

1. Быстрый поиск авторов. За 59 секунд система рассылает уведомления экспертам, авторы предлагают цены.
2. Стоимость в 2-3 раза ниже посредников. Общаясь с автором напрямую, пользователи сервиса экономят время, деньги.
3. Строгий отбор лучших специалистов. Биржа Napishem проверяет исполнителей по собственной трехэтапной методике, требующей подтверждения образования, телефонного собеседования, испытательного срока.
4. Гарантия возврата. Работы низкого качества подлежат 100 % компенсации по решению арбитража.
5. Автоматическая проверка на антиплагиат. Выполненные задания на 93% уникальны.

1. Оперативная служба поддержки, работающая до 24.00 по Москве. Персональный менеджер.
2. Внесение правок на странице заказа в течение 30 дней. Доработка задач по технической механике, линейному программированию, экологии, педагогике, пахт в период гарантийного срока длится 7 дней. Коррективы выполняются автором бесплатно.
3. Официальный договор оферты защищает клиентов на юридическом уровне.

Детали работы авторы обсуждают с заказчиком. Оплату получают после проверки, принятия задания. Личные данные подрядчиков, клиентов на 100 % защищены.

Оформление заказа на решение задач специалистами сервиса «Напишем» занимает минимум времени, сил:

• пользователи заполняют регистрационную форму;
• составляют задание по информатике, управленческому учету, по праву и юриспруденции, кинематике, сопромату;
• указывают сроки выполнения, дополнительные условия;
• получают отклики авторов;
• выбирают лучшего эксперта;
• вносят авансовый платеж;
• получают, проверяют готовый заказ.

Заказ услуги по решению задач конкретным подрядчиком происходит в личном кабинете. Необходимо открыть страницу автора, нажать кнопку «Сделать заказ».

Оценка стоимости решения задач соответствует принципу аукциона. Средняя цена, предлагаемая исполнителями, составляет 150 рублей/задача. Сайт работает по предоплате. Размер аванса указывается исполнителем, составляет 25-100%. Решение недорогих задач занимает 2 часа.

Оплата заявок проводится различными способами, наиболее распространены: банковские карты, «Киви», Яндекс.Деньги.

5. Всё сдал

Всё сдал работает 2011 года, за короткий период компания помогла решить задачи 5000 клиентам. Сотрудники площадки работают удаленно, снижая себестоимость готовых работ. Для поддержания хорошей репутации сервиса авторы компании проходят тестирование. Интегрированный калькулятор обеспечивает предварительный расчет стоимости услуг, учитывая сложность решаемых задач, дату сдачи, процент уникальности.

Лучшие стороны площадки Всё сдал

Популярность компании «Всё сдал» обусловлена рядом преимуществ:

1. Уникальность. Отдельные работы сопровождаются скриншотами результатов проверки на антиплагиат.
2. Скорость. Более 90% заявок команда Всё сдал сдает досрочно.
3. Качество. Клиенты получают возможность частично изучить работу до момента сдачи. Учебный материал отвечает ГОСТам, требованиям образовательных заведений, пожеланиям клиентов.
4. Решение координатных задач, неравенств, простых, дифференциальных уравнений — от руки, в печатном исполнении. Предпочтительный вариант клиент указывает при создании заявки.
5. Бесплатная доработка. Гарантия выполненных задач длится 3 месяца.
6. Удобная оплата. «Всё сдал» принимает платежи банковскими картами, е-кошельками.
7. Акции. Недорого оформлять решение задач помогают специальные бонусы, скидки.

Качество услуг Всё сдал подтверждено цифрами: 20 000 студентов ежегодно пользуются сервисом, 5 200 экспертов работает в компании, 85 000 заявок сервис обрабатывает за год.

Пользователям сервиса предлагается решение задач по различным дисциплинам:

• физика;
• геометрия;
• программирование;
• аудит;
• торговля;
• гражданское право;
• химия;
• прикладная механика;
• теория вероятности.

Всё сдал предлагает заполнить электронную заявку по форме сайта. Точная цена работы формируется менеджером за 2 часа. Клиент внесет авансовый платеж размером 30%, оставшиеся средства — после исполнения заявки. Сервис обеспечивает конфиденциальность, клиенты не указывают полную контактную информацию, хранит данные в в зашифрованном виде

Средняя цена решения задач специалистами Всё сдал — 600 рублей. Минимальный срок исполнения заявки — 6 часов. На главной странице сайта доступен промокод, дающий на первый заказ скидку 5 %. Сервис также предлагает скидки по 15% для клиента, друзей, при совместном оформлении работы. Задачи для экзаменов создаются одинаковые, заказав решение заданий всей группой – стоимость значительно уменьшится. Личный менеджер проконтролирует ход работы, проверит соответствие начальному заданию, решит вопросы правок, доработок.

Источник: zadach-reshenie.ru

Заказать быстрое решение задач по любым предметам

Решим любую задачу, объясним любое решение или пример в срок!

Почему выгодно заказать именно в Zaochnik?

Мы пишем качественно

Наши авторы — практикующие преподаватели вузов и колледжей, профессора, кандидаты и доктора наук, а это значит, что ваша работа, в любом случае, будет выполнена качественно. Наши специалисты глубоко погружены в свои предметы, знают, как грамотно оформить работу в соответствии со всеми стандартами и ГОСТами и придерживаются правила: «Репутация превыше всего». Именно поэтому вы не встретите у нас просто скачанных работ из интернета.

Мы предоставляем крутые гарантии

Гарантийный срок на все работы, кроме дипломной и диссертации, составляет 2 месяца. Гарантия начинает действовать с того момента, когда вы получите готовую работу. Если понадобится внести правки, мы сделаем это абсолютно бесплатно (если они соответствуют первоначальным требованиям: данным, которые вы указали в заявке). А еще, мы сопроводим вас до защиты или сдачи работы и поддержим на каждом этапе.

Мы выполняем работы в срок

Мы не понаслышке знаем, как важно для вас, получить работу вовремя, поэтому выполняем работы точно в срок, чтобы вам не пришлось лишний раз волноваться. Всю ответственность мы берем на себя. Вы можете спокойно заниматься вещами, которые действительно важны для вас.

Как работает наш сервис

Как оформить заказ на решение задач

Оформляете заявку

Бесплатно рассчитываем стоимость

Вы вносите предоплату 25%

Эксперт выполняет работу

Вносите оставшуюся сумму

И защищаете работу на отлично!

Узнай бесплатно стоимость работы

Мы уже помогли 2 000 000+ студентов. Не хотите присоединиться?

Мы всегда рядом!

Отзывы о выполнении решения задач

✅ Профессиональная помощь в решении любых учебных задач. ✅ Соблюдение требований и сроков. ✅ Низкие цены. Заказать решение задач с гарантией сдачи и договором. Оставляй заявку!

Учусь в экономическом техникуме на втором курсе. Обычно задачи по экономике решаю самостоятельно, еще и другим помогаю. Но в это раз преподаватель задал нереально много, еще и сроки сжатые, плюс другие предметы, да и жить когда-то надо, и отдыхать. В общем, решила обратиться за помощью и заказала готовые задачи на заочник.ком. Сделали быстро и без ошибок, взяли не дорого.

Я довольна!

25 Сентябрь 2022

Не ожидал, что получу готовые решения всех задач так быстро. У нас даже наши отличники не всегда знают решения сложных задач. А здесь помощь пришла очень быстро, буквально через несколько часов после того, как я сбросил скан задания. Разумеется все задачи и примеры были решены верно, за что и получил отличную оценку. Спасибо, буду еще по возможности обращаться к вам за помощью.

24 Сентябрь 2022

Мой любимый сайт уже второй год. В начале было страшно даже не за деньги, а за качество работы, чтобы преподаватели не придирались. Но никто ничего не заметил 🙂 Работу получаю всегда четко в срок, надеюсь так будет и дальше. Нравится онлайн формат заказа, не нужно никуда идти. Заказал, оплатил, получил и ни одного лишнего движения.

Пока только положительные впечатления.

17 Сентябрь 2022

С математикой я не дружу от слова совсем. Но так уж получилось, что Математический анализ один из самых сложных предметов в этом семестре. Преподаватель дал целую кучу задач и выделил минимальный срок на выполнение- 3 дня. Самостоятельно осилить их я не смог, поэтому заказал на Заочнике. Спасибо менеджеру, который быстро подобрал мне автора который разбирается в тематике.

К счастью, исполнитель попался толковый и выполнил заказ точно в срок. Преподаватель остался доволен моей работой и по достоинству её оценил.

11 Сентябрь 2022

Решение задач по экономике то еще приключение, приходится учитывать множество показателей, очень легко ошибиться, тратится много времени. Преподаватель в университете обозначил задачу решить несколько десятков заданий. Решил не париться и обратиться к специалистам. Выбрал данный ресурс. Сделали все быстро, решения правильные (преподаватель уже проверил).

09 Сентябрь 2022

Я абсолютно довольна сервисом Заочник, соотношением цены и качества, сроками выполнения заказа. Исполнитель нашёлся быстро и ответственно подошёл к решению задач. Работа была сдана мне уже на следующий день. Преподаватель остался доволен качеством и поставил соответствующий высокий бал. Благодарю вас за это и при случае непременно обращусь сюда ещё раз.

08 Сентябрь 2022

Протянул с решением задач по высшей математике. Оставались сутки до сдачи задания. На своих соседей по общаге особой надежды не было. Зато настоящая помощь пришла оперативно. Буквально через 3 часа после оформления заявки на сайте мне прислали решение с правильными ответами по электронке.

Времени на проверку особо не было. Но, как оказалось, это делать и не нужно было. Все решения были верными.

07 Сентябрь 2022

Хочу выразить огромную благодарность сервису Заочник и исполнителю который помогал мне решить задачи по налоговому праву. Исполнитель оказался очень компетентным в данной тематике, серьёзно подошёл к выполнению моего заказа, сдал работу в срок и даже дополнил работу заметками с подробными объяснениями. Стоимость очень дешёвая для такой работы, я бы советовала сайту повышать тарифы, всё-таки качество соответствует))

05 Сентябрь 2022

Как только у меня намечается завал на учёбе, то я тут же бегу за помощью компетентных авторов на Заочник) в этот раз заказывала решение задач по высшей математике, автор молодец выполнил работу качественно и в срок, дополнил подробными объяснениями, да такими что я даже сама немного поняла как это решать, хотя по натуре я типичный гуманитарий) отдельно хочу выделить невысокую цену за работу, если вы бедный студент, то для вас это будет вполне доступно поэтому смело пользуйтесь.

04 Сентябрь 2022

Уже не первый раз заказываю здесь решение задач для ВУЗа. На личном опыте убедилась, что авторы выдают качественный материал, а если вдруг всё-таки требуется какие-то правки, то исполнитель учтет все требования и исправит так как нужно. В целом я очень довольна сотрудничеством с Заочником, работа предоставляется всегда в указанный срок (а иногда даже раньше). Ну и конечно не последнюю роль играет стоимость, даже с постоянно ограниченным бюджетом, я могу себе позволить заказать работу онлайн, а всё потому что цены здесь адекватные и доступные студентам.

Маргарита (4 курс)

Вас проконсультирует

Личный помощник (менеджер)

• Ответит головой за сроки
• Сделает всё, чтобы решить вашу проблему
• Проконтролирует выполнение услуги
• Подберет лучшего эксперта по вашей задаче

Универсальный солдат (сотрудник колл-центра)

• Поможет описать вашу задачу
• Обучит работе с личным кабинетом
• Проконтролирует выполнение услуги

Персональный «Пушкин» (Эксперт)

• Откликнется на вашу проблему
• Проанализирует пути решения
• Объяснит материал
• Убедится, что вы все поняли

Шерлок Холмс (сотрудник отдела Контроля Качества)

• Придирчивый и внимательный: не даст расслабиться экспертам
• Проверит текст на уникальность сотней специальных программ
• Просканирует каждый миллиметр оформления на соответствие нормам и ГОСТу

Часто задаваемые вопросы о решении задач

• Кто будет выполнять работу?

Вашу работу будет выполнять практикующий преподаватель вуза, профессор, кандидат или доктор наук. Кто именно будет выполнять, зависит от степени сложности вашей работы.

Стоимость работы зависит от количества страниц, процента уникальности и срока выполнения.

Мы знаем, как для вас важно, чтобы работа была готова вовремя, поэтому выполняем все заказы в срок. В случае форс-мажора со стороны клиента мы максимально входим в положение и делаем всё возможное, чтобы всё получилось. В случае форс-мажора со стороны автора ваш заказ отдают в отдел срочных заказов, и он выполняется вне очереди. Мы делаем всё, чтобы выполнить работу вовремя.

Когда наступит гарантийный срок (он начинается с того момента, когда вам присылают готовую работу), мы бесплатно внесем правки, если вам понадобится, сопроводим вас до сдачи или защиты работы, будем постоянно на связи, если возникнут вопросы. На дипломные и диссертации у нас бессрочная гарантия, на все остальные виды работы – 2 месяца.
*Обращаем ваше внимание, что бесплатно мы вносим правки только в том случае, если они соответствуют первоначальным требованиям в заказе, т.е. тем, которые вы указали в заявке.

Конечно, можно. Даже бесплатно. Бесплатно мы вносим правки в том случае, если они соответствуют первоначальным требованиям в заказе (тем, которые вы указали в заявке). Платно вносим тогда, когда требуется что-то такое, чего не было в условиях заявки (переписать работу, поменять тему и т.д.).

Решение задач по предметам

Решение задач по механике

Решение задач по маркетингу

Решение задач по банковскому делу

Решение задач по менеджменту

Решение задач по логике

Решение задач по информатике

Решение задач по экономике

Решение задач по высшей математике

Кто обращается за решением задач в Zaochnik

Решение задач – один из распространенных видов проверки знаний. Учащиеся практически любой специальности сталкиваются с таким заданием на зачетах и экзаменах. Курсовые и дипломные работы часто предполагают демонстрацию нахождения ответа. Поэтому студенты перегружены примерами по физике, математике, механике, химии, биологии и другим предметам.

Не всегда можно справиться с заданиями с помощью решебника или найти толкового исполнителя на бирже. В таком случае нужна помощь профессионалов. Образовательный сервис Zaochnik оказывает такие услуги недорого.

Как получить задачи с решением

Чтобы оформить заказ и быстро получить результат, оставьте заявку на сайте. Опишите свой проект в полях формы, прикрепите нужные файлы или фото с условиями. Отметьте, насколько срочно вам нужен результат. Все эти данные отправляются менеджеру на обработку для определения цены.

1. Менеджер свяжется с вами, расскажет об условиях сотрудничества и ответит на оставшиеся вопросы.
2. Если вы согласны с прайсом, заключаем договор.
3. После внесения части денег заказ передается автору.
4. В финале написания проект согласовывается с заказчиком.
5. Внесение остатка средств – заключительный этап, после которого вы получаете результат.

Кто поможет решить задачу к нужному сроку

Заказывать проекты у нас и купить их у сторонних исполнителей – большая разница. Не каждый может помогать профессионально. Сделать задания, например, по термеху не каждому по плечу. Для этого нужна серьезная теоретическая подготовка, умение применить эти знания в конкретной ситуации. То же касается ПСО – права социального обеспечения.

Решатель должен выдавать быстрый результат, а не тратить время на поиск информации.

Автор из нашего штата, который будет выполнять ваш заказ, имеет подтвержденную квалификацию. В нашем центре работают преподаватели университетов, научные и медицинские сотрудники, экономисты, юристы и представители других сфер. Мы найдем нужного исполнителя, опыт которого соответствует требованиям вашего заказа. Любой срочный проект будет сделан вовремя.

Почему решенные задачи не вызывают вопросов у преподавателей

Любой студенческий запрос быстро обрабатывается. Для этого достаточно заполнить заявку или написать консультанту. Решать задания будут преподаватели и сотрудники-практики. Покупать дополнительные услуги не потребуется. Вы получите:

• Последовательное выполнение всех действий с пояснениями.
• Бесплатное внесение корректировок до полного согласования с заказчиком.
• Дополнительную проверку работы отделом контроля качества перед завершением покупки.

Вам не придется стоять в очередях для совершения оплаты или получения готового заказа. Платежи и доставка производятся через Интернет. Поэтому наши услуги доступны не только для Москвы, но и для других городов.

Сколько стоит сделать задачу в Zaochnik

На сайте можно получать помощь в вычислениях бесплатно. Мы разработали раздел с математическими калькуляторами, который позволяет тренироваться в расчетах, видеть подробные действия и ответ.

Платно оказываются услуги по выполнению заданий на заказ. Стоимость для разных проектов отличается. Простое задание обойдется дешево – от 150 р. Составление комплексного проекта выйдет дороже. Менеджер проведет оценку объема и сложности заказа и на их основе определит итоговую сумму.

От объема и сложности задания зависит не только денежный вопрос, но и сроки готовности. Уже через пару часов вы получите ответ для уравнения или другое задание. На контрольной или экзамене мы сопроводим вас онлайн. Присылайте фотографию с условием, наш сотрудник сделает все расчеты и перешлет картинку с результатом.

Источник: zaochnik.com

Решение метрических задач в начертательной геометрии с примерами

К метрическим задачам относятся задачи на определение натуральной величины отрезков, расстояний углов, площадей плоских фигур.

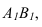
Определение натуральной величины отрезка и углов наклона к плоскостям проекций методом прямоугольною треугольника Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка, а вторым — разность расстояний концов отрезка от той плоскости, на которой ведется построение. При этом угол между гипотенузой и катетом проекций является углом наклона отрезка к той плоскости, ряльной величины выполнено на горизонтальной проекции. Поэтому одним катетом прямоугольного треугольника, является горизонтальная проекция

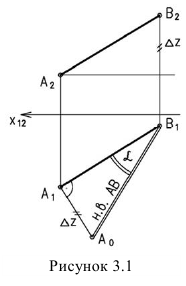
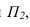
Если необходимо определить угол наклона отрезка АВ к плоскости то построение прямоугольного треугольника ведется на фронтальной проекции.

Решение метрических задач методами преобразовании проекций

Положении геометрических образов, при которых расстоянии и углы не искажаются на плоскостях проекций

Метрические характеристики объектов на чертежах не искажаются, если геометрические образы занимают частное положение относительно плоскостей проекций.

Приведем некоторые из них.

1. Прямая проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.2).

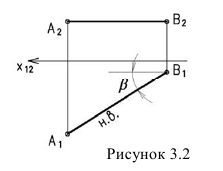
— угол наклона к плоскости

2. Расстояние от точки до прямой проецируется в натуральную величину, если прямая проецирующая (рисунок 3.3).

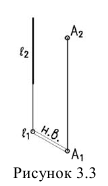
3. Расстояние между параллельными прямыми проецируется в натуральную величину, если прямые проецирующие (рисунок 3.4).

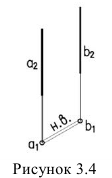
4. Расстояние между скрещивающимися прямыми проецируется в натуральную величину, если одна из прямых проецирующая (рисунок 3.5).

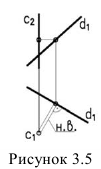
5. Угол между плоскостями (двугранный угол) проецируется в натуральную величину, если ребро угла проецирующее (рисунок 3.6).

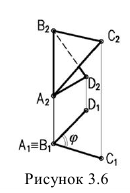
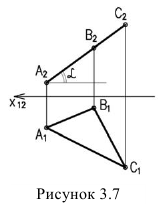
6. Угол наклона плоскости к плоскости проекций проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.7)

7. Расстояние от точки до плоскости проецируется в натуральную величину, если плоскость проецирующая (рисунок 3.8)

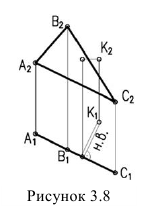
8. Любая плоская фигура проецируется в натуральную величину, если она параллельна плоскости проекций (рисунок 3.9а,б)

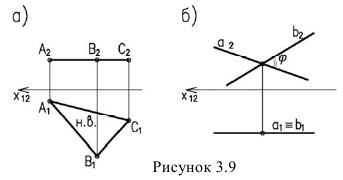
Таким образом, для решения метрических задач целесообразно данный объект привести в частное положение с тем, чтобы на одной из новых проекций получить более простое решение задачи.

Для такого перехода и служат способы преобразования проекций.

Существует несколько способов преобразовании проекций: способ вращения вокруг осей перпендикулярных плоскостям проекций, способ плоскопараллельного перемещения, способ замены плоскостей проекций и др.

Четыре основных задачи преобразовании проекций

Этими способами решаются четыре основные задачи:

• Задача 1. Прямую общего положения преобразуем в линию уровня (одно преобразование).
• Задача 2. Прямую общего положения преобразуем в проецирующую (два преобразования)
• Задача 3. Плоскость общего положения преобразуем в проецирующую (одно преобразование)
• Задача 4. Плоскость общего положения преобразуем в плоскость уровня (два преобразования)

Решение 1-ой и 2-ой задачи преобразовании проекций методом вращении, плоскопараллельного перемещении и замены плоскостей проекций

Способ вращения

Способ вращения заключается в том, что геометрические образы вращаются вокруг осей перпендикулярных плоскостям проекций до занятия ими какого-либо частного положения относительно плоскостей проекций. При этом одна проекция точки перемещается по окружности, вторая — но прямой параллельной оси проекций.

На рисунке 3.10 вокруг осивращаем отрезок ЛВ до положения параллельного плоскости(1 задача). Далее вращением вокруг осиполученный отрезок до положения перпендикулярного плоскости На отрезок с проецируется в точку

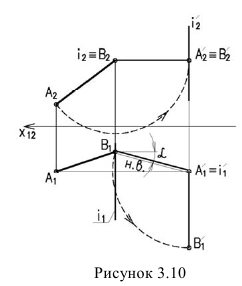
Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения является разновидностью способа вращения (вращение без закрепленных осей), т.е. положение объекта можно преобразовывать путем перемещения его параллельно одной плоскости проекций, одновременно изменяя его положение относительно другой плоскости проекций до занятия им какого-либо частного положения.

На рисунке 3.11 сначала АВ переводим из общего положения в положение горизонтальное. При этом должно быть равно по величина находим в пересечении вертикальных линий связи и линий параллельных оси (1 задача). Далее отрезок перемещаем до положения перпендикулярного оси При этом На фронтальной проекции отрезок с проецируется в точку (2 задача).

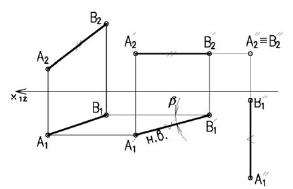
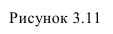
Способ замены плоскостей проекций

Сущность способа замены плоскостей проекций заключается в том, что старая система плоскостей проекций заменяется на новую, с таким расчетом, чтобы относительно новой системы плоскостей, геометрический образ занял какое-то частное положение. При этом нужно помнить, что линии связи будут перпендикулярны относительно новой оси проекций и расстояния от новой оси проекций до новой проекции точки равно расстоянию от старой проекции точки до старой оси.

На рисунке 3.12 произведена первая замена плоскость заменена на новую фронтальную плоскость параллельную прямой АВ. При этом новая ось проводится параллельно проекции Линии связи проводятся перпендикулярно оси и на них от откладываются координаты z точек А и В (1 задача).

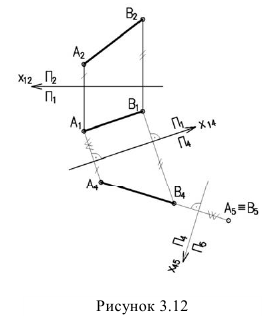
Далее прямую АВ преобразуем в проецирующую. Для этого проводим новую ось перпендикулярно проекции. Т.к. параллельна оси , расстояние до проекций будет одинаковое и прямая спроецируется в точку (2 задача)

Решение 3-ой и 4-ой задачи преобразовании проекций методом плоскопараллельного перемещения и замены плоскостей проекций

Так как метод вращения является более громоздким, рассмотрим решение 3-ей и 4-ой задачи преобразования методом плоскопараллельного перемещения и методом замены плоскостей проекций.

Способ плоскопараллельного перемещения

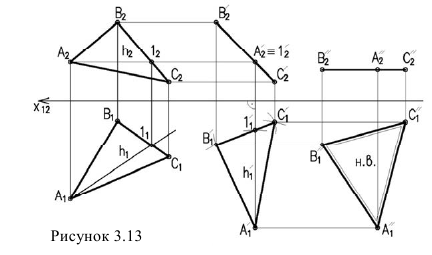
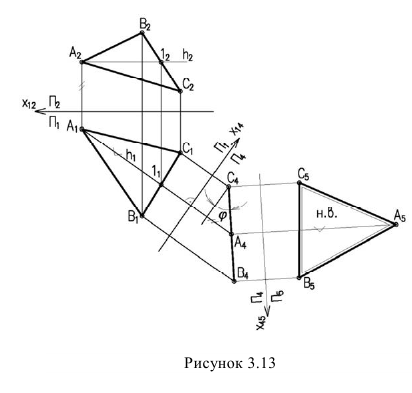
Для того чтобы плоскость из общего положения перевести в проецирующее, нужно иметь ввиду, что при этом ее горизонталь или фронталь должна быть перпендикулярна плоскости проекций. Поэтому на рисунке 3.13 проведена горизонталь Далее располагаем перпендикулярно оси Откладываем на ней отрезок и циркулем строим треугольник равный по величине На фронтальной проекции треугольник проецируется в линию (3 задача).

Чтобы плоскость треугольника перевести в положение плоскости уровня, достаточно полученную фронтальную проекцию расположить параллельно оси при этом на горизонтальной проекции треугольник проецируется в натуральную величину (4-я задача)

Способ замены плоскостей проекций

При решении задачи методом замены (рисунок 3.14) новую ось проводим перпендикулярно горизонтали тогда на новую фронтальную плоскость треугольник спроецируется в линию, т.е. станет перпендикулярным (3-я задача). Чтобы плоскость перевести в положение плоскости уровня, необходимо новую ось провести параллельно плоскости На новую плоскость треугольник спроецируется в натуральную величину.

Для того, чтобы методами преобразования решить любую метрическую задачу, необходимо определить какую из четырех основных задач преобразования необходимо решать в каждом конкретном случае.

Метрические задачи

Метрические задачи — это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.

Главным вопросом метрических задач является вопрос о построении перпендикуляра к прямой или плоскости. Построение взаимно перпендикулярных прямых было рассмотрено ранее.

Из элементарной геометрии известно, что прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. В качестве этих пересекающихся прямых наиболее целесообразно использовать горизонталь и фронталь плоскости. Это объясняется тем, что только в этом случае прямой угол будет проецироваться в натуральную величину на соответствующие плоскости проекций. На рисунке 5.1 приведен пространственный чертеж, на котором из плоскости а (из точки А) восстановлен перпендикуляр АВ. Из приведенного изображения можно выяснить методику построения проекций перпендикуляра к плоскости: горизонтальная проекция перпендикуляра к плоскости проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости, а фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости. Таким образом, необходимо выполнить следующий алгоритм проведения проекций перпендикуляра к плоскости:

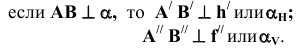
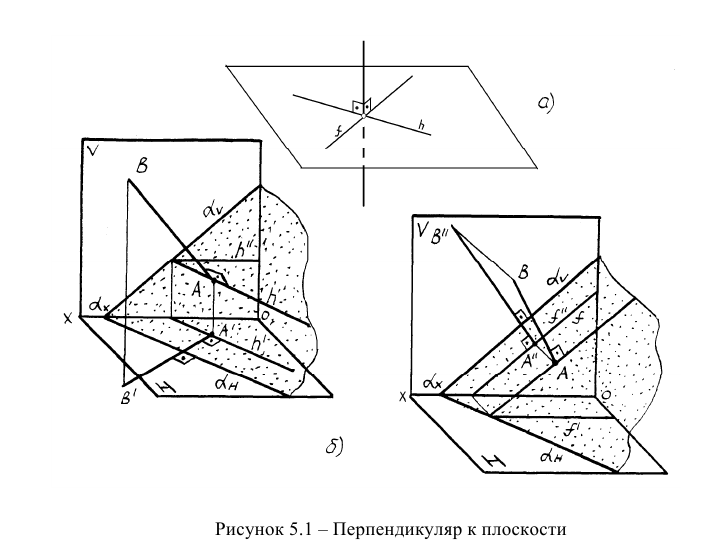
Построение перпендикуляра к плоскость и восстановление перпендикуляра из плоскости называется прямой задачей, а построение плоскости, перпендикулярной к прямой — обратной задачей. Обе задачи решаются по одному и тому же вышеописанному алгоритму. При этом плоскость, перпендикулярную заданной прямой, можно задать следами или пересекающимися горизонталью и фронталью.

На рисунке 5.2 показано решение прямой (а) и обратной (б) задач. В прямой задаче из точки A треугольника AВС восстановлен перпендикуляр, в обратной задаче через точку К проведена плоскость, перпендикулярная прямой АВ. Плоскость задана пересекающимися горизонталью и фронталью.

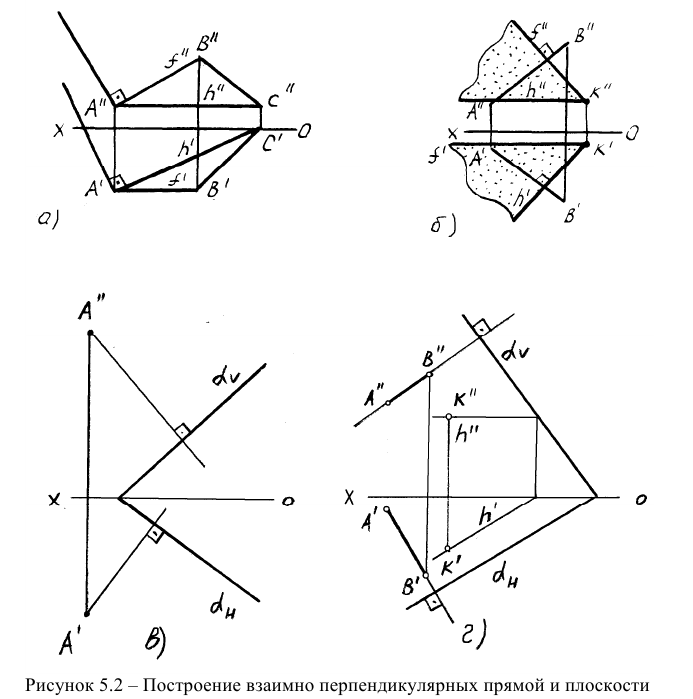
Здесь же приведены примеры прямой и обратной задач, если плоскость задана следами. В прямой задаче (в) из точки Л построен перпендикуляр на плоскость, в обратной (г) — через точку К проведена плоскость перпендикулярно прямой АВ.

Определение расстояний между геометрическими объектами

Среди этих задач можно выделить следующие задачи: расстояние от точки до плоскости, расстояние от точки до прямой, расстояние между двумя параллельными прямыми, расстояние между двумя скрещивающимися прямыми, расстояние между двумя параллельными плоскостями и другие. В общем случае все задачи сводятся к определению расстояний между двумя точками.

Чтобы определить расстояние от точки до плоскости, необходимо выполнить ряд логических действий:

1. Из точки опустить перпендикуляр на заданную плоскость;
2. Найти точку встречи перпендикуляра с плоскостью;
3. Определить НВ расстояния между заданной и найденной точками.

Задача на определение расстояния от точки до прямой решается по следующему плану:

1. Через точку к провести плоскость, перпендикулярную заданной прямой;
2. Найти точку встречи М заданной прямой с проведенной плоскостью;
3. Соединить полученные точки (это будет перпендикуляр из точки на прямую);
4. Определить НВ перпендикуляра.

Пространственная модель решения второй задачи представлена на рисунке 5.3. Рассмотренная задача относится также к задачам на перпендикулярность двух прямых.

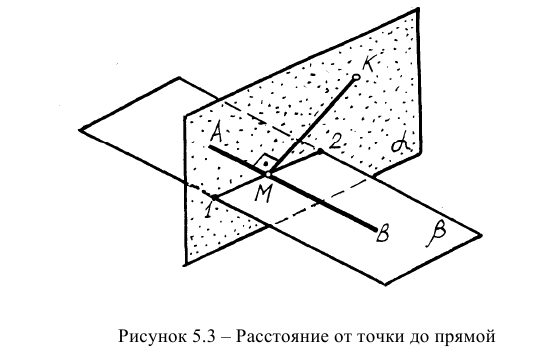
Другие упомянутые задачи на определение расстояний легче решаются методами преобразования эпюра, которые будут рассмотрены в последующих разделах.

Перпендикулярность плоскостей

Плоскость перпендикулярна другой плоскости, если она содержит прямую, перпендикулярную другой плоскости (рисунок 5.4а). Таким образом, для того, чтобы провести плоскость, перпендикулярную другой, необходимо сначала провести перпендикуляр к заданной плоскости, а затем через него провести искомую плоскость. На рисунке 5.46 представлена задача: через точку К провести плоскость, перпендикулярную плоскости треугольника AВС. Искомая плоскость задана двумя пересекающимися прямыми, одна из которых перпендикулярна заданной плоскости.

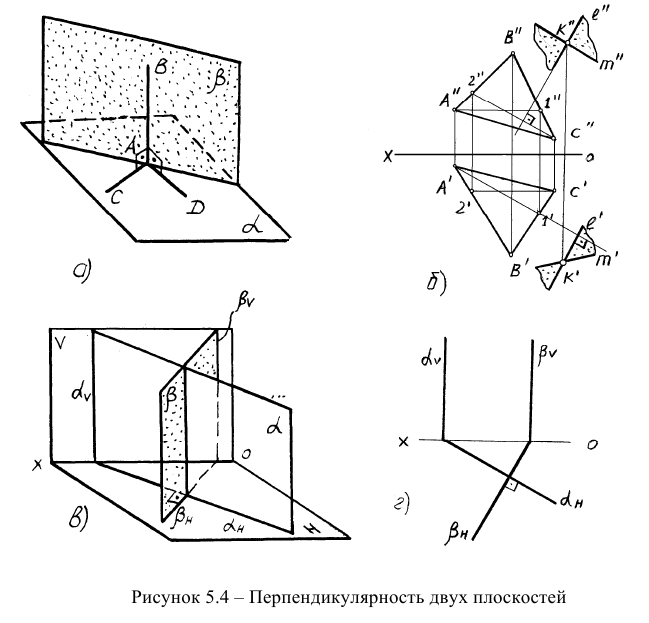
Если две плоскости являются одноименными плоскостями частного положения (например, горизонтально- или фронтально-проецирующими), то при перпендикулярности плоскостей их собирательные следы будут перпендикулярны друг другу (рисунок 5.4в,г).

Если плоскости являются плоскостями общего положения, то при их перпендикулярности одноименные следы не будут взаимно перпендикулярны. Другими словами, перпендикулярность одноименных следов плоскостей общего положения не является достаточным условием для перпендикулярности самих плоскостей.

Определение углов между прямой и плоскостью и между двумя плоскостями

Определение углов между геометрическими объектами является трудоемкой задачей, если её решать традиционными геометрическими способами. Так, например, задачу на определение угла между прямой и плоскостью (рисунок 5.5) можно решить способом, алгоритм которого содержит следующие операции:

1. Определить точку встречи прямой АВ с плоскостью а;
2. Из точки В построить перпендикуляр на плоскость;
3. Найти точку встречи перпендикуляра с плоскостью;
4. Точки К и N соединить и определить НВ угла BKN.

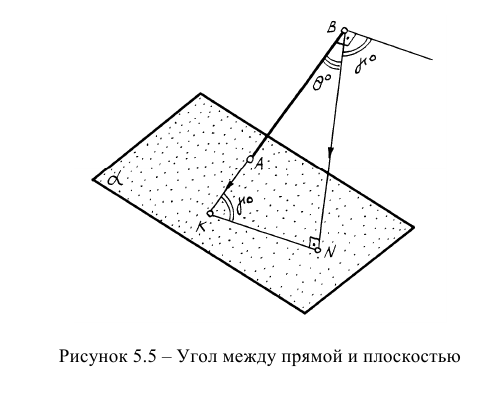
Однако задача может быть значительно упрощена, если использовать способ решения задачи с помощью дополнительного угла. Дополнительным углом назовем угол между заданной прямой АВ и перпендикуляром BN, обозначенный через Из приведенного рисунка видно, что, если из точки В прямой построить на плоскость перпендикуляр, определить НВ дополнительного угла то искомый угол определится по формуле:

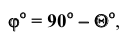
которую можно решить графически, достроив угол до 90°.

То же самое можно сказать о задаче на определение двугранного угла, то есть угла между двумя плоскостями (рисунок 5.66). Первый способ (геометрический) достаточно трудоемок. Он заключается в пересечении угла вспомогательной плоскостью а, перпендикулярной ребру АВ, построении линий пересечения KN и KL и определении натуральной величины угла NKL.

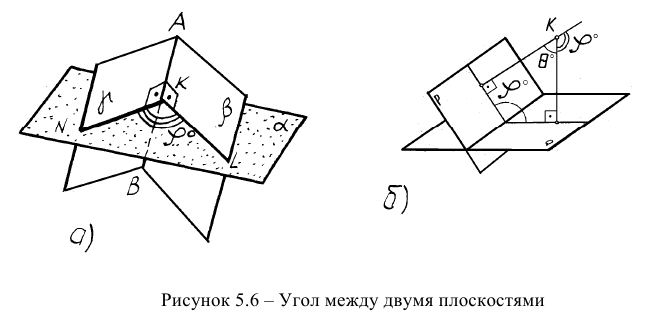
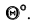
С помощью дополнительного угла задача решается следующим образом. В растворе двугранного угла (рисунок 5.6в) берут любую точку К и строят из неё перпендикуляры на обе плоскости двугранного угла, которые образуют дополнительный угол Далее определяют НВ дополнительного угла и дополняют его (графически) до 180 градусов, исходя из формулы:

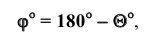
Дополненный угол будет искомым.

Натуральную величину дополнительного угла в обеих задачах наиболее целесообразно определять методом вращения вокруг горизонтали или фронтали, который будет изложен в последующих темах.

Пример: Из любой вершины треугольника АВС восстановить перпендикуляр длиной 40 мм.

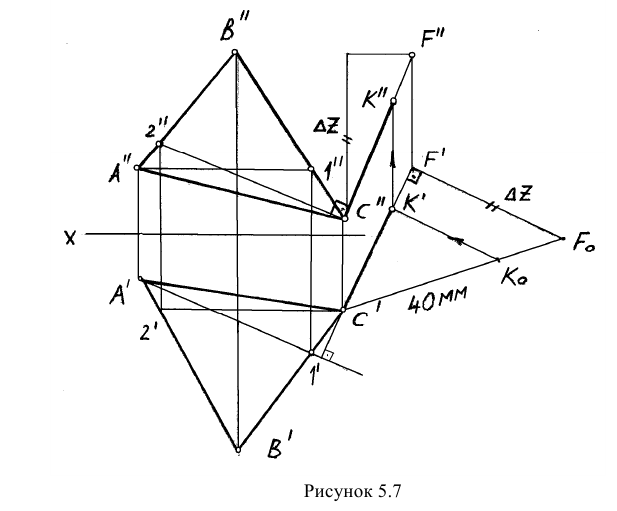
Решение: Сначала необходимо в плоскости треугольника АВС провести горизонталь и фронталь для того, чтобы построить проекции восстановленного перпендикуляра. Далее из точки С проводим проекции перпендикуляра согласно рассмотренному выше алгоритму о перпендикуляре к плоскости.

Для того, чтобы отложить 40 мм, необходимо определить НВ ограниченного отрезка перпендикуляра CF (точку F берем произвольно). НВ отрезка CF определяем методом прямоугольного треугольника на горизонтальной проекции CF. Полученную точку К возвращаем на проекции по теореме Фалеса. Получаем проекции перпендикуляра длиной 40 мм (рисунок. 5.7).

Пример: Найти расстояние от точки А до плоскости, заданной следами

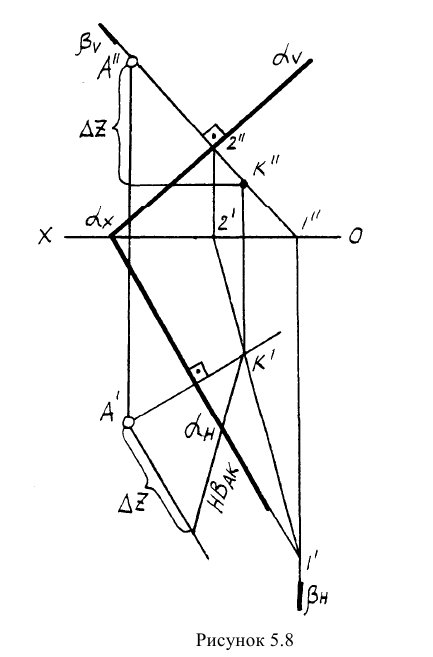
Решение: Из точки А строим перпендикуляр на заданную плоскость. Проекции перпендикуляра проводим перпендикулярно следам. Далее находим точку встречи перпендикуляра с заданной плоскостью с помощью вспомогательной фронтально-проецирующей плоскости Находим линию пересечения плоскостей (линия 1-2) и точку встречи в месте пересечения горизонтальной проекции перпендикуляра с линией 1-2. Методом прямоугольного треугольника определяем НВ расстояния АК (рисунок 5.8).

Пример: Определить расстояние от точки К до прямой AВ.

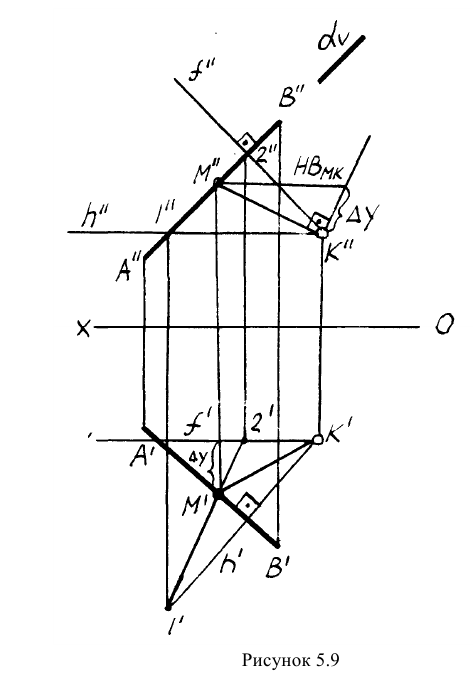
Решение: Через точку К проводим плоскость, перпендикулярную заданной прямой. Плоскость задаем пересекающимися горизонталью и фронталью. Их проекции проводим согласно алгоритму о перпендикуляре к плоскости (обратная задача). Далее находим точку встречи прямой AВ с проведенной плоскостью (точка М). Определяем натуральную величину КМ методом прямоугольного треугольника (рисунок 5.9).

Примеры метрических задач

Задачи, в которых определяются различные геометрические величины -расстояния между объектами, длины отрезков, углы, площади и т.д. называются метрическими. Решение многих метрических задач, например задач на определение кратчайших расстояний, требует построения перпендикулярных прямых и плоскостей.

Перпендикулярность является частным случаем пересечения прямых, прямой и плоскости или двух плоскостей. Необходимо установить соотношения, по которым строятся проекции перпендикулярных прямых и плоскостей.

Теорема о проекциях прямого угла

Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 10.1).

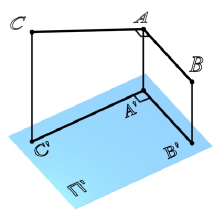
Рис. 10.1. Теорема о проекциях прямого угла

Дано :BAC = 90°; AB || П’

Доказать, что C’A’A’B’

Доказательство: если AB||П’, то A’B’||AB, но AA’П’^AA’A’B’ значит ABAA,AB плоскости CAA’C’, тогда и A’B’ CAA’C’. Следовательно,CA’A’B’.

На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П1 в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П2 — если одна из них фронталь (рис. 10.2,а).

Условие перпендикулярности скрещивающихся прямых (рис. 10.2,б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

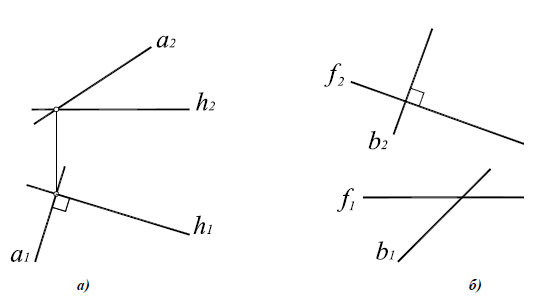
Рис. 10.2. Перпендикулярные прямые:
а -пересекающиеся a1 h1 a h ;
б -скрещивающиеся b2 2 b

Линии наибольшего наклона плоскости

Прямые, лежащие в плоскости и перпендикулярные линиям уровня этой плоскости, называются линиями наибольшего наклона к соответствующей плоскости проекций (рис. 10.3). Так, прямая, лежащая в плоскости и перпендикулярная горизонтали плоскости, называется линией наибольшего наклона к горизонтальной плоскости проекций, а прямая, перпендикулярная фронтали — линией наибольшего наклона к фронтальной плоскости проекций.

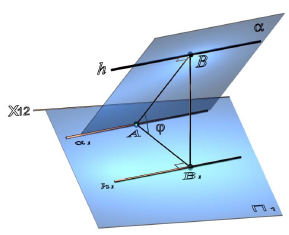
Угол между линией наибольшего наклона и ее проекцией на соответствующую плоскость равен углу наклона плоскости к плоскости проекций (см. рис. 9.15).

Рис. 10.3. Линия наибольшего наклона плоскости а к П1:
а — плоскость общего положения; h ∈α — горизонталь плоскости а; AB h — линия наибольшего наклона;
φ = AB, AB 1 — угол наклона плоскости а к П1

Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:
Если прямая а перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция — фронтальной проекции фронтали плоскости.

Например, при построении прямой а, перпендикулярной плоскости α(ABC) (рис. 10.4,а), в плоскости строятся линии уровня — горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция — фронтальной проекции фронтали плоскости.

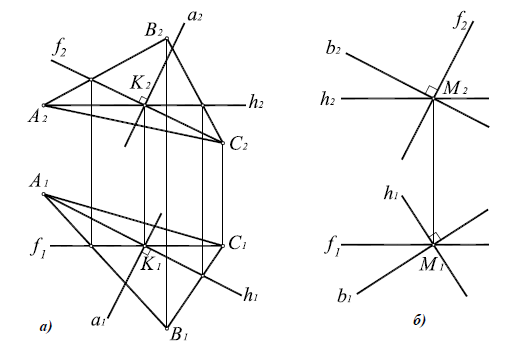
Рис. 10.4. Перпендикулярность прямой и плоскости:

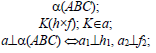
а -построение прямой, перпендикулярной плоскости:

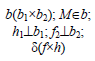
б -построение плоскости, перпендикулярной прямой:

Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 10.4,б)

Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 10.5,а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.
Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 10.5,б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.

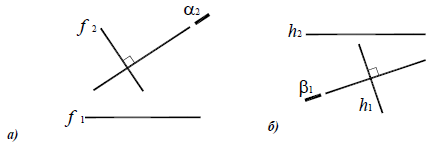
Рис. 10.5. Перпендикулярность прямой и проецирующей плоскости:
а -построение прямой, перпендикулярной плоскости;
б -построение плоскости, перпендикулярной прямой

Взаимная перпендикулярность плоскостей

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, построение взаимно перпендикулярных плоскостей сводится к построению перпендикулярных прямой и плоскости. Например, чтобы через произвольную точку А провести плоскость, перпендикулярную плоскости a(× h) (рис. 10.6), достаточно построить прямую n,перпендикулярную плоскости α(×h): n1h1; n22. Вторая прямая m, определяющая искомую плоскость, может быть задана произвольно — как пересекающая прямую n или параллельная ей.

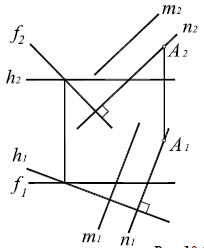
Рис. 10.6. Перпендикулярность двух плоскостей

Дано: α(h × ) ; A (A1, A2).

Построить: A ∈ β α .

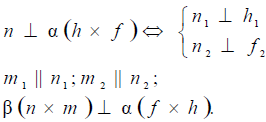
Определение метрических задач

Традиционно задачи, связанные с измерением длин, углов, площадей и объемов относят к метрическим. В основе решения этих задач лежит определение длины отрезка и, как производной от этого, площади плоской фигуры.

Определение длины отрезка

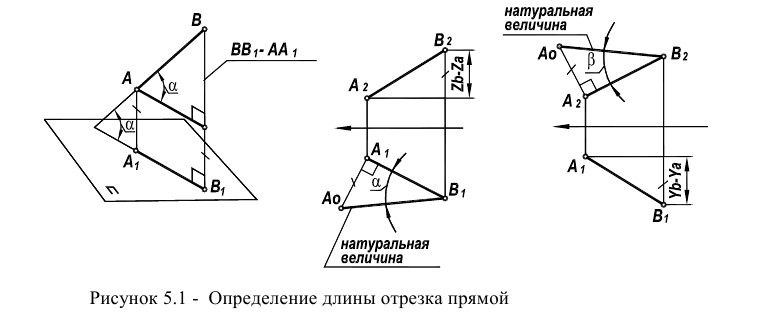
Одним из наиболее распространенных методов (рисунок 5.1) является метод прямоугольного треугольника (так его называют в начертательной геометрии) или метод ортогональных дополнений (название, принятое в линейной алгебре).

Идея метода базируется на следующем. Истинная величина отрезка AВ является гипотенузой прямоугольного треугольника, один из катетов которого, является проекцией отрезка AВ на плоскость проекции а второй катет -разница координат концов отрезка для оси, отсутствующей в рассматриваемой плоскости проекции (ортогональное дополнение). Угол между проекцией и гипотенузой этого треугольника (а) определяет наклон прямой к соответствующей плоскости проекции.

На комплексном чертеже возможно решение как на плоскости так и на плоскости При правильных построениях . Углы а и -углы наклона отрезка прямой АВ к плоскости соответственно.

Определение площади треугольника

Определение площади треугольника и величины плоского угла можно свести к известной задаче построения треугольника по трем сторонам.

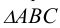
Для этого достаточно, используя рассмотренный выше способ прямоугольного треугольника, найти по порядку истинные величины сторон (в соответствии с рисунком 5.2), а затем на свободном месте построить треугольник по трем сторонам.

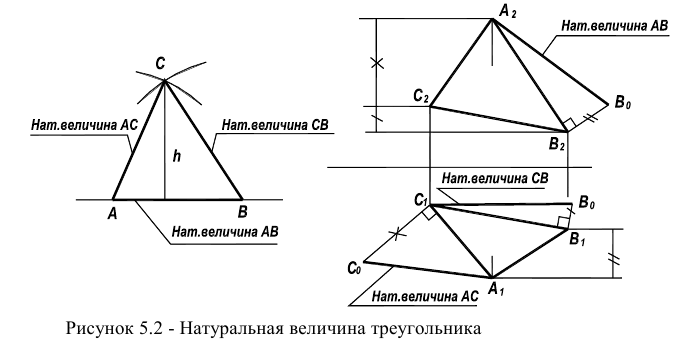
Величина плоского угла между двумя любыми сторонами этой фигуры может быть измерена на истинной величине треугольника.

Проецирование прямого угла

Решение многих задач Начертательной геометрии связано с необходимостью построения на чертеже взаимно перпендикулярных прямых и плоскостей. Базой для этого служит умение строить прямые углы на комплексном чертеже.

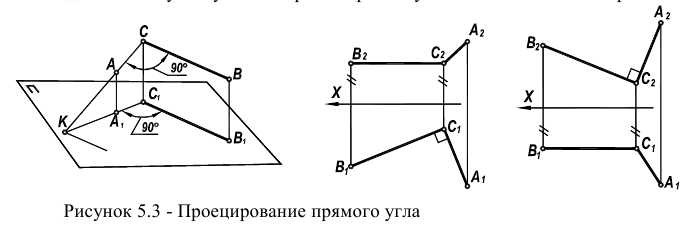
Известная в теории чертежа теорема (приведем ее без доказательства) утверждает, что прямой угол (в соответствии с рисунком 5.3) проецируется на

соответствующую плоскость проекций вез искажения, если одна из его сторон параллельна этой плоскости проекций, а вторая — ей не перпендикулярна.

Перпендикулярность прямых и плоскостей

Выше уже отмечалось, что в трехмерном Евклидовом пространстве отсутствует полная параллельность, то же самое можно сказать и о перпендикулярности. Понятие перпендикулярности так же, как и параллельности, вводится через определение.

Перпендикулярность прямой и плоскости

Считают, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся (любым) прямым этой плоскости.

При решении задачи возможны два варианта: проведение перпендикулярной прямой к плоскости из внешней точки и из точки, лежащей в плоскости.
Рассмотрим возможность проведения перпендикуляра из точки К, лежащей в плоскости общего положения Р, заданной следами (рисунок 5.4).

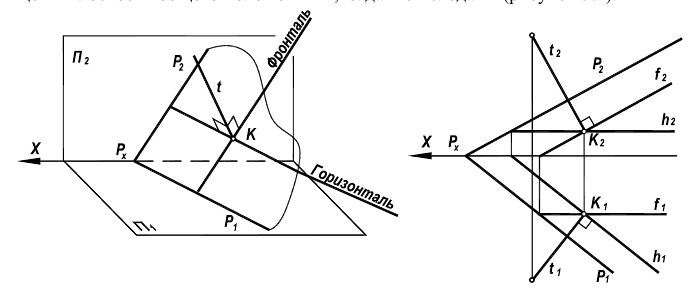
Рисунок 5.4 — Перпендикулярность прямой и плоскости

В плоскости Р (через точку К) проводятся горизонталь h и фронталь f. Прямые, перпендикулярные соответствующим проекциям линий уровня в соответствии с теоремой о проецировании прямого угла и данным выше определением, могут быть приняты за проекции прямой .

В том случае, когда точка К не лежит в плоскости Р, решение задачи аналогично (рисунок 5.5).

Поскольку положение точки пересечения искомого перпендикуляра не определено, решение соответствует следующей схеме:

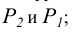
а) в плоскости проводятся горизонталь h (через точку В) и фронталь f (через точку A), в случае задания плоскости следами за фронталь и горизонталь принимаются соответствующие следы плоскости

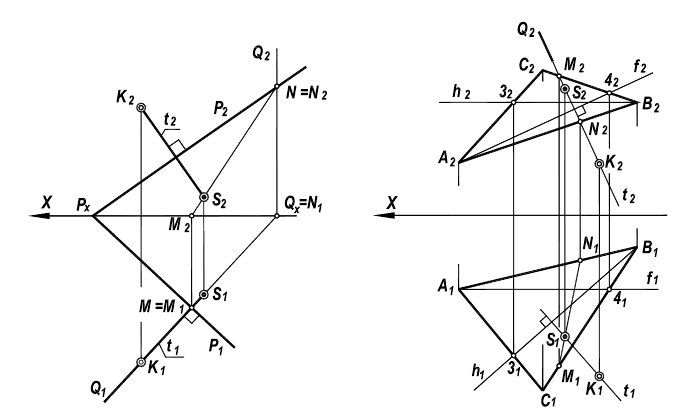
Рисунок 5.5 — Перпендикуляр к плоскости

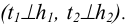
б) из внешней точки К к соответствующим проекциям линий уровня (следам) проводятся перпендикулярные прямые- Линия t принимается за перпендикуляр, опущенный из точки К к плоскости Р;

в) определяется точка S пересечения этого перпендикуляра t и плоскости.

Расстояние от точки до плоскости

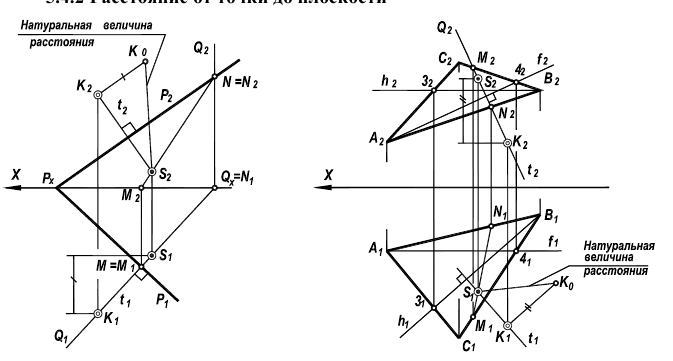
Рисунок 5.6 — Расстояние от точки до плоскости

Задачу на определение расстояние от точки до плоскости (рисунок 5.6) можно свести к решению уже известных задач на построение перпендикуляра к плоскости (рисунок 5.5) и определения натуральной величины отрезка прямой (рисунок 5.1)

Перпендикулярность плоскостей

Считают, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.

Задача может ставиться, как проведение плоскости, перпендикулярной заданной, проходящей через точку или прямую.

При проведении искомой плоскости через точку, как и в предыдущем случае, возможны два варианта проведения плоскости перпендикулярной заданной: через точку, лежащую в плоскости и через точку вне ее (рисунок 5.7).

Точно такой же вариант возникает и при проведении перпендикулярной плоскости через прямую (лежащую в исходной плоскости или не лежащую).

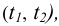
Рассмотрим вариант построения плоскости, проходящей через точку. Пусть точка А лежит в плоскости Р. Линии перпендикулярные соответствующим проекциям линий уровня (следам), определят перпендикуляр t к плоскости Р.

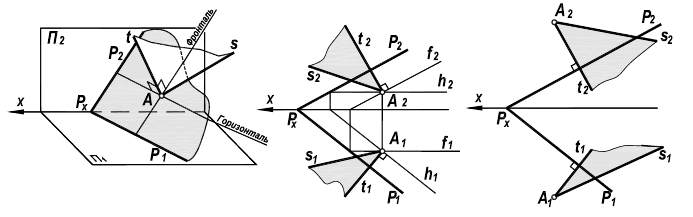
Рисунок 5.7 — Перпендикулярность плоскостей
Проведение через точку А произвольной прямой s позволяет определить плоскость Q, которая будет перпендикулярна плоскости Р.

Если точка А лежит вне плоскости Р, то решение аналогично. Проведение через точку А перпендикуляра t и произвольной прямой s определит плоскость Q, которая также, по определению, будет перпендикулярна плоскости Р.

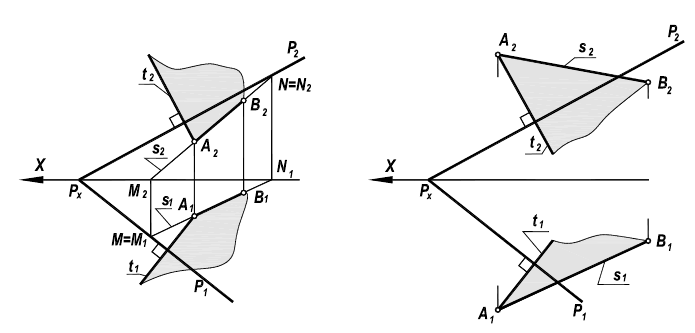
Решение задачи на проведение плоскости через прямую аналогично решению задачи по проведению плоскости через точку. Достаточно вместо произвольной прямой s использовать заданную прямую АВ. И тогда, в соответствии с рисунком 5.8, задача сведется к проведению перпендикуляра t к плоскости Р (из точки, лежащей в плоскости или лежащей вне ее).

Рисунок 5.8 — Перпендикулярность плоскостей

Определение натуральных величин геометрических элементов

1. Определить натуральную величину отрезка общего положения:

• способом прямоугольного треугольника;
• способом замены плоскостей проекций преобразовать в прямую уровня;
• способом вращения вокруг проецирующей оси преобразовать в прямую уровня.

2. Определить натуральную величину плоскости общего положения (замкнутого отсека):

• способом замены плоскостей проекций преобразовать в плоскость уровня;
• способом вращения вокруг линии уровня преобразовать в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать в плоскость уровня.

Определение расстояния между геометрическими элементами (образами)

1. Определить расстояние от точки до прямой общего положения:

• способом замены плоскостей проекций преобразовать плоскость, заданную прямой и точкой, в плоскость уровня (задачи 3 и 4 преобразования; прямую и точку рассматривать как плоскость);
• способом замены плоскостей проекций преобразовать прямую общего положения в проецирующую прямую (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную прямой и точкой, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить через заданную точку плоскость, перпендикулярную к прямой, и определить точку пересечения последней с плоскостью.

2. Определить расстояние между параллельными прямыми:

• способом замены плоскостей проекций преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня (задачи 3 и 4 преобразования);
• способом замены плоскостей проекций преобразовать две параллельные общего положения в проецирующие прямые (задачи 1 и 2 преобразования);
• способом вращения вокруг линии уровня преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня, ограничив ее замкнутым отсеком;
• способом плоскопараллельного перемещения преобразовать плоскость, заданную параллельными прямыми, в плоскость уровня;
• способом задания плоскости, перпендикулярной к прямой (3-й тип задач), построить плоскость через любую точку, принадлежащую одной из прямых, перпендикулярную ко второй прямой, и определить точку пересечения этой плоскости со второй прямой.

3. Определить расстояние между скрещивающимися прямыми, преобразовав одну из прямых в проецирующую (задачи 1 и 2 преобразования).

4. Определить расстояние от точки до плоскости:

• по теме «Перпендикулярность» – провести перпендикуляр к плоскости, построить точку пересечения этого перпендикуляра с заданной плоскостью и найти любым способом натуральную величину построенного отрезка (см. пункт 1);
• способом замены плоскостей проекций преобразовать плоскость общего положения в плоскость проецирующую.

5. Определить расстояние от точки до поверхности вращения:

• способом замены плоскостей проекций преобразовать плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня (задача 4 преобразования);
• способом вращения вокруг проецирующей оси повернуть плоскость, проведенную через точку и ось вращения поверхности, в плоскость уровня.

Определение углов наклона геометрических элементов к плоскостям проекций H и V

1. Определить углы наклона прямой общего положения к плоскостям проекций H и V:

• способом прямоугольного треугольника построить на двух проекциях натуральные величины отрезка и определить углы наклона прямой;
• способом замены плоскостей проекций преобразовать прямую общего положения в горизонтальную, а затем во фронтальную прямую (задача 1 преобразования);
• способом вращения вокруг соответствующей проецирующей оси преобразовать прямую общего положения в горизонтальную и во фронтальную прямые.

2. Определить угол наклона прямой к заданной плоскости общего положения:

• из любой точки прямой опустить перпендикуляр к плоскости;
• способом вращения вокруг линии уровня преобразовать построенную плоскость, заданную прямой и перпендикуляром, в плоскость уровня;
• искомый угол будет дополнять построенный угол до 90°.

3. Определить величину двухгранного угла, если на чертеже есть линии пересечения плоскостей, образующих двухгранный угол (ребро):

• способом замены плоскостей проекций преобразовать ребро двухгранного угла в проецирующую прямую (задачи 1 и 2 преобразования).

4. Определить угол между двумя плоскостями общего положения, если на чертеже нет линии пересечения заданных плоскостей (ребра):

• задача решается косвенным путем, для чего из любой точки пространства следует опустить перпендикуляры к заданным плоскостям, которые, в свою очередь, задают вспомогательную плоскость, перпендикулярную к этим плоскостям;
• эту вспомогательную плоскость способом вращения вокруг линии уровня следует преобразовать в плоскость уровня, определив угол между перпендикулярами (преобразование вспомогательной плоскости в плоскость уровня возможно и другими способами – ее плоскопараллельным перемещением или заменой плоскостей проекций);
• искомый угол будет дополнять построенный угол до 180° (углом между плоскостями считают угол острый).

Структуризация материала тринадцатой лекции в рассмотренном объеме схематически представлена на рис. 13.1 (лист 1). На последующих листах 2–7 компактно приведены иллюстрации к этой схеме для визуального повторения изученного материала при его повторении (рис. 13.2–13.7).

Метрические задачи:

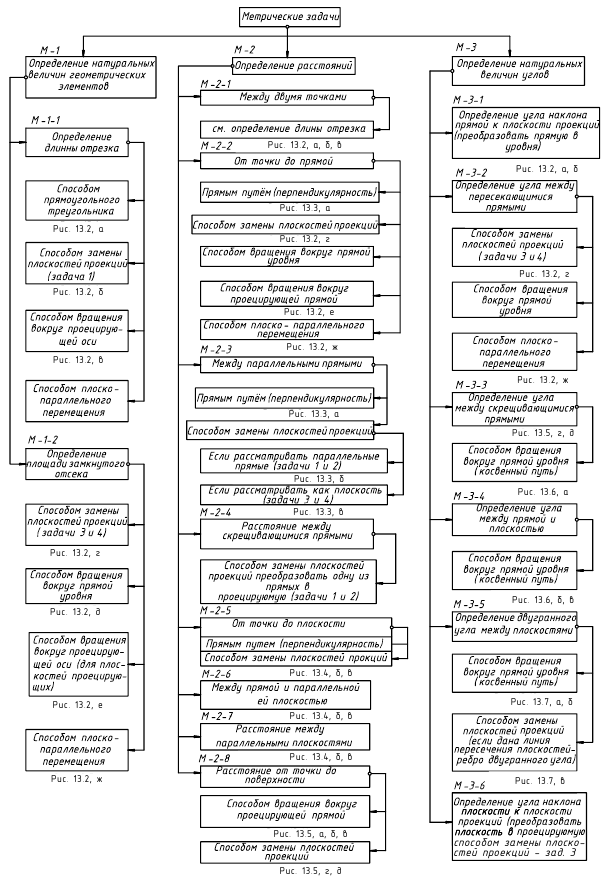
Определение натуральной величины геометрических элементов:

1. Определение длины отрезка

Способ прямоугольного треугольника

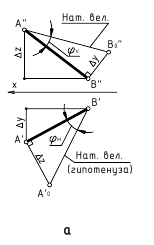
Способ замены плоскостей проекций (задача 1)

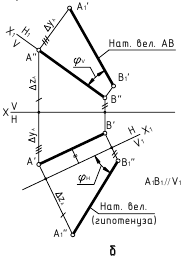
Способ вращения вокруг проецирующей оси

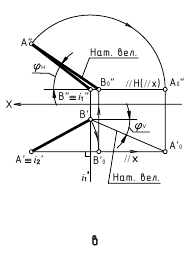
2. Определение площади замкнутого отсека

Способ замены плоскостей проекций (задачи 3 и 4)

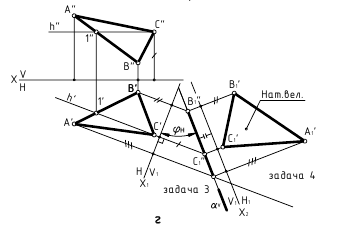
Способ вращения вокруг прямой уровня (горизонтали)

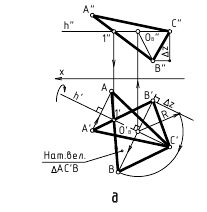
Способ вращения вокруг проецирующей оси i(i V)

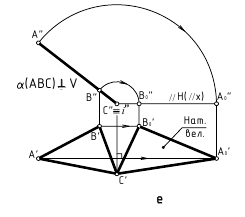
Способ плоско-параллельного перемещения (переноса)

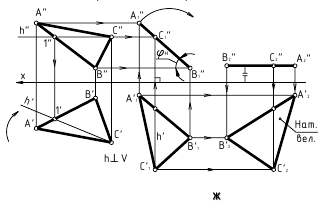
Определение расстояний:

1. Расстояние между точками — определяется величиной отрезка, соединяющего эти точки

2. Расстояние от точки до прямой — определяется величиной перпендикуляра, опущенного из точки к прямой

а. Прямой путь (перпендикулярность)

б. Способ замены плоскостей проекций: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис. 13.2, г)

в. Способ вращения вокруг прямой уровня: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, д)

г. Способ плоскопараллельного переноса: определить натуральную величину плоскости, которую определяют точка и прямая (см.рис.13.2, ж)

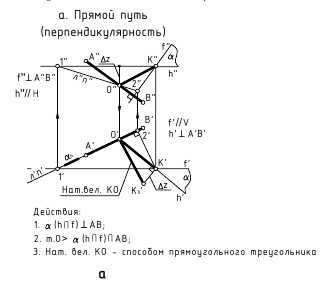
3. Расстояние между параллельными прямыми — определяется величиной перпендикуляра, проведённого из произвольной точки одной прямой к другой прямой

а. Способ замены плоскостей проекции (рассматриваем две прямые) — задачи 1 и 2 (преобразовать прямые общего положения AB и CD в проецирующие)

б. Способ замены плоскостей проекции (рассматриваем плоскость, которую определяют параллельные прямые) — задачи 3 и 4 (определить натуральную величину плоскости ? (AB//СВ))

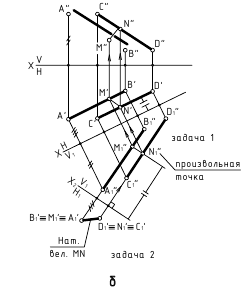
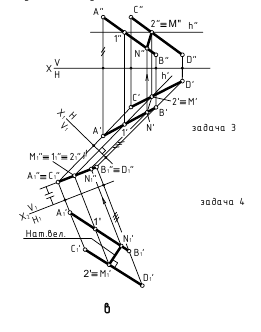
4. Расстояние между скрещивающимися прямыми — определяется величиной перпендикуляра, проведённого от одной из прямых, преобразованной в точку, к другой прямой (задачи 1 и 2 замены плоскостей проекции).

Способ замены плоскостей проекций — задачи 1 и 2

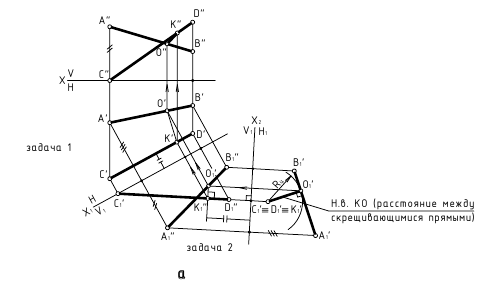
5. Расстояние от точки до плоскости — определяется величиной перпендикуляра, проведённого из точки на плоскость до точки его пересечения с этой плоскостью.

а. Прямой путь (перпендикулярность)

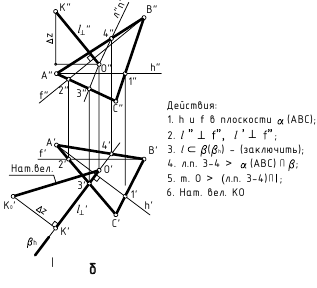
б. Способ замены плоскостей проекций (плоскость преобразовать в проецирующую — задача 3)

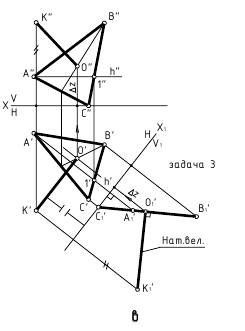
6. Расстояние между прямой и параллельной ей плоскостью — определяется величиной перпендикуляра, проведённого из произвольной точки на прямой к плоскости.

7. Расстояние между параллельными плоскостями — определяется величиной отрезка перпендикуляра, опущенного из точки одной плоскости на другую плоскость (до точки пересечения с другой плоскостью).

8. Расстояние от точки до поверхности

a. Cпособ вращения вокруг проецирующей оси

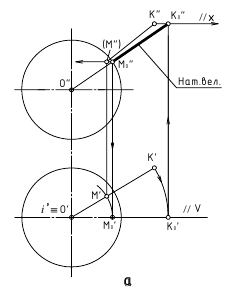
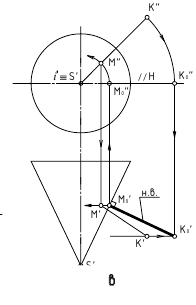
б. Способ замены плоскостей проекции

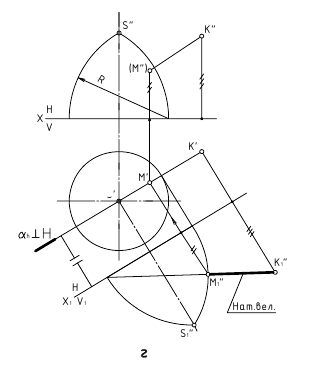
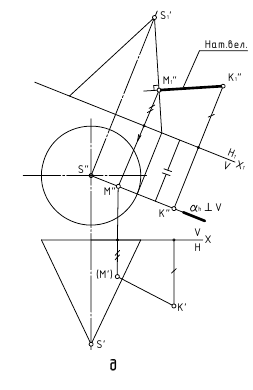
Определение величин углов:

1. Угол φ между скрещивающимися прямыми — определяется плоским углом, образованным двумя пересекающимися прямыми, проведёнными из произвольной точки пространства параллельно скрещивающимся прямым (рис. 13.6, а)

Способ вращения вокруг линии уровня

Дано:
а и b — скрещивающиеся прямые
Требуется:
∠φ — ?

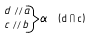
Решение:
1.
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости α(d ∩с)

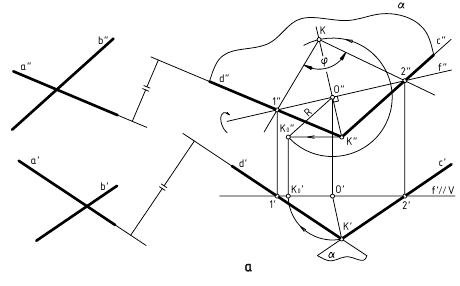
2. Угол φ между прямой и плоскостью — определяется углом между прямой и её проекцией на эту плоскость.

Дано:
α(h ∩ f);
AB — прямая общего положения
Требуется:
∠φ — ?

Решение:
1. l α(h ∩ f);
l» f»;
l’ h’;
2. ∠φ — вращением вокруг фронтали, проведённой в построенной плоскости β(AB∩l)

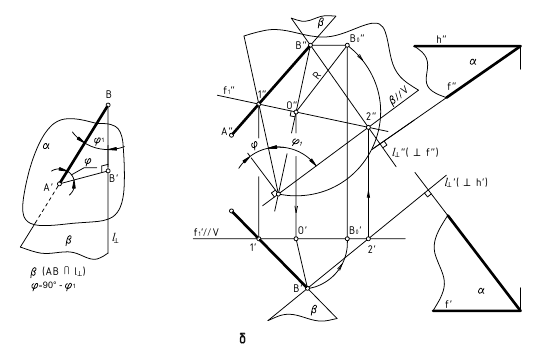
3. Угол φ между плоскостями α и β — определяется линейным углом, образованным двумя прямыми, по которым некоторая плоскость γ, перпендикулярная плоскостям (или их ребру), пересекает эти плоскости (углом между плоскостями считают острый угол).

а. Если на чертеже нет ребра (линии пересечения заданных плоскостей) — угол φ определяется способом вращения вокруг линии уровня (рис. а)

Дано:
(m // h); (а ∩ b).
Требуется:
∠φ — ?
Решение:
1. провести в заданной плоскости фронтали и горизонтали;

2. из произвольной точки пространства D (D’, D») провести перпендикуляры l1 и l2 к заданными плоскостям, которые определяют плоскость γ(l1 ∩ l2);
3. ∠φ — вращением вокруг горизонтали h3, проведённой в построенной плоскости γ(l1 ∩ l2).

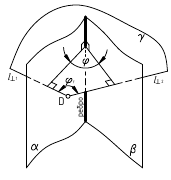
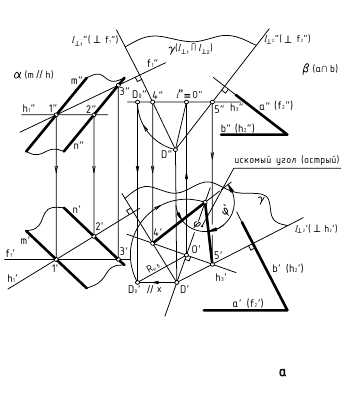
б. Если на чертеже есть ребро (линия пересечения заданных плоскостей) — угол φ определяется способом замены плоскостей проекций (задачи 1 и 2, рис. б)

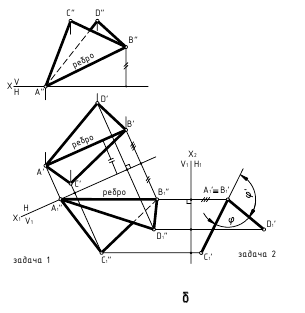
ребро АВ двугранного угла преобразовать двумя заменами в проецирующую прямую.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник: www.evkova.org