Резонанс в строительстве это

Вибрации в конструкциях и механизмах, в зависимости от характера колебаний, могут быть периодическими и случайными. Случайные вибрации представляют собой набор непериодических колебаний. Анализ случайных вибраций основывается на статистике. Примерами случайных вибраций могут служить: ветровые нагрузки на здание, вибрации в авиационной, ракетной, железнодорожной и автомобильной технике, возникающие в процессе эксплуатации.

У случайной вибрации есть ряд особенностей, которые вызывают определенные сложности при исследовании проблемы, а именно:

1. Случайная вибрация не может быть описана точными математическими соотношениями.
2. Невозможно точно предсказать значения параметров случайной вибрации в ближайший момент времени.
3. Можно с определенной вероятностью предсказать только то, что мгновенное значение амплитуды вибрации попадает в произвольно выбранный интервал значений от x1 до x1+Δx (рисунок 1).

Резонанс. Теория, примеры и практика

Рисунок 1 – Пример случайной вибрации

Периодические колебания, напротив, могут быть описаны точными математическими соотношениями и представлены как ряд Фурье. Поэтому для упрощенного описания поведения конструкции, например, в автомобилестроении, применяется данный идеализированный вариант модели описания колебаний системы.

При эксплуатации автомобиля его компоненты неизбежно испытывают вибрации (автоколебания или вынужденные колебания). При продолжительном воздействии вибрации в деталях и узлах накапливаются напряжения, что может привести к так называемой усталости металла.

Усталость металла – это процесс постепенного накопления повреждений, то есть даже при небольших деформациях в конструкции могут возникать и развиваться трещины (рисунок 2). В первую очередь в конструкции могут разрушиться наиболее нагруженные места, такие как неразъемные соединения, и, как следствие, к ним предъявляются наиболее высокие требования.

Рисунок 2 – Разрушение коленчатого вала вследствие развития усталостной трещины

Особо пагубное влияние на срок службы транспортного средства оказывает явление резонанса. Как известно, резонанс возникает при совпадении частоты внешнего воздействия с частотой собственных колебаний этой системы. При резонансе происходит резкое возрастание амплитуды колебаний системы, что приводит к большим деформациям и, как следствие, к разрушению конструкции.

Таким образом, важной задачей является проведение тестов на вибрацию для определения долговечности конструкций. В настоящее время существует возможность проводить данные эксперименты виртуально, средствами численного моделирования, в частности, с помощью ПО Ansys.

Выбор инструмента моделирования

Для определения отклика конструкции на воздействие сил, меняющихся во времени, традиционно используется одна из систем анализа Ansys Mechanical: Harmonic Response (Гармонический отклик/Гармонический анализ), Random Vibration (Случайные вибрации) или Transient Analysis (Временной анализ/Анализ переходных процессов) и пр. Сфера применения данных систем для расчета различна.

Резонанс

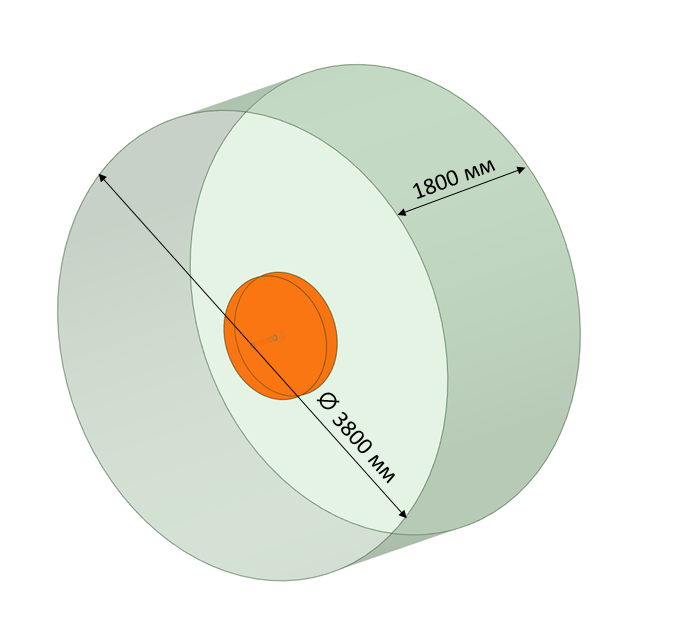
Рисунок 3 – Компоненты Ansys Workbench для решения задач вибрации

В данной статье подробнее остановимся на использовании инструментов Harmonic Response и Transient Analysis для моделирования вибрационных тестов. Гармонический анализ позволяет определять установившийся отклик системы на воздействие, действующее на конструкцию по гармоническому закону. Переходные колебания, происходящие в начале возбуждения, не учитываются в гармоническом анализе. Данный расчет также не учитывает нелинейность – как физическую, так и геометрическую.

Ниже представлено определяющее уравнение для гармонического анализа.

Рисунок 4 – Основные положения, заложенные в гармоническом анализе

Для более полного анализа отклика конструкции используется Transient Analysis. Динамический анализ переходных процессов используется для определения динамического отклика конструкции под влиянием любых меняющихся во времени сил и воздействий. В отличие от гармонического анализа, используя данный метод, мы можем учитывать нелинейности любого типа.

В случае анализа переходных процессов мы имеем дело с более общим уравнением, отличающимся от определяющего уравнения гармонического анализа тем, что в правой части стоит произвольная (но меняющаяся во времени) нагрузка.

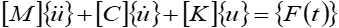
Таким образом, если нагрузка, зависящая от времени, не подчиняется гармоническому закону или же необходим учет нелинейного поведения материала, больших перемещений, то выбор очевиден – Transient Analysis. Но стоит отметить, что данный тип анализа требует больших вычислительных ресурсов, и время расчета намного выше, чем при гармоническом анализе.

Постановка задачи

В качестве примера рассмотрим автомобильный спойлер, представленный на рисунке 4, изготовленный из стали (стойки и закрылки) и алюминия (лезвие). Вибрация воздействует на спойлер с частотой 48 Гц и ускорением вибрации 32 мм/с 2 , направленным перпендикулярно поверхности закрылков. Необходимо обеспечить длительную прочность конструкции в течение 1.5 часов виброиспытаний.

Рисунок 5 – Геометрия спойлера

Определим усталостную долговечность конструкции под воздействием заданной циклической нагрузки. Долговечность конструкции определяется при помощи кривой Веллера (S-N кривой), представляющей собой зависимость напряжений, при которых происходит разрушение материала, от числа этих циклов. Пример данной кривой для стали 3 представлен на рисунке 6.

Рисунок 6 – Пример кривой усталости (S-N кривой) для Ст3

Определение собственных частот колебаний

Анализ конструкции под воздействием вибрации начинается с определения собственных частот и форм колебаний этой конструкции для выявления возможной близости расчетной частоты к резонансной.

Для рассматриваемой конструкции спойлера самая близкая собственная частота к расчетной – 48,32 Гц. Форма колебаний, соответствующая данной частоте, представляет собой колебания вдоль оси Y, то есть колебания перпендикулярно лезвию спойлера (рисунок 7).

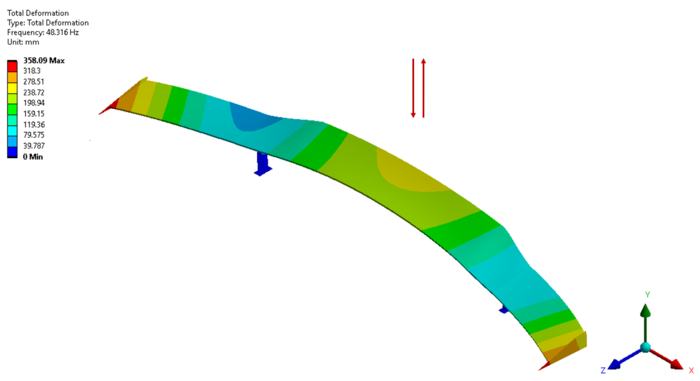
Рисунок 7 – Форма колебаний на резонансной частоте

Решение задачи Harmonic Response VS Transient Structural

Для определения времени работы конструкции в данном режиме проведем гармонический анализ. Спойлер закреплен на корпусе автомобиля по основаниям стоек, ускорение вибрации направлено перпендикулярно лезвию спойлера (вдоль оси Y).

В результате расчета получаем распределение напряжений, представленное на рисунке 8. Мы видим, что максимум достигается в месте сужения стойки. Данный факт обусловлен наличием концентратора напряжений.

Вообще, при создании конструкции, которая должна работать безотказно под воздействием повторяющихся (усталостных) нагрузок, необходимо, по возможности, избавляться от концентраторов напряжений, которыми могут являться: острые углы, переходы валов на другой диаметр, сварные соединения и так далее. Для каждого из видов концентраторов напряжений применяются различные действия по уменьшению величины напряжений в них. Для острых углов – это скругления достаточного радиуса; для сварных швов – более качественное выполнение сварки с зачисткой поверхности шва.

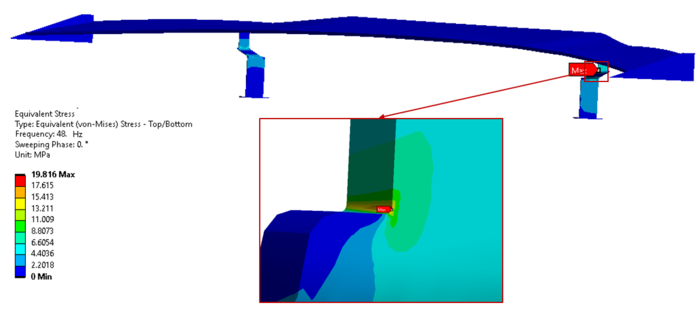
Рисунок 8 – Распределение эквивалентных напряжений, МПа

Теперь узнаем, насколько долговечен спойлер с имеющейся конструкцией стоек. Срок жизни будем определять согласно усталостной кривой Веллера для стали (рисунок 9).

Рисунок 9 – Кривая Веллера, используемая в расчете

На рисунке 10 представлена долговечность конструкции в часах. Время жизни стойки составляет чуть больше получаса, что говорит о необходимости внесения конструктивных изменений.

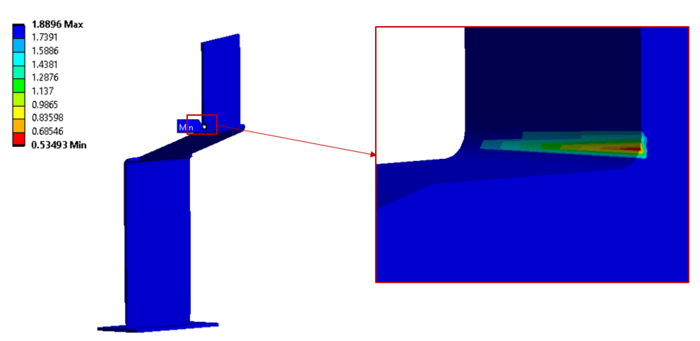
Рисунок 10 – Долговечность стойки спойлера, часы

Для обеспечения требуемой долговечности конструкции возможно внесение одного или нескольких конструкционных изменений. Такими изменениями для расчетного объекта могут быть:

1. Увеличение толщины конструкции.
2. Удаление концентраторов напряжений из модели.
3. Предотвращение появления ослабленных сечений (особенно в местах закрепления).

В нашем случае увеличим радиус скругления концентратора с 0.05 мм до 0.25 мм. Теперь минимальное время жизни спойлера, согласно гармоническому анализу, составляет более полутора часов (рисунок 11), что соответствует поставленным требованиям.

Рисунок 11 – Долговечность стойки спойлера, часы

Для верификации проведем расчет измененной конструкции в Transient Structural с учетом нелинейности. На рисунке 12 представлено распределение эквивалентных напряжений. Максимальное значение напряжений возникает в начале колебательного процесса, и далее амплитуда напряжений выходит на плато.

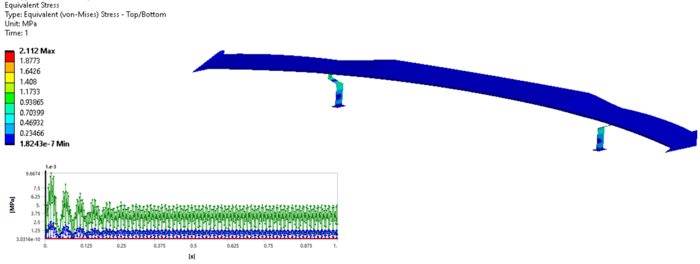
Рисунок 12 – Распределение эквивалентных напряжений, МПа

Долговечность конструкции после конструктивных изменений удовлетворяет требованиям поставленной задачи (рисунок 13).

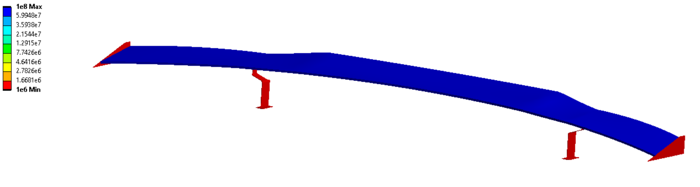
Рисунок 13 – Долговечность конструкции, циклы

Конструкции, на работу которых накладываются условия обеспечения усталостной долговечности, необходимо подвергать вибрационным испытаниям: первичным и после каждого конструкционного изменения. При таком подходе натурные вибрационные тесты экономически неэффективны, поэтому всё чаще их заменяют виртуальными испытаниями.

В ходе виртуального вибрационного теста с помощью ПО Ansys подобран оптимальный радиус скругления для конструкции стоек. Внесенное конструкционное изменение обеспечивает требуемую долговечность конструкции спойлера.

Источник: multiphysics.ru

резонанс конструкции

3.14 резонанс конструкции: Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных колебаний изделия.

3.12 Резонанс конструкции — явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных колебаний конструкции изделия (ГОСТ 30630.0.0).

Примечание — Настоящее определение применяют также к понятию «Резонанс промежуточной конструкции».

3.12 Резонанс конструкции — явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных колебаний конструкции изделия (ГОСТ 30630.0.0).

Примечание — Настоящее определение применяют также к понятию «Резонанс промежуточной конструкции».

Смотри также родственные термины:

3.1.15 резонанс конструкции (изделия) : Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два и более раз при постоянном внешнем воздействии, возникающих на частотах вибрационных нагрузок, близких к частоте собственных (свободных) колебаний изделия — по ГОСТ 24346.

3.16 резонанс конструкции изделия: Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных колебаний конструкции изделия.

Словарь-справочник терминов нормативно-технической документации . academic.ru . 2015 .

Полезное

Смотреть что такое «резонанс конструкции» в других словарях:

резонанс конструкции — Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных колебаний конструкции изделия (ГОСТ 30630.0 … Справочник технического переводчика

резонанс конструкции изделия — Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных колебаний изделия [ГОСТ 20.57.406 81]… … Справочник технического переводчика

резонанс конструкции изделия — 3.16 резонанс конструкции изделия: Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два раза и более при постоянном внешнем воздействии, возникающее на частотах вибрационных нагрузок, близких к частоте собственных… … Словарь-справочник терминов нормативно-технической документации

резонанс конструкции (изделия) — 3.1.15 резонанс конструкции (изделия) : Явление увеличения амплитуды вынужденных колебаний конструкции изделия в два и более раз при постоянном внешнем воздействии, возникающих на частотах вибрационных нагрузок, близких к частоте собственных… … Словарь-справочник терминов нормативно-технической документации

Резонанс — 9 Резонанс По ГОСТ 24346 80 Источник: ГОСТ 26382 84: Двигатели газо … Словарь-справочник терминов нормативно-технической документации

Резонанс — (франц. resonance, от лат. resono звучу в ответ, откликаюсь) явление резкого возрастания амплитуды вынужденных колебаний (См. Вынужденные колебания) в какой либо колебательной системе (См. Колебательные системы), наступающее при… … Большая советская энциклопедия

РЕЗОНАНС — (франц. resonance, от лат. resono звучу в ответ, откликаюсь) более или менее резкое возрастание амплитуды А установившихся вынужденных колебаний системы, когда частота w внеш. воздействия на колебат. систему приближается к к. л. из частот соо её… … Большой энциклопедический политехнический словарь

Земной резонанс вертолёта — самовозбуждающиеся связанные колебания лопастей винта вертолёта в плоскости его вращения и фюзеляжа или другой поддерживающей винт, конструкции, вызывающие перемещения втулки винта в плоскости его вращения. Колебания лопастей происходят из за… … Энциклопедия техники

«земной резонанс» — вертолёта — самовозбуждающиеся связанные колебания лопастей винта вертолёта в плоскости его вращения и фюзеляжа или другой, поддерживающей винт, конструкции, вызывающие перемещения втулки винта в плоскости его вращения. Колебания лопастей… … Энциклопедия «Авиация»

«земной резонанс» — вертолёта — самовозбуждающиеся связанные колебания лопастей винта вертолёта в плоскости его вращения и фюзеляжа или другой, поддерживающей винт, конструкции, вызывающие перемещения втулки винта в плоскости его вращения. Колебания лопастей… … Энциклопедия «Авиация»

Источник: normative_reference_dictionary.academic.ru

Резонанс в строительстве это

Постановка задачи. Явление Резонанса.

До сих пор мы решали основную задачу сопротивления материалов, определяли размеры поперечных сечений частей конструкции и выбирали для них материал лишь при статическом действии нагрузок.

Статическое действие нагрузок имеет место, когда при передаче давления от одной части конструкции на другую или при действии объемных сил механическое движение этих частей не меняется с течением времени. В этом случае каждый элемент конструкции находится в равновесии под действием внешних нагрузок и напряжений.

Постоянство движения характеризуется тем, что скорость рассматриваемых деталей и каждой их части не меняется — отсутствует ускорение частиц этих элементов. Наличие же ускорения частиц рассматриваемого тела или соприкасающихся с ним деталей характеризует уже воздействие динамической нагрузки. Так, давление земли на подпорную стенку будет статической нагрузкой, так как ни стенка, ни земляная масса не движутся, — скорость их постоянна и равна нулю.

Точно так же статическим будет действие поднимаемого груза на канат при постоянной скорости подъема груза. Наоборот, это действие будет динамическим, если груз поднимается с ускорением. Динамическую нагрузку испытывают шатуны паровых машин и двигателей внутреннего сгорания, так как отдельные элементы их движутся с переменной скоростью. В качестве других примеров конструкций, работающих на динамическую нагрузку, можно указать на фундамент машины, имеющей вращающиеся части, расположенные внецентренно относительно оси вращения, — они будут испытывать центростремительное ускорение; можно указать на фундамент и шток парового молота, так как боек молота при ковке теряет свою скорость за очень короткий период времени, что связано с сообщением ему весьма больших ускорений.

Уже из этих примеров видно, что на практике мы можем встречаться с различными видами ускорения рассматриваемой детали или соприкасающихся с ней тел; оно может быть постоянным по величине и направлению или только по направлению; может быть знакопеременным.

При переменных и знакопеременных напряжениях мы встречаемся с явлением разрушения от постепенно развивающейся трещины — с явлением усталости. При резком изменении скорости движения элемента конструкции в зависимости от передачи на него давлений от соседних деталей, когда имеет место явление удара, может обнаружиться хрупкость в таких материалах, которые при статическом действии нагрузок оказывались пластичными. Поэтому при проверке прочности деталей конструкций, подвергающихся действию динамических нагрузок, приходится интересоваться влиянием этих нагрузок не только на величину напряжений в детали, но и на сопротивляемость материала.

Влияние ускорений точек деталей конструкции на напряженное состояние материала может быть учтено следующим образом. Если какое-либо тело движется с ускорением, то это значит, что на него передаются (к нему приложены) силы (давления) от других тел; по закону равенства действия и противодействия оно передает на эти тела равные приложенным силам и противоположно направленные реакции, называемые силами инерции. Это рассуждение применимо также и к каждому элементу движущегося с ускорением тела; этот элемент будет передавать на прилегающие части материала усилия, равные силе инерции этого элемента.

Таким образом, при ускоренном движении частей конструкции в них возникают добавочные вполне реальные напряжения, которые эквивалентны статическим напряжениям, вызванным силами инерции; от каждого элемента стержня на соседние части материала будут передаваться такие напряжения, как будто бы к нему была приложена соответствующая сила инерции.

Отсюда получаем практическое правило для определения напряжений в части конструкции, точки которой испытывают ускорения: надо вычислить эти ускорения и в дополнение к внешним силам, действующим на рассматриваемый элемент конструкции, нагрузить его соответствующими силами инерции. Дальше следует вести расчет так, как будто на стержень действует статическая нагрузка.

Здесь надо различать три случая. Если величина и расположение внешних сил, приложенных к рассматриваемому элементу, не зависят от его деформаций, если эти деформации не изменяют характера движения стержня, то ускорения его точек вычисляются по правилам кинематики твердого тела, и учет динамических воздействий сводится к добавочной статической нагрузке соответствующими силами инерции. Это имеет место в большинстве практически важных случаев (за исключением удара).

Если при этом ускорение будет меняться, то, как правило, возникнут колебания рассматриваемой части конструкции, которые могут в некоторых случаях дать явление, резонанса, связанное с резким увеличением деформаций и напряжений. Эти напряжения могут достигать весьма большой величины и будут прибавляться к тем, которые учитываются путем введения в расчет статической нагрузки силами инерции.

Наконец, могут быть случаи (удар), когда величина ускорений, а значит, и соответствующих сил инерции будет зависеть от деформируемости рассматриваемых элементов; в этом случае при вычислении сил инерции приходится использовать и данные сопротивления материалов.

Способ проверки прочности для каждого из указанных случаев покажем на примерах.

Влияние резонанса на величину напряжений.

Если на балке расположена машина с вращающимся грузом, имеющим эксцентриситет по отношению к оси вращения (Рис.1,). то

Рис.1. Расчетная схема неуравновешенного ротора машины

Сила инерции груза будет вызывать в балке напряжения и деформации, периодически меняющие свой знак. Балка будет совершать колебания с периодом, равным периоду вращения груза. Это будут так называемые вынужденные колебания. Если период вынужденных колебаний совпадет с периодом свободных колебаний стержня, то мы получим явление резонанса, при котором амплитуда (размах) колебаний будет резко расти с течением времени. Наличие сил трения, сопротивление воздуха и т. д. ограничивают на практике рост этой амплитуды; однако она может достичь очень большой величины, значительно превышающей те деформации, которые испытывала бы конструкция под действием ускорений той же величины, но не меняющих знака.

Известен случай, когда при резонансе угол закручивания вала увеличился в шесть раз по сравнению с тем углом, который был до наступления резонанса, — это был случай поломки коленчатых валов двигателей «Цеппелина» при первом его перелете через Атлантический океан.

Таким образом, явление резонанса, если оно длится некоторое время, а не сбивается немедленно по возникновении, ведет к постепенному росту деформаций и пропорциональных им напряжений в конструкции, что может вызвать поломку. Поэтому, как правило, при проектировании конструкций, испытывающих переменные ускорения с постоянным периодом, необходимо избежать возникновения явления резонанса.

Так как период раскачивающих (возмущающих) сил обычно является заданным, то в распоряжении проектировщика остается лишь период собственных свободных колебаний конструкции, который надо подобрать так, чтобы он в должной мере отличался от периода изменений возмущающей силы.

Вопросы, связанные с определением периода, частоты и амплитуды свободных и вынужденных колебаний, рассматриваются в курсах теоретической механики. Поэтому ограничимся лишь приложением полученных там выводов к определению напряжений и проверке прочности элементов конструкции при колебаниях.

Вычисление напряжений при колебаниях.

Упругая система, выведенная каким-либо путем из равновесия, приходит в колебательное движение. Колебания происходят около положения упругого равновесия, при котором в нагруженной системе имели место статические деформации и соответствующие им статические напряжения ( или — в зависимости от вида деформации). При колебаниях к статическим деформациям добавляются динамические, зависящие от вида колебательного движения и от величины размаха (амплитуды) колебаний. В связи с этим изменяются и напряжения . Таким образом, при расчете колеблющейся системы на прочность необходимо уметь вычислять динамические добавки к статическим деформациям и соответствующим им напряжениям.

Во многих случаях характер колебаний системы может быть определен одной какой-нибудь величиной (одной координатой). Такие системы называются системами с одной степенью свободы; таковы, например, растянутая или сжатая незначительного веса пружина с грузом на конце, совершающая продольные колебания; небольшого (сравнительно с грузом Q) собственного веса балка, изображенная на Рис.2, колеблющаяся в направлении, перпендикулярном к ее оси, и т. п.

Рис.2. Динамическая модель колебаний системы с одной степенью свободы.

При колебаниях систем с одною степенью свободы полные деформации системы в каком либо сечении могут быть найдены путем сложения статической деформации с добавочной деформацией при колебаниях. Для проверки прочности системы, очевидно, необходимо найти наиболее опасное сечение с наибольшей в процессе колебаний суммарной величиной деформации. В простейших случаях для этого потребуется сложить наибольшую статическую деформацию с наибольшей амплитудой колебаний А, т. е.

Пока система деформируется в пределах упругости, напряжения пропорциональны деформациям. Поэтому

— коэффициент динамичности при колебаниях. Условие прочности в этом случае должно иметь такой вид:

Таким образом задача нахождения динамических напряжений и проверки прочности при колебаниях может быть сведена к определению статических напряжений и коэффициента динамичности . Так как последний зависит от величины А, то нужно уметь определять наибольшее значение амплитуды колебаний в разных случаях.

Как известно, дифференциальное уравнение движения колеблющегося груза Q в случае свободных колебаний можно представить в виде уравнения равновесия, в котором кроме внешней силы (веса груза Q) и силы упругого сопротивления системы учитывается также и сила инерции:

Здесь х — координата, полностью определяющая положение груза Q во время колебаний; Р — полное упругое сопротивление системы при колебаниях; — так называемая восстанавливающая сила (добавочное упругое усилие, возникающее в системе в результате перемещения точки приложения груза Q на расстояние х при колебаниях), которую в пределах упругости можно считать пропорциональной координате х (); с — коэффициент пропорциональности, представляющий собой усилие, необходимое для того, чтобы вызвать равную единице статическую деформацию системы в направлении действия груза Q. Если статическая деформация от груза Q равна , то .

Решение уравнения (1) приводит к таким формулам для вычисления частоты и периода свободных колебаний:

Свободные колебания невесомого тела суть простые гармонические колебания с частотой (периодом), равной частоте (периоду) колебаний математического маятника, длина которого равна статической деформации системы от груза Q. Так, например, если груз Q растягивает призматический стержень,

при изгибе балки на двух шарнирных опорах грузом Q посредине пролета

Если на упругую систему, кроме груза Q и силы упругого сопротивления системы Р, в том же направлении действует периодически меняющаяся возмущающая сила S и сила сопротивления среды R, то дифференциальное уравнение движения груза Q при колебаниях также может быть представлено в виде уравнения равновесия, подобного уравнению (1):

Силу сопротивления среды R на практике в довольно большом числе случаев можно считать пропорциональной первой степени скорости колебательного движения, т. е. . Если возмущающая сила S меняется по синусоидальному закону:

где , а — частота возмущающей силы, то уравнение (2) может быть переписано так:

Здесь — так называемый коэффициент затухания колебаний,

a — найденная выше частота свободных колебаний системы, возникающих при отсутствии как возмущающей силы S так и силы сопротивления R.

Решение уравнения (3) приводит к такому выражению для амплитуды А вынужденных колебаний при наличии сил сопротивления:

— статическая деформация системы от наибольшей величины возмущающей силы S (). Отношение амплитуды вынужденных колебаний А к величине деформации называется коэффициентом нарастания колебаний :

Таким образом, формула (35.21) для динамического коэффициента получает теперь такой вид:

В этом выражении не учтена амплитуда собственных колебаний системы, которая может иметь сколько-нибудь существенное значение лишь в самом начале процесса колебаний; при наличии сил сопротивления она довольно быстро уменьшается с течением времени.

На рис.3 приведены графики изменения коэффициента нарастания колебаний в зависимости от величины отношения при разных значениях коэффициента затухания колебаний n ( отношения ). Если частота изменения возмущающей силы близка к частоте свободных колебаний системы, т. е. , и если величина коэффициента затухания колебаний сравнительно невелика, то знаменатели формул и для A и будут очень малыми, амплитуда колебаний и коэффициент нарастания колебаний будут очень большими. В этом случае даже небольшая возмущающая сила может вызвать высокие напряжения (явление резонанса).

Рис.3. Амплитудно-частотные характеристики системы.

С увеличением сил сопротивления явление резонанса становится все менее заметным. Заметим, однако, что силы сопротивления значительно уменьшают величину амплитуды вынужденных колебаний только вблизи от резонанса при других величинах отношения — влияние сил сопротивления незначительно.

Из рис. 3 видно, что если частота изменения возмущающей силы S очень мала, то амплитуда колебаний приближается к величине , коэффициент нарастания колебаний стремится к единице и наибольшие напряжения в системе могут быть вычислены как статические напряжения от груза Q и наибольшего значения возмущающей силы S.При очень большой частоте изменения возмущающей силы S амплитуда колебаний и коэффициент нарастания колебаний стремятся к нулю, груз Q можно рассматривать как неподвижный; поэтому наибольшее напряжение в системе равно статическому напряжению от груза Q.

Это обстоятельство имеет очень большое практическое значение; оно используется при конструировании разного рода поглотителей колебаний, сейсмографов, вибрографов и других приборов. В машиностроении амортизаторы, предохраняющие основания машин от усилий, возникающих при колебаниях, подбираются так, чтобы частота собственных колебаний машины на амортизаторах была значительно меньше частоты изменения возмущающей силы.

Учет массы упругой системы при колебаниях.

Если колеблющаяся система, несущая груз Q, обладает довольно значительной распределенной массой (число степеней свободы, следовательно, велико), то упрощенные расчеты, будут иметь уже значительную погрешность. В этом случае дифференциальные уравнения движения составляются с учетом массы системы. При решении подобного рода задач удобнее исходить не из условий равновесия, а из закона сохранения энергии.

Полагая, что количество энергии, сообщенное системе при выведении ее из положения равновесия и представляющее собой сумму кинетической и потенциальной энергии груза и упругой системы, при свободных колебаниях остается постоянным, получаем уравнение

Это уравнение показывает, что при колебаниях происходит непрерывный процесс преобразования энергии из одного вида в другой, не сопровождающийся какими-либо потерями энергии. Когда упругая система достигает одного из крайних положений, в котором скорость колебательного движения равна нулю, а следовательно, равна нулю и кинетическая энергия (T=0), потенциальная энергия груза и системы достигает наибольшего значения ; наоборот, в положении равновесия и .

Заметим, что принцип, положенный в основу этого уравнения, применим лишь для систем с одной степенью свободы, так как закон сохранения энергии не учитывает обмена энергии, происходящего в системах с несколькими степенями свободы. Таким образом, решение задачи о колебаниях системы с большим числом степеней свободы здесь сводится к простейшей задаче и мы сможем приближенно найти лишь одну (первую) частоту свободных колебаний.

Рассмотрим теперь некоторые примеры использования исходного уравнения.

В качестве первого примера исследуем колебания груза Q, подвешенного к нижнему концу призматического стержня длиной l, площадью поперечного сечения F и удельным весом (Рис. 4). Выведенный из положения равновесия и затем предоставленный самому себе груз начнет совершать продольные колебания около положения равновесия. Составим выражения для U и Т колеблющейся системы: груз — стержень.

Рис.4. Расчетная схема колебаний подвешенного груза

Потенциальная энергия системы по сравнению с положением равновесия изменится на , где — потенциальная энергия системы в начальный момент (в положении равновесия), a — в момент t.

Потенциальную энергию груза Q в начальный момент обозначим через ; потенциальная энергия стержня в тот же момент равна , где — статическая деформация стержня от груза Q.

В момент t, когда груз переместится на расстояние х и стержень получит такую же дополнительную деформацию х, потенциальная энергия груза уменьшится на Qx, а сила упругого сопротивления стержня и статическая деформация его увеличатся в отношении . Поэтому

Кинетическая энергия системы складывается из кинетической энергии груза и стержня . Кинетическая энергия груза . При вычислении кинетической энергии стержня учтем, что в некоторый момент t скорость груза и нижнего конца стержня равна х’, а верхнего — нулю. Скорости промежуточных сечений будут иметь значения, заключающиеся между этими двумя.

Предположим, что при колебаниях перемещения всех сечений стержня по отношению к закрепленному концу меняются по тому же закону, что и при статическом растяжении, т. е. пропорционально расстоянию от закрепленного сечения. Таким образом, если нижнее сечение стержня переместилось на величину х, то сечение, отстоящее от места защемления на , переместится на величину , скорость этого сечения будет равна . Живая сила элемента стержня длиной , отстоящего на от закрепленного конца, будет равна:

Кинетическая энергия всего стержня будет равна сумме величин , т.е.

Таким образом, живая сила стержня равна живой силе груза, имеющего массу , т. е. равную трети массы стержня, и двигающегося с той же скоростью х’, что и груз Q. Полная же кинетическая энергия системы груз — стержень будет:

Подставляя Т и выражение U (4) в уравнение (5), дифференцируем последнее по t и находим:

Здесь — статическая деформация от груза . Полученное дифференциальное уравнение движения с учетом массы колеблющегося стержня отличается от полученного ранее уравнения только величиной множителя при х и полностью совпадает с ним, если пренебречь массой стержня. Поэтому поправка на массу стержня, которую нужно ввести в предыдущие расчеты, состоит в том, что при определении частоты свободных колебаний стержня статическая деформация его вычисляется не от груза Q, но от груза Q, сложенного с одной третью веса стержня. Таким образом, учет массы колеблющегося стержня уменьшает частоту свободных колебаний и увеличивает их период. Величину называют приведенной массой стержня.

Источник: toehelp.ru

Явление резонанса

Резонансная новость, резонансный томограф, трансформатор, преобразователь и даже резонансная черта. Что общего у этих словосочетаний? Резонанс — это физический термин или бытовой? Как открытия Галилео Галилея в области маятников и музыкальных струн помогли современным ученым изобрести радио, телевизор и даже смартфоны? Обо всем этом и даже больше мы поговорим в сегодняшней статье.

22 сентября 2022

· Обновлено 27 сентября 2022

Колебания и частота

Но сначала нам нужно сделать небольшой шаг назад: прежде чем обсуждать понятие резонанса, вспомним, что такое колебания.

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Движение качелей, приливы и отливы, качание маятника — все это примеры колебательного движения.

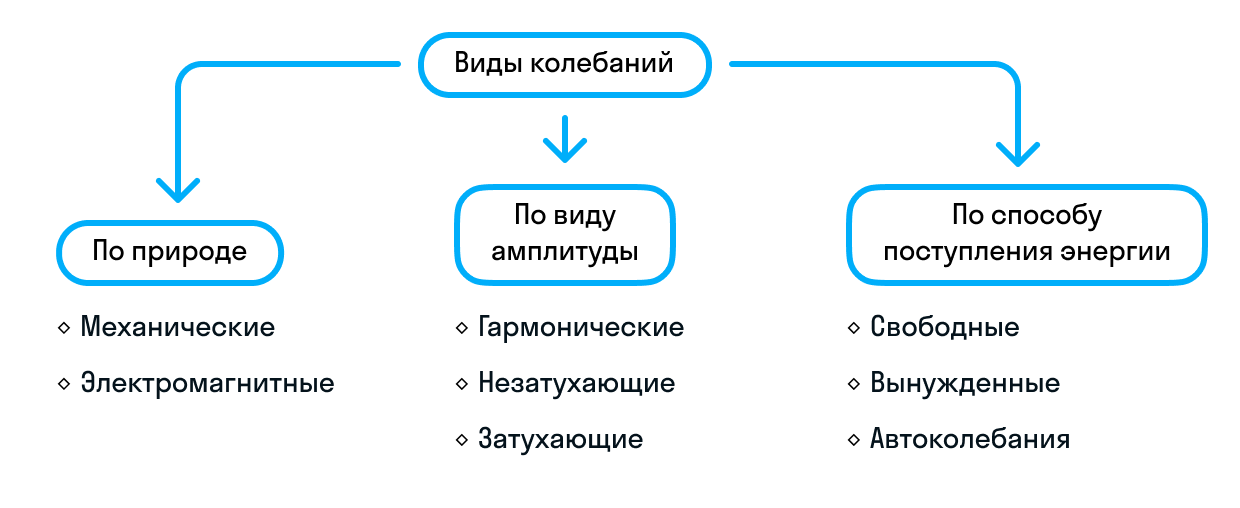
Виды колебаний

Колебания классифицируют по-разному. Если говорить об их природе, то можно выделить механические и электромагнитные колебания. В обоих случаях происходит периодическое изменение физической величины, только при механических колебаниях это изменение ускорения, скорости и координаты тела, а при электромагнитных — напряжения,силы тока и заряда.

По способу поступления энергии колебания делятся на свободные, вынужденные и автоколебания.

Свободные колебания — колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия. Например: колебание струны гитары, движение шарика на нити, изменение положения качелей или ветки дерева, с которой спрыгнул кот.

Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил. К ним можно отнести качание ветки из-за ветра, работу иглы швейной машинки и всех электрических приборов, движение поршня в ДВС.

Автоколебания — незатухающие колебания, которые существуют за счет поступления энергии в систему под ее же управлением. Это и сокращение сердца, и транзисторы, и колебания маятника в часах. Подумайте и ответьте самостоятельно, почему эти примеры нам подходят?

По виду амплитуды колебания делятся на:

гармонические (физическая величина изменяется с течением времени по гармоническому закону — закону синуса или косинуса);

затухающие (колебания, энергия которых уменьшается с течением времени);

незатухающие (колебания, энергия которых с течением времени не изменяется).

Характеристики колебаний

Помимо классификации, колебания характеризуются определенными физическими терминами, которые позволяют описать колебания количественно.

Амплитуда колебаний — максимальное значение смещения или изменения переменной величины.

Если мы рассмотрим волновое движение как пример колебания, то гребни волны (максимальное и минимальное значение функции) будут показывать её амплитуду.

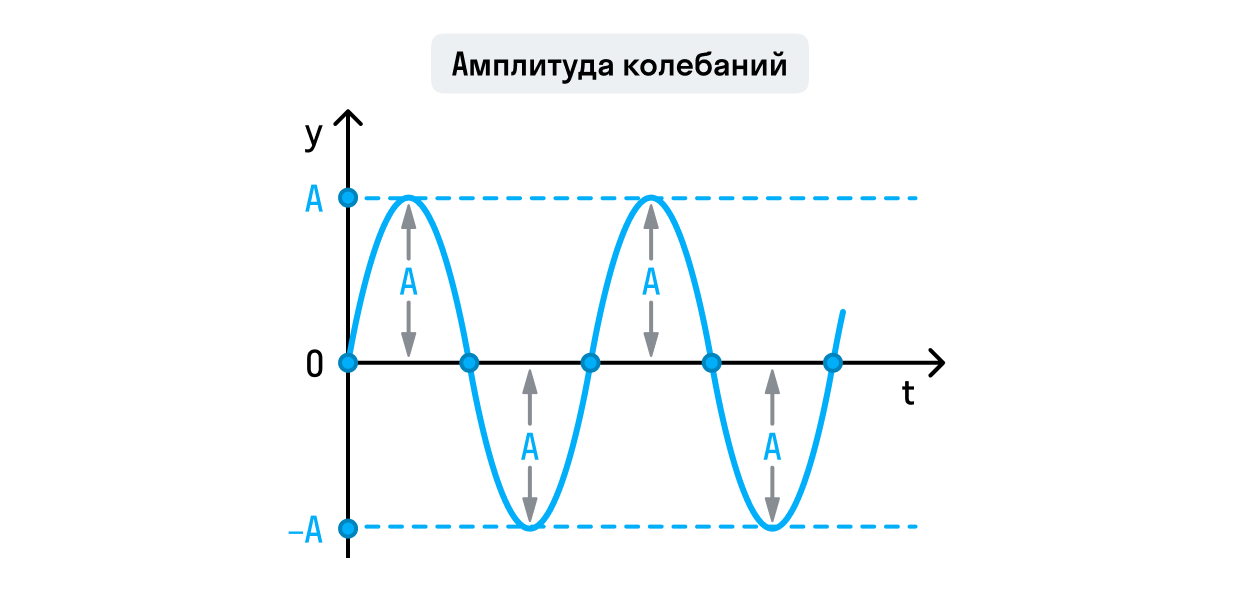
Если мы говорим о движении маятника, то амплитуда — это максимальное расстояние, на которое смещается тело от точки равновесия.

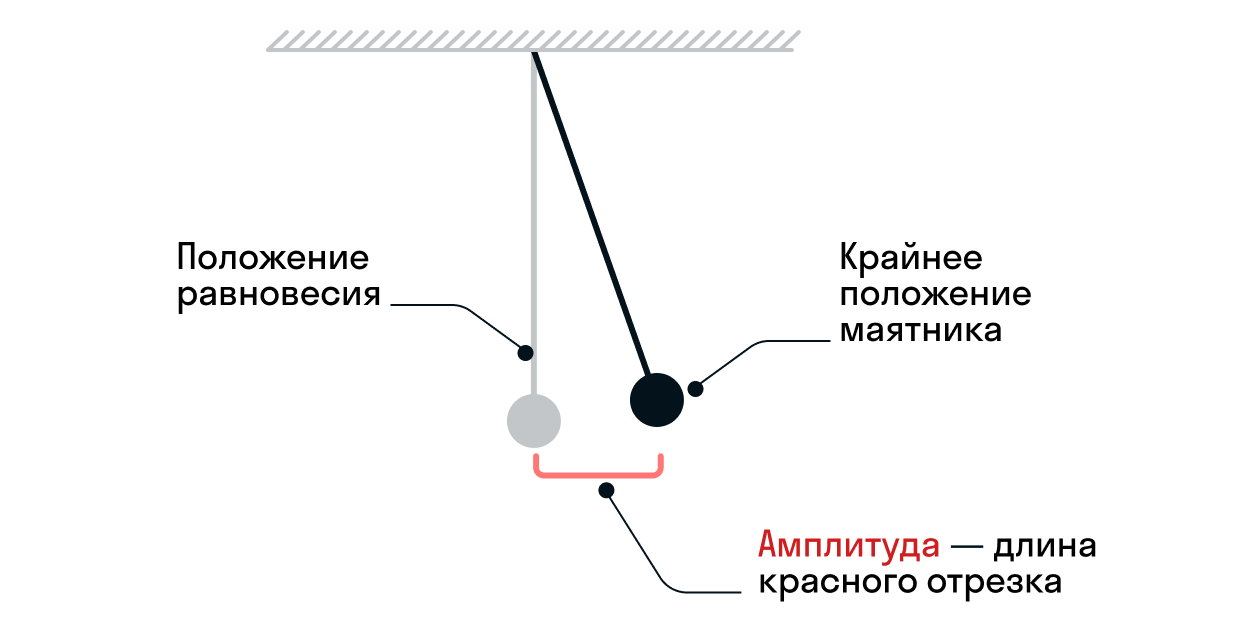
Так как колебания — это повторяющиеся движения, можно говорить о частоте и периоде колебаний.

Период колебаний — это время, за которое происходит одно колебание. В физике обозначается буквой и измеряется в секундах.

где — время колебаний, — количество колебаний.

Частота колебаний — величина, обратная периоду. Она показывает, какое количество колебаний происходит в единицу времени, и измеряется в герцах.

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Суть явления резонанса

Теперь мы готовы пойти дальше и выяснить, что такое резонанс в физике.

Резонанс (от лат. resono — откликаюсь) — это достижение максимальной амплитуды колебаний системой.

Как это может произойти? Рассмотрим еще одно определение:

Резонанс в физике — это отклик колебательной системы на периодическое воздействие внешней силы, проявляющееся в синхронизации частот колебаний системы с частотой внешнего воздействия, что влечет за собой явление резкого возрастания амплитуды вынужденных колебаний этой системы.

Приведем пример резонанса.

Представьте, что ваш маленький братишка или сестренка качается на качелях. Чтобы раскачать их еще сильнее, вы стоите рядом и прикладываете силу, еще больше отталкивая качели из состояния равновесия. Чтобы амплитуда действительно увеличилась, вам необходимо стоять в правильном месте и толкать в верный промежуток времени, иначе ничего не получится.

У вас нет маленьких родственников? Тогда садитесь на качели сами! Даже если вы сильно раскачаетесь, без дополнительного воздействия качели быстро остановятся. А значит, вы должны помогать им раскачиваться, подталкивая их своим телом в правильном направлении, причем в нужную секунду. Таким образом частота ваших движений должна полностью совпадать с частотой колебаний качелей, и тогда можно бесстрашно взмыть под самые небеса!

Резонансная частота — частота вынуждающей силы, равная собственной частоте колебательной системы, при которой достигается максимальная амплитуда.

Резонанс возникает в любых упругих средах: твердых, жидких и газообразных, главное — это наличие резонансной частоты.

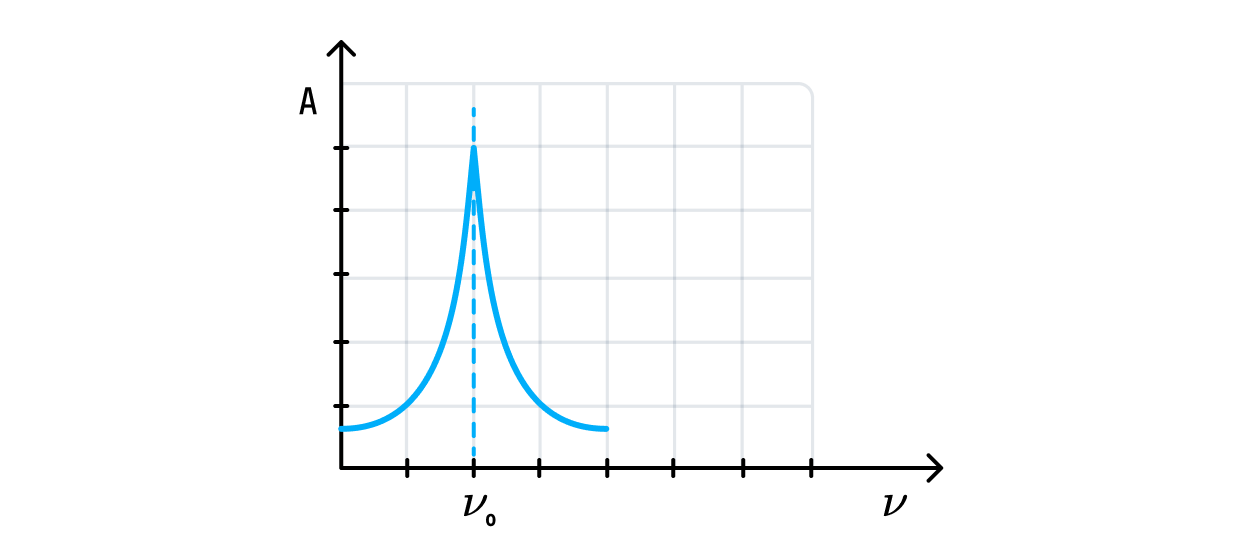
На графике представлена зависимость амплитуды от частоты вынуждающей силы. Как мы видим, существует такая частота, при которой достигается максимальное отклонение от точки равновесия. График функции стремительно возрастает, достигает наивысшей точки, а затем также стремительно убывает, а значит, постоянное увеличение частоты не даст лучшее отклонение — здесь важно вовремя остановиться.

Явление резонанса может нести как пользу, так и вред: из-за него происходит обрушение зданий и сооружений, но он же является основой, главным фактором в работе музыкальных инструментов.

Виды резонанса

В физике рассматриваются следующие типы резонанса:

Помимо этого, в обычной жизни мы используем такие устойчивые выражения, как общественный и когнитивный резонанс. Давай подробнее рассмотрим все эти виды!

Механический резонанс

Механический резонанс — это резонанс, вызванный механическим воздействием.

Сюда можно отнести наш пример с качелями, а еще раскачивание и обрушение моста под действием ветра.

Существует историческое подтверждение этому явлению: 7 ноября 1940 года двухкилометровый Такомский мост в США полностью обрушился. Порывы ветра отклоняли мост в одну сторону, создавая колебания, которые не могло погасить сопротивление воздуха, и из-за упругости конструкции движение по ветру начиналось вновь и вновь. В конечном итоге амплитуда движения стала настолько большой, что мост не выдержал и рухнул.

Механический резонанс очень часто возникает во время строительства, когда частота колебаний частей объекта совпадает с частотой внешних сил (ветра, рабочих инструментов), поэтому инженеры и строители бдительно следят за этими показателями.

Электрический резонанс

Электрический резонанс — это увеличение токов и напряжений на отдельных участках цепи при изменении частоты гармонического сигнала.

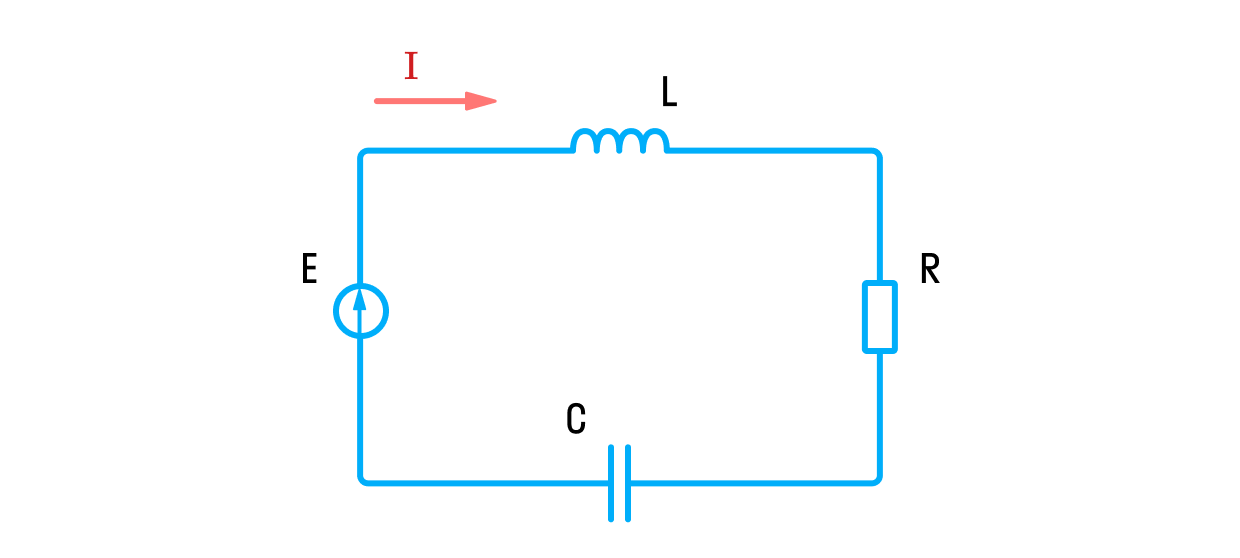
Резонанс в электрических цепях возникает при обмене энергией между емкостными элементами — конденсаторами и индуктивными элементами — катушками, которые включены в данную цепь. Амплитуда достигает максимального значения на определённой частоте, когда индуктивная и ёмкостная составляющие системы уравновешены, и энергии могут свободно циркулировать между магнитным полем катушки и электрическим полем конденсатора. Магнитное поле индуктивного элемента порождает электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в катушке. Этот процесс способен повторяться многократно.

Более подробно об этих явлениях вы можете прочитать в нашей статье «Колебательный контур».

Условие возникновения резонанса в электрической цепи можно выразить формулой где — резонансная частота, — индуктивность катушки, — ёмкость конденсатора.

Различают резонанс токов (при параллельном соединении катушки и конденсатора) и резонанс напряжений (при последовательном соединении элементов).

На принципах электрического резонанса функционируют такие приборы, как электрические резонансные трансформаторы, катушка Теслы и многие современные электронные устройства.

Акустический резонанс

С исследования именно этого вида резонанса всё и началось! Галилео Галилей в 1602 году исследовал маятники и струны различных музыкальных инструментов. Открытия, сделанные им, позволили сделать ряд выводов и создать новую отрасль физики — учение о звуковых колебаниях.

Акустический резонанс — это явление, при котором акустическая система усиливает звуковые волны, частота которых совпадает с одной из ее собственных частот вибрации (ее резонансными частотами).

Благодаря акустическому резонансу музыкальные инструменты способны работать, воспроизводить звучание особенным образом. Большую роль в этом играет форма инструмента. Звук, который издает струна, попадает внутрь корпуса и вступает там в резонанс со стенками, что в итоге многократно усиливает его. Грушевидная форма гитары, определенная длина флейты, форма барабана не являются результатом случайного выбора — с древних времен, путем проб и экспериментов, именно это строение каждого инструмента было выбрано из-за наилучшего акустического резонанса.

Характеристики струны также влияют на этот показатель: акустический резонанс зависит от длины, массы и силы натяжения струны.

Формула для расчета частоты резонанса в акустике:

где — частота резонанса, — сила натяжения, — масса единицы длины струны, а m — полная масса струны.

Акустический резонанс играет большую роль и для нашего слуха. Благодаря нему наружное ухо усиливает звуки средней частоты, составляющие основную часть спектра речи, а также различает высоту звука и его тембр.

Общественный резонанс — событие, на которое общество дает яркий отклик.

Когнитивный резонанс — полное совпадение во взглядах и мнениях.

Многие слова и устойчивые выражения, которые мы используем в повседневной жизни, основаны на физических явлениях и законах. Резонанс, инерция, энергия, напряжение и многие другие термины встречаются нам ежедневно, но знаем ли мы, что они на самом деле означают?

Приходите на онлайн-курсы физики школы Skysmart: на них вы научитесь не только мастерски обращаться с научной терминологией, но еще и станете настоящим экспертом в исследовании мира через призму физики! А заодно подготовитесь к экзаменам и повысите оценки в школе.

Источник: skysmart.ru