В школе новостройке в каждой из двух аудиторий может находиться либо кабинет информатики

Решение логических задач с помощью составления логических выражений Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т.е. записать на

В школе новостройке в каждой из двух аудиторий может находиться либо кабинет информатики

3. Решение истинностных задач

Данный тип задач можно решать тремя методами: методом рассуждений, табличным методом и с помощью логических выражений, с помощью построения таблиц истинности и приведения задачи к системе логических уравнений.

Перед началом Турнира «Четырех» болельщики высказали следующие предположения по поводу своих кумиров:

А) Макс победит, Билл – второй;

В) Билл – третий, Ник – первый;

С) Макс – последний, а первый – Джон.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Ник, Билл, Макс?

1) Есть «точная» информация, которая не подвергается сомнению: каждый из болельщиков оказался прав в одном прогнозе.

1. Макс победит, Билл – второй;
2. Билл – третий, Ник – первый;
3. Макс – последний, а первый – Джон.

3) Известно, что каждый из болельщиков только в одном из прогнозов был прав (то есть, из двух высказываний одно истинно, а другое – ложно).

4) Пусть первый болельщик угадал, что Макс победит, тогда третий болельщик ошибся в двух предположениях, а это не соответствует «точной» информации.

5) Пусть первый болельщик угадал, что Билл занял второе место, тогда второй болельщик предсказал первое место Нику, следовательно, по предположению третьего, Макс занял последнее место, а Джон – оставшееся третье место.

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

1) Запишем высказывания трех болельщиков в форме таблицы (заголовок строки обозначает место в турнирной таблице):

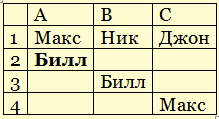
2) Считая, что два человека не могут оказаться на одном месте, начнем «раскручивать» эту таблицу с той строчки, где больше всего информации (в данном случае – с первой).

• «C» ошибся, поставив на первое место Джона;
• учитывая, что каждый один раз угадал, а второй ошибся, получается, что «C» угадал, что Макс будет на четвертом месте;
• но мы предположили, что Макс – на первом месте (а не на четвертом), следовательно, получили противоречие; это значит, что Макс все-таки не на первом месте
• таким образом, в первом прогнозе «А» ошибся, это значит, что во втором он угадал, и Билл действительно занял второе место:

• так как Билл – второй, он не может быть на третьем месте, поэтому из прогноза «Б» следует, что Ник – первый:

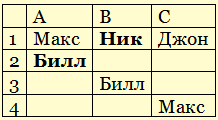
• если Ник на первом месте, там не может быть Джон, поэтому из ответов «С» (среди которых должен быть один верный, и один неверный), сразу находим, что Макс занял четвертое место:

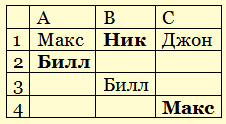
4) осталось только определиться с Джоном – ему досталось единственное «свободное» третье место; окончательный список победителей:

В школе-новостройке в каждой из двух аудиторий может находится либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайней мере, в одном из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истины, либо обе ложны. Помогите проверяющему найти кабинет информатики.

Решение (способ 3, логические выражения):

Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:

А = «В первой аудитории находится кабинет информатики»;

В = «Во второй аудитории находится кабинет информатики».

Отрицания этих высказываний:

¬ А = «В первой аудитории находится кабинет физики»;

¬ В = «Во второй аудитории находится кабинет физики».

Х = А ˅ В.

Высказывание на второй двери:

Утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего запишется следующим образом:

Подставим вместо X и Y соответствующие формулы:

Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:

В соответствии закона непротиворечия:

Далее упростим второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания:

В соответствии с законом непротиворечия:

В результате получаем:

Построим таблицу истинности для полученного выражения:

Проанализировав данные таблицы истинности имеем, что в первой аудитории находится кабинет физики, а во второй – кабинет информатики.

Задача 1. В школе — новостройке в каждой из двух аудиторий может находиться либо кабинет информатики , либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайне мере, в одной из этих аудиторий размещается кабинет информатики », а на второй аудитории – табличку с надписью « Кабинет физики находится в другой аудитории ». Проверяющему, который пришел в школу , известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики . Ответ. Слайд 9. Задача 2. На вопрос «Кто из твоих учеников изучал логику?» учитель ответил: «Если логику изучал Андрей, то изучал и Борис.

Решение логических задач с помощью составления логических выражений

Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т.е. записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.

При формализации необходимо учитывать следующее соответствие между логическими операциями и правилами русского языка:

• Отрицание – частица «не»;

• Дизъюнкция – союз «или»;

• Конъюнкция – союзы «и», «а», «но», «хотя», «однако»;

• Эквиваленция – слова «в том и только в том случае», «тогда и только тогда» и другие;

• Импликация – слова «если, то».

Рассмотрим пример. В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На аудиториях повесили шутливые таблички. На первой аудитории повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках или обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.

Переведем условие на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:

A – «В первой аудитории находится кабинет информатики»;

B – «Во второй аудитории находится кабинет информатики».

Тогда отрицаниям этих высказываний будут соответствовать:

— Высказывание, содержащееся на табличке первой аудитории, соответствует логическому выражению: X=A B.

— «В первой аудитории находится кабинет физики»,

— «Во второй аудитории находится кабинет физики»,

— Высказывание, содержащееся на табличке второй аудитории, соответствует логическому выражению: Y= .

Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные, в соответствии с законом исключенного третьего записываются следующим образом: = 1.

Подставим вместо X и Y соответствующие формулы:

Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения: = .

В соответствии с законом непротиворечия: = .

Упростим теперь второе слагаемое. В соответствии с законом де Моргана и законом двойного отрицания: = .

В соответствии с законом непротиворечия: .

В результате получаем: .

Полученное логическое выражение оказалось простым и поэтому его можно проанализировать без построения таблицы истинности. Для того чтобы выполнялось равенство , обе логические переменные должны быть равны 1, а соответствующие им высказывания истинны.

Ответ: В первой аудитории находится кабинет физики, а во второй – кабинет информатики.

В школе в каждой из двух аудиторий может находиться либо кабинет информатики , либо кабинет физики. На аудиториях повесили шутливые таблички, про которые известно, что они либо обе истинны, либо обе ложны. На первой аудитории повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики », а на второй аудитории — табличку с надписью « Кабинет физики находится в другой аудиторци». Определите, какой кабинет размещается в каждой из аудиторий . Переведем условие задачи на язык алгебры логики. Так как в каждой из аудиторий может находиться кабинет информатики , то пусть

Уроки 63 — 73
§3.2. Алгебра логики

В школе в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На аудиториях повесили шутливые таблички, про которые известно, что они либо обе истинны, либо обе ложны. На первой аудитории повесили табличку «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории — табличку с надписью «Кабинет физики находится в другой аудиторци». Определите, какой кабинет размещается в каждой из аудиторий.

Переведем условие задачи на язык алгебры логики. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:

А — «В первой аудитории находится кабинет информатики».

В — «Во второй аудитории находится кабинет информатики».

Поскольку в каждой аудитории обязательно размещается какой-либо из этих двух кабинетов, отрицания этих высказываний будут соответствовать:

А — «В первой аудитории находится кабинет физики».

B — «Во второй аудитории находится кабинет физики».

Высказывание, содержащееся на табличке первой аудитории, соответствует логическому выражению:

X = A ∨ В.

Высказывание, содержащееся на табличке второй аудитории, соответствует логическому выражению:

Y = А .

Содержащееся в условии задачи утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные, соответствует истинности функции эквивалентности :

Выразим функцию эквивалентности через базовые логические функции и получим:

(X & Y) ∨ ( X & Y ) = 1.

Подставим вместо X и Y соответствующие логические выражения:

((A ∨ В) & А ) ∨ ( (А ∨ В) & А = 1.

Упростим сначала первое слагаемое. В соответствии с правилом дистрибутивности умножения относительно сложения:

((A ∨ В) & А ) = (A & А ) ∨ (В & А ).

В соответствии с законом непротиворечия:

(A & А ) ∨ (В & А ) = 0 ∨ (В & А ).

В соответствии с правилом исключения констант:

0 ∨ (В & А ) = (В & А ).

Упростим теперь второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания:

( (А ∨ В) & А = А & B & А)= А & А & B ).

В соответствии с законом непротиворечия:

А & А & B ) = (0 & B ) = 0.

В результате преобразований первого и второго слагаемых получаем:

(B & А ) ∨ 0 = 1.

В соответствии с правилом исключения констант:

(B & А ) = 1.

Полученное логическое выражение оказалось простым, и поэтому его можно проанализировать без построения таблицы истинности. Для того чтобы выполнялось равенство, обе логические переменные должны быть равны 1, а соответствующие им высказывания истинны:

В — «Во второй аудитории находится кабинет информатики».

А — «В первой аудитории находится кабинет физики».

Таким образом, логическая задача решена: в первой аудитории находится кабинет физики, а во второй — кабинет информатики.

В школе — новостройке в каждой из двух аудиторий может находиться либо кабинет информатики , либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку "По крайней мере, в одной из этих аудиторий размещается кабинет информатики ", а на второй аудитории – табличку с надписью " Кабинет физики находится в другой аудитории ". … Переведем условие задачи на язык логических высказываний. Так как кабинет информатики может находиться в каждой аудитории , то пусть: А="В первой аудитории находится кабинет информатики ". В="Во второй аудитории находится кабинет информатики ". Отрицания этих высказываний