Многое, что окружает нас в жизни, если смотреть с позиции геометрии, — это линии и поверхности простых и сложных форм. Поверхности широко используются в различных областях науки и техники при создании очертаний различных технических форм или как объекты инженерных исследований.
Основные понятия и определения
Поверхность как объект инженерного исследования может быть задана следующими основными способами: а) уравнением; б) каркасом; в) определи гелем; г) очерком.
Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает поверхность как множество точек, координаты которых удовлетворяют уравнению вида F (х,у, z) = 0.
В начертательной геометрии поверхность на чертеже задается каркасом, определителем, очерком.
При каркасном способе поверхность задастся совокупностью некоторого количества линий, принадлежащих поверхности. В качестве линий, образующих каркас, как правило, берут семейство линий, получающихся при пересечении поверхности рядом параллельных плоскостей. Этот способ используется при проектировании кузовов автомобилей, в самолето — и судостроении, в топофафии и т. п.
Штукатурка: все о материале и выравнивании стен | Секреты, советы и опыт профессионала
Поверхность, образованная движущейся в пространстве линией, на чертеже может быть задана определителем поверхности.
Определителем поверхности называется совокупность геометрических фигур и связей между ними. позволяющих однозначно образовать поверхность в пространстве и задать ее на чертеже.
Способ образования поверхности движущейся в просфанстве линией называют кинематическим.
Линию, образующую при своем движении в пространстве данную поверхность называют образующей (производящей).
Образующая при своем движении может изменять свою форму или оставаться неизменной. Закон перемещения образующей можно, в частности, задать неподвижными линиями, на которые при своем движении опирается образующая. Эти линии называются направляющими.
На чертеже при задании поверхности ее определителем строятся проекции направляющих линий, указывается, как находятся проекции образующей линии. Построив ряд положений образующей линии, получим каркас поверхности. Пример образования поверхности кинематическим способом показан на рис. 96.

В качестве образующей а этой поверхности взята плоская кривая. Закон перемещения образующей задан двумя направляющими m и n и плоскостью а. Образующая а скользит по направляющим, все время оставаясь параллельной плоскости a.
Различают геометрическую и алгоритмическую часть определителя поверхности. Определитель имеет следующую форму записи Ф( Г ) [ А ], где Ф — обозначение поверхности; ( Г ) -геометрическая часть определителя, в ней перечисляются все геометрические фигуры, участвующие в образовании поверхности и задании ее на чертеже; [А ] — алгоритмическая часть определителя — в ней записывается алгоритм формирования поверхности.
Определитель поверхности выявляется путем анализа способов образования поверхности или се основных свойств. В общем случае одна и та же поверхность может быть образована несколькими способами, поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший. Например, боковая поверхность прямого кругового цилиндра может быть образована четырьмя способами (рис. 97):

а) как след, оставляемый в пространстве прямой а при ее вращении вокруг оси m (рис. 97,а).
Определитель поверхности — Ф ( а,m ) [ A1]:
б) как след, оставляемый в пространстве кривой линией b при ее вращении вокруг оси m (рис. 97,6).
Определитель поверхности — Ф ( b,m ) [ A2];
в) как след, оставляемый в пространстве окружностью с при поступательном перемещении ее центра О вдоль оси m. при этом плоскость окружности все время остается перпендикулярной к этой оси (рис. 97,в).
Определитель поверхности — Ф ( а,m ) [ A3]:
г) как огибающую всех положений сферической поверхности р постоянного радиуса, центр которой перемещается по оси m (рис.97,г).
Определитель поверхности -Ф ( p,m ) [ A4].
Наиболее простым из рассматриваемых будет определитель Ф ( а,m ) [ A1].
Задание поверхности на чертеже каркасом или определителем не всегда обеспечивает наглядность ее изображения. В некоторых случаях поверхность целесообразнее задавать ее очерком.
Очерком поверхности называется проекция проецирующей цилиндрической поверхности, огибающей заданную поверхность.
По известному уравнению поверхности или се определителю, или очерку всегда можно построить каркас поверхности.
Многообразие поверхностей требует их систематизации. Для поверхностей, образованных кинематическим способом в основу систематизации положен их определитель.
В зависимости от вида образующей поверхности разделяются на два класса:
класс 1 — поверхности нелинейчатые (образующая — кривая линия);
класс 2 — поверхности линейчатые (образующая — прямая линия).
Поверхности нелинейчатые
Поверхности нелинейчатые подразделяют на поверхности с образующей переменного вида (изменяющей свою форму в процессе движения) и на поверхности с образующей постоянного вида.
Нелинейчатые поверхности с образующей переменного вида
К нелинейчатым поверхностям с образующей переменного вида относятся:
1. Поверхность общего вида. Такая поверхность образуется перемещением образующей переменного вида а по криволинейной направляющей т (рис. 98).

2. Каналовая поверхность. Эта поверхность образуется движением плоской замкнутой линии, плоскость которой определенным образом ориентирована в пространстве (рис. 99).

Площадь, ограниченная образующей, монотонно изменяется в процессе ее движения но направляющей. Например, каналовую поверхность имеет переходный участок, соединяющий два трубопровода разной формы.
3. Циклическая поверхность — частный случай каналовой поверхности, когда образующая — окружность, радиус которой монотонно изменяется (рис. 100).

Примером циклической поверхности может быть корпус духового музыкального инструмента.
Нелинейчатые поверхности с образующей постоянного вида
К нелинейчатым поверхностям с образующей постоянного вида относятся:
1. Поверхность общего вида. Такая поверхность может быть образована движением произвольной кривой линии а по направляющей m (рис. 101).

2. Трубчатая поверхность. Образующей трубчатой поверхности является окружность постоянного радиуса. Плоскость окружности при ее движении остается перпендикулярной к направляющей (рис. 102).

Примером трубчатой поверхности может быть поверхность проволоки круглого сечения.
Поверхности линейчатые
Линейчатые поверхности образуются движением прямой (образующей) по заданному закону. В зависимости от закона движения образующей получаем различные линейчатые поверхности.
Линейчатые поверхности с тремя направляющими
К линейчатым поверхностям с тремя направляющими относятся:
1. Поверхность косого цилиндра. Такая поверхность может быть образована движением прямолинейной образующей по трем криволинейным направляющим (рис. 103).

2. Поверхность дважды косого цилиндроида. Эта поверхность образуется в том случае, когда две направляющие кривые, а третья -прямая линия (рис. 104).

3. Поверхность дважды косого коноида получается в том случае, когда одна из направляющих — кривая, а две других — прямые линии (рис. 105).

4. Поверхность однополостного гиперболоида образуется в случае, когда направляющие — три скрещивающиеся прямые, параллельные одной плоскости. Пример. Найти недостающие проекции точек А» и В’ принадлежащих поверхности однополостного гиперболоида (рис. 106).

P e ш е н и е. Для определения недостающей проекции точки, воспользуемся признаком принадлежности ее поверхности: точка принадлежит поверхности; если она принадлежит какой-либо линии этой поверхности.
Для данной линейчатой поверхности при построении проекций образующей сначала задается ее горизонтальная проекция, а затем находится фронтальная. Поэтому через известную горизонтальную проекцию точки A’ проводим проекцию образующей а’2, определяем ее фронтальную проекцию а2″, на которой по линии связи найдем искомую фронтальную проекцию точки A».
Для определения недостающей горизонтальной проекции точки В’ выполним следующие построения:
1. Построим ряд образующих заданной поверхности a1,a2,a3,a4 .
2. На фронтальной плоскости проекций через известную проекцию точки В» проведем проекцию вспомогательной линии b’ принадлежащей заданной поверхности и пересекающей образующие.
3. По известным фронтальным проекциям точек пересечения проекции линии b» с образующими а1″, а2″, а3″, а4″ найдем горизонтальные проекции этих точек. Соединив их плавной линией, построим горизонтальную проекцию вспомогательной линии b’ на которой по линии связи найдем искомую проекцию точки В’.
К линейчатым поверхностям с тремя направляющими относятся, например, поверхности гребных винтов судов и пропеллеров самолетов. В архитектуре и строительстве они используются при возведении крытых зданий стадионов, рынков, вокзалов.
Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана)
К линейчатым поверхностями с двумя направляющими плоскостью параллелизма относятся:
1. Поверхность прямого цилиндроида. Такая поверхность может быть образована движением прямолинейной образующей по двум направляющим m и n в том случае, когда они — гладкие кривые линии, причем одна из них — плоская кривая, плоскость которой β перпендикулярна плоскости параллелизма a (n ⊂ β, β ⊥ a) (рис. 107).

2. Поверхность прямого коноида. Эта поверхность получается в том случае, когда одна направляющая — кривая линия, а вторая -прямая, причем она перпендикулярна плоскости параллелизма
a( n ⊥ a) (рис. 108). Поверхность прямого коноида используется в гидротехническом строительстве для формирования поверхности устоев мостовых опор.

3. . Такая поверхность образуется в том случае, когда две направляющие — скрещивающие прямые (рис. 109). Поверхность косой плоскости применяется в инженерно — строительной практике для формирования поверхностей откосов, насыпей, железнодорожных и автомобильных дорог, набережных, гидротехнических сооружений в местах сопряжения имеющих различные углы наклона.

Линейчатые поверхности с одной направляющей (торсы)
Торсы являются развертываемыми поверхностями — они могут быть совмещены с плоскостью без складок и разрывов. К торсовым поверхностям относятся:
1. Поверхность с ребром возврата. Эта поверхность образуется движением прямолинейной образующей, во всех своих положениях касательной к пространственной кривой, называемой ребром возврата.
2. Цилиндрическая поверхность. Данная поверхность образуется движением прямолинейной образующей, скользящей по кривой направляющей и остающейся параллельной своему исходному состоянию (рис.110).

3. Коническая поверхность. Эта поверхность образуется движением прямолинейной образующей, скользящей по кривой направляющей и проходящей во всех своих положениях через одну и ту же неподвижную точку S (рис. 111).
Источник: forkettle.ru
Поверхности на чертеже
Поверхность – это двумерное топологические многообразие. На чертежах под поверхностью понимается наружная сторона чего либо, обладающая заданными базовыми характеристиками и свойствами.
Поверхности на чертеже по ГОСТу
Ключевым параметром поверхности является шероховатость, каждый чертеж должен иметь условное обозначение, которое позволит расшифровать и обработать нужным образом поверхность. Все требования перечислены в ГОСТ 2.309-73, который входит в ЕСКД, единую систему конструкторской документации. Название документа «Шероховатость поверхностей».
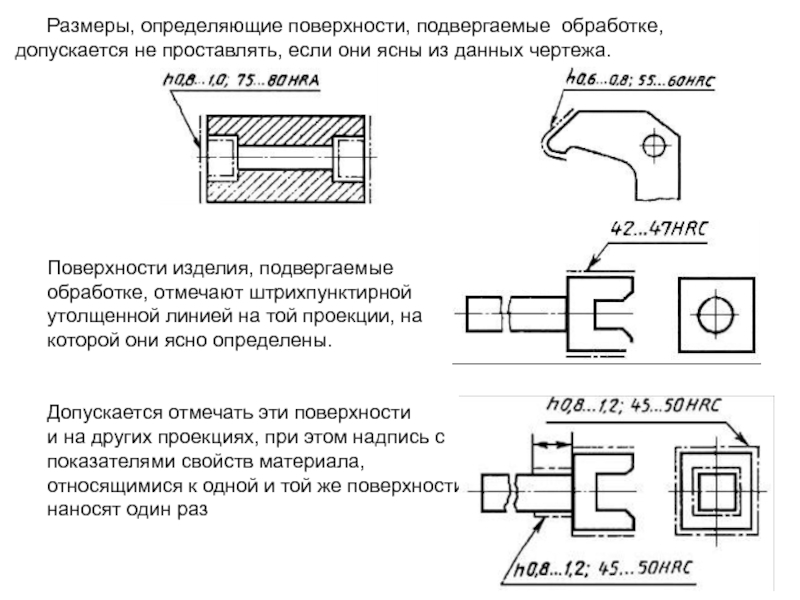
Рисунок 1. Поверхности на чертеже по ГОСТу
Условное обозначение шероховатости
Для обозначения шероховатости используется условный знак, показанный на рисунке 2. Знак состоит из условного обозначения направления неровности, базовой длины, способа обработки и других указаний. Шероховатость указывается для всех поверхностей изделия, если иное не обосновано требованиями конструкции. Для двусторонних изделий шероховатость задают для каждой из сторон.
Нормируются не только шероховатость, но и допуски, отклонения. Для придания нужных характеристик поверхности формы или тела, на чертеже приводят указание (задание) о процессе обработки, к примеру лазерная резка, фрезерование, сверление, прорезание, протягивание, растачивание и прочее.
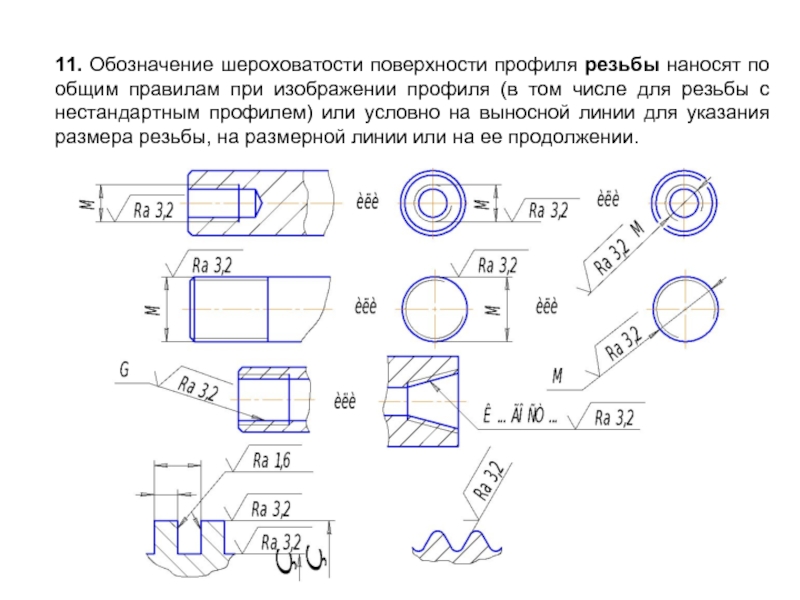
Рисунок 2. Условное обозначение шероховатости
Типы направлений поверхности на чертеже
Согласно требованиям ГОСТа различают 6 типов направлений неровностей:
- если линии идут перпендикулярно, то неровность наносят перпендикулярно линии, к которой относится поверхность;
- если линии идут параллельно, то неровность наносится вдоль линии, к которой относится поверхность.;
- если линии имеют пересечение, то выполняется перекрещивание в двух направлениях. В условном обозначении используется символ креста;
- если линии располагаются произвольно, то используют различные направления. Обозначается на условном знаке буквой «М»;
- если линии идут кругообразно, то нервности располагаются по кругу по отношению к центру;
- если линии идут радиально, то неровности располагаются согласно указанному рисунку, расходящемуся из центра.
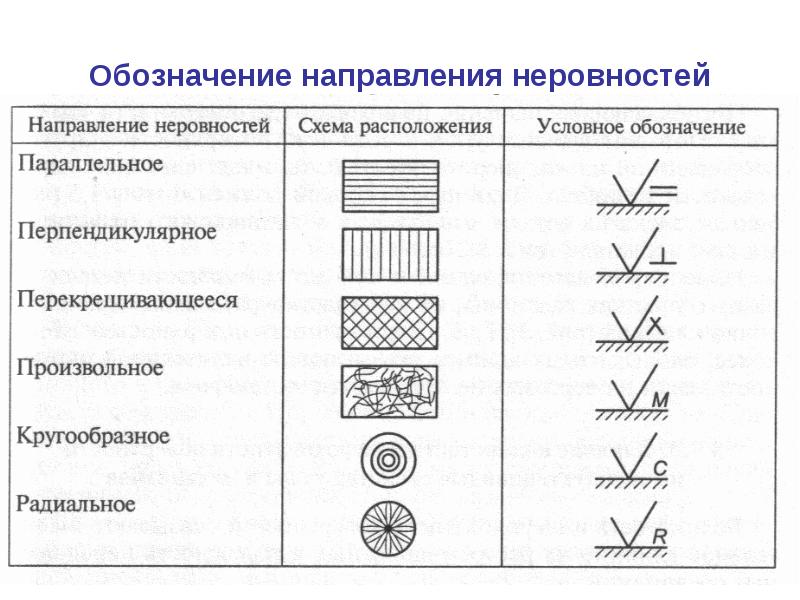
Рисунок 3. Типы направлений неровности поверхности
Виды поверхностей
В зависимости от назначения поверхностей выделяют следующие их виды:
- соединительные или ограничительные поверхности могут выступать в роли корпуса, стенок, фиксаторов, обычно их среднее арифметическое отклонение профиля составляет от 20 до 2,5 мкм;
- установочные поверхности соприкасаются между собой, но их расположение по отношению друг к другу не меняется, поэтому их среднее арифметическое отклонение профиля составляет от 20 до 2,5 мкм;
- рабочие поверхности используются в механизмах, они являются основной частью двигателей и насосов, совершая взаимное перемещение относительно друг друга. Их среднее арифметическое отклонение профиля составляет от 2,5 до 0,16 мкм;
- к специальным поверхностям относят внешние корпуса механизмов, их среднее арифметическое отклонение профиля составляет от 5 до 1,25 мкм;
- отдельно выделяют органы управления приборами, их среднее арифметическое отклонение профиля составляет от 0,63 до 0,08 мкм.
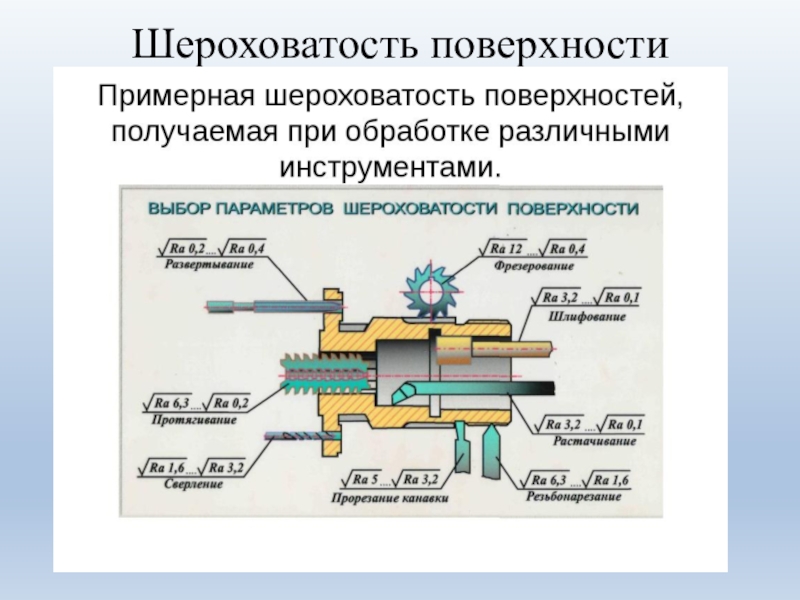
Рисунок 4. Способы обработки поверхностей
Указание на чертежах допусков формы и расположения поверхностей
Для правильного изображения геометрических элементов, деталей и изделий используется ряд условных обозначений, относящихся либо к форме, либо к расположению. К первой группе относятся допуск плоскостности, а также допуск прямолинейности. Помимо этого допуск круглости, допуск цилиндричности, а также допуск профиля продольного сечения. Отдельно выделяют допуски расположения, в которые входят допуски наклонов, симметричности, а также допуск параллельности, допуск перпендикулярности, допуск соосности, позиционный допуск и допуск пересечения осей.
В технических требованиях помимо условного обозначения приводится указание элемента, баз, и зависимость допуска от расположения.
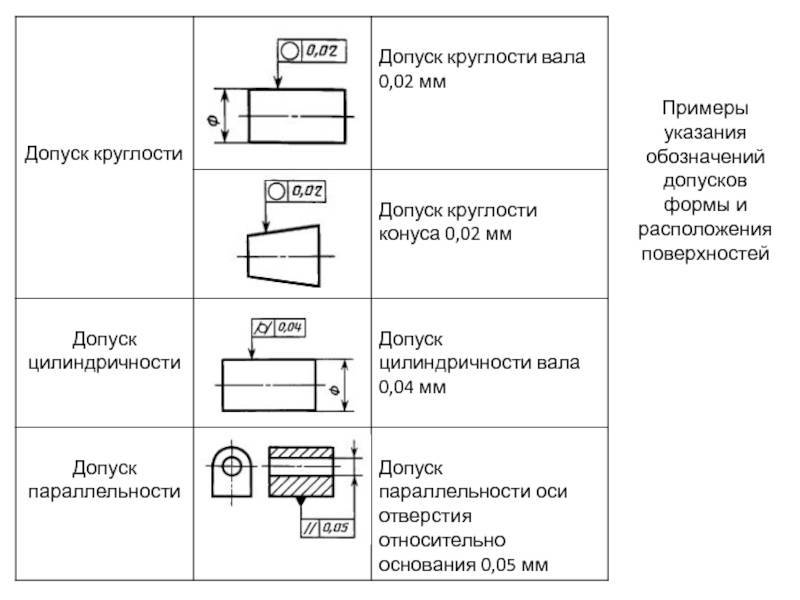
Рисунок 5. Допуски формы и допуски расположения
Проекции поверхностей на чертеже
При выполнении комплексного чертежа мы получаем отображение, называемое очерк поверхности, на нем мы видим наиболее важные линии и точки, полученные через проецирующие на плоскость лучи. Через массив проецирующих лучей можно получить цилиндрическую поверхность. Для конической поверхности фронтальный очерк на плоскость будет соответствовать равнобедренному треугольнику.
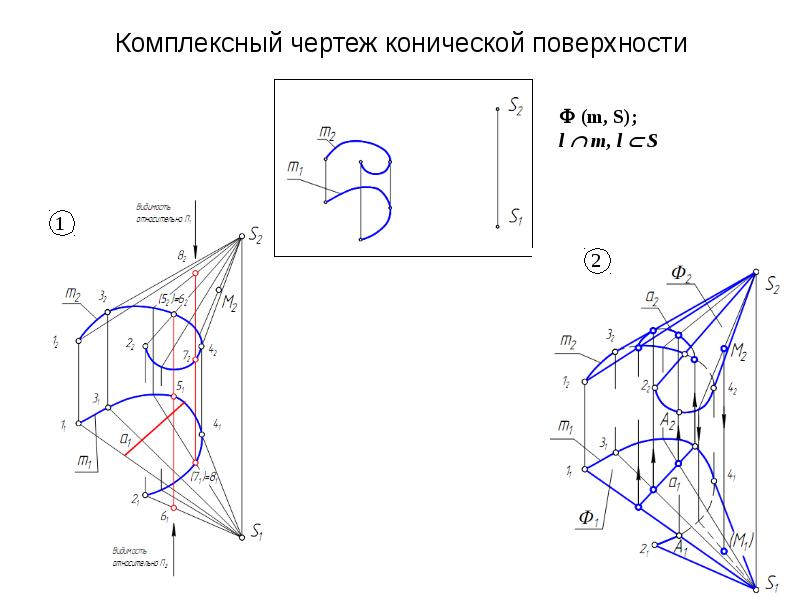
Рисунок 6. Комплексный чертеж поверхности
Как задается поверхность в программе Компас
При разработке модели часто стоит задача создания поверхностей, к примеру это может быть покрытие или поверхность корпуса детали, с помощью которой можно будет выполнить несколько разверток.
Для того, чтобы создать плоскость объемного предмета в первую очередь создаем эскиз траектории для будущей поверхности вращения, затем выбираем на панели «Поверхности» и указываем тип построения. Через инструмент «Поверхность соединения» можно создать единую деталь из нескольких поверхностей.
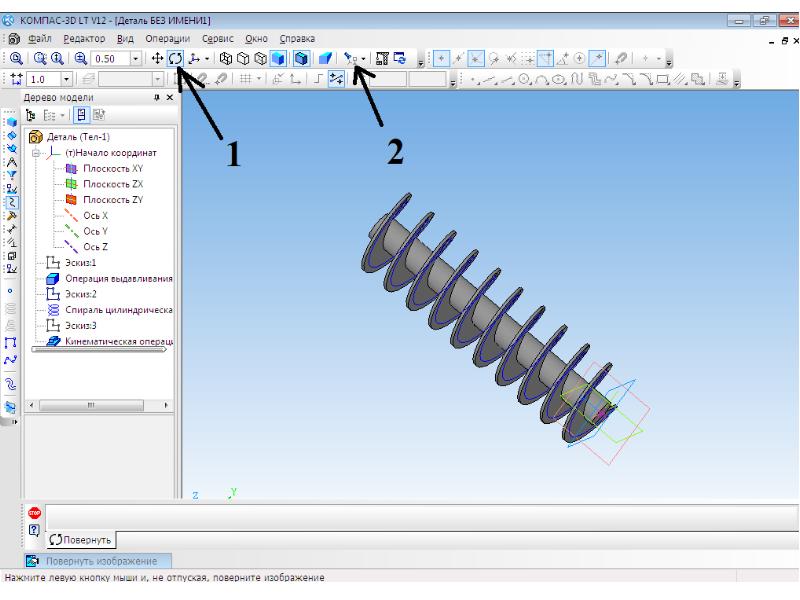
Рисунок 7. Поверхность в Компас
Ответы на вопросы
Какие существуют способы задания поверхностей?
В литературе приведено три способа задания поверхностей, а именно аналитический, кинематический и каркасный.
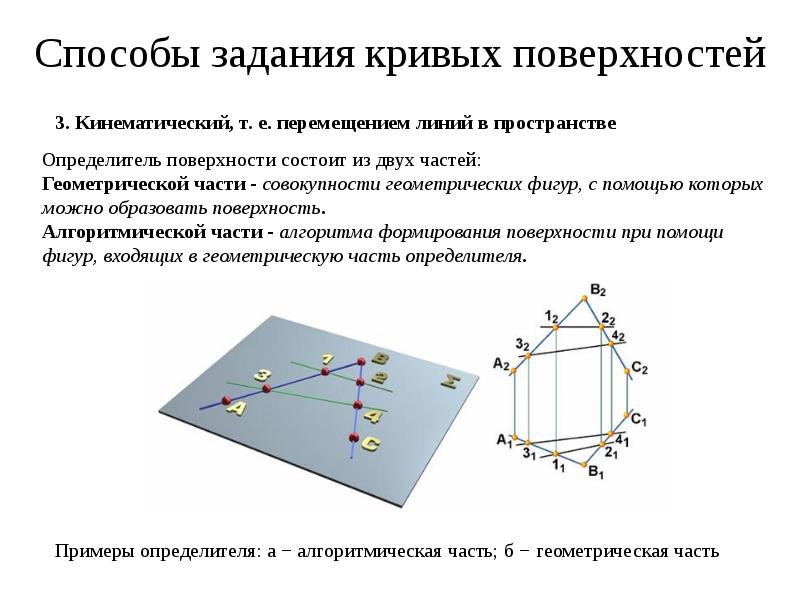
Рисунок 8. Кинематический способ задания поверхностей
Какие признаки используют для классификации поверхностей?
Поверхности различают по способу задания, закону движения образующей, по виду образующей, по закону изменения формы образующей и по признаку развертывания. В механике, в промышленности в основном применяют поверхности вращения, винтовые и полученные путем сдвига. Отмечается, что сложно выделить единый признак классификации заданной поверхности, что создает путаницу, так как разные поверхности могут относиться одновременно к разным группам.

Рисунок 9. Признаки классификации поверхностей
Как задается поверхность на чертеже?
Поверхность (сферическая, призматическая, торсовая, криволинейная, с прямолинейной образующей, с поступательным движением образующей и другие) считается заданной, если можно дать однозначный ответ на вопрос о том какие точки ей принадлежат.
Источник: spravochnick.ru
Тема 6. Поверхности
6.1. Поверхности в технике и строительстве. Образование поверхности и ее задание на чертеже. 6.2. Классификация поверхностей.
6.3. Многогранники. Образование поверхностей некоторых многогранников. Точки на поверхности гранных геометрических тел. Общие принципы построения разверток гранных поверхностей.
6.4. Поверхности вращения. Образование некоторых поверхностей вращения. Точки на поверхности геометрических тел вращения. Общие принципы построения разверток поверхностей вращения.
6.5. Поверхности винтовые и циклические. 6.6. Проекции геометрических тел с вырезом. Построение разверток геометрических поверхностей с нанесением линии выреза.
6.7. Развертки наклонных геометрических тел
6.1. Поверхности в технике и строительстве. Образование поверхности и ее задание на чертеже
Мир поверхностей многогранен и безграничен. Он простирается от элементарных, простых до сложнейших, причудливых форм поверхностей и их сочетаний. По разнообразию форм и свойств, по той роли, которую они играют в науке, технике, строительстве, архитектуре, поверхности не имеют себе равных среди других геометрических образов.
С точки зрения начертательной геометрии многое из того, что нас окружает — это линии и поверхности простых и сложных форм, и все, что создается человеком (конструкции, объекты, сооружения и т. д.), ограничивается этими поверхностями.
Поверхность в начертательной геометрии определяется как непре-
рывное множество последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону и называемой образующей поверхности.
Обязательным условием перемещения образующей в пространстве при образовании поверхности является пересечение ее с неподвижными линиями пространства, называемыми направляющими поверхности . Кроме этого должен быть указан характер движения образующей по направляющим. На рис. 57 показан процесс образования некоторой поверхности. В качестве образующей взята плоская кривая линия m , которая скользит по двум направляющим n 1 и n 2 , оставаясь все время параллельной плоскости β. Точка A , принадлежащая образующей m , перемещается по кривой n 1 . Такой способ образования поверхности называется кинематическим, и он позволяет задать любую поверхность Ф определителем. Определителем поверхности называется необходимая и достаточная совокупность геометрических фигур и связей между ними, которые однозначно задают (определяют) поверхность Φ .
Рис. 57. Кинематический способ образования поверхности
Определитель поверхности Φ может быть записан в виде структурной формы:
На рис. 58 показано образование некоторых поверхностей в начертательной геометрии кинематическим способом:
призматической поверхности — прямая образующая m перемеща-
ется по ломанной направляющей n , сохраняя параллельность заданному направлению S (рис. 58, а );
цилиндрической поверхности — прямая образующая m перемеща-
ется по кривой направляющей n , сохраняя параллельность заданному направлению S (рис. 58, б );
пирамидальной поверхности — прямая образующая m перемеща-
ется по ломанной направляющей n , проходя через постоянную точку (вершину) S (рис. 58, в );
конической поверхности — прямая образующая m перемещается по кривой направляющей n , проходя через постоянную точку (верши-
Рис. 58. Образование некоторых поверхностей
На чертеже поверхность может быть задана:
определителем поверхности (например, проекциями образующих и направляющих);
каркасом — упорядоченное множество точек или линий, принадлежащих поверхности. Каркас может быть точечным и линейным. Точечным каркасом называют совокупность точек на поверхности, достаточно точно определяющих эту поверхность. Линейным каркасом называют совокупность линий, имеющих единый закон образования и связанных между собой определенной зависимостью. Для получения линейного каркаса поверхность пересекается параллельными плоскостями, линии пересечениякоторых споверхностьюиобразуютее каркас;
очерком — след на плоскости проекции проецирующей цилиндрической поверхности, огибающей данную поверхность. Задание поверхности очерком обеспечивает наглядность изображения поверхности и облегчает чтение чертежа.
Поверхность считается заданной, если относительно любой точки пространства можно решить задачи о принадлежности ее данной поверхности.
6.2. Классификация поверхностей
Классификация поверхностей на протяжении длительного периода времени является предметом научных исследований. Это связано с тем, что за ее основу можно взять разные критерии, например характер образующей, признак развертывания и др. В основу классификации поверхностей может быть также положен и их определитель.
Принимая во внимание геометрическую часть определителя — вид линии, определяющей поверхность, все поверхности можно разделить на два класса: линейчатые и нелинейчатые.
Линейчатые — это поверхности, образующая которых прямая линия. Нелинейчатыми или криволинейными называются поверхности, образующая которых является кривой линией.
I. Линейчатые поверхности подразделяются на следующие виды: развертываемые (торсовые) поверхности, которые можно совместить с плоскостью без складок и разрывов. К ним относят конические (образующие пересекаются в одной точке); цилиндрические (образующие параллельны между собой и оси́вращения); поверхности с ребром возврата (образующие — множество касательных линий к
заданной пространственной кривой, называемой ребром возврата); неразвертываемые поверхности, которые невозможно совмес-
тить с плоскостью без разрывов и складок. Они подразделяются на поверхности с плоскостью параллелизма (все образующие параллельны какой-либо плоскости) и поверхности без плоскости параллелизма.
Разверткой называется плоская фигура, полученная при совмещении поверхности (или ее отсека) с плоскостью путем изгибания.
Свойства разверток поверхностей : сохранение длин линий, углов между линиями и площади, ограниченной замкнутым контуром.
В зависимости от формы направляющих и их расположения
в пространстве можно получить различные поверхности, относящиеся к классу линейчатых поверхностей:
1. Линейчатые поверхности с тремя направляющими: поверхность общего вида (косой цилиндр с тремя направляю-
поверхность дважды косого цилиндроида ; поверхность дважды косого коноида ; поверхность однополостного гиперболоида .
2. Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана):
поверхность прямого цилиндроида ; поверхность прямого коноида ; косая плоскость .
Линейчатые поверхности с двумя направляющими и без плоско-
поверхность косого цилиндроида ; поверхность косого коноида ; дважды косая плоскость .
3. Линейчатые поверхности с одной направляющей — торсы:
поверхность с ребром возврата ; коническая поверхность ; цилиндрическая поверхность ; плоскость .
II. Нелинейчатыеповерхности подразделяютсянаследующиевиды:
1. Нелинейчатые поверхности с постоянной образующей:
поверхность общего вида ; трубчатая поверхность .
2. Нелинейчатые поверхности с переменной образующей:
поверхность общего вида ; каналовая поверхность ; циклическая поверхность .
Согласно алгоритмической части определителя, характеризующей
закон движения образующей, линейчатые и нелинейчатые поверхности можно разделить на три подкласса:
поверхности параллельного переноса , образованные поступатель-
ным перемещением образующей; поверхности вращения , образованные вращением образующей;
поверхности винтовые , образованные винтовым перемещением образующей.
Поверхности вращения в зависимости от вида образующей подразделяются на несколько групп:
сфера, тор, глобоид (образующая — окружность);
эллипсоид вращения (образующая — эллипс); гиперболоид вращения (образующая — гипербола); параболоид вращения (образующая — парабола);
поверхность вращения общего вида (образующая — произвольная кривая линия).
Все поверхности в зависимости от вида направляющей, которая может быть ломаной, прямой или кривой линией, подразделяются на гранные поверхности и кривые.
Гранными называют поверхности, в образовании которых участвуют правильные многоугольники. Кривыми называют поверхности, в образовании которых участвуют плоские кривые линии правильной формы. При этом если направляющей является окружность, то полу-
чают поверхность вращения .
Часть пространства, ограниченная со всех сторон поверхностью,
называется геометрическим телом.
Образование поверхностей некоторых многогранников. Точки на поверхности гранных геометрических тел.
Общие принципы построения разверток гранных поверхностей
Многогранники относят к гранным поверхностям. Эти поверхности являются закономерными (т. е. образующая такой поверхности перемещается по определенному закону), линейчатыми и развертываемыми.
Многогранником называют геометрическое тело, ограниченное со всех сторон плоскими многоугольниками. Плоские многоугольники являются его гранями, а линии пересечения граней — его ребрами. Концы ребер многогранника называются его вершинами. Образующая гранной поверхности есть прямая, направляющая — ломаная линия.
На ортогональном чертеже многогранник задается проекциями его вершин (точками), ребер (отрезками прямых) и граней (плоскими фигурами). На рис. 59 показан пример изображения многогранника на ортогональном чертеже. Вершины многогранника заданы точками A , B , C и S , ребра — отрезками прямых AB , AC , BC , AS , BS и CS , а грани — треугольниками ABC , ABS , BCS и ACS . Проекции ребер многогранника, образующих его внешний контур, на ортогональном чертеже всегда видимы. Видимость остальных ребер многогранника определяется методом конкурирующих точек (см. тему 2).
Рис. 59. Проекции многогранника ABCS
Многогранники и многогранные поверхности нашли широкое применение в технике, строительстве и архитектуре: пирамиды, башни, крепости, крыши домов, мостовые опоры, перекрытия и т. д. Из всего многообразия гранных поверхностей рассмотрим наиболее известные: призматическую и пирамидальную поверхности.
Призматической называется поверхность, образующая которой, перемещаясь в пространстве, остается параллельной самой себе.
Призмой называется многогранник, две грани которого конгруэнтны, а остальные пересекаются по параллельным прямым.
По числу боковых граней различают призмы трехгранные, четырехгранные и т. д. Призма, все боковые грани которой являются прямоугольниками, т. е. ребра перпендикулярны основанию призмы, называется прямой . Призма является правильной , если ее основаниями служат правильные многоугольники, и высота проходит через ее центр. У правильных многогранников все грани являются равными правильными многоугольниками и все двугранные углы их конгруэнтны.
Проецирование прямой призмы начинают с горизонтальной проекции (рис. 60). Основания призмы будут проецироваться на горизонтальную плоскость проекций П 1 в натуральную величину, так как они расположены параллельно плоскости П 1 . На фронтальную и профильную плоскости проекций основания призмы проецируются в виде прямых, параллельных оси проекций.
Грани призмы перпендикулярны горизонтальной плоскости проекций. На фронтальной и профильной плоскостях проекций они будут выполняться в виде прямоугольников различной величины. Сечением прямой призмы плоскостью, параллельной горизонтальной плоскости проекций П 1 , является многогранник.
Каждая грань призмы представляет собой плоскость и, следовательно, проекции точки, принадлежащей поверхности, определяют ис-
ходя из принадлежности точки плоскости. Точка, принадлежащая плоскости, лежит на линии, принадлежащей также данной плоскости. Проекции точки, заданной на поверхности призмы, определяют с помощью образующих и линий проекционной связи. При этом помнят, что призматическая поверхность является проецирующей и все точки, принадлежащие данной поверхности, будут проецироваться на плоскость П 1 на ее очерк. Найдя проекции образующей, переносят на нее с помощью линий проекционной связи проекции данной точки
Рис. 60. Проекции точек на поверхности прямой призмы
При построении развертки любой геометрической фигуры необходимо вначале определить натуральные величины оснований и ребер или образующих геометрического тела, используя способы преобразования плоскостей проекций .
При построении развертки прямой призмы ее основания, являясь горизонтальными плоскостями уровня, проецируются на горизонтальную плоскость проекций в натуральную величину. Грани прямой призмы являются горизонтально-проецирующими плоскостями, ребра призмы — горизонтально-проецирующими прямыми, которые на плоскость П 1 проецируются в точки, а на плоскости П 2 и П 3 — в натуральную величину. Следовательно, для построения развертки прямой призмы никаких дополнительных построений не требуется.
Развертка прямой призмы производится методом раскатки (рис. 61). Положение точек, принадлежащих поверхности призмы, определяется следующим образом: заложение a каждой точки берется с горизонтальной проекции призмы, превышение b точек — с фронтальной или профильной проекций призмы (см. рис. 60).
Рис. 61. Развертка прямой призмы
Пирамидальной называется поверхность, образующая которой при перемещении проходит через одну и ту же точку пространства.
Пирамидой называется многогранник, одна грань которого (основание) представляет собой многоугольник, остальные грани являются треугольниками с общей вершиной S .
По числу углов многоугольника основания различают пирамиды треугольные, четырехугольные и т. д. Если вершина пирамиды S проецируется ортогонально (перпендикулярно) в центр тяжести ее основания, то такая пирамида называется прямой . Прямая пирамида, основанием которой является правильный многоугольник, называется правильной пирамидой.
Рис. 62. Проекции точек на поверхности прямой пирамиды, получаемые с помощью образующей
Проецирование прямой пирамиды начинают с горизонтальной проекции (рис. 62). Основание пирамиды будет проецироваться на горизонтальную плоскость проекций П 1 в натуральную величину, так как оно расположено параллельно плоскости П 1 . На фронтальную и профильную плоскости проекций основание пирамиды проецируется в виде прямой, параллельной оси проекций. Грани пирамиды в зависимости от их количества могут занимать общее и частное положение по отношению к плоскостям проекций и проецируются на них в виде треугольников различной величины.
Сечением прямой пирамиды плоскостью, параллельной горизонтальной плоскости проекций П 1 , является многогранник. Каждая грань пирамиды представляет собой плоскость, и, следовательно, проекции точки, принадлежащей поверхности, определяют исходя из принадлежности точки плоскости. Проекции точки, заданной на поверхности пирамиды, определяют с помощью прямой, лежащей в плоскости, или образующей, соединяющей основание пирамиды с его вершиной S .
Следует помнить, что точка, принадлежащая плоскости, лежит на линии, принадлежащей также данной плоскости. Найдя проекции образующей, переносят на нее с помощью линий проекционной связи проекции данной точки (см. рис. 62). Вместо образующей для определения проекций точки можно использовать вспомогательную плоскость уров-
Рис. 63. Проекции точек на поверхности прямой пирамиды, получаемые с помощью вспомогательной плоскости уровня
При построении развертки прямой пирамиды вначале определяют натуральные величины ее основания и ребер. Так в данном примере основание пирамиды, являясь горизонтальной плоскостью уровня, проецируется на горизонтальную плоскость проекций в натуральную величину. Грани прямой пирамиды являются плоскостями общего по-
ложения, ребра пирамиды, как правило, — прямыми общего положения и, в частном случае (см. рис. 62 и 63), — прямыми уровня, которые на плоскости П 2 или П 3 проецируются в натуральную величину. Следовательно, для построения развертки прямой пирамиды требуются дополнительные построения в том случае, если ребра пирамиды являются прямыми общего положения. Тогда, применяя способы преобразования плоскостей проекций (чаще способ вращения), определяют натуральные величины ребер пирамиды (см. рис. 51).
Развертку прямой пирамиды производят методом треугольников (триангуляции) (рис. 64). Положение точек, принадлежащих поверхности пирамиды, определяют следующим образом: заложение a каждой точки берут с горизонтальной проекции пирамиды, превышение b точек — с фронтальной или профильной проекций пирамиды
Рис. 64. Развертка прямой пирамиды
6.4. Поверхности вращения. Образование некоторых поверхностей вращения.
Точки на поверхности геометрических тел вращения. Общие принципы построения разверток поверхностей вращения
Поверхности вращения относят к кривым поверхностям, в образовании которых участвуют плоские кривые линии правильной формы. Поверхность вращения образуется путем вращения любой линии, например MN , вокруг другой неподвижной прямой линии 0 N (рис. 65).
Неподвижная прямая 0 N называется осью вращения , линия MN — образующей поверхности вращения. Плоскость, перпендикулярная к оси вращения, при пересечении с поверхностью вращения
образует в сечении окружность, называемую параллелью . Самая большая окружность называется экватором , самая малая — горлом . Любая секущая плоскость, проходящая через ось вращения, называется меридиональной плоскостью , линия ее пересечения с поверхностью
вращения — меридианом . Меридиан, лежащий в плоскости, параллельной фронтальной плоскости проекций П 2 , называется главным меридианом . Он определяет очерк поверхности вращения на плоскости П 2 .
Рис. 65. Образование поверхности вращения
Каждая точка, принадлежащая поверхности вращения, обязательно принадлежит какой-либо одной параллели и какому-либо одному меридиану (образующей).
По виду образующей различают:
линейчатые поверхности вращения ; нелинейчатые поверхности вращения .
I. Линейчатые поверхности вращения относятся к развертывае-
мым поверхностям. Образующей такой поверхности является прямая, направляющей — кривая линия. К этой группе поверхностей относят:
конические; цилиндрические и др.
Цилиндрической называется поверхность, образующая которой при перемещении вокруг оси вращения остается ей параллельной.
Цилиндром называется геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон, принятой за ось вращения (рис. 66). Цилиндр может быть прямым или наклонным.
Проецирование прямого кругового цилиндра с вертикальной осью вращения аналогично проецированию призмы. Основаниями цилиндра являются конгруэнтные круги. При оси вращения, перпендикулярной горизонтальной плоскости проекций П 1 , горизонтальная проекция цилиндра будет в виде круга, фронтальная и профильная проекции — в виде прямоугольников. Сечением прямого кругового цилиндра плос-
костью, перпендикулярной к его оси, является круг. При вычерчивании проекций прямого кругового цилиндра вначале выполняются оси симметрии (вращения) тела. Затем основание в виде окружности, потом фронтальная и профильная проекции геометрического тела. Проекции точки, заданной на поверхности цилиндра, определяют с помощью образующих и линий проекционной связи.
При этом помнят, что цилиндрическая поверхность является проецирующей, и все точки, принадлежащие данной поверхности, будут проецироваться на плоскость П 1 на ее очерк (см. рис. 66).
Рис. 66. Проекции точек на поверхности прямого цилиндра
При построении развертки данного прямого цилиндра его основания, являясь горизонтальными плоскостями уровня, проецируются на горизонтальную плоскость проекций П 1 в натуральную величину. Поверхность прямого цилиндра является горизонтально-проецирующей. Все точки, принадлежащие данной поверхности, будут проецироваться на горизонтальную плоскость проекций П 1 на ее очерк. Образующая такой поверхности — горизонтально-проецирующая прямая, которая на фронтальную плоскость проекций П 2 и профильную плоскость проекций П 3 проецируется в натуральную величину. Следовательно, для построения развертки прямого цилиндра никаких дополнительных построений не требуется.
Развертка прямого цилиндра производится методом раскатки (рис. 67). Основание цилиндра (окружность) с помощью циркуля разбивается на шесть, восемь или двенадцать равных частей. Положение точек, принадлежащих поверхности цилиндра, определяется следую-
щим образом: заложение a каждой точки берется с горизонтальной проекции цилиндра, превышение b точек — с фронтальной или профильной проекций цилиндра (см. рис. 66).
Рис. 67. Развертка прямого цилиндра
Конической называется поверхность, образованная перемещением прямой образующей, проходящей через неподвижную точку (вершину) S по кривой направляющей.
Конусом называется геометрическое тело, образованное вращением прямоугольного треугольника вокруг катета, принятого за ось вращения. Конус может быть прямым или наклонным . Это зависит от того, перпендикулярны или наклонены к его основанию образующие.
Рис. 68. Проекции точек на поверхности прямого конуса, получаемые с помощью образующей
Проецирование прямого кругового конуса с вертикальной осью вращения аналогично проецированию пирамиды (рис. 68). Основанием конуса является окружность, с выполнения которой следует начинать чертеж конуса. При оси вращения, перпендикулярной горизонтальной плоскости проекций П 1 , горизонтальная проекция конуса будет в виде круга, фронтальная и профильная проекции — в виде треугольников с вершиной S . Сечением прямого кругового конуса плоскостью, перпендикулярной к его оси, является круг.
Проекции точки, заданной на поверхности конуса, определяют с помощью образующей, соединяющей основание конуса с его вершиной S . Следует помнить, что точка, принадлежащая поверхности, лежит на линии, принадлежащей также данной поверхности. Найдя проекции образующей, переносят на нее с помощью линий проекционной связи проекции данной точки (см. рис. 68). Вместо образующей для определения проекций точки можно использовать вспомогательную параллель (рис. 69).
Рис. 69. Проекции точек на поверхности прямого конуса, получаемые с помощью вспомогательной параллели
При построении развертки прямого кругового конуса его основание, являясь горизонтальной плоскостью уровня, проецируется на горизонтальную плоскость проекций в натуральную величину. Образующая прямого конуса является прямой частного положения (фронтальной уровня или профильной уровня) и на плоскости П 2 или П 3 проецируется в натуральную величину. Следовательно, для построения развертки прямого конуса дополнительные построения не требуются.
Развертка прямого конуса производится методом раскатки (рис. 70). Основание конуса (окружность) с помощью циркуля разбивается на шесть, восемь или двенадцать равных частей. Положение точек, принадлежащих поверхности конуса, определяется следующим образом: заложение a каждой точки берется с горизонтальной проекции конуса, превышение b точек — с фронтальной или профильной проекций конуса (см. рис. 68).
Рис. 70. Развертка прямого конуса
II. Нелинейчатые поверхности вращения относятся к неразвер-
тываемым поверхностям. Образующей и направляющей такой поверхности являются кривые линии.
Поверхностью вращения общего вида называют поверхность, об-
разованную вращением произвольной кривой (плоской или пространственной) вокруг оси вращения поверхности (рис. 71).
Рис. 71. Поверхность вращения общего вида
Проекции точки, заданной на поверхности общего вида, определяются с помощью параллели, проведенной через заданную точку. Радиус параллели измеряется от оси поверхности до ее очерка. Следует помнить, что точка, принадлежащая поверхности, лежит на линии, также принадлежащей данной поверхности. К этой группе поверхностей относят:
шаровые; торовые и др.
Сферой ( шаром ) называется геометрическое тело, образованное вращением окружности вокруг ее диаметра, принятого за ось вращения (рис. 72). Центр вращающейся окружности является центром сферы. Сфера проецируется на все плоскости проекций в виде равных окружностей одинакового радиуса. Самая большая окружность — экватор.
На горизонтальную плоскость проекций он проецируется в виде круга, на фронтальную и профильную плоскости проекций — в виде прямой линии, параллельной оси проекций 0 х . Соответственно, главный меридиан на плоскость П 1 проецируется в прямую линию, параллельную оси проекций 0 х , а на фронтальную и профильную плоскости проекций — в виде круга (см. рис. 72). Сечением сферы плоскостью, перпендикулярной к ее оси, является круг.
Рис. 72. Проекции точек на поверхности сферы
Тором называется геометрическое тело, образованное вращением окружности вокруг оси, лежащей в плоскости окружности, но не проходящей через ее центр. Тор является открытым (кольцо), если ось вращения поверхности не пересекает эту окружность, т. е. находится за ее пределами (рис. 73, а ), и закрытым , если ось вращения поверхности пересекает или касается окружности (рис. 73, б ).
Источник: studfile.net