На сухом академическом языке сопромата и бухучета эта народная мудрость будет звучать примерно так (кого это не интересует, может сразу переходить к примеру расчета):
Расчет любой строительной конструкции начинается с выбора расчетной схемы. Принимаемая расчетная схема должна как можно больше соответствовать рассматриваемой ситуации и при этом максимально упрощать расчет.
Финансовые и временные затраты на расчет будут компенсированы экономией на строительных материалах и оптимизацией строительных процессов.
С точки зрения строительной механики стена каркасного дома может рассматриваться как прямоугольник, состоящий из двух вертикальных и двух горизонтальных стержней, соединенных шарнирами. Вертикальные стержни АD и ВС — это крайние стойки стены, горизонтальные стержни АВ и DC в принятой модели расчетной схемы — это верхнее и нижнее перекрытие.
Такой прямоугольник может выдерживать только вертикальную нагрузку. Даже очень незначительная горизонтальная или наклонная нагрузка, например сосредоточенная сила Q, приложенная к одному из верхних шарниров прямоугольника, превращает прямоугольник сначала в параллелограм с достаточно большой высотой, а потом и вовсе складывает его (рисунок 217.2.б)) без изменения длины самих стержней:
Лекция «Перекрытия и покрытия гражданских зданий. Диафрагмы жесткости»
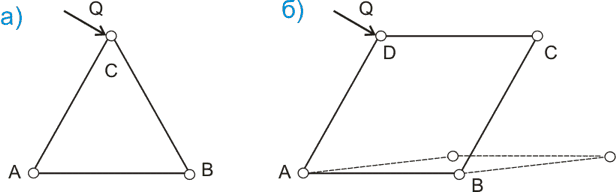
Система из трех стержней, соединенных шарнирами (рисунок 217.2.а)) является геометрически неизменяемой. Как ни прикладывай силу Q к шарниру С, треугольник будет оставаться треугольником. Изменение геометрических размеров стержней возможно только в результате деформации.
Чтобы растянуть или сжать стержни на рисунке а), нужно приложить значительно большую силу, чем требуется для сложения карточного домика на рисунке б).
Прямоугольник — это геометрически изменяемая система.
Количество стоек (вертикальных стержней) на геометрическую изменяемость системы не влияет. Это будут стержни, параллельные стержням АD и ВС, и также шарнирно прикрепленные к двум горизонтальным стержням. Поэтому прямоугольник все равно будет складываться в параллелограмм (мы продолжаем рассматривать модель, а не реальную ситуацию, в модели это возможно).
Чтобы сделать прямоугольник геометрически неизменяемой системой, нужно добавить в систему пятый элемент — стержень, соединяющий шарниры АС или DB. Таким образом прямоугольник разбивается на два треугольника, проблема вроде бы решена, но в реальной жизни разместить вертикальные брусья — стойки и наклонный брус — укосину в одной плоскости никак не возможно без ослабления сечения брусьев. Но не увеличивать же из-за этого толщину стены в 1.5-2 раза? Как тут быть? Рассмотрим возможные варианты:
1. Стены каркасного дома — это стойки (вертикальные стержни), обшитые листовым материалом с двух сторон .
Стойки (1) — это ребра жесткости клетки — они имеют большое сопротивление как сжатию, так и растяжению. Листовой материал — это гибкая оболочка, она имеет большое сопротивление только при растяжении. Чем больше толщина листового материала, тем больше сопротивление сжатию и тем больше оснований рассматривать такую оболочку, как 5 элемент в системе.
Монтаж ригеля на диафрагму жесткости
В этом случае стойки рассчитываются на вертикальные нагрузки от перекрытий, покрытий и вышележащих стен. А листовой материал — на горизонтальные нагрузки от ветра, землетрясений и др.
2. Стены каркасного дома дополнительно усилены диафрагмой жесткости .
В этом случае все горизонтальные нагрузки воспринимает диафрагма, а листовой материал обеспечивает дополнительную надежность конструкции (в частности увеличивает жесткость стоек из плоскости стены) и в расчете на прочность не нуждается.
3. Стены дополнительно усилены одним или двумя диагональными стержнями — укосинами, прирезанными по длине пролетов между стойками.
В этом случае более правильно вести комплексный расчет, т.е. учитывать несущую способность и укосин и листового материала.
Наиболее простым для расчетов является второй вариант, диафрагму жесткости можно рассчитать вручную с помощью простого калькулятора, в крайнем случае достаточно листа бумаги и карандаша. Именно этот вариант мы ниже и рассмотрим.
Расчет пластин на продольную нагрузку в рамках теории сопротивления материалов выполняется очень приблизительно, так как любая пластина — это не отдельный стержень, а решетка, состоящая из множества вертикальных и горизонтальных стержней с жестким, а не шарнирным соединением в узлах.
Такая система стержней является статически неопределимой. Каждый узел — это примерно 4 степени статической неопределимости или четыре дополнительных уравнения в общей системе уравнений.
Для таких расчетов используются различные модели теории упругости (например метод предельного равновесия или метод конечных элементов), согласно которым необходимо выполнить большое количество математических операций с использованием того или иного программного обеспечения. Чем больше узлов (соединений 4 стержней) или элементов (элементарных пластин между стержнями), тем больше точность расчета.
Все из-за того, что пластина при деформациях — это уже не плоский элемент, а часть поверхности некоего объемного тела с определенным радиусом кривизны.
Примечания:
1. Самая надежная стойка — это бревно. У бревна круглое сечение, а значит моменты инерции и сопротивления одинаковы относительно любой из выбранных осей, все оси главные.
Но бревно — это сучки, задоринки, радиус изгиба нейтральной оси бревна, нелинейно изменяющиеся по высоте размеры поперечного сечения, позволяющие равномерно распределять нагрузку на древесину, и прочие детали, не вписывающиеся в максимально упрощенную геометрию сопромата.
Гораздо проще, когда сечение стержня одинаковое сверху и снизу стрежня. При расчете рассматривается самое нижнее сечение стержня, как наиболее нагруженное с учетом собственного веса стержня. И такие стержни имеются в наличии — это оцилиндрованный брус. Но работать с оцилиндрованным брусом не так удобно, как с брусьями прямоугольного сечения, да и стоит он дорого.
Брус квадратного сечения — менее надежная стойка, так как имеет одинаковые моменты инерции и сопротивления только относительно двух главных осей, но больше в принципе и не нужно.
Самая ненадежная стойка — это брус ярко выраженного прямоугольного сечения, когда высота сечения в несколько раз больше ширины. Например у бруса 20х5 см момент инерции относительно оси х в 16 раз больше момента инерции относительно оси у. Соответственно такая стойка будет достаточно жесткой в плоскости стены и достаточно гибкой в перпендикулярной плоскости.
Для увеличения жесткости стоек нужны дополнительные горизонтальные связи между ними. Они уменьшают расчетную длину стоек, а значит увеличивают жесткость. Роль дополнительных горизонтальных связей очень хорошо выполняет обшивка стоек листовым материалом с двух сторон.
Пример расчета фермы — диафрагмы жесткости стержневой системы.
Планируется строительство каркасного дома-пристройки к основному зданию. Размеры в плане 6х18 м, высота этажа 3 м:

При действии ветровой нагрузки на стены по оси А самая большая горизонтальная нагрузка будет на внутренние стены по осям 3 и 4. Для наглядности рассмотрим место установки диафрагмы в одной из наружных стен по цифровой оси, так как наружные стены имеют больше дверных и оконных проемов и мест для установки диафрагмы меньше:
Ферма-диафрагма устанавливается как можно ближе к середине пролета стены для того, что наиболее равномерно распределить момент, возникающий при действии ветровой нагрузки.
Так как остальные стержни только передают горизонтальные нагрузки, то диафрагма жесткости и есть тот жестко закрепленный рычаг, на который действует ветровая нагрузка.
Нижнее перекрытие — это неподвижная жесткая опора, верхнее перекрытие — это скользящая жесткая опора.
Момент будет примерно поровну передаваться не только на левую и правую от диафрагмы жесткости части стены, но и на верхнее и нижнее перекрытие.
Как изменяется значение изгибающего момента слева и справа от точки приложения изгибающего момента можно посмотреть отдельно (расчетные схемы 3.1 и 3.2).
В итоге мы получаем вертикальную стойку сквозного сечения, расчет которой отличается от расчета горизонтальной балки на шарнирных опорах только тем, что касательные напряжения, определяемые по эпюре «Q», будут максимальными посредине балки, а не у опор (расчетная схема 2.1 для обычной балки).
У фермы — это растяжение или сжатие в центральном наклонном стержне.
После просчета геометрии ферма будет иметь следующие размеры:

Ну и собственно сам расчет:
1. При расчетной плоской ветровой нагрузке 100 кг/м 2 , действующей на 6 метров ширины стены по оси А, равномерно распределенная горизонтальная линейная нагрузка q на стену по оси 3 или 4 составит:
q = 6·100 = 600 кг/м.
2. При пролете l = 3 метра реакции опор составят:
А = В = ql/2 = 600·3/2 = 900 кг
3. При угле наклона 45 градусов максимальная сжимающая или растягивающая сила, действующая на наклонный стержень, составит:
N = A/cos45° = 900/0.707 = 1273 кг
4. На контактных площадках стыков наклонных стержней с горизонтальными связями (показаны на рисунке 779.3 оранжевым цветом) и с вертикальными стойками эта сила будет действовать не вдоль волокон и не поперек волокон, а под углом 22.5° к нейтральным осям стержней. Для упрощения расчетов эти напряжения можно рассматривать, как действующие поперек волокон, соответственно расчетное сопротивление древесины сжатию в этом случае составляет:
5. Требуемая площадь контактной площадки составит:
S = N/Rсж = 1273/18 = 71 см 2
6. При высоте сечения бруса, используемого и для стоек и для наклонных стержней и для горизонтальных связей фермы h = 20 см требуемая ширина контактной площадки составляет:
b = S/h = 71/20 = 3.53 см
7. При принятой общей ширине опорной площадки 5.3 + 1.8 = 7.1 см требуемая прочность стыков обеспечена с запасом прочности 7.1/3.53 = 2 раза.
Вот и весь расчет.
Примечание: При варианте 3 — распределении одного или двух наклонных стержней на несколько пролетов между стойками — укосины могут рассматриваться как наклонные стержни с одной или двумя скользящими шарнирными опорами, так как крепление укосин к стойкам любыми нагелями — слабое препятствие для скольжения опоры.
Например, несущая способность одного нагеля диаметром 1 см будет не более:
Тс = 50сd = 50·5·1 = 250 кг
Потребуются дополнительные меры по обеспечению неподвижности шарнирных опор. Это или врезка в стойки, а значит ослабление сечения стоек. Или нашивка на стойки дополнительных брусков с двух сторон с общей длиной каждого примерно равной длине стойки. Или комплексный расчет, о котором говорилось выше.
На этом пока все.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)).
Источник: doctorlom.com