В таких задачах всегда присутствуют одни и те же величины, их три:
— первая величина — это время, за которое выполняется та или иная работа. Обозначают время буквой t.
— вторая величина — объём работы: сколько сделано деталей, налито воды, вспахано полей и так далее. Обозначим объем буквой О.
— третья величина — производительность. По сути, это скорость работы. Обозначим производительность буквой П.
Скорость любой работы, т.е. производительность можно определить, как объём работы, сделанной за какое-то время.
Получим формулу для производительности: П = О : t.
Пример. Токарь делает 5 деталей в час. Сколько деталей он сделает за 7 часов?
Пример. Токарь делает 5 деталей в час. Ему нужно сделать 20 деталей. За какое время он выполнит эту работу?
Ответ: 4 часа
Пример. Красная Шапочка и Волк очень любят пирожки. Волк может съесть 24 пирожка за 4 часа, а Красная Шапочка — 35 пирожков за 7 часов. У Волка в корзинке 30 пирожков, а у Красной Шапочки — 20. Кто съест свои пирожки раньше, если они начали есть одновременно?
Где НЕЛЬЗЯ Покупать себе УЧАСТОК? #строительстводома #доммечты #строительство
Определим производительности Волка и Красной Шапочки. Волк съест 24 пирожка (объём работы) за 4 часа (время). Значит, его производительность: П = О:t = 24:4 = 6 пирожков в час.
Производительность Красной Шапочки: П = О:t = 35:7 = 5 пирожков в час.
Посчитаем сколько времени затратит каждый на свои пирожки.
У Волка 30 пирожков. Значит, затратил времени: t = О:П= 30:6 = 5 часов.
Красная Шапочка потратила на свои 20 пирожков: t = О:П = 20:5 = 4 часа.
Красная Шапочка опередила Волка на один час.
Ответ: Красная Шапочка.
Как определить производительность в следующих задачах:
— труба заполняет бассейн за 3 часа. (объем работы — бассейн — 1 бассейн);
— бригада строителей строит дом за 150 дней. (объем работы — дом — 1 дом);
— трактор вспахивает поле за 12 часов. (объем работы — поле — 1 поле).
Следовательно, в задачах объем работы равен 1.
Задачи на совместную работу
Совместная работа возникает, когда несколько человек (бригад, насосов, тракторов и т.д.) выполняют одну и ту же работу вместе, причем они работают с разными скоростями.
Пример. Одна труба может наполнить бассейн за четыре часа. Вторая — за шесть часов. За какое время заполнится бассейн, если обе трубы включить одновременно?
Так как трубы работают вместе, складывают их производительности.
Для первой трубы, которая заполняет 1 бассейн за 4 часа: П = О:t = 1:4, т.е. за час первая труба заполнит 1/4 бассейна.
Для второй трубы: П = О:t = 1:6, т.е. вторая труба заполнит за час 1/6 бассейна.
Вместе, при совместной работе, трубы заполнят за час: 1/4 + 1/6 = 5/12 — две трубы за 1 час.
Объём работы 1 бассейн. Совместная производительность 5/12 бассейна в час.
t = О:П = 1 : 5/12 = 12/5 = 2,4 (ч.)
Ответ:2,4 часа.
УПРАЖНЕНИЯ
1. а) Одна труба заполняет бассейн за 3 ч, а вторая — за 5 ч. За какое время заполнится бассейн, если будут работать две трубы одновременно? Выберите правильное значение:
Строительство дома от фундамента до ландшафтного дизайна! Мы снимали этот ролик с 2016 года!
б) Один насос заполняет бак за 4 ч, а второй — за 2 ч. За какое время заполнится бак, если будут работать два насоса одновременно? Выберите правильное значение:
а) Производительность первой трубы — 1/3, производительность второй трубы — 1/5. Общая производительность — 1/3+1/5. Для нахождения затраченного времени при совместной работе разделим объем работы -1 на производительность: 1:(1/3+1/5).
2. а) Два строителя вместе сложили стену за 10 дней, один из них мог бы выполнить эту работу за 16 дней. За сколько дней может выполнить эту работу второй? Выберите правильное значение:
б) Одна наборщица может набрать рукопись за 12 ч, а две, работая вместе, — за 8 ч. За сколько часов выполнит эту работу вторая наборщица? Выберите правильное значение:
Решение:
а) Производительность первого строителя — 1/16, о бщая производительность — 1/10. Производительность второго строителя — 1/10-1/16. Для нахождения затраченного времени вторым строителем разделим объем работы -1 на производительность: 1:(1/10-1/16).
Ответ: 2.
3. а) Папа выполняет всю работу за 4 ч, а его сын— за 7 ч. Какую часть работы они сделают вместе за 1 ч?
б) Мама выполняет всю работу за 1 ч, а дочь эту же работу выполняет за 2 ч. Какую часть работы они сделают вместе за 1 ч?
Решение:
а) Производительность папы — 1/4, производительность сына — 1/7. Производительность общая: 1/4+ 1/7=11/28 всей работы за 1 час.
Ответ: 11/28 работы.
4. а) При одновременной работе 6 комбайнов уберут все поле за 14 ч. За сколько часов уберут поле 8 комбайнов?
б) При одновременной работе 7 комбайнов уберут поле за 14 ч. За сколько часов уберут поле 10 комбайнов?
Решение:
а) 1) 6*14=84 (ч) — понадобится одному комбайну, чтобы убрать все поле.
2) 84 : 8= 10,5 (ч) — понадобится 8 комбайнам, чтобы убрать все поле.
Ответ: 10,5 часов
5. а) 18 студентов, работая по 6 ч в день, прополют все поле все поле. Сколько понадобится студентов, чтобы прополоть это поле за то же время, если они будут работать по 9 ч в день?
б) 12 студентов, работая по 8 ч в день, соберут все яблоки в саду. Сколько понадобится студентов, чтобы убрать все яблоки в этом саду за то же время, если они будут работать по б ч в день?
Решение:
а) 1) 6*18=108 (ч) — понадобится одному студенту, чтобы прополоть все поле.
2) 108 : 9= 12(ст.) — понадобится, чтобы прополоть все поле, работая по 9 ч в день.
Ответ: 12 студентов.
6. а) Производительности дочери и мамы относятся как 2:3. Работая вместе, они прополют огород за 12 ч. За сколько часов прополет огород каждая, работая отдельно?
б) Производительности труда папы и сына относятся как 3 : 5. Работая вместе, они выполнят работу за 15 ч. За сколько часов каждый справится с данной работой, работая отдельно?
Решение:
а) Пусть х — коэффициент пропорциональности, тогда производительность дочери — 2х, а мамы — 3х. Производительность при совместной работе 2х+3х=5х. Объем работы равен 12*5х=60х.
1) 60х:2х=30 (ч) — затратит дочь.
2) 60х:3х=20 (ч) — затратит мама.
Ответ: 30 часов; 20 часов.
7. а) Заказ на печать учебников типография должна была выполнить по плану за 15 дней. Но уже за три дня до срока типография выполнила план, так как печатала ежедневно по 2 тыс. учебников сверх плана. Сколько учебников напечатала типография?
б) Заказ на выпуск станков завод должен был выполнить за 30 дней. Но за три дня до срока завод выполнил заказ, так как выпускал ежедневно по 3 станка сверх плана. Сколько станков выпустил завод?
Решение:
а) Пусть х учебников в день типография должна была печатать по плану, но печатала х+2000 учебников день.
1) 15-3=12 (дн.) — потратила типография на заказ.
15х — количество заказанных учебников, 12(х+2000) — количество напечатанных учебников. Эти количества равны. Составим и решим уравнение:
15х=12(х+2000),
15х=12х+24000,
3х=24000,
х=8000 (м.) — в день должна была печатать типография.
2) 8000*15=120000 (м.) — напечатала типография.
Ответ: 120000 учебников.
8. а) При совместной работе двух погрузчиков железнодорожный состав был загружен за 4 ч 12 мин. Сколько времени потребуется на загрузку такого же железнодорожного состава каждым погрузчиком, если одним из погрузчиков железнодорожный состав можно загрузить на 8 ч быстрее, чем другим?
б) При совместной работе двух кранов работа была выполнена за 2 ч 6 мин. Сколько времени потребуется для выполнения этой работы каждым краном, если один может выполнить ее на 4 ч быстрее другого?
Решение:
а) Пусть х — время загрузки состава первым погрузчиком, тогда х+8 — время загрузки состава вторым погрузчиком.
Производительность первого погрузчика — 1/х, второго погрузчика — 1/(х+8). Совместная производительность 1/х+1/(х+8)=(2х+8)/(х(х+8)).
Время совместной работы равно 1 : (2х+8) /(х(х+8))=х(х+8)/(2х+8).
По условию время равно 4 ч 12 мин = 4,2 ч. Составим и решим уравнение:
х(х+8)/(2х+8)=4,2,
х(х+8)=4,2(2х+8),
х1=6 (ч) — понадобится первому погрузчику, х2=(0,4-11,6):2=-5,6 — не подходит по условию задачи.
1) 6+8=14 (ч) — понадобится второму погрузчику.
Ответ: 6 часов, 14 часов.
9. а) Бассейн наполняется через две трубы за 6 ч. Через первую трубу бассейн наполняется на 5 ч быстрее, чем через вторую. За какое время может быть наполнен бассейн через каждую трубу в отдельности?
б) Бак наполняется через две трубы за 2 ч. Через первую трубу бак наполняется на 3 ч быстрее, чем через вторую. За какое время может быть наполнен бак через каждую трубу в отдельности? (№ 6.4.30 [7])
Решение:
а) Пусть х — время заполнения первой трубой, тогда х+5 — время заполнения второй трубой.
Производительность первой трубы 1/х, второй трубы 1/(х+5). Совместная производительность 1/х+1/(х+5)=(2х+5)/(х(х+5)).
Время совместной работы равно 1 : (2х+5) /(х(х+5))=х(х+5)/(2х+5).
По условию время равно 6 ч. Составим и решим уравнение:
х(х+5)/(2х+5)=6,
х(х+5)=6(2х+5),
х1=10 (ч) — понадобится первой трубе, х2=(7-13):2=-3 — не подходит по условию задачи.
1) 10+5=15 (ч) — понадобится второй трубе.
Ответ: 10 часов, 15 часов.
10. а) Двое плиточников облицевали стены за 12 ч. Если бы сначала первый облицевал половину стен, а затем второй — вторую половину, то облицовка была бы выполнена за 25 ч. За какое время мог бы облицевать стену каждый плиточник в отдельности?
б) Двое каменщиков сложили стену за 6 ч. Если бы сначала первый выложил половину стены, а затем второй — вторую половину стены, то вся стена была бы сложена за 12,5 ч. За какое время мог бы сложить эту стену каждый каменщик в отдельности?
Решение:
а) Пусть первый работал х часов, второй — у часов. Производительность первого 1/х, второго 1/у. При совместной работе их время равно 1: (1/х+1/у) =12.
Если первый и второй делают по половине работы, то их время равно 0,5:(1/х) +0,5:(1/у)=25. Решим систему из двух уравнений:
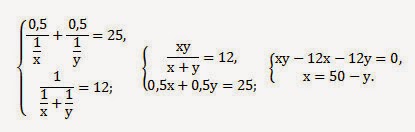
у1=20 (ч) — работал второй, х1=50-20=30 (ч) — работал первый.
у2=30 (ч) — работал второй, х1=50-30=20 (ч) — работал первый.
Ответ: 20 часов, 30 часов.
11. а) Рабочий копал траншею. Когда он проработал 7 ч, к нему присоединился второй рабочий. Вместе они проработали 2 ч. За сколько часов может выкопать траншею каждый рабочий, работая отдельно, если первому нужно на это на 4 ч больше, чем второму?
б) Один рабочий работал 9 ч, после чего к нему присоединился другой рабочий. После 7 ч совместной работы они выполнили всю работу. За сколько часов мог бы выполнить работу каждый рабочий, работая самостоятельно, если первому нужно для этого на 3 ч больше, чем второму?
Решение:
а) Пусть х — время работы первого, тогда х-4 — время работы второго.
Производительность первого — 1/х, второго — 1/(х-4).
Объем работы первого — 1/х*(7+2), объем работы второго — 1/(х-4)*2. Весь объем равен 1.
Составим и решим уравнение:
9/х + 2/(х-4)=1,
11х-36=х(х-4),
х1=3 (ч) — понадобится первому, 1) 3-4=-1(ч) — не подходит по условию задачи.
х2=12 ( ч) — понадобится первому, 2) 12-4=8 (ч) — понадобится второму.
Ответ: 12 часов, 8 часов.
12. а) Двое рабочих выполняют некоторую работу. После 45 мин совместной работы первый был переведен на другую работу и второй рабочий закончил оставшуюся часть работы за 2 ч 15 мин. За какое время мог бы выполнить всю работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 ч больше, чем первому? (№6.5.34 [7])
б) Бассейн может наполняться водой из двух кранов. Если открыть первый кран на 10 мин, а второй — на 20 мин, то бассейн будет наполнен. Если первый кран открыть на 5 мин, а второй — на 15 мин, то заполнится — бассейна. За какое время из каждого крана в отдельности может заполниться весь бассейн?
Решение:
а) Пусть х — время первого, тогда х+1 — время второго. Производительность первого 1/х, производительность второго 1/(х+1). Вместе они работали 45 мин=0,75 ч и выполнили (1/х + 1/(х+1)) * 0,75 часть работы. Второй за 2ч 15 мин=2,25 ч выполнил 1/(х+1)*2,25 часть работы. Составим и решим уравнение:
(1/х + 1/(х+1)) * 0,75 + 1/(х+1)*2,25 =1,
4х 2 -11х-3=0,
D=( 13) 2
х1=3 (ч) — понадобится первому,
х2=(11-13):2= -1 не подходит по условию задачи.
1) 3+1=4 (ч) — понадобится второму.
Ответ: 3 часа, 4 часа.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Два экскаватора различной мощности роют котлован. Работая отдельно, первый может вырыть котлован за 5 дней, второй — за 7 дней. За сколько дней они выроют котлован, работая совместно? Выберите правильное значение:
1) (7+5):2; 2) 1: (7+5); 3) 1: (1/7+1/5).
2. Одна из труб может наполнить бассейн за 3 ч, вторая — за 5 ч. За сколько часов наполнится бассейн, если открыть сразу две трубы? Запишите выражение для решения задачи.
3. Два экскаватора роют траншею. Работая отдельно, первый может вырыть траншею за 10 дней, второй — за 16 дней. За сколько дней они выроют траншею, работая совместно?
4. Водоем заполняется первой трубой за 5 ч, а второй трубой за 4 ч. За сколько часов наполнится водоем, если будут одновременно работать две трубы?
5. Две наборщицы должны были набрать по 120 страниц каждая. Вторая наборщица набирала за 1 ч на 5 страниц меньше, чем первая, поэтому закончила работу на 2 ч позже. Сколько страниц в час набирала первая наборщица?
6. Две бригады рабочих должны по плану изготовить 240 деталей. Первая бригада работала 6 ч, а вторая — 5 ч. Сколько деталей в час изготавливала каждая бригада, если первая делала на 4 детали в час меньше, чем вторая?
7. По плану колхоз каждый день должен был засевать по 20 га. Начав сев, колхоз ежедневно засевал на 5 га больше, чем было предусмотрено планом, поэтому сев был закончен на 2 дня раньше срока. Определите засеянную площадь.
8. Два каменщика сложили стену за 20 дней. За сколько дней выполнил бы эту работу каждый из них в отдельности, если известно, что первому пришлось бы работать на 9 дней больше, чем второму?
9. Теплоход загружается подъемными кранами. Сначала в течение 4 ч работали три крана одинаковой мощности, затем к ним присоединились еще два крана большей мощности, и через 3 ч после этого загрузка была закончена. Если бы все краны начали работать одновременно, то погрузка была бы закончена за 6 ч. За какое время выполнят погрузку один кран меньшей мощности и один кран большей мощности, работая вместе?
10. Вода из трех кранов заполнила резервуар за 12 минут, причем первый кран был открыт 4 минуты, и за это время было заполнено 40 % резервуара. За сколько минут заполнил бы резервуар каждый кран, если известно, что второй кран за 5 минут наливает столько воды, сколько третий кран за 6 минут?
Источник: mathembs.blogspot.com
Разделяй и Властвуй. Разбор задач

Решение задач с помощью метода «Разделяй и Властвуй» или по-английски «Divide and Conquer» является одним из базовых методов по ускорению алгоритмов. Примером тому служит переход от квадратичной сложности пузырьковой сортировки или сортировки вставками к сложности при сортировке слиянием. Или переход от линейной сложности к логарифмической, при реализации поиска элемента в отсортированном массиве (см. бинарный поиск).
В этой статье мы рассмотрим два примера задач с пояснениями и кодом, в которых будет использоваться этот подход.
Для начала сформулируем, разделение и властвование. Решение задачи с помощью данного подхода обладает следующими тремя свойствами:
- Разделить входные данные на меньшие подмножества.
- Решить подзадачи рекурсивно.
- Объединить решения подзадач в решение исходной задачи.
Задача №1
Дан унимодальный массив, состоящий из уникальных элементов. Будем называть массив унимодальным, если его элементы, стоящие до максимума, расположены в порядке возрастания, а элементы, стоящие после максимума, расположены в порядке убывания. Требуется предоставить алгоритм, возвращающий максимальный элемент такого массива за логарифмическое () время.
Решение
Очевидным способом найти максимум в произвольном массиве, является проход по всем его элементам с сохранением текущего наибольшего элемента.
Когда массив будет исчерпан, в переменной max будет записан наибольший из элементов. Сложность такого подхода эквивалентна линейной, поскольку необходимо просмотреть каждый элемент из возможных.
Унимодальный массив обладает двумя примечательными свойствами, которые позволяют оптимизировать поиск.
- Известно, что в таком массиве максимум находится по соседству с меньшими элементами, т.е. предыдущий и следующий за ним элементы гарантировано меньше искомого. Воспользуемся этим свойством, чтобы задать основной базовый случай, в котором мы завершаем поиск наибольшего элемента.
- Если мы смотрим на произвольный элемент массива и видим, что элементы, стоящие после него убывают, то не имеет смысла искать среди них максимум, поскольку он находится раньше. То же верно и для элементов, возрастающих до рассматриваемого. Этот момент помогает сократить число рассматриваемых элементов массива
Оценка сложности
При первом запуске данного алгоритма, если его длина больше трёх, и если серединный элемент не оказался искомым, то независимо от того, как велико , следующий вызов будет работать только с элементами, среди которых максимум должен найтись по свойству 2. Во время второго и всех последующих вызовов этого алгоритма количество элементов, принимаемых к рассмотрению, сокращается вдвое. Этот процесс продолжается до тех пор, пока не будет выполнен базовый случай по количеству элементов (два и менее элементов), либо базовый случай из свойства 1.
Деление массива надвое до достижения базового случая не может продолжаться больше, чем раз, а в каждый из этих вызовов совершается константное, не зависящее от число операций. Отсюда следует вывод, что сложность представленного алгоритма .
Задача №2
Дан неупорядоченный массив из элементов, где является степенью двойки. Требуется предоставить алгоритм, который находит второй по величине элемент массива, осуществляя не более операций сравнения.
Решение
Если первую задачу, можно решить, зная как работает бинарный поиск, то в этой нам потребуется чуть больше смекалки. Давайте подумаем, как можно решить эту задачу прямолинейно и сколько операций сравнения в этом случае мы используем.
Будем проходить по массиву и поддерживать два числа max и second_largest.
Подсчитаем количество сравнений
Лучшим возможным вариантом может быть сравнение. Происходит это, когда условие первого if выполняется на каждой итерации цикла (это даёт сравнения), и добавляется одно сравнение до цикла. Такое поведение может быть достигнуто на упорядоченном по возрастанию массиве.
Рассмотрим убывающий массив. В этом случае сравнение в if выполняется каждую итерацию, но управление передаётся в ветку elif , где также выполняется еще одно сравнение. Получается, что суммарно операций сравнения в случае убывающего массива, с учетом первого сравнения до цикла, будет равняться .
Как можно сократить это близкое к операций число до ? Попробуем искать максимум, путём разбиения доступных элементов на две части и последующего поиска наибольших значений в них.
Рассмотрим массив, состоящий из элементов 9, 18, 3, 5, 25, 1, 5, 19. Зеленым цветом на диаграме выделен максимум этих чисел. Смотря снизу вверх, видно, что максимум находится путём сравнений двух чисел, наибольших в своём подмножестве.

В этом случае количество сравнений для поиска максимума равно сумме: . Чтобы найти second_largest, потребуется рассмотреть все элементы, с которыми сравнивался max (на диаграмме они выделены желто-оранжевым). Поиск максимального среди них потребует операцию, поскольку элементов в этом маленьком списке не больше, чем глубина дерева минус один.
Осталось только реализовать этот алгоритм:
Количество операций сравнения алгоритма выше как раз равно . Этот факт можно показать в числах, если завести глобальную переменную — счетчик.
Подход к решению задач — «Разделяй и Властвуй» не является самым простым концептом в программировании, но зато его легко идентифицировать. Зачастую, когда требуется решить задачу поиска объекта среди других объектов с заданной логарифмической сложностью, скорее всего от вас ожидают применения этого подхода, основанного на рекурсивных вызовах на двух подможествах данных. Это не правило, но два подтверждения этой гипотезе мы разобрали в этой статье.
Информация
[1] Условия задач взяты из книги «Algorithms Illuminated: Part 1: The Basics» от Tim Roughgarden. [2] Решения авторские.
Данную статью я подготовил в преддверии старта курса «Алгоритмы и структуры данных» от OTUS. Узнать подробнее о курсе можно тут.
Источник: habr.com
Помогите решить задачу:
Найди верный ответ на вопрос ✅ «Помогите решить задачу: Первая бригада построит дом а 54 дня, а вторая бригада за 27 дней. За сколько дней две бригады построят дом при . » по предмету Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч
Всем привет. В магазине в 1 день продали 35%, во 2 — 28%всеховощей, А в 3 — оставшиеся 333 кг. Сколько кг овощейбыло в магазине первоначально?
Главная » ⭐️ Математика » Помогите решить задачу: Первая бригада построит дом а 54 дня, а вторая бригада за 27 дней. За сколько дней две бригады построят дом при совместной работе?
Источник: urokam.net
5.3 Примеры решения некоторых задач
Даны производственные возможности двух стран в двух товарах (в тыс. тонн в год):
| Нефть | 1680 | 320 |
| Сталь | 2340 | 200 |
По этим данным требуется посчитать абсолютное и сравнительное преимущество.
Сразу заметим, что абсолютное преимущество по этим данным посчитать нельзя. Вспомним определение абсолютного преимущества: способность производить больше товара с теми же затратами ресурсов. Поскольку нам не даны затраты ресурсов ни в каком виде, то абсолютное преимущество, то есть производительность, определит нельзя. Россия, хоть и производит больше нефти и стали, может тратить на их производство в разы больше ресурсов, чем Англия.
Для того, чтобы посчитать сравнительное преимущество, посчитаем альтернативные издержки каждого товара в каждой стране.
АИ(нефть) = = 1.39
АИ(сталь) = = 0.72
АИ(нефть) = = 0.63
АИ(сталь) = = 1.6
Полученные результаты можно представить в таблице:
| нефть | 1.39 | 0.63 |
| сталь | 0.72 | 1.6 |
Видно, что альтернативные издержки по нефти ниже у Англии (0.63 меньше чем 1.39), а по стали ниже у России (0.72 ниже чем 1.6). Из этого следует, что Англия имеет сравнительное преимущество в нефти, а Россия – в стали.
Разберем чуть более сложную задачу
Даны затраты времени на 1 тонну производимой продукции
| Сыр | 20 | 40 |
| Вино | 100 | 25 |
Необходимо определить абсолютные и сравнительные преимущества.
Вспомним, что абсолютное преимущество это способность производить больше продукции при одинаковых затратах ресурсов, или же способность иметь меньшие затраты ресурсов на одинаковое количество производимой продукции. Для нашей задачи воспользуемся второй частью определения. Затраченное время можно воспринимать как ресурс. Поскольку затраты времени на одинаковое количество сыра (1 тонна) меньше в Швеции, она имеет абсолютное преимущество в сыре. Аналогично, Португалия имеет абсолютное преимущество в вине.
Для определение сравнительного преимущества посчитаем, сколько товара может производить каждая страна в 1 час
| Сыр | 1/20 | 1/40 |
| Вино | 1/100 | 1/25 |
Далее посчитаем в табличном виде альтернативные издержки каждого товара в каждой стране:
| Сыр | 20/100 | 40/25 |
| Вино | 100/20 | 25/40 |
Из таблицы видно, что наименьшие альтернативные издержки сыра имеет Швеция, а наименьшие альтернативные издержки в вине – Португалия. Следовательно, Швеция имеет сравнительное преимущество в сыре, а Португалия в вине.
Обобщим некоторые правила определения абсолютных и сравнительных преимуществ.
- При сравнении двух экономик одна из них может иметь абсолютное преимущество как в одном товаре, так и в нескольких товарах, так и ни в одном.
- Если одна экономика имеет сравнительное преимущество в одном товара, то другая экономика обязательно имеет сравнительное преимущество в другом товаре.
- Если страны имеют одинаковые альтернативные издержки производства двух товаров, то ни одна из них не имеет сравнительного преимущества, и в этом случае их КПВ имеют одинаковый угол наклона. Только в этом случае разделение труда не имеет смысла.
Давид Рикардо первым указал на то, что выгода от торговли определяются не производительностью (абсолютным преимуществом), а относительными издержками производства товаров (относительным, или сравнительным преимуществом). Для того, чтобы эффективно торговать с другой страной, данной экономике не нужно иметь более высокую производительность в обмениваемом благе, а достаточно производить его с меньшими альтернативными издержками.
Это имеет огромное практическое значение. Например, США производительнее Эквадора и в производстве программного обеспечения, и в выращивании бананов. Но это не означает, что США не будет торговать с Эквадором ни одним товаром. Поскольку альтернативные издержки бананов ниже в Эквадоре, он будет специализироваться на производстве бананов и торговать ими.
США, напротив, имеет более низкие альтернативные издержки производства программного обеспечения, и будет торговать им. Таким образом, каждая страна торгует тем товаром, при производстве которого ресурсы используются наиболее оптимальным способом. Каждая экономика обнаруживает, что ей выгоднее специализировать на товаре с наименьшими альтернативными издержками и получать второй товар от другой экономики в процессе обмена, вместо того, чтобы самостоятельно производить второй товар.
Рассмотрим задачу поиска выгоды от торговли
Даны затраты в часах на одну тонну
| Сыр | 20 | 40 |
| Вино | 100 | 25 |
Требуется найти выгоду для каждой страны от обмена 1 тонны вина на 3 тонны сыра.
Для того, чтобы найти выгоду от обмена, необходимо определить, на каком товаре будет специализироваться каждая экономика в рамках международного разделения труда. Здесь нам поможет уже знакомое правило: страна специализируется на том товаре, альтернативные издержки которого минимальны, то есть в котором имеет сравнительное преимущество.
Мы уже нашли сравнительные преимущества для этой задачи (см. выше): Швеция имеет сравнительное преимущество в сыре, а Португалия в вине. Следовательно, при установлении торговых отношений между этими двумя странами Швеция будет специализироваться на сыре, а Португалия – на вине.
Швеция меняет 3 тонны сыра на 1 тонну вина у Португалии. Для того, чтобы произвести 3 тонны сыра, Швеция затрачивает 3*20=60 часов. Следовательно, для получения 1 тонны вина от Португалии ей нужно затратить 60 часов. Но если бы она захотела произвести вино самостоятельно, ей пришлось бы потратить 100 часов. Ее выгодна от специализации и торговли составила 40 часов.
Португалия меняет 1 тонну вина на 3 тонны сыра у Швеции. Для производства 1 тонны вина она затрачивает 25 часов. Следовательно, для получения 3 тонн сыра от Швеции, ей нужно потратить 25 часов. Но если бы она захотела произвести сыр самостоятельно, ей пришлось бы затратить 3*40=120 часов. Следовательно, ее выгода от торговли составила 95 часов.
В предыдущем примере мы увидели, что специализация и торговые отношения ведут к взаимной выгоде участников торговли. Это происходит так, потому что каждая страна реализует свое сравнительное преимущество, которое заключается в более низкой относительной цене производства товара (то есть более низкий альтернативных издержках его производства). Иными словами, в этих условиях страна обнаруживает, что ей выгодно не производить весь набор товар внутри себя, а специализироваться, и устанавливать торговые отношения с другими странами.
Но любой ли обмен ведет к взаимной выгоде? Нет, потому что все зависит от пропорции обмена. Если бы в нашем пример 1 тонна вина менялась на 1 миллион тонн сыра, то это было бы крайне выгодно Португалии, и совсем невыгодно Швеции. Торговля уже не была бы взаимовыгодной и торговые отношения между странами не установились бы.
Как определить торговый диапазон взаимовыгодной торговли? Рассмотрим, как он устанавливается, на примере нашей задачи про Швецию и Португалию.
Вспомним, что нам даны затраты времени на 1 тону продукции:
| Сыр | 20 | 40 |
| Вино | 100 | 25 |
Также вспомним, что из этой таблицы можно легко получить альтернативные издержки (см. задачу выше)
| Сыр | 20/100 | 40/25 |
| Вино | 100/20 | 25/40 |
При таких альтернативных издержках Швеция будет специализироваться на сыре, а Португалия на вине. Выделим продукт, на котором будет специализироваться каждая экономика:
| Сыр | 0.2 | 1.6 |
| Вино | 5 | 0.625 |
Швеция, производя сыр, имеет альтернативные издержки 0.2. Это означает, что вместо производства 1 тонны сыра она может производить 0.2 тонны вина. При какой пропорции обмена сыра на вино Швеция будет вступать в торговые отношения? Ответ звучит так: Швеция будет менять сыр на вино, когда за 1 тонну сыра она сможет получить БОЛЬШЕ, чем 0.2 тонны вина.
Если она получит от торговли ровно 0.2 тонны вина, то Швеции все равно, производить вино самостоятельно или же получать его у Португалии. Если Швеция получит от торговли меньше чем 0.2 тонны вина, то ей будет выгодно производить его самостоятельно, и торговля не состоится.
Аналогично, Португалия будет менять вино на сыр, когда за 1 тонну вина он получит БОЛЬШЕ, чем 0.625 тонн сыра. Это означает, что Португалия хочет получить за 1 тонну сыра МЕНЬШЕ, чем 1.6 тонн вина.
Пересечение интересов Швеции и Португалии находится в диапазоне 1 СЫР ∈ (0.2;1.6)ВИНА. Это и есть диапазон взаимовыгодной торговли, то есть диапазон таких отношений обмена, который устроит одновременно обе экономики. Если мы захотим найти подобный диапазон как вино от сыра, от он будет выглядеть так: 1 ВИНО ∈ (0.625;5)СЫРА. Нетрудно увидеть, что диапазон взаимовыгодной торговли лежит между альтернативными издержками экономик.
Правило:
диапазон взаимовыгодной торговли лежит между альтернативными издержками рассматриваемых участников торговли.
Рассмотрим способы решения типовых задач на установление торговых отношений между экономиками. В подобных задачах как правило даны первоначальные возможности двух отдельных экономик (их КПВ), и заданное торговое отношение. Необходимо найти, каким образом торговля может улучшить положение каждой из экономик.
Первым шагом решения подобных задач является обнаружение сравнительных преимуществ, которые позволят нам определить, каким товаром будет торговать данная экономика. Далее мы начинаем производить обмен товарами между экономиками, придерживаясь заданной пропорции обмена. При взаимовыгодной торговле экономика выходит за рамки своей первоначальной КПВ, это и есть выгода от торговли. Получаемая в результате торговле новая КПВ (которая всегда лежит в области выше-правее первоначальной КПВ) иногда называется кривая торговых возможностей, или КТВ.
Рассмотрим две страны с начальными КПВ:
Требуется найти новый вид КПВ экономик при торговом отношении 1А=1В.
Посчитав альтернативные издержки каждого товара в каждой экономике, мы обнаружим, что Россия специализируется на товаре А, а США на товаре В. Диапазон взаимовыгодной торговли: 1А ∈ (0.5;2)В. То есть заданное торговое отношение 1А=1В принадлежит диапазану взаимовыгодной торговли.
Начнем рассматривать экономику России. Она специализируется на товаре А. Следовательно, перед началом торговли она находится в левой верхней точке КПВ с координатами (0;200). Далее по пропорции 1А=1В она начинает менять свой товар А на товар В, получаемый из США. Россия хочет поменять 200 товаров А и получит за них 200 товаров В. Поскольку у экономики США имеется в наличии 200 товаров В, то при торговле между Россией и США 2000 товаров А будет обменено на 200 товаров В.
В результате КПВ (вернее КТВ) стран примут следующий вид:
Мы видим, что в результате торговли и Россия, и США расширили свои возможности.
Рассмотрим тот же пример, но с другой пропорцией обмена: 1А=1.5В
Построение КТВ при данной пропорции обмена начнем опять же с России. Россия, специализируясь на товаре А, производит его в размере 200 единиц. Пропорция обмена 1А=1.5В предполагает, что 200 А будут обменены на 300В. Но 300В нет у США, которая может предложить только 200В для обмена. Значит, для того, чтобы забрать 200В у США, России нужно предложить = 133товаров A. Россия, начиная торговлю с точки 200А, отдает США 133A и получаем взамен 200 товаров В. Когда обмен окончен, Россия имеет 200 товаров В и одновременно остаток товара А, который не был обменен (200 — 133 = 66). КПВ России выглядит следующим образом:
Для того, чтобы завершить построение КПВ России, заметим, что из точки с координатами (200;66) Россия может увеличить производство В, пожертвовав для этоого товаром А. Для того, чтобы посчитать, сколько В можно произвести вместо имеющихся 66A, достаточно вспомнить, что внутреннии альтернативные издержки производства одного товара А в России составляет 0.5 товара В. То есть вместо 66A Россия может произвести 33. В итоге крайняя левая точка КПВ имеет координату 233 ( = 200 + 33). У КПВ появился перелом. Заметим, что получившийся участок КПВ параллелен первоначальной КПВ, поскольку на этом участке Россия закончила торговлю и вернулась к выбору между производством двух товаров с внутренними альтернативными издержками.
Теперь построим КПВ США. США, начиная торговлю в точке 200В, по пропорции обмена 1А=1.5В (что эквивалентно пропорции 1B = A), хочет поменять 200В на 133товаров A ( = 200 * ). Россия располагает возможностями поставить 133товара A. Поэтому новая КПВ США не будет иметь изломов:
Таким образом, решая задачи на построение КТВ при заданной пропорции обмена, важно помнить о том, что КТВ может выглядеть как ломаная линия. Появление излома зависит от того, хватает ли у противоположной стороны товара для того, чтобы удовлетворить потребности данной стороны.
В ряде зада на КПВ требуется найти оптимальную точку производства двух товаров, зная их соотношение (пропорцию).
Фирма имеет два завода, которые могут производить плееры и батарейки. Фирма продает комплекты, состоящие из одного плеера и четырех батареек. Возможности каждого завода представлены следующими КПВ:
Требуется определить, какое максимальное количество комплектов сможет продать данная фирма.
В качестве первого шага мы построим общую КПВ (алгоритм ее построения уже был рассмотрен ранее):
Далее мы изобразим прямую, которая отвечает за отношение плееров к батарейкам. Нам дано, что 1 комплект состоит из 1 плеера и 4 батареек. Это может быть записано как пропорция . Эта пропорция говорит нам о том, что батареек должно быть в 4 раза больше чем плееров.
Пользуясь данной пропорцией, получим уравнение прямой линии:
плеер = батарейка
Прямая, отвечающая за данное уравнение, выходит из начала координат и проходит выше точки (300;40). В это легко убедиться, подставив в уравнение прямой горизонтальную координату = 300. Тогда вертикальная координата этой точки будет равна 75 ( = * 300), что выше, чем 40.
Решение задачи находится в точке пересечения линии пропорции и КПВ. Для того, чтобы найти эту точку, нам необходимо найти уравнение верхнего участка КПВ. Сделаем это способом нахождения уравнения прямой линии по двум заданным точкам.
Напишем уравнение прямой линии в общем виде:
плееры = a + b * батарейки,
где коэффициент а отвечает за параллельный сдвиг данной прямой, а коэффициент b – за ее угол наклона. Подставим в уравнение общего вида две имеющихся точки с координатами (0;100) и (300;40):
Решая данную систему, получаем a = 100, b = -. В результате уравнение верхнего участка КПВ выглядит так:
плееры = 100 — 0.2 * батарейки
Теперь найдем точку пересечения полученного уравнения верхнего участка КПВ и уравнения пропорции:
Решение данной системы: батарейка = 222.2 плеер = 55.5
То есть фирма может произвести максимально 55.5 комплектов.
Если нам нужно дать решение в целых числах, то мы должны будем выбрать первую целочисленную точку на прямой плеер = * батарейка, которая лежит ВНУТРИ области КПВ. Очевидно, что в нашем случае это точка плеер=50, батарейка=200. Следовательно, фирма может произвести 55 комплектов при условии целочисленного решения.
Источник: n2tutor.ru